Received 9 September 2014; revised 19 October 2014; accepted 2 November 2014

ABSTRACT

Studying liquid water in a frame of band theory shows that varying a reduction-oxidation (RedOx) potential of aqueous solution can be identified as shifting Fermi level in its band gap. This medium becomes the reductive one when Fermi level is shifting to the conduction band due to populating hydroxonium level 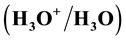by electrons and transforming water in a hypo-stoichiometric state,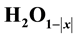. Opposite in the hyper-stoichiometric one 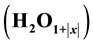Fermi level is shifting to the valence band due to populating hydroxide level 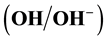by holes and the aqueous solution becomes the oxidative one. The energy difference between these electronic levels is estimated of 1.75 eV. It is shown that the standard half-reactions and the typical aqueous electrodes fix their RedOx potential only by the electrons and holes populations 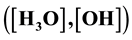of these local electronic levels in the band gap of non-stoichiometric water in the corresponding solutions.

Keywords:

Liquid water, Band Gap, Fermi level, Hydroxonium ion, Hydroxide ion

1. Introduction

The electronic properties of liquid water and its solutions have been studied by different research groups [1] -[9] . In particular, a density of states (DOS) in liquid water and its electronic band gap, which separates the molecular orbitals occupied by electrons from the unoccupied ones, have merited the attention for fundamental studying. They are not well understood in comparison with thermodynamics and microstructure of water but are important for understanding water as participant and medium of electrochemical reactions [2] .

The main difficulty in producing reliable theoretical predictions of the electronic properties of liquid water lies in the necessary compromise between the level of accuracy at which the system can be described and the thorough sampling of the phase-space, as required for converged computational quantities [1] . At that, the dominant view is that pure liquid water can be described as an amorphous insulator with a wide band gap, 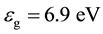, and an electronic affinity, [2] .

Several strategies have been considered to simplify the study of disordered systems: use of clusters of increasing size to model the liquid, “mean-field” approaches, use of periodically repeated small unit cells, and hybrid approaches, which use different combinations of quantum and classical methods to describe the two subsystems [1] . From uncorrelated super-molecular structure generated by the Monte-Carlo simulation, quantum mechanical calculations based on Hartree-Fock method [3] , density functional theory (DFT) with a modified functional exchange-correlation functional [4] , and ab initio molecular-dynamic simulation using DFT in the Kohn-Sham formulation with plane wave basis set [5] have been carried out to study the electronic properties of liquid water, in particular DOS and the liquid water band gap. These results [6] [7] give a large band gap as a difference between electron energies at the top of valence band and the bottom of conduction band [2] .

Allowed local electronic states have to be in the band gap of liquid water similar to impurity levels in the band gap of solid insulators occupied and not occupied by electrons [6] [8] . The most interested species of them are the occupied-by-electrons level of hydroxide ions, 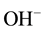, and the vacant one of hydroxonium ions,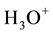. However, the electrochemical properties of these aqueous ions have not been understood in the frame of electronic band theory so far [8] . Just filling up this gap is the subject of the present paper.

2. The Electronic Levels of Hydroxonium and Hydroxide Ions

The electronic properties of water are extremely interesting since water can influence many electrochemical processes with dissolved constituents of aqueous solution by their actively participating in these processes [1] . Perhaps the most important reaction of water is its reversible self-dissociation by emerging hydroxonium ions, 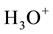, and the hydroxide ones, , which is described by the chemical reaction [7] [9] :

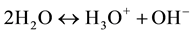(1)

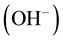In the frame of electronic band theory, these inherent constituents of liquid water can be described as local carriers of vacant and occupied-by-electrons energy levels, 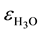and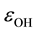, disposed symmetrically nearby the band-gap middle which is Fermi level, , of stoichiometric water, , as shown in Figure 1(a). Generally, Fermi level, , is a total electrochemical potential of water in any thermodynamic state and composition. It is a precisely defined thermodynamic quantity threshold of 50%-population of the all allowed electronic levels in the band gap of liquid water at any temperature [10] [11] .

As seen in Figure 1(a), the bulk electron affinity, , of stoichiometric water is equal to 6.45 eV which agrees with data [5] [6] [9] but it is considered here only as a specific case. In Figure 1(b), Fermi level, , of hypo-stoichiometric water is controlled by the electron population of the energy level, , as a hydroxon-

ium-radical concentration, , where is the constant of hydrated dissociation of hydro-

gen molecule in water up to. Opposite, Fermi level, , of hyper-stoichiometric state of liquid wa-

ter is controlled by hole population of the energy level, , as a hydroxyl concentration, ,

where is the constant of hydrated dissociation of oxygen molecule in water up to. These different electrochemical states of liquid water characterize by the following standard half-reactions [12] .

(2)

(3)

at, , , , , , T = 298 K [13] . Then, we have for (2) and for (3) accordingly. It means that the electronic level, , is mostly vacant as hydroxonium ions, , due to the fixed is below (see Figure 1(b), left) and the energy level, , is occupied by electrons as hydroxide ions since this Fermi level is essentially above.

The forcedly variable Fermi level, , in the band gap of liquid water is determined rigorously by the ratio of

the concentrations: and, as portions of vacant and occupied by

electrons energy levels, and, fixed in the band gap of liquid water. These proportions are given by Fermi-Dirac statistics which can be simplified to Maxwell-Boltzmann distribution of electrons and holes in the corresponding energy levels [10] [11] :

(4)

(5)

where T is Kelvin temperature, and is Boltzmann constant equal to 8.62 × 10^?5 eV/K.

So, we submit the values of, , , and for half-reactions (2) and (3) in these

Equations and obtain:,. Here, Fermi levels, , , for

the non-stoichiometric states of liquid water are the confines of its thermodynamic stability.

From the well known requirement of [5] , we find:, and hence, the electronic energy levels of inherent water constituents:

(6)

(7)

where (see Figure 1(a)). In changing of aqueous solution, the composition deviation, x, of non-stoichiometric water, , will be defined by equation [14] [15]

(8)

and one can show that the hypo-stoichiometric state, , at |x| < 10^?6 is achieved in acidic solution

easier than in the basic one by shifting Fermi level to the conduc-

tion band.

Opposite, the hyper-stoichiometric one, , also at |x| < 10^?6 is achieved in basic solution

easier than in the acidic one by shifting Fermi level to the valence band.

At the same time, Fermi level is mostly sensitive to the non-stoichiometry amount, x, in the hypo-stoi- chiometric basic solution and in the hyper-stoichiometric acidic one because the concentrations of hydroxonium and hydroxide ions as inherent water species have to be in the ratio [16]

(9)

with the dissociation constant K_w = 10^?14 M² at T = 298 K. Reduction-Oxidation (RedOx) potential of an aqueous solution is measured by Standard Hydrogen Electrode (SHE) with the half-reaction [12]

(10)

Directly identifying this electrode by means of congruous Fermi level, , in the band gap of liquid water, we can find Fermi level, , for each standard aqueous electrodes using only the two fixed electronic energy levels, and, in the band gap of water.

3. Electronic Identifying Some Standard Aqueous Electrodes

For illustrating this identification, we consider the following half-reactions [12] :

(11)

(12)

(13)

in addition to the half-reaction (10) which is characterized by and as it

is shown above for the half-reaction (2). We obtain by substituting and

in the Equation (4) and find using (6). Then, the RedOx of hydroxonium level is

, which confines below RedOx variations of any strong acidic solution due to very

limited hydroxonium level population:, that is illustrated by Figure 2.

Similarly, we can find the RedOx of Standard Oxygen Electrode (11). Substituting and

in the Equation (5), we obtain and which

gives for the half-reaction (11).

For (12), we also have but which gives according to the Equation (9). Substituting the values of and in the Equation (5), we obtain ε_OH − ε_F(12) = 0.113 eV and Fermi level equal to which gives for the half- reaction (12).

Finally, we can find the RedOx potential of the Electrode (13) in the basic solution with

and in accordance with data for the half-reaction (2). From the Equation (9), we obtain

and when substitute the values of and in the Equation (4). Then, which gives.

4. Discussion of Results

The electronic band structure of spatially-separated different aqueous electrodes is essentially differed from the one of an electric contact between them via an ion-exchanging membrane shown in Figure 3.

One can see that, the electrochemical cell generates the negative voltage relative to the standard hydrogen electrode when Fermi levels of these electrodes are equated. Here, in the specific case of Standard Electrodes (10) and (12), the SHE has the positive charge and the band-gap model of liquid water allows visualizing correctly the deformed electronic energy levels of aqueous solutions near the ion-exchanging membrane.

Using this method for identifying the RedOx potentials of the following half-reactions [12] :

(14)

(15)

we can assay the effect of in aqueous solutions. Here,.

From the Equation (9), we obtain. In rating for these half-reactions, we use the

exponential proportion between the values of hydrated dissociation energy of, , and in aqueous

solution [13] :, and. Then, we obtain

for Electrode (14). Substituting and in Equation (5), it is easy to obtain

and Fermi level which conforms to the RedOx potential of half-

reaction (14) inasmuch as.

Opposite, the Standard Electrode (15) of two oxidants as gaseous oxygen and liquid hydrogen peroxide is characterized by the negative effect of this combination. Indeed, for RedOx = 0.695 V of this electrode, Fermi

level is equal to that is higher than and of the

mono-oxidant electrodes (12) and (14) accordingly. It implies that gaseous oxygen and liquid hydrogen peroxide force out each other from water because the actual concentration of hydroxide radicals in it as the electrode (15)

is reduced up to that is practically equal to zero for liquid water and essentially lesser than

for the half-reaction (12) and for the one (14). Therefore, water actu-

ally does not involve in the half-reaction (15) and free oxygen is reduced only up to hydrogen peroxide.

5. Conclusions

The liquid water is considered in the frame of electronic band theory with accentuating the guessed energy levels, and, in the band gap for inherent constituents of liquid water as hydroxonium and hydroxide

ions. Their radicals are interpreted here as electron and hole population of the corresponding levels located symmetrically nearby the middle of the band gap with.

In this model, the specific concentration of hydroxonium radicals, , in the aqueous solution at the

given determines uniquely Fermi level, , as the electrochemical potential of water by the ratio

or for the dissolved hydroxyls, , at the given in the aqueous

solution.

It is shown that such the variation of Fermi level allows describing the typical half-reactions and aqueous electrodes. For this, only two allowed electronic levels in the band gap of liquid water, and, unoc-

cupied and occupied by electrons are quite enough.

At the same time, the forced transformation of liquid water in the hypo-stoichiometric state, for

example, by its electric reduction is realized when Fermi level, , is shifting to the electronic level, , and higher. In this process, the pure liquid water is converted simply into solution of the hydrated atoms of hydrogen,.

Opposite, the hyper-stoichiometric water, , is characterized by shifting Fermi level to the level,

, and lower. In this process, the liquid water is simply enriched by dissolved hydroxyl radicals, , as

dissociated and hydrated oxidants: half-oxygen, , or half-hydrogen-peroxide,. It is

shown that two-oxidant solution of and is less effective than the mono-oxidant one.

Such theoretical approach closely relates the electrochemistry of aqueous solutions with the specification of electron population of allowed levels in the band gap of liquid water.

Acknowledgements

Author is pleased to the Russian foundation of basic research (RFBR) for supporting this work (grant # 13-08-00826a).

Cite this paper

AlexanderShimkevich, (2014) Electrochemical View of the Band Gap of Liquid Water for Any Solution. World Journal of Condensed Matter Physics,04,243-249. doi: 10.4236/wjcmp.2014.44027

References