Received 8 May 2014; revised 14 June 2014; accepted 2 July 2014

ABSTRACT

The general expressions, based on the Fermi distribution of the free electrons, are applied for calculation of the kinetic coefficients in donor-doped silicon at arbitrary degree of the degeneracy of electron gas under equilibrium conditions. The classical statistics lead to large errors in estima- tion of the transport parameters for the materials where Fermi level is located high above the conduction band edge unless the effective density of randomly moving electrons is introduced. The obtained results for the diffusion coefficient and drift mobility are discussed together with practical approximations applicable for non-degenerate electron gas and materials with arbitrary degree of degeneracy. In particular, the drift mobility of randomly moving electrons is found to depend on the degree of degeneracy and can exceed the Hall mobility considerably. When the ef- fective density is introduced, the traditional Einstein relation between the diffusion coefficient and the drift mobility of randomly moving electrons is conserved at any level of degeneracy. The main conclusions and formulae can be applicable for holes in acceptor-doped silicon as well.

Keywords:

Donor-Doped Silicon, Electrical Conductivity, Thermal Noise, Einstein Relation, Diffusion Coefficient, Drift Mobility, Hall Mobility

1. Introduction

Silicon is the main material for electronics during the last fifty years. Its basic parameters have been intensively treated theoretically and experimentally [1] -[18] . Diffusion coefficient and drift mobility are necessary for characterization of material quality and electronic transport properties. In spite of the importance of these

quantities for device applications, such as bipolar transistors, the results on heavily doped regions are quite limited, while accurate values of electron mobility and diffusion coefficient are essential for advanced engi- neering. The theoretic problem for silicon and gallium arsenide usually has been treated through the Monte Carlo simulation [2] - [4] . 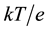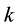The ratio of the classical value of the diffusion coefficient over the mobility for the majority- and minority-carriers satisfies the Einstein relation and equals where is the Boltzmann constant, 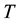is the absolute temperature, and is the elementary charge [5] - [11] . Most published papers assume this relation to hold only for non-degenerate materials. Therefore, at thermal equilibrium, the diffusion coefficient 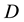of charge carriers in a degenerate semiconductor is often related to the mobility through the modified relation [2] [3] [5] - [8] :

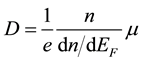, (1)

where 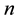is the total density of free electrons in the conduction band and 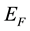is the Fermi energy. Similar relation is used for holes. Equation (1) can be transformed into:

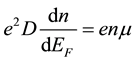(2)

where both sides mean the conductivity. But as it will be shown later the quantity 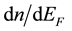in Equation (2) left side is proportional to the effective density of randomly moving electrons, while the expression 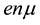contains the total electron density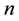; this is wrong for degenerate silicon because the main contribution comes from the randomly moving electrons, located near the Fermi energy, while the contribution due to the electrons located deep below the Fermi level is next to zero because of limitations induced by the Pauli principle [19] - [21] . The randomly moving electrons not only determine the electric conduction and electron diffusion, but also electron heat capacity, electron thermal noise, electron heat conduction and other dissipative phe- nomena [22] .

The electron Hall factor determined as the ratio of the Hall mobility over the drift mobility for non-degenerate semiconductors yields the values above unity [12] [13] . In some cases, the Hall factor of holes varies from 0.882

to 0.714 at 300 K over the acceptor density range 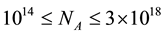cm⁻³ [14] . The factor tends to unity

when the degenerate case is approached since the averaging of relaxation time 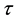over energy yields the value at the Fermi energy. In spite of huge amount of investigations, there are some unsolved problems of drift mobility and diffusion coefficient in silicon with high level of degeneracy of electron gas. We are going to illustrate that Equations (1) and (2) are not applicable for degenerate electron gas in silicon. Section 2 deals with the basic expressions. Section 3 presents and discusses the results of calculations for donor-doped silicon at any degree of degeneracy of electron gas.

2. Basic Expressions of Electrical conductivity characteristics for Homogeneous Materials with one Type of Free carriers at Any Degree of Degeneracy of Electron gas

The total density of the free electrons in the conduction-band is

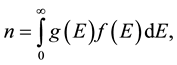(3)

where is the electron energy above the conduction band edge, is the density of states (DOS) at the given energy, and is the Fermi distribution function for electrons

(4)

and is the chemical potential.

From the Fermi-Dirac statistics directly follows that the effective density of electrons taking part in the random motion and, thus, in all kinetic processes depends not only on the DOS of electrons and Fermi

distribution function, but it depends also on the probability that any of such electron

can leave the occupied energy level at a given temperature [19] - [21] :

(5)

or

, (6)

because

. (7)

The term represents the probability density of the randomly moving electrons:

, (8)

and meets all requirements of the probability theory. Here it should be pointed that for materials with degenerate electron gas the total density of electrons is the fixed quantity, while the effective density of randomly moving electrons is the stochastic variable. So, there are two parameters to characterize the free electron gas in metals and other materials with highly degenerate electron gas: the total density of the free electrons in conduction band and the effective density of randomly moving electrons.

Comparison of functions and for different normalized chemical potentials are

shown in Figure 1. From this figure it seen that, when. In this

case the classical statistics is applicable, and.

An approval of Equation (5) also follows from the general relation between the electrical conductivity σ and the diffusion coefficient of electrons [22] [23] :

. (9)

After simple calculation of the derivative one obtains:

(10)

where expression

is the same Equation (5) for the effective density of randomly moving electrons. Equation (10) unambiguously shows that the conductivity in all cases is determined by the effective density of randomly moving charge carriers determined through Equation (5) rather than the total free electron density in the conduction band. The total density can be used for determination of conductivity only for materials with non-degenerate electron gas.

Thus, the conductivity (Equation (10)) also can be presented as

, (11)

where is the drift mobility of randomly moving charge carriers in the homogeneous materials with one type of the charge carriers (either electrons or holes). From this general relationship, which is applicable in all cases, one immediately gets the Einstein relation

. (12)

In [20] , accounting the concept of randomly moving charge carriers there were derived the following general relations, which are valid at any degree of degeneracy of electron gas in isotropic materials with one type of charge carriers:

For drift mobility:

. (13)

or

; (14)

for electrical conductivity:

; (15)

for diffusion coefficient:

(16)

for drift velocity:

; (17)

where factor

(18)

shows, how many times the mean kinetic energy of randomly moving charge carrier is larger than. The average kinetic energy of randomly moving electron is defined by

. (19)

3. Applications of the Basic Relations to Transport Features of Donor-Doped Silicon

According to the above presented relations, one can evaluate the characteristics of donor-doped silicon with shallow donors (completely ionized at room temperature, K). Illustrations of Equations (3) and (5) for donor-doped silicon are presented in Figure 2. The effective density of randomly moving electrons (shaded area) for highly degenerate material is many times lower than the total density of free electrons n in the conduction band of silicon.

Here for calculation instead of chemical potential the Fermi level energy was used, because the difference between these quantities is about 0.01% even at room temperature [24] .

Figure 3 presents the dependence of the Fermi energy E_F and average kinetic energy of randomly electrons on the total electron density n in the conduction band of silicon. The Fermi energy was calculated from Equation (3), and was obtained from Equation (19). The average kinetic energy of randomly moving electrons in nSi for the total electron density n smaller than 10¹⁸ cm⁻³ equals, but for cm⁻³, and does not depend on temperature.

Comparison of the effective density of randomly moving electrons with the total density of free elec- trons in conduction band of is presented for room temperature in Figure 4. Here

. (20)

It illustrates that the effective density of randomly moving electrons equals the total density of free electrons only when the shallow donor density is smaller than cm⁻³. However, a sharp decrease is found at high densities, and the ratio is well below unity at cm⁻³.

The effective density of randomly moving electrons dependence on the total density of free elec- trons in at K is shown in Figure 5. It shows that the effective density of randomly moving

electrons at cm⁻³, but for cm⁻³.

The diffusion coefficient of randomly moving electrons in nSi can be determined from Equation (16):

. (21)

The obtained results are presented in Figure 6. Here the resistivity dependence on the total free electron density in conduction band data have been taken from [25] - [28] , and the effective density of randomly moving electrons has been used from Figure 5.

The increase of the diffusion coefficient of randomly moving electrons at cm⁻³ is due to the increase of the average kinetic energy of the randomly moving electrons (Figure 3).

From Equation (15) follows that the drift mobility of randomly moving electrons can be obtained from the conductivity or resistivity measurement results [25] - [28] , when the dependence of the density of randomly moving electrons on the total density of the free electrons (from Equation (3)) is taken into account:

. (22)

Comparison of drift and Hall [25] [26] mobilities for donor-doped silicon is presented in Figure 7. It is seen that the drift mobility of randomly moving electrons in silicon at high doping levels can be many times higher than the Hall mobility.

The electron relaxation time at the Fermi level at room temperature is the same for all homogeneous metals and highly degenerate semiconductors and equals [29] :

; (23)

where is the Plank constant. At highly degenerate the Hall mobility of electrons cm²/Vs (Figure 7), it corresponds to, while the drift mobility can be many times higher, because it also depends on the kinetic energy of the randomly moving electrons. The relaxation time dependence on the total density of free electrons in at K, defined by using mobility data (Figure 7) and Equations (14) and (23) is presented in Figure 8. Here the effective mass of conduction of [25] [26] for cm⁻³, and for cm⁻³. The relaxation time dependence on the total density of free electrons in conduction band can be approximated by such relation:

; (24)

here is in cm⁻³.

a. c. conductivity usually is represented in the following form [24] :

, (25)

and the relative permittivity for as:

; (26)

where

. (27)

Here is the plasma frequency. Accounting the basic Equation (15) for d. c. conductivity, the plasma frequency can be described as:

. (28)

The plasma frequency dependence on parameter for is shown in Figure 9. These results are near to that presented in [30] .

The dielectric function (Equation (26)) vanishes at, i.e. longitudinal vibrations (or the density oscillations of free electrons) of this frequency can appear in the electron gas even in absence of external excitations.

Usually the plasma frequency is presented in the following form [24] [31] [32] :

. (29)

For silicon the density of states in conduction band is expressed as [24] [33]

, (30)

[32] is the effective mass of the density of states. In this case, for silicon, it is il- lustrated in Figure 10. As it is seen there is a good coincidence of digital values of these quantities.

Though both Equations (28) and (29) give the same digital value of the plasma frequency, but it does not mean that all free electrons at high doping levels take part in collective oscillations. As it was shown for drift velocity (Equation (17)), the effective force acting to randomly moving electron in materials with highly degenerate electron gas is times higher than in non-degenerate case. Equation (28) is valid only then, when the average kinetic energy of electron. Coincidences of digital results from Equations (28) and (29) for highly degenerate materials are only then, when the Fermi surface is spherical or the density of states is parabolic. For materials with composite density of states (with non-spherical Fermi surfaces) Equation (29) is not valid [24] [34] . In principle, the expression (29) is misleading, because from it follows that all free electrons at high degenerate of electron gas take part in plasma oscillations. But this is not true, because the applied external electric field can only change the energy of randomly moving electrons, which energy is located near to the Fermi energy, while the contribution due to the electrons located deep below the Fermi level

is near to zero due to limitations of the Pauli principle.

Terahertz (THz) plasma frequency range (see Figure 9) of silicon is very important for science and tech- nology [32] [35] - [38] . In [31] [39] , it is shown that reflectivity of electromagnetic waves has a minimum near to plasma frequency, and there the absorption by free charge carriers is increased [40] . This effect is used for THz radiation detection and fabrication of THz imaging cameras with plasma-wave-based silicon MOSFET detectors [41] [42] .

4. Conclusions

This work tries to attract attention to interpretation of transport properties of degenerate semiconductors and to possible large errors caused when classical statistics is applied for estimation of transport parameters for heavily doped silicon. The general expressions for effective density of randomly moving electrons, their diffusion coefficient, drift mobility, and conductivity are presented and illustrated for electrons in silicon. The calculated values of effective density of randomly moving electrons, their diffusion coefficient, drift mobility, and plasma frequency for donor-doped silicon at any degree of degeneracy there are presented at room temperature. The comparison between the hall mobility and the drift mobility of randomly moving electrons is made and their specific behavior at high level of degeneracy is explained. The presented general expressions are valid for holes as well.

It is unambiguously shown that under equilibrium conditions the Nyquist formula, and the Einstein relation are always fulfilled for one type of charge carriers in homogeneous materials. The form of relation does not depend on the non-parabolicity of conduction band or on mechanism of scattering of charge carriers: The ex- pressions of the Nyquist formula and the Einstein relation remain the same.

Acknowledgements

This study was funded by European Social Fund under Global Grant measure No. VP1-3.1-ŠMM-07-03-040.

Cite this paper

ViliusPalenskis, (2014) Transport of Electrons in Donor-Doped Silicon at Any Degree of Degeneracy of Electron Gas. World Journal of Condensed Matter Physics,04,123-133. doi: 10.4236/wjcmp.2014.43017

References