World Journal of Condensed Matter Physics
Vol.4 No.2(2014), Article ID:45666,4 pages DOI:10.4236/wjcmp.2014.42011
Entanglement of E8E8 Exceptional Lie Symmetry Group Dark Energy, Einstein’s Maximal Total Energy and the Hartle-Hawking No Boundary Proposal as the Explanation for Dark Energy
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 16 January 2014; revised 27 February 2014; accepted 19 March 2014
ABSTRACT
The present note is concerned with two connected and highly important fundamental questions of physics and cosmology, namely if E8E8 Lie symmetry group describes the universe and where cosmic dark energy comes from. Furthermore, we reason following Wheeler, Hartle and Hawking that since the boundary of a boundary is an empty set which models the quantum wave of the cosmos, then it follows that dark energy is a fundamental physical phenomenon associated with the boundary of the holographic boundary. This leads directly to a clopen universe which is its own Penrose tiling-like multiverse with energy density in full agreement with COBE, WMAP and Type 1a supernova cosmic measurements.
Keywords:E8 Exceptional Lie Symmetry Group, Dark Energy, Einstein’s Relativity, E-Infinity Theory, Wheeler Boundary of a Boundary, Hartle-Hawking No Boundary Proposal, Penrose Tiling Multiverse

1. Introduction
The exceptional E8 Lie symmetry group played a major role in condensed matter physics and developing various superstring theories as well as high energy physics (see Ref. 1 and references therein). It was also used for instance by the present author in quantum cosmology and in connection with the issue of dark energy [1] -[8] . The present short analysis continues in this direction and presents a very short and hopefully convincing derivation of the dark energy density of the cosmos, namely E(D) = mc2(21/22) which together with the ordinary energy density E(O) = mc2/22 adds to Einstein’s famous density E = mc2, where m is the mass and c is the speed of light [1] -[4] . We note that the present analysis is partially motivated by the considerable success of using E8 topology in condensed matter physics theory and experiment [9] [10] . Finally we give a global justification of the entire present theory by invoking Wheeler’s boundary of a boundary principle [11] [12] and the HartleHawking no boundary proposal [13] [14] . We stress that our confidence in our explanation of dark energy [11] - [23] stems not only from its simplicity and agreement with Wheeler, Hartle and Hawking’s analysis but mainly from the agreement with the most recent accurate measurements [6] -[9] and observations [23] .
2. Analysis
Let us start by assuming the universe to be described by E8 world and a second E8 shadow world [1] . This adds to |E8E8| = 496 dimensions. We split these dimensions into 3 + 1 = 4 dimensions related to the classical relativistic domain while 496  4 = 492 belongs to Hardy’s maximal generic entanglement regime. It follows then that the net dimensional effect of the 492 internal dimensions is the intersection of 492 and P(Hardy) =
4 = 492 belongs to Hardy’s maximal generic entanglement regime. It follows then that the net dimensional effect of the 492 internal dimensions is the intersection of 492 and P(Hardy) = 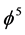 [1]
[1]
[2] . Consequently, we have in addition to 3 + 1 = 4 space dimensions  hidden dimensions which together with D = 4 make up the 26 dimensions of Bosonic strings [1] [2] . However if we look at the fact that E8E8 and not only E8 describes the entity of entanglement, then our dark dimensions are really (22) (2) = 44 dimensions. The ratio of energy reduction from 3 + 1 = 4 dimensions is thus
hidden dimensions which together with D = 4 make up the 26 dimensions of Bosonic strings [1] [2] . However if we look at the fact that E8E8 and not only E8 describes the entity of entanglement, then our dark dimensions are really (22) (2) = 44 dimensions. The ratio of energy reduction from 3 + 1 = 4 dimensions is thus . This should be then taken into account as a Weyl-Nottale scaling in
. This should be then taken into account as a Weyl-Nottale scaling in  so that we may write [1] -[4]
so that we may write [1] -[4]
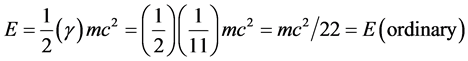 (1)
(1)
Needless to say we could have argued the case slightly differently using Einstein’s density E = mc2 where D(1) = 4 is already taken into account so that 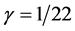 where
where . The calculation would fit seamlessly and become exact by simply using the transfinite exact value of |E8E8|, namely [1] -[4]
. The calculation would fit seamlessly and become exact by simply using the transfinite exact value of |E8E8|, namely [1] -[4]
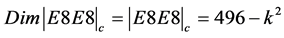 (2)
(2)
where , i.e. k is the twist in the magnitude of Hardy’s quantum entanglement, i.e.
, i.e. k is the twist in the magnitude of Hardy’s quantum entanglement, i.e.
 . (3)
. (3)
In other words we are subtracting from 496 the Hardy entanglement of four entangled dimensions. Consequently the exact dark internal dimensions are
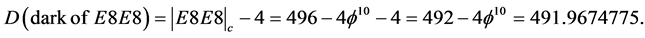 (4)
(4)
To find the net real non-entangled weight we intersect the above with Hardy’s entanglement and find
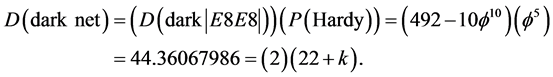 (5)
(5)
Now we can start from  of Newton or E = mc2 maximal energy density of Einstein and find in the first case
of Newton or E = mc2 maximal energy density of Einstein and find in the first case 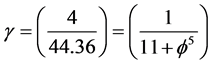 and in the second case
and in the second case . Either way we arrive at [17] -[21]
. Either way we arrive at [17] -[21]
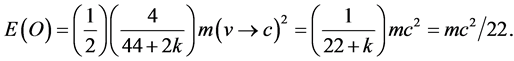 (6)
(6)
The dark energy density is consequently [17] -[21]
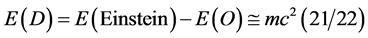 (7)
(7)
exactly as established in previous publications[1] -[4] .
3. Wheeler, Hartle and Hawking Global Justification of Dark Energy
In this section we outline a global justification for the physical existence of dark energy [22] . Our main strategy is to link dark energy to the extension of Wheeler’s boundary of a boundary principle [11] [12] to the no boundary proposal of Hartle-Hawking [13] [14] . In turn this proposal is revised in such a manner as not to equate zero with empty as originally done by Wheeler [11] [12] . By contrast we take here the mathematically more stringent notion of equating emptiness not with the non empty zero set but with the truly empty set denoted traditionally with the Scandinavian letter Ø [15] [16] . This is far from being only a mathematical requirement because the zero set models the quantum particle while the empty set models the quantum wave as has been well established in the last two years [17] -[20] . Seen that way it becomes abundantly clear that the boundary of the holographic boundary of our universe is an empty set [1] -[4] [17] -[22] . In other words dark energy constituting 95.5% of the total energy density must be contained in the Hartle-Hawking wave function of the cosmos located at the boundary of the holographic boundary of a Penrose tiling-like universe which is open and closed, i.e. clopen as well as being its own multiverse as reasoned sometime ago [22] and confirmed by recent observations [23] . It follows then that the dark energy density is given by 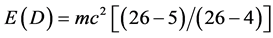 where 26 is the number of Bosonic strings, 5 is the dimensionality of Kaluza-Klein spacetime and 4 is Einstein’s spacetime dimensions [17] -[20] . We have thus a very persuasive mental picture and a satisfactory geometrical topological model to go with it. In this picture we live in the Penrose multiverse space surrounded with 4.5% ordinary energy and experience local attractive gravity while at the boundary of the holographic boundary of our compactified hyperbolic fractal Klein-Penrose universe which has 95.5% dark energy we have negative gravity pulling the universe apart [3] [17] -[20] .
where 26 is the number of Bosonic strings, 5 is the dimensionality of Kaluza-Klein spacetime and 4 is Einstein’s spacetime dimensions [17] -[20] . We have thus a very persuasive mental picture and a satisfactory geometrical topological model to go with it. In this picture we live in the Penrose multiverse space surrounded with 4.5% ordinary energy and experience local attractive gravity while at the boundary of the holographic boundary of our compactified hyperbolic fractal Klein-Penrose universe which has 95.5% dark energy we have negative gravity pulling the universe apart [3] [17] -[20] .
4. Conclusion
The present analysis shows once more the unity of theoretical physics and cosmology in a simple but impressive way [1] -[4] . Using E8E8 exceptional Lie symmetry group of superstring theory, an exact expression for the ordinary and dark components of the cosmic energy density are obtained which are in full agreement with measurements [1] [6] -[8] . Thus we can state with reasonable confidence that E8 describes our universe and its dark energy just as it describes fundamental experiments in condensed matter physics [9] [10] . These conclusions and the theory behind them find a global convincing justification in our way of interpreting the work of Wheeler, Hartle and Hawking where the universe is viewed as a compactified Klein-Penrose disc representing a ‘t Hooft-Susskind hologram of a multiverse. Since the boundary of this holographic boundary is an empty set, then it follows that it is equivalent to a Hartle-Hawking quantum wave for the cosmos and contains the 95.5% dark energy density. Very recent observation seems to confirm this picture [23] .
References
- El Naschie, M.S. (2013) A Unified Newtonian-Relativistic Quantum Resolution of the Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light. International Journal of Modern Nonlinear Theory and Application, 2, 43-54. http://dx.doi.org/10.4236/ijmnta.2013.21005
- El Naschie, M.S. (2013) From Yang-Mills photon in Curved Spacetime to Dark Energy Density. Journal of Quantum Information Science, 3, 121-126. http://dx.doi.org/10.4236/jqis.2013.34016
- El Naschie, M.S. (2014) Pinched Material Einstein Spacetime Produces Accelerated Cosmic Expansion. International Journal of Astronomy and Astrophysics, 4, 80-90. http://dx.doi.org/10.4236/ijaa.2014.41009
- El Naschie, M.S. (2014) Capillary Surface Energy Elucidation of the Cosmic Dark Energy-Ordinary Energy Duality. Open Journal of Fluid Dynamics, 4, 15-17. http://dx.doi.org/10.4236/ojfd.2014.41002
- El Naschie, M.S. (2014) Why E Is Not Equal to mc2. Journal of Modern Physics, in Press.
- Linder, E., (2008) Dark Energy. “Scholarpediablog”. The Peer-Reviewed Open Access Encyclopedia, Scholarpedia, 3, Article ID: 4900.
- Amendola, L. and Tsujikawa, S. (2010) Dark Energy. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511750823
- Copeland, E.J., Sami, M. and Tsujikawa, S. (2006) Dynamics of Dark Energy. arXiv: hep-th/0603057V3
- Coldea, R. et al. (2010) Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E8 Symmetry. Science, 327, 177-180. http://dx.doi.org/10.1126/science.1180085
- El Naschie, M.S. (2013) The Quantum Entanglement behind the Missing Dark Energy. Journal of Physics and Applications, 2, 88-96.
- Kheyfets, A. and Wheeler, J.A. (1986) Boundary of a Boundary Principle and Geometric Structure of Field Theories. International Journal of Theoretical Physics, 25, 573-580.
- Wheeler, J.A. (1989) Information, Physics, Quantum the Search for Links. The 3rd International Symposium Foundations of Quantum Mechanics, Tokyo, 310-336.
- Hartle, J. and Hawking, S. (1983) Wave Function of The Universe. Physical Review D, 28, Article ID: 2960. http://dx.doi.org/10.1103/PhysRevD.28.2960
- Hartle, J. and Hawking, S. (2008) No-Boundary Measure of the Universe. Physical Review Letters, 100, Article ID: 201301. http://dx.doi.org/10.1103/PhysRevLett.100.201301
- Henle, J.M.(1986) An Outline of Set Theory. Springer, New York. http://dx.doi.org/10.1007/978-1-4613-8680-3
- Devlin, K. (1993) The Joy of Sets. Springer, New York (in Particular See p. 5).
- El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrödinger Quantum Wave. Journal of Modern Physics, 4, 591-596. http://dx.doi.org/10.4236/jmp.2013.45084
- El Naschie, M.S. (2013) Nash embedding of Witten’s M-Theory and the Hawking-Hartle Quantum Wave of Dark Energy. Journal of Modern Physics, 4, 1417-1428. http://dx.doi.org/10.4236/jmp.2013.410170
- El Naschie, M.S. and Helal, A. (2013) Dark energy Explained via the Hawking-Hartle Quantum Wave and the Topology of Cosmic Crystallography. International Journal of Astronomy and Astrophysics, 3, 318-343. http://dx.doi.org/10.4236/ijaa.2013.33037
- Helal, M.A., Marek-Crnjac, L. and He, J.-H. (2013) The Three Page Guide to the Most Important Results of M. S. El Naschie’s Research in E-Infinity and Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145. http://dx.doi.org/10.4236/ojm.2013.34020
- Marek-Crnjac, L. (2013) Cantorian Space-Time Theory—The Physics of Empty Sets in Connection with Quantum Entanglement and Dark Energy. Lambert Academic Publishing, Saarbrücken.
- El Naschie, M.S., Marek-Crnjac, L., He, J.-H. and Helal, M.A. (2013) Computing the Missing Dark Energy of a Clopen Universe Which Is Its Own Multiverse in Addition to Being Both Flat and Curved. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 3, 3-10.
- Grossman, L. (2014) Ripples of the Multiverse. New Scientist, 221, 8-10. http://dx.doi.org/10.1016/S0262-4079(14)60557-1

