World Journal of Condensed Matter Physics
Vol.4 No.1(2014), Article ID:42847,9 pages DOI:10.4236/wjcmp.2014.41004
“Smart Design” of Quantum Wells and Double-Quantum Wells Structures
![]()
Faculty of Mathematics and Natural Sciences, University of Rzeszow, Rzeszow, Poland.
Email: tralle@univ.rzeszow.pl
Copyright © 2014 Igor Tralle, Klaudiusz Majchrowski. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Igor Tralle, Klaudiusz Majchrowski. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 30th, 2013; revised December 3rd, 2013; accepted January 6th, 2014
KEYWORDS
Inverse Scattering Problem Method; Quantum Wells and Superlattices; Predetermined Energy Spectrum; Bargmann Reflectionless Potentials
ABSTRACT
In the work, we propose an approach to “smart design” of heterostructures (quantum wells and superlattices) based on the combination of Inverse Scattering Problem Method and the direct solution of the eigenvalue problem for the Schrödinger equation with reconstructed potentials. Potential shape reconstructed in this way can be substituted then by some approximation, so that the output spectrum obtained by solving the Schrödinger equation with such approximated potential, differs only slightly from the input one. In our opinion, the approach can be used in many applications, for instance, for developing the new electronic devices such as tunable THz detectors.
1. Introduction
In recent years, we have been witnessing the rapid progress in nanoelectronics which is already on the way to continue the outstanding successes of microelectronics. This became possible among others, due to the development of technologies and techniques, such as, Molecular Beam Epitaxy (MBE), which enables depositing thin layers of different materials, one on the top of another, with almost atomic precision. The last one in its turn, gives the possibility to produce a variety of low-dimensional structures which are the basis for constructing a great many novel devices.
Recently, step by step, the approach to the semiconductor heterostructures design comes into being, which perhaps could be termed as smart design and whose aim is to tailor the heterostructure shapes in order to obtain the predetermined characteristics (see [1-3]). In some of the cases, the “smart design” approach is based on the Inverse Scattering Problem Method (ISP) (see [2] and especially [4]). In others, when the space dependence of charge carriers effective mass is also taken into accountit is based on different techniques [5]. The paper [4], and then [6], in which the main ideas of [4] were implemented, were devoted mainly to the design of quantum filters with the predetermined reflection and transmission properties. On the other hand, the “palette” of quantum well (QW) potentials which are in use, is still limited to a few most popular ones, rectangular, parabolic or at most, semiparabolic or triangular [7,8] and this circumstance obviously restricts the possibility to choose and control the energy spectrum of QWs and the devices based on them. Meantime, in different areas of possible applications of the low-dimensional structures, one often needs to have a specific kind of spectrum known beforehand and a question arises: how to produce the QW with a predetermined spectrum? At least from the theorist’s point of view, the question can be reformulated as follows: suppose that the spectrum of QW is known, and that is to say one knows the number of quantum levels and the energy distances between them (remember that the spectrum is not necessarily equidistant as in the case of parabolic QW or similar to the spectrum of rectangular well); can one reconstruct the QW-potential which supports this spectrum? An affirmative answer to this question would make quantum engineering more flexible and provide the opportunity to develop multitude of novel devices.
The already cited papers [4,6] tackled the difficult problem of complex transmission and reflection coefficients reconstruction, if the potential does not support the bound states. As it was stated in [4], if bound states are present, knowledge of the accessible scattering data is not sufficient for unique recovery of the potential. One can notice, however, that, if from the very beginning, one restricts the searching for the shape of the potentials to some definite class of possible potentials, the uniqueness of potential reconstruction can be restored. As a matter of fact, this is the consequence of the theorem proved by B. M. Levitan and M. G. Gasymov [9,10]. This fact was rediscovered later by a group of theorists from Fermi Lab at Batavia (USA), who dealt with numerical simulation of quarkonium [11,12]. Surprisingly, it turns out that if one tries to solve the inverse problem with the aid of reflectionless Bargmann potentials which, above all, are symmetric, which is V(x) = V(−x), it suffices to know only the positions of energy levels, without knowing the normalizing constants of wave functions. There is also another problem with the QW potential reconstruction: this problem, as most of inverse problems, is ill-posed; this fact was emphasised also in [4] (However, there is certain well-posedness of the ISP in one dimension, in the sense that the mapping from the scattering data to potential is continuous in proper topology).
In our particular case, it means that if the “input” spectrum of QW changes even slightly, the potential shape can change essentially and in unpredictable manner. But if the potential of QW is already established to a first approximation by means of, saying ISP-method, the problem of finding the “proper” potential can be reduced to well-posed problem.
So, in the present work, we address the following issues. At first, using the “smart design” approach and ISPmethod, we reconstruct the shape of symmetric QW with pre-determined energy spectrum, and then using the direct approach based on the numerical solution of eigenvalue problem for corresponding Schrödinger equation, we find more realistic potential shapes of QW and coupled-QW, which in our opinion can be produced by means of existing fabrication techniques. The paper is organized as follows: in Section 2, for the reader’s convenience, we outline briefly the ISP-method in its relation to the QWpotential reconstruction; in Section 3, we present the results of numerical simulations. The discussion is summed up in Conclusion which ends the paper.
2. ISP Method and Reconstruction of Quantum Well Potentials
As we already mentioned, one often needs to know, how to reconstruct the QW-potential provided that the spectrum supported by this potential is known beforehand. One can look at the problem also as follows: suppose we have a set of “scattering data”, whatever it means; we do not define them precisely right now. Can we find a potential which produces this set of data? An affirmative answer to this question was obtained for the first time by mathematicians I. M. Gel’fand, B. M. Levitan [10,13] and V. A. Marchenko [14] (see also [15]). They elaborated a method of potential reconstruction by means of spectral or scattering data which is now known under the name of Inverse Scattering Problem Method (ISP). We shall term their method or approach also as a GLM-method (approach). In a particular case of QW, the question is reduced to the following: suppose we have a number of quantum levels with the given distances between them; what potential shape (or which form of) QW should be in this case; or in other words, can we find the potential of QW, if the spectrum and the depth of QW are given? As we mentioned in the Introduction, the provisional positive answer to this question was obtained by means of the ISP-method in [2]. Here, for the sake of consistency and reader’s convenience, we outline the main ideas of GLMapproach only very briefly. Our basic physical model is the single-particle model of the electron trapped in a potential (QW) which supports a number of bound states, while its dynamics is described by single-band (conduction band) effective mass approximation for the envelope wave function.
Consider the eigenvalue problem of the Schrödinger equation with the potential V(x) in one space dimension
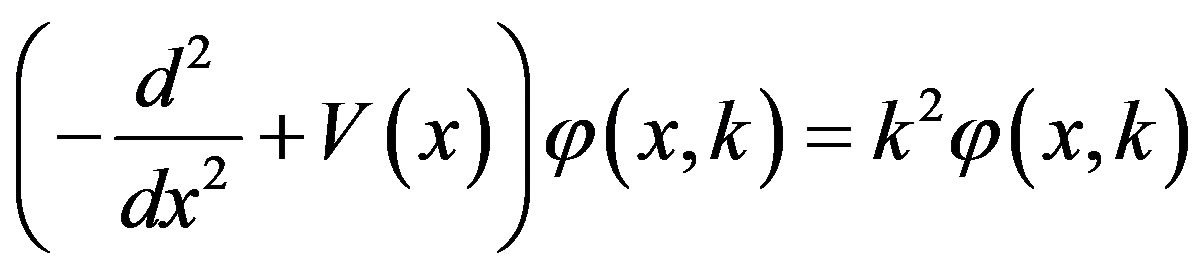 , (1)
, (1)
(here we assume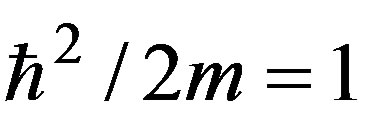 ). The GLM-method may be viewed as a dispersion theory for the Schrödinger wave function of (1). From the solution to (1) with k complex, one can define Jost functions
). The GLM-method may be viewed as a dispersion theory for the Schrödinger wave function of (1). From the solution to (1) with k complex, one can define Jost functions  and
and 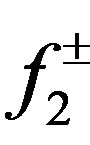 which are analytic in the upper-half k-plane with the following asymptotic behavior
which are analytic in the upper-half k-plane with the following asymptotic behavior

and construct a meromorphic function Φ(x,k) as
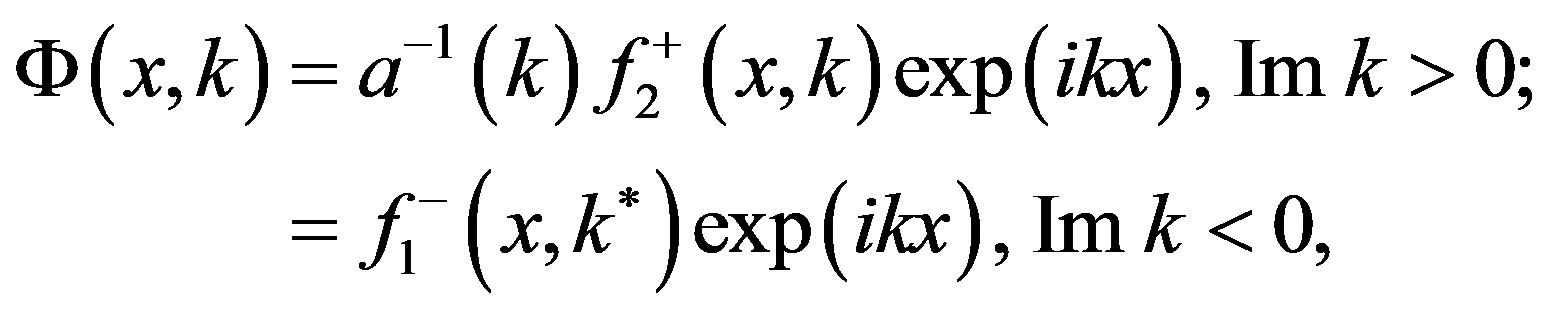
where a−1(k) is a conventional transmission coefficient.
Thus, Φ(x,k) is completely determined by its singularity structure which consists of a cut along the real k-axis and some number, say, N of bound-state poles on the positive imaginary axis. The spectral weight of the cut is essentially the scattering-state wave function multiplied by the reflection coefficient, both evaluated at real k. Similarly, the pole residues are essentially constants times bound-state wave functions. Upon Fourier transformation the dispersion relation for Φ becomes the Marchenko integral equation [16] (see also [15] for details) which determines the wave functions. The inverse problem of the potential reconstruction by means of scattering data can be reduced, generally speaking, to solving an integral equation
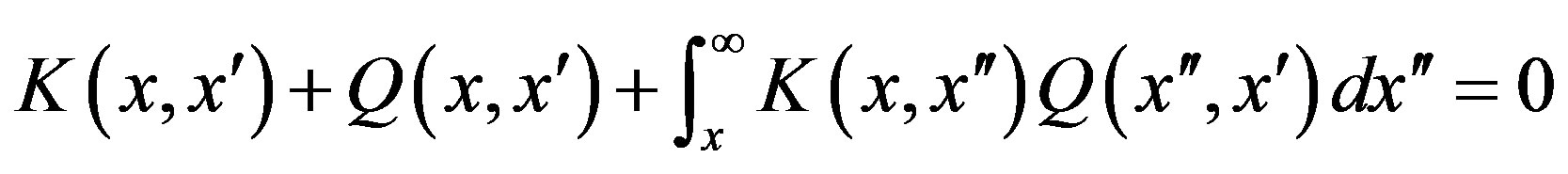
and thereupon, to a simple differentiation of its kernel
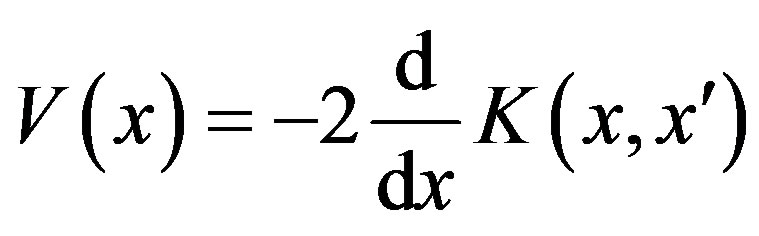
which is given entirely in terms of the reflection coefficient and 2N bound-state parameters. Here
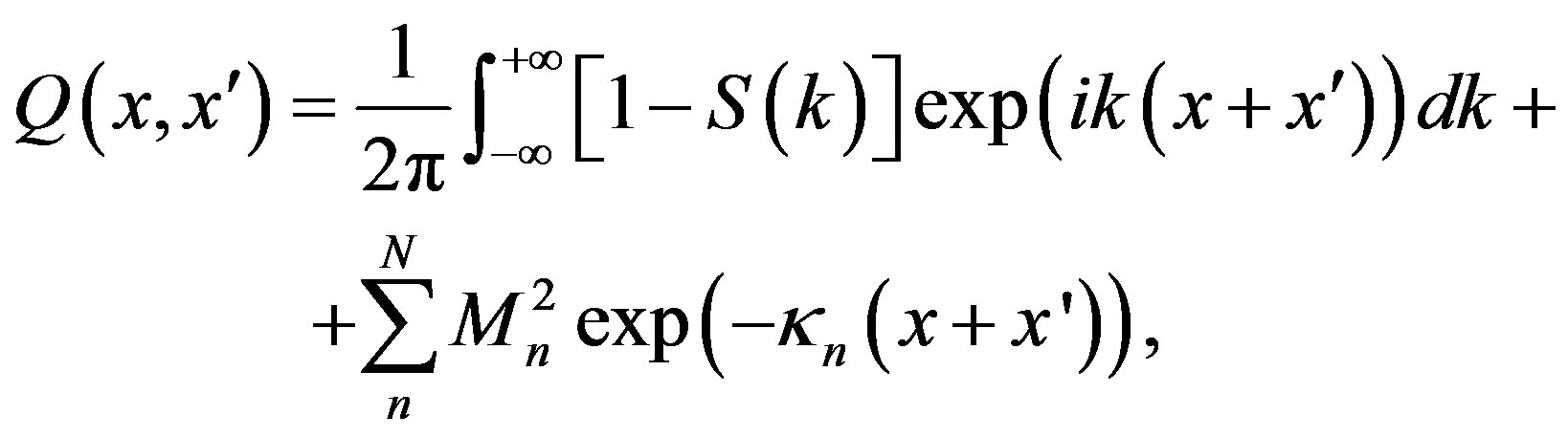
where S(k), En and 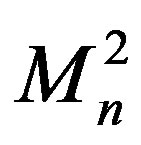 are scattering data: S(k) is a scattering matrix, En = (iκn)2 are bound-state energies and
are scattering data: S(k) is a scattering matrix, En = (iκn)2 are bound-state energies and 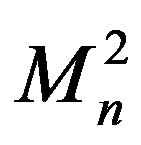 are its normalization constants.
are its normalization constants.
If the reflection coefficient can be represented by rational functions of k, the Marchenko equation can be solved exactly by algebraic technique. The most simple case corresponds to a reflection coefficient vanishing for all real k(S(k) = 1); then the expression for Q(x, x') contains only the sum over the bound states, and the integral equation reduces to a system of N linear algebraic equations with respect to the kernel K(x, x'). The potential V(x) also can be reconstructed by means of 2N parameters. Half of the parameters are N bound-state energies En, n = 1, 2,··· N, while the others are the normalizing constants 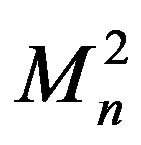 which in Nuclear Physics are assumed to be obtained from scattering data as
which in Nuclear Physics are assumed to be obtained from scattering data as . This choice corresponds to the transparent and symmetric potentials. These 2N numbers supply a complete set of the parameters for the solution of inverse problem to exist and be unique. Obviously, in the case of QWs a second half of the scattering data (the normalizing constants) is inaccessible. It turns out however, that the way out actually exists. The possibility to reconstruct the infinitely deep and symmetric potentials solely by means of bounded states was established for the first time by B. M. Levitan and M. G. Gasymov who proved the so called Two Spectra Theorem [9,10]. The meaning of this theorem in brief is the following: to reconstruct symmetric potentials V(x) = V(−x), it suffices to know only the positions of energy levels without knowing the normalizing constants. This fact was re-discovered later by H. B. Thacker, C. Quigg and J. L. Rosner [11] who modeled the confining potentials binding massive quarks and antiquarks in meson systems. They were able even to fit approximately the lower parts of infinitely deep wells (parabolic, harmonic oscillator, linear and rectangular wells) by means of a limited number of levels whose positions are known, using some additional technical trick which is termed a stabilizing parameter.
. This choice corresponds to the transparent and symmetric potentials. These 2N numbers supply a complete set of the parameters for the solution of inverse problem to exist and be unique. Obviously, in the case of QWs a second half of the scattering data (the normalizing constants) is inaccessible. It turns out however, that the way out actually exists. The possibility to reconstruct the infinitely deep and symmetric potentials solely by means of bounded states was established for the first time by B. M. Levitan and M. G. Gasymov who proved the so called Two Spectra Theorem [9,10]. The meaning of this theorem in brief is the following: to reconstruct symmetric potentials V(x) = V(−x), it suffices to know only the positions of energy levels without knowing the normalizing constants. This fact was re-discovered later by H. B. Thacker, C. Quigg and J. L. Rosner [11] who modeled the confining potentials binding massive quarks and antiquarks in meson systems. They were able even to fit approximately the lower parts of infinitely deep wells (parabolic, harmonic oscillator, linear and rectangular wells) by means of a limited number of levels whose positions are known, using some additional technical trick which is termed a stabilizing parameter.
In accordance with what was said above, one has to search for the solution of our problem among the potentials of a special class of reflectionless and symmetric potentials V(x) = V(−x). Suppose that one-dimensional potential V(x) can be represented by the function 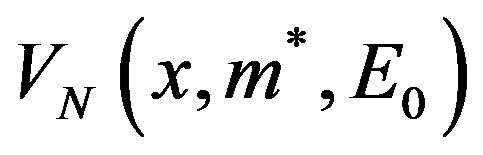 which obeys the following conditions:
which obeys the following conditions:
• VN supports precisely N bounded states of the quantum system with the effective mass m*. The boundstate energies coincide with the energies ε1, ε2, ···, εN, of the levels within the QW;
• limx®¥VN = E0. The last value can be considered as a depth of QW.
Arranging the binding energies k2 = E0 − εn in a descending order so that k1 > k2 >··· > kN, and  refers to the ground-state energy, one can use for QW potential reconstruction the technique developed by Schonefeld et al. [12] for studying the convergence of the reflectionless approximation to the confining potentials. Omitting the intermediate calculations, we give here only the final results:
refers to the ground-state energy, one can use for QW potential reconstruction the technique developed by Schonefeld et al. [12] for studying the convergence of the reflectionless approximation to the confining potentials. Omitting the intermediate calculations, we give here only the final results:
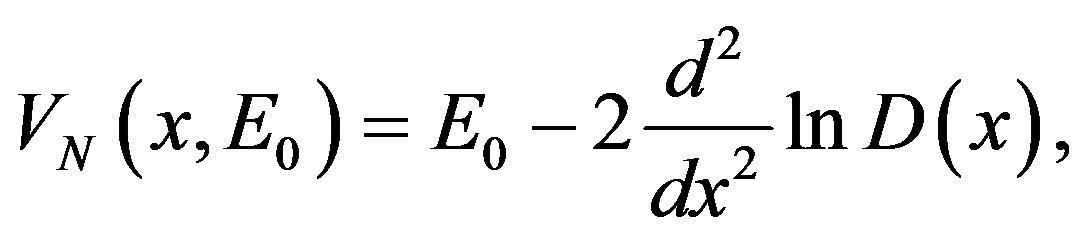 (2)
(2)
where
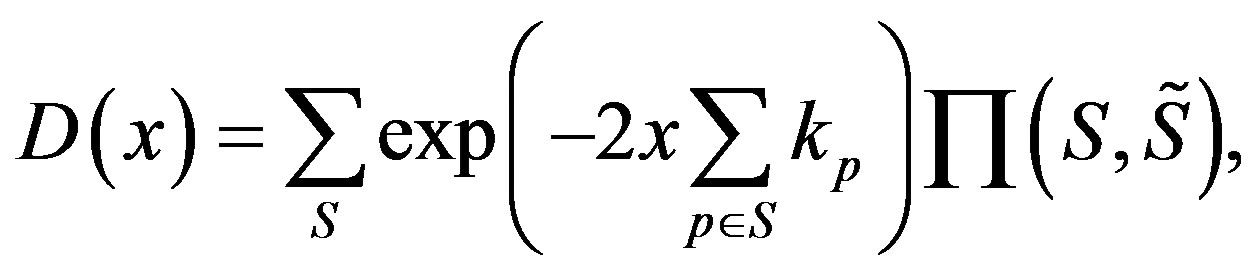
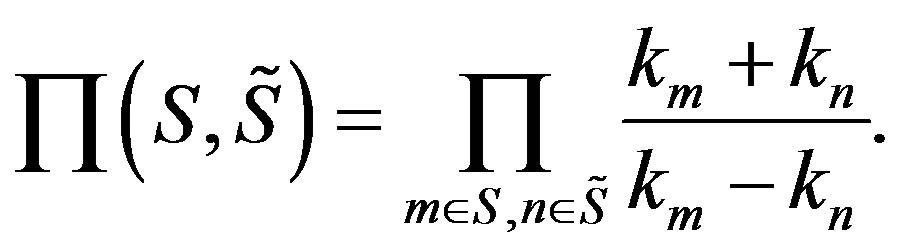
Here the sum ranges over all subsets S of {1, 2, ···, N} including the empty set and the full set, while  denotes the complement of the set S. Notice that in spite of apparent simplicity, these formulae possess the complicated inner structure; thus, due to the sum which runs over all subsets of a set of N elements, the calculations become practically impossible without use of computer already at N = 4.
denotes the complement of the set S. Notice that in spite of apparent simplicity, these formulae possess the complicated inner structure; thus, due to the sum which runs over all subsets of a set of N elements, the calculations become practically impossible without use of computer already at N = 4.
3. Results of Numerical Calculations and Discussion
To aim at doing corresponding calculations, the computer program was elaborated in the MatLab environment, which enables to reconstruct the QW potential based on the preset energy spectrum.
The implemented algorithm enables to calculate the potential for the arbitrary number N of quantum levels in accordance with the formulae (2). As the input parameters of the applet one has to choose the width and depth of QW, the number of quantum levels and the effective mass of charge carriers, while in the output one gets the reconstructed potential. The software includes the additional algorithm for the solution of eigenvalue problem for Schrödinger equation with the potential V(x), reconstructed in previous step. Due to this, one can immediately and directly check the correctness of the obtained results. To sum up, the software works according to the following scheme:
1) At the input one should define the desirable energy spectrum, the charge carriers effective mass and to the first approximation, the width and depth of QW;
2) On the base of these data, an implemented algorithm calculates the shape of the potential;
3) In the next step we solve the eigenvalue problem (direct problem) for the Schrödinger equation with the potential V(x), reconstructed in previous step;
4) One calculates the relative error, i.e. is the difference between the preset energy spectrum and the one obtained in the step 3).
It turns out, that the depth and width of QW defined as input parameters, play the role of germ and are not sufficient for the difference between the input spectrum and that obtained after potential reconstruction to be sufficiently small. That is why the software is equipped with the algorithm whose task is to minimize this difference. It goes through the nearest vicinity of the given parameters (the width and depth of QW) with some tolerance, simultaneously determining the minimum of relative errors in accordance with the chosen measure.
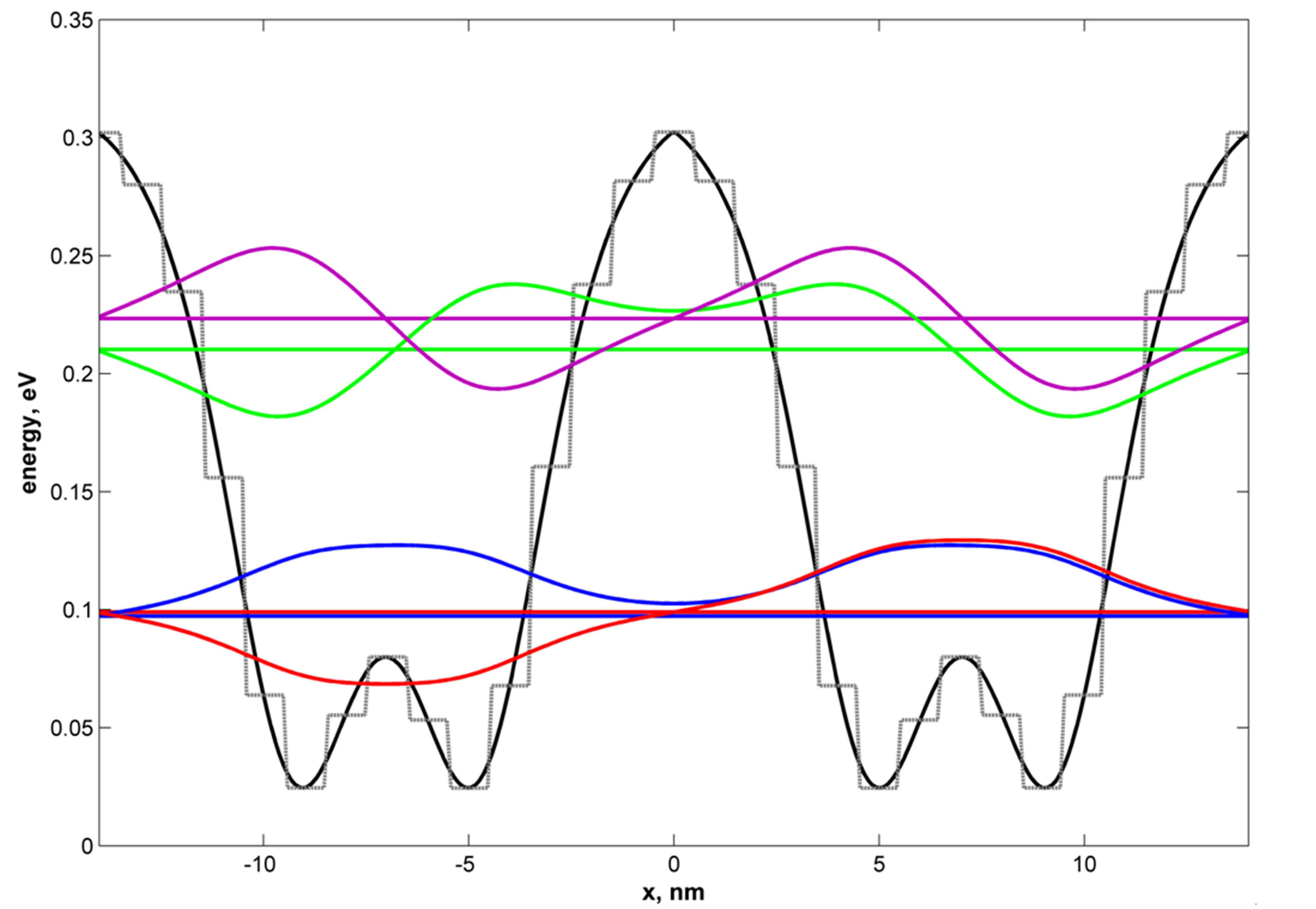
As an example of the of simulations made by means of the program, in Figure 1 the shape of the QW potential is presented, which supports two energy levels, while in Figure 2 the potential of the two coupled QW is shown. Such double-QW structure can be considered as the base of super-lattice, since the energy splitting due to tunneling determines the sub-band width in the super-lattice.
In Figure 1 and Figure 2 it is seen that the QW potential shapes are not trivial and another question immediately arises: is it possible to produce these QWs by means of available techniques (say, MBE-technique)? Very probable, that the answer to this question is also affirmative.
The point is, that as it was already mentioned in Introduction, ISP like the most inverse problems is illposed. There are two definitions of ill-posedeness, the one is belonged to J. Hadamard [17] and another to A. Tikhonov [18]. Since these two definitions in some circumstances coincide and the difference is of no importance for our discussion, let us recall the first of them.
Let we have two metric spaces (Z, U) equipped with
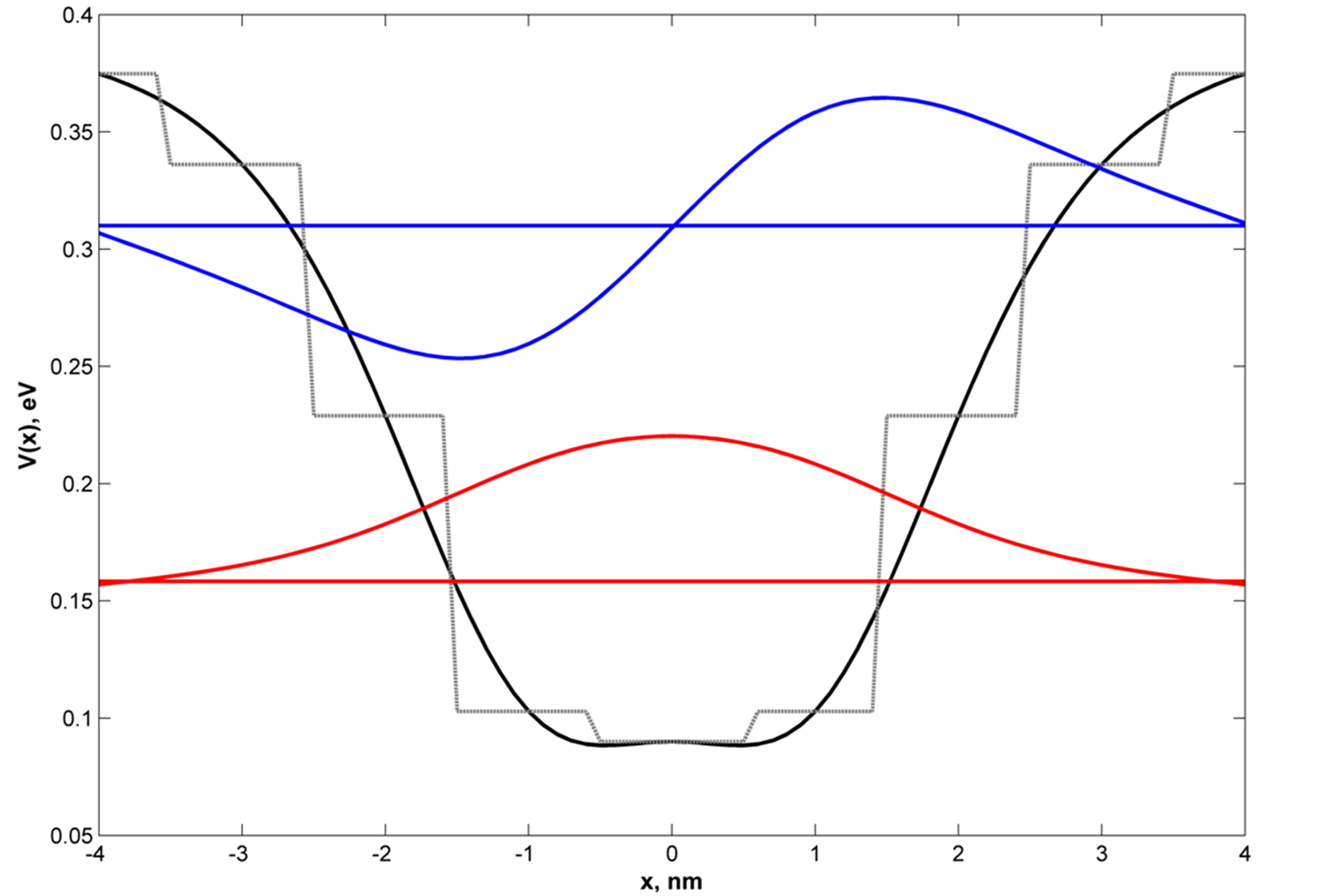
Figure 1. Example of QW-potential with predetermined spectrum reconstructed by means of ISP method. Black solid curvepotential reconstructed by ISP-method; dashed line-step-like approximation. Colored lines and curves (in red and blue) are the energy levels and corresponding wave functions (For the values of energies see Table 1).

Figure 2. Double-quantum-well structure constructed on base of the QW depicted in Figure 1. The splitting due to tunneling is clearly seen in case of excited level, while for the ground state the splitting is practically negligible (for the numerical values see Table 1).
the corresponding metrics ρZ and ρU. Following Hadamard, we call the problem well-posed on the pair of spaces (Z, U), where Z is the “solution space” and U is the “initial condition space”, if:
• for every 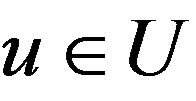 there is the solution
there is the solution • the solution is unique• for every ε > 0 such δ(ε) exists, that for any u1, u2 Î U from the condition ρU(u1, u2) ≤ δ(ε) another one, namely ρZ(z1, z2) ≤ ε immediately follows.
• the solution is unique• for every ε > 0 such δ(ε) exists, that for any u1, u2 Î U from the condition ρU(u1, u2) ≤ δ(ε) another one, namely ρZ(z1, z2) ≤ ε immediately follows.
Violation of any of these conditions renders the problem ill-posed. In our particular case that means that if the initial (input) spectrum of QW changes even slightly, the potential shape can change essentially and in unpredictable manner. But if the potential of QW is already established by ISP procedure, the problem of finding the “proper” potential can be reduced to well-posed problem. Indeed, substituting the reconstructed by the ISP-method potential by its step-like (or other desirable) approximation, we could hope that the output spectrum of QW should not change too much with respect to input one. In this work we have found the step-like approximation for the initial potentials and as it is clearly seen from Figures 1-4, the changes in input and output spectra are indeed almost negligible, but the potential shapes become more realistic to be produced by existing fabrication techniques.
To our opinion, the developed approach can have numerous applications, one of them is the construction of tunable detectors for THz radiation. For instance, the authors of [19] proposed the intersubband transitions in GaAs coupled-quantum-wells for use as such detector for the range of 2 - 5 THz. Our results (see Figure 4) show that intersubband transitions in double-quantum-well structure can be used for detection the radiation of about 19 THz as well as a hundred times higher frequencies of about 230 THz; the full account will be published elsewhere, here we only mention the main features of such device. As it can be easily shown, some transitions between two-split states (ground and excited) resulted from the tunneling between coupled symmetric wells are parity forbidden. However, in the external electric field these transitions become allowed. They correspond to the frequency region of about 19 THz. The transitions between ground state (whose splitting is negligible) and the twosplit excited states of corresponding parity are allowed even in zeroth external electric field. Their frequencies are just in the range of about 230 THz. Varying the electric field across the structure, one can make the detector tunable for a wide range of THz frequencies. Since our software enables to calculate not only the energy spectrum of the structure in question, but the wave functions of the charge carriers too, we can calculate the other important characteristics of the device as well, for instance, the oscillator strengths of the transitions.
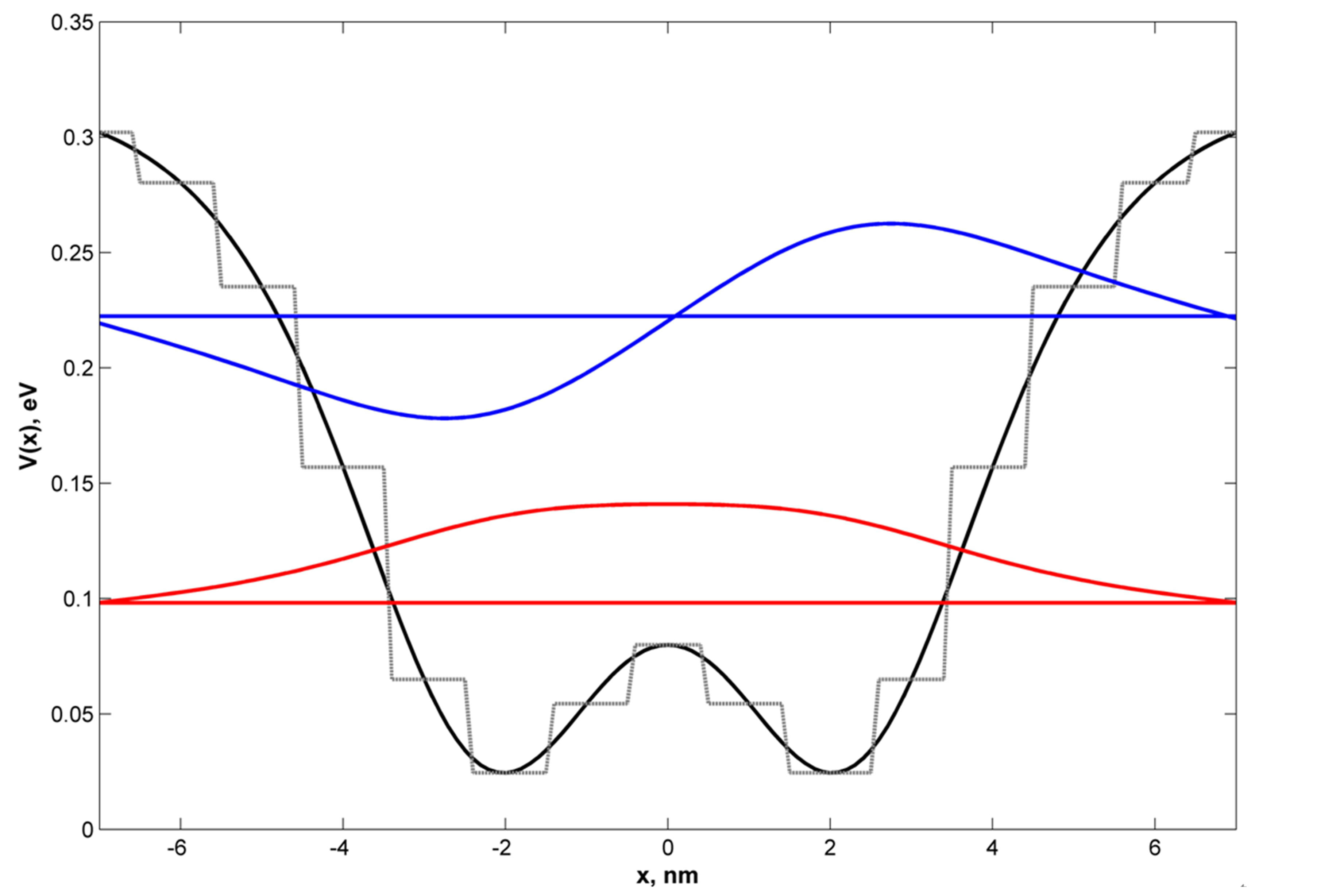
Figure 3. Another example of QW-potential with predetermined spectrum reconstructed by means of ISP method. Denotations are similar to that ones in Figure 1.
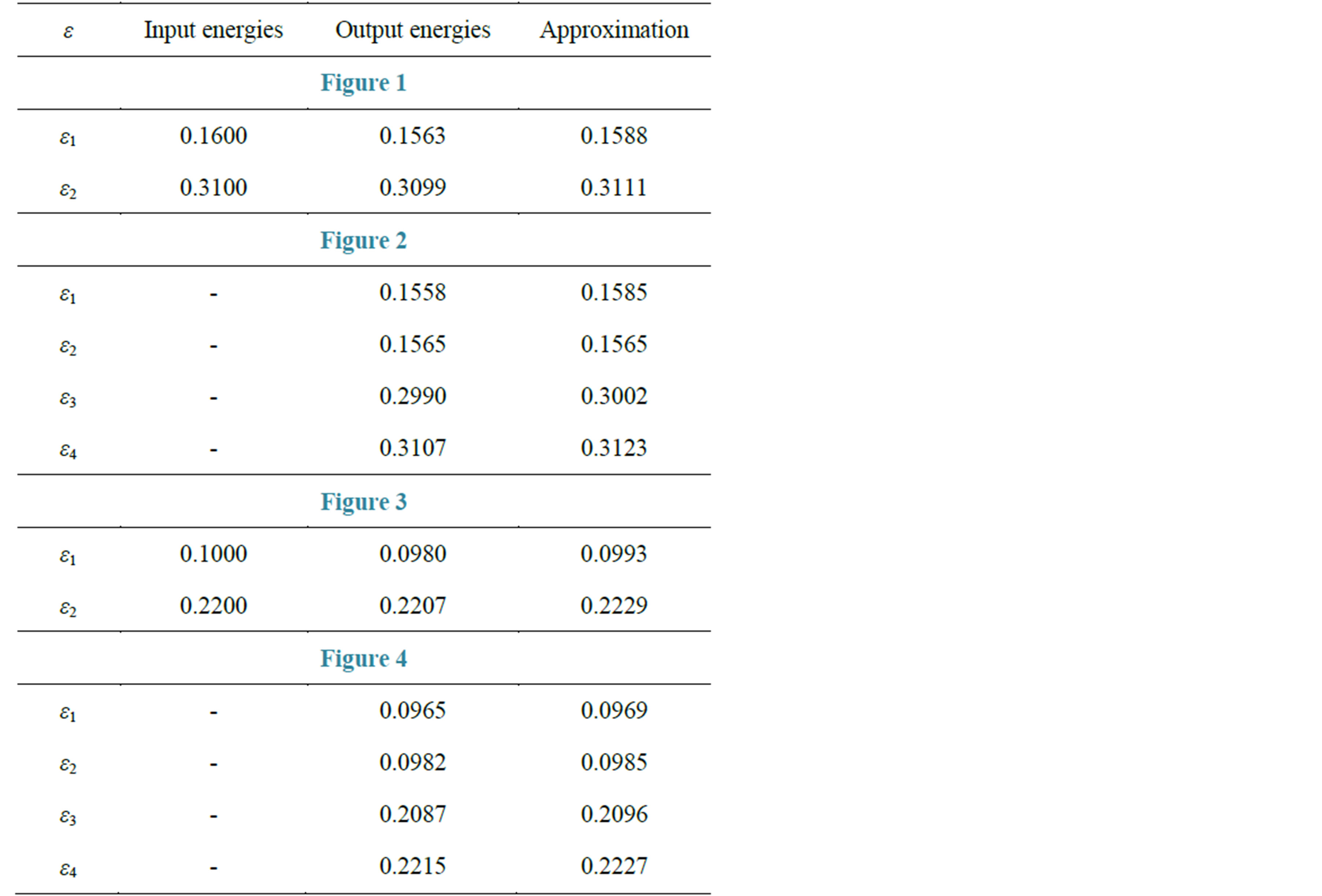
Table 1. Energy spectrum of QWs and double-QW structures presented in Figures 1-4. First column—input energy spectrum (predetermined); second column—energy spectrum obtained as a result of making optimization; third column—output energy spectrum obtained after step-like approximation (all energies are in eV).
As another example of possible applications of the technique developed in the work, consider the next situation. It is well-known that one of the most attractive features of the devices based on QWs, for instance resonant tunneling transistors or more general, resonant tunneling structures (RTS), is the discreteness of their energy spectrum. Very often however, it can be revealed only at very low temperature of about few K. The point is that the energy distances between the quantum levels are of the order of ~meV, while the quantum level width can be also of the same order at higher temperature (room temperature, for instance) and hence, for the levels not to overlap, one should have the temperature of about few K. Only at such temperatures the peak-to-valley ratio of so called I-V-characteristic of RTS is sufficient to resolve the tunnel current peaks. So, for the different applications it is desirable to have RTS which could operate at higher temperature (ideally, at room temperature).
Suppose now that we have the desirable spectrum of QW, in other words, we simply set the number of quantum levels with the distances between them in such a way that they do not overlap at higher temperature. It means that the spacings between the levels are chosen to be about ~2.5 kBT. Of course, having in mind real structure, we should restrict the number of quantum levels to some reasonable value, say 3, 4 to 6 at most, since the depth of QW can be about 0.2 - 0.4 eV.
The effective potentials reconstructed by means of ISP procedure and satisfying these requirements at 77 K and 130 K are shown in Figures 5 and 6.

Figure 5. Example of QW-potential supporting 4 energy levels which do not overlap (see the text) at 77 K. The colored lines and curves (in blue, red, crimson and green) correspond to the energy levels and wave functions (for all numerical values see Table 2).
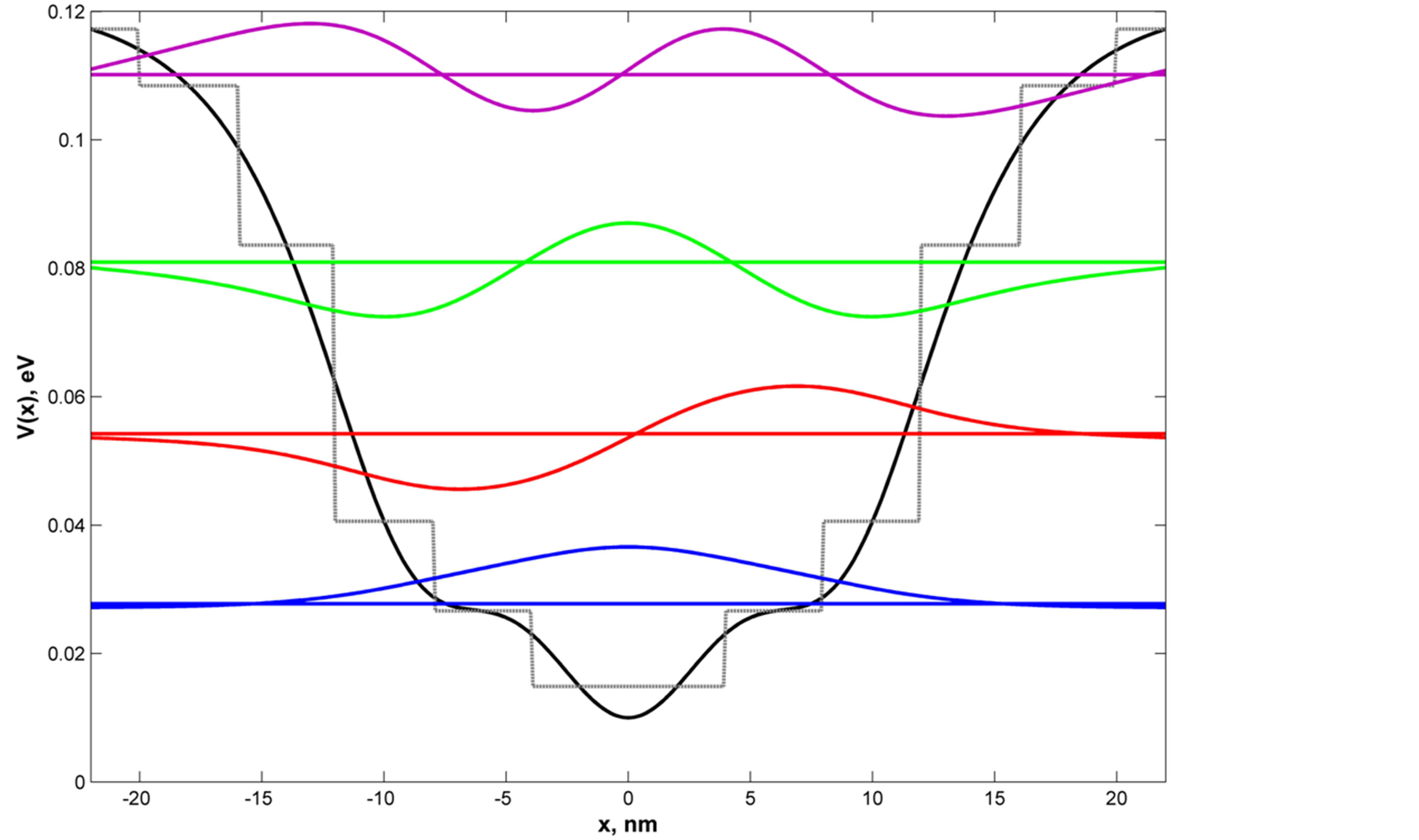
Figure 6. Example of QW potential supporting 4 energy levels which do not overlap at 130 K (all numerical values are in Table 2).
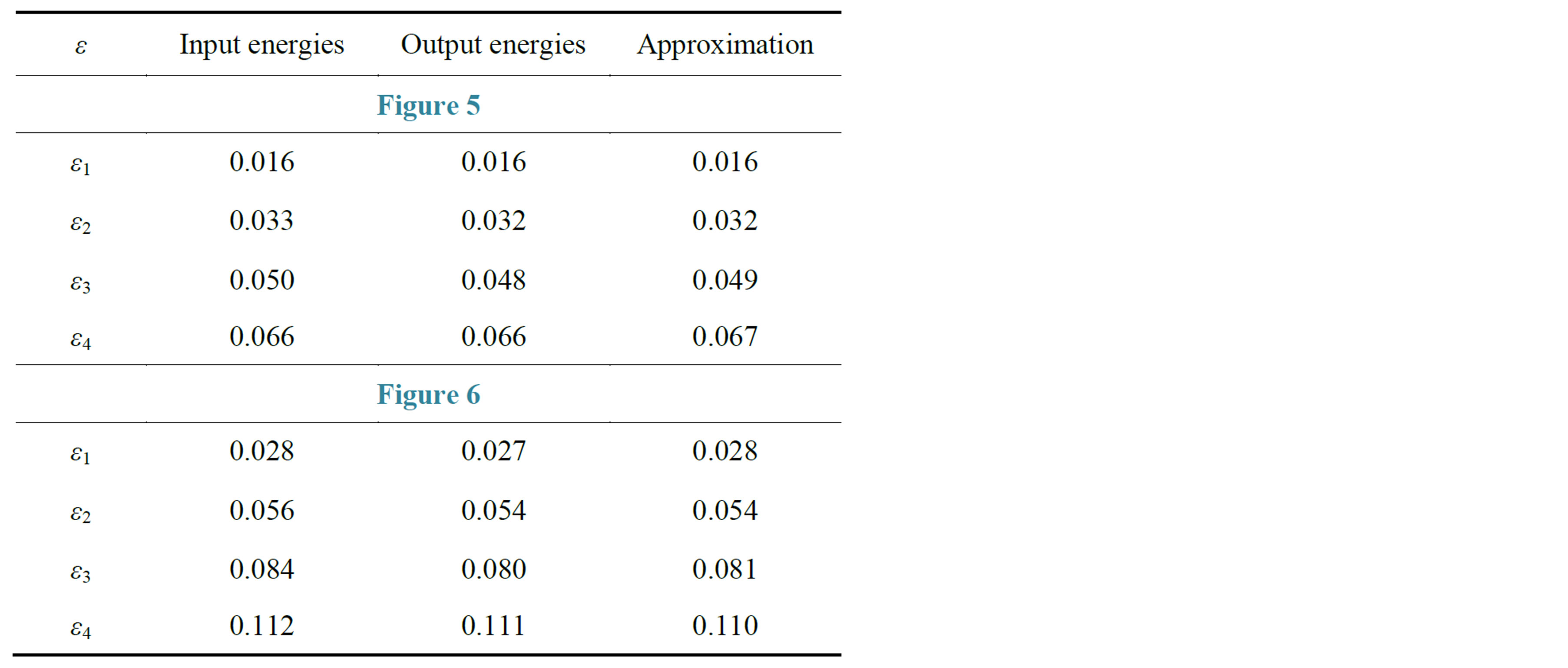
Table 2. Energy spectrum of QWs presented in Figures 5 and 6. All denotation are similar to that ones in Table 1.
4. Conclusion
In this work, we propose an approach to “smart design” of nanostructures (quantum wells and superlattices) based on the combination of Inverse Scattering Problem Method and the direct solution of the eigenvalue problem for the Schrödinger equation with reconstructed potential afterwards. The problem of potential reconstruction of QWs with predetermined spectrum for the class of Bargmann symmetric potentials can be solved directly, if one knows solely the energies of quantum levels without possessing the knowledge of normalizing constants of the wave functions. The obtained potential shapes are often too complicated to be produced by means of even very advanced technique such as MBE. It turns out however, that, reconstructed in this way, potential shape can be substituted by some approximation (say, step-like approximation), and thus the output spectrum obtained by the direct solving of corresponding Schrödinger equation with such approximated potential differs only slightly from the input one. This is the consequence of the simple fact that direct problem in most of the cases is well-posed problem, while the inverse problem of potential reconstruction is ill-posed. We illustrated developed approach by various numerical results. In our opinion, it can be used in many practical applications, for instance, developing the new electronic devices such as tunable THz detectors, as well as many others.
Acknowledgments
The authors are greatly acknowledged to Prof. J. Łusakowski of Warsaw University and to Prof. R. Hryniv of University of Rzeszow for fruitful discussions and valuable comments.
This work was done due to support from the Centre for Innovation and Transfer of Natural Sciences and Engineering Knowledge at the University of Rzeszow.
REFERENCES
- V. Milanović and Z. Ikonić, “Optimization of Nonlinear Optical Rectification in Semiconductor Quantum Wells Using the Inverse Spectral Theory,” Solid State Community, Vol. 104, No. 8, 1997, pp. 445-450. http://dx.doi.org/10.1016/S0038-1098(97)00396-7
- I. Tralle and G. Petrov, “On the Semiconductor Well Engineering,” Molecular Physics Reports, Vol. 23, 1999, pp. 199-202.
- S. Tomić, V. Milanović and Z. Ikonić, “Quantum Well Shape Tailoring via Inverse Spectral Theory: Optimizing Resonant Second-Harmonic Generation,” Journal of Physics: Condensed Matter, Vol. 10, No. 29, 1998, pp. 6523- 6532. http://dx.doi.org/10.1088/0953-8984/10/29/012
- D. Bessis and G. A. Mezincescu, “Design of Semiconductor Heterostructures with Preset Electron Reflectance by Inverse Scattering Techniques,” Microelectronics Journal, Vol. 30, No. 10, 1999, pp. 953-974. http://dx.doi.org/10.1016/S0026-2692(99)00059-2
- A. A. Suzko and I. Tralle, “Reconstruction of Quantum Well Potentials via the Intertwining Operator Technique,” Acta Physica Polonica B, Vol. 39, No. 3, 2008, pp. 545- 567.
- S. A. Sofianos, G. J. Rampho, H. A. Donfack, I. E. Lagaris and H. Leeb, “Design of Quantum Filters with Pre-Determined Reflection and Transmission Properties,” Microelectronics Journal, Vol. 38, No. 2, 2007, pp. 235-244. http://dx.doi.org/10.1016/j.mejo.2006.11.006
- T. Wojtowicz, G. Karczewski and J. Kossut, “Excitons in Novel Diluted Magnetic Semiconductor Quantum Structures,” Thin Solid Films, Vol. 306, No. 2, 1997, pp. 271- 282. http://dx.doi.org/10.1016/S0040-6090(97)00284-8
- K. Kowalik, A. Kudelski, J. A. Gaj, T. Wojtowicz, O. Krebs and P. Voisin, “In-Plane Optical Anisotropy of Parabolic and Half-Parabolic Cd1-xMnxTe Quantum Wells,” Solid State Community, Vol. 126, No. 8, 2003, pp. 467- 471. http://dx.doi.org/10.1016/S0038-1098(03)00190-X
- B. M. Levitan and M. G. Gasymov, “Determination of Differential Equation by Two of Its Spectra,” Russian Mathematical Surveys, Vol. 19, No. 2, 1964, pp. 3-63.
- B. M. Levitan, “Inverse Sturm-Liouville Problems,” Nauka, Moscow, 1984.
- H. B. Thacker, C. Quigg and J. L. Rosner, “Inverse Scattering Problem for Quarkonium Systems,” Physical Review D, Vol. 18, No. 1, 1978, pp. 274-287. http://dx.doi.org/10.1103/PhysRevD.18.274
- J. F. Schonefeld, W. Kwong, J. L. Rosner, C. Quigg and H. B. Thacker, “On the Convergence of Reflectionless Approximations to Confining Potentials,” Annals of Physics, Vol. 128, No. 1, 1980, pp. 1-28. http://dx.doi.org/10.1016/0003-4916(80)90055-X
- I. M. Gel’fand and B. M. Levitan, “On the Determination of a Differential Equation from Its Spectrum Function Izv. Akad. Nauk SSSR Ser. Mat.,” Vol. 15, No. 4, 1951, pp. 309-360.
- V. A. Marchenko, “Spectral Theory of Sturm-Liouville Operators,” Nauk. Dumka, Kiev, 1972.
- B. N. Zakhariev and A. A. Suzko, “Direct and Inverse Problems. Potentials in Quantum Scattering,” Springer-Verlag, Berlin, 1990.
- Z. S. Agranovich and V. A. Marchenko, “Sturm-Liouville Operators and Their Applications,” Nauk. Dumka, Kiev, 1977.
- J. Hadamard, “Le Probleme de Cauchy et les Équations aux Derives Partiels Linéaires Hyperboliques,” Hermann, Paris, 1932.
- A. N. Tikhonov and V. Ya. Arsenin, “Methods of Solution of Ill-Posed Problems,” Nauka, Moscow, 1979.
- A. M. Tomlinson, C. C. Chang, R. J. Stone, R. J. Nicholas, A. M. Fox, M. A. Pate and C. T. Foxon, “Intersubband Transitions in GaAs Coupled-Quantum-Wells for Use as a Tunable Detector at THz Frequencies,” Applied Physics Letters, Vol. 76, No. 12, 2000, pp. 1579-1581. http://dx.doi.org/10.1063/1.126101