World Journal of Condensed Matter Physics
Vol.2 No.4(2012), Article ID:24477,4 pages DOI:10.4236/wjcmp.2012.24031
Magnetic-Field Effects on Donor Impurity States in a Quantum Well
![]()
1Kuang-Chi Institute of Advanced Technology, Shenzhen, China; 2Department of Applied Mathematics, Donbass State Engineering Academy, Kramatorsk, Ukraine.
Email: qulaser@gmail.com
Received June 7th, 2012; revised July 10th, 2012; accepted July 23rd, 2012
Keywords: Quantum Well; Impurity; Binding Energy; Magnetic Field
ABSTRACT
Green’s function technique is used to obtain the solution of Shredinger equation for impurity states in a quantum well (QW) under the magnetic field. Binding energy of impurity states is defined as poles of the wave function. We studied effects of the magnetic field magnitude and impurity position on the binding energy. The calculations were performed for both ground and excited states. The dependences of binding energies versus impurity position and magnetic field are presented for GaAs/Al0.3Ga0.7As QW.
1. Introduction
Since Bastard calculated [1] the impurity binding energy in QW for the very first time many works on this subject have been published. Their main purpose is to determine the binding energy of impurity states. By changing this important parameter, for instance by external fields, it is possible to control the free carrier’s concentration, and thus affect many physical properties of the structure: low-temperature behavior of the kinetic characteristics, the type of conductivity, electronic mobility, optical properties.
This paper is devoted to the investigations of the magnetic field effects on shallow impurity states (IS) in semiconductor quantum well. Variational techniques [1-5] are most frequently used for this aim. But it is necessary to note that the accuracy of the variational method cannot be estimated. Besides, most of variational calculations are restricted by weak-field and strong-field cases. In [6] the numerical method is used for finding the solution for wave function (WF) as expansion on plane wave basis. Then the problem is reduced to a task of determination of eigen vectors (envelope functions) and eigen values (binding energy) of rather large matrices. An alternative nonvariational method to calculate the binding energy of impurity states in a QW was developed in [7]. The electron wave function was constructed through the Green’s function of corresponding Schredinger equation. Similar scheme is used in the present paper. Our method allowed to receive the binding energy and wave functions of IS in a QW under magnetic field of arbitrary strength. Also, the presented method led to recalculation of results for QW levels in a magnetic field. We used our method for various impurity location and values of magnetic fields in GaAs/Al0.3Ga0.7As QW.
2. Theoretical Background
To calculate wave functions and binding energy of impurity states in a QW under magnetic field we need to solve the appropriate Shredinger equation. Then for energy gap (below the first QW level) we will receive the solution describing localized impurity states. Impurity states belonging to the second and higher QW levels are in the continuum and, therefore, resonant. In this case the solutions of Shredinger equation will correspond to a superposition of impurity and free electron states. And as a result we have band structures and wave functions modified by impurity potential [8]. Positions of impurity states, which are on the background of the continuum, can be defined as the poles of the WF. This approach is implemented in the present work.
Within the framework of an effective-mass approximation, the Hamiltonian in the presence of a magnetic field B that is perpendicular to the plane of a QW can be written as
 (1)
(1)
where m^(m||) are the transverse (longitudinal) electron masses,

Coulomb interaction between an electron and the impurity ion, V(z): Square-well confinement potential, e: Unit charge, k: Permittivity, k0: Dielectric constant, z0: Position of impurity atom.
The origin of coordinates in the plane of QW coincides with the position of the impurity (the growth axis of QW is taken as the z axis). Cylindrical coordinates are used: (R, q, z) are the distances and angle describing the position of an electron.
Because of the axial symmetry of the system, angular momentum projection onto the z axis is conserved Lz = h m (m = 0, ±1, ±2,··· (Magnetic quantum number)), and their eigen functions exp(imz) determine the dependence of the unknown electron wave function versus an angle q: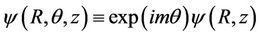 . Solving the one-dimensional Schrödinger equation
. Solving the one-dimensional Schrödinger equation
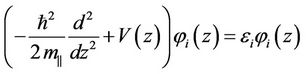
we get the basis for an expansion of the WF:
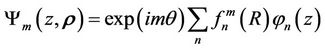 (2)
(2)
Substituting (2) in (1), we obtain a system of differential equations.
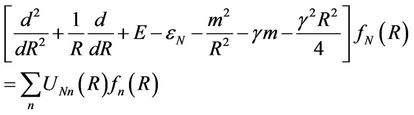 (3)
(3)
where .
.
In (3) we use dimensionless variables, introduced as units of distance (Bohr radius ab), energy (Rydberg R*) and measure of the magnetic field respectively
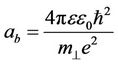 ,
, 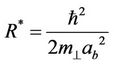 ,
, 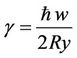
where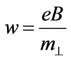 —frequencies.
—frequencies.
To construct the solutions of (3) we introduce the Green’s function GN(R, R') via the equation

Thus the expression for fN(R) can be written as
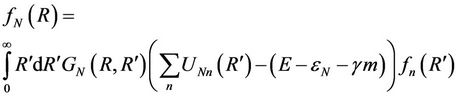 (4)
(4)
The Green’s function GN(R, R′) is given by

where I, K are the standard Bessel function of order m/2.
The Green’s function can be written directly for the left part of Equation (3). In this case it would dependent on the energy and would have different formulas for the gap and continuum (see for example [7]). From this point of view the above presented expressions have their own advantages: The Green function has an identical kind for all energy range; by equating the impurity potential to zero we can receive the solution for magnetic subbands.
The integrand in (4) is a decreasing function of distance R, so that for sufficiently large R the integral can be cut at some value Rmax and replaced by the finite sum
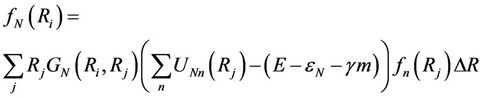 (5)
(5)
where j is the number of equidistant pieces of length DR on the interval [0, Rmax].
Expression (5) can be rewritten as

where the operator A presents the matrix, whose terms are defined as

Unlike the work [6] energy here is not eigenvalue of the matrix, but is a parameter on which the matrix elements depend.
The determinant of matrix A should be equal to zero for the existence of the solution of the system (5):
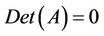 (6)
(6)
The solution of the Equation (6) allows finding the impurity binding energy for various impurity location and values of the magnetic fields.
3. Discussion
The impurity binding energy was calculated for GaAs/ Al0.3Ga0.7As QW of width d = 125A. Such structure has been calculated by R. Chen et al. [5]. This means that we can compare our results with those obtained in that work.
We used the values dR = 0.1 and Rmax = 10 in the calculations. The increase of Rmax and (or) change of dR did not change the result. In general a change in the result with a change of calculation parameters is determined by the oscillations of the Bessel functions. The argument of Bessel’s function (gR2) predicts that as a magnetic field increases n times the value of Rmax should increase 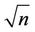 times. Taking into account the fact that the values of magnetic fields generally used in the experiments are more than 1 Тesla, for which the result is steady at Rmax = 10, such situation is not seen as critical. Let us notice, that the similar situation is observed in a plane wave basis expansion method [6], however this method operates with a larger matrix, whose size is 20 times more than in the present works. Therefore, the presented method will be more effective for the cases of small magnetic fields.
times. Taking into account the fact that the values of magnetic fields generally used in the experiments are more than 1 Тesla, for which the result is steady at Rmax = 10, such situation is not seen as critical. Let us notice, that the similar situation is observed in a plane wave basis expansion method [6], however this method operates with a larger matrix, whose size is 20 times more than in the present works. Therefore, the presented method will be more effective for the cases of small magnetic fields.
The comparison between the results of the present work and [5] is shown in Figure 1. As it is seen they are in qualitative and quantitative agreement.
The position of the impurity states for the case of edge doping is also shown.
A well known Coulomb expression tells us about the inverse relationship between charge energy interactions and distance. Since the maximum of the electron wave function at the first QW level is in the center, then the offset of the impurity atom to the edge will increase a distance between the ion and the electron, and thus the binding energy will decrease (as it is seen in Figure 1 for the states m = 0). However, the binding energy of the excited states is reduced slightly when impurity atom move to the edge. The thing is that the maximum of the wave functions for excited states is shifted from the center both along the z-axis and the xy-plane. Therefore the displacement of the impurity atom only along the z axis, within the width of QW, has no essential effect on the binding energy.
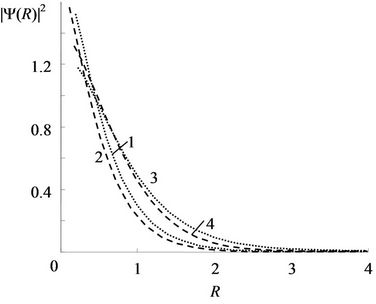
The increase of a magnetic field increases the localization of impurity wave function (Figure 2). The effect is negligible for the ground state, and clearly exhibits itself for the excited state. This is not surprising since the electron WF in a QW under magnetic field is described by the factor , which will be essential especially for excited states, as they have a maximum for large r.
, which will be essential especially for excited states, as they have a maximum for large r.
4. Conclusions
In conclusion, Green’s function technique is used to obtain the solution of Schrödinger equation for impurity states in a square QW under magnetic field. Results of our calculations are in agreement with the data of other authors. We studied the effects of the impurity position
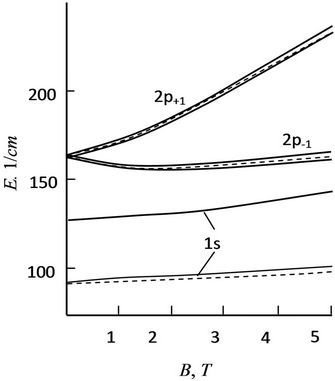
Figure 1. Impurity binding energy as function of applied magnetic field B. Solid line—present work; dashed—[5]. For the same states the lower curves (as well as dashed lines) refer to the case of doping in the center, top—to the edge of QW.
 (a)
(a)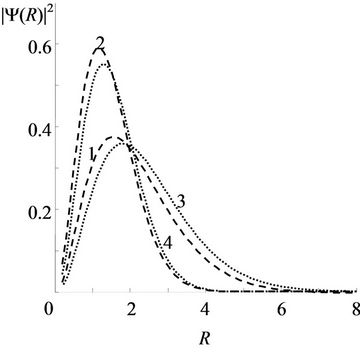 (b)
(b)
Figure 2. (a) Probability density |Y(R)|2 for donor state m = 0 in QW as a function of applied magnetic field B and impurity location z0. B(T): 1,3 – 1; 2,4 – 5; z0: 1,2 – 0; 3,4 – 1.0; (b) As for (a) but for a state m = –1.
and magnitude of magnetic field on the binding energy. A displacement of the impurity atom from the center to the edge has a different effect on the ground and excited states. The binding energy of the ground state reduces significantly, while for the excited states it changes insignificantly. The increase of the magnetic field increases the space localization of the wave functions.
Our method does not depend on either additional parameters or physical assumptions; it allows taking into account other QW subbands, demonstrating stable and steady results at the increase or change of calculation parameters Rmax and dR.
5. Acknowledgements
This work was supported in part by the Russian-Ukrainian project grant 06-02-12 (U) and by grants from the project of Introducing Innovation Research Team by Guangdong Province No. CXB 2011092 10101A, CXB 2011092 10103A.
REFERENCES
- R. L. Green and K. K. Bajaj, “Effect of Magnetic Field on the Energy Levels of a Hydrogenic Impurity Center in GaAs/Ga1−xAlxAs Quantum-Well Structures,” Physical Review B, Vol. 31, No. 2, 1985, pp. 913-918. doi:10.1103/PhysRevB.31.913
- N. Nguen, J. X. Zang, R. Ranganathan, B. D. McCombe and M. L. Rustgi, “Energy Levels of a Hydrogenic Impurity in GaAs/Ga1−xAlxAs Multiple-Quantum-Well Structures with Narrow Barriers in a Magnetic Field,” Physical Review B, Vol. 48, No. 19, 1993, pp. 14226-14231. doi:10.1103/PhysRevB.48.14226
- D. M. Larsen, “Excited States of Donors in Quantum Wells in a Magnetic Field,” Physical Review B, Vol. 44, No. 11, 1991, pp. 5629-5634. doi:10.1103/PhysRevB.44.5629
- G. Brozak, B. D. Mccombe, D. M. Larsen, “Potential and Magnetic Field Confinement of Shallow Donor Impurities in Semiconductor Quantum Wells,” Physical Review B, Vol. 40, No. 2, 1989, pp. 1265-1270. doi:10.1103/PhysRevB.40.1265
- R. Chen, J. P. Cheng, D. L. Lin, B. D. McCombe and T. F. George, “Excited States of Hydrogenic Impurities in Quantum Wells in Magnetic Fields,” Journal of Physics: Condensed Matter, Vol. 7, No. 18, 1995, p. 3577. doi:10.1088/0953-8984/7/18/021
- V. Ya Aleshkin and L. V. Gavrilenko, “Calculation of the States of Shallow Donors in Quantum Wells in a Magnetic Field Using Plane Wave Expansion,” Semiconductors, Vol. 39, No. 1, 2005, pp. 54-57. doi:10.1134/1.1852645
- A. A. Abramov, “Resonant Donor States in Quantum Well,” Modern Physics Letters B, Vol. 25, No. 2, 2011, p. 89. doi:10.1142/S0217984911025493
- A. A. Abramov, Y. G. Belichenko and V. N. Tulupenko, “The Influence of the Ionized Impurity Delta-Layer Potential in the Quantum Well on Impurity Binding Energy,” Journal of Applied Physics, Vol. 109, No. 7, 2011, Article ID: 064303. http://jap.aip.org/resource/1/japiau/v109/i6/p064303_s1?bypassSSO=1

