Soft Nanoscience Letters
Vol. 3 No. 3 (2013) , Article ID: 34635 , 10 pages DOI:10.4236/snl.2013.33011
Structure and Mechanical Behavior of Cellulose Nanofiber and Micro-Fibrils by Molecular Dynamics Simulation
![]()
1Department of Mechanical Engineering, Faculty of Engineering Science, Kansai University, Suita, Japan; 2KYOCERA Corporation, Kyoto, Japan.
Email: saitou@kansai-u.ac.jp
Copyright © 2013 Ken-ichi Saitoh et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 30th, 2013, revised May 3rd, 2013; accepted May 12th, 2013
Keywords: Cellulose; Nanofiber; Molecular Dynamics; Wiredrawing; Mechanical Properties; Biomaterial; Twist Angle
ABSTRACT
Cellulose nanofiber (CNF) and CNF micro-fibrils (CNF-MFs) are computationally modeled by molecular dynamics with united atom (UA) methodology of polymers. Structural stability and mechanical properties of these materials are focused on. Diffusion coefficient decreases with increase of the number of shells in CNF-MF. The structure of CNF-MFs with crystalline alignment is totally stabilized with twist which is an accumulation of torsion angles at Glycosidic bonds between monomers inside CNFs. Unique fiber drawing simulation, where a single CNF fiber is taken out of CNF-MF structure, is first conducted. The CNF fiber which is drawn out stretches up to relatively large strain, with linear increase of tensile stress. The computation results show that, the larger the number of shell structure of CNF-MF is, the larger the stretch and the stress of drawn fibers are.
1. Introduction
Cellulose substance is known to be the elementary constituent of plants and bacteria. As natural materials, plants, wood and tree are put in use with ecological benefit. A basic element of cellulose substances is a small molecular chain which is composed of many pieces of a nano-sized structure of “cellulose monomer”. As the second leveled structure of cellulose molecules, cellulose micro-fibril (MF) is constructed [1]. It is interesting from mechanical engineering viewpoint that, even though plants, tree and wood are natural biomass, they are basically made up of this single unit like synthetic polymers. Excellent application in engineering will be realized in the future by these natural materials, together with development of complicated hierarchical structures along the size scale [2].
Recently, exploration of cellulose nanofiber (CNF) has been developed as a new material. Some engineers are proposing that CNF may be made into an optically transparent sheet [3] and new type of composite [4]. It is supposed that strength and toughness required for these new materials will be realized by optimized design of CNF from nano-scale. However, since CNF is too small to be observed experimentally, it is expected that theoretical and computational modeling and simulation will provide in advance much insight and information for unknown material properties of CNF. By analyzing CNF with computational methodology, we can also approach general structure, behavior and property of other nano-scale fibers with only the atomic or molecular size. Examples will be found in “collagen” fibers [5] in animals’ hard-tissue, or inorganic “nanowire” made of metallic elements (e.g. gold nanowire [6] and magnesium nanowire [7]) or semiconductor elements (e.g. silicon/carbon nanotube and nanowire [8]). In fact, the mechanical behavior and useful properties of these nano-sized materials have to be clarified more.
In plants, tree or wood, microscopically cellulose molecules form CNF micro-fibrils (CNF-MFs), their sizes range from several tens nanometer in a diameter. Strictly speaking, detailed structure of a fibril depends on the kind of cellulose in natural species. However, it has already clarified that these CNF-MFs are essentially constructed from a bundle gathering chain molecules which orient with parallel alignment. In some experiments, a CNF-MF can be chemically separated out from cellulose material and is observed to have almost the same unit as a natural CNF-MF.
In order to acquire mechanical properties and behavior of CNF or CNF-MF, computational modeling and simulation of the material are worthwhile studying and will be necessary for future development of this field. In this paper, we should study on molecular dynamics (MD) modeling of CNF and are about to start to link the modeling to macroscopic behavior.
In microscopic scale, as stated above, cellulose molecule is constructed from a monomer, which is called β-D-glucose. The all-atom (AA) model of β-D-glucose and its polymerization have been considered [9]. There are intra-molecule bonding as well as hydrogen bonding and van-der-Waals bonding (intermolecular interactions). The AA model is certainly more precise, but in order to obtain dynamic behavior of molecule, we should use more coarse-grained modeling such as united atom (UA) method for polymer structure. MD studies of bulk structure have been done for Cellulose I [10] and Cellulose II [11], but any CNF-MF model, to our knowledge, has not calculated yet. In this paper, we are originally developing a new UA model of CNF and are utilizing it to the MD simulation of CNF-MFs.
The purpose of this study is to clarify the mechanical behavior, such as deformation and strength, of CNF and CNF-MF. In particular, we will discuss the stability of CNF-MFs depending on shell (crystalline) structure, and will evaluate the durability of a single fiber by a unique fiber drawing (wiredrawing) test. These studies will contribute to the future development in the field of upcoming CNF-related research, in which experimental facts are somewhat relying on computational predictions. It is supposed by the authors that the simulation is advantageous in making theoretical insight and in predicting unknown behavior of CNF and CNF-MFs.
The present paper is organized as follows. In the following section, we explain about the atomistic modeling of CNF and provide its verification. Then, the results on stability of CNF-MFs, and their tensile (fiber drawing) testing of CNF-MF structures are shown. These results are discussed, and then conclusion is made.
2. Theory and Method
2.1. Microscopic Structure of Cellulose Molecule
CNF is the elementary structure which is basis for all cellulose-originated materials, such as paper, plants and trees. The monomer structure of cellulose molecule has already been theoretically predicted as shown in Figure 1. A lot of cellulose monomers are polymerized and become a fiber with long chain shape. Then, these chains form a micro-fibril (CNF-MF), which usually has a crystalline structure and is recognized as higher-order struc-

Figure 1. All-Atom (AA) model of cellulose molecule.
ture when cellulose molecules are growing and aggregating. However, crystalline state of cellulose is likely to present many polymorphs. For example, there exist cellulose I-IV, or cellulose I-α and I-β, and so on [1]. In constructing a theoretical model, we downscale our view into ultimate (the smallest) scale of the material, where a cellulose exists as a single fiber (one molecule). Then, a theoretical model of CNF-MF is built up as an aggregation of these molecules with some crystalline alignment.
The atomic conformation of cellulose monomer is shown in Figure 1. Two identical hydrocarbon groups, called β-D-glucoses, are linked each other and compose an unit of cellulose. Carbon (C) atoms are in six-membered ring of each glucose group, but they are not in the same plane and they show a “chair-shaped” coordination. Being linked each other by common oxygen (O) atom (ester bond), glucose groups are polymerized into a large polymer.
Each molecule is interacting mainly by hydrogen bonding. Consequently, many molecules are aligned in the same direction to be packed into a crystal structure. The famous crystal model is called Meyer-Misch type, which presents three-dimensional monoclinic or triclinic crystal unit [12]. Since monomers are arranged in the “chair-shaped” configuration, as shown in Figure 1, a long molecule seems to be naturally parallel to adjacent one, accompanied by slight displacement in longitudinal direction. However, the detailed three-dimensional structure of CNF-MF has not been completely deterred mined yet.
2.2. United Atom Modeling of Cellulose Molecule
In this paper, we use a coarse graining methodology in molecular modeling. Since usually in MD simulations, only the limited number of atoms can be calculated mainly due to the limitation of computer resources now available. Therefore, many coarse-graining methods, such as UA method [13] and coarse-grained MD (CGMD) [14], have been proposed in molecular modeling. In this study, the UA method is adopted for the modeling of cellulose molecules.
However, as for potential function, we should rely on full version of interatomic interactions inside cellulose molecule. The well-established and reliable interaction theory and data are found in CHARMM (Chemistry at HARvard Macromolecular Mechanics) force field [15], and we can adopt it to the AA model. The detail of the AA model can be referred in [9], omitting here. The present UA model is useful because it can provide mechanical properties of CNF and CNF-MFs which are comparable to those produced by more precise AA model. Based on the AA model of cellulose monomer shown in Figure 1, the UA model of cellulose monomer is constructed as shown in Figure 2, here. Since H atom is relatively light weight, atomic groups, CH, CH2 and OH, which are taking H atoms inside, are defined as a single particle as well as an O atom. Both these atomic groups and single atom are called united atom (UA). The number of UAs in the cellulose monomer is reduced to 22, from 44 in AA model. UAs are positioned at the point of center atom (C or O) of each. Geometrical parameters are shown in Table 1. The potential function and parameters for UAs are summarized in Tables 2-6, respectively. (These tables are including the potential function form used there.)

Figure 2. United-Atom (UA) model for cellulose molecule.

Table 1. Parameters of united atom (UA) model.
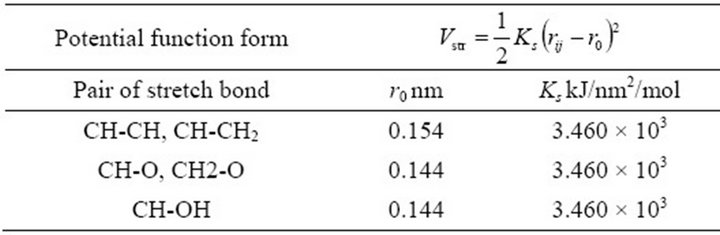
Table 2. Stretch potential (for UA model).

Table 3. Bending potential (for UA model).
Electric charge of H is included in UA (for example, when electric charges are C = α and H = β in AA model, then the electric charge of the resulted UA (CH2) becomes α + 2β), so that total charge of the monomer is equivalent between AA and UA models. Note that the polarization of electric charge (electric moment) is not considered in the present model. By using this UA model, almost the same energy and conformation of monomer as the AA model is obtained in equilibrium condition.
The reason why the present UA model will be effectively utilized as an approximation of the AA model is that, though vibration behavior of cellulose monomer is not completely identical, but it is comparable. This is verified by normal mode analysis (NMA) performed for cellulose monomer. In NMA, by assuming harmonic vibration around the energy minimum of each atomic motion, set of eigenvalue and amplitude of atomic vibration (normal modes) are calculated [16].
Figure 3 is the results of root mean square (RMS) value obtained by NMA, comparing between AA model (42 atoms) and UA model (22 UAs). In AA model, only atoms corresponding to UA model (except H) are observed. Since straight solid line depicted on the graph shows the 1:1 ratio for AA and UA models, it is found that AA model slightly tends to show larger amplitude for atomic vibration. This tendency is typically observed in lower temperature like 200 Kelvin. However, for 300 Kelvin or larger, some atoms vibrate with wider range of fluctuation for both models and they seem to result in almost identical vibration. It is concluded that, as for atomic vibration, the present UA model is sufficient to be used as approximation of AA model.
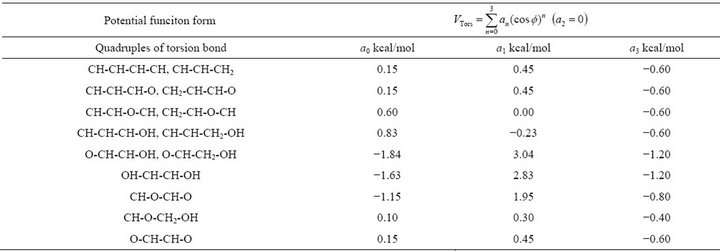
Table 4. Torsion potential (for UA model).

Table 5. Electrostatic potential (for UA model).

Table 6. Buckingham potential (for UA model).
2.3. Calculation Model and Condition: Computation Model of CNF and CNF-MFs
As explained above, cellulose monomers are polymerized and become a long chain structure called CNF. The polymerization in CNF is carried out by oxygen bridging with a firm covalent bond. When these CNFs aggregate, van-der-Waals and electrostatic (Coulomb) forces play an important role, though these forces produce mechanically weak and breakable bonding. Generally speaking, crystal alignment called Meyer-Misch structure is ob-
 (a)
(a) (b)
(b)
Figure 3. Comparison of RMS between AA and UA models. (a) 200 K. (b) 300 K.
tained [12]. The crystal shows parallelogram unit in cross section as shown in Figure 4, and its lattice constants are reported a = 0.735 nm and b = 0.835 nm [17]. Besides, these CNFs are bundled and are made into a fibril structure.
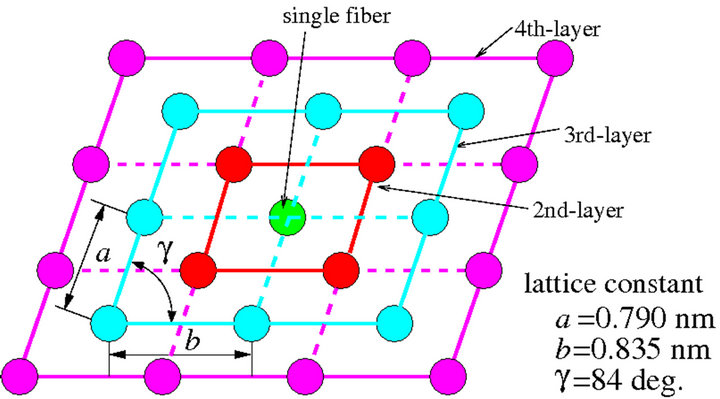
Figure 4. Meyer-Misch crystalline structure of cellulose nanofiber micro-fibrils (CNF-MFs).
The aspect ratio (length/diameter) of CNF-MF is chosen around 100 in our model, so accordingly each single polymer molecule should be composed of 30 monomers. In our model, at the core of the crystal, a molecular chain is primarily placed. And then molecular chains, in 2nd-layer, 3rd-layer, ..., are sequentially located in a parallel fashion so as to cover the centered fiber. The number of molecules are 5 up to 2nd-layer, 13 up to 3rd-layer and 25 up to 4th-layer. It is true that the structural stability of CNF-MF depends on length of polymers, but our models are using the same molecular length and the present study are focusing on the effect of shell structures. Figure 5 and Table 7 show structural parameters and properties of computation models of CNF and CNF-MFs.
3. Results and Discussions
3.1. Structural Stability of CNF-MFs
3.1.1. Evaluation of Diffusivity by MSD
Atomic diffusivity in a molecule can be estimated from mean square displacement (MSD) of each atomic (UA) members. When molecules are moving, MSD is directly monitored from atomic displacement which is difference between the reference position  and the current position
and the current position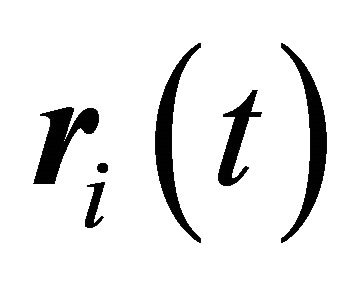 , by taking into account displacement of the center of mass of the molecule
, by taking into account displacement of the center of mass of the molecule 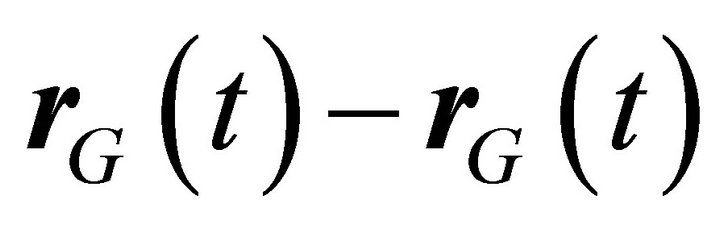 as,
as,
 (1)
(1)
where t0 is the time of origin. The MSD is directly obtained from MD calculation with the condition as shown in Table 8.
According to Einstein’s law, time ratio of increase of MSD is in proportion to diffusion coefficient D [18]. That is,
 (2)
(2)
where Nmolecule is the number of molecules in a CNF-MF. The result is shown in Figure 6. Plots of D in each struc-
 (a)
(a) (b)
(b)
Figure 5. Cellulose nanofiber (CNF) and micro-fibril (CNF-MF) models by United Atom method for MD.
tures can be approximated by straight line, which means that D obeys the Arrhenius relation. The linear relation is, above all, realized for single fiber. To the contrary, in the shell-structured like 2-layered or 3-layered CNF-MF, atoms in an inside molecule are restrained by forces exerted from atoms in surrounding molecules. Consequently, diffusivity of shell-structured CNF-MF is smaller than that of the single fiber. This means that CNF-MF is more structurally stable than single CNF fiber at the same condition.
3.1.2. Twisted Structure of CNF-MF Observed in Structural Relaxation
Here, we would like to investigate on twisted structure found in relaxed CNF-MF. Figure 7 shows structural change of CNF single fiber and CNF-MFs (2-, 3- and 4-layered). Since these CNF-MFs are not constrained at both ends, their atoms move freely and they prone to be curled up into a lump. This tendency is remarkable for single fiber and lower-layered CNF-MF. This behavior is induced by atomic diffusion inside molecule, discussed above. Theoretically speaking, it is understood that conformational entropy of molecules should decrease by aggregation and condensation. By observing equilibrium molecular configuration, conformational entropy seems to be lower with increase of the number of layers in CNF-MFs. It also means that intermolecular interaction plays an important role for stabilization of layered fibrils. Especially for closed-packed crystalline structure of molecules, such as Meyer-Misch type applied in our model, the whole layered structure becomes stable since

Table 7. The structural properties of CNF fiber and CNF-MF models.

Table 8. Calculation conditions for obtaining MSD and diffusion simulation.

Figure 6. Diffusion coefficient of atoms (UAs) in CNF and CNF-MFs.
intermolecular force is strong between molecules.
As atomic configuration (in Figure 7) is viewed in longitudinal direction, it is discovered that CNF-MFs are twisted from one end to another end. Although initial twist angle of molecule is zero, molecule has been collectively twisted and stabilized during structural relaxation process. This twist is caused by finding the energetically lowest configuration among molecules. The total twist angle averaged over all molecules is around 15 - 17 degrees, which is obtained by accumulating atomic twist angle at every glycosidic (glucose-O-glucose) bond. The specific twist angle θ’ = θ/l comes to be approximately 0.5 degree per 1 nm of molecule, where θ is total
 (a)
(a) (b)
(b) (c)
(c)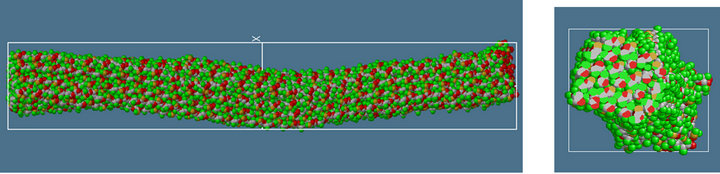 (d)
(d)
Figure 7. Atomic and molecular configuration of CNF and CNF-MFs (after structural relaxation for 40 ps, at constant temperature of 10 Kelvin.). (a) single CNF (side view), cross-section; (b) 2-layered CNF-MF (side view), cross-section; (c) 3-layered CNF-MF (side view), cross-section; (d) 4-layered CNF-MF (side view), cross-section.
twist angle (averaged) and l is length of molecule. Figure 8 shows the time change of θ during structural relaxation of the 2-layered. It shows that twist of molecules occurs in the early stage of relaxation and then that twist is retained with just a slight fluctuation.
3.2. Mechanical Behavior of CNF-MF
3.2.1. Fiber Drawing Test for CNF-MF Models
In order to investigate the strength and deformation of CNF-MF, we conduct a unique testing, in which a centered single fiber is drawn out from other molecules forming fibril shells. This fiber drawing test is motivated,

Figure 8. Time transition of twist angle of CNF-MF during relaxation (2-layered CNF-MF).
in reference to an existing material testing where an actual fiber (such as cotton fiber with diameter of several micrometers) is extracted from a woven textile sheet [19].
The detail of the present drawing test is as follows. As shown in Figure 9, a single cellulose molecular fiber is drawn out of shell-structured CNF-MF. The moving velocity of atoms in the end region of the fiber, which are located within the length of one monomer of cellulose, is all constrained to be v = 175 m/s. On the other hand, atoms in the other end region of the rest of CNF-MF structure are totally fixed in the space (i.e. v = 0 m/s). For example, in the case of 2-layered CNF-MF, only the centered molecule is to be pulled out of other four molecular fibers. The move velocity in MD simulation is quite high compared with usual experiment, technically because the simulation is intended to be carried out in very short duration. Therefore, the dependency on drawing velocity is still interesting and is left for further research. Drawing tests for 2-, 3- and 4-layered CNF-MFs are conducted. The calculation parameters are summarized in Table 9.
We would like to mention the reason why this type of testing is chosen here. Any molecular fiber never gets broken in stretching along fiber direction because intra-molecular potentials for stretching, bending and torsion are all made not to be broken in the present model. However, dissociation of molecules would occur easily in the lateral direction of CNF-MF, where hydrogen bonding, i.e. intermolecular potential, is responsible for molecular aggregation. Certainly, other behavior concerning fibrous material, such as tearing test of fibers into small pieces, may be interesting, but, as a mechanically simple testing, fiber drawing test is adopted here.
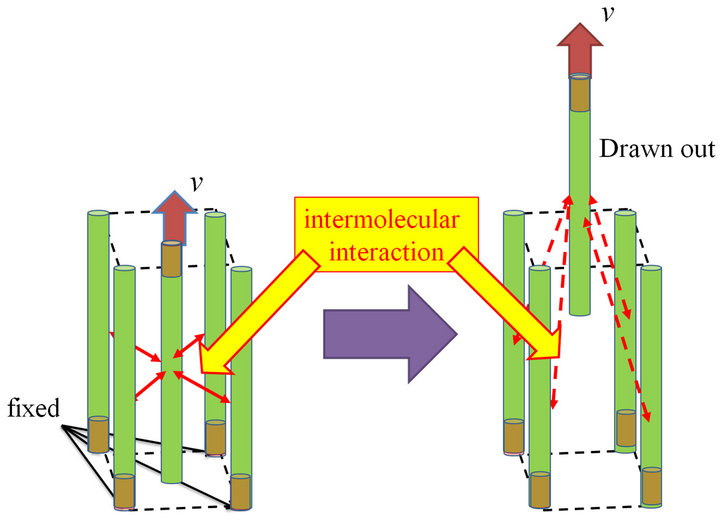
Figure 9. Schematic of fiber drawing test: a single CNF fiber is pulled out of a CNF-MF structure.

Table 9. Values for fiber drawing simulation of CNF-MFs.
3.2.2. Result of Fiber Drawing Test
Figure 10 shows examples of snapshots in the fiber drawing test for 2-layered CNF-MF. Before pulling the centered fiber, the CNF-MF structure has already curved. Pulling starts, whereas the centered fiber does not immediately come out of the CNF-MF shell until it regains an original straight shape. The centered fiber is stretched for the time being; finally it begins to be pulled out. The rest of fibers in the CNF-MF keep shell structure (a hollow shell is manufactured).
It is found that, while the centered fiber is being pulled, twist angle observed between monomers reduces from the equilibrium angle. Figure 11 shows the magnitude of the change of twist angle during drawing test. As confirmed, increase of angle is observed until the centered fiber has completely pulled out. In fact, this increase occurs so as to reduce equilibrium twist angle.
This fact suggests an interesting behavior of CNF-MF in loading. A certain twist angle is necessary for molecular fibers to be packed themselves and the twist is “stored” inside CNF-MF structure in equilibrium condition. But, when tensile force is applied to just one fiber to pull out the fiber out of the structure, the drawn fiber goes out of remaining shell structure, adjusting the twist of the structure.
Figure 12 shows stretch of the drawn fiber. Strain of the centered fiber εA and that of others εB can be defined,

Figure 10. General conformation change of CNF-MF during fiber drawing process (2-layered CNF-MF model).

Figure 11. Transition of twist angle of single fiber during drawing test.
as for longitudinal component, by
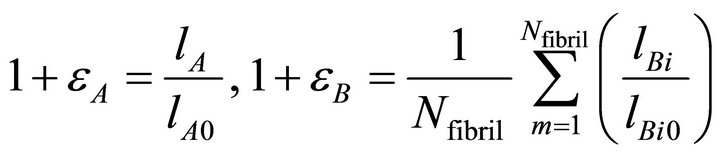 (3)
(3)
where lA and lBi are fiber lengths during drawing test, lA0 and lBi0 are those before relaxation, and Nfibril means the number of molecules in shell (s). After the system is equilibrated, molecular fibers has already shrunk slightly. As found in Figure 12, strain εA is completely in proportion to the distance moved by the end region of the drawn fiber. It is understood that friction force between the center and others acts as resistance of dissociation motion. The energy of friction (as strain energy) is given by both elasticity of the drawn fiber and molecular interaction between fibers. On the other hand, the strain of fi
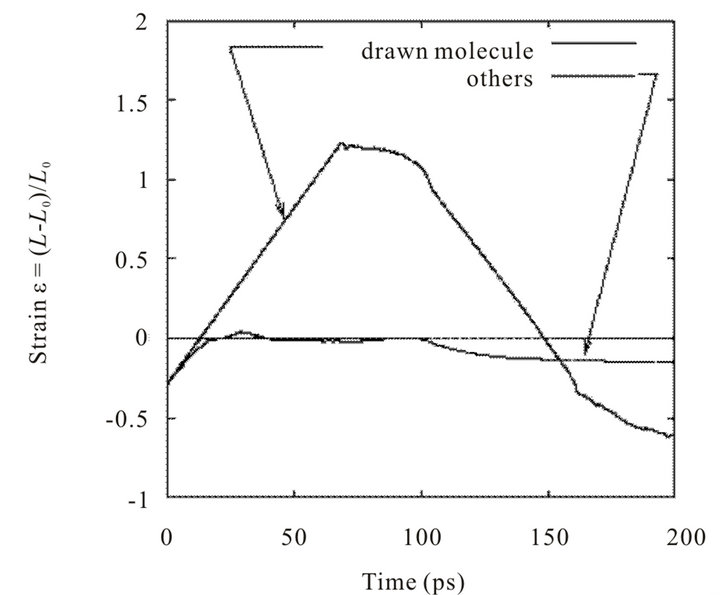
Figure 12. Elongation of CNFs (drawn fiber and others, 2-layered model).
bers in outer shell is less than 0, which means that those remaining fibers do not stretch themselves but preserve their stable length.
Comparison of elongation of fiber between 2-, 3- and 4-layered CNF-MFs is shown in Figure 13. When the number of supporting fibers in shell structures is larger, the structure becomes more stable. The graph also shows that ratio of elongation to the displacement is almost the same for all models before extraction completes. The maximum elongation is found in 4-layered CNF-MF.
The Cauchy stress is straightforwardly defined as force vector divided by its cross-section at an arbitrary body surface [20]. In the present drawing test, the tensile force Fα can be directly collected from atoms in the drawn molecule, and then the normal component of Cauchy stress σαα is calculated by
 (4)
(4)
where A is area of the cross-section. As for CNF-MF, A is estimated as an area occupied by the crystal unit as shown in Figure 4. Figure 14 shows the averaged stress during drawing test. As naturally predicted, the order of maximum stress is like: (2-layered) < (3-layered) < (4-layered). It is guessed that longitudinal stiffness of the drawn fiber is identical, but total friction force between fibers is augmented in larger CNF-MFs. This result reveals that increase of the number of shell structures leads to larger resistance to separation of a single fiber from CNF-MF structure.
4. Conclusions
In this study, structural stability and mechanical behavior of cellulose nanofiber (CNF) are investigated by using
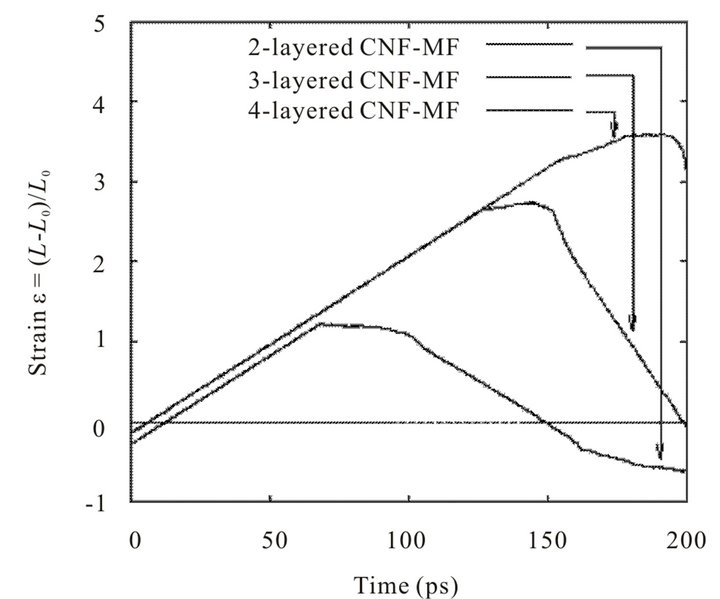
Figure 13. Elongation of CNF fiber during drawing test (comparison between 2-, 3- and 4-layered models).

Figure 14. Averaged stress in CNF-MF during fiber drawing test (comparison between 2-, 3- and 4-layered models).
molecular dynamics (MD) with united atom (UA) modeling. In particular, unique mechanical testing where the single fiber is drawn out from CNF micro-fibril (CNF-MF) is conducted and the mechanical response is observed. The following results are obtained.
1) By utilizing UA method, molecular chain model of CNF structure is made from polymerization of cellulose monomers. Potential parameters of UA are derived from all-atom (AA) model and the MD calculation can be carried out. This UA model is verified as for vibrating motion by normal mode analysis of monomers.
2) Atomic diffusion in CNF fiber and CNF-MF is basically obeys Arrhenius relation. At high temperature, the diffusion coefficient of multi-layered CNF-MF reaches that of single CNF fiber.
3) CNF-MF preserves equilibrium structure with a certain twist angle (estimation is around 16 degrees, which is accumulated at every glycoside bond).
4) In fiber drawing test, where one CNF fiber is pulled out from CNF-MF structure, the equilibrium twist angle cancels. The friction between the drawn fiber and others is large. Therefore, the larger the number of shell structures is, the larger the stretch and the stress of drawn fiber are.
5. Acknowledgements
This study is partly supported by the “Strategic Project to Support the Formation of Research Bases at Private Universities: Matching Fund Subsidy from MEXT (Ministry of Education, Culture, Sports, Science and Technology) (2012-2013)”.
REFERENCES
- D. Klemm, H. P. Schmauder and T. Heinze, “Cellulose,” In: S. De Baets, E. Vandamme and A. Steinbüchel, Eds., Biopolymers, Vol. 6, Wiley-VCH, Weinheim, 2001, pp. 275-287.
- Cellulose Gakkai, “Cellulose no Jiten,” (in Japanese) Asakura Syoten, Tokyo, 2000. pp. 219-253.
- M. Nogi, S. Iwamoto, A. N. Nakagaito and H. Yano, “Optically Transparent Nanofiber Paper,” Advanced Materials, Vol. 21, No. 16, 2009, pp. 1595-1598. doi:10.1002/adma.200803174
- T. Nishino, I. Matsuda and K. Hirao, “All-Cellulose Composite,” Macromolecules, Vol. 37, No. 20, 2004, pp. 7683-7687. doi:10.1021/ma049300h
- J. Buehler, “Nanomechanics of Collagen Fibrils under Varying Coss-Link,” Journal of the Mechanical Behavior of Biomedical Materials, Vol. 1, No. 1, 2008, pp. 59-67. doi:10.1016/j.jmbbm.2007.04.001
- Q. Pu, Y. Leng, L. Tsetseris, H. S. Park, S. T. Pantelides and P. T. Cummings, “Molecular Dynamics Simulations of Stretched Gold Nanowires: The Relative Utility of Different Semiempirical Potentials,” Journal of Chemical Physics, Vol. 126, No. 14, 2007, Article ID. 144707. doi:10.1063/1.2717162
- L. Hui and F. Pederiva, “Helical Multishell Structures of Magnesium Nanowires,” Journal of Applied Physics, Vol. 96, No. 4, 2004, pp. 2214-2220. doi:10.1063/1.1765866
- D. Li, Y. Wu, P. Kim, L. Shi, P. Yang and A. Majumdar, “Thermal Conductivity of Individual Silicon Nanowires,” Applied Physics Letters, Vol. 83, No. 14, 2003, pp. 2934- 2396. doi:10.1063/1.1616981
- S. Neyertz, A. Pizzi, A. Merlin, B. Maigret, D. Brown and X. Deglise, “A New All-Atom Force Field for Crystalline Cellulose I,” Journal of Applied Polymer Science, Vol. 78, No. 11, 2000, pp.1939-1946. doi:10.1063/1.468791
- J. F. Matthews, C. E. Skopec, P. E. Mason, P. Zuccato, R. W. Torget, J. Sugiyama, M. E. Himmel and J. W. Brady, “Computer Simulation Studies of Microcrystalline Cellulose I,” Carbohydrate Research, Vol. 341, No. 1, 2006, pp. 138-152. doi:10.1016/j.carres.2005.09.028
- H. Miyamoto, M. Umemura, T. Aoyagi, C. Yamane, K. Ueda and K. Takahashi, “Structural Reorganization of Molecular Sheets Derived from Cellulose II by Molecular Dynamics Simulations,” Carbohydrate Research, Vol. 344, No. 9, 2009, pp. 1085-1094. doi:10.1016/j.carres.2009.03.014
- K. H. Meyer and L. Misch, “Positions des Atomes Dans le Nouveau Modèle Spatial de la Cellulose,” Helvetica Chimica Acta, Vol. 20, No. 1, 1937, pp. 232-244. doi:10.1002/hlca.19370200134
- H. Fukunaga, J. Takimoto and M. Doi, “A Coarse-Graining Procedure for Flexible Polymer Chains with Bondedand Nonbonded Interactions,” Journal of Chemical Physics, Vol. 116, No. 18, 2002, pp. 8183-8190. doi:10.1063/1.1469609
- T. Kinjo and S. Hyodo, “Equation of Motion for Coarse-Grained Simulation Based on Microscopic Description,” Physical Review E, Vol. 75, No. 5, 2007, pp. 1-9. doi:10.1103/PhysRevE.75.051109
- “CHARMM force field” http://www.charmm.org/
- D. A. Pearlman , D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham III, S. DeBolt, D. Ferguson, G. Seibel and P, Kollman, “AMBER, a Package of Computer Programs for Applying Molecular Mechanics, Normal Mode Analysis, Molecular Dynamics and Free Energy Calculations to Simulate the Structural and Energetic Properties of Molecules,” Computer Physics Communications, Vol. 91, No. 1-3, 1995, pp. 1-41. doi:10.1016/0010-4655(95)00041-D
- J. Sugiyama, “Crystal Structure of Cellulose-Personal Overview of the Main Stream Idea,” Sen’i Gakkaishi, (in Japanese) Vol. 62, No. 7, 2006, pp. 183-187. doi:10.2115/fiber.62.P_183
- M. P. Allen and D. J. Tildesley, “Computer Simulation of Liquids,” Oxford University Press, Oxford, 1989.
- M. Valizadeh, S. A. H. Ravandi, M. Salimi and M. Sheikhzadeh, “Determination of Internal Mechanical Characteristics of Woven Fabrics Using the Force-balance Analysis of Yarn Pullout Test,” Journal of the Textle Institute, Vol. 99, No. 1, 2008, pp. 47-55. doi:10.1080/00405000701567712
- Y. C. Fung and P. Tong, “Classical and Computational Solid Mechanics,” World Scientific, Singapore, 2001.

