International Journal of Astronomy and Astrophysics
Vol.07 No.02(2017), Article ID:76819,21 pages
10.4236/ijaa.2017.72008
Periodic Orbits of the First Kind in the Autonomous Four-body Problem with the Case of Collision
M. R. Hassan1, Md. Aminul Hassan2, Payal Singh3, Vinay Kumar4, R. R. Thapa5
1Department of Mathematics, S. M. College, T. M. Bhagalpur University, Bhagalpur, India
2GTE, Bangalore, India
3Research Scholar, T. M. Bhagalpur University, Bhagalpur, India
4Department of Mathematics, Zakir Hussain College, University of Delhi, New Delhi, India
5Department of Mathematics, P. G. Campus, Tribhuvan University, Biratnagar, Nepal
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 1, 2017; Accepted: June 9, 2017; Published: June 12, 2017
ABSTRACT
In this manuscript, the existence of periodic orbits of collision of the first kind has been discussed on the model of Autonomous Four-body Problem by the method of analytic continuation given by Giacaglia [1] and Bhatnagar [2] [3] . For the existence of periodic orbits, Duboshin’s criterion [4] has been satisfied and it has been confirmed by analyzing the Poincare surfaces of section (PSS) [5] . Also it has been shown that the case of collision given by Levi-Civita [6] [7] is conserved by the method analytic continuation. In all sections of this manuscript, equilateral triangular configuration given by Ceccaroni and Biggs [8] has been considered. In this model, third primary of inferior mass (in comparison of the other primaries) is placed at the equilibrium point  of the R3BP.
of the R3BP.
Keywords:
Autonomous Four-Body Problem, Regularization, Periodicity, Poincare Surfaces of Section, Collision Orbit, Zero Velocity Curves

1. Introduction
We know that the four most popular methods of proving the existence of periodic orbits are:
(i) the method of analytic continuation,
(ii) the process of equating Fourier coefficients of equal frequencies,
(iii) the application of fixed point theorem given by Poincare,
(iv) the method of power series.
Giacaglia [1] used the method of analytic continuation to examine the existence of periodic orbits of collision in the Restricted Three-body Problem (R3BP). Bhatnagar [2] generalized the problem in elliptic case. The problem of Giacaglia [1] was further extended by Bhatnagar [3] in the R4BP by taking the primaries at the vertices of an equilateral triangle. With different perturbations like oblateness, triaxiality, photogravitation, Pointing-Robertson drag effects of the primaries, the existence of periodic orbits of collision in the R3BP and in the R4BP, have been studied by different authors in two and three-dimensional co-ordinate system during the period of last three decades of the 20th century but nobody established the proper mathematical model of the R4BP. Recently Ceccaroni and Biggs [8] has studied the autonomous coplanar CR4BP by taking the third primary of comparatively inferior mass at the triangular equilibrium point 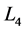 of R3BP and with an extension to low-thrust propulsion for application to the future science mission.
of R3BP and with an extension to low-thrust propulsion for application to the future science mission.
In present paper, we have proposed to study the existence of periodic orbits of first kind in the Autonomous Four-body Problem by the method of analytic continuation. By using Poincare surfaces of section (PSS), the conditions for the existence of periodic orbits given by Duboshin [4] have been confirmed. For collision case, we have applied the criterion given by Levi-Civitas [6] [7] and it is satisfied by our model.
2. Equations of Motion
Let 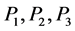 be the three massive bodies of masses
be the three massive bodies of masses 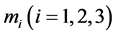 respectively, where
respectively, where 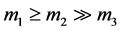 and the fourth body of mass
and the fourth body of mass 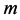 be at
be at . These bodies are moving in the same plane under some restrictions as follows:
. These bodies are moving in the same plane under some restrictions as follows:
The fourth body at  of mass
of mass  is assumed to be of infinitesimal mass not influencing the motion of
is assumed to be of infinitesimal mass not influencing the motion of  but motions of
but motions of 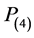 is being influenced by the motions of
is being influenced by the motions of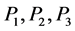 . Further, we have assumed that the mass
. Further, we have assumed that the mass 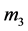 at
at 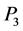 is taken small enough, so that it can’t influence the motion of the dominating primaries
is taken small enough, so that it can’t influence the motion of the dominating primaries  and
and 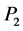 and it is placed at any one of the triangular libration points (Lagrangian Points) of the classical restricted three body problem. Since the third primary can’t influence the motions of
and it is placed at any one of the triangular libration points (Lagrangian Points) of the classical restricted three body problem. Since the third primary can’t influence the motions of  and
and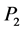 , so the centre of rotation of the system remains at the barycentre of two main primaries
, so the centre of rotation of the system remains at the barycentre of two main primaries 







Let the line joining 








Figure 1. Configuration of four-body problem.
ments of 



Let 


where 
The total gravitational force acting on 

Let 



The Equation of motion of the infinitesimal mass 

Since the synodic frame are revolving with constant angular velocity 


In cartesian form, the equations of motion of the infinitesimal mass 

Also the linear velocity of the infinitesimal mass 

If 


If mass of the infinitesimal body is supposed to be unity, then the kinetic energy of the infinitesimal mass is given by

Let 


Combination of Equations ((9) and (10)) yields

The gravitational potential of the body of mass 

then, total gravitational potential at 

The Hamiltonian of the infinitesimal body of unit mass is given by

Let 

then
The coordinates of 
Clearly










where

is the reduced Hamiltonian corresponding to canonically conjugate variables 

3. Regularization at the Singularity
In our Hamiltonian 



with

where 

Clearly,


Also,

Thus the Hamiltonian 


Let us introduce pseudo time 

Thus the regularized Hamilton-canonical equations of motion of the infinitesimal body corresponding to the Hamiltonian

where the regularized Hamiltonian 

Let us write


4. Generating Solution (i.e., Solutions When
For generating solutions, we shall choose 


where 
Since 


Putting

It may be noted that this differential equation is exactly the same as in Giacaglia [1] and Bhatnagar [2] [3] and therefore the solution of Equation (29) can be written by the method of separation of variables, as

where 
Let us introduce a new quantity 


Combination of Equations (29) and (30) yields

where


where 

From Equation (33), we conclude that for general solution; we need only two arbitrary constants as 

Let us introduce the parameters 

where 


It may be noted that for 


We introduce a parameter 

From Equations (33), (35) and (36), we get

Again from Equation (25)
Thus the equations of motion associated with 

where 

Now from 

Also 
and 
Thus from the above relations, we have

From Equation (32), we get

From Equation (30),
where

where
If we take 


From the second equation of system (41), we get the argument as

Since

hence for the problem generated by Hamiltonian 

The variables 


where 
When 


where 
The original synodic cartesian co-ordinates in a non-uniformly rotating system are obtained from Equations (18) and (20), when

The sidereal cartesian co-ordinates are obtained by considering the transformations

where 

where 
In terms of canonical variables introduced, the complete Hamiltonian may be written as

The equations of motion for the complete Hamiltonian are

Equation (49) forms the basis of a general perturbation theory for the present problem. The solution described by Equations ((44) and (45)) and is periodic if 
where 

The periods of 




5. Existence of Periodic Orbits When
Here we shall follow the method given by Chaudhary [9] to prove the existence of periodic orbits. Let 

Integrating these equations with respect to

These are the generating solutions of two-body problems. The generating solution will be periodic with the period

when 

Following Poincare [5] , the general solution in the neighbourhood of the generating solution, may be given as

where 
The necessary and sufficient conditions for the existence of periodic solution are

Restricting our solution only up to the first order infinitesimals, the equations of motion may be written as


where
Expanding 

Rejecting the second order term


and
The Equation (55) gives
Equation (45) gives

By solving the Equations (54)-(57), we can find the values of


(i)
(ii)
(iii)
where 

Now,
From Equation (43),
then

From the Equation (26)
where

Thus

Taking only zero order terms i.e., for

where
Now from equations of system (52)

and from Equation (63)
where

Here 





But 




Now choosing suitably

and
Thus,

Now,
As 
Thus,
Using Equation (65), we get
Thus the conditions for the existence of periodic orbits given by Duboshin [4] are satisfied i.e., in the region of motion of the infinitesimal body, periodic orbits exist.
6. Poincare Surfaces of Section (PSS)
In this previous section, we have shown that Duboshin’s condition [4] for the existence of periodic orbits when

together with the Jacobi Integral

To study the motion of the infinitesimal body by PSS, it is necessary to know its position 






The techniques of PSS suggest to determine the regular or chaotic nature of the trajectories. If there are smooth, well-defined island then the trajectory is likely to be regular and the islands correspond to oscillation around a periodic orbit. As the curves shrink down to a point, the points represent a periodic orbit as per Kolmogorov-Arnold-Moser (KAM) theory. Any fuzzy distribution of points in surfaces of section, implies that trajectory is chaotic. In Figure 2, for 








7. Periodic Orbits of Collision When
Levi-Civita [6] [7] proved that the invariant relation for collision orbits can be analytically continued from the one that corresponds to the problem of two bo-
Figure 2. Poincare Surface of Section for
Figure 3. Poincare Surface of Section for
Figure 4. Poincare Surface of Section for
Figure 5. Region Plot of ZVCs for
Figure 6. Contour Plot of ZVCs for
dies. Bhatnagar [2] [3] has developed this as


for sufficiently small 

Further, he has proved that, in particular, such relation is uniform integral of the differential equation of motion along any collision orbit. He has also proved this integral is a power series in terms of the distance from the origin and the series is convergent through the radius of convergence is generally small. In section (5), we have shown that periodicity is conserved by analytic continuation. Let us show that the condition of collision is also conserved by analytic continuation.
Figure 7 shows the geometrical configuration of collision orbits. In order to show the validity of that continuation, we shall consider orbits corresponding to the case when

from the origin and return to it after

where
Figure 7. Geometrical configuration of collision orbits.
Therefore, the condition of Equation (69) became,

But,

Thus from Equations ((70) and (71))

Here the Equation (71) corresponds to the Equation (68), so it is easy to say that the collision orbits exist.
8. Discussions and Conclusion
In section 1 of this paper, historical background has been sketched with original and previous contributions. In section 2, the equations of motion of the infinitesimal mass moving under the gravitational field of the three primaries situated at the vertices of an equilateral triangle taken by Ceccaroni and Biggs [8] . In this the reduced Hamiltonian 




Cite this paper
Hassan, M.R., Hassan, Md. A., Singh, P., Kumar, V. and Thapa, R.R. (2017) Periodic Orbits of the First Kind in the Autonomous Four-body Problem with the Case of Collision. International Journal of Astronomy and Astrophysics, 7, 91-111. https://doi.org/10.4236/ijaa.2017.72008
References
- 1. Giacaglia, E.O. (1967) Periodic Orbits of Collision in the Restricted Problem of Three Bodies. Astronomical Journal, 72, 386-391.
https://doi.org/10.1086/110237 - 2. Bhatnagar, K.B. (1969) Periodic Orbits of Collision in the Plane Elliptic Restricted Problem of Three Bodies. National Institute of Science India, 35A, 829-844.
- 3. Bhatnagar, K.B. (1971) Periodic Orbits of Collision in the Plane Circular Problem of Four Bodies. Indian Journal of Pure and Applied Mathematics, 2, 583-596.
- 4. Duboshin, G.N. (1964) Analytical and Qualitative Methods (Russian). Celestial Mechanics, 178-184.
- 5. Poincare, H. (1905) Lecons de Mécanique Céleste. Gauthier-Villars, Paris, 1.
- 6. Levi-Civita, T. (1903) Traiettorie singolari ed urti nel problema ristreto deri teri corpi. Annali di Mathematica Pura ed Applicata, 9, 1-32.
- 7. Levi-Civita, T. (1906) Sur la résolution qualitative du probleme restrient des trios corps. Acta Mathematica, 30, 305-327.
https://doi.org/10.1007/BF02418577 - 8. Ceccaroni, M. and Biggs, J. (2012) Low-Thrust Propulsion in a Coplanar Circular Restricted Four body Problem. Celestial Mechanics and Dynamical Astronomy, 112, 191-219.
https://doi.org/10.1007/s10569-011-9391-x - 9. Choudhry, R.K. (1966) Existence of Periodic Orbits of the Third Kind in the Elliptic Restricted Problem of the Three Bodies and the Stability of the Generating Solution. Proceedings of the National Academy of Sciences India Section A, 36, 249-264.
Definitions
Bary-Centre: It is the center of mass of two or more bodies that are orbiting each other, or the point around which they both orbit.
Synodic Co-ordinate System: The co-ordinate system, in which the xy-plane rotates in the positive direction with an angular velocity equal to that of the common velocity of one primary with respect to the other keeping the origin fixed, is called synodic co-ordinate system.
Reduced Mass: Mass ratio of the smaller primary to the total mass of the primaries or the non-dimensional mass of the smaller primary is known as reduced mass of the smaller primary.
Regularization: The process of elimination of the singularity from the force function is known as regularization.
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact ijaa@scirp.org





























































