International Journal of Astronomy and Astrophysics
Vol.06 No.04(2016), Article ID:72193,17 pages
10.4236/ijaa.2016.64032
An Advanced Multi-Band Acousto-Optical Radio-Wave Spectrometer with Multi-Channel Frequency Processing for Astrophysical Studies
Alexandre S. Shcherbakov, Miguel Chavez Dagostino, Adan Omar Arellanes*, Eduardo Tepichin
National Institute for Astrophysics, Optics and Electronics, Puebla, Mexico

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 7, 2016; Accepted: November 20, 2016; Published: November 23, 2016
ABSTRACT
We present an advanced schematic arrangement of the radio-wave spectrometer with a few parallel optical arms for processing the data flow. This arrangement includes two principal novelties. First of them consists in the proposed design, where each individual optical arm exhibits its original performances providing parallel multi-band observations within a few different scales simultaneously. These optical arms have the beam shapers providing both the needed incident light polarization and apodization to increase the dynamic range. After parallel acousto-optical processing, data flows of all the optical arms are united by the joint CCD matrix on the stage of the combined electronic data processing. The second novelty is in usage of unique wide- aperture bastron-based acousto-optical cell providing one of the best performances at the middle-frequencies (about 500 MHz) in comparison with the other available crystalline materials in this range. Such multi-band capabilities have a number of applications in astrophysical scenarios at different scales: from objects in the distant universe to planetary atmospheres in the Solar system. Thus one yields the united versatile instrument, which provides comprehensive studies of astrophysical objects simultaneously with precise synchronization in various frequency ranges.
Keywords:
Precise Acousto-Optical Spectrum Analysis, Frequency Bandwidth and Resolution, Wide-Aperture Crystalline Cell, Astronomical Instrumentation

1. Introduction
Spectroscopic techniques have been a powerful tool for investigating the physics of astronomical phenomena since its very first use in stellar classification by father Angelo Secchi in the mid-1800s. To date, this technique is used pan-chromatically. From space it has been possible to investigate the absorption and emission line spectra of highly ionized multi-electronic atoms (Fe, Si, O, Mg, Ne, etc.) whose prints appear mainly at X-ray and Extreme Ultraviolet regimes. At lower frequencies, molecular (electronic, vibrational, and rotational) transitions dominate the infrared and (sub-)millimeter spectra on a variety of celestial bodies and have been studied from the ground at the available atmospheric windows, as well as from space when the atmospheric opacity precludes ground based observations.
The analysis of spectra at radio frequencies (1 - 250 GHz) is of particular importance for the investigation of the physical and chemical properties of astronomical objects in a number of astrophysical scenarios; from studies of the high red-shift universe to planetary atmospheres in the solar system. Different astrophysical contexts require, in general, different capabilities. For instance, at large distances when extragalactic objects cannot be resolved, a rather coarse resolution (of a few 10s of MHz) is sufficient to detect the most prominent molecular emission lines (CO, HCN). In this particular frame- work, the detection of emission lines not only allows the investigation of the physical properties of the gas (such as density), but also to determine, through the wavelength displacement of the spectral lines, the red-shift of the objects and hence their distances (see, e.g. [1] ).
In the nearby extragalactic universe, the resolution requirements are more demanding, since in many cases, spectral lines are less broadened by velocity dispersion. In this intermediate scale context, some of the current investigations are focused in identifying faint molecular lines that can contribute in tracing the effects of significantly distinct environments in the star formation rate of galaxies with prominent star formation (Starbursts and Active Galactic Nuclei) [2] .
More locally, galactic studies on the gas content of star forming regions and around young and relatively mature stars require higher resolutions (of a few KHz). For these global cases the bandwidth needs are also different, although it should be mentioned that it is desirable to have the largest possible bandwidth to collect data on several molecular species simultaneously. These requirements have been nicely summarized in figure 8.12 of Ref. [3] that we reproduce here for easy reference as Figure 1. In this plot the horizontal axes provide, for a central band of 230 GHz, the required resolution in kHz (lower axis) and km/s (upper axis) for a diversity of astrophysical projects, ranging from the distant Universe, through nearby galaxies and studies of the galactic center, to hot molecular cores in star forming regions.
As indicated above, the resolution requirements increases from left to right, from about 30 MHz needed for high-z galaxies, to the very high resolution demanded by analyses of molecular gas in galactic scenarios. The necessary bandwidth for each case is depicted by the two vertical axes given in frequency and km/s units on the left and right axes, respectively. Correspondingly, the vertical and horizontal lines provide a rough indication of the resolution and bandwidth, denoted in the figure as RSB (Red- shift Search Receiver Band, see below), WB (wide band) and NB (narrow band). The
Figure 1. Demands on resolution and bandwidth by various scientific niches under development or proposed for the LMT. From the red-shift determination for primeval galaxies, with a required bandwidth (BW) of >10,000 km/s, and a resolution of δν ~ 100 km/s; through galactic surveys and high velocity sources: BW ~ 300 km/s, δν ~ 1 km/s; to the molecular analysis of Giant molecular clouds (GMC) and dark clouds: BW ~ 20 - 50 km/s, δν ~ 0.01 - 0.1 km/s. Circles and squares represent the needs at two wave bands: 1 and 3 mm, respectively. When completed, the LMT is expected to have a battery of instruments that will allow different modes: NB = narrow band mode; WB = wide band mode; RSB = redshift receiver spectrometer. The proposed AO spectrometer design would be able to simultaneously collect data at these set-ups. Figure reproduced under permission of Gopal Narayanan and Peter Schloerb university of Massachusetts at Amherst.
circles and squares indicate, respectively, these requirements for two representative wavelength bands: 1 and 3 millimeters.
In general, the different demands are fulfilled by independent instruments working at a given astronomical facility. Such is the case, for example, of the two spectrometers, the Red-shift Search Receiver (RSR) [4] , and the Second Quabin Optical Imaging Array (SEQUOIA) [5] , in use or planned for the Alfonso Serrano Large Millimeter Telescope [6] , which cover two quite different spectral resolutions and are primarily intended, respectively, for studies of distant galaxies and objects in the Milky Way. For more detail on some of the astrophysical galactic scenarios, the reader is referred to [7] and [8] , and references therein.
Whilst there are currently a number of multi-band radio wave continuum cameras in operation at different astronomical infrastructures, such as the SCUBA-2 at the James Clerk Maxwell Telescope [9] that is sensitive to 450 and 850 microns, to our knowledge there are not similar multi-frequency capabilities in spectrometers. In this paper, we present a novel optical design of a spectrometer that not only incorporates the advantages provided by the acousto-optical (AO) techniques, but allows the simultaneous collection of data at three different resolutions. We want to remark that, within the proposed design, the number of central frequencies can be easily expandable to more bands.
2. General Characterization of the Advanced Spectrometer
Within this article, a pioneer approach to designing a prototype of the acousto-optic spectrometer for radio-astronomy is schematically analyzed as well as preliminary confirmed by both the practical estimations and proof-of-principal experiments. The advances under this proposal reflect the next step in a progress in this field that includes principally higher level of parallelism in a wideband analogue signal processing with various frequency performances simultaneously and selecting the most appropriate AO materials for the desirable algorithm of processing.
As it had been described recently [8] , any arrangement of the AO radio-wave spectrometer is based on injecting ultra-high-frequency (UHF) radio-signals into a wide- aperture AO cell through effective piezoelectric transducer. Similar signals give birth to a large amount of dynamic diffraction acoustic gratings. Each grating is conditioned by a frequency harmonic of the incoming radio-wave signal that deflects the preliminary expanded incident monochromatic optical beam. This is why, the incident optical beam is converted into a large amount of individual optical beams creating individual parallel frequency channels for the corresponding partial radio-wave signal processing. As a result, the intensities of individual optical beams are governed by the amplitudes and phases of frequency harmonics from the incoming radio-wave signal. Then, all the individual optical beams are focused by the Fourier-integrating lenses on a CCD photo- detector for the subsequent electronic processing. Consequently, optical parallelism works together with electronic accuracy.
The principal difference of the schematic arrangement presented here in comparison with the one described in [8] , consists in the fact that we now develop the scheme with a few spatially parallel optical arms for data flow processing. Now, each individual spatial arm exhibits its own original performances to provide parallel multi-band observations of astrophysical objects within a few different scales simultaneously. Similar possibility is based on designing each of these spatial optical arms perfectly independently from one another. As a result, one can exploit different materials for AO cells operating within various regimes at different frequency ranges and light wavelengths from completely independent sources of the coherent light. Moreover, these spatial optical arms have now the beam shapers providing both the needed states of the incident light beam polarization in each arm and the required apodization for the incident light beams to suppress side lobes in the Fourier-transform plane, i.e. to increase the dynamic range of processing system as a whole.
Finally, after parallel AO processing, all these data flow are united by the joint matrix CCD photo-detector already on the stage of a high-bit-rate combined electronic data processing. After parallel AO processing, data flows of all the optical arms are united by the joint CCD matrix on the stage of the combined electronic data processing. At this point one yields at the united versatile instrument, which provides comprehensive studies of astrophysical objects simultaneously with precise synchronization in various frequency scales. At the moment, we have restricted ourselves by only the three similar spatial optical arms for data processing (see Figure 2) and for simplicity sake only one optical arm of this three-arm schematic arrangement is shown in Figure 3 in detail.
The first spatial arm of data processing represents almost a replica of the optoelectronic scheme described previously [8] , so that it need not a lot of additional comments. Nevertheless, it now uses the single frequency solid-state laser CL-442-025-S (CrystaLaser) at optical wavelength λ = 442 nm to decrease the spot size d due to d ~ λ. It is based on a low frequency and extremely effective tellurium dioxide (TeO2) AO cell with the central frequency of analysis close to 60 - 80 MHz and the frequency bandwidth below 80 MHz. The other novelty is related to the increased optical aperture of the TeO2 AO cell by 6 cm, which improves the frequency resolution in comparison with the recently presented data. The second arm is oriented to the spectrum analysis of let’s say middle-frequency radio-wave signals with the central frequencies of 350 - 500 MHz and the frequency bandwidth about 100 - 300 MHz. This spatial arm can exploit the AO cells based on such a unique effective AO crystal as bastron (Sr0.75Ba0.25Nb2O6) that operates in the visible range at λ = 671 nm.
The third arm of processing is intended for direct spectrum analysis of UHF radio- wave signals whose the central frequencies exceed 1.5 GHz and the frequency bandwidth are over 300 MHz. At the moment, the third spatial arm oriented to an AO cell based on rather specific cut of a lithium niobate (LiNbO3) crystal providing the anomalous regime of light scattering in the near infrared range at λ ≈ 1150 nm. Potentially, one can already have imagined the fourth spatial arm directed to reaching the frequency bandwidths over 1 GHz with the corresponding growth of the central frequencies. In practice, the most adequate approach for providing such bandwidths can
Figure 2. Schematic arrangement of the spatial arms in an advanced AO spectrometer (horizontal view).
Figure 3. The second spatial arm for a new prototype of the AO spectrometer (vertical view).
be based on either the phased-array technique [10] or on a novel technique for the piezoelectric transducer design developed by Gnewuch et al. [11] .
Each of the enumerated spatial optical arms for spectrum analysis within the prototype under discussion consists of a few optical or optoelectronic sub-systems, namely:
1) Rather powerful coherent light source controlling the linear polarization state and operating in a single frequency regime with small (about 1 - 3 mrad) beam divergence;
2) Beam shaper providing the desirable degree of linear polarization as well as the needed expansion and apodization of that beam;
3) The AO cell represents by itself specifically operating opto-electronic sub-systems, which determine the main performances of taken spatial arm;
4) Fourier-transform system including the integrating lens with an individual row of the CCD-matrix (see Figure 2 and Figure 3).
The three AO cells are key components of an advanced spectrometer under proposal, since exactly this triplet of devices is responsible for the efficiency of data processing, the frequency resolution and bandwidth of analysis, i.e. the precision of radio-signals detection. There are various criteria for choosing optimal AO cells crystalline materials; one can require, for example, a large light scattering efficiency or an increased angular range of optical beam scanning, or a minimized acoustic losses to provide the highest possible frequencies of operation, etc.
Together with this, even an individual spatially one-channel AO cell provides a multi-channel (a thousand channels or more) parallel processing in the frequency domain in such a way that practical frequency range of AO cell’s operation can be varied in wide limits to be adequate to the observational needs of modern radio-astronomy. These needs are widely varied from the frequency bandwidth ∆f ≈ 40 MHz and the frequency resolution δf ≥ 15 KHz to ∆f ≈ 300 MHz or more and δf ≥ 100 KHz with the number of parallel processing channels in the frequency domain (or, equivalently, the number of resolvable spots) N ≈ (2 − 3) × 103 as the case requires. These performances can be achieved at the top of modern technology exploiting specially designed AO cells based on specifically selected crystalline materials and regimes of their operations as it has been noted above.
Within our today’s aims, one can mention first of all the successful arrangement and detailed characterization of the above-mentioned sub-systems for the second arm with the specially designed wide-aperture AO cell based on the bastron single crystal, which is unique for practical applications.
This pioneer AO cell works at optical wavelength λ = 671 nm, which combines the convenience of operating in just the visible range with good enough transparency of this material with dark red light, from the single frequency solid-state laser CL-671- 050-S (Crysta Laser). The bastron-based AO cell of 6 cm aperture is theoretically able (see section 3) to manage the UHF radio-wave signals whose best performances can be estimated at the central frequency about of 500 MHz, frequency bandwidth close to 260 MHz and frequency resolution better 92 KHz providing the number N ≈ 2.7 × 103 of resolvable spots or, what is the same, the number of parallel frequency channels for spectral data processing.
The beam shaper included a variable optical attenuator, a Glan-Taylor linear polarizer, and a specially designed 4-prism beam expander for achieving the apodization by the tunable Gaussian profile. During its characterization rather precise adjusting the incident light beam had been realized. The processing part of this spatial arm embraces three key components. The first of them is the above-mentioned unique bastron AO cell with active optical aperture 60 × 2 mm. The second one is a fragment of the 3-inch achromatic doublet lens (Edmund Optics) with the focal length of about 85 cm, while the third component represents the second row of at least a 3-row multi-pixel CCD- matrix whose pixel has not more than 7 µm width. The performed characterization demonstrates that each individual optical beam can shape a spot whose main lobe has about 14 - 21 µm width, so that such a lobe lights usually two or three pixels in the corresponding row of CCD-matrix providing optimal resolution from viewpoint of the sampling theorem. General optical scheme of the second, i.e. the middle-frequency spatial arm for a new prototype under consideration, is depicted in Figure 3.
3. Potential Performances of the Bastron Crystalline AO Cell
3.1. Efficiency of Normal Light Scattering with a Given Bandwidth
The AO interaction leads to deflection of the incident light beam by an angle that is directly proportional to the frequency of the applied electric and, consequently, acoustic signal. One of the most important parameters for an AO cell, included into the Fourier processing, is the number of resolvable spots N in the image plane, which corresponds to the number of resolvable frequencies in the Fourier-transform plane. The number N can be determined as a ratio of the maximal light beam deflection angle ∆θ to the beam divergence δθ ≈ λ/D (with the refractive index n ≈ 1 for the air), where D is the linear size of that beam, i.e. N = ∆θ(λ/D). The above-noted proportionality inherent in the Fourier transform makes it possible to explain ∆θ = λ∆f/V in terms of the frequency bandwidth ∆f and acoustic wave velocity V. Then, due to the transition time of passing an acoustic wave through an AOC with an aperture coinciding with D is τ = D/V, one can write
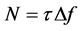 (1)
(1)
It is seen from Equation (1) that if both the AO cell’s-aperture D and, consequently, the transition time τ are fixed, so that growing the number N can only be provided by increasing the bandwidth ∆f. In so doing, the highest efficiency of light scattering is extremely desirable of course. However, the scattered light intensity depends on the angular-frequency mismatch η as well, which is conditioned by a wide range of varying the wave vectors of acoustic waves. The dependencies of the maximum scattered light intensity on the squared acoustic power parameter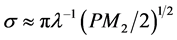 , which combines contributions of the material and the acoustic power, where M2 is the figure of AO merit and P is the acoustic power density [12] [13] were analyzed for a triplet of the relative frequency bandwidths Δf/f0 = 0, 0.25, and 0.5 (here, f0 is the central acoustic frequency within the bandwidth ∆f [14] .
, which combines contributions of the material and the acoustic power, where M2 is the figure of AO merit and P is the acoustic power density [12] [13] were analyzed for a triplet of the relative frequency bandwidths Δf/f0 = 0, 0.25, and 0.5 (here, f0 is the central acoustic frequency within the bandwidth ∆f [14] .
One can find that the efficiencies about 50% are approximately the same for all the taken values of the relative frequency bandwidth when σ2 ≈ π/4. By this it means that the maximum scattered light intensity will be almost the same for every frequency component under analysis with σ2 ≈ π/4 or, in the other words, the magnitude σ2 ≈ π/4 provides minimal variations of the scattered light intensity versus the applied frequency of a signal within the bandwidth ∆f at the cost of decreasing the interaction efficiency by about 50%.
3.2. The Expected Number of Resolvable Spots for the Bastron AO Cell
The above-mentioned number of resolvable spots N characterizes either the number of frequency channels for parallel analysis or the frequency resolution inherent in processing optical system. The frequency bandwidth ∆f of each AO cell depends on the chosen regime of light scattering. In the case of normal regime associated with a one-fold non- collinear light scattering, one can assume that the angle θ0 of light incidence is rather small, so that cosθ0 ≈ 1, and the frequency bandwidth of a one-fold light can be expressed as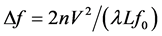 . When the acoustic power density P is not too high and acoustic wave attenuation can be characterized as a moderate one, the frequency resolution of AO cell is given by δf ≈ V/D at the level of 0.405 [12] . Thus, the number of resolvable spots can be expressed as
. When the acoustic power density P is not too high and acoustic wave attenuation can be characterized as a moderate one, the frequency resolution of AO cell is given by δf ≈ V/D at the level of 0.405 [12] . Thus, the number of resolvable spots can be expressed as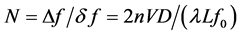 .
.
Now, one can analyze a few factors limiting the number of resolvable spots as a function of the frequency parameters [14] , and the main attention will be paid to a dependence on the frequency bandwidth ∆f. For this purpose, one can use the above-moti- vated preferable option ∆f ≈ f0/2. Then, one can use the recently described approach to estimating the number N of resolvable spots, restricted by at least three physically independent limitations conditioned by aperture, geometry, and acoustic attenuation (see, e.g. [8] ). After that, however, a one-fold normal non-collinear light scattering has to be considered for available and effective modern crystalline materials with Γ ≤ 10 dB/ (cm∙GHz2) to make the best choice.
Within such an analysis the bastron (Sr0.75Ba0.25Nb2O6) had been chosen for the application to the second spatial optical arm. The selection of tetragonal Sr0.75Ba0.25Nb2O6- crystal (its point-symmetry group is 4 mm) is conditioned first of all by its quite acceptable figure of merit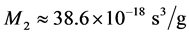 , desirable for sufficiently effective operating of the AO cell, together with rather low acoustic wave attenuation that potentially allows us the design of a wide-aperture AO cell, proving the improved frequency resolution within a 500 MHz frequency range. Then, one need take the normal process of light scattering by the longitudinal elastic mode passing along the [001] axis, which yield V = 5.5 × 105 cm/s, λ = 671 nm, n = 2.3, and Γ = 4 dB/(cm∙GHz2) can be expected. This set of the bastron’s data looks preferable in comparison with traditionally exploited crystals as the lead molybdate (PbMoO4), z-cut tellurium dioxide (z ? TeO2), and gallium phosphide (GaP) [15] . At a glance, the bastron crystal has slightly yellow color, so that the dark red laser beam is rather desirable for this material to maximize its optical transmission (staying together with that in the visible range, which makes, in its turn, much simpler adjusting optical scheme within experiments and later exploitation). The required numerical estimates for the optical apertures D = 4, 5, 6, 7 cm; the attenuation factors along the full aperture B = 3, 4, 5, 6 dB/aperture, and the Klein- Cook parameter Q = 3π, 4π, 5π, have been calculated and depicted in Figure 4. One can see that the chosen unique bastron-based AO cell with, for example, a wide optical aperture D = 6 cm, Q > 5π, and B ≈ 6 dB/aperture is able to provide N ≈ 2700 at f0 ≈ 500 MHz within the bandwidth ∆f ≈ ~250 MHz together with the frequency resolution δf = V/D ≈ 91.7 kHz, which is rather good for similar central acoustic frequency.
, desirable for sufficiently effective operating of the AO cell, together with rather low acoustic wave attenuation that potentially allows us the design of a wide-aperture AO cell, proving the improved frequency resolution within a 500 MHz frequency range. Then, one need take the normal process of light scattering by the longitudinal elastic mode passing along the [001] axis, which yield V = 5.5 × 105 cm/s, λ = 671 nm, n = 2.3, and Γ = 4 dB/(cm∙GHz2) can be expected. This set of the bastron’s data looks preferable in comparison with traditionally exploited crystals as the lead molybdate (PbMoO4), z-cut tellurium dioxide (z ? TeO2), and gallium phosphide (GaP) [15] . At a glance, the bastron crystal has slightly yellow color, so that the dark red laser beam is rather desirable for this material to maximize its optical transmission (staying together with that in the visible range, which makes, in its turn, much simpler adjusting optical scheme within experiments and later exploitation). The required numerical estimates for the optical apertures D = 4, 5, 6, 7 cm; the attenuation factors along the full aperture B = 3, 4, 5, 6 dB/aperture, and the Klein- Cook parameter Q = 3π, 4π, 5π, have been calculated and depicted in Figure 4. One can see that the chosen unique bastron-based AO cell with, for example, a wide optical aperture D = 6 cm, Q > 5π, and B ≈ 6 dB/aperture is able to provide N ≈ 2700 at f0 ≈ 500 MHz within the bandwidth ∆f ≈ ~250 MHz together with the frequency resolution δf = V/D ≈ 91.7 kHz, which is rather good for similar central acoustic frequency.
These estimations show that N does not exceed the values of about 1500 or 3000 as a maximum for any crystal. This is why the obtained numbers N reflect evidently the physical limitation peculiar to the normal regime of an AO interaction in anisotropic materials.
4. Estimating Performances of the LiNbO3-Based AO Cell for Direct Analysis of Ultra-High-Frequency Radio-Wave Signals
To provide direct spectrum analysis of UHF radio-wave signals the LiNbO3-based AO cell operating in the anomalous light scattering regime with wide-bandwidth tangential phase matching with so-called “optimal matching” can be chosen. As it had been shown in [16] , due to taking similar modified geometry of anomalous AO interaction exactly two acoustic wave vectors will intersect the internal optical surface of refractive indices. Therefore, the precise Bragg matching can be fulfilled at a pair of different acoustic frequencies. As a result, close to perfectly symmetric profile of the frequency band-shape will be potentially formed, so that two maxima of a new band-shape will be situated at frequencies almost equidistant from the central tangentially matching frequency. In this case, both the central frequency fC and the frequency bandwidth ΔfA the for anomalous light scattering are given by [17] .
(a) , (b)
, (b)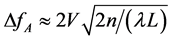 (2)
(2)
where n is the average refractive index and L = L0 is the initial length of AO interaction.
Figure 4. The combined diagram illustrating effect of a triplet of the restricting factors in a bastron AO cell. The solid slowly growing lines are related to N1, the chosen apertures D are equal to 4, 5, 6, and 7 cm. The dashed line regards to N2 in the case of Q = 3π, 4π, and 5π. The solid hyperbolic-like falling curves illustrate N3 and reflect contributions of the acoustic attenuation; the attenuation factors B are equal to 3, 4, 5, and 6 dB along the aperture.
Expression for ΔfA in Equation (2) does not include the frequency fC in the contrast with the corresponding formula for ΔfN ~ 1/fC, leading to fast increasing ΔfN when the central frequency fC grows.
The above-mentioned approach can be illustrated by the following numerical estimations for a one-fold light scattering in lithium niobate crystalline AO cell operating in the regime of anomalous light scattering with wide-bandwidth tangential phase matching.
The main values NE and NO of the refractive indices inherent in a lithium niobate crystal are markedly dispersive; for instance, NE ≈ 2.208, NO ≈ 2.967 at λ = 633 nm and NE ≈ 2.152, NO ≈ 2.227 at λ = 1150 nm [18] , so that their difference i.e. the birefringence has a tendency to fall as the optical wavelength λ grows. This is why choosing the optical wavelength represents a degree of freedom to vary the central frequency fC, as it is seen from Equation (2), in such a way that the frequency fC can be lowered, for example, to suppress the effect of acoustic losses, via increasing the optical wavelength. In lithium niobate crystal, one can choose the process using the S[100] 35˚ Y-acoustic mode, so that , n ≈ 2.2 in this case, and select λ = 1150 nm with L = 0.2 cm. Using Equation (2), one can calculate ΔfA ≥ 300 MHz and fC ≈ 1727 MHz, while ΔfN ≈ 13.3 MHz at the same central frequency fC and other parameters. For the taken set of material parameters, estimating the Klein-Cook parameter at the minimal frequency in the range, i.e. at
, n ≈ 2.2 in this case, and select λ = 1150 nm with L = 0.2 cm. Using Equation (2), one can calculate ΔfA ≥ 300 MHz and fC ≈ 1727 MHz, while ΔfN ≈ 13.3 MHz at the same central frequency fC and other parameters. For the taken set of material parameters, estimating the Klein-Cook parameter at the minimal frequency in the range, i.e. at 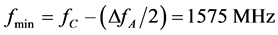 gives
gives
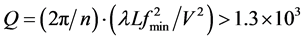 , which provides the Bragg regime of scattering at fmin. The obtained data mean that ΔfA/fC ≈ 17.5%, which can be improved, evidently, only through exploiting much more complicated and expansive phased-array technique for arranging the piezoelectric transducer [16] .
, which provides the Bragg regime of scattering at fmin. The obtained data mean that ΔfA/fC ≈ 17.5%, which can be improved, evidently, only through exploiting much more complicated and expansive phased-array technique for arranging the piezoelectric transducer [16] .
In this case, N is again limited by the independent agents mentioned previously, but they have to be partially modified because now the above-exploited in section 3 approximation Δf ≈ f0/2 cannot be applied. In so doing, one can use the expression
 , (3)
, (3)
which does not depend on the frequency. The second limitation is not actual now due to the Klein-Cook parameter is high enough even at the minimal frequency in the range of processing. The second limitation is not actual practically due to the carried out above estimation of the Klein-Cook parameter even at the minimal frequency in the range of processing. At the same time, the acoustic attenuation can be extremely important for acoustic waves at the UHF. One can take B ≈ 10 dB/aperture as an acceptable level of acoustic losses along the AO cell’s aperture and find an allowable aperture D as
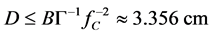 , (4)
, (4)
due to Γ ≈ 1 dB/(cm∙GHz2) [15] . However, one has to note here that the information related to the attenuation level for this acoustic mode is rather contradictory, so that the taken value of Γ ought to be considered as a reference one. Substituting Equation (4) into Equation (3), one can find
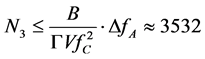 . (5)
. (5)
By this it means that one can expect N ≥ 3500 resolvable spots with the LiNbO3-cell under consideration, while the corresponding frequency resolution δf = V/D is close to about 100 KHz.
The efficiency of anomalous AO interaction with wide-bandwidth tangential phase matching in a crystal can be characterized by the modified figure of merit
 , where no and ne are the corresponding refractive indices, ρ = 4.7 g/cm3 is the material density of a lithium niobate crystal, and peff is the corresponding effective photo-elastic constant. To determine the magnitudes of both peff and M2 one can apply the recently developed approach [13] to the case of the slowest shear acoustic wave passing along the [100]-axis in a LiNbO3-crystal with the displacement vector is oriented along the direction 35˚ to the [010]-axis. As a result, the maximum value of photo-elastic constant is |peff,max| ≈ 0.15, while the maximum for M2 depends radically on the magnitude of the available refractive indices as well. For the above- chosen case of λ = 1150 nm, one can estimate the AO figure of merit by the value
, where no and ne are the corresponding refractive indices, ρ = 4.7 g/cm3 is the material density of a lithium niobate crystal, and peff is the corresponding effective photo-elastic constant. To determine the magnitudes of both peff and M2 one can apply the recently developed approach [13] to the case of the slowest shear acoustic wave passing along the [100]-axis in a LiNbO3-crystal with the displacement vector is oriented along the direction 35˚ to the [010]-axis. As a result, the maximum value of photo-elastic constant is |peff,max| ≈ 0.15, while the maximum for M2 depends radically on the magnitude of the available refractive indices as well. For the above- chosen case of λ = 1150 nm, one can estimate the AO figure of merit by the value 



One can find from this plot that LiNbO3-based AO cell under discussion is able potentially to provide the efficiency of light scattering up to 36% per one Watt of the applied acoustic power within a 0.405 level of a maximum frequency bandwidth close to 300 MHz.
5. Experimental Data
The bastron-based AO cell of 6 cm aperture is able theoretically (see section 3) to manage the radio-wave signals whose the best performances can be estimated at the central
Figure 5. Theoretical band-shape for LiNbO3 AO cell operating in the anomalous regime with wide-bandwidth tangential phase matching.
frequency about 500 MHz, frequency bandwidth close to 250 MHz and frequency resolution about 91.7 KHz providing potentially N ≈ 2720 resolvable spots. Testing of the second spatial optical arm of a new prototype under consideration, had been preliminary carried out with the currently available Bragg AO cell made of the bastron single crystal, which had an active optical aperture of 60 × 2 mm. To minimize the optical absorption in this material the dark-red light (the wavelength is 671 nm, the refractive index n ≈ 2.3) with linear polarization state of the incident light had been chosen. The normal process of light scattering by pure longitudinal elastic mode propagating along the [001]-axis with the acoustic wave velocity 
Within the first part of experiments, specially designed wide-aperture AO cell based on the unique bastron (Sr0.75Ba0.25Nb2O6) single crystal had been inserted in the above- described second spatial optical arm of that schematic arrangement representing a layout of an AO spectrometer (see section 2). Namely, it consists of the solid-state laser CL-671-050-S/CrystaLaser/(λ = 671 nm, the output optical power about 50 mW); the bastron-based AO cell of 6 cm aperture that is able potentially to manage the UHF radio-wave signals at the central frequency ~500 MHz; a four-prism beam expander, a large-aperture 3-inch achromatic doublet lens (Edmund Optics), and a multi-pixel CCD linear photo-detector. A bastron-based AO cell was illuminated by the single- frequency light beam expanded and polarized linearly in a plane of light scattering, which includes the acoustic beam inside the bastron-based AO cell. Such a state of polarization gave maximal transmission and desirable Gaussian apodization of the prism beam expander because the plane of optical beam expansion was coinciding with the plane of light polarization. Moreover, this polarization state provided the highest efficiency of light scattering within the chosen orientation of a crystal.
The Bragg regime of AO interaction can be provided only if the angle of light incidence on undoutedly thick dynamic acoustic grating satisfies the necessary Bragg condition as well as if the Klein-Cook parameter Q realizes the inequality



The piezoelectric transducer of that AO cell with the interaction length L = 1.0 cm had been made of a thin lithium niobate (Y + 36˚)-cut crystalline plate. It generated pure longitudinal acoustic mode with rather low losses of electro-acoustic conversion slightly exceeding 2 dB, due to a fact that the acoustic impedance of this lithium-ni- obate crystal cut is equal to

The electronic scheme for optimal connection of the sweep-generator with that port of the AO cell’s, i.e. in fact with the lithium niobate transducer, included a two-section wide-band matching circuit of the lumped electronic components accompanied by a two-cascade resistance step-down transformer assembled out of micro-coaxial cables. This electronic circuit was used to make as wide and uniform as possible the frequency band-shape even at the coast of decreasing the efficiency of the AO cell in part. The single-frequency longitudinal mode with the acoustic power density up to 0.3 mW/mm2 was generated at the swept carrier frequency during the experiments. The efficiency of AO interaction with the pure longitudinal acoustic mode was limited by about 10% to keep the linearity of potential analysis.
Figure 6 illustrates the normalized plot of the detected frequency band-shape exhibited by the wide-aperture bastron-based AO cell under investigation. Experimentally achieved non-uniformity of this band-shape was not exceeding approximately 9%. Full width of the measured band-shape at a 0.405 level of a maximum can be estimated by the value ΔfM ≈ 258 MHz (see Figure 6).
Estimating the frequency resolution peculiar to the bastron-based AO cell within the frames of the above-described optical system (including the multi-pixel CCD-array
Figure 6. Experimentally obtained frequency band-shape of a 60-mm aperture bastron AO cell with ΔfM ≈ 258 MHz at a 0.405 level of a maximum.
with 7 µm × 200 µm pixels) had been performed at the wavelength 671 nm as well. Two types of measurements had been carried out with a loaded AO cell, i.e. with radio-wave signal applied at the electronic port of that bastron-based AO cell. The first type of measurements had been performed at the central acoustic frequency 500 MHz with total acoustic wave attenuation 
Our experimental results had been obtained using the achromatic integrating lens (Edmund Optics) with F = 85 cm at the light wavelength 671 nm, so that theoretically 





The second type of measurements had been carried out using Gaussian apodization of the incident light distribution to demonstrate an opportunity of suppressing side lobes and increasing potential dynamic range of data processing within the second spatial optical arm of a prototype under design. In so doing, a few profiles for Gaussian apodization had been shaped exploiting the above-mentioned 4-prism beam expander due to rotating each prism individually and adjusting rather large angles of light incidence as accurate as possible. At the output of expander, these profiles had been checked
Figure 7. Light intensity profiles of an individual resolvable spot for the 6-cm aperture bastron- based crystalline AO cell with the applied input UHF radio-wave signal at fM ≈ 500 MHz.
using a linear diaphragm of about 30 microns width in combination with a wide-aper- ture silicon photo-detector sliding together along a 60 mm optical aperture of the expander’s last prism. Two typical light distributions for the cases β ≈ 2 and β ≈ 6 are presented in Figure 8. As a result, the chosen profile of the incident lighting was close to the distribution 
In this case, the acoustic carrier frequency was again about fM ≈ 500 MHz with total acoustic wave attenuation close to B ≈ 6 dB/aperture. Figure 9 shows the normalized light intensity profile with the spot size about of 14.7 microns with significantly suppressed side lobes, which look as a noise trace at the bottom of this plot. The maximum of this profile can be adequately estimated using the plot related to B = 6 dB/aperture at β ≈ 6 in Figure 8.
6. Conclusions
In this paper, we have presented an innovative design of a multi-band acousto-optic spectrometer with a few spatially parallel optical arms for the combined processing of
Figure 8. Two examples of the incident light distribution with Gaussian apodizations provided experimentally by a 4-prism beam expander (horizontal axes is measured in mm).
Figure 9. Light intensity profiles of a resolvable spot for the bastron-based crystalline AO cell with the applied input radio-wave signal at fM ≈ 500 MHz with Gaussian apodization of the incident light distribution; β ≈ 6.
their data flow. Similar schematic arrangement permits the simultaneous exploitation of three or more bands at different resolutions and bandwidths, which makes it a highly versatile instrument in a number of astrophysical scenarios. The design is based on the use of a few, currently the three, different AO cells, and one of them, which is based on unique bastron crystal, represents specific subject of our interest as well as the object of advanced studies at the current stage of development.
This pioneer AO cell worked at optical wavelength λ = 671 nm, which combines the convenience of operating in just the visible range with good enough transparency of this material with dark red light. It has been demonstrated experimentally that the bastron- based AO cell of 6 cm aperture is practically able to manage the UHF radio-wave signals at the central frequency about fM ≈ 500 MHz within the frequency bandwidth ~258 MHz at the frequency resolution about 113.5 kHz providing the number N ≈ 2174 of resolvable spots or parallel frequency channels for spectral data analysis. Together with this, the potential of a UHF lithium niobate AO cell, operating in the anomalous light scattering regime with wide-bandwidth tangential phase matching has been estimated theoretically. The progressed characterization has shown a possibility of exploiting such an AO cell directly at the central frequency fM ≈ 500 MHz within the frequency bandwidth ~260 MHz with the needed efficiency. Additionally, practical aspects of realizing the Gaussian apodization in a multi-band AO spectrometer have been experimentally examined as well.
Finally, one can note that, as it has been indicated in the introductory section, the proposed design of a multi-band spectrometer will allow us the construction of a versatile instrument that can be used in virtually every astronomical context, with the advantage that data in three or even more bands can be obtained at the same time. This not only reduces time overheads associated with instrument changes, but allows us to extract valuable data in at least two distinct wave bands. It becomes achievable for the first time to our knowledge due to after parallel acousto-optical processing, data flows of all the optical arms are united by the joint CCD matrix on the stage of the combined electronic data processing. At this point, one yields at the really united astrophysical instrument, which provides comprehensive studies of astronomical objects simultaneously with precise synchronization in various frequency scales.
Acknowledgements
We would like to thank CONACyT for financial support through grant CB-256961 and 61237.
Cite this paper
Shcherbakov, A.S., Dagostino, M.C., Arellanes, A.O. and Tepichin, E. (2016) An Advanced Multi-Band Acousto-Optical Radio-Wave Spectrometer with Multi-Channel Frequency Processing for Astrophysical Studies. International Journal of Astronomy and Astrophysics, 6, 393- 409. http://dx.doi.org/10.4236/ijaa.2016.64032
References
- 1. Yun, M.S., et al. (2012) Deep 1.1 mm-Wavelength Imaging of the GOODS-S Field by AzTEC/ASTE—II. Redshift Distribution and Nature of the Sub-Millimeter Galaxy Population. MNRAS, 420, 957-985.
http://dx.doi.org/10.1111/j.1365-2966.2011.19898.x - 2. Snell, R.L., et al. (2011) The Redshift Search Receiver 3 mm Wavelength Spectra of 10 Galaxies. The Astronomical Journal, 141, No. 2.
http://dx.doi.org/10.1111/j.1365-2966.2011.19898.x - 3. Carrasco, E., Aretxaga, I. and Irvine, W.M. (2006) The Large Millimeter Telescope. Instituto Nacional de Astrofisica, Optica y Electronica, 139.
- 4. Erickson, N., Narayanan, G., Goeller, R. and Grosslein, R. (2007) An Ultra-Wideband Receiver and Spectrometer for 74 -110 GHz. From Z-Machines to ALMA: (Sub)Millimeter Spectroscopy of Galaxies 375 of Astronomical Society of the Pacific Conference Series, 71.
- 5. Narayanan, G., Heyer, M.H., Brunt, C., Goldsmith, P.F., Snell1, R. and Li, D. (2008) The Five College Radio Astronomy Observatory CO Mapping Survey of the Taurus Molecular Cloud. The Astrophysical Journal Supplement Series, 177, 341.
http://dx.doi.org/10.1086/587786 - 6. Chavez, M. and Hughes, D. (2013) New Quests in Stellar Astrophysics III: A Panchromatic View of Solar-like Stars, with and without Planets. Proceedings of the Conference a Panchromatic View of Solar-like Stars, Astronomical Society of the Pacific Conference Series, Vol. 472, 279.
- 7. Chavez, M., Shcherbakov, A.S., Arellanes, A.O. and Chavushyan, V. (2013) High-Resolu-tion Broadband Millimeter-Wave Astrophysical Spectrometer with Triple Product Acousto-Optical Processor. International Journal of Astronomy and Astrophysics, 3, 421-430.
http://dx.doi.org/10.4236/ijaa.2013.34050 - 8. Shcherbakov, A.S. and Luna Castellanos, A. (2014) Developing an Advanced Prototype of the Acousto-Optical Radio-Wave Spectrometer for Studying Star Formation in the Milky Way. International Journal of Astronomy and Astrophysics, 4, 128-144.
http://dx.doi.org/10.4236/ijaa.2014.41012 - 9. Holland, W.S., Bintley, D., Chapin, E.L., et al. (2013) SCUBA-2: The 10 000 Pixel Bolometer Camera on the James Clerk Maxwell Telescope. MNRAS, 430, 2513-2533.
http://dx.doi.org/10.1093/mnras/sts612 - 10. Goutzoulis, A.P. and Pape, D.R. (1994) Design and Fabrication of Acousto-Optic Devices. In: Goutzoulis, A.P. and Kludzin, V.V., Chapter 1, Principles of Acousto-Optics, Marcel Dekker, NY, 1-68.
- 11. Gnewuch, H., Zayler, N.K., Pannell, C.N., Ross, G.W. and Smith, P.G.R. (2000) Broadband Monolithic Acousto-Optic Tunable filter. Optics Letters, 25, 305-307.
http://dx.doi.org/10.1364/OL.25.000305 - 12. Shcherbakov, A.S., Arellanes, A.O. and Nemov, S.A. (2013) Transmission Function of Collinear Acousto-Optical Interaction Occurred by Acoustic Waves of Finite Amplitude. Journal of the Optical Society of America B, 30, 3174-3183.
http://dx.doi.org/10.1364/JOSAB.30.003174 - 13. Shcherbakov, A.S., Arellanes, A.O. and Nemov, S.A. (2013) Transmission Function of the Collinear Acousto-Optical Filter Controlled by Acoustic Waves of the Finite Amplitude. Optical Engineering, 52, 064001.
http://dx.doi.org/10.1117/1.OE.52.6.064001 - 14. Young, E. and Yao, S.-K. (1981) Design Considerations for Acousto-Optic Devices. Proceedings of the IEEE, 69, 54-64.
http://dx.doi.org/10.1109/PROC.1981.11920 - 15. Chang, I.C. (1995) Chapter 12, Acousto-Optic Devices and Applications. In: Bass, M., Ed., Handbook of Optics, Vol. II., McGraw-Hill, United States.
- 16. Goutzoulis, A.P. and Pape, D.R. (1994) Design and Fabrication of Acousto-Optic Devices. In: Pape, D.R., Gusev, O.V., Kujakov, S.V., Chapter 2, Design of Acousto-Optic Deflectors, Marcel Dekker, NY, 69-122.
- 17. Dixon, R. (1967) Acoustic Diffraction of Light in Anisotropic Media. IEEE Journal of Quantum Electronics, 3, 85-93.
http://dx.doi.org/10.1109/JQE.1967.1074447 - 18. Shaskolskaya, M.P. (1988) Handbook of Acoustical Crystals. Nauka, Moscow, Russia.










