International Journal of Astronomy and Astrophysics
Vol.06 No.03(2016), Article ID:70003,18 pages
10.4236/ijaa.2016.63021
Evolution of the “f” Family Orbits in the Photo Gravitational Sun-Saturn System with Oblateness
Niraj Pathak1, V. O. Thomas2
1Department of Mathematics, Dharmsinh Desai University, Nadiad, India
2Department of Mathematics, The Maharaja Sayajirao University of Baroda, Vadodara, India
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 January 2016; accepted 21 August 2016; published 24 August 2016
ABSTRACT
We analyze the periodic orbits of “f” family (simply symmetric retrograde periodic orbits) and the regions of quasi-periodic motion around Saturn in the photo gravitational Sun-Saturn system in the framework of planar circular restricted three-body problem with oblateness. The location, nature and size of these orbits are studied using the numerical technique of Poincare surface of sections (PSS). In this paper we analyze these orbits for different solar radiation pressure (q) and actual oblateness coefficient of Sun Saturn system. It is observed that as Jacobi constant (C) increases, the number of islands in the PSS and consequently the number of periodic and quasi-periodic orbits increase. The periodic orbits around Saturn move towards the Sun with decrease in solar radiation pressure for given value of “C”. It is observed that as the perturbation due to solar radiation pressure decreases, the two separatrices come closer to each other and also come closer to Saturn. It is found that the eccentricity and semi major axis of periodic orbits at both separatrices are increased by perturbation due to solar radiation pressure.
Keywords:
Restricted Three Body Problem, Sun-Saturn System, “f” Family Periodic Orbits, Region of Quasi Periodic Orbits, Photo Gravitation, Oblateness, Poincare Surface of Section

1. Introduction
Restricted three body problem (RTBP) describes the motion of massless body which moves under the gravitational effect of two finite masses called primaries. The primaries are supposed to move in circular orbits around their center of mass on account of their mutual attraction. Usually Sun and anyone of its planets are taken as primaries. The secondary body is taken as the satellite of the primary planet or asteroid or comet or artificial satellite.
The RTBP has many applications in the solar system dynamics. [1] is fundamental book on the RTBP. [2] studied the locations of the stationary points and their linear stability in the RTBP by considering the bigger primary as source of radiation and smaller primary as oblate spheroid. A large number of periodic orbits were generated and categorized in different families according to their properties or nature by [3] in the framework of RTBP. Poincare surface of section (PSS) is widely used for analyzing periodic, quasi periodic and chaotic orbits. [4] provided a detailed analysis of periodic orbits using PSS technique. As per Kolmogorov-Arnold-Moser (KAM) theory, a fixed point on the Poincare surface of section represents a periodic orbit in the rotating frame, and the closed curves around the point correspond to the quasi-periodic orbits. [5] analyzed the location and stability of periodic and quasi-periodic orbits in the Earth-Moon system. [6] and [7] analyzed the PSS for Earth-Moon system and Sun-Mars system. They have identified periodic, quasi-periodic solutions and chaotic regions. [8] also studied PSS for Saturn Titan system for periodic orbits, quasi-periodic and chaotic regions. [9] analyzed the family “f” orbits around smaller primary under RTBP for different systems. They studied numerous systems in ideal condition. [5] [10] - [12] have shown that the stability of periodic orbits of f family is lost due to third-order resonances. The same phenomenon has been explicitly shown in [13] . Recently, [14] analyzed Sun and Saturn centered periodic orbits with solar radiation pressure and oblateness and found that there is a non negligible effect of solar radiation pressure on position and geometry of secondary body orbit. In this paper we have studied family “f” orbits and their stability for Sun Saturn system with perturbation. Here Sun is a source of radiation and Saturn is considered as oblate spheroid. So, actual coefficient of oblateness for Saturn is taken into account and for different values of solar radiation pressure we analyzed family “f” orbits around Saturn.
2. Equations of Motion
The solar radiation pressure force Fp changes with the distance by the same law as the gravitational attraction force Fg and acts opposite to it. It is possible to consider that the result of the action of this force leads to reducing the effective mass of the sun [7] . Thus, the sun’s resultant force acting on the particle is
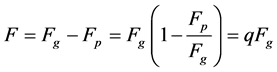 (1)
(1)
where 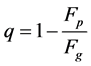 is the mass reduction factor constant for the given particle. We follow the notation and ter-
is the mass reduction factor constant for the given particle. We follow the notation and ter-
minology of [1] and [15] . The perturbed mean motion n of Saturn is given by,
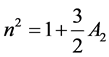 (2)
(2)
where,
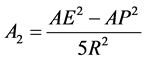 (3)
(3)
Here AE and AP represent equatorial and polar radii of Saturn and R is the distance between Sun and Saturn. The unit of mass is chosen equal to the sum of the primary masses and the unit of length is equal to their separation. The unit of time is such that the Gaussian constant of gravitation is unity in the unperturbed case. The usual dimensionless synodic coordinate system Oxy is used to express the motion. The origin of the system is positioned at the center of mass of the primaries while the more massive and less massive primaries always lie on the Ox axis at P(−μ, 0) and Q(1−μ, 0), respectively. Following [2] , the equations of motion of the third body are
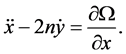 (4)
(4)
And
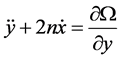 (5)
(5)
where,
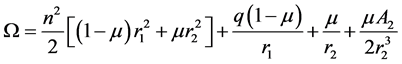 (6)
(6)
Here
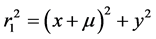
And
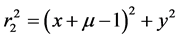 (7)
(7)
Also,
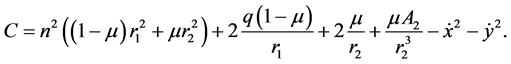 (8)
(8)
which is Jacobi constant of integration.
3. Poincare Surface of Section
The Poincare surface of section (PSS) technique is a method for determining the regular or chaotic nature of the trajectory. The numerical technique of PSS has been utilized by a large number of researchers to generate periodic and quasi-periodic orbits [6] - [9] . For the PSS technique, the equations of motion are integrated in (x, y) variables using a Runge-Kutta Gill fourth order variable or fixed step-size integrator. The initial conditions are selected along the x-axis. By defining a plane, say y = 0, in the resulting three dimensional space the values of and 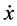 can be plotted every time the particle has y = 0, whenever the trajectory intersects the plane in a particular direction, say
can be plotted every time the particle has y = 0, whenever the trajectory intersects the plane in a particular direction, say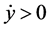 . It is noted that the resulting 3D space is reduced to a 2D subspace by considering a fixed value of the Jacobi constant. We have constructed PSS on the x,
. It is noted that the resulting 3D space is reduced to a 2D subspace by considering a fixed value of the Jacobi constant. We have constructed PSS on the x, 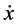 plane. The initial values were selected along the Ox-axis by using intervals of length 0.001. Time interval is 0.001which is step size for Runge-Kutta Gill fourth order integration method. A PSS contains discrete points of trajectories.
plane. The initial values were selected along the Ox-axis by using intervals of length 0.001. Time interval is 0.001which is step size for Runge-Kutta Gill fourth order integration method. A PSS contains discrete points of trajectories.
4. Results
For Sun-Saturn system the mass of Sun m1 = 1.9881 × 1030 kg, mass of Saturn m2 = 568.36 × 1024 kg [7] [15] .
Thus,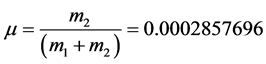 .
.
Also equatorial radius of Saturn is 60,268 km, polar radius of Saturn is 54,364 km. and distance between Sun and Saturn is 1,433,000,000 km. So, according to the equation 3 the oblateness coefficient is calculated as 6.59158 × 10−11.
q = 1 means that there is no perturbation due to solar radiation pressure and q < 1 indicates that we are including perturbation due to solar radiation pressure. For a given q, selection of C is not arbitrary. By solving Equation 8 w.r.t. 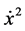 and by setting in to this equation y = 0 and
and by setting in to this equation y = 0 and 

Figure 2 shows PSS corresponding to C = 3.018. Here we ignore solar radiation pressure (i.e. q = 1). Figure 3 shows one major island. Center of the island gives Saturn centered simply symmetric retrograde periodic orbit at x = 0.987101 which is elliptic in shape. This orbit is categorized as family “f” orbit. Saturn centered periodic orbits being elliptic in shape; it is possible to obtain its semi major axis and eccentricity.
Table 1. Range of Jacobi constant for different solar radiation pressure q.
Figure 1. Excluded region for different solar radiation pressure q.
Figure 2. PSS for C = 3.018, q = 1.
Figure 3. PSS for C = 3.018, q = 1, center of the island showing Saturn centered orbit at x = 0.987101.
The semi-major axis a and eccentricity e of the Saturn centered orbits are given by [4] .


where,


And

Period T of Saturn’s orbit is given by
using Equation 2. For Saturn, T = 0.283185306868965 and A2 = 6.59158 × 10−11. From Kepler’s third law semi major axis of Saturn’s orbit is obtained as a = 1.000867863227069. Table 2 shows the analysis of Saturn centered periodic orbits. From each pair of q and C, we have calculated center of island x, semi major axis a, eccentricity e, diameter D (which is difference between two end points of Saturn centered orbit on Sun-Saturn line) and the period T of Saturn centered orbit. L, R and A represent, respectively, the left tip, the right tip and the amplitude (R-L) of the island whose center x gives Saturn centered periodic orbit.
From Table 2 it is observed that for a given C, as q decreases, the location of Saturn centered periodic orbits move towards Saturn, which supports the fact that solar radiation pressure acts opposite to the gravitational force. It is also observed from Table 2 that for a given C, as q decreases, semi major axis a, eccentricity e and diameter D of Saturn centered periodic orbits decrease. Thus, it is concluded that due to perturbation of solar radiation pressure, size of Saturn centered periodic orbits decrease. It is also observed from Table 2 that for a given C, as q decreases, semi major axis a, eccentricity e and diameter D of Saturn centered periodic orbits decrease. This shows that due to perturbation of solar radiation pressure, size of Saturn centered periodic orbits decrease.
In Table 3, for each arbitrary selected values of q, we have displayed the numerical estimates of x, a, e, T, L, R and A for different permitted values of C. It is clear that for a given q, as C increases location of periodic orbit moves towards Saturn. Diameter D of Saturn centered periodic orbits decrease as C increases. Figure 4 shows that the location L of Saturn centered orbits move towards Saturn and diameter D decreases as C increases for a given q. From Table 3 and Figure 5 it can be noticed that a increases with C up to certain value of C and then shows a sudden increment in a. For instance, for q = 1 and C = 2.995, Saturn centered periodic orbit is located at x = 0.93334. Semi major axis of this orbit is 1.0648, whereas, Saturn centered periodic orbit corresponding to q = 1 and C = 3.006 is located at x = 0.97585 has semi major axis 1.2361 which is clearly a sudden increment in semi major axis.
From Figure 6 it is observed that, for each q, eccentricity e decreases up to certain value of C and then increases suddenly as C increases. For instance, for q = 1, C = 2.995 Saturn centered periodic orbit is at x = 0.93334. Eccentricity e of this orbit is 0.1255, whereas, Saturn centered periodic orbit corresponding to q = 1, C = 3.006 is located at x = 1.2361. Eccentricity e of this orbit is 0.2116 which shows sudden increment in eccentricity.
Table 2. Analysis of Saturn centered periodic orbits for different values of q and C.
Table 3. Analysis of Saturn centered periodic orbits.
Figure 4. Location and diameter of Saturn centered periodic orbits.
Figure 5. Semi major axis of Saturn centered periodic orbits.
Each point in the island around its center corresponds to a quasi-periodic orbit. The largest of these islands is the one with the maximum amplitude of oscillation that are still stable. The regular regions of PSS are defined by a periodic orbit surrounded by an area of quasi-periodic orbits. The regular regions can be interpreted as regions of stability in the sense that outside them the motion is certainly unstable (chaotic) and inside them the motion is in general regular.
Figures 7-10 give the size of the stability region for q = 1, 0.9845, 0.9645 and 0.9345 respectively. The left and right tips of the island are plotted by green and red curves, respectively. It is seen that in each figure there are two separatrices where stability of the periodic orbit is zero as the size of the island is zero at separatrix. For each PSS corresponding to (q, C), we get two separatrices. We have analyzed the stability curve for three stages, which are divided by two separatrices. In the first stage, the quasi periodic orbit oscillates around the periodic
Figure 6. Eccentricity of Saturn centered periodic orbits.
Figure 7. Stability of Saturn centered periodic orbits for q = 1.
orbits in such a way that the farthest point from the Saturn is in the line of conjunction is a pericenter. Stability of periodic orbit decreases up to first separatrix. At the first separatrix stability becomes zero as island disappears. In the second stage, island reappear and consequently the stability increases. Then size of the island starts decreasing up to second separatrix where again the island disappears. In the third stage, the quasi periodic orbit oscillates around the periodic orbit in such a way that the closest point to the Saturn in the line of conjunction is pericenter. After second separatrix, island reappears and consequently the stability increases.
From Figures 11-20, it can be shown that there is a transition in the way the quasi periodic orbit oscillates about the periodic orbit before and after the separatrix due to third order resonance. The disappearance of the region of stability is caused by the intersection of the central periodic orbit and the unstable periodic orbit lying at the three corners of the triangular stability region [12] .
Figure 8. Stability of Saturn centered periodic orbits for q = 0.9845.
Figure 9. Stability of Saturn centered periodic orbits for q = 0.9645.
For q = 1, size of stability region increases for values of C in the range [2.6 2.9]. Stability is maximum at C = 2.9 and then decrease till first separatrix obtained at C = 2.9928. Again size of stability region increases and then decrease for small interval of C. Second separatrix obtained at C = 2.999. Again size of stability region increases.
Figures 11-15 shows PSS of islands for q = 1corresponding to C = 2.991, 2.9928, 2.995, 2.999 and 3.0 respectively. Figure 11 and Figure 14 are PSS of first and second separatrix for q = 1. Separatrices lies between two opposite direction islands as shown in Figure 11, Figure 13 and Figure 13, Figure 15.
For q = 0.9345 size of stability region increases for values of C in the range [2.18, 2.68]. For q = 0.9345 at C = 2.86 and 2.867. Figure 17 and Figure 19 are PSS of separatrices for q = 0.9345. Figure 16 and Figure 18 and Figure 18 and Figure 20 are in opposite direction for q = 0.9345.
Figure 10. Stability of Saturn centered periodic orbits for q = 0.9345.
Figure 11. C = 2.991 and q = 1.
Reduction in q increases perturbation due to solar radiation pressure which affects location, shape, size and stability of periodic orbits located at center of separatrix.
Table 4 and Figure 21 shows the variation in location of periodic orbits at both separatrices. Red and green curves show variation in location of periodic orbit at first and second separatrix respectively. It is observed that as the q moves towards 1, the location of periodic orbits at both separatrices moves towards Saturn. Figure 22 shows that variation in value of C corresponding to both separatrices as a function of q. Red and green curves are corresponding to first and second separatrices. It is clear that as q moves towards 1, value of C corresponding to both separatrices moves towards 3. Figure 23 shows difference between two Jacobi constants corresponding to first and second separatrices for given q. It is concluded that the difference between corresponding Jacobi constant decreases as q decreases up to 0.9845 and then increases slightly. Figure 24 shows distance between location of both separatrices for each q. it can be seen that the difference between location of two periodic
Figure 12. First separatrix for C = 2.9928 and q = 1.
Figure 13. C = 2.995 and q = 1.
orbits at both separatrices decreases as q drops to the value 0.9845 and then slightly increases. The effect of solar radiation pressure on the semi-major axis and eccentricity of the periodic orbits are shown in Figure 25 and Figure 26. Red, green and magenta curves show behavior of location of periodic orbit at separatrices, its semi major axis and eccentricity respectively. Figure 25 and Figure 26 shows behavior of periodic orbits at first and second separatrices respectively. It is found that q is responsible for increment in e and a of periodic orbits at both separatrices.
5. Conclusion
The present paper analyses the effect of radiation pressure and oblateness on family “f” of periodic orbit (PO) in the Sun-Saturn system. It is observed that radiation pressure has significant influence on evolution of family “f” of PO. As radiation pressure increases the admissible value of C decreases and PO shifts towards Saturn. Also the geometric parameters of the orbits such as diameter, eccentricity and semi major axis decrease. An increment in C increases the semi-major axis of f family of periodic orbits, the eccentricity decreases up to certain
Figure 14. Second separatrix for C = 2.999 and q = 1.
Figure 15. C = 3.0 and q = 1.
Figure 16. C = 2.855 and q = 0.9345.
Figure 17. First separatrix for C = 2.86 and q = 0.9345.
Figure 18. C = 2.865 and q = 0.9345.
Figure 19. Second separatrix for C = 2.867 and q = 0.9345.
Figure 20. C = 2.869 and q = 0.9345.
Table 4. Analysis of periodic orbit at separatrices.
Figure 21. Location of separatrices for Sun-Saturn system as a function of q.
Figure 22. Value of C corresponding to the separatrices in Sun-Saturn system as a function of q.
Figure 23. Difference between the values of C corresponding to the separatrices as a function of q.
Figure 24. Distance between the two separatrices in Sun-Saturn system as a function of q.
Figure 25. Location of periodic orbit (PO) at first separatrix, semi major axis and eccentricity of PO.
Figure 26. Location of periodic orbit (PO) at second separatrix, semi major axis and eccentricity of PO.
value of C and then shows a sudden increase in its value. Diameters of these periodic orbits decrease slowly, but after certain value of C, there is a sudden decrement in value of diameter of periodic orbits. It is also observed that as solar radiation pressure decreases, the location of PO orbits at both separatrices moves towards Saturn. Also, as q moves towards 1, value of Jacobi constant corresponding to both separatrices moves towards 3. It is concluded that the difference between corresponding Jacobi constant decreases as q decreases up to 0.9845 and then increases slightly. It can be seen that the difference between location of two periodic orbits at both separatrices decreases as q drops to the value 0.9845 and then slightly increases. In other words, as the perturbation due to solar radiation pressure decreases, the two separatrices come closer to each other and also come closer to Saturn. It is found that the eccentricity and semi major axis of periodic orbits at both separatrices are increased by perturbation due to solar radiation pressure. The evolution of the family of periodic orbits can be divided into three stages separated by two separatrices. These are caused by the 3:1 resonance. That is, the bifurcation of the basic family f with the family f 3 of triple periodic orbits branching from f at these values of the Jacobi constant. There is a change in the direction of the islands around the periodic orbits before and after these separatrice. In other words, there is a change in the way the quasi-periodic orbits oscillate around the periodic orbits before and after these separatrices. Family f can be used for patching of trajectory of satellite, that is, joining of two or more orbits to obtain a trajectory.
Acknowledgements
The authors thank Pooja Dutt, Applied Mathematics Division, Vikram Sarabhai Space Centre (ISRO), Thiruvananthapuram, India for her constructive comments for separatix analysis. They also thank the associate editor and referees for their constructive comments, which helped in bringing this paper to the present form.
Cite this paper
Niraj Pathak,V. O. Thomas, (2016) Evolution of the “f” Family Orbits in the Photo Gravitational Sun-Saturn System with Oblateness. International Journal of Astronomy and Astrophysics,06,254-271. doi: 10.4236/ijaa.2016.63021
References
- 1. Szebehely, V. (1967) Theory of Orbits. Academic Press, San Diego.
- 2. Sharma, R.K. (1987) The Linear Stability of Libration Points of the Photo Gravitational Restricted Three Body Problem When the smaller Primary Is an Oblate Spheroid. Astrophysics and Space Science, 135, 271-281.
http://dx.doi.org/10.1007/BF00641562 - 3. Broucke, R.A. (1968) Periodic Orbits in the Restricted Three-Body Problem with Earth-Moon Masses. Technical Report, 32, Jet Propulsion Lab., Pasadena.
- 4. Murray, C.D. and Dermot, S.F. (1999) Solar System Dynamics. Cambridge University Press, Cambridge.
- 5. Winter, O.C. (2000) The Stability Evolution of a Family of Simply Periodic Lunar Orbits. Planetary and Space Science, 48, 23-28.
http://dx.doi.org/10.1016/S0032-0633(99)00082-3 - 6. Dutt. P. and Sharma, R.K. (2010) Analysis of Periodic and Quasi-Periodic Orbits in the Earth-Moon System. Journal of Guidance, Control, and Dynamics, 33, 1010-1017.
http://dx.doi.org/10.2514/1.46400 - 7. Dutt. P. and Sharma, R.K. (2011) Evolution of Periodic Orbits in the Sun-Mars System. Journal of Guidance, Control, and Dynamics, 34, 635-644.
http://dx.doi.org/10.2514/1.51101 - 8. Safiyabeevi, A. and Sharma, R.K. (2011) Oblateness Effect of Saturn on Periodic Orbits in the Saturn-Titan Restricted Three-Body Problem. Astrophysics and Space Science, 333, 245-261.
- 9. Dutt. P. and Sharma, R.K. (2012) On the Evolution of the “f” Family in the Restricted Three-Body Problem. Astrophysics and Space Science, 340, 63-70.
http://dx.doi.org/10.1007/s10509-012-1039-0 - 10. Hénon, M. (1970) Numerical Exploration of the Restricted Problem. VI. Hill’s Case: Non-Periodic Orbits. Astronomy and Astrophysics, 9, 24-36.
- 11. Douskos, C., Kalantonis, V. and Markellos, P. (2007) Effect of Resonances on the Stability of Retrograde Satellite. Astrophysics and Space Science, 310, 245-249.
http://dx.doi.org/10.1007/s10509-007-9508-6 - 12. Dutt, P. and Sharma, R.K. (2011) Evolution of Periodic Orbits near the Lagrangian Point L2. Advance in Space Research, 47, 1894-1904.
http://dx.doi.org/10.1016/j.asr.2011.01.024 - 13. Perdiou, A.E., Perdios, E.A. and Kalantonis, V.S. (2012) Periodic Orbits of the Hill Problem with Radiation and Oblateness. Astrophysics and Space Science, 342, 19-30.
http://dx.doi.org/10.1007/s10509-012-1145-z - 14. Pathak. N., Sharma, R.K. and Thomas, V.O. (2016) Evolution of Periodic Orbits in the Sun-Saturn System. International Journal of Astronomy and Astrophysics, 6, 175-197.
http://dx.doi.org/10.4236/ijaa.2016.62015 - 15. Sharma, R.K. and Subbarao, P.V. (1976) Stationary Solutions and Their Characteristic Exponents in the Restricted Three-Body Problem When the More Massive Primary Is an Oblate Spheroid. Celestial Mechanics, 13, 137-149.
http://dx.doi.org/10.1007/BF01232721





























