International Journal of Astronomy and Astrophysics
Vol.05 No.03(2015), Article ID:59484,10 pages
10.4236/ijaa.2015.53020
Collinear Libration Points in the Photogravitational CR3BP with Zonal Harmonics and Potential from a Belt
Jagadish Singh1, Joel John Taura2
1Department of Mathematics, Faculty of Science, Ahmadu Bello University, Zaria, Nigeria
2Department of Mathematics and Computer Science, Federal University, Kashere, Nigeria
Email: jgds2004@yahoo.com, taurajj@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 April 2015; accepted 6 September 2015; published 9 September 2015
ABSTRACT
We have studied a reformed type of the classic restricted three-body problem where the bigger primary is radiating and the smaller primary is oblate; and they are encompassed by a homogeneous circular cluster of material points centered at the mass center of the system (belt). In this dynamical model, we have derived the equations that govern the motion of the infinitesimal mass under the effects of oblateness up to the zonal harmonics J4 of the smaller primary, radiation of the bigger primary and the gravitational potential generated by the belt. Numerically, we have found that, in addition to the three collinear libration points Li (i = 1, 2, 3) in the classic restricted three-body problem, there appear four more collinear points Lni (i = 1, 2, 3, 4). Ln1 and Ln2 result due to the potential from the belt, while Ln3 and Ln4 are consequences of the oblateness up to the zonal harmonics J4 of the smaller primary. Owing to the mutual effect of all the perturbations, L1 and L3 come nearer to the primaries while Ln3 advances away from the primaries; and L2 and Ln1 tend towards the smaller primary whereas Ln2 and Ln4 draw closer to the bigger primary. The collinear libration points Li (i = 1, 2, 3) and Ln2 are linearly unstable whereas the Ln1, Ln3 and Ln4 are linearly stable. A practical application of this model could be the study of motion of a dust particle near a radiating star and an oblate body surrounded by a belt.
Keywords:
Circular Restricted Three-Body Problem, Photogravitational, Zonal Harmonic Effect, Potential from the Belt

1. Introduction
In celestial mechanics, one amidst various inspiring subject is the restricted three-body problem (R3BP). The problem entails three bodies: two primary bodies having finite masses moving under their mutual gravitational attraction and the third with a negligible-mass (infinitesimal) body, whose motion is influenced by the primaries. If the primaries move on circular orbits about their common centre of mass, it is termed as the circular R3BP (CR3BP). Then, the objective of this CR3BP is to determine the motion of the infinitesimal mass. [1] and [2] gave a detailed description of the solution of the CR3BP. They showed that if the primary bodies were fixed in a rotating coordinate system, five libration points existed. That is the points where the infinitesimal mass can remain permanent, if placed there with zero velocity. Three of the points
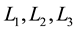 are on the line linking the primaries, whereas the other two
are on the line linking the primaries, whereas the other two
 are in equilateral triangular alignment with the primaries. The collinear points
are in equilateral triangular alignment with the primaries. The collinear points
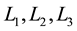 are linearly unstable, while the triangular points
are linearly unstable, while the triangular points
 are linearly stable for the mass ratio of the primaries less than 0.03852.
are linearly stable for the mass ratio of the primaries less than 0.03852.
Researches on the sites and stability of the libration points of the CR3BP with perturbations have achieved ample attention in recent times. [3] indicated that small particles were equally influenced by the gravitation and light radiation force as they moved toward luminous celestial bodies. [4] [5] established that the presence of direct solar radiation pressure caused a variation in the sites of the libration points of the CR3BP. He called the CR3BP, photogravitational when one or both of the masses of the primaries were discharges of radiation. Researchers [6] -[10] have examined the existence of libration points and their linear stability in the photogravitational CR3BP.
[11] [12] studied a modified CR3BP by considering the influence from a belt (circular cluster of material points) for planetary systems and found that the likelihood to get libration points around the inner part of the belt was greater than the one nigh the outer part. The impact of the belt makes the configuration of the dynamical system altered such that new libration points emerge under certain condition [13] - [16] .
The primaries in CR3BP are generally considered to be spherical in shape, whereas in real situations, numerous celestial bodies are non-spherical (e.g. the Earth, Jupiter, Saturn, Regulus stars are oblate). The oblateness of the planets causes large deviations from a two-body orbit. The most salient instance of disturbance due to oblateness in the solar system is the orbit of the fifth satellite of Jupiter, Amalthea. This planet is extremely oblate and the satellite’s orbit is exceptionally small that its line of apsides progresses approximately 900˚ in one year [17] . This vindicates the incorporation of oblateness of the primaries in the study of CR3BP [18] - [25] .
The orbital effects of the oblateness up to the quadrupole, i.e. J2, and the octupole, i.e. J4, on the orbital motion of a particle in the field of a non-spherical body have been worked out in the general case of an arbitrarily oriented spin axis [26] . [22] certified that the sites of the triangular libration points and their linear stability were influenced by the oblateness up to J4 of the bigger primary in the CR3BP. [27] examined the effects of photogravitational force and oblateness in the perturbed restricted three-body problem. [15] analyzed analytically and numerically the effects of oblateness up to J2 of the smaller primary and gravitational potential from the belt on the linear stability of libration points in the photogravitational CR3BP. [16] explored the combined effect of radiation and oblateness up to J2 of both primaries, together with additional gravitational potential from the circumbinary belt on the motion of an infinitesimal body in the binary stellar systems within the frame work of CR3BP. [9] studied the effects of oblateness up to J4 of the smaller primary and gravitational potential from a belt, on the linear stability of triangular libration points in the photogravitational CR3BP. [24] looked at the effects of oblateness of both primaries up to zonal harmonic J4 and gravitational potential from the belt on the linear stability of the triangular libration points in the CR3BP.
Here, our intention is to look into the resultant effect of radiation of the bigger primary, oblateness up to the zonal harmonic J4 of the smaller primary and gravitational potential from the belt on the sites and stability of collinear libration points in the CR3BP.
The manuscript is structured in five units. Unit 2 deals with the mathematical formulation of the problem, while Unit 3 is dedicated to the determination of the sites of the collinear libration points. The linear stability of collinear points and the conclusion are presented in Units 4 and 5 respectively.
2. Mathematical Formulation of Model
2.1. The Problem
Let
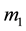 and
and
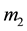 be the masses of the primaries with
be the masses of the primaries with , and let
, and let
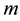 be the mass of the infinitesimal body moving in the plane of motion of the primaries. The positions of the primaries are defined with respect to a rotating coordinate frame oxyz whose x-axis overlaps with the line connecting them and whose origin coincides with the center of mass of
be the mass of the infinitesimal body moving in the plane of motion of the primaries. The positions of the primaries are defined with respect to a rotating coordinate frame oxyz whose x-axis overlaps with the line connecting them and whose origin coincides with the center of mass of
 and
and . The y-axis is perpendicular to the x-axis and the z-axis is normal to the orbital plane of the primaries. Let r1 be the distance between m and m1, r2 the distance between m and m2; and R the distance between
. The y-axis is perpendicular to the x-axis and the z-axis is normal to the orbital plane of the primaries. Let r1 be the distance between m and m1, r2 the distance between m and m2; and R the distance between
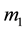 and
and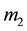 . The coordinates of m1, m2 and m are (x1, 0), (x2, 0) and (x, y) correspondingly. Our aim is to find the equations of motion of
. The coordinates of m1, m2 and m are (x1, 0), (x2, 0) and (x, y) correspondingly. Our aim is to find the equations of motion of
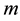 under the influence of radiation of
under the influence of radiation of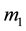 , oblateness up to J4 of the smaller primary, and a circumbinary belt centred at the origin of the coordinate system oxyz (see Figure 1).
, oblateness up to J4 of the smaller primary, and a circumbinary belt centred at the origin of the coordinate system oxyz (see Figure 1).
2.2. The Kinetic Energy
The kinetic energy (K.E) of the infinitesimal body in the barycentric coordinate system oxyz rotating about z-axis with uniform angular velocity
 Figure 1, is given as
Figure 1, is given as
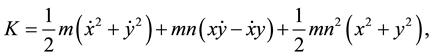 (1)
(1)
where over dot represents differentiation with respect to time t.
2.3. Force Due to Radiation Pressure
Now, since the radiation pressure force



where

2.4. Potential Due to an Oblate Body
In free space the gravitational potential exterior to an oblate body with its mass distributed symmetrically about its equator, can be expanded in terms of Legendre polynomials in the form

Figure 1. The planar configuration of the problem.
[28] . Equation (3) is expressed in standard spherical coordinates, with f the longitude and q representing the angle between the body’s symmetry axis and the vector to a particle ro (i.e., the colatitudes). Ro is the mean radius of the oblate body. The terms


J2n are dimensionless coefficients that characterize the size of non spherical components of the potential, called the zonal harmonic coefficients. Since the present study is concerned with planar problem, assuming the equatorial plane of the smaller primary coincides with the plane of motion, then with

We denote the oblateness coefficient for the smaller primary as Bi,
2.5. Potential Due to the Belt
The gravitational potential from belt (circular cluster of material points) centered at the origin of a coordinates system oxyz, Figure 1 as specified by [29] is

where






2.6. The Potential Energy of the Infinitesimal Body
The potential energy of the infinitesimal body, under the influence of the oblateness up to J4 of smaller primary, radiation of the bigger primary and the circumbinary belt, now takes the form

with


2.7. The Equations of Motion
We start from Lagrangian (L) of the problem which is the kinetic energy minus the potential energy of the infinitesimal body. That is
or

where
Subsequently, we obtain the equations of motion of the infinitesimal body as

To covert the variables to non dimensional, we choose unit for the mass as the sum of the masses of the primaries, the unit of length as the distance between the primaries and unit of time is such that the gravitational
constant is unit. Consequently,



dimensionless synodic coordinate system, the equations of motion (10) reduce to

with

and n is the mean motion, given by [24] as


3. Locations of Collinear Libration Points
We now search for possible collinear libration points of the infinitesimal mass in the rotating reference frame. The libration points are positions of gravitational balance between the primaries. At these points the two finite masses would exert zero net force on the infinitesimal mass, in effect, allowing the infinitesimal mass to have zero velocity in the rotating frame of reference. That is the libration points satisfy

and

Now, an evident solution of Equation (15) is y = 0, corresponding to the collinear libration points (the libration points which lie on the x-axis). This deciphers to

Equation (16) reduces to those of [1] , in the absence of the perturbations. That is when

with three collinear points



If we consider the effects of the potential from the belt only (i.e.

[16] showed that whenever



(18) will have five collinear points (Figure 3).
Now, using Equation (16) and with the help of the MATLAB (R2007b) software package, we obtain the coordinates of the collinear libration points for different cases as classified in the following order which are portrayed in Table 1:
1) Absence of radiation, oblateness and potential from the belt (classical case).
2) Radiation of the bigger primary only.
3) Potential from the belt only.
4) Oblateness of the smaller primary up to J2 only.
5) Oblateness of the smaller primary up to J4 only.
6) Radiation of the bigger primary, oblateness of the smaller primary up to J4 and potential from the belt.
The combined effect of these perturbations on the collinear points is given in Table 2.
In the absence of the perturbations (i.e.




Figure 2. Disposition of the collinear points in the classical case.
Figure 3. Disposition of the collinear points under the effects of the belt.
Table 1. Positions of the collinear points when µ = 0.35, q1 = 0.98, B1 = 0.01, B2 = 0.005 and Mb = T = 0.01, rc = 0.8789.
Table 2. Combined effects of the perturbations on the collinear points when m = 0.35, T = 0.01, rc = 0.8789.
potential from the belt only (i.e.

4. Linear Stability of the Collinear Points
To study the stability of a libration point (x0, y0), we employ small displacement






The superscript “0” indicates that the partial derivatives have been evaluated at the libration point under consideration (x0, y0).
Let solutions of the equations of (19) be


On expanding the determinant we obtain the characteristic equation equivalent to the variational equations of (19) as

Now, we obtain the second partial derivatives as:
Figure 4. Disposition of the collinear points under the combined effects of the perturbations.

The partial derivatives computed at any collinear libration points (x0, 0), are



Substituting these values in Equation (21), the characteristic equation reduces to

where
The libration point is stable if all the roots of the characteristic equation (26) are either negative real numbers or distinct pure imaginary numbers or real parts of the complex numbers are negative.
The roots of the characteristic equation (26) for the libration points Li (i = 1, 2, 3), Lnj (j = 1, 2, 3, 4) of Table 1 are presented in Tables 3-9 correspondingly.
Studying Tables 3-9, we find that all the collinear libration points Li (i = 1, 2, 3) and Ln2 are unstable (Table 3, Table 4, Table 5, Table 7), whereas the additional new collinear points Ln1, Ln3 and Ln4 are stable (Table 6, Table 8, Table 9).
5. Conclusion
The collinear libration points are investigated in a modified CR3BP when the bigger primary is a source of radiation, the smaller primary is an oblate spheroid; and the bodies are surrounded by a belt (circular cluster of material points). We have established the equations that govern the motion of the infinitesimal body under the
Table 3. Stability of L1.
Table 4. Stability of L2.
Table 5. Stability of L3.
Table 6. Stability of Ln1.
Table 7. Stability of Ln2.
Table 8. Stability of Ln3.
Table 9. Stability of Ln4.
influence of radiation of the bigger primary, oblateness up to the zonal harmonics J4 of the smaller primary and gravitational potential from the belt. The equations are affected by the aforementioned perturbations. Numerically, we have determined the positions of the collinear libration points and investigated the resultant effect of the aforesaid perturbations on them. It is found that in count to the three libration points L1, L2, L3 in the classical problem, there emerge four new collinear points which we call Ln1, Ln2, Ln3 and Ln4. Ln1 and Ln2 arise from the effect of the potential from the belt, whereas Ln3 and Ln4 stem from the influence of the oblateness up to the zonal harmonics J4 of the smaller primary. Due to the pooled impact of the aforesaid perturbations, the collinear points L1 and L3 advance toward the primaries while Ln3 moves away from the primaries; and L2 and Ln1 tend towards the smaller primary as Ln2 and Ln4 come closer to the bigger primary. Despite the influence of radiation of the bigger primary, oblateness up to the zonal harmonics J4 of the smaller primary and gravitational potential from the belt, the collinear libration points Li (i = 1, 2, 3) as in the classical case, remain unstable. However, all the additional new collinear points are stable except Ln2. The existence of stable new collinear points can be utilized as stations for artificial satellites.
Cite this paper
JagadishSingh,Joel JohnTaura, (2015) Collinear Libration Points in the Photogravitational CR3BP with Zonal Harmonics and Potential from a Belt. International Journal of Astronomy and Astrophysics,05,155-165. doi: 10.4236/ijaa.2015.53020
References
- 1. Szebehely, V. (1967) Theory of Orbits: The Restricted Problem of Three Bodies. Academic Press, New York.
- 2. Valtonen, M. and Karttunen, H. (2006) The Three-Body Problem. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511616006 - 3. Poynting, J.H. (1903) Radiation in the Solar System: Its Effect on Temperature and Its Pressure on Small Bodies. Philosophical Transactions of the Royal Society of London A, 202, 525-552.
http://dx.doi.org/10.1098/rsta.1904.0012 - 4. Radzievskii, V.V. (1950) The Restricted Problem of Three-Body Taking Account of Light Pressure. Astronomicheskii-Zhurnal, 27, 250-256.
- 5. Radzievskii, V.V. (1953) The Space Photogravitational Restricted Three-Body Problem. Astronomicheskii-Zhurnal, 30, 225.
- 6. Bhatnagar, K.B. and Chawla, J.M. (1979) A Study of the Lagrangian Points in the Photogravitational Restricted Three-Body Problem. Indian Journal of Pure and Applied Mathematics, 10, 1443-1451.
- 7. Simmons, J.F.L., McDonald, J.C. and Brown, J.C. (1985) The Three-Body Problem with Radiation Pressure. Celestial Mechanics, 35, 145-187.
http://dx.doi.org/10.1007/BF01227667 - 8. Das, M.K., Narang, P., Mahajan, S. and Yuasa, M. (2008) Effect of Radiation on the Stability of Equilibrium Points in the Binary Stellar Systems: RW-Monocerotis, Krüger 60. Astrophysics Space Science, 314, 261.
http://dx.doi.org/10.1007/s10509-008-9765-z - 9. Singh, J. and Taura, J.J. (2014) Stability of Triangular Libration Points in the Photogravitational Restricted Three-Body Problem with Oblateness and Potential from a Belt. Journal of Astrophysics and Astronomy, 35, 107-119.
http://dx.doi.org/10.1007/s12036-014-9299-4 - 10. Singh, J. and Taura, J.J. (2015) Triangular Libration Points in the CR3BP with Radiation, Triaxiality and Potential from a Belt. Differential Equations and Dynamical System.
http://dx.doi.org/10.1007/s12591-015-0243-0 - 11. Jiang, I.G. and Yeh, L.C. (2004) The Drag-Induced Resonant Capture for Kuiper Belt Objects. Monthly Notices of the Royal Astronomical Society, 355, L29-L32.
http://dx.doi.org/10.1111/j.1365-2966.2004.08504.x - 12. Jiang, I.G. and Yeh, L.C. (2004) On the Chaotic Orbits of Disk-Star-Planet Systems. The Astronomical Journal, 128, 923-932.
http://dx.doi.org/10.1086/422018 - 13. Jiang, I.G. and Yeh, L.C. (2003) Bifurcation for Dynamical Systems of Planet-Belt Interaction. International Journal of Bifurcation and Chaos, 13, 617-630.
http://dx.doi.org/10.1142/s0218127403006807 - 14. Yeh, L.C. and Jiang, I.G. (2006) On the Chermnykh-Like Problems: II. The Equilibrium Points. Astrophysics and Space Science, 306, 189-200.
http://dx.doi.org/10.1007/s10509-006-9170-4 - 15. Kushvah, B.S. (2008) Linear Stability of Equilibrium Points in the Generalized Photogravitational Chermnykh’s Problem. Astrophysics and Space Science, 318, 41-50.
- 16. Singh, J. and Taura, J.J. (2013) Motion in the Generalized Restricted Three-Body Problem. Astrophysics and Space Science, 343, 95-106.
http://dx.doi.org/10.1007/s10509-012-1225-0 - 17. Moulton, F.R. (1914) An Introduction to Celestial Mechanics. 2nd Edition, Dover, New York.
- 18. Sharma, R.K. (1987) The Linear Stability of Libration Points of the Photogravitational Restricted Three-Body Problem When the Smaller Primary Is an Oblate Spheroid. Astrophysics and Space Science, 135, 271-281.
http://dx.doi.org/10.1007/BF00641562 - 19. Kalvouridis, T.J. (1997) The Oblate Spheroids Version of the Photo-Gravitational 2+2 Body Problem. Astrophysics and Space Science, 246, 219-227.
http://dx.doi.org/10.1007/BF00645642 - 20. Singh, J. and Umar, A. (2013) Application of Binary Pulsars to Axisymmetric Bodies in the Elliptic R3BP. Astrophysics and Space Science, 348, 393-402.
http://dx.doi.org/10.1007/s10509-013-1585-0 - 21. Abdul Raheem, A. and Singh, J. (2006) Combined Effects of Perturbations, Radiation and Oblateness on the Stability of Equilibrium Points in the Restricted Three-Body Problem. Astronomical Journal, 131, 1880-1885.
http://dx.doi.org/10.1086/499300 - 22. Abouelmagd, E.I. (2012) Existence and Stability of Triangular Points in the Restricted Three-Body Problem with Numerical Applications. Astrophysics and Space Science, 342, 45-53.
http://dx.doi.org/10.1007/s10509-012-1162-y - 23. Singh, J. and Taura, J.J. (2014) Effects of Triaxiality, Oblateness and Gravitational Potential from a Belt on the Linear Stability of L4,5 in the Restricted Three-Body Problem. Journal of Astrophysics and Astronomy, 35, 729-743.
http://dx.doi.org/10.1007/s12036-014-9308-7 - 24. Singh, J. and Taura, J.J. (2014) Effects of Zonal Harmonics and a Circular Cluster of Material Points on the Stability of Triangular Equilibrium Points in the R3BP. Astrophysics and Space Science, 350, 127-132.
http://dx.doi.org/10.1007/s10509-013-1719-4 - 25. Singh, J. and Taura, J.J. (2014) Combined Effect of Oblateness, Radiation and a Circular Cluster of Material Points on the Stability of Triangular Libration Points in the R3BP. Astrophysics and Space Science, 351, 499-506.
http://dx.doi.org/10.1007/s10509-014-1860-8 - 26. Renzetti, G. (2013) Satellite Orbital Precessions Caused by the Octupolar Mass Moment of a Non-Spherical Body Arbitrarily Oriented in Space. Journal of Astrophysics and Astronomy, 34, 341-348.
http://dx.doi.org/10.1007/s12036-013-9186-4 - 27. Abouelmagd, E.I. (2013) The Effect of Photogravitational Force and Oblateness in the Perturbed Restricted Three-Body Problem. Astrophysics and Space Science, 346, 51-69.
http://dx.doi.org/10.1007/s10509-013-1439-9 - 28. Peter, I.D. and Lissauer, J.J. (2007) Planetary Science. Cambridge University Press, New York.
- 29. Miyamoto, M. and Nagai, R. (1975) Three-Dimensional Models for the Distribution of Mass in Galaxies. Publications of the Astronomical Society of Japan, 27, 533-543.











