International Journal of Astronomy and Astrophysics
Vol.05 No.02(2015), Article ID:57067,4 pages
10.4236/ijaa.2015.52012
Five Dimensional String Universes in Lyra Manifold
Mahbubur Rahman Mollah1, Kangujam Priyokumar Singh2, Koijam Manihar Singh3
1Department of Mathematics, Commerce College Kokrajhar, Kokrajhar, BTC, Assam, India
2Department of Mathematical Sciences, Bodoland University, Kokrajhar, BTC, Assam, India
3Department of Mathematics Sciences, National Institute of Technology Manipur, Imphal, India
Email: mr.mollah123@gmail.com, pk_mathematics@yahoo.co.in, drmanihar@rediffmail.cim
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 February 2015; accepted 8 June 2015; published 11 June 2015
ABSTRACT
Considering five dimensional plane symmetric metric, we discuss a model universe with different situations, by solving the modified Einstein field equations within the framework of Lyra geometry. We obtain many interesting realistic solutions governing the present day model of the universe. Physical and kinematical properties of the models are discussed in detail.
Keywords:
Cosmic Strings, Lyra Geometry, Dark Energy, Evolution, Clouds, Early Universe, Dark Matter

1. Introduction
A lot of remarkable knowledge of cosmology is made by various experimental and theoretical results which have been made still today. But still now it is difficult to explain exactly the physical situation of the formation of our universe at the very early stage. To describe the events at the early stages of the universe, we are required to develop and study the concept of string theory. It is believed that universe may have many phase transitions after big-bang.
Einstein formulation of General Relativity is the foundation of other geometric theories in order to explain the actual gravitational phenomena. A more general theory in which both gravitation and electromagnetism were described geometrically was proposed by [1] . Later, [2] suggested a modification of Riemannian geometry by introducing a gauge function which removed the non-integrability condition of the length of a vector under parallel transport, which was known as Lyra’s geometry. In Lyra’s geometry, the connection is metric preserving as Riemannian geometry, and length transfers as integrable in contrast to Weyl’s geometry. He also introduced a gauge function into the structure-less manifold, as a result of which a displacement field arose naturally. This alternating theory is of interest since it produces effects similar to Einstein’s theory.
Many authors have investigated cosmology in Lyra’s geometry with both a constant displacement field and time dependent one. Also cosmological models in the frame work of Lyra’s geometry in different contexts are investigated by [3] - [11] . Cosmological models based on Lyra’s manifold with constant displacement field vector were also studied by Bhamra [12] - [18] . But with this condition it is found as one of conveniences and there is no priori reason for it. Recently, several authors like [19] - [24] have studied cosmological models in the frame work of Lyra’s geometry in various contexts.
We know that the constant vector displacement field in Lyra’s geometry plays the role of cosmological constant in the normal general relativistic study as suggested by [25] . Also, [26] shows that the scalar-tensor treatment based on Lyra’s geometry predicts the same effects, within observational limits, as the Einstein theory.
As the necessity of study of higher-dimensional space-time in this field aiming to unify gravity with other in- teractions, the concept of extra dimension is relevant in cosmology, particularly for the early stage of universe and theoretically the present four dimensional stage of the universe may have been preceded by a multi-dimen- sional stage. So, in this paper we discussed about the five dimensional cosmological models in Lyra’s geometry by considering plane symmetric metric with some conditions to find out some solutions which were realistic with the observational facts.
2. Field Equations and Their Solutions
Here we consider the five dimensional plane symmetric metric in the form
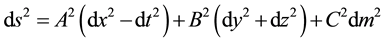 (1)
(1)
where A, B and C are functions of time “t” only.
Einstein’s field equations based on Lyra’s Geometry is
 (2)
(2)
where we use the units in which 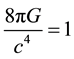 (Wesson 1992; Baysal et al. 2001; Bali and Dave 2002), and
(Wesson 1992; Baysal et al. 2001; Bali and Dave 2002), and  is the displacement vector defined by
is the displacement vector defined by
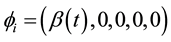 (3)
(3)
The energy momentum tensor of cosmic strings is
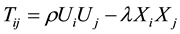 (4)
(4)
where, 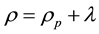 , is the energy density of the cloud of string,
, is the energy density of the cloud of string,  being the rest energy density of particles attached to the strings and λ is the string tension density.
being the rest energy density of particles attached to the strings and λ is the string tension density. 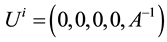 is the five velocity vector for the cloud of particles and
is the five velocity vector for the cloud of particles and  is the direction of strings. Moreover the directions of strings satisfies
is the direction of strings. Moreover the directions of strings satisfies
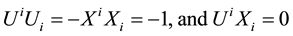 (5)
(5)
Using the commoving coordinate system and Equations (3), (4) and (5), the field equations (2) for the metric (1) yield
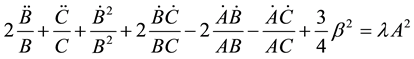 (6)
(6)
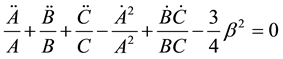 (7)
(7)
 (8)
(8)
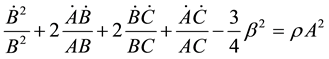 (9)
(9)
Now, (7) and (8) give
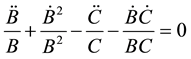 (10)
(10)
A solution of (10) is


Thus, (11) and (12) together with (7) and (8) give

And

Now from (9), we have,

And from (6), we have,

Therefore, from the relation 

For the metric (1), the expansion factor 

and

Therefore, from Equations (18) and (19) we have

Here, the deceleration parameter 

3. Physical Interpretations of the Solutions
In the universe we obtain here, it is seen that the energy density has a finite value at the beginning and then it gradually decreases until it shrinks almost to zero at infinite time. The string tension density is also found to be a decreasing function of time until it almost tends to zero as time tends to infinity. Here, with the advent of time, the density of the string decreases more rapidly than density of the particles attached to them. Thus, our universe ultimately becomes a universe dominated by particles, where strings are becoming invisible in course of time. Here, for our universe, we see that the special dimensions expand isotropically, implying the expansion of our universe which bears testimony to our universe being a realistic one.
Moreover, from the expressions of the expansion factor and deceleration parameter obtained here, it can be inferred that our universe is expanding, but the rate of expansion is decreasing slowly until at infinite time where it is expanding at a constant rate. Here, the gauge function 

Interacting with the pressureless matter here, the displacement vector can play the same role as a cosmological constant (term). Thus, it will be nice to study further whether the displacement vector plays a role in disturbing the rate of expansion of the universe.
Though our model universe seems to be anisotropic in the beginning it will become gradually an isotropic one until it becomes perfectly isotropic at time given by
anisotropic parameter is produced in this universe, its anisotropy does not promote anisotropy in the expansion, and thus in course of time our universe becomes an isotropic one.
References
- Weyl, H. (1918) Sitzungsberichte Der Preussischen Akademie Der Wissenschaften. Academy Wiss, Berlin, 465.
- Lyra, G. (1951) Über-eine Modifikation der Riemannschen Geometrie. Mathematische Zeitschrift, 54, 52-64. http://dx.doi.org/10.1007/BF01175135
- Pradhan, A. and Kumar, S.S. (2009) Plane Symmetric Inhomogeneous Perfect Fluid Universe with Electromagnetic Field in Lyra Geometry. Astrophysics and Space Science, 321, 137-146. http://dx.doi.org/10.1007/s10509-009-0015-9
- Pradhan, A. and Mathur, P. (2009) Inhomogeneous Perfect Fluid Universe with Electromagnetic Field in Lyra Geometry. Fizika B, 18, 243-264. (gr-qc/0806.4815)
- Pradhan, A. and Yadav, P. (2009) Accelerated Lyra’s Cosmology Driven by Electromagnetic Field in Inhomogeneous Universe. International Journal of Mathematics and Mathematical Sciences (IJMMS), 2009, Article ID: 471938, 20 p. http://dx.doi.org/10.1155/2009/471938
- Pradhan, A. (2009) Cylindrically Symmetric Viscous Fluid Universe in Lyra Geometry. Journal of Mathematical Physics, 50, 022501-022513. http://dx.doi.org/10.1063/1.3075571
- Pradhan, A., Amirhashchi, H. and Zainuddin, H. (2011) A New Class of Inhomogeneous Cosmological Models with Electromagnetic Field in Normal Gauge for Lyra’s Manifold. International Journal of Theoretical Physics, 50, 56-69. http://dx.doi.org/10.1007/s10773-010-0493-0
- Pradhan, A. and Singh, A.K. (2011) Anisotropic Bianchi Type-I String Cosmological Models in Normal Gauge for Lyra’s Manifold with Constant Deceleration Parameter. International Journal of Theoretical Physics, 50, 916-933. http://dx.doi.org/10.1007/s10773-010-0636-3
- Yadav, A.K. (2010) Lyra’s Cosmology of Inhomogeneous Universe with Electromagnetic Field. Fizika B, 19, 53-80.
- Agarwal, S., Pandey, R and Pradhan, A. (2011) LRS Bianchi Type II Perfect Fluid Cosmological Models in Normal Gauge for Lyra’s Manifold. International Journal of Theoretical Physics, 50, 296-307. http://dx.doi.org/10.1007/s10773-010-0523-y
- Singh, R.S. and Singh, A. (2012) A New Class of Magnetized Inhomogeneous Cosmological Models of Perfect Fluid Distribution with Variable Magnetic Permiability in Lyra Geometry. Electronic Journal of Theoretical Physics, 9, 265- 282.
- Bhamra, K.S. (1974) A Cosmological Model of Class One in Lyra’s Manifold. Australian Journal of Physics, 27, 541- 547. http://dx.doi.org/10.1071/PH740541
- Kalyanshetti, S.B. and Waghmode, B.B. (1982) A Static Cosmological Model in Einstein-Cartan Theory. General Relativity and Gravitation, 14, 823-830.
- Soleng, H.H. (1987) Cosmologies Based on Lyra’s Geometry. General Relativity and Gravitation, 19, 1213-1216.
- Sen, D.K. and Vanstone, J.R. (1972) On Weyl and Lyra Manifolds. Journal of Mathematical Physics, 13, 990-994. http://dx.doi.org/10.1063/1.1666099
- Karade, T.M. and Borikar, S.M. (1978) Thermodynamic Equilibrium of a Gravitating Sphere in Lyra’s Geometry. General Relativity and Gravitation, 9, 431-436.
- Reddy, D.R.K. and Innaiah, P. (1986) A Plane Symmetric Cosmological Model in Lyra Manifold. Astrophysics and Space Science, 123, 49-52. http://dx.doi.org/10.1007/BF00649122
- Reddy, D.R.K. and Venkateswarlu, R. (1987) Birkhoff-Type Theorem in the Scale Covariant Theory of Gravitation. Astrophysics and Space Science, 136, 191-194.
- Asgar, A. and Ansary, M. (2014) Accelerating Bianchi Type-VI0 Bulk Viscous Cosmological Models in Lyra Geometry. Journal of Theoretical and Applied Physics, 8, 219-224. http://dx.doi.org/10.1007/s40094-014-0151-7
- Kumari, P., Singh, M.K. and Ram, S. (2013) Anisotropic Bianchi Type-III Bulk Viscous Fluid Universe in Lyra Geometry. Advances in Mathematical Physics, 2013, Article ID: 416294. http://dx.doi.org/10.1155/2013/416294
- Asgar, A. and Ansary, M. (2014) Bianchi Type-V Universe with Anisotropic Dark Energy in Lyra’s Geometry. The African Review of Physics, 9, 145-151.
- Zia, R. and Singh, R.P. (2012) Bulk Viscous Inhomogeneous Cosmological Models with Electromagnetic Field in Lyra Geometry. Romanian Journal of Physics, 57, 761-778.
- Asgar, A. and Ansary, M. (2014) Exact Solutions of Axially Symmetric Bianchi Type-I Cosmological Model in Lyra Geometry. IOSR Journal of Applied Physics (IOSR-JAP), 5, 1-5. www.iosrjournals.org
- Panigrahi, U.K. and Nayak, B. (2014) Five Dimensional Stiff Fluids with Variable Displacement Vector in Lyra Manifold. International Journal of Mathematical Archive, 5, 123-128. www.ijma.info
- Halford, W.D. (1970) Cosmological Theory Based on Lyra’s Geometry. Australian Journal of Physics, 23, 863-869. http://dx.doi.org/10.1071/PH700863
- Halford, W.D. (1972) Scalar-Tensor Theory of Gravitation in a Lyra Manifold. Journal of Mathematical Physics, 13, 1699-1703. http://dx.doi.org/10.1063/1.1665894

