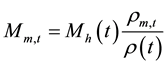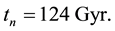International Journal of Astronomy and Astrophysics
Vol.05 No.01(2015), Article ID:54869,7 pages
10.4236/ijaa.2015.51004
Distribution of Mass and Energy in Five General Cosmic Models
Fadel A. Bukhari
Department of Astronomy, Faculty of Science, King Abdulaziz University, Jeddah, KSA
Email: fdbukhari@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 March 2015; accepted 17 March 2015; published 20 March 2015
ABSTRACT
Distributions of the universe horizon distance and universe horizon volume were investigated in the light of five general cosmic models which were constructed in a previous study. Both distributions increase so slowly up to t ≈ 21.5444 Myr, then they start raising very fast up to t ≈ 60 Gyr. Afterwards, they increase again very slowly until t ≈ 124 Gyr. Distributions of mass of radiation, matter and dark energy within the horizon volume of the universe were also studied in the five general cosmic models. The masses of both radiation and matter decrease gradually with time while the mass of dark energy increases. The mass of radiation prevailed in the early universe up to t ≈ 34627.5 - 55916.2 yr, where it becomes equal to the mass of matter. Then the mass of matter dominated until t ≈ 9.4525 - 10.0632 Gyr, where it becomes equal to the mass of dark energy. Thenceforward, the mass of dark energy prevails the universe. The cosmic space becomes approximately matter empty in the so far future of the universe.
Keywords:
General Cosmic Models, Distribution of Mass and Energy

1. Introduction
In a previous study [1] the distribution of density parameters of radiation, matter and dark energy were investigated in details in five general cosmic models. Hence, it would be interesting to study the distributions of equivalent mass of radiation, mass of matter and equivalent mass of dark energy within the horizon volume of the universe in the general models.
Therefore, it is necessary to start this study by investigating the distributions of the horizon distance and horizon volume of the universe in the general models at different time intervals depending on the bases discussed in [2] . Description of methodology is given in Section 2 while algorithm would be illustrated in Section 3. Results and discussion are presented in Section 4. Conclusion is shown in Section 5.
2. Methodology
We have seen in [2] that the horizon distance and horizon volume of the universe at the present time are respectively
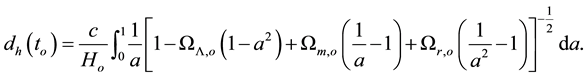 (1)
(1)
 (2)
(2)
where 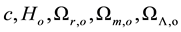 are all defined as in [1] . Thus the horizon distance of the universe at any given time is
are all defined as in [1] . Thus the horizon distance of the universe at any given time is
 (3a)
(3a)
Consequently the change in the horizon distance of the universe in the time interval between two instants of scale factors 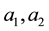 is written as
is written as
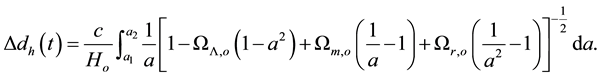 (3b)
(3b)
The horizon volume of the universe at any given time is
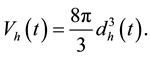 (4)
(4)
It is also obvious from [2] that the total density of the universe is given by
 (5)
(5)
where
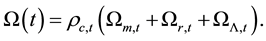 (6)
(6)
 (7)
(7)
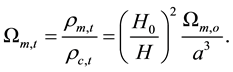 (8)
(8)
 (9)
(9)
 (10)
(10)
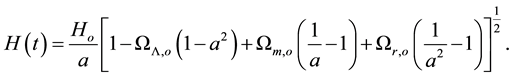 (11)
(11)
Hence, the total mass within the horizon volume of the universe at any given time is expressed as
 (12)
(12)
The mass of matter , the equivalent mass of radiation
, the equivalent mass of radiation 
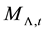
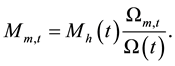
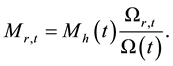
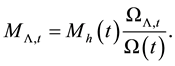
The cosmic time is given by Equation (16) in [1] as
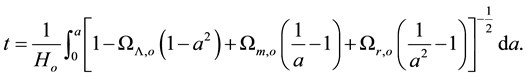
Thus the time interval between two instants with scale factors 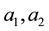
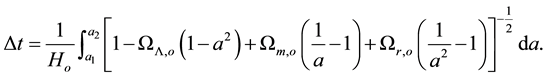
3. Algorithm
In determination of the distributions of 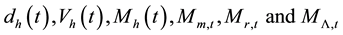
i) Set 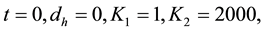


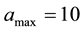
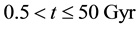
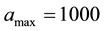
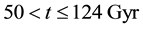
ii) Compute
iii) Start general DO loop 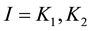
iv)
v) Calculate new value of cosmic time t numerically using(16-b), where
vi) Determinate new value of the universe horizon distance 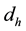
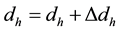
vii) Obtain the corresponding values of 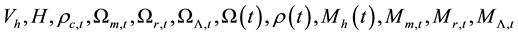
viii) Continue the general DO loop.
4. Results and Discussion
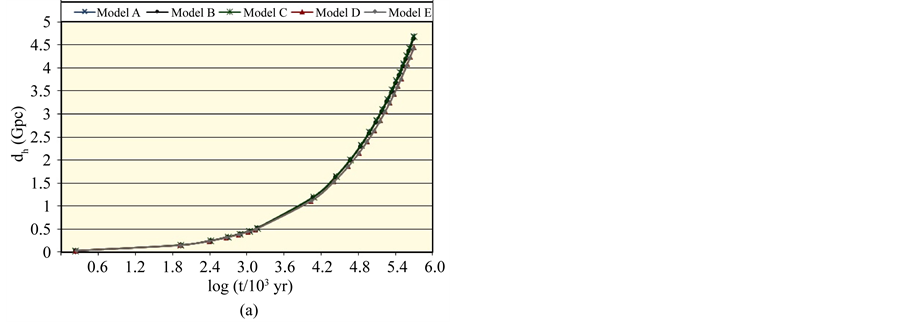
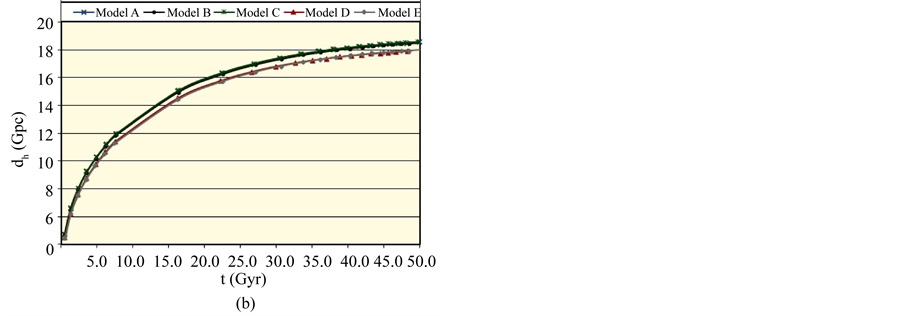
The distribution of the universe horizon distance in the general models up to 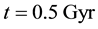
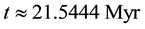
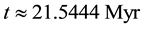
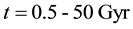
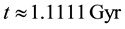
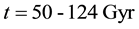
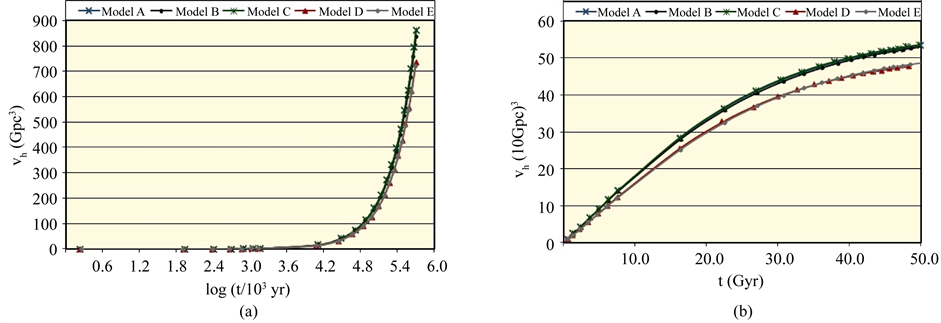
Figure 1. The distribution of the universe horizon distance in the general cosmic models (a) up to t = 0.5 Gyr; (b) in the range t = 0.5 - 50 Gyr; (c) in the range t = 50 - 124 Gyr.
Table 1 shows the universe horizon distances in the general models at special times. These times are the time of radiation-matter mass equivalence
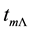
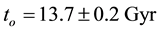
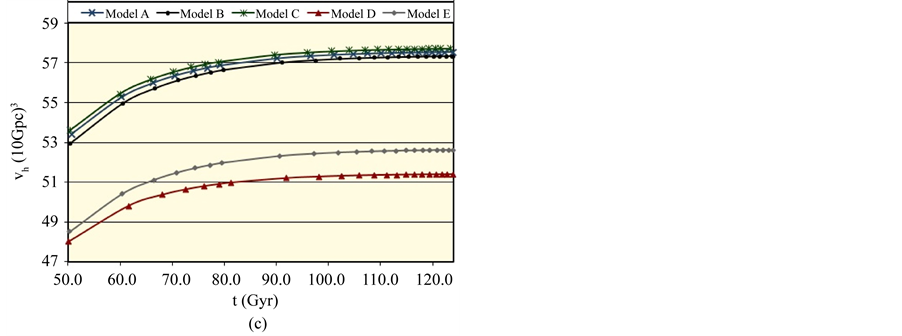
The results illustrated in Figures 1(a)-(c) are supported by those displayed in Figures 2(a)-(c) which show the distributions of the universe horizon volume in the general models in the ranges up to t = 0.5 Gyr, t = 0.5 - 50 Gyr and t = 50 - 124 Gyr respectively. Table 2 presents the universe horizon volumes in the general models at the special times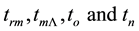
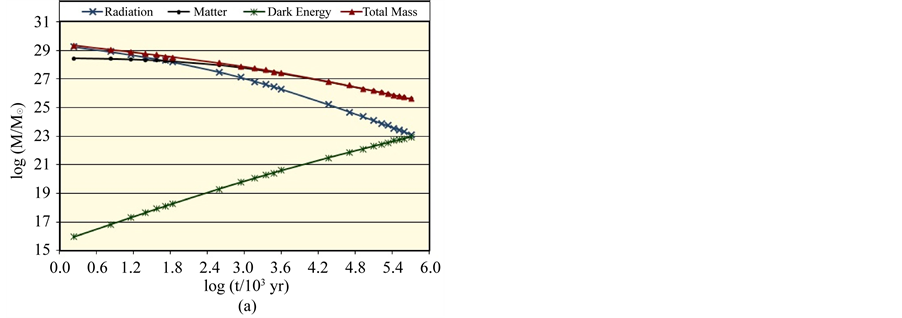
The distribution of mass and energy within the universe horizon volume of the universe in any general model up to 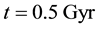



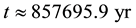
The distribution of mass and energy within the universe horizon volume of the universe in any general model in the range 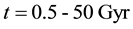
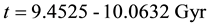
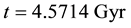
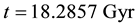
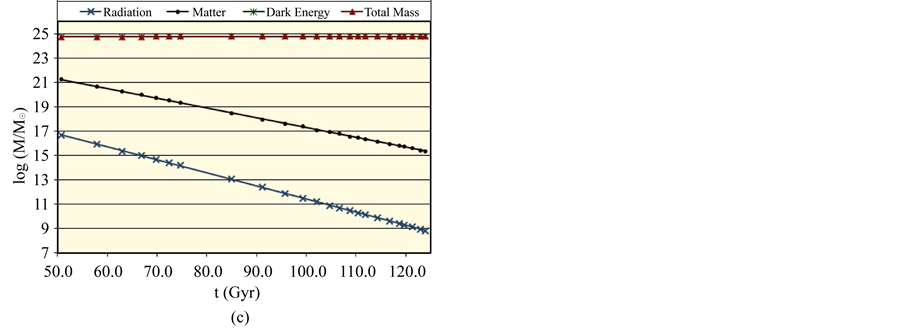
The distribution of mass and energy within the universe horizon volume in any general model in the range
Table 1. Horizon distances of the universe in the general cosmic models at special times.
Figure 2. The distribution of the universe horizon volume in the general cosmic models (a) up to t = 0.5 Gyr; (b) in the range t = 0.5 - 50 Gyr; (c) in the range t = 50 - 124 Gyr.
Table 2. Horizon volumes of the universe in the general cosmic models at special times.
Figure 3. The distribution of mass and energy within the universe horizon volume in any general cosmic model (a) up to t = 0.5 Gyr; (b) in the range t = 0.5 - 50 Gyr; (c) in the range t = 50 - 124 Gyr.
Table 3. Cosmic times at which 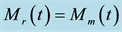
Table 4. Cosmic times at which 
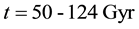
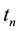
Table 8 shows the equivalent number of the Coma-like clusters to the mass of matter within the universe horizon volume 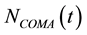
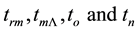
5. Conclusion
In this article distributions of the universe horizon distance and universe horizon volume were determined in the five general cosmic models which were established previously. The two distributions were found increasing slowly up to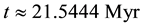
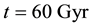
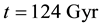
Table 5. Cosmic times at which 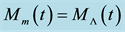
Table 6. Masses of radiation, matter and dark energy within the universe horizon volume in the general cosmic models at
Table 7. Masses of radiation, matter and dark energy within the universe horizon volume in the general cosmic models at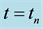
Table 8. Equivalent number of the Coma-like clusters to the mass of matter within the universe horizon volume in the general cosmic models at special times.
universe up to 
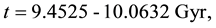
References
- Bukhari, F.A. (2013) Five General Cosmic Models. Journal of King Abdulaziz University: Science, 25.
- Bukhari, F.A. (2013) Cosmological Distances in Five General Cosmic Models. International Journal of Astronomy and Astrophysics, 3, 183-188.