International Journal of Astronomy and Astrophysics
Vol.04 No.04(2014), Article ID:52103,8 pages
10.4236/ijaa.2014.44054
Two Unified Algorithms for Fundamental Planetary Ephemeris
Mohamed Adel Sharaf1, Abdel-Naby Saad Saad2,3, Aisha Abdu Alshaery4
1Department of Astronomy, Faculty of Science, King Abdulaziz University, Jeddah, KSA
2Department of Astronomy, National Research Institute of Astronomy and Geophysics, Cairo, Egypt
3Department of Mathematics, Qassim University, Buraidah, KSA
4Department of Mathematics, College of Science for Girls, King Abdulaziz University, Jeddah, KSA
Email: Sharaf_adel@hotmail.com, Saad6511@gmail.com, alshaary@hotmail.com
Academic Editor: Michael Smith, University of Kent, UK
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 September 2014; revised 25 October 2014; accepted 17 November 2014
ABSTRACT
In the present paper, we established two unified algorithms. The first algorithm is for the transformations between J2000.0 Keplerian orbital elements and B1950.0 elements, while the second is for the transformations between the equatorial orbital elements and the ecliptic orbital elements. Mathematica Modules of the algorithms are given together with some numerical applications.
Keywords:
Spherical Astronomy, Precession, Ephemeris, Orbit Determination

1. Introduction
Precession is a change in the orientation of the rotational axis of a rotating body. In astronomy, precession refers to any of several slow changes in an astronomical body’s rotational or orbital parameters, and especially to the Earth’s precession of the equinoxes. The shift in the position of the Earth’s axis and of the ecliptic caused by forces exerted by the Sun, Moon and planets not only causes a slight change in the angle between the equator and the ecliptic, but also a shift of the vernal equinox by about 1.5˚ per century (1’ per year). This effect is negligibly small for casual observing, but is an important correction for precise observations. To get accurate observations, the International Astronomical Union (IAU) 2000 recommended significant improvements in the definition of the International Celestial Reference System (ICRS) [1] . It follows that changes in Earth’s orbital parameters (e.g. orbital inclination, the angle between Earth’s rotation axis and its plane of orbit) is important to the study of Earth’s climate, in particular to the study of past ice ages.
For precise calculations therefore, the equinox of the coordinate system used must be stated. The equinoxes most frequently used are the equinox of date, equinox J2000 and equinox B1950 [2] and [3] . “Equinox of the date” means that the values used are those for the equator, ecliptic, and vernal equinox for actual date under con- sideration. Such daily alteration of the coordinate system is sensible if one requires the coordinates of a planet, for example, for use in conjunction with the setting circles on an equatorial mounted telescope, or on a transit circle. Since the shift in the Earth’s axis, the orientation of the polar axis of a telescope will also alter. On the other hand, if one wants to study the actual spatial motion of a planet then it is better to use a fixed equinox, such as that for Julian Epoch J2000 (2000 January 1.5 = JD = 2451545.0), which was generally introduced in 1984. Before that, the older equinox B1950 has been used for a long time, and was employed for many stellar catalogues and atlases (such as the SAO Star Catalog and Atlas Coell). The beginning of the Basselian year 1950 (1950 Jan.0.9232 = JD 2433282.423).
On the other hand, there are two standard reference planes to specify the orbits of celestial objects, the equatorial plane of the Earth and the ecliptic plane (the plane of Earth’s orbit around the Sun). However, due to precession, the equatorial and the ecliptic planes are slowly changing their positions relative to the background stars [4] .
In this paper, we established two new unified computational algorithms each one is applicable to get ephemeris in both directions simultaneously. That is to mean it can be used as a switch between: 1) J2000.0 Keplerian orbital elements and B1950.0 elements and 2) between the equatorial orbital elements and the ecliptic orbital elements. Such artifices do not exist in any other numerical ephemeris methods. Furthermore, in our algorithms the number of the utilized equations was reduced via applying some mathematical operations, a matter, which facilitates the computations. Mathematica Modules for the two algorithms are also included.
Finally, it should mentioned that, although all numerical ephemeris methods utilize the same equations, but their accuracy may be differ greatly depending on a) the computational package adopted for their evaluation; b) the form of the equations, such that, the more they are explicit, the more their satiability and accuracy will be.
Due to the quite simple explicit forms of the reduced equations of our algorithms, and the usages of the most power full computational packages of Mathematica, consequently as regarding to that two points a & b, our algorithms may be more accurate than that given by JPL system or other numerical ephemeris methods.
2. Basic Formulations
2.1. Duality of Theorems Relating to the Spherical Triangle
The duality of theorems relating to the spherical triangle [5] was stated as: Any theorem relating the sides and angles of any spherical triangle will remain true when the angles are changed into the supplements of the corresponding sides and the sides into the supplements of the corresponding angles.
2.2. Transformation Formulae between J2000.0 and B1950.0 Keplerian Elements
Given the six orbital elements 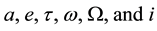 in the B1950.0 reference system, one may compute the corresponding orbital elements for J2000.0-based system (dented by primes):
in the B1950.0 reference system, one may compute the corresponding orbital elements for J2000.0-based system (dented by primes):
・ 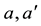 : Semi-major axes in B1950.0, J2000.0 systems.
: Semi-major axes in B1950.0, J2000.0 systems.
・ 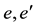 : Eccentricities in B1950.0, J2000.0 systems.
: Eccentricities in B1950.0, J2000.0 systems.
・ 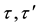 : Pre-center passage times in B1950.0, J2000.0 systems.
: Pre-center passage times in B1950.0, J2000.0 systems.
・ 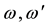 : Argument of pre-center in B1950.0, J2000.0 systems.
: Argument of pre-center in B1950.0, J2000.0 systems.
・  : Longitude of the ascending node in B1950.0, J2000.0 systems.
: Longitude of the ascending node in B1950.0, J2000.0 systems.
・ 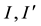 : Inclination in B1950.0, J2000.0 systems.
: Inclination in B1950.0, J2000.0 systems.
where 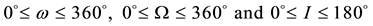 such that for direct motion I ranges from 0˚ to 90˚; for retrograde motion ranges from 90˚ to 180˚. Clearly,
such that for direct motion I ranges from 0˚ to 90˚; for retrograde motion ranges from 90˚ to 180˚. Clearly, 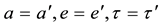 while the angles
while the angles 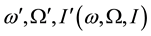 are computed from
are computed from 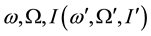 as will be shown soon.
as will be shown soon.
Figure 1 represents the relationship between B1950.0 and J2000.0 reference frames and the orbital plane. The numerical values for the angles 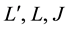 [6] are
[6] are  These values were computed using the values of
These values were computed using the values of  as
as  .
.
Figure 1. The relation between the reference systems B1950.0, J2000.0 and the orbital plane.
2.2.1. The Basic Equations for the Transformation
Applying the duality property (see Section 2.1) to the spherical triangle ABC of Figure 1, we get





From the spherical triangle ABC of Figure 1 we get





Clearly the right hand side of each of the Equations (2) contained mixture of the unknown quantities (dented by primes) and known quantities (without primes) e.g.






2.2.2. The Basic Equations for the Transformation 
By the same way as above, we get for the transformation from 





3. Unified Transformation Formula for J2000.0 and B1950.0 Keplerian Elements
For practical applications, we can unified the two sets of Equations (1) and (2) as:







where
・ 
・ 
・ h, an integer takes the values 

・ 


・ 


・ 
・ The unified formulae for the required elements 





4. Transformation Formulae between Equatorial and Ecliptic Orbital Elements
Let the equatorial orbital elements of celestial body, be denoted by 


From the spherical triangle gNL we get:



Figure 2. The orbit in space with respect to the fundamental planes.
Figure 3. Equatorial and ecliptic orbital elements of celestial body.


Equations (7) are to be used to obtain 

Also





5. Unified Transformation Formulae for Equatorial and Ecliptic Orbital Elements
For practical applications, we can unify the two sets of Equations (7) and (8) as:





where
・ 
・ 
・ h, an integer takes the values 

・ 


・ 


Since the right hand side of each of the above equations is known (note 




6. Computational Developments of J2000.0 and B1950.0 Keplerian Elements Transformations
6.1. Mathematica Module: KeplerB1950TJ2000
・ Purpose
Transfer the Keplerian orbital elements with respect to reference system B1950.0 to the Keplerian orbital elements with respect to reference system J2000.0 and vice versa.
・ Input

・ Output
・ 
・ User defined procedures
Module: arctan (Appendix A).
Module: angle (Appendix A).
・ Module list
6.2. Numerical Examples
Table 1 gives the transformations of the orbital Kepler elements 1950.0 to the corresponding elements J2000.0 and vice versa as computed from the above Module.
7. Computational Developments of Equatorial and Ecliptic Orbital Elements Transformations
7.1. Mathematica Module: TranElements
・ Module list
7.2. Numerical Examples
Table 2 gives the transformations of the ecliptic orbital elements to the equatorial orbital elements and vice versa.
Table 1. The transformations of the orbital Kepler elements 1950.0 to the corresponding elements J2000.0 and vice versa.
Table 2. Transformations of the ecliptic orbital elements to the equatorial orbital elements and vice versa.
In concluding, the present paper introduced two unified and simple algorithms that are capable of executing calculations in both directions and in one program run to the 1) transformations between J2000.0 Keplerian orbital elements and B1950.0 elements and 2) transformations between the equatorial orbital elements and the ecliptic orbital elements. The algorithms are elaborated using Mathematica package, which is qualified for accurate computations. The proposed algorithms are checked by numerical examples given in Table 1 and Table 2.
References
- Capitaine, N. and McCarthy, D. (2004) American Astronomical Society Meeting 204, #28.01. Bulletin of the American Astronomical Society 36, p.694.
- Standish, E.M. (1982) Conversion Positions and Proper Motions from B1950.0 to the IAU System at J2000.0. Astronomy and Astrophysics, 115, 20-22.
- Murray, C.A. (1989) The Transformation of Coordinates between the Systems of B1950.0 and J 2000.0, and the Principal Galactic Axes Referred to J2000.0. Astronomy and Astrophysics, 218, 325-329.
- Aoki, S., Soma, M., Kinoshita, H. and Inoue, K. (1983), Conversion Matrix of Epoch B1950.0 FK 4-Based Positions of Stars to Epoch J2000.0 Positions in Accordance with the New IAU Resolution. Astronomy and Astrophysics, 128, 263-267.
- Todhunter, M.A. (1925) Spherical Trigonometry. Macmillan & Co., London.
- Seidelmann, P.K. (2005) Explanatory Supplement to the Astronomical Almanac. University of Science Books, Sausalito.
Appendix A: The User Defined Procedures
A-1 User defined procedure: angle
Mathematica Module: angle
・ Purpose
To reduce the angle x in radian to the interval
・ Input
The value of x
・ Output
The angle
・ User defined procedures
None
・ Module list
angle x_ : Module, Mod x, 2
・ Notes
1. The above procedure is valid for positive as well as for negative angles.
2. For all values 
3. The given angle x and the reduced angle are the same if
A-2 User defined procedure: Arctan (y/x)
When the inverse function of “tan” is taken an ambiguity arises which has to be cleared up. The angle 







Mathematica Module: arctan
・ Purpose
To find the correct quadrant of the angle 
・ Input
Y, x
・ Output
The angle 
・ User defined procedures
None
・ Module list
・ Notes
The usage of the Mathematica built in ArcTan[y/x] and the function arctan[y, x] of the above procedure for calculating the angle 
・ If 
・ 

・ 

・ If 
・ 
The only case in which ArcTan[y/x] = arctan[y, x] is when












