International Journal of Astronomy and Astrophysics
Vol.4 No.3(2014), Article
ID:48864,8
pages
DOI:10.4236/ijaa.2014.43040
Period Correction and Evolutionary Status of the MACHO Eclipsing Binary System 47.2135.29
Nematollah Riazi1, Maysam Rezvani2
1Physics Department, Shahid Beheshti University, Evin, Tehran, Iran
2Physics Department, Shiraz University International Division, Shiraz, Iran
Email: n_riazi@sbu.ac.ir
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 June 2014; revised 1 July 2014; accepted 1 August 2014
ABSTRACT
The eclipsing binary system which is catalogued in MACHO as 47.2135.29 is analyzed in detail for orbital elements and absolute parameters based on the MACHO observations and the latest values for the distance modulus of LMC. The period of the system is found more accurately, by minimizing the dispersion in the folded light curves. The binary is found to be a young semi-detached binary and is potentially a beta Lyrae system.
Keywords:MACHO, Eclipsing Binaries, Light Curve Analysis

1. Introduction
Eclipsing binary systems have been used for a long time by astronomers to extract reliable information about physical properties (like masses and radii) of stars. They are particularly important since they can be observed even in nearby galaxies [1] . They are also important since they can serve as a means to calibrate other distance indicators [2] -[4] . The MACHO project was a collaboration between astronomers of the Mount Stromolo and Siding Spring observatories, using a 50 inch telescope [5] . Observations included the Large and Small Magellanic Clouds and the Galactic Bulge, using two filters in the blue (4400 - 5900 Å) and red (5900 - 7800 Å) and a 2048 * 2048 CCD imaging system [6] . 11.9 million stars were observed during a 7-year period, leading to a rich database of photometric data. Every object in the database is catalogued by the field number (1 to 82 for LMC and 201 to 213 for SMC), and also the tile number which can have overlap with neighboring tiles. The object identifier is thus in the form Field.Tile.Sequence. The project, although aimed at detecting gravitational lensing by massive dark halo objects, provided a valuable by-product observation of thousands of eclipsing binaries in LMC [7] -[12] . A catalogue of 3031 MACHO EBs in the LMC was published by Derekas, Kiss, and Bedding [13] ; they analyzed a list of 6835 stars classified as possible EBs in the MACHO database. These 6835 possible EBs were identified by their position in the space of parameters such as color, magnitude, and period, more ascribable to eclipses rather than pulsations. In [13] , the authors presented an analysis of the MACHO eclipsing binary light curves in LMC which have been online since 2001. The main aim of these authors was to measure period changes and search for eclipsing binaries with pulsating components. They also reported the general properties of the sample, re-classification, newly determined periods, the color-magnitude diagram and periodluminosity distributions.
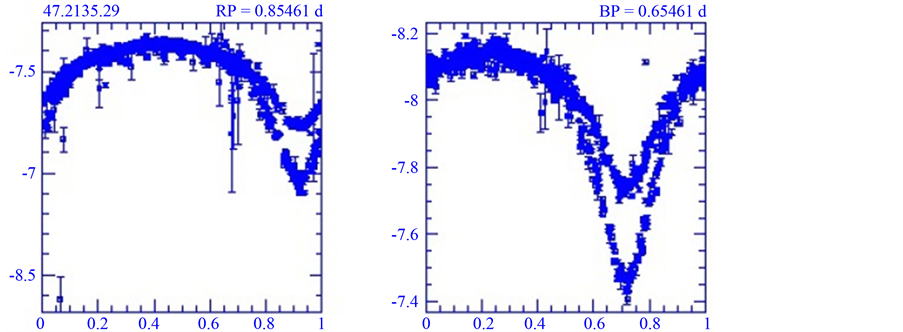
The star 47.2135.29 which is located at RA 4h53m13.555 and Dec-67deg45m14.82s, was observed 792 times, each time with a 300 s exposure time. The mean instrumental magnitude is reported to be −7.588 in red and −8.111 in blue. The period of the system is reported to be 0.85461 days in the MACHO data base [14] , which leads to the tentative light curves shown in Figure 1 and Figure 2.
2. Period Determination and HJD of Minimum
It is obvious from Figure 1 and Figure 2 that the tentative period reported in the database is almost half the actual value. The automated periods were obtained by the Super-smoother algorithm [10] and this algorithm can
 (a) (b)
(a) (b)
Figure 1. The raw light curves of 47.2135.29, based on the tentative period reported in the MACHO data base for red (a) and blue (b) filters.
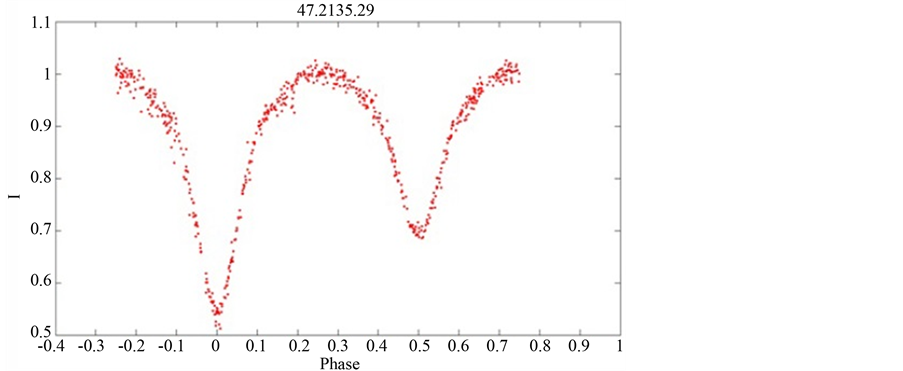
Figure 2. The revised and normalized light curve (normalized intensity versus orbital phase) of 47.2135.29, based on the corrected period (1) for red filter.
lead to incorrect periods at least in two ways: 1) When the depth of the secondary minimum is very shallow, the program cannot detect it and the period obtained is twice the real period, and 2) When the depths of the primary and secondary minima is near to each other, the program cannot distinguish between them and the period reported is half the real value. The case (2) is what is happening in Figure 1. Therefore, we continue with the revised period
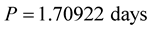 (1)
(1)
As reported by [13] , the period histogram of the MACHO eclipsing binaries shows two modes with periods between 1 and 2 days, while a good proportion of the sample (about 600 stars) have periods between 10 and 200 days. Our star, therefore belongs to the first mode. Note that in these light curves, appropriate phase shifts are implemented to bring the primary minimum to phase 0 or 1, which is a standard practice in eclipsing binary light curves. The correct amount of the phase shift is obtained by fitting a parabola to the primary minima. The phases are calculated using the standard relation
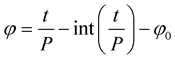 (2)
(2)
in which P is he corrected period, t is the time and φ0 is the required phase shift to bring the primary minimum to the zero phase. Using the calculated phase shift φ0, the modified Julian Date of the primary minimum is found to be
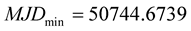 (3)
(3)
Finally, we have converted the instrumental magnitudes to light intensities for each filter which are normalized to one at the out-of-eclipse, maximum light phase. The resulting corrected and normalized light curves for the R and B filters are shown in Figure 2 and Figure 3.
3. Modeling
Eclipsing binary light curve analysis normally requires radial velocity information from the velocity curves. Since no velocity curve is reported yet for the system under investigation, we have used a different approach, using the fact that the system belongs to LMC which has a well estimated distance modulus [6] [15] . It is interesting to note that eclipsing binaries have served as a very useful means to estimate the distance to nearby galaxies (including LMC and SMC) and therefore help to calibrate the cosmological distance scale [3] [12] [15] . The fairly accurately known distance to the system enables us to achieve a consistent absolute solution for the system as explained below. Fortunately, there are reliable computer programs which model an eclipsing binary system to the desired accuracy [16] -[20] . These programs, require, as input, parameters like the mass ratio, inclination angle, Roche potentials, limb and gravity darkening coefficients, etc. The output is the synthesized

Figure 3. The revised and normalized light curve (normalized intensity versus orbital phase) of 47.2135.29, based on the corrected period (1) for blue filter.
light and velocity curves for the specified filter. Some morphological indications from the observational light curve help to a great extent the initial guesses we need to start with. The final set of system parameters is then approached by successive improvements, or by using optimization routines provided by the computer programs. The apparent magnitude, together with the reported distance modulus 18.43 m of the system [3] [6] enables us to find the absolute magnitude (and therefore the total out-of-eclipse luminosity) of the system:
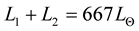 (4)
(4)
We then need an estimate of the mass ratio of the system. To this end, we have used the ratio of the secondary to primary minimum depths of the light curves which is an indicator of the surface temperature ratios. The surface temperatures, in turn, depend on the masses of the components. Using the standard physical properties of main sequence and giant stars available for model stars (e.g. [21] ), we were able to reach to a reasonable initial guess for the mass ratio and surface temperatures. Note, however, that these are only initial guesses and they were iteratively improved to the final self-consistent solution. Also, note that we had to find the corresponding stellar masses from the model tables in such a way that the combined luminosity of the system satisfies Equation (4). The most difficult part of the job is to find reasonable values of the Roche potentials. For a contact system, the Roche potentials of the components assume their critical values which are known once the mass ratio is known. We can therefore start with the contact configuration, motivated by the continuous variations of the outside eclipse light curve which indicates strong proximity effects in the system. Other input parameters are chosen accordingly, and the initial guess light curves which are obtained in this way are shown in Figure 4 and Figure 5. What remains is to optimize this initial guess towards the final best fit solution. The resulting optimum light curves parameters are given in Table1 Note that we have adopted the wavelengths 6850 Å for the red filter and 5150 Å for the blue filter which are the median wavelengths of the corresponding filters used in the observations.
4. Roche Model and Evolutionary Status of the System
Figure 6 shows the geometrical shape of the components of the system compared to the critical Roche lobes. It can be seen that the secondary is considerably distorted and fills its critical Roche lobe. The primary is less distorted and is well inside its critical lobe. We therefore expect the system to exhibit mass transfer effects and period changes which can be looked for in future observations. The predicted velocity curve of the system is shown in Figure 7. Since the luminosities of the components do not differ too much, we predict the system to be a double lined spectroscopic binary. The solution obtained here is consistent with both components being on the main sequence with absolute parameters M1 = 6 Mʘ, M2 =3.8 Mʘ, L1 = 400 Lʘ and L2 = 270 Lʘ. Since the two stars are fairly massive main sequence stars, we conclude that they should be quite young with an age less that 8 × 107 yrs. The calculated positions of the primary and secondary stars on an observational HR diagram are shown in Figure 8, where the background observational diagram is taken from [21] ).
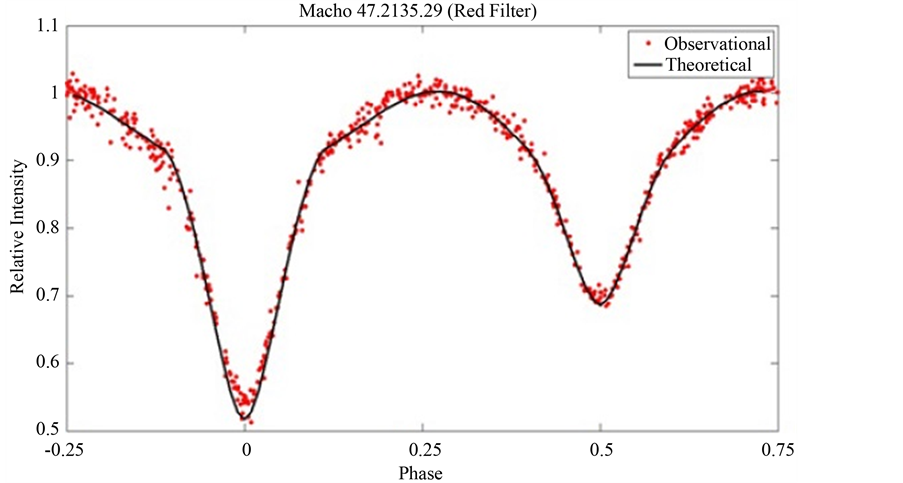
Figure 4. The revised and normalized light curve (normalized intensity versus orbital phase) of 47.2135.29, based on the corrected period (1) for red filter, together with the synthesized light curve.

Figure 5. The revised and normalized light curve (normalized intensity versus orbital phase) of 47.2135.29, based on the corrected period (1) for blue filter, together with the synthesized light curve.


Figure 6. The geometrical shape of the system, together with the critical Roche lobes of the system.
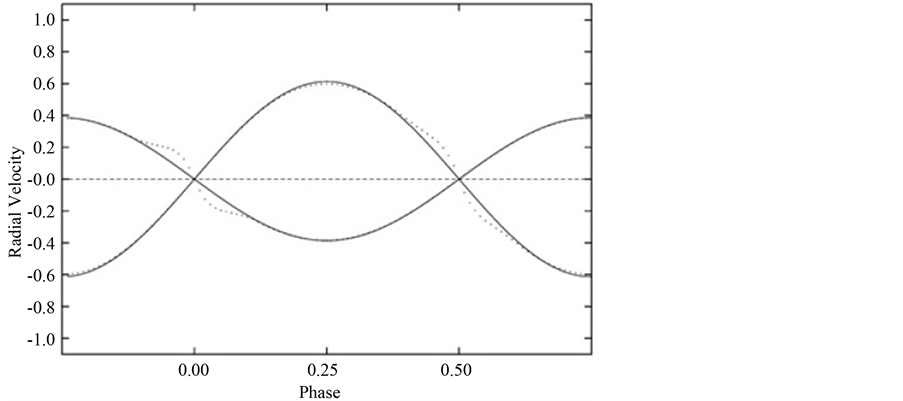
Figure 7. The predicted velocity curve of the system.
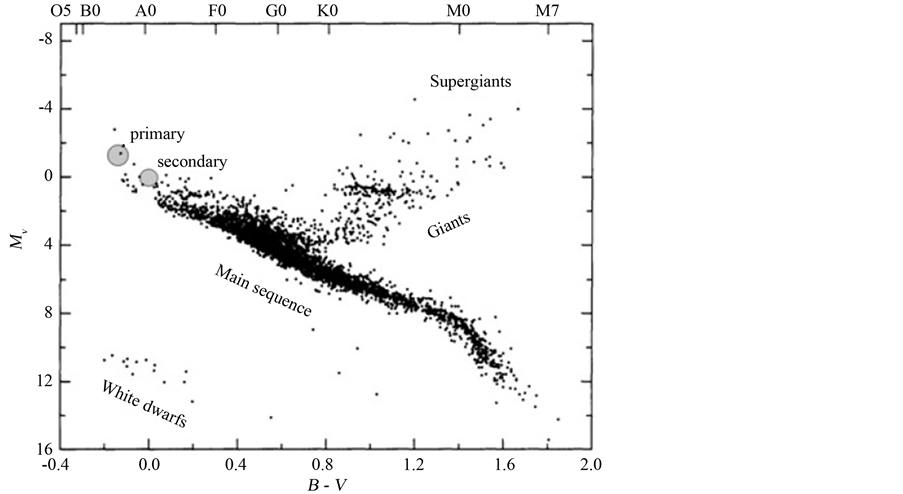
Figure 8. The calculated position of the components of the system on the HR diagram (the background HR diagram is taken from [21] ).
5. Concluding Remarks
The MACHO project continues to provide a valuable database for studying secular variations over a relatively long time-scale (of order of a decade or so). These include search for period variations and other detailed studies of binaries with pulsating components [13] . In the present paper, the orbital and geometrical parameters of the LMC eclipsing binary system MACHO 47.2135.29 were determined for the first time. The absolute properties of the system components were calculated, using the estimated distance modulus of LMC [3] [6] [15] . It was found that MACHO47.2135.29 is a young, semi-detached (potentially beta-Lyrae type) binary system with an age of no more than about 80 million years. Beta-Lyrae stars are semi-detached, massive binary systems with deformed components. One component of the system is usually evolved away from the main sequence and fills its Roche lobe. Mass is therefore transferred to its companion via the first Lagrangian point. Their light curve shows continuous light variations and very broad minima. Some of them show periodic light changes [22] [23] . The fact that the period of the system is toward the short distribution of periods in beta Lyrae confirms the components not being giants, since otherwise one would expect a much longer period. The predicted velocity curve and the position of the components on HR diagram were also reported. An evolving semi-detached binary system is expected to undergo mass transfer which implies interesting observational consequences including period change and line emission characteristics [19] [24] [25] . Unfortunately, none of these observations is available yet and our results provide a tentative basis for comparison with possible future observations.
Acknowledgements
N. Riazi acknowledges the support of Shahid Beheshti University Research Council.
References
- Ribas, I., et al. (2005) First Determination of the Distance and Fundamental Properties of an Eclipsing Binary in the Andromeda Galaxy. Astrophysical Journal, 635, L37-L40. http://dx.doi.org/10.1086/499161
- Vilardell, F., et al. (2010) The Distance to the Andromeda Galaxy from Eclipsing Binaries. Annual Review of Astronomy & Astrophysics, 509, Article No. A70. http://dx.doi.org/10.1051/0004-6361/200913299
- Salaris, M. and Groenewegen, M.A.T. (2002) An Empirical Method to Estimate the LMC Distance Using B-Stars in Eclipsing Binary Systems. Astronomy & Astrophysics, 381, 440-445. http://dx.doi.org/10.1051/0004-6361:20011528
- Bonanos, A.Z., et al. (2006) The First DIRECT Distance to a Detached Eclipsing Binary in M33. Astrophysics and Space Science, 304, 207-209. http://dx.doi.org/10.1007/s10509-006-9112-1
- http://www.macho.mcmaster.ca
- Macho Project Data Access Portals. http://wwwmacho.anu.edu.au/Data/MachoData.html
- Cook, K.H., Alcock, C., Allsman, H.A., et al. (1995) Variable Stars in the MACHO Collaboration Database. In: Stobie, R.S. and Whitelock, P.A., Eds., Astrophysical Applications of Stellar Pulsation, ASP Conference Series, 83, 221.
- Alcock, C., et al. (2000) The MACHO Project: Microlensing Results from 5.7 Years of Large Magellanic Cloud Observations. The Astrophysical Journal, 542, 281-307. http://dx.doi.org/10.1086/309512
- Alcock, C., et al. (2001) The MACHO Project: Microlensing Detection Efficiency. The Astrophysical Journal Supplement Series, 136, 439-462. http://dx.doi.org/10.1086/322529
- Alcock, C., et al. (2001) The MACHO Project LMC Variable Star Inventory. X. The R Coronae Borealis Stars. The Astrophysical Journal, 554, 298-315. http://dx.doi.org/10.1086/321369
- Faccioli, L., Alcock, C., Cook, K., Prochter, G.E., Protopapas, P. and Syphers, D. (2007) Eclipsing Binary Stars in the Large and Small Magellanic Clouds from the MACHO Project: The Sample. The Astronomical Journal, 134, 1963- 1993. http://dx.doi.org/10.1086/521579
- Derekas, A., Kiss, L.L. and Bedding, T.R. (2007) Eclipsing Binaries in the MACHO Database: New Periods and Classifications for 3031 Systems in the Large Magellanic Cloud. The Astrophysical Journal, 663, 249-257. http://dx.doi.org/10.1086/517994
- Harries, T.J., Hilditch, R.W. and Howarth, T.J. (2003) Ten Eclipsing Binaries in the Small Magellanic Cloud: Fundamental Parameters and Cloud. Monthly Notices of the Royal Astronomical Society, 339, 157-172. http://dx.doi.org/10.1046/j.1365-8711.2003.06169.x
- Derekas1, A., Kiss, L. and Bedding, T.R. (2007) Eclipsing Binaries in the Macho Database: New Periods and Classifications for 3031 Systems in the Large Magellanic Cloud. arXiv:astro-ph/0703137v1.
- NASA/IPAC Extragalactic Database. Results for Large Magellanic Cloud. http://ned.ipac.caltech.edu
- Guinan, E.F., Fitzpatrick, E.L., DeWarf, L.E., Maloney, F.P., Maurone, P.A., Ribas, I., et al. (1998) The Distance to the Large Magellanic Cloud from the Eclipsing Binary HV 2274. The Astrophysical Journal, 509, L21-L24. http://dx.doi.org/10.1086/311760
- Wilson, R.E. (1998) Computing Binary Star Observables. University of Florida Documents, Gainesville.
- Kallrath, J. and Milone, E.F. (2009) Eclipsing Binary Star: Modeling and Analysis. Springer, New York. http://dx.doi.org/10.1007/978-1-4419-0699-1
- Bradstreet, D.H. (1993) Binary Maker 2.0—An Interactive Graphical Tool for Preliminary Light Curve Analysis. Department of Physical Science, Springer, New York.
- Bradstreet, D.H. (2005) Fundamental of Solving Eclipsing Binary Light Curves Using Binary Maker 3.0. Society of Astronomical Sciences Inc., The NASA Astrophysics Data System.
- Ostlie, D.A. and Carroll, B.W. (1996) An Introduction to Modern Stellar Astrophysics. Addison Wesley, Boston.
- van Hamme, W., Wilson, R.E. and Guinan, E.F. (1995) Periodic Light Curve Changes for Beta Lyrae. Astronomical Journal, 110, 1350. http://dx.doi.org/10.1086/117609
- Huang, S. (1963) An Interpretation of Beta Lyrae. Astrophysical Journal, 138, 342. http://dx.doi.org/10.1086/147648
- Hilditch, R.W. (2001) An Introduction to Close Binary Stars. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139163576
- Kallrath, J. and Milone, E.F. (1999) Eclipsing Binary Stars. Springer, Berlin. http://dx.doi.org/10.1007/978-1-4757-3128-6


