International Journal of Astronomy and Astrophysics
Vol.3 No.2A(2013), Article ID:33027,7 pages DOI:10.4236/ijaa.2013.32A004
A Model for a Spherically Symmetric Space Generated by a Spherical Gravitational Source and a Gravitational Medium with Constant Mass Density
Dorodnitsyn Computing Center, Russian Academy of Sciences, Moscow, Russia
Email: nnpopov@mail.ru
Copyright © 2013 Nikolaj N. Popov, Vladimir I. Tsurkov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 28, 2013; revised March 30, 2013; accepted April 7, 2013
Keywords: Spherically Symmetric Space with Discontinuous Scalar Curvature; Generalized Schwarzschild Metric; Radial Geodesic; Black Hole; Dark Energy
ABSTRACT
A metric on a spherically symmetric space generated by a spherical source of gravity and filled with a gravitational medium is constructed, and criteria for the continuity of this metric on the entire space (which is equivalent to the absence of black holes) are found. Properties of radial geodesics under various constraints on the size of the gravitational source, its mass, and the mass density of the gravitational medium are studied.
1. Introduction
This paper considers a model for the spherically symmetric space generated by a volume source of gravity having the shape of a ball of radius r1 placed in a gravitational medium, which represents dark energy uniformly filling the entire space [1]. If the gravitational source were a point source, then the metric on the space would inevitably have a discontinuity at some finite distance from the source (which essentially means the presence of a black hole) and a discontinuity at the point where the gravitational source is located. However, in the model with a volume source of gravity, which is physically more realistic, the metric has no discontinuities under certain conditions on the size of the source and on the mass densities of the source and dark energy.
The question of how particles move in such a space inside and outside the volume source of gravity naturally arises. The accepted idea of the motion of point bodies in the case of a point gravitational source is described in [2, 3]. It is assumed that, in a certain neighborhood of the point source, bodies are attracted by the source according to Newton’s law, while outside this neighborhood (at sufficiently large distances), the presence of dark energy causes repulsion from the source according to Hubble’s law; thus, the radial velocity of particles is directly proportional to their distance from the source. Such a picture is typical of radial geodesics with respect to the absolute time s. These are precisely the geodesics subject to constraints with respect to the radial parameter r, which leads to the violation of the principle that a material body cannot travel faster than light. But if geodesics with respect to the world time t [4] are considered, then, even in the simplest case of a point gravitational source, the motion along radial geodesics obey more complicated laws, without the violation of the principle prohibiting motion faster than light.
The purpose of this paper is to describe properties of radial geodesics in the case of a volume source of gravity under various constraints on the parameters of the physical model.
2. Description of the Model and Its Basic Equations
Suppose given a pseudo-Riemannian spherically symmetric 4-space with signature 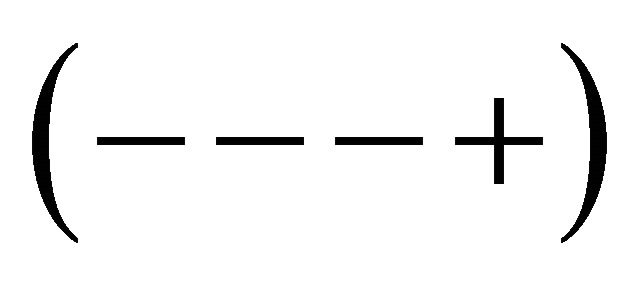 and a ball of radius
and a ball of radius 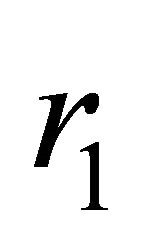 with constant mass density
with constant mass density  at the center of symmetry of this space. The entire space, including the ball, is uniformly filled with dark energy of constant mass density
at the center of symmetry of this space. The entire space, including the ball, is uniformly filled with dark energy of constant mass density . The material ball (which may be a star or some other astronomical object) and dark energy determine the geometric properties of the space. Mathematically, the geometric properties of any pseudo-Riemannian space are completely determined by its metric
. The material ball (which may be a star or some other astronomical object) and dark energy determine the geometric properties of the space. Mathematically, the geometric properties of any pseudo-Riemannian space are completely determined by its metric . The interrelation between the mass distribution density
. The interrelation between the mass distribution density  in the space and the metric tensor
in the space and the metric tensor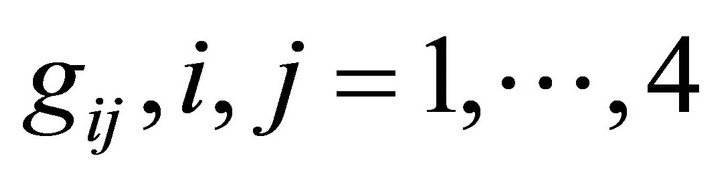 , is described by the Equation (5)
, is described by the Equation (5)
 (1)
(1)
where 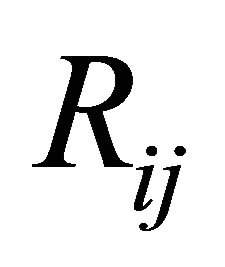 is the Ricci tensor, which is defined by
is the Ricci tensor, which is defined by
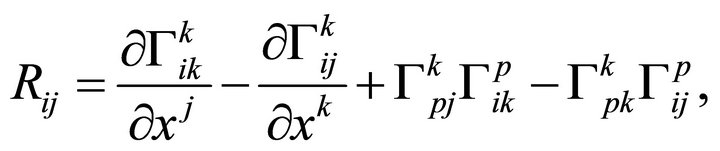 (2)
(2)
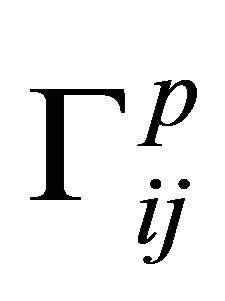 is the Christoffel symbol defined by
is the Christoffel symbol defined by
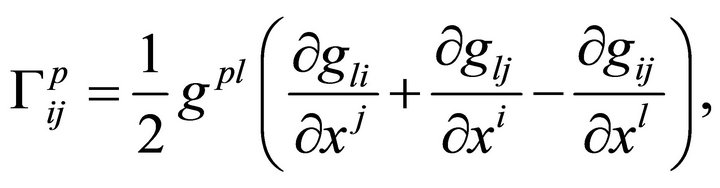 (3)
(3)
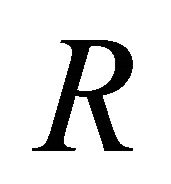 is the scalar curvature defined by
is the scalar curvature defined by
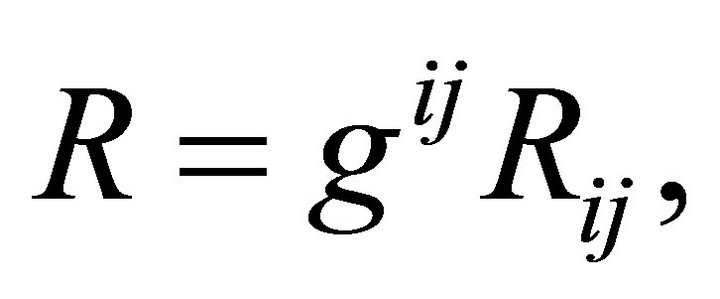 (4)
(4)
 is the gravitational constant; and
is the gravitational constant; and  is the speed of light. Throughout the paper, summation over repeated indices is implied. Equation (1) directly implies the following relation between the scalar curvature
is the speed of light. Throughout the paper, summation over repeated indices is implied. Equation (1) directly implies the following relation between the scalar curvature  of the pseudo-Riemannian space and the distribution density
of the pseudo-Riemannian space and the distribution density  of the matter mass:
of the matter mass:
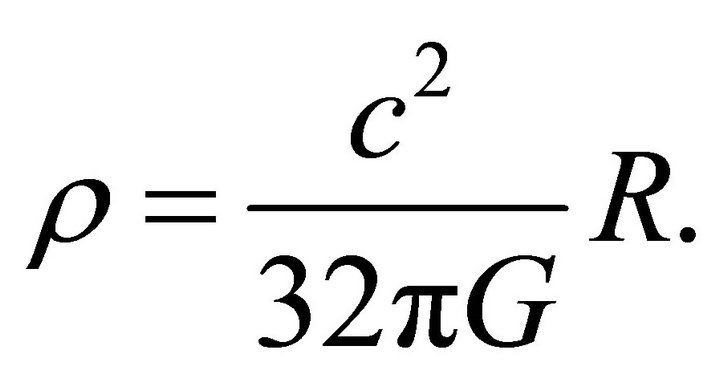 (5)
(5)
According to relation (5), the specification of the distribution density of the matter mass in the space is equivalent to the specification of the scalar curvature field of the pseudo-Riemannian space. The mass distribution density is governed by the gravitational field of the interaction of masses. According to the presently accepted point of view, the gravitational field is the metric on the pseudo-Riemannian space. Thus, the basic physical notions of gravitational theory, such as the density of the matter mass and the gravitational field, are interpreted in the language of differential geometry as the scalar curvature (up to proportionality) and the metric on the pseudo-Riemannian space, respectively. They are related by
 (6)
(6)
this is a direct consequence of (1). Note that the system of Equations (5) and (6) is equivalent to (1).
3. The General Form of a Static Spherically Symmetric Metric
A static spherically symmetric metric can be represented in spherical coordinates 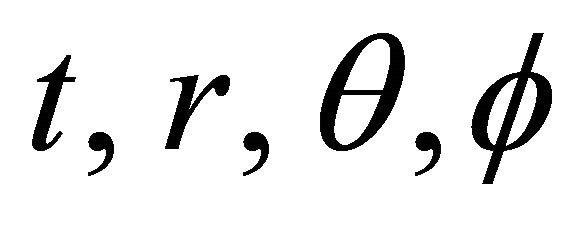 as
as
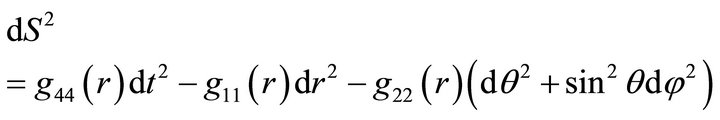 (7)
(7)
where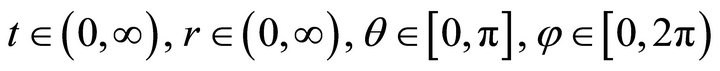 , and
, and , and
, and  are unknown positive functions. It follows from general geometric properties of a spherically symmetric space that the function
are unknown positive functions. It follows from general geometric properties of a spherically symmetric space that the function  must satisfy the condition
must satisfy the condition
 (8)
(8)
According to relations (2)-(5), the system (6) of gravity equations with respect to the components of metric (7) can be represented in the form
 (9)
(9)
where  and
and  is the distribution density of the matter mass, which generally depends on the radial parameter
is the distribution density of the matter mass, which generally depends on the radial parameter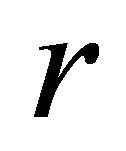 . In [5], it was shown that if
. In [5], it was shown that if 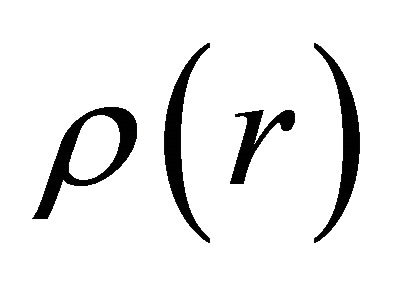 is a piecewise constant function having at most countably many discontinuities with respect to the parameter
is a piecewise constant function having at most countably many discontinuities with respect to the parameter  and
and 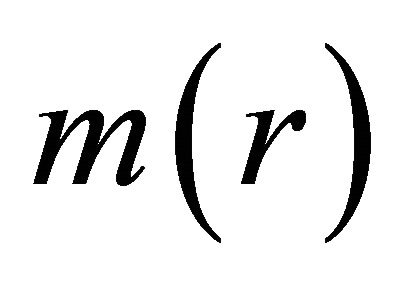 is the mass of a ball of radius
is the mass of a ball of radius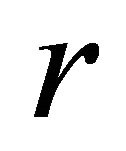 , then the spherically symmetric metric satisfying the system of Equations (9) has the form
, then the spherically symmetric metric satisfying the system of Equations (9) has the form
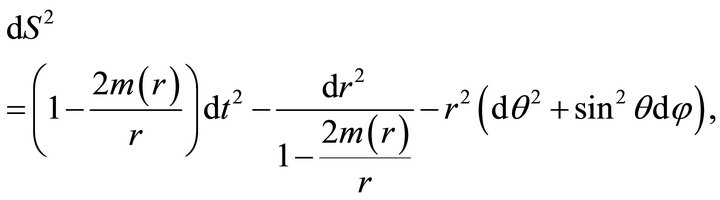 (10)
(10)
where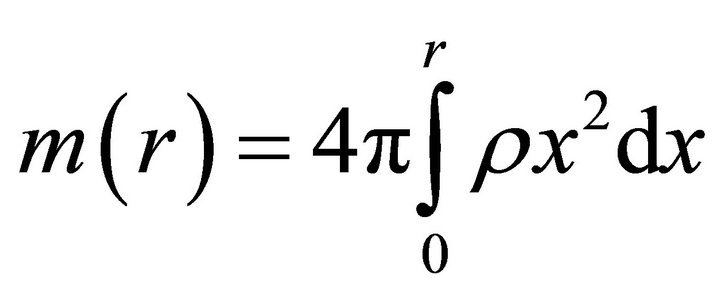 . The system of units used for measuring physical quantities is chosen so that
. The system of units used for measuring physical quantities is chosen so that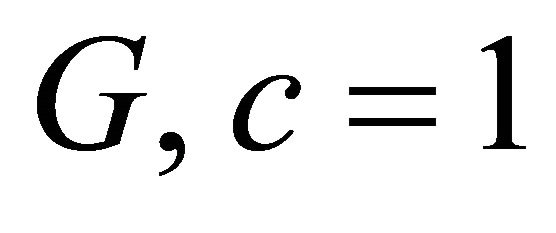 . Metric (10) is a generalization of the Schwarzschild metric to the case of an arbitrary spherically symmetric mass distribution in a space with piecewise constant density
. Metric (10) is a generalization of the Schwarzschild metric to the case of an arbitrary spherically symmetric mass distribution in a space with piecewise constant density . Note that metric (10) satisfies system (9) only on domains of continuity of the density.
. Note that metric (10) satisfies system (9) only on domains of continuity of the density.
4. Equations for Geodesics and First Integrals
We seek equations for geodesics by using the Lagrangian formalism. Let us introduce a Lagrangian of the form
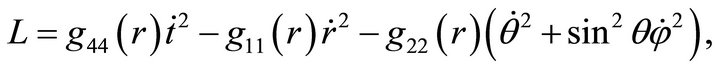 (11)
(11)
where  and
and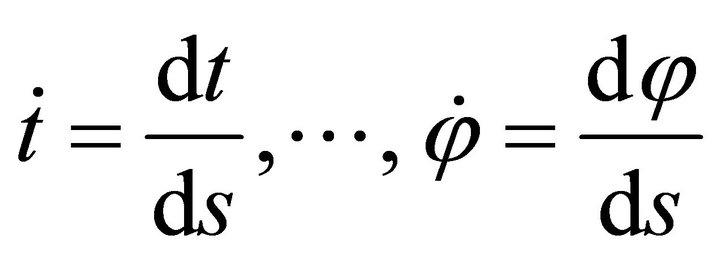 .
.
Substituting Lagrangian (11) into the Euler-Lagrange equation

where x is one of the parameters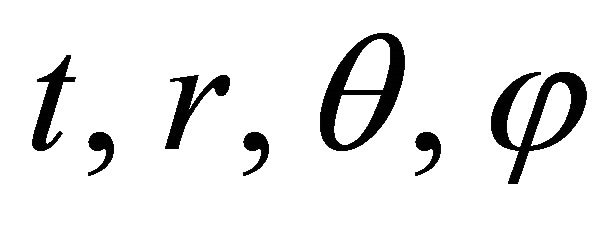 , we obtain the following system of equations for the geodesics with respect to the parameter
, we obtain the following system of equations for the geodesics with respect to the parameter :
:
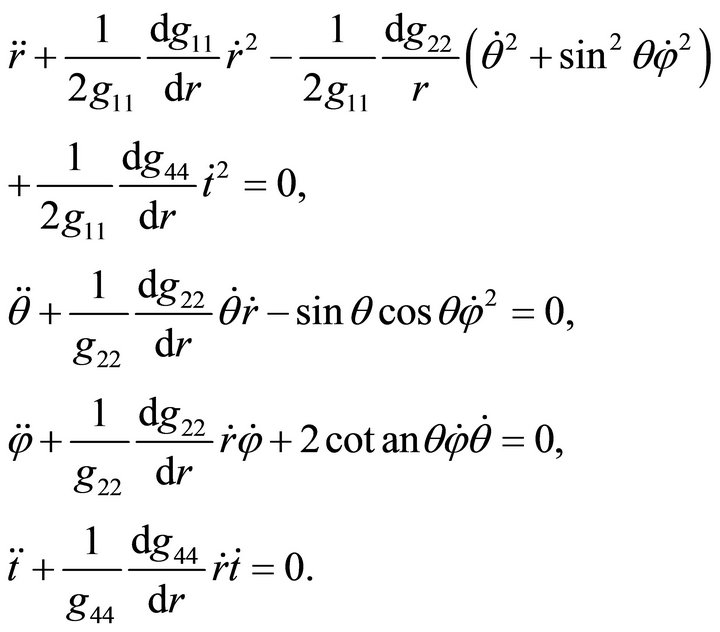 (12)
(12)
The system of differential Equation (12) can be integrated in the general form without any simplifying assumptions. As a result, we obtain
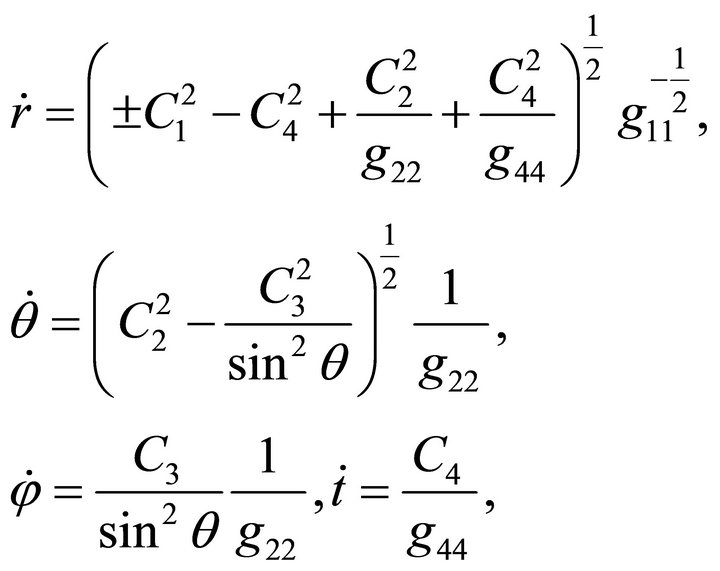 (13)
(13)
where 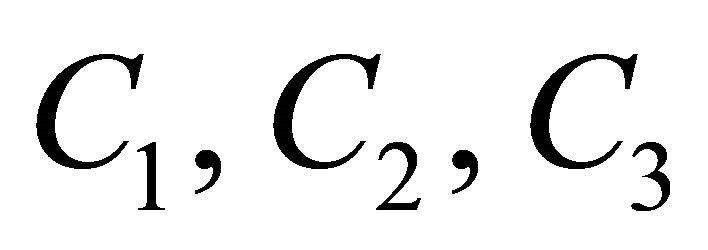 and
and  are integration constants;
are integration constants;  and
and  must satisfy the condition
must satisfy the condition
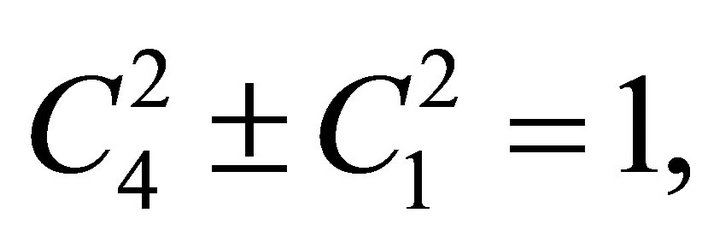 (14)
(14)
and  and
and  can be chosen arbitrarily. The physical meaning of
can be chosen arbitrarily. The physical meaning of  is the angular momentum
is the angular momentum 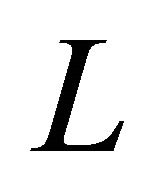 of the rotating body, and
of the rotating body, and  is the kinetic energy
is the kinetic energy  of the moving body. The functions
of the moving body. The functions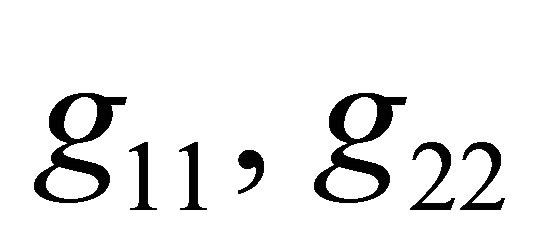 , and
, and  are
are
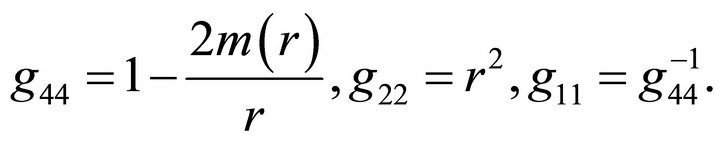
5. The Radial Geodesics with Respect to the Absolute Time s
We consider the radial geodesics in the equatorial planei.e., satisfying the conditions 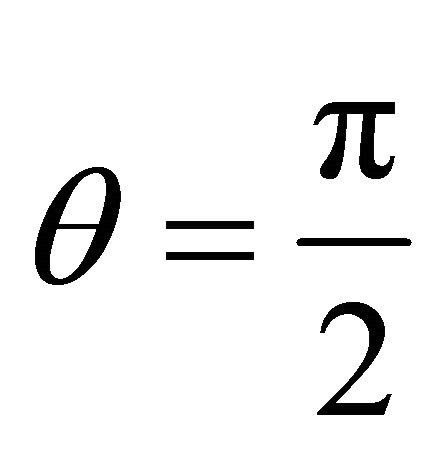 and
and . According to (12), we have
. According to (12), we have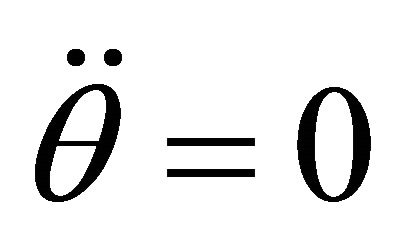 ; therefore,
; therefore,  remains constant during the motion along the geodesic, and
remains constant during the motion along the geodesic, and . The condition for a geodesic in the equatorial plane to be radial is
. The condition for a geodesic in the equatorial plane to be radial is
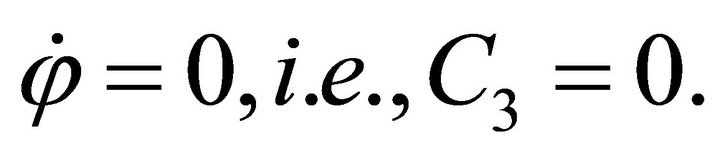
The radial geodesics with respect to the absolute time  are given by the equations
are given by the equations
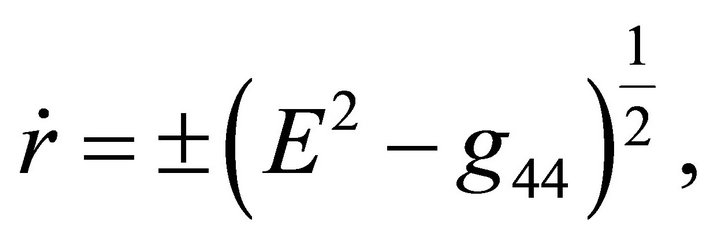 (15)
(15)
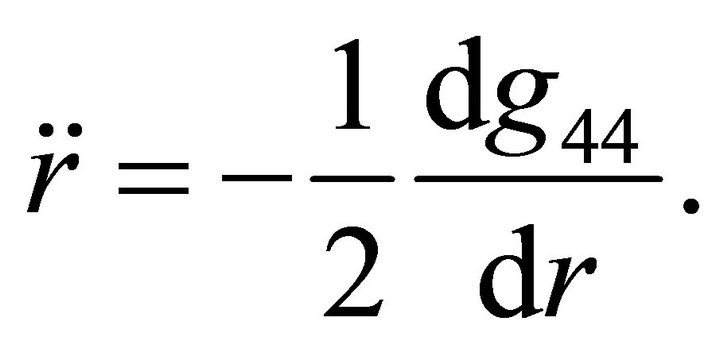 (16)
(16)
For the model considered in this paper, we have
 at
at  and
and
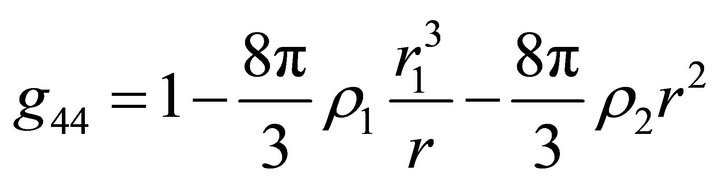 at
at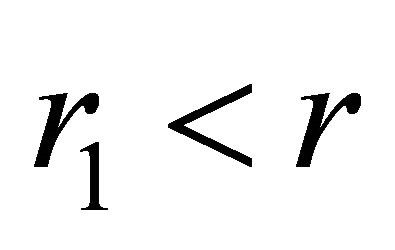 . Outside the ballthe acceleration and the velocity have the form
. Outside the ballthe acceleration and the velocity have the form
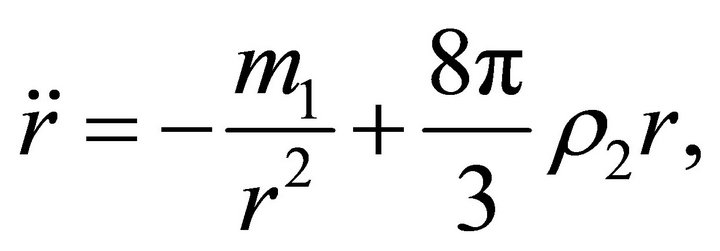 (17)
(17)
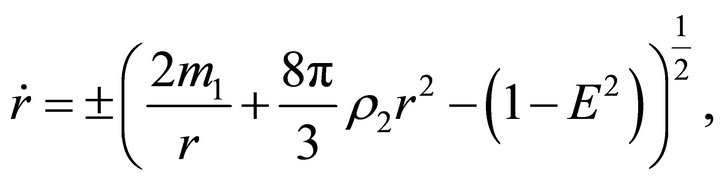 (18)
(18)
where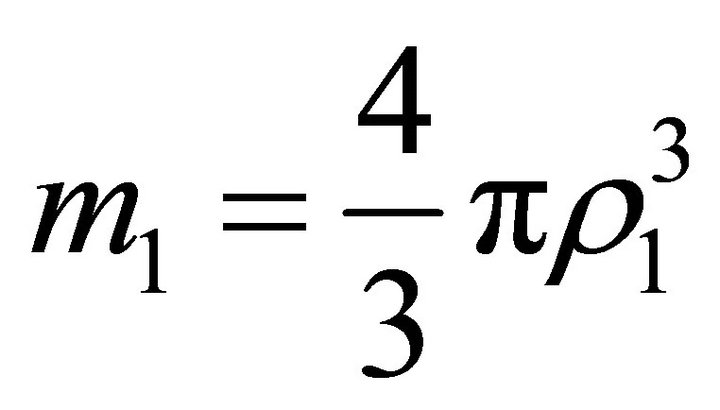 . Inside the ball, the acceleration and the velocity have the form
. Inside the ball, the acceleration and the velocity have the form
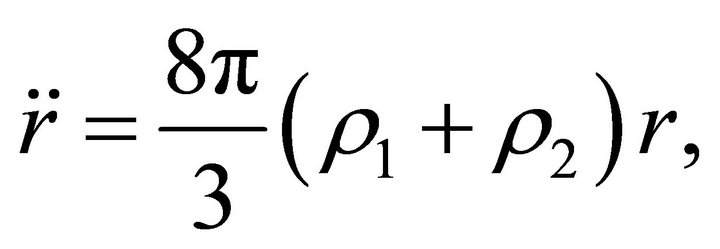 (19)
(19)
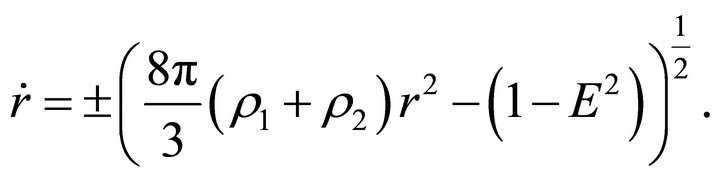 (20)
(20)
Thus, outside the ball, on the interval 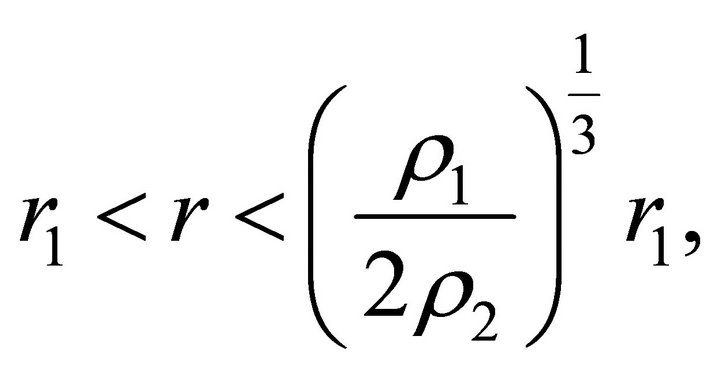
where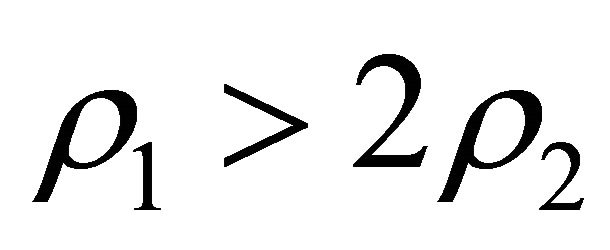 , a test body experiences the action of an attractive force, while at
, a test body experiences the action of an attractive force, while at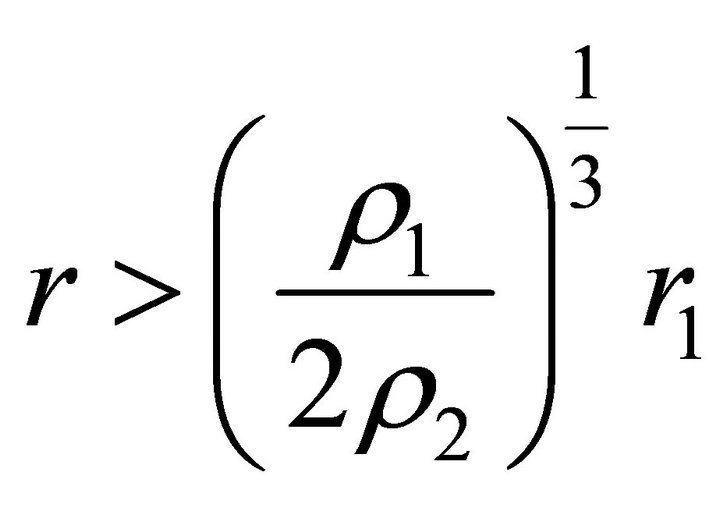 , it experiences the action of a repulsive force. Inside the ball, a test body experiences the action of a braking force, and the acceleration is positive up to the center of the ball, at which it vanishes.
, it experiences the action of a repulsive force. Inside the ball, a test body experiences the action of a braking force, and the acceleration is positive up to the center of the ball, at which it vanishes.
If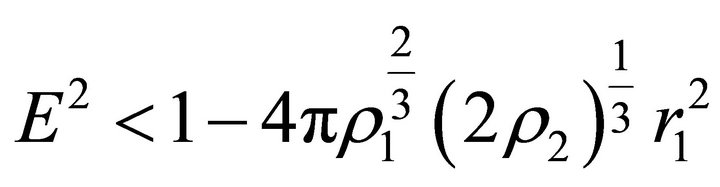 , then the velocity outside the ball, which is determined by (18), vanishes at two points
, then the velocity outside the ball, which is determined by (18), vanishes at two points 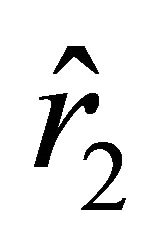 and
and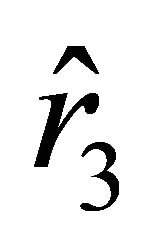 . For the inequalities
. For the inequalities  to hold, it is necessary that
to hold, it is necessary that . Thusif
. Thusif
 (21)
(21)
then 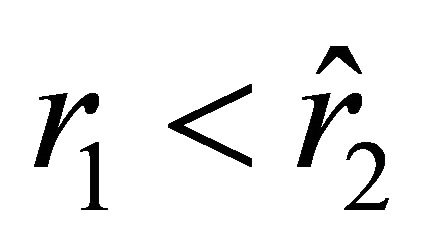 and
and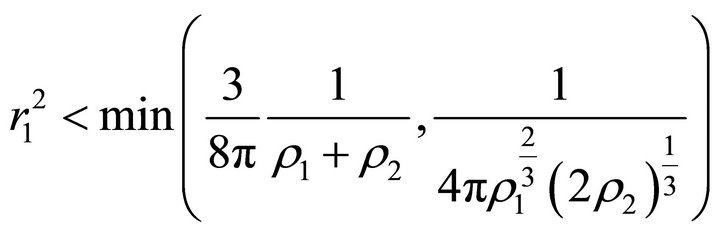 .
.
The motion of the particle begins at the rest position characterized by 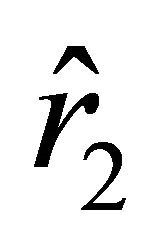 in the direction of the ball if the sign in (18) is “
in the direction of the ball if the sign in (18) is “ .” The acceleration of the test body on the interval
.” The acceleration of the test body on the interval 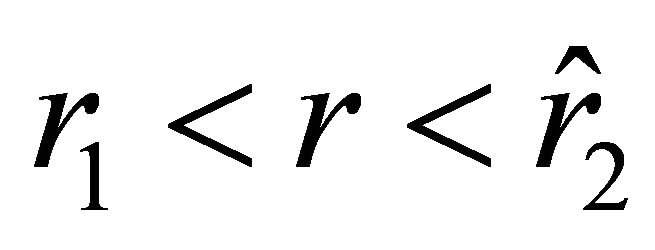 is negative, i.e., the particle experiences an attractive force. As the particle passes through the surface of the ball, its velocity remains continuous, while the acceleration jumps by
is negative, i.e., the particle experiences an attractive force. As the particle passes through the surface of the ball, its velocity remains continuous, while the acceleration jumps by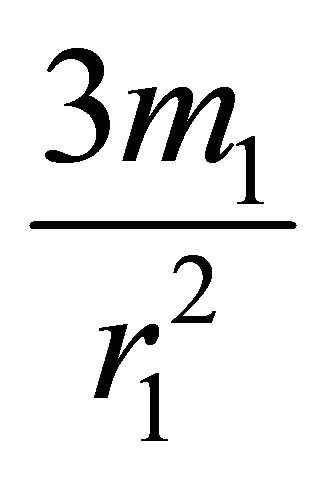 .
.
On the part  of the trajectory inside the ball, the particle is subject to a braking force, and it stops at the position characterized by the radial parameter
of the trajectory inside the ball, the particle is subject to a braking force, and it stops at the position characterized by the radial parameter 
Another motion from the rest state starts at the position characterized by the parameter . If the sign in (18) is “+,” then the motion of the particle starts at
. If the sign in (18) is “+,” then the motion of the particle starts at 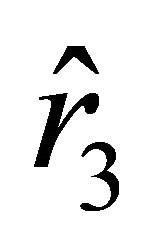 with positive acceleration, because
with positive acceleration, because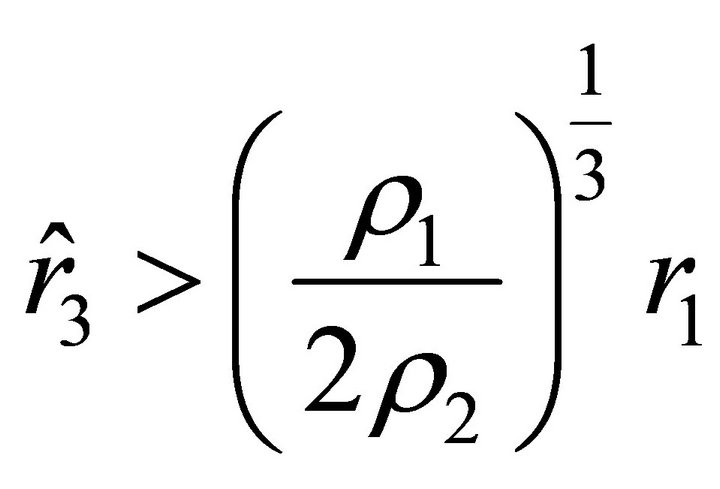 . According to (17) and (18), the acceleration and the velocity of the particle unboundedly increase with
. According to (17) and (18), the acceleration and the velocity of the particle unboundedly increase with , which contradicts the principle that a body cannot travel faster than light.
, which contradicts the principle that a body cannot travel faster than light.
If , then the velocity of a test body does not vanish at any point outside the ball; inside the ball, it vanishes at the radial parameter
, then the velocity of a test body does not vanish at any point outside the ball; inside the ball, it vanishes at the radial parameter
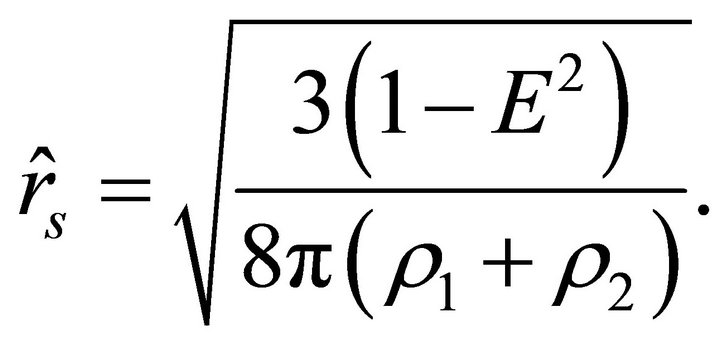
If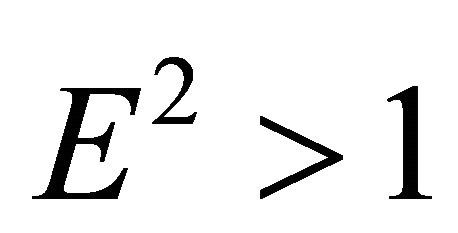 , then (18) and (20) imply that the velocity of the particle nowhere vanishes, and (17) and (18) imply that as the radial parameter
, then (18) and (20) imply that the velocity of the particle nowhere vanishes, and (17) and (18) imply that as the radial parameter  unboundedly increases, the velocity and the acceleration unboundedly increase as well.
unboundedly increases, the velocity and the acceleration unboundedly increase as well.
6. Radial Geodesics with Respect to the World Time t
We proceed to consider the radial geodesics with respect to the world time . In this case, we have
. In this case, we have
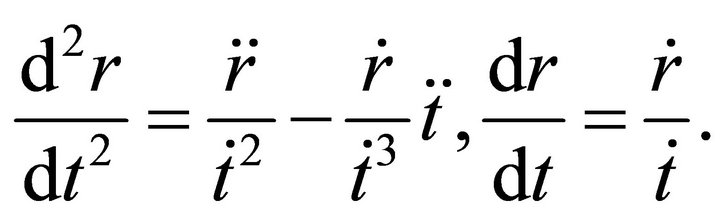
Taking into account (15) and (16), we obtain
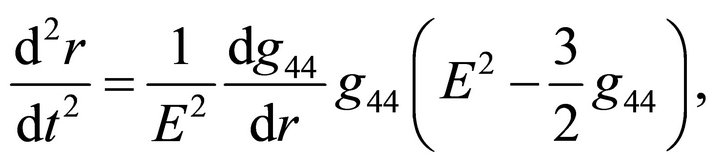 (22)
(22)
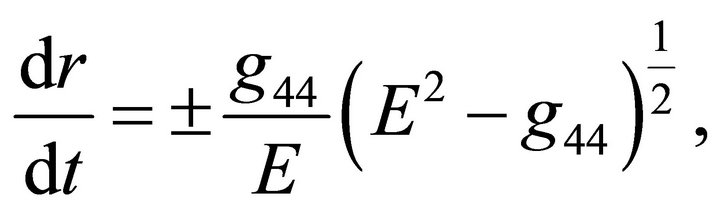 (23)
(23)
where 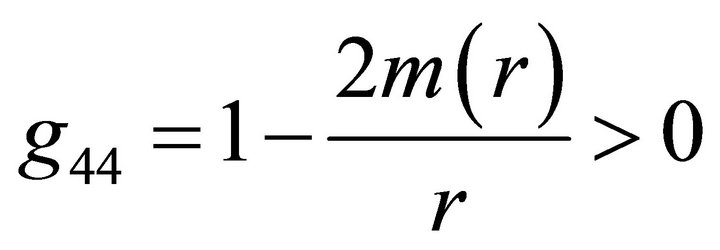 at
at . For the model considered in this paper, we have
. For the model considered in this paper, we have 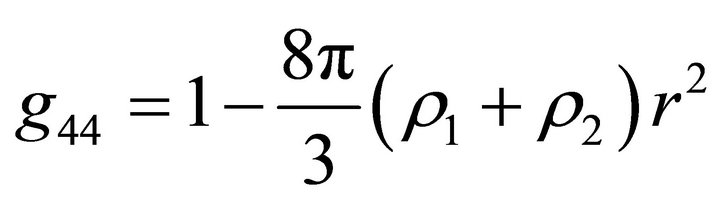 if
if  and
and  if
if ; i.e.inside the ball, the space is described by the de Sitter metric [6], and outside the ball, it is described by the Schwarzschild-de Sitter metric. Formulas (22) and (23) for the acceleration and velocity outside the ball take the form
; i.e.inside the ball, the space is described by the de Sitter metric [6], and outside the ball, it is described by the Schwarzschild-de Sitter metric. Formulas (22) and (23) for the acceleration and velocity outside the ball take the form
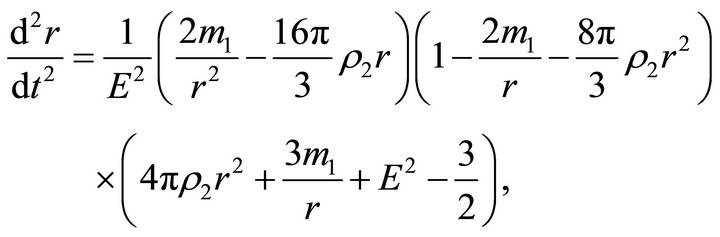 (24)
(24)
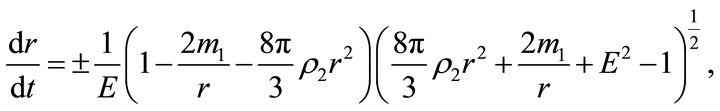 (25)
(25)
and inside the ball, they take the form
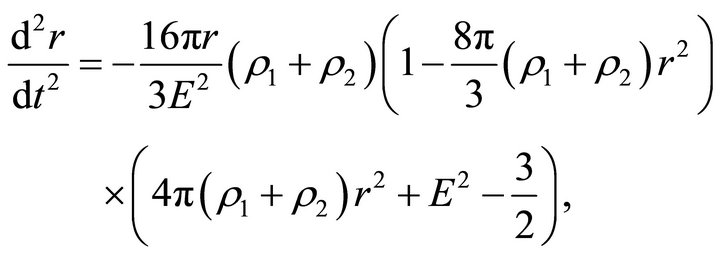 (26)
(26)
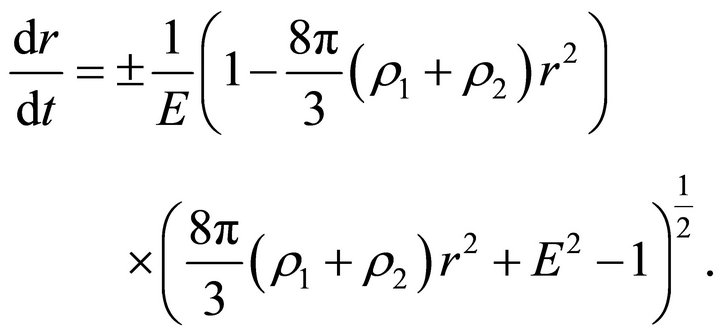 (27)
(27)
The radial geodesics can be divided into the two classes of trajectories determined by the conditions  and
and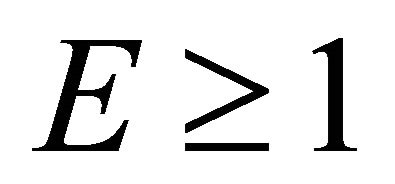 . We conventionally refer to the trajectories from the first class as bounded and to those from the second class as unbounded [7]. In the next section, we consider these cases in more detail.
. We conventionally refer to the trajectories from the first class as bounded and to those from the second class as unbounded [7]. In the next section, we consider these cases in more detail.
6.1. Bounded Radial Geodesics
Consider the radial trajectories of particles whose motion starts from a rest state at some finite distance outside the ball determined by 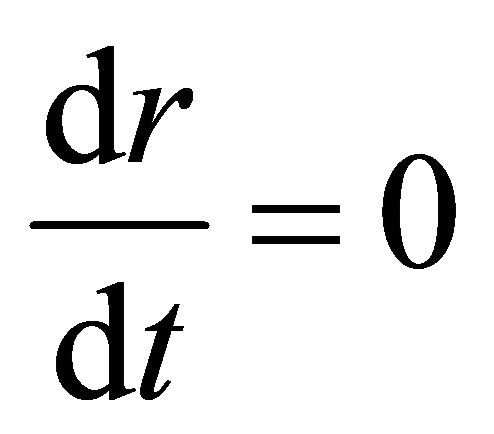 under the condition
under the condition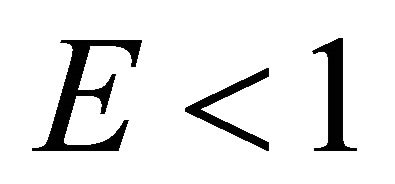 .
.
According to (25), we have either
 (28)
(28)
or
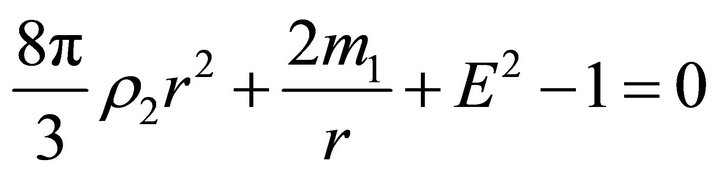 (29)
(29)
Since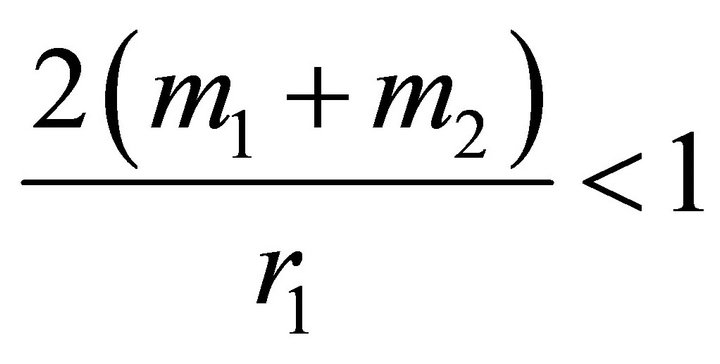 , where
, where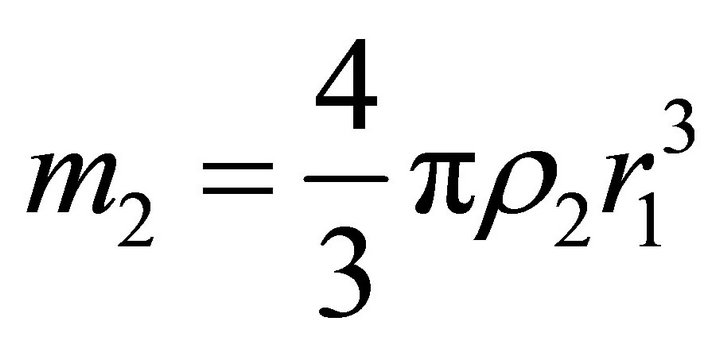 , it follows that Equation (28) has two positive roots
, it follows that Equation (28) has two positive roots  and
and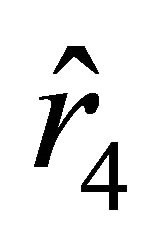 , and
, and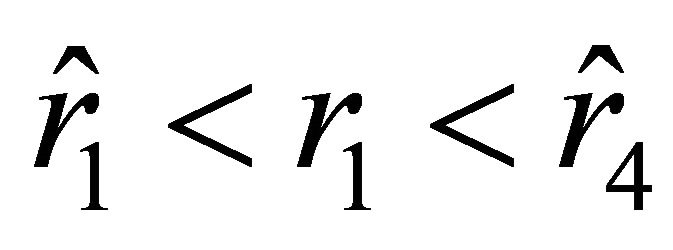 . Equation (27) has two positive roots only if
. Equation (27) has two positive roots only if
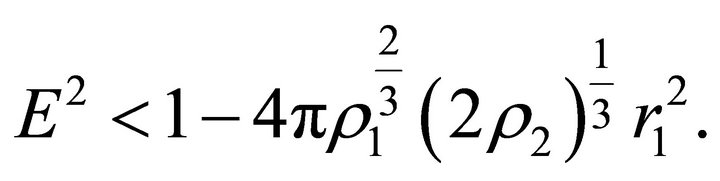
We denote the roots of Equation (29) by 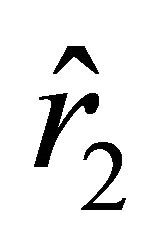 and
and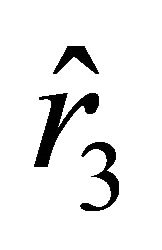 ; these roots are arranged with respect to the roots
; these roots are arranged with respect to the roots 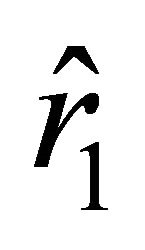 and
and 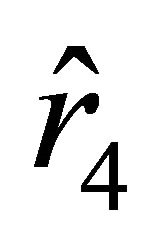 as
as 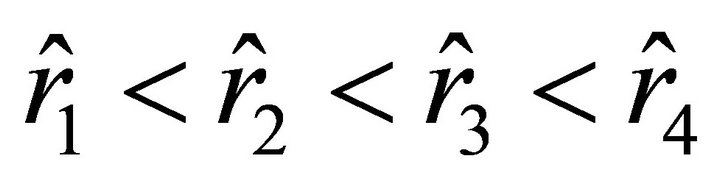 (this follows from the condition
(this follows from the condition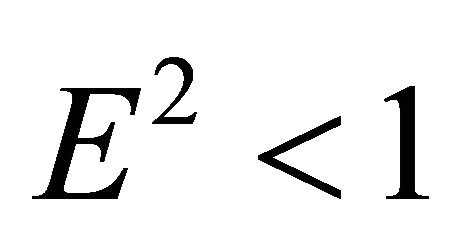 ). Let us find the values of the radial parameter
). Let us find the values of the radial parameter  at which the acceleration vanishes. According to (24), these values are determined by the equations
at which the acceleration vanishes. According to (24), these values are determined by the equations
 (30)
(30)
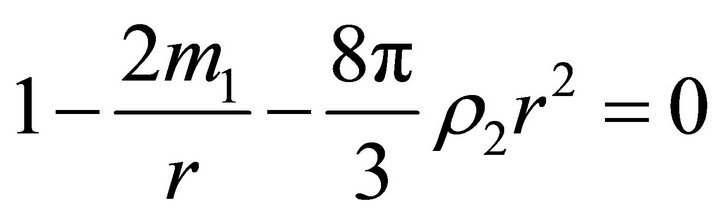 (31)
(31)
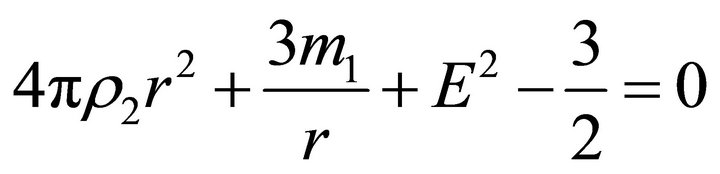 (32)
(32)
We are interested in the case where the root  of Equation (30) satisfies the inequality
of Equation (30) satisfies the inequality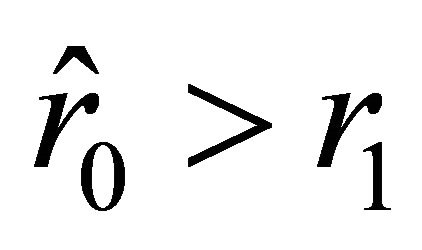 . This happens if
. This happens if . Equation (32) has positive roots if
. Equation (32) has positive roots if
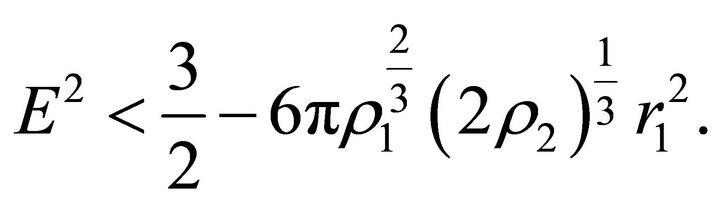
We denote these roots by 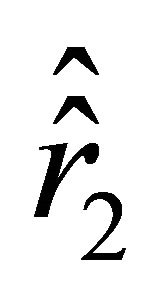 and
and . It follows from the inequality
. It follows from the inequality 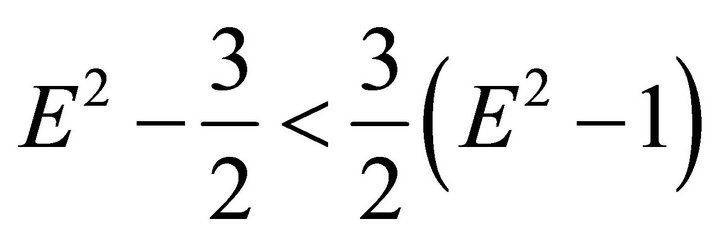 that the positive roots of Equations (29)-(32) (if they exist) are arranged as
that the positive roots of Equations (29)-(32) (if they exist) are arranged as 
Consider the possible patterns of behavior of the radial geodesics.
(a1) Suppose that
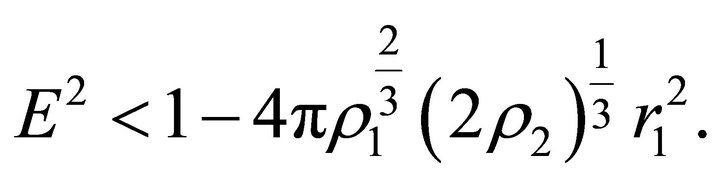 (33)
(33)
Then (33) implies
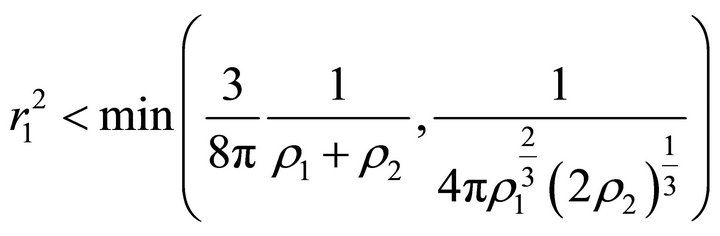 . Suppose also that
. Suppose also that
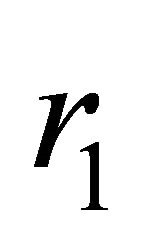 belongs to the interval
belongs to the interval . Then the inequality
. Then the inequality
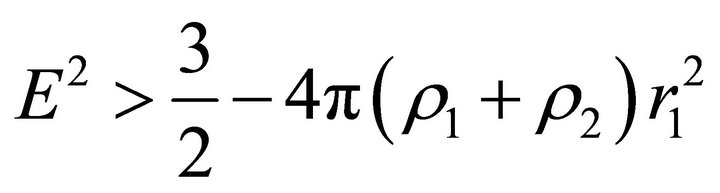 (34)
(34)
must hold. Relations (33) and (34) imply
 (35)
(35)
Condition (35) holds if 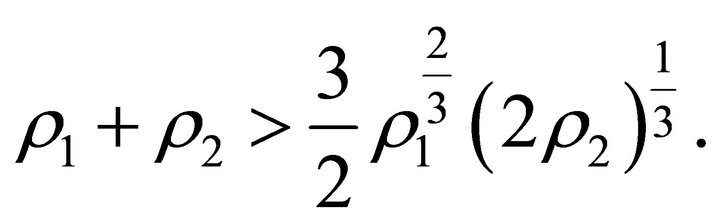
The motion starts at the rest position characterized by the parameter  toward the ball if the sign in (25) is “
toward the ball if the sign in (25) is “ .” The acceleration of the particle on the interval
.” The acceleration of the particle on the interval  is negative, i.e., the particle experiences the action of the attractive force. On the interval
is negative, i.e., the particle experiences the action of the attractive force. On the interval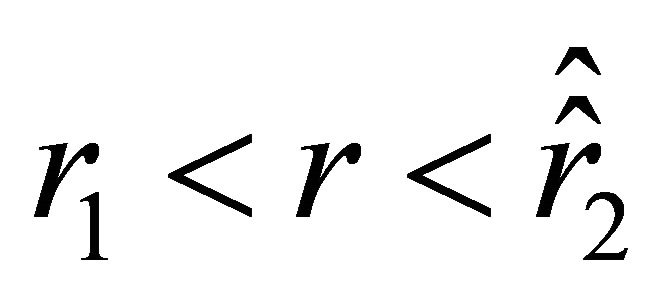 , the acceleration is positive, i.e., the particle is repelled. According to (24)-(27), on the surface of the ball, the acceleration jumps, while the velocity remains continuous. The acceleration inside the ball vanishes at those points where the radial parameter
, the acceleration is positive, i.e., the particle is repelled. According to (24)-(27), on the surface of the ball, the acceleration jumps, while the velocity remains continuous. The acceleration inside the ball vanishes at those points where the radial parameter  takes the values
takes the values
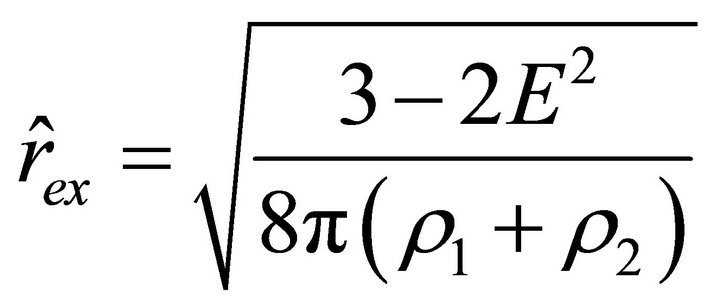 and
and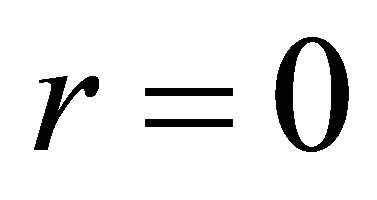 , and the velocity vanishes when r takes the value
, and the velocity vanishes when r takes the value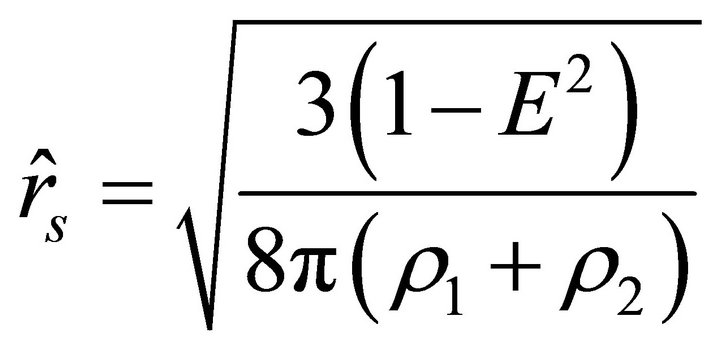 . The acceleration of a test body inside the ball remains negative on the interval
. The acceleration of a test body inside the ball remains negative on the interval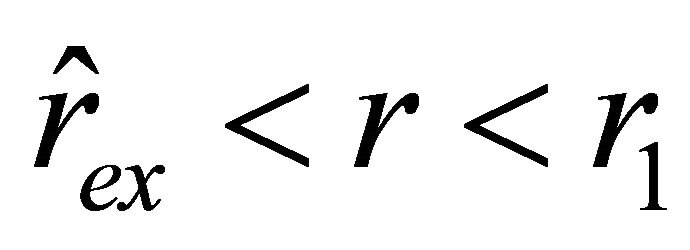 , while on the interval
, while on the interval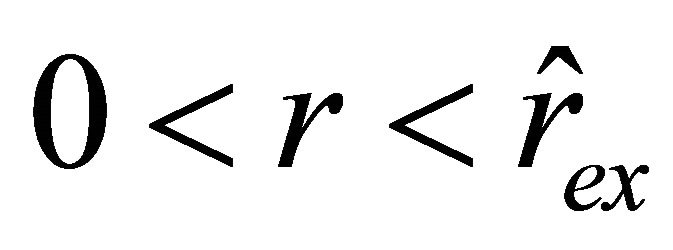 , it becomes positive, i.e., the particle slows down until it stops in the position characterized by the radial parameter
, it becomes positive, i.e., the particle slows down until it stops in the position characterized by the radial parameter .
.
Consider another motion from the rest state, which starts at the position determined by the radial parameter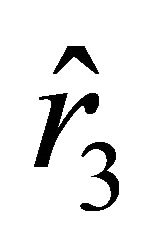 . In this position, the initial velocity vanishes, and the acceleration is positive. The sign in (25) is “+.” On the interval
. In this position, the initial velocity vanishes, and the acceleration is positive. The sign in (25) is “+.” On the interval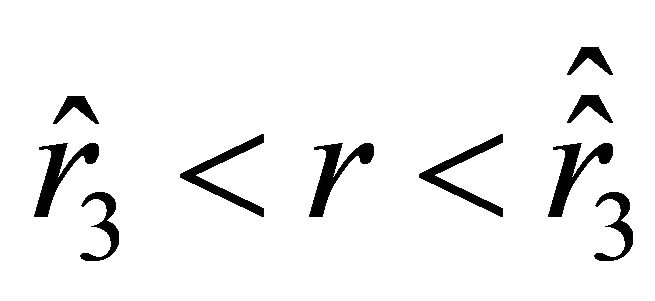 , acceleration (24) is positive, and the particle experiences repulsion. On the interval
, acceleration (24) is positive, and the particle experiences repulsion. On the interval , the acceleration becomes negative, while the velocity remains positive. As the particle approaches the position characterized by the radial parameter
, the acceleration becomes negative, while the velocity remains positive. As the particle approaches the position characterized by the radial parameter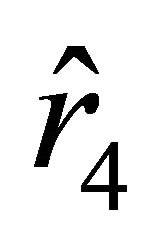 , the acceleration and the velocity tend to zero. The particle cannot reach the boundary characterized by
, the acceleration and the velocity tend to zero. The particle cannot reach the boundary characterized by 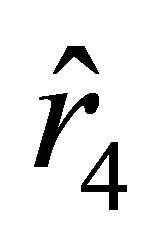 in finite time t.
in finite time t.
(a2) Suppose that condition (33) holds and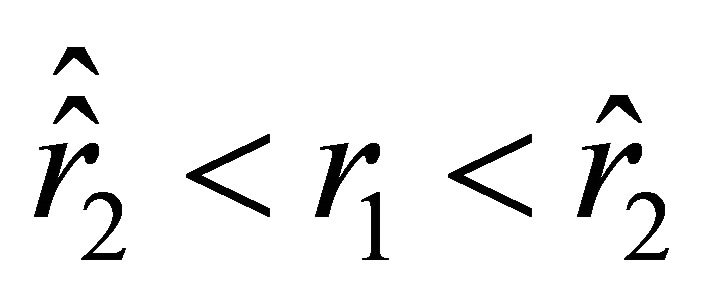 .
.
This means that . If
. If
 , then
, then
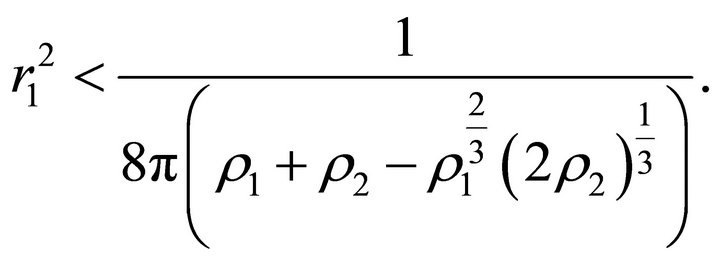
The least positive root  determines the initial position of the motion of a particle from a state of rest toward the ball if the sign in (25) is “
determines the initial position of the motion of a particle from a state of rest toward the ball if the sign in (25) is “ .” The acceleration and the velocity of the particle on the interval
.” The acceleration and the velocity of the particle on the interval 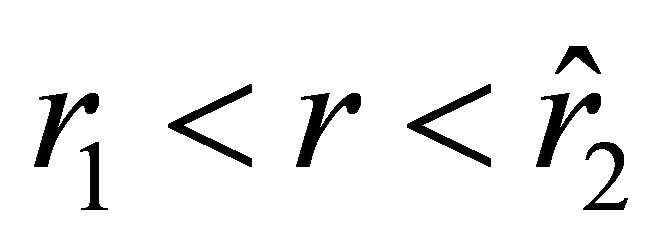 are negative. On this interval, the particle experiences attraction. It reaches the surface of the ball in finite time, moving with continuous velocity and discontinuous acceleration. The motion of a test body inside the ball is the same as in the previous case.
are negative. On this interval, the particle experiences attraction. It reaches the surface of the ball in finite time, moving with continuous velocity and discontinuous acceleration. The motion of a test body inside the ball is the same as in the previous case.
The motion from the state of rest determined by the parameter 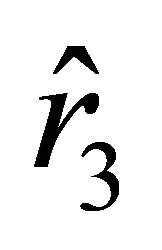 is similar to that considered above. Other variants of particle motion are not possible when the dark energy density is sufficiently small and for this reason will not be considered here. In cases (a1) and (a2), as well as in those cases which have not yet been considered here, the motion from a state of rest under the condition
is similar to that considered above. Other variants of particle motion are not possible when the dark energy density is sufficiently small and for this reason will not be considered here. In cases (a1) and (a2), as well as in those cases which have not yet been considered here, the motion from a state of rest under the condition 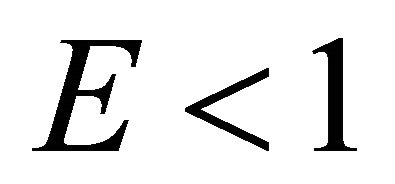 is bounded by
is bounded by .
.
6.2. Unbounded Radial Geodesics
In this section, we consider several behavior patterns of radial geodesics satisfying the condition .
.
(a1) Suppose that
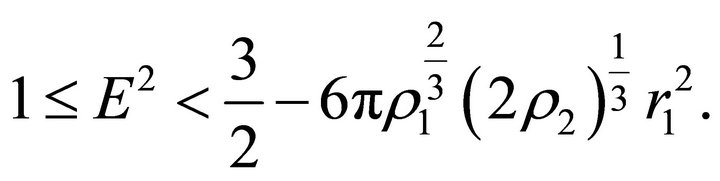 (36)
(36)
Then .
.
Equation (32) has positive roots, and 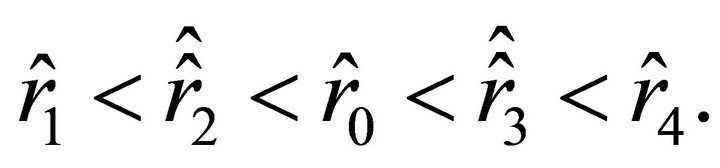
Suppose that 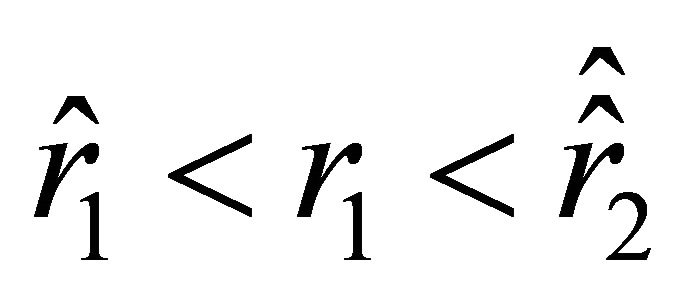 (this is possible if
(this is possible if
 ); then the acceleration is negative on the interval
); then the acceleration is negative on the interval , positive on the interval
, positive on the interval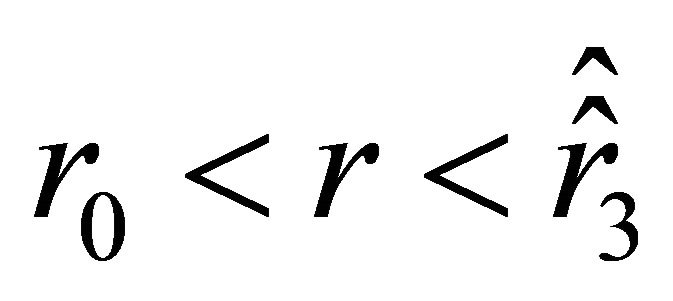 , again negative on the interval
, again negative on the interval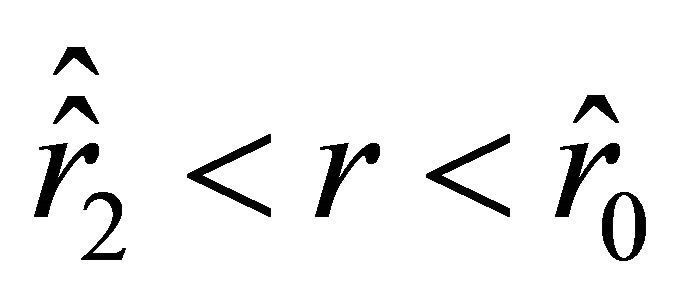 , and positive on the interval
, and positive on the interval . Inside the ball, on the interval
. Inside the ball, on the interval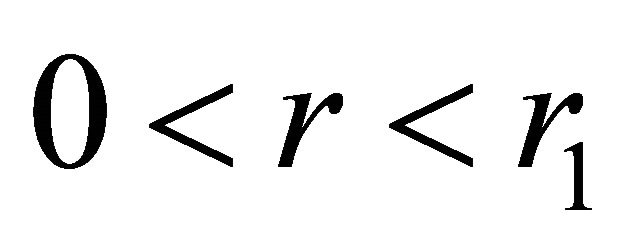 , the acceleration is negative. The velocity does not change sign on the interval
, the acceleration is negative. The velocity does not change sign on the interval . If the velocity is contained in (25) with the sign “
. If the velocity is contained in (25) with the sign “ ,” then the motion of the particle starts at the unstable equilibrium position determined by the radial parameter
,” then the motion of the particle starts at the unstable equilibrium position determined by the radial parameter 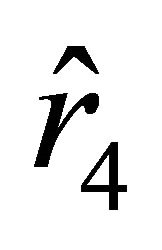 toward the ball. Successively passing through attraction and repulsion zones, the particle arrives at the center of the ball with velocity
toward the ball. Successively passing through attraction and repulsion zones, the particle arrives at the center of the ball with velocity 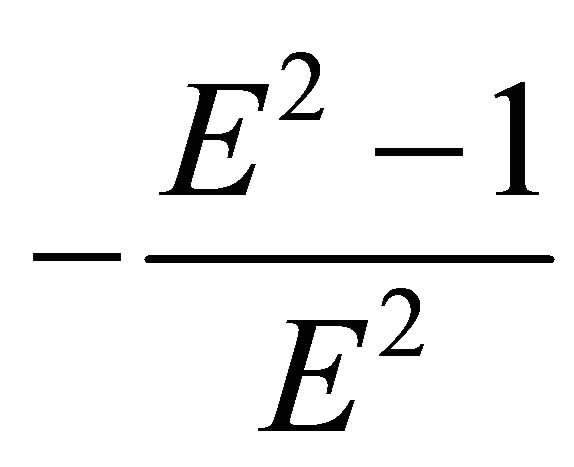 and continues to move in the same direction; now the particle moves away from the center of the ball with positive velocity toward the boundary characterized by the radial parameter
and continues to move in the same direction; now the particle moves away from the center of the ball with positive velocity toward the boundary characterized by the radial parameter  but does not reach it in any finite time
but does not reach it in any finite time .
.
(a2) Suppose that condition (36) holds and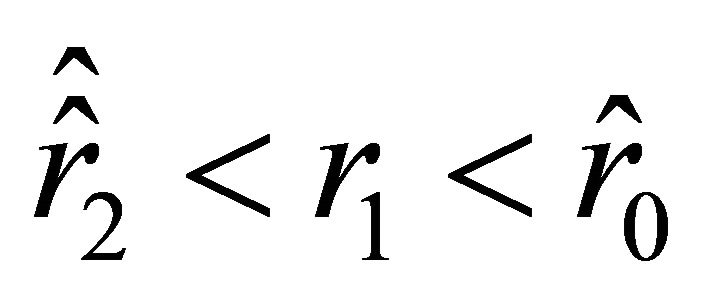 .
.
Then the acceleration is negative on the interval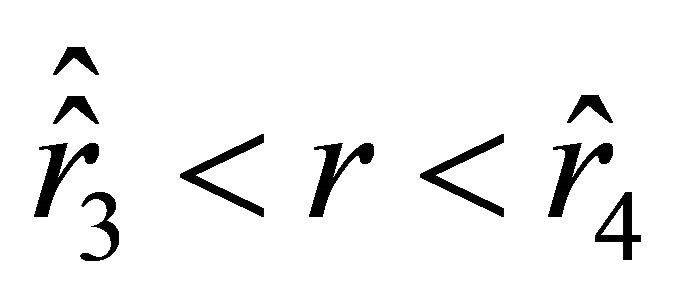 , positive on the interval
, positive on the interval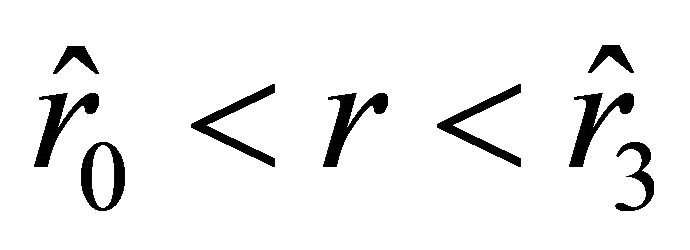 , and negative again on the interval
, and negative again on the interval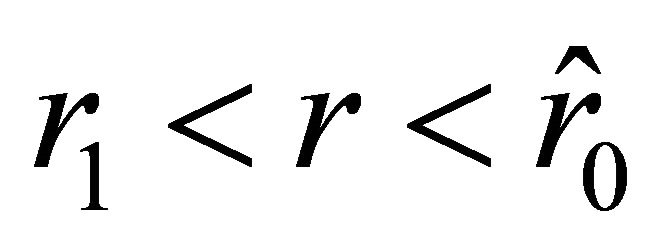 . The motion of the particle starts from the unstable equilibrium position determined by the radial parameter
. The motion of the particle starts from the unstable equilibrium position determined by the radial parameter  toward the ball if the sign in (25) is “
toward the ball if the sign in (25) is “ .” Successively passing attraction and repulsion zones, the particle reaches the boundary at the antipodal point characterized by the radial parameter
.” Successively passing attraction and repulsion zones, the particle reaches the boundary at the antipodal point characterized by the radial parameter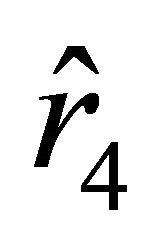 . Formally, we might also consider motions from the unstable equilibrium state determined by
. Formally, we might also consider motions from the unstable equilibrium state determined by 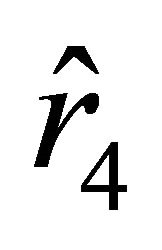 with positive velocity and acceleration in the direction away from the ball. However, at
with positive velocity and acceleration in the direction away from the ball. However, at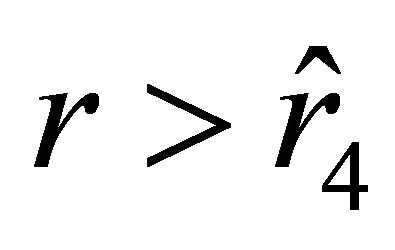 , the signature of the space changes, which is mathematically inadmissible. Physically, such a motion would lead to the violation of the principle that a material body cannot travel faster than light.
, the signature of the space changes, which is mathematically inadmissible. Physically, such a motion would lead to the violation of the principle that a material body cannot travel faster than light.
(a3) Suppose that 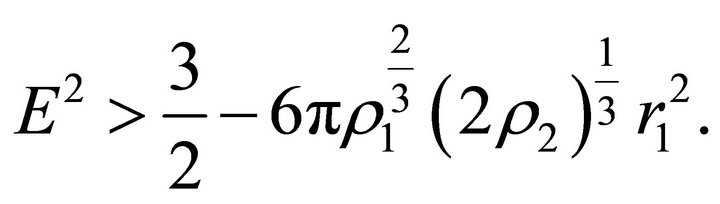
Then Equation (32) has no positive roots, and 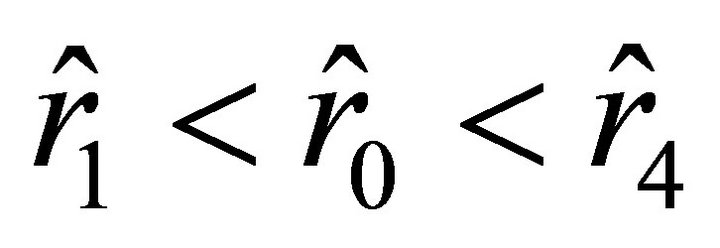 . The condition
. The condition 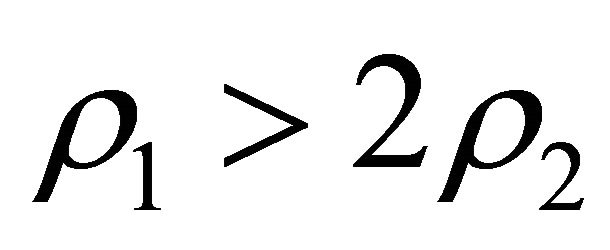 implies
implies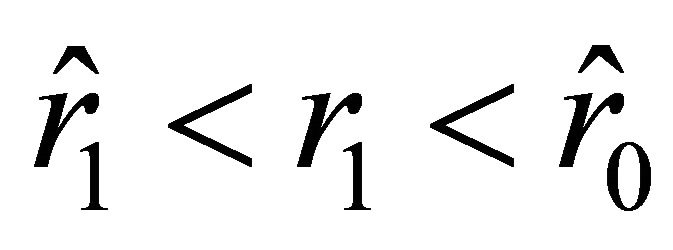 . The acceleration vanishes at the points
. The acceleration vanishes at the points 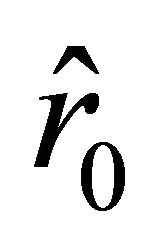 and
and 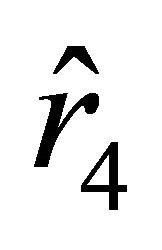 outside the ball and at the point
outside the ball and at the point  inside the ball. The velocity vanishes only at the point
inside the ball. The velocity vanishes only at the point . The acceleration is negative on the interval
. The acceleration is negative on the interval  and positive on the interval
and positive on the interval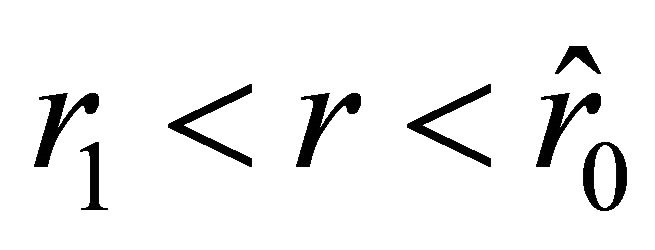 . Inside the ball, on the interval
. Inside the ball, on the interval , the acceleration is negative, i.e., the particle experiences attraction.
, the acceleration is negative, i.e., the particle experiences attraction.
The motion of the particle starts from the unstable equilibrium state characterized by the parameter 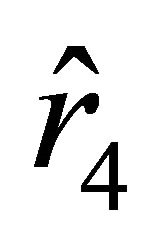 toward the ball if the sign in (25) is “
toward the ball if the sign in (25) is “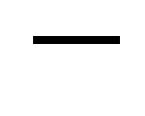 ”. The particle experiences the action of an attractive force, which changes for a repulsive force near the surface of the ball. Inside the ball, the force is again attractive. Successively passing through attraction and repulsion zones, the particle approaches the boundary characterized by the parameter
”. The particle experiences the action of an attractive force, which changes for a repulsive force near the surface of the ball. Inside the ball, the force is again attractive. Successively passing through attraction and repulsion zones, the particle approaches the boundary characterized by the parameter 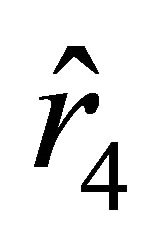 but does not reach it in finite time.
but does not reach it in finite time.
7. Conclusion
The analysis of properties of the radial geodesics with respect to the world time  performed in this paper shows that these geodesics do not leave a certain spherically symmetric domain, provided that the radial motion starts at an interior point of this domain. This indirectly indicates that the presence of dark energy in a space renders this space finite and closed. Indeed, if the space was filled only with dark energy, i.e., if it had everywhere constant positive scalar curvature, then, as de Sitter showed in [6], this would be a finite closed elliptic space. Apparently, the finiteness and closedness of such a space must be preserved when a material body is placed inside it. However, the behavior of the radial geodesics with respect to the absolute time
performed in this paper shows that these geodesics do not leave a certain spherically symmetric domain, provided that the radial motion starts at an interior point of this domain. This indirectly indicates that the presence of dark energy in a space renders this space finite and closed. Indeed, if the space was filled only with dark energy, i.e., if it had everywhere constant positive scalar curvature, then, as de Sitter showed in [6], this would be a finite closed elliptic space. Apparently, the finiteness and closedness of such a space must be preserved when a material body is placed inside it. However, the behavior of the radial geodesics with respect to the absolute time  is alerting. Thus, the question on the finiteness and the closedness of the space in the model considered above remains open and requires additional analysis.
is alerting. Thus, the question on the finiteness and the closedness of the space in the model considered above remains open and requires additional analysis.
REFERENCES
- S. Permutter, et al., “Measurements of Ω and Λ from 42 High-Redshift Supernovae,” The Astrophysical Journal, Vol. 517, No. 2, 1999, pp. 565-586. doi:10.1086/307221
- A. G. Ries, et al., “Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant,” The Astronomical Journal, Vol. 116, No. 3, 1998, pp. 1009-1038.
- A. D. Chermin, “Dark Energy and Universal Antigravitation,” Physics-Uspekhi, Vol. 51, No. 3, 2008, pp. 253- 282.
- L. D. Landau and E. M. Lifshiz, “The Field Theory,” Nauka, Moscow, 1973.
- N. N. Popov, “A Geometric Interpretation of Gravity Theory,” Advances in Systems Science and Application, Vol. 12, No. 3, 2012, pp. 53-66.
- W. de Sitter.,” On Einstein’s Theory of Gravitation and Its Astronomical Consequences,” Monthly Notices of the Royal Astronomical Society, Vol. 78, No. 3, 1917, pp. 3-28.
- S. Chandrasekhar, “The Mathematical Theory of Black Holes,” Clarendon Press, Oxford, 1983.

