International Journal of Astronomy and Astrophysics
Vol. 3 No. 2 (2013) , Article ID: 32353 , 9 pages DOI:10.4236/ijaa.2013.32011
Creating a “Faraday Ghost” inside the Rotation Measure Synthesis Technique, through a Wide Observational “Gap” in Wavelength Coverage
National Research Council Canada, National Science Infrastructure Portfolio, Victoria, Canada
Email: jacques.vallee@nrc-cnrc.gc.ca
Copyright © 2013 Jacques P. Vallée. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 16, 2013; revised February 17, 2013; accepted February 26, 2013
Keywords: Magnetic Fields; Radio Polarization; Galactic Magnetic Fields; Spiral Galaxies
ABSTRACT
Several recently published Faraday rotation measures (RM) derived using the novel RM synthesis technique are likely in error. If a set of polarimetric observations contains a large gap in the wavelength coverage, the rotation measure determination is sometimes ambiguous; this is also true even when two long wavelength ranges are observed but are separated by a wide gap. Essentially, there are 180˚ ambiguities in the observed Position Angle of the electric polarisation vector between the two wavelength ranges; these ambiguities are not resolved because the extent of wavelengths2 covered, within each of the two ranges, is too small to uniquely determine the RM in isolation. We find that unphysical “Faraday ghosts” can be mathematically constructed with a np ambiguity (±180˚ times an integer) at predictable polarization position angles when using only two wavelength ranges separated by a gap, as a function of the width of the gap (Equation (4)). Our computations suggest an empirical correlation between an observational gap between two wavelength ranges and the appearance of “Faraday ghosts”.
1. Introduction
Studies of the magneto-ionic medium in galaxies make use of the “angular rotation of the plane of polarisation”, ΔPA, of the electric vector in the plane of the incoming electromagnetic wave while travelling in a magnetized medium, known as Faraday rotation. In turn, these studies yield magnetic field information and maps for objects in the Milky Way [1] and beyond [2]. In the interstellar medium, Faraday rotation occurs, in which the position angle [PA] of the electric vector at maximum intensity changes with the observing wavelength λ:
 (1)
(1)
where ΔPA is in radians, λ is in m, and RM [radians/m2] is the rotation measure. The PA of the electric vector of the photon at λ0 cm wavelength is perpendicular to the magnetic field in the emitting region, in the optically-thin synchrotron emission. Thus a “linear RM” is defined as the slope in a plot of PA versus wavelength squared. Numerous uses of this linear RM technique have been made ([3,4]; etc.).
The Faraday Depth [FD] is defined as:
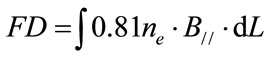 (2)
(2)
where ne is the free electron density [cm−3], B// [mG] is the magnetic field parallel to the line of sight [l-o-s], and L [pc] is the length along the l-o-s. The total RM is the linear sum of the individual RM contributions from the radio emitter (a galaxy or a quasar, say), and all along the way including from the ionosphere of the Earth, provided that the emitting medium is separated from the Faraday rotating medium. Numerous maps of nearby galaxies have recently shown their Faraday depth, or grossly speaking their own RM for a Faraday-thin medium. Singularities in the RM can arise when the magnetic field along the line of sight changes direction; when Blos = 0 the net zero magnetic field along the l-o-s gives rise to Faraday caustic [5].
In the linear Rotation Measure technique, the np ambiguity (±180˚ times an integer) is tested by adding a different n value to the polarization position angles, and solved by a least-squares fit [lsf] of the slope in a plot of the observed linear polarisation position angle as a function of the square of the observing wavelength. This minimization can provide a valuable estimate of RM, as it finds the proper integer “n” value through a statistical analysis.
A newer RM synthesis [RMS] technique has been proposed recently, to perform a transformation from the observational position-angle versus l2 space to the computational Faraday depth space, to obtain the characteristic RM. Here the integral of the observed linear polarization parameters (Stokes Q and U) over the observed wavelengths can in principle be inverted by a transform function, in order to give the run of the polarized intensity as a function of the Faraday depth of an emitting object from the observer. No intervention is currently made in RM synthesis to insert the proper integer “n” value, when using widely separated wavelengths (say, many observations near l22 cm and many more elsewhere near l18 cm). Secondary, faint RM components thus appear— but are they physically real?
In B10 ([6], their sect.3.4), there is a discussion of three indicators of the reliability of these faint components: they do not occur towards the brightest low dispersion components; the Faraday depth separation of these secondary components varies from source to source, while the instrumental sidelobe response does not; and the faint positive and negative-shifted components from a complementary distribution of each other, rather than a repetition in detail. Yet, doubts remain, since counter-arguments can be made (see below). a) Here the observed data shown here (see below) are all from high signal to noise polarized objects (as compared to others) previously selected as such by B10 [6] and H09 [7]; b) In each case discussed so far, these two FD ghosts are located on both sides of the RM corresponding to the expected (3rd) physical disk solution to the np ambiguity (see below); c) Broad similarities and small differences between the two FD ghosts are computed for a galaxy. In maps of Right Ascension and Declination coordinates [RA/Dec], their “ghosts” are distributed in a broadly similar way (suggesting a basic common error), yet with some slight differences (suggesting different noise at different RA/Dec).
Here, our goal is to evaluate the alleged physical presence of multiple Faraday RM recently proposed in the literature, for the galaxies NGC5194, NGC 6946, and quasar 2236 + 3420. To show their probable unphysical (or ghost) properties, we create a model showing the observed and predicted ghosts, and evaluate their chance probability. Methodologically, we summarize in Section 2 the linear RM technique to solve the ambiguity in observed position angle of the linear polarisation. In Section 3, we review the newer RM synthesis technique. In Section 4, we look at recent cases in detail, comparing their computed Faraday depths with the actual linear polarisation angles at each wavelength.
2. The Linear RM Technique, Used to Solve the Ambiguity of n Times 180˚
To properly compute the RM and remove the ambiguity in 180˚ of each observed position angle, one must set up a scheme, be it statistical (a, b), neighbourly (c, d) or physically grounded (e). In (a), the least-squares fit method is often used, to do a least-squares-fit of successive trial RM, after adding as many times 180˚ as needed to bring a position angle near a trial RM, with a cut-off at 10,000 rad/m2 ([8,9]) and proper care to isolate a suitable range of wavelength l pertinent to a single physical ré- gime [10]. In (b), the maximum-likelihood with the MacDonald-Bunimovitch method is used [11]. In (c), one uses the RM from two adjacent positions in the sky to assist the computations at a given (RA/Dec) point [12], denying a jump of 180˚ over such a short adjacent physical space. In (d), the RM from two very near wavelengths are used [13], denying a jump of 180˚ over such a short wavelength range. In (e), one selects a range of observing wavelengths short enough to encompass only one physical regime. Broten et al. [3] selected polarization observations in one physical wavelength range, to cover one physical regime. They found four physical regimes for a typical elliptical radio galaxy [10]: 1) a variable emission from the nucleus of the optical galaxy; 2) a two-component, side-side depolarization (from the twin radio lobes, at short l cm); 3) one-component, Faradaythick régime (from one lobe, at long l cm); and 4) onecomponent, Faraday-thin régime (from one radio lobe, at mid l cm).
3. The RM Synthesis Technique, Employed via an Inversion with Gaps
New mathematical techniques to compute the RM have been proposed, to complement the linear RM technique. Others include the uses of Stokes Q and U parameters with wavelength [14], or a wavelet deconvolution ([15, 16]), or a compressed sensing/sparse solution [17]. Sparse solutions seek the smallest number of components required to fit an observed Faraday depth spectrum [17]. The main new one frequently employed is the Rotation Measure synthesis technique (as discussed below). The integral of the observed linear polarization Stokes Q and U, over the observed wavelengths, can in principle be inverted, in order to give the run of the polarized intensity as a function of the Faraday depth of an emitting object from the observer [18]. At wavelengths without observational data (or gaps), the mathematical inversion will assume something in the gaps (possibly a wrong assumption) or nothing there (zero amplitude, definitely a wrong assumption), and hence the inversion result will show a RM deviation (ghost-like) from the physical reality—creating the “ghosts of the gaps”!
We must solve the lack of observations at l2 < 0 (unobservable gap). Unobservable negative wavelengths will require an assumption in the inversion process. Different assumptions, made to cover the observational gap in negative l2, could lead to different reconstructions (or to create unphysical ghosts).
We must solve the observational gaps in l2 > 0 (instrumental gap). Unobserved positive wavelengths, in between or outside observed positive wavelengths, will require some data filtering, or employing an assumption in the inversion process. An assumption of symmetry can be used. In [15], the Faraday dispersion function F (a.k.a. the fraction of polarized emission with the Faraday depth f) is assumed to be symmetric (+) or antisymmetric (−) with respect to the observed maximum of emission at fo, producing the observed complex polarized intensity P:
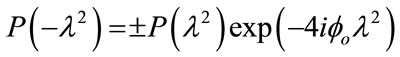 (3)
(3)
Between these two (+ or −) options, they choose only the + sign in their subsequent paper (their Equation (15) in Ref. [16]) as they claimed that “realistic objects mainly look like even objects in Faraday depth space”. Different assumptions, made to cover the observational gaps in positive l2, could lead to different results or “ghost”.
A selective filter can be used. Some employed the RM synthesis technique using data at l20 cm (with many observed channels), and added data at l13 cm (with many observed channels) but only if the l13 cm data agreed independently with the l20 cm data (Section 3 in [19]), assuming that the RM found at l20 cm should also be dominating at l13 cm. Van Eck et al. [20] used both the linear RM technique and the RM synthesis technique for extragalactic point sources, with VLA observations near a frequency of 1365 and also near 1485 MHz. Using the linear RM technique, they found the RM near 1365 and near 1485 MHz (and the proper “n” integer value). If these results differed, they discarded the results; the remaining “well-behaved” sources were processed through the RM synthesis technique. Their final galactic magnetic field model is similar to that elsewhere (see picture 33 in Ref. [2]).
There are some known problems in the RM synthesis technique. It is difficult to reproduce the correct phase information in the presence of multiple RM components [15]. The RM synthesis technique lacks the equivalent of a reduced chi-squared value (r) to get the “goodness of fit”, so the solution can “converge” to an incorrect RM value [21]—having computed r in a plot of the PA versus l2, using the RM slope equal the RM synthesis value, they then rejected the RM synthesis value if r is > 2. Farnsworth et al. [14] studied the RM resulting from different techniques in six WSRT areas: Aries, Coma SW, Coma NW, Coma NE 1259 + 2758, A1453 + 4025 and B 1620 + 6012, and found the RM synthesis technique to give differing results in 1 case out of 7 (their lists 6 to 12).
4. Evaluations of Multiple Faraday Depths from the RM Synthesis Technique
Here, we perform an evaluation of claims of the presence of several multiple Faraday depths in galaxies or quasars, having employed interferometric observations. Table 1 here shows many published multiple Faraday depths data from the literature, using RM synthesis. All observations were made near l18 cm and near l22 cm, but without observations located in between these two wavelengths l.
Figure 1 shows the histogram of the data in Table 1, where one can see a group of central Faraday depths (true data), and another group for negative Faraday depths (at left, with negative ghosts), and an analogous group (at right, with positive ghosts). The width of each of the 3 groups is large, near 150 rad/m2.
Figure 2 shows the same objects from Table 1, except that the central Faraday depths (true data, in Table 1) are subtracted from the negative Faraday depths (giving the left peak). Also, the central Faraday depths (true data) are subtracted from the positive Faraday depths (giving the peak at right). The width of each of the 2 peaks now is quite narrow, about 75 rad/m2, but the difference in two independent distributions should have a larger width.
Figure 3 is an artist’s conception of the published data, showing a simplified sketch of the observed quasar data (Picture 3b in Ref. [7]; source 2236 + 3420 in List 2 of [7]) as thick continuous slanted lines. The small observed deviations could slightly broaden the main RM value at −185 rad/m2, but not create a ghost elsewhere. Also shown is one of their fits at RM = −185 rad/m2 (thin continuous line), with the data at top left being the same data
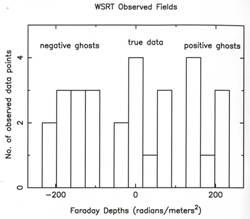
Figure 1. Histogram of the Faraday depths data in Table 1, where one can see a group of central Faraday depths, and at left another group for negative Faraday depths, and an analogous group at right. All data were computed with the RM Synthesis technique.
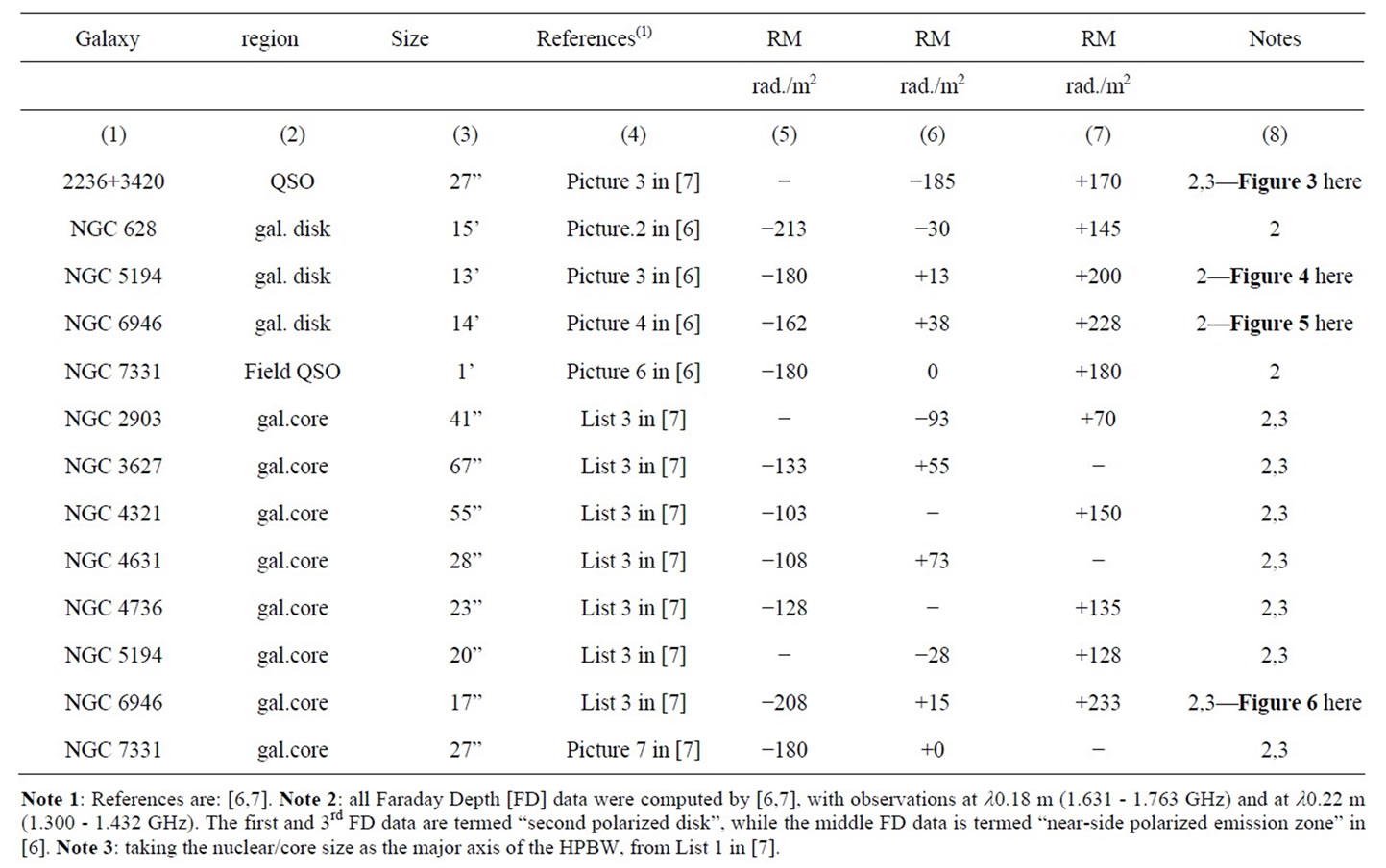
Table 1. Published multiple Faraday Depths, from the RM synthesis technique.

Figure 2. Histogram of the same objects from Table 1, except that the central Faraday depths (true data) is subtracted from the negative Faraday depths (giving the left peak). Also, the central Faraday depths (true data) is subtracted from the positive Faraday depths (giving the peak at right).
at bottom left to which we added 180 degrees in order to resolve the ambiguity on polarization position angle. We show their second FD at +170 rad/m2 [dashed line] and another one with an ambiguity of 180˚ [dotted line]. For this ghost, the RM synthesis assigned an amplitude of 1/6 of that of the primary Faraday depth near –185 rad/m2 (see their picture 3a). The dotted line is an RM ghost (Equation (4) below, with n = +1).
It could thus be assumed that the same n times 180-degree problem will come up at other ghost Faraday depths, obeying the relation:
 (4)
(4)
with “n” being a positive or negative integer (0, +1, −1, +2, −2, ···), and where two observing bands have been employed (here, one near l18 cm and the other near l22 cm).
Figure 4 is an artist’s conception of the published data (the PA data are not published). It shows the computed data for the NGC5194 galaxy (Picture 7 at right panel and List 3 in [7]; Pictures 1 and 3 in [6]) as thick continuous slanted lines. Also shown is one of their fits at RM = +13 rad/m2 (thin continuous line). This fit is good, as per the usual criteria of fit. They (Picture 3 in reference [6]) proposed a 2nd and a 3rd fit in Faraday depth, namely at +200 and –180 rad/m2. We show two dashed lines with very similar RM values, rising from the middle of the l18 cm position angle data towards the l22 cm position angle data (after adding or subtracting one times 180 degrees to them).
For this NGC galaxy, at these 2nd and 3rd Faraday depths, the RM synthesis code assigns a positive ampli-
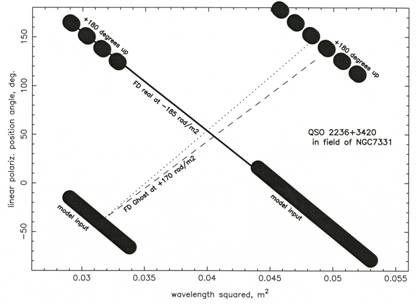
Figure 3. Artist’s conception of the observed linear polarization position angle at each observing wavelength squared, with the 180˚ ambiguity model. The observed quasar data (Picture 3b in Ref. [7]; source 2236 + 3420 in List 2 in Ref. [7]) are simplified as thick continuous slanted lines. Also shown is their fit at RM = −185 rad/m2 (thin continuous line), with the data at top left being the same data at bottom left plus 180˚. The dashed line is the observed ghost from the RM synthesis technique [7] and the dotted line is the linear RM-modeled ghost (Equation (1)).
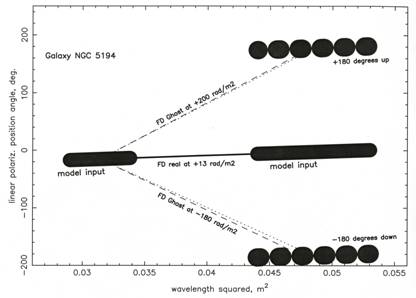
Figure 4. Artist’s conception of the observed linear polarization position angle at each observing wavelength squared, with the 180˚ ambiguity model. The observed PA data were not published. This plot is for the NGC5194 galaxy (Picture 7 at right panel and List 3 in Ref. [7]; Picture 1 and List 3 in Ref. [6]) seen as thick continuous slanted lines. Also shown is their fit at RM = +13 rad/m2 (thin continuous line). The dashed lines are the ghosts from the RM synthesis technique [6] and the dotted lines are the linear RM-modeled ghosts (Equation (1)).
tude of 1/5 of that of the primary Faraday depth (their picture 3). For most of the remaining galaxies listed in our Table 1, we find a pattern for their 2nd and 3rd Faraday depths (same pattern as for Figures 3 and 4 here): a “ghost” Faraday depth (dashed lines in Figure 4) can be linked to the set of observed l22 cm position angles by adding or subtracting 180 degrees to them (Figure 3).
Figure 5 is an artist’s conception for the published data (the PA data are not published). It shows the computed data for the NGC6946 galaxy (Picture 7 at right panel and List 3 in Ref. [7]; Pictures 1 and 4 in Ref. [6]). Other symbols are the same as in previously used.
Figure 6 is an artist’s conception of the published data (the PA data are not published). It shows the computed data for the central nucleus of this same galaxy (Picture 7 at right panel and List 3 in Ref. [7]). B10 [6] proposed a 2nd and a 3rd Faraday depths for the whole galaxy, namely at +228 and –162 rad/m2.
We show two dashed lines with very similar RM values, rising from the middle of the l18 cm position angle
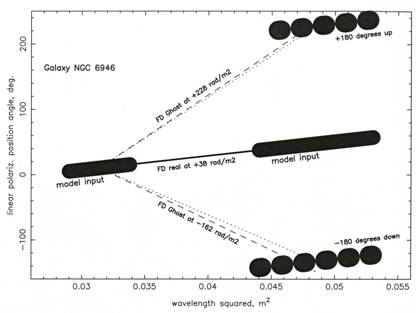
Figure 5. Artist’s conception of the observed linear polarization position angle at each observing wavelength squared, with the 180˚ ambiguity model. The observed PA data were not published. The plot is for the whole galaxy NGC6946 (Picture 7 at right panel and List 3 in Ref. [7]; Pictures 1 and 4 in Ref. [6]). The dashed lines are the ghosts from the RM synthesis technique [6] and the dotted lines are the linear RM-modeled ghosts (Equation (1)).
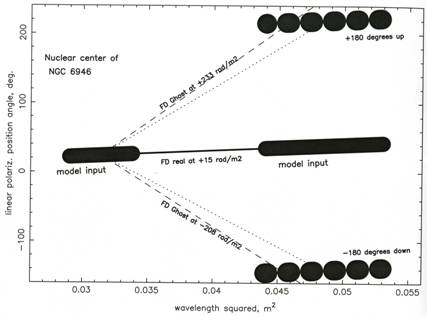
Figure 6. Artist’s conception of the observed linear polarization position angle at each observing wavelength squared, with the 180˚ ambiguity model. The observed PA data were not published. The plot is for the central nucleus of the galaxy NGC6946 (Picture 7 at right panel and List 3 in Ref. [7]). The dashed lines are the ghosts from the RM synthesis technique [7] and the dotted lines are the linear RM-modeled ghosts (Equation (1)).
data towards the l22 cm position angle data (after adding or subtracting one times 180 degrees to them).
Table 2 here shows some of the Ghost Faraday depths obtained from the RM synthesis technique (data from Table 1), and the corresponding RM from the linear RM technique when adding 180˚ to the observed PA. While Table 1 shows 5 sources with 2 symmetric Faraday Ghosts (with n = 1), only one Faraday Ghost in seen in 8 sources (with n = 1). In no case did the FD “ghosts” reported in Table 1 have an ambiguity of 2p (with n = 2).
Figure 7 shows the Ghost Faraday Depths from the RM synthesis technique (vertical) versus the RM from the linear RM technique when adding an ambiguity of 180˚. The solid line is drawn with the ideal case of: [Ghost RMS FD] = [RM with an 180˚ ambiguity]. The dashed line shows the best least-squares fit. This suggests that the Ghosts are likely correlated with an ambiguity of 180˚. Probability statistics were made on the data in Figure 7 and Table 2. The linear correlation coefficient was found to be r = 0.996 in Figure 7. For two variables (RM synthesis and linear RM) assumed to be uncorrelated, the chance probability that in a random sample of 7 objects one gets a linear correlation coefficient r > 0.996 is less than 0.1% [22]. Our linear RM with one 180˚ ambiguity matches well the RM synthesis ghosts with a probability >99.9%.
5. Conclusion
When there is a wide observational gap in wavelength, such as in all the cases discussed here with data only near l22 cm and near l18 cm, and no data at l19 cm nor at l20 cm, the missing data (which could have revealed the n times 180˚ value) are not there to inform the subsequent modeling. In the linear RM technique, using the position angle versus wavelength squared plane, this is prevented by doing a set of actions to effectively choose the best RM slope through a standard least-squares fit ([8-10]).
In the RMS technique, [23] suggested that the 180- degree ambiguity could manifest itself in the sidelobes of the RM transfer function. [24] used both the linear RM technique and the RM synthesis technique near 350 MHz, and found that the RM synthesis technique may yield an erroneous Faraday structure in the presence of multiple RM components. They found that two nearby RM components would “interfere” to create structures in Q and U, causing the RM synthesis technique to “put power” at values other than the input model RM.
Here we evaluated the alleged physical presence of multiple Faraday RM recently proposed in the literature, obtained through the RM synthesis technique, for the galaxies NGC5194, NGC 6946, and quasar 2236 + 3420 (Tables 1 and 2). Figures 1 and 2 show narrow ghosts being symmetric on both sides of the real Faraday depths. This suggest an unphysical mathematical issue. We suggest a possible correlation between the wide absence of observations at wavelength in between two observed ranges (l18 cm range and l22 cm range, say), and the presence of Faraday ghosts rotation measures (Equation (4)). We create a model (Figures 3 to 6) showing the observed (RM synthesis values) and predicted ghosts, and evaluate their chance probability (Figure 7). Our models show that an unphysical Faraday ghost can be easily created when adding or subtracting 1 or more times 180 degrees to the l22 cm data, starting from the l18 cm position angle data. We found evidence at >99.9% level of an empirical correlation between the “ghosts” in Faraday depths obtained from the RM synthesis technique

Table 2. Ghost RM synthesis Faraday Depths, and linear RM least-squared fit with 180˚ ambiguity.

Figure 7. Comparison of the Faraday Ghosts as observed from the RM synthesis technique (y-axis) versus those modeled from the linear RM technique with an inserted ambiguity of 180˚ (x-axis). The straight line is for an ideal match (RM synthesis value = linear RM value), and the dashed line is the best least-squared fitted line to the data.
and the RM needed to link the two wavelength coverages (around l18 cm, around l22 cm). Actual telescope observations in-between the two wavelength bands (above l19 cm and below l21 cm) could support this explanation.
REFERENCES
- J. P. Vallée, “Magnetic Fields in the Nearby Universe, as Observed in Solar and Planetary Realms, Stars, and Interstellar Starforming Nurseries,” New Astronomy Reviews, Vol. 55, No. 3-4, 2011, pp. 23-90. doi:10.1016/j.newar.2011.01.001
- J. P. Vallée, “Magnetic Fields in the Galactic Universe, as Observed in Supershells, Galaxies, Intergalactic and Cosmic Realms,” New Astronomy Reviews, Vol. 55, No. 3-4, 2011, pp. 91-154. doi:10.1016/j.newar.2011.01.002
- N. W., Broten, J. M. MacLeod and J. P. Vallée, “Catalogue of Unambiguous (Faraday-Thin, One-Component, Spectrum-Selected) Rotation Measures for Galaxies and Quasars,” Astrophysics and Space Science, Vol. 141, No. 2, 1988, pp. 303-331. doi:10.1007/BF00639497
- J. C. Brown and A. R. Taylor, “The Structure of the Magnetic Field in the Outer Galaxy from Rotation Measure Observations through the Disk,” Astronomical Journal, Vol. 563, No. 1, 2001, pp. L31-L34. doi:10.1086/338358
- M. R. Bell, H. Junklewitz and T. A. Ensslin, “Faraday Caustics. Singularities in the Faraday Spectrum and Their Utility as Probes of Magnetic Field Properties,” Astronomy and Astrophysics, Vol. 535, No. A85, 2011, pp. 1-14.
- R. Braun, G. Heald and R. Beck, “The Westerbork SINGS Survey. III. Global Magnetic Field Topology,” Astronomy and Astrophysics, Vol. 514, No. A42, 2010, pp. 1-19.
- G. Heald, R. Braun and Edmonds, “The Westerbork SINGS Survey. II Polarization, Faraday Rotation, and Magnetic Fields,” Astronomy and Astrophysics, Vol. 503, No. 2, 2009, pp. 409-435. doi:10.1051/0004-6361/200912240
- J. P. Vallée, “A Study of the Linear Polarization of Radio Galaxies and Quasars,” Ph.D. Thesis, University of Toronto, Toronto, 1973.
- J. P. Vallée and P. P. Kronberg, “The Rotation Measures of Radio Sources and Their Interpretation,” Astronomy & Astrophysics, Vol. 43, No. 2, 1975, pp. 233-242.
- J. P. Vallée, “The Rotation Measures of Radio Sources and Their Data Processing,” Astronomy and Astrophysics, Vol. 86, No. 1, 1980, pp. 251-253.
- S. Sarala and P. Jain, “A Circular Statistical Method for Extracting Rotation Measures,” Monthly Notices of the Royal Astronomical Society, Vol. 328, No. 2, 2001, pp. 623-634. doi:10.1046/j.1365-8711.2001.04932.x
- K. Dolag, C. Vogt and T. A. Ensslin, “PACERMAN-I. A New Algorithm to Calculate Faraday Rotation Maps,” Monthly Notices of the Royal Astronomical Society, Vol. 358, No. 3, 2005, pp. 726-731. doi:10.1111/j.1365-2966.2005.08851.x
- A. A Ruzmaikin and D. D. Sokoloff, “The Calculation of Faraday Rotation Measures of Cosmic Radio Sources,” Astronomy and Astrophysics, Vol. 78, No. 1, 1979, pp. 1-6.
- D. Farnsworth, L. Rudnick and S. Brown, “Integrated Polarization of Sources at λ ~ 1 m and New Rotation Measure Ambiguities,” Astronomical Journal, Vol. 141, No. A191, 2011, pp. 1-28.
- P. Frick, D. Sokoloff, R. Stepanov and R. Beck, “Wavelet-Based Faraday Rotation Measure Synthesis,” Monthly Notices of the Royal Astronomical Society, Vol. 401, No. 1, 2010, pp. L24-L28. doi:10.1111/j.1745-3933.2009.00778.x
- P. Frick, D. Sokoloff, R. Stepanov and R. Beck, “Faraday Rotation Measure Synthesis for Magnetic Fields of Galaxies,” Monthly Notices of the Royal Astronomical Society, Vol. 414, No. 3, 2011, pp. 2540-2549. doi:10.1111/j.1365-2966.2011.18571.x
- M. Andrecut, J. M. Stil and A. R. Taylor, “Sparse Faraday Rotation Measure Synthesis,” Astronomical Journal, Vol. 143, No. A33, 2012, pp. 1-12.
- B. J. Burn, “On the Depolarization of Discrete Radio Sources by Faraday Dispersion,” Monthly Notices of the Royal Astronomical Society, Vol. 133, No. 1, 1966, pp. 67-83.
- S. A. Mao, B. M. Gaensler, M. Haverkorn, E. G. Zweibel, G. J. Madsen, N. M. McClure-Griffiths, A. Shukurov and P. P. Kronberg, “A Survey of Extragalactic Faraday Rotation at High Galactic Latitude: The Vertical Magnetic Field of the Milky Way toward the Galactic Poles,” Astronomical Journal, Vol. 714, No. 2, 2010, pp. 1170-1186. doi:10.1088/0004-637X/714/2/1170
- C. L. Van Eck, J. C. Brown, J. M. Stil, K. Rae, S. A. Mao, B. M. Gaensler, A. Shukurov, A. R. Taylor, M. Haverkorn, P. P. Kronberg and N. M. McClure-Griffiths, “Modeling the Magnetic Field in the Galactic Disk Using New Rotation Measure Observations from the Very Large Array,” Astronomical Journal, Vol. 728, No. A97, 2011, pp. 1-14.
- S. A. Mao, N. M. McClure-Griffiths, B. M. Gaensler, J. C. Brown, C. L. van Eck, M. Haverkorn, P. P. Kronberg, J. M. Still, A. Shukurov and A. R. Taylor, “New Constraints on the Galactic Halo Magnetic Field Using Rotation Measures of Extragalactic Sources toward the Outer Galaxy,” Astronomical Journal, Vol. 755, No. A21, 2012, pp. 1-15.
- P. R. Bevington, “Data Reduction and Error Analysis for the Physical Sciences,” McGraw-Hill, New York, 1969, pp. 310-311.
- M. A. Brentjens and A. G. de Bruyn, “Faraday Rotation Measure Synthesis,” Astronomy and Astrophysics, Vol. 441, No. 3, 2005, pp. 1217-1228. doi:10.1051/0004-6361:20052990
- D. Farnsworth, L. Rudnick and S. Brown, “Integrated Polarization of Sources at λ ~ 1 m and New Rotation Measure Ambiguities,” Astronomical Journal, Vol. 141, No. A191, 2011, pp. 1-18.

