International Journal of Astronomy and Astrophysics
Vol.3 No.3(2013), Article ID:36509,9 pages DOI:10.4236/ijaa.2013.33027
Antigravity—Its Manifestations and Origin
1Institute of Mathematics, Academy of Sciences, Prague, Czech Republic
2Department of Mathematics, Catholic University of America, Washington DC, USA
Email: krizek@cesnet.cz, somer@cua.edu
Copyright © 2013 Michal Křížek, Lawrence Somer. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 11, 2013; revised June 13, 2013; accepted June 20, 2013
Keywords: Hubble Parameter; Dark Energy; Antigravity; Cosmological Constant; Gravitational Aberration; Conservation of Energy and Momentum Law; Solar System
ABSTRACT
Dark energy has been introduced in order to explain the observed acceleration of the expansion of our Universe. It seems to be distributed almost uniformly and it has an essential influence on the present value of the Hubble constant which characterizes the rate of this expansion. The Newtonian theory of gravitation is formulated so that the laws of conservation of energy and momentum hold. However, the Universe is designed so that the total amount of energy is slowly, but continually increasing, since its expansion is accelerating. Our examples show that even the Solar System and also our Galaxy imperceptibly expand thanks to dark energy whose origins are tiny antigravity forces. We claim that these forces appear due to the finite speed of gravitational interaction, which causes gravitational aberration effects. We show that effects of dark energy are observable; they are not only globally, but also in local systems. These effects can be measured and are comparable with the present value of the Hubble constant.
1. Introduction
There is a tendency among physicists to state that dark energy can only manifest itself on cosmological scales by definition. However, there is an underlying reality which our model of dark energy tries to capture. In this paper, we provide many examples that give evidence that in reality there are manifestations of dark energy on local scales as small as the Solar System.
The validity of physical laws is verified by measurements. Nevertheless, absolutely exact measurement instruments cannot be constructed. Hence, we are not able to check by measurements whether generally accepted physical laws (such as the conservation of energy law or the conservation of momentum law) are valid for an arbitrary number of decimal digits.
The law of conservation of energy belongs to the basic pillars of current physics. The Newtonian theory of gravitation is formulated in such a way that the law of conservation of energy is valid absolutely and exactly. However, is this law valid also in the real world that is only modeled by Newton’s theory or Einstein’s theory of general relativity? We will apply a wide interdisciplinary approach to answer this question. We will present more than 10 real-world examples that illustrate why the law of conservation of energy is not valid absolutely and exactly. Firstly we survey a number of astrobiological, astronomical, geometrical, geophysical, geochronometrical, heliophysical, climatological, paleontological, and observational arguments showing that the Solar System slowly expands by a speed of approximately v = 5 m·yr−1· au−1. comparable to the present value of the Hubble constant recalibrated to 1 au = 149,597,870,700 m, i.e.
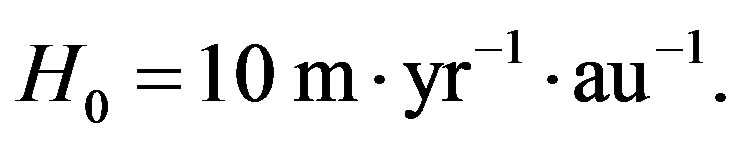 (1)
(1)
Such a large expansion rate cannot be explained by the decrease of the solar mass nor by solar wind or by tidal forces (see [1]). This, of course, contradicts Kepler’s laws, and thus also the law of conservation of energy taking into account that the Solar System is sufficiently isolated from the gravitational influence of other stars. For instance, the closest star (except for our Sun), Proxima Centauri acts on the Earth with about a million times smaller gravitational force than does Venus.
Dark energy has an essential influence on the expansion of our Universe and there is no reason to assume that dark energy would somehow avoid the Solar System or the interior of our Galaxy. In [2,3] we show that the average recession speed 5.2 m/yr of the Earth from the Sun guarantees an almost constant solar flux on the Earth during the last 3.5 billion years, since the luminosity of the Sun slowly and continually increases. This would, of course, guarantee very stable conditions for the development of life. Zhang, Li, and Lei in their groundbreaking paper [4] present other independent arguments showing that the Earth-Sun distance increases several meters per year. We give more details on this topic in Section 2.
The repulsive force, which is responsible for the expansion of the Solar System and other gravitationally bounded systems, is called antigravity. It is not a new fifth physical force, but only a secondary effect of the gravitational force caused by the finite speed of gravitational interaction producing gravitational aberration effects. (Similarly, the strong force, which holds quarks together, has a secondary effect, which keeps atomic nuclei together.)
In this paper we assert that the presence of dark energy leads to small discrepancies from exact conservation of energy within the Solar System. Some authors claim (see e.g. [5,6]) that dark energy has no influence on the Solar System. In Section 3 we show where these authors fail and from where we get dark energy, i.e., what is the mysterious origin of dark energy?
2. Manifestations of Dark Energy
2.1. Manifestation of Dark Energy in the Solar System
According to [7,8], the expansion of our Universe accelerates due to dark energy that has a repulsive character. In [1,3,9] we give more than ten examples showing that some tiny antigravity forces can be detected even in the Solar System. Introducing dark energy into the Solar System, a number of classical paradoxes can be explained, such as the Faint Young Sun Paradox, the very large orbital momentum of our Moon and Triton, the formation of Neptune and the Kuiper belt, an unexplained residual in the orbit of Neptune, the existence of Saturn’s rings, rivers on Mars, the Tidal Catastrophe Paradox of the Moon, and migration of planets.
A decrease of the solar luminosity of only 2% caused ice ages in the past. Life on Earth originated approximately 3.5 Gyr ago. However, in that time the luminosity of the Sun was about 77% of the current value and since then it has increased approximately linearly (see Figure 1 and [10]). In [2] it was shown that the recession speed
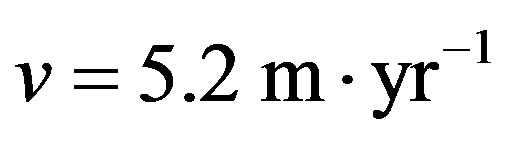 (2)
(2)
of the Earth from the Sun is just right to enable the almost constant influx of solar energy from the origin of life on Earth up to the present. By (1) this corresponds to the expansion rate 0.52 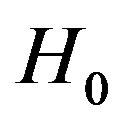 due to dark energy and
due to dark energy and
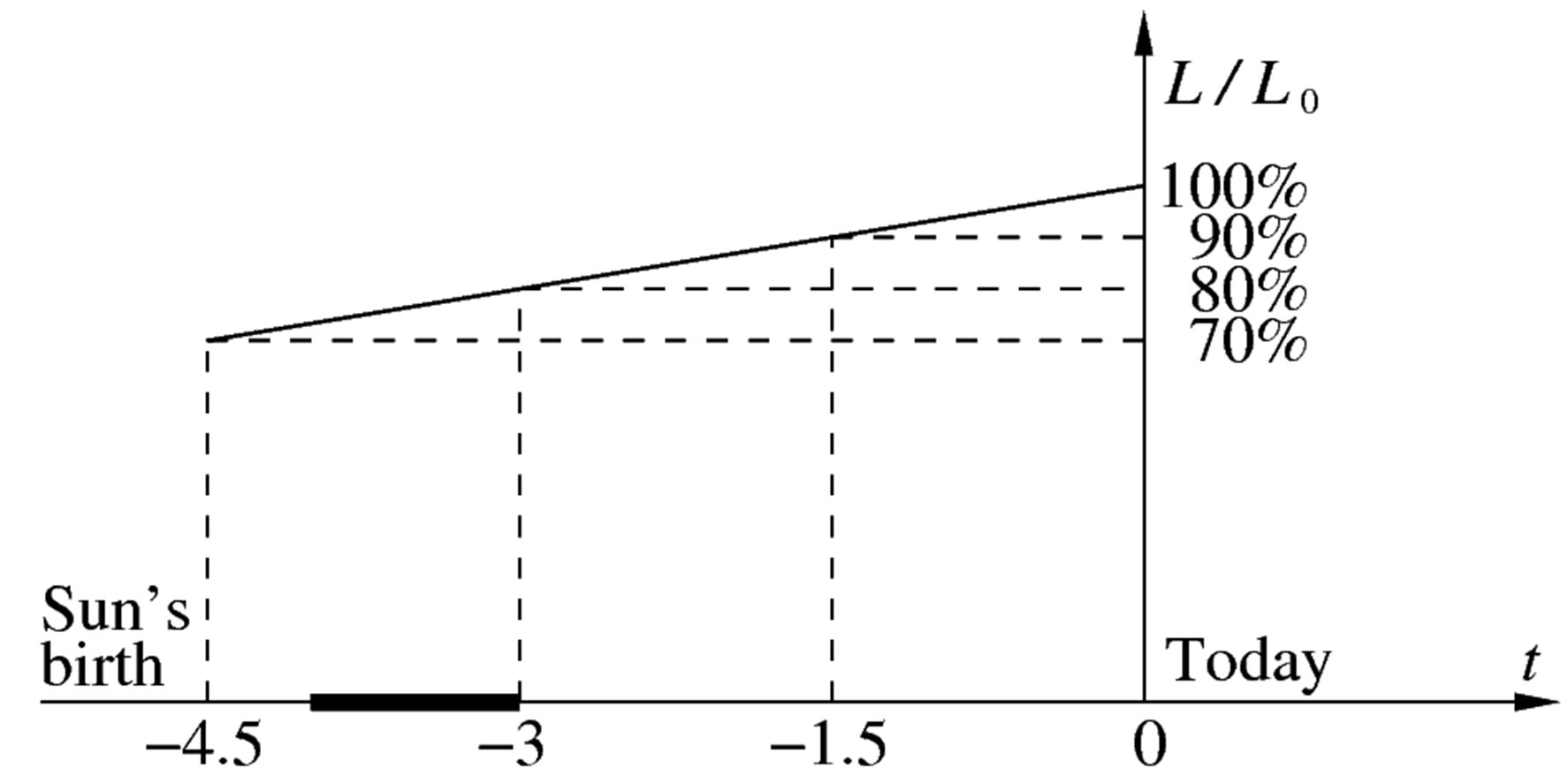
Figure 1. Relative luminosity 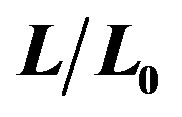 of the Sun from the origin of the Solar System up to the present. The time
of the Sun from the origin of the Solar System up to the present. The time  is given in Gyr.
is given in Gyr.
represents further support for the Anthropic Principle [3]. In other words, the amount of dark energy that is continually produced by the Earth-Sun system lies in a narrow interval that enabled the origin of intelligent life.
A similar recession speed to (2) was independently derived by Zhang et al. in [4, Figures 3 and 4]. Using sophisticated paleontological and computational methods, they showed that the average Earth-Sun distance increases very roughly at the rate of 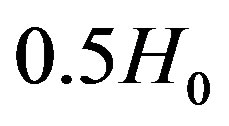 (cf. (4) and (6)), where
(cf. (4) and (6)), where
 (3)
(3)
is the Hubble constant (1) characterizing the expansion of the Universe at present. By a detailed analysis of growth patterns on many fossil corals they found that during the last 500 million years the Earth-Sun distance increased about 3 million km. This yields an average recession speed
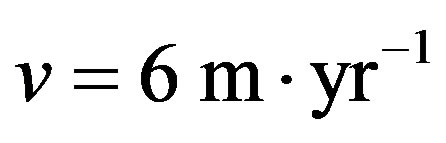 (4)
(4)
which is of the same order as the above-mentioned Hubble constant (1).
Zhang et al. in their seminal paper [4] investigated solar and lunar data (which are independent) of hundreds of fossil patterns from the whole world. To reduce the error in the calculations it is necessary to have at least four consecutive years of data. The main idea of their method can be explained by the following example.
By means of calculating the number of layers deposited during one year in fossil corals Zhang, Li, and Lei found that in the Devonian era (370 million years ago) each year had about 405 days. However, each day was shorter at that time—about 21.3 hours, since the rotation of the Earth slows down due to tidal forces. The Earth’s rotational history is known from many papers on paleorotation. In this way we obtain that the length of the sidereal year in the Devonian era was about 31,055,400 seconds, whereas the present value is
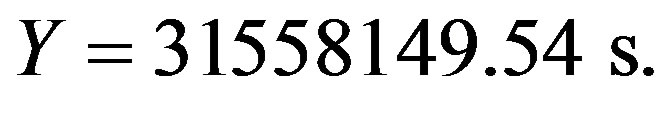 (5)
(5)
Kepler’s third law enables us to derive that the semimajor axis of Earth’s orbit was only 148.1 million km, i.e. shorter than it is now. From this we find an average recession speed
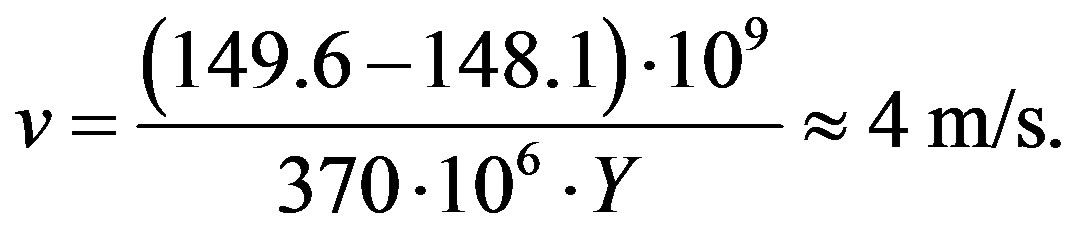 (6)
(6)
By [2,3] Mars was also closer to the Sun 3 - 4 Gyr ago when there were rivers on its surface and when it contained a large liquid ocean in the northern hemisphere. Let us take a closer look at situation on Mars by means of the Stefan-Boltzmann law. The intensity of radiation of the black body (Sun) is equal to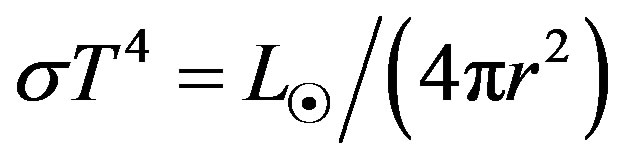 , where
, where 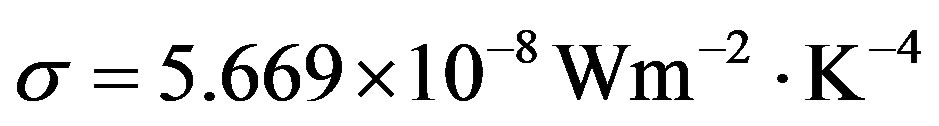 is the Stefan-Boltzmann constant,
is the Stefan-Boltzmann constant, 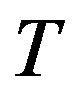 is the equilibrium temperature,
is the equilibrium temperature, 
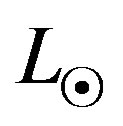 is the total solar power and r is the distance from the Sun. Since the surface of Mars is four times larger than its maximal cross section, the surface equilibrium temperature is given by
is the total solar power and r is the distance from the Sun. Since the surface of Mars is four times larger than its maximal cross section, the surface equilibrium temperature is given by
 (7)
(7)
where 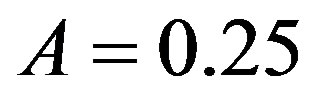 is the present value of the Bond albedo. In this case the absorbed energy is equal to the emitted energy.
is the present value of the Bond albedo. In this case the absorbed energy is equal to the emitted energy.
The theoretical value as given in (7) is in good agreement with the overall average temperature 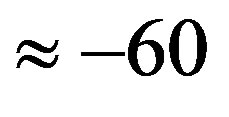 ˚C that was measured by the Vikings, Pathfinder, etc. It is deeply below the freezing point of water. However, the luminosity of the Sun 3 - 4 Gyr ago was only 75% of its present value (see the emphasized interval in Figure 1), since the Sun is a star on the main sequence of the HertzsprungRussell diagram. Then by (7) we get only
˚C that was measured by the Vikings, Pathfinder, etc. It is deeply below the freezing point of water. However, the luminosity of the Sun 3 - 4 Gyr ago was only 75% of its present value (see the emphasized interval in Figure 1), since the Sun is a star on the main sequence of the HertzsprungRussell diagram. Then by (7) we get only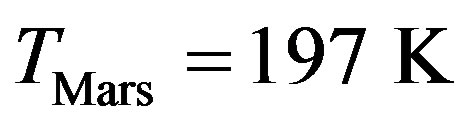 . For such a low temperature the greenhouse effect cannot guarantee an average temperature around the freezing point of water even though Mars had a denser atmosphere, higher radioactivity, and more volcanism. For example, the present greenhouse effect on the Earth increases the average temperature if Earth would not have an atmosphere by about 29 degrees so that the average temperature on the Earth is about 15˚C (see Figure 2). Moreover, Mars had a larger albedo (cf. (7)) than now, since there were water clouds feeding hundreds of large rivers (see [1]). We further note that if Mars were to be 180 million km rather than 225 million km from the Sun when it originated, then its average recession speed would be 10 m/yr which is comparable to the value of the Hubble constant given in (1).
. For such a low temperature the greenhouse effect cannot guarantee an average temperature around the freezing point of water even though Mars had a denser atmosphere, higher radioactivity, and more volcanism. For example, the present greenhouse effect on the Earth increases the average temperature if Earth would not have an atmosphere by about 29 degrees so that the average temperature on the Earth is about 15˚C (see Figure 2). Moreover, Mars had a larger albedo (cf. (7)) than now, since there were water clouds feeding hundreds of large rivers (see [1]). We further note that if Mars were to be 180 million km rather than 225 million km from the Sun when it originated, then its average recession speed would be 10 m/yr which is comparable to the value of the Hubble constant given in (1).
If Mars were substantially closer to the Sun, then Jupiter was closer as well, since otherwise Mars would have larger dimensions.
According to measurements by means of laser retroreflectors installed on the Moon, the average distance 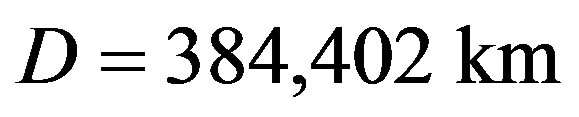 between Earth and the Moon increases
between Earth and the Moon increases
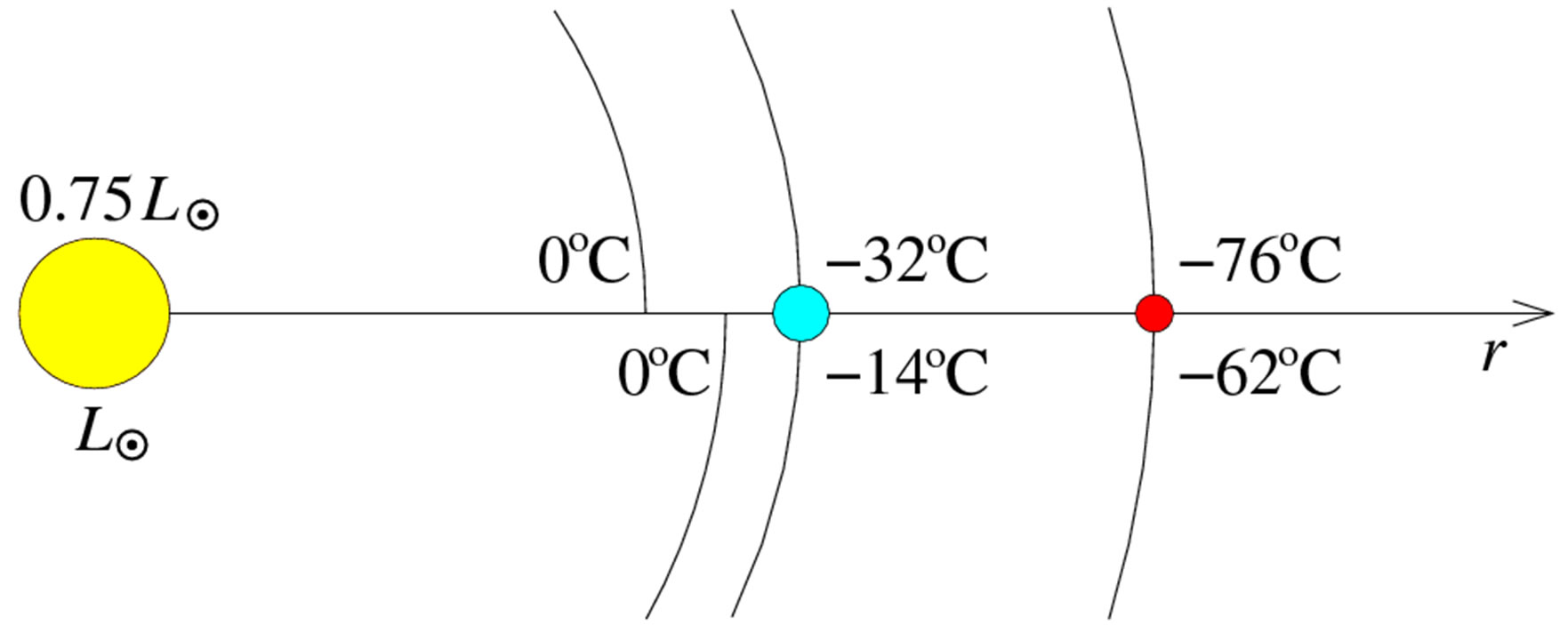
Figure 2. The equilibrium temperature according to the Stefan-Boltzmann law (7) for the albedo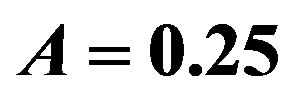 . Temperatures in the upper part correspond to the luminosity
. Temperatures in the upper part correspond to the luminosity  and in the lower part to the present luminosity
and in the lower part to the present luminosity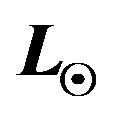 . The radii of the circles are respectively 117, 134, 150, and 225 million km. The Sun is yellow, Earth is blue and Mars is red.
. The radii of the circles are respectively 117, 134, 150, and 225 million km. The Sun is yellow, Earth is blue and Mars is red.
about 3.84 cm/yr. Nonetheless, only 55% of this value can be explained by tidal forces (see [2] for details). The missing part
 (8)
(8)
could again be due to dark energy. This value is also comparable with the Hubble constant recalibrated to the distance D, namely
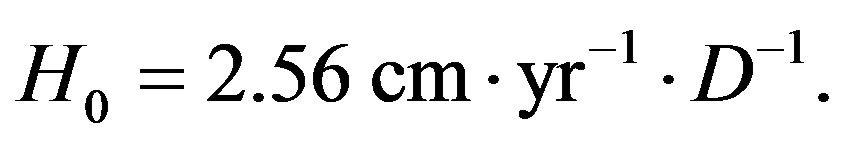
The corresponding expansion rate due to dark energy is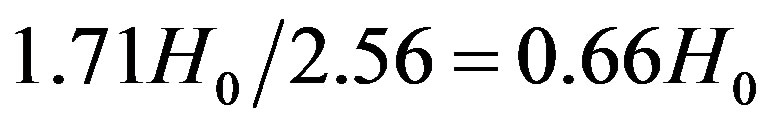 .
.
Other satellites of the planets are also affected by antigravity forces. In particular, the so-called fast satellites that are below the stationary orbit of a planet, where the orbital and rotational periods are equal, should approach their mother planet along spiral trajectories due to tidal forces. By Kepler’s third law the radius of the stationary orbit is
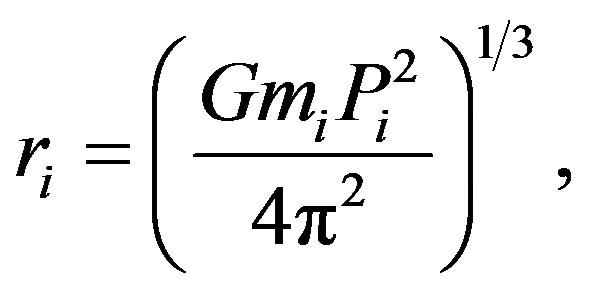 (9)
(9)
where 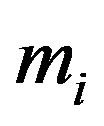 is the mass of the
is the mass of the 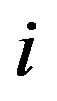 th planet and
th planet and 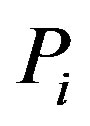 is its sidereal rotational period. However, dark energy causes a repulsive force that acts in the opposite direction and has approximately the same size as tidal forces. This makes trajectories of fast satellites stable for billion years (see [3]). Dark energy thus prevents all fast satellites from crashing into their mother planets.
is its sidereal rotational period. However, dark energy causes a repulsive force that acts in the opposite direction and has approximately the same size as tidal forces. This makes trajectories of fast satellites stable for billion years (see [3]). Dark energy thus prevents all fast satellites from crashing into their mother planets.
Consider e.g. Neptune’s satellite Larissa whose orbit has radius 73,548 km which is close to 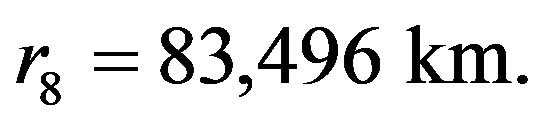 Since the rotation of Neptune slows down due to tidal forces by Triton and other satellites, it is not clear where Larissa was 4.5 Gyr ago. At that time the stationary orbit was by (9) much smaller and by the Newtonian theory Larissa is continually approaching Neptune. This shows that Larissa is floating by antigravity forces due to dark energy.
Since the rotation of Neptune slows down due to tidal forces by Triton and other satellites, it is not clear where Larissa was 4.5 Gyr ago. At that time the stationary orbit was by (9) much smaller and by the Newtonian theory Larissa is continually approaching Neptune. This shows that Larissa is floating by antigravity forces due to dark energy.
It is an open problem how Neptune could be formed as far away as 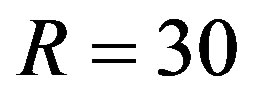 au from the Sun, where the original protoplanetary disc was relatively sparse and all motions are very slow (by Kepler’s third law its mean speed is only 5.4 km/s). Assuming that the average Neptune-Sun distance increases roughly at the rate of
au from the Sun, where the original protoplanetary disc was relatively sparse and all motions are very slow (by Kepler’s third law its mean speed is only 5.4 km/s). Assuming that the average Neptune-Sun distance increases roughly at the rate of 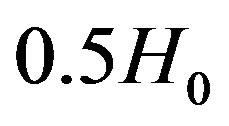 due to dark energy (as in previous examples), we find by (1) that Neptune could be formed several astronomical units closer to the Sun
due to dark energy (as in previous examples), we find by (1) that Neptune could be formed several astronomical units closer to the Sun 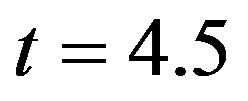 Gyr ago on the orbit with radius
Gyr ago on the orbit with radius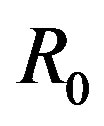 . From the relation
. From the relation 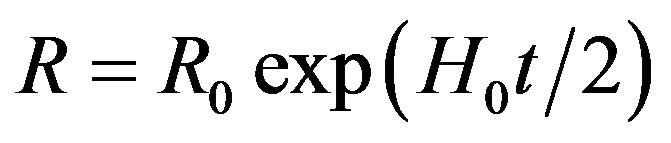 we have
we have
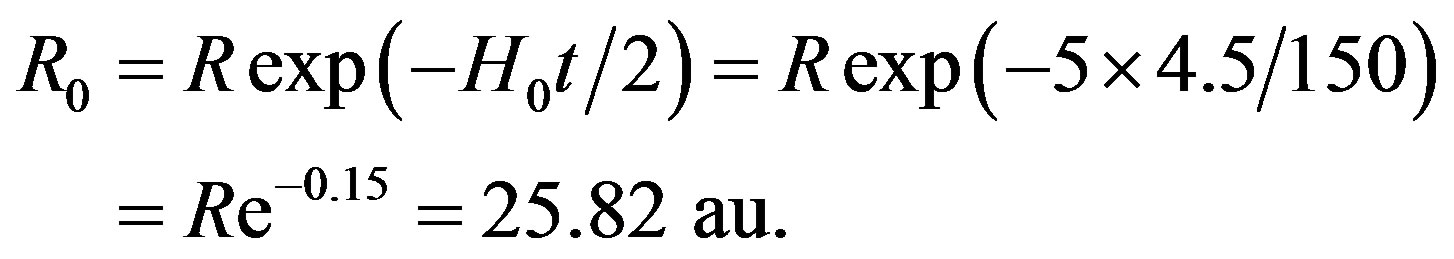
Another hypothesis states that some star had flown closely to the Solar System which could also contribute to the current distant position of Neptune. Other models, like the Nice model [11], assume that several Gyr ago two giant planets exchanged their orbits to keep the total energy conserved. Nevertheless, this scenario has several drawbacks:
1) It is well known that the classical non-colliding N-body problem has a unique global solution and that this problem is not stable in the Lyapunov sense. This means that extremely small variations in initial data cause large errors in the final state after billion of years. Moreover, the backward integration of the current situation does not show that two giant planets would exchange their orbits billion years ago. If the backward integration does not give the initial situation, then the numerical simulation is incorrect due to the Lyapunov instability;
2) The validity of the Newtonian theory of gravity (with infinite speed of gravitational interaction) is supposed over an extremely long time interval of 4.5 Gyr and the influence of dark energy and the finite speed of gravitational interaction are not taken into account;
3) In the Nice model it is not clear what would happen with very rich families of satellites (moons) of giant planets during their close encounter, even though the authors of this model assert that satellite systems survived during their numerical simulation of the exchange.
2.2. Do Galaxies Expand Due to Dark Energy?
A positive answer to the above question is based on the following 10 independent observational facts:
1) There is no reason to assume that dark energy would somehow avoid the interior of galaxies, since it is distributed almost uniformly throughout the Universe and it acts also locally in the Solar System as shown in the previous subsection.
2) Recently several observational arguments were published that confirm the expansion of galaxies themselves. For instance, Bouwers et al. [12] found that galaxies subtly grow with cosmic time. Also Trujillo et al. [13] discovered that the size of massive galaxies increases with time. By [14] superdense massive galaxies were quite common in the early universe with redshift  and they are very exceptional in the nearby universe. Also early-type galaxies were smaller and denser at earlier times (see [15]). Based on the above facts (see also [16-18], etc.) we claim that dark energy essentially contributed to the expansion of galaxies. By [19] the density of some galaxies for
and they are very exceptional in the nearby universe. Also early-type galaxies were smaller and denser at earlier times (see [15]). Based on the above facts (see also [16-18], etc.) we claim that dark energy essentially contributed to the expansion of galaxies. By [19] the density of some galaxies for 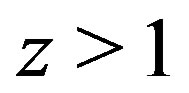 is even comparable with the density of present globular clusters, i.e., on average one star in one pc3.
is even comparable with the density of present globular clusters, i.e., on average one star in one pc3.
3) The density distribution of galaxies in space 10 - 13 Gyr ago was much larger than at present, since the Universe was smaller. For instance, for the redshift 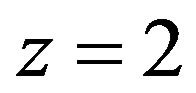 (which roughly corresponds to the Hubble Field South), when space was
(which roughly corresponds to the Hubble Field South), when space was 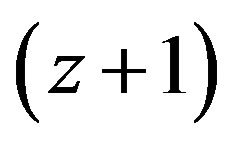 times smaller, the density of galaxies in the unit volume is on average
times smaller, the density of galaxies in the unit volume is on average 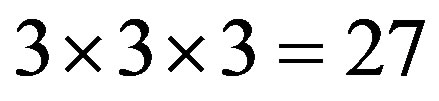 times higher. Since protogalaxies at that time were smaller, this higher accumulation is not observed. They only seem to be larger, since the space for
times higher. Since protogalaxies at that time were smaller, this higher accumulation is not observed. They only seem to be larger, since the space for  was three times smaller (see [1] for the time-lens principle or [20, p. 319]).
was three times smaller (see [1] for the time-lens principle or [20, p. 319]).
Suppose to the contrary that galaxies do not change their sizes. The right part of Figure 3 illustrates what we would see at cosmological distances, provided galaxies would have a constant size. On the left, five galaxies are schematically sketched in the unit volume corresponding to . In the same volume, there is on average 5 × 33 = 135 crammed galaxies for
. In the same volume, there is on average 5 × 33 = 135 crammed galaxies for 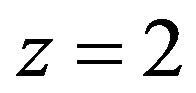 and 5 × 53 = 625 tightly crammed galaxies for
and 5 × 53 = 625 tightly crammed galaxies for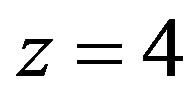 . However, this is not observed, since galaxies were smaller at that time.
. However, this is not observed, since galaxies were smaller at that time.
4) According to [21], the measured stellar mass density in galaxies with 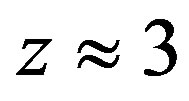 is up to eight times higher than for galaxies in our neighborhood. These very distant galaxies cca 11 Gly far away are seen to have been roughly a factor two times smaller than they are seen now. They have grown from some smaller protogalaxies.
is up to eight times higher than for galaxies in our neighborhood. These very distant galaxies cca 11 Gly far away are seen to have been roughly a factor two times smaller than they are seen now. They have grown from some smaller protogalaxies.
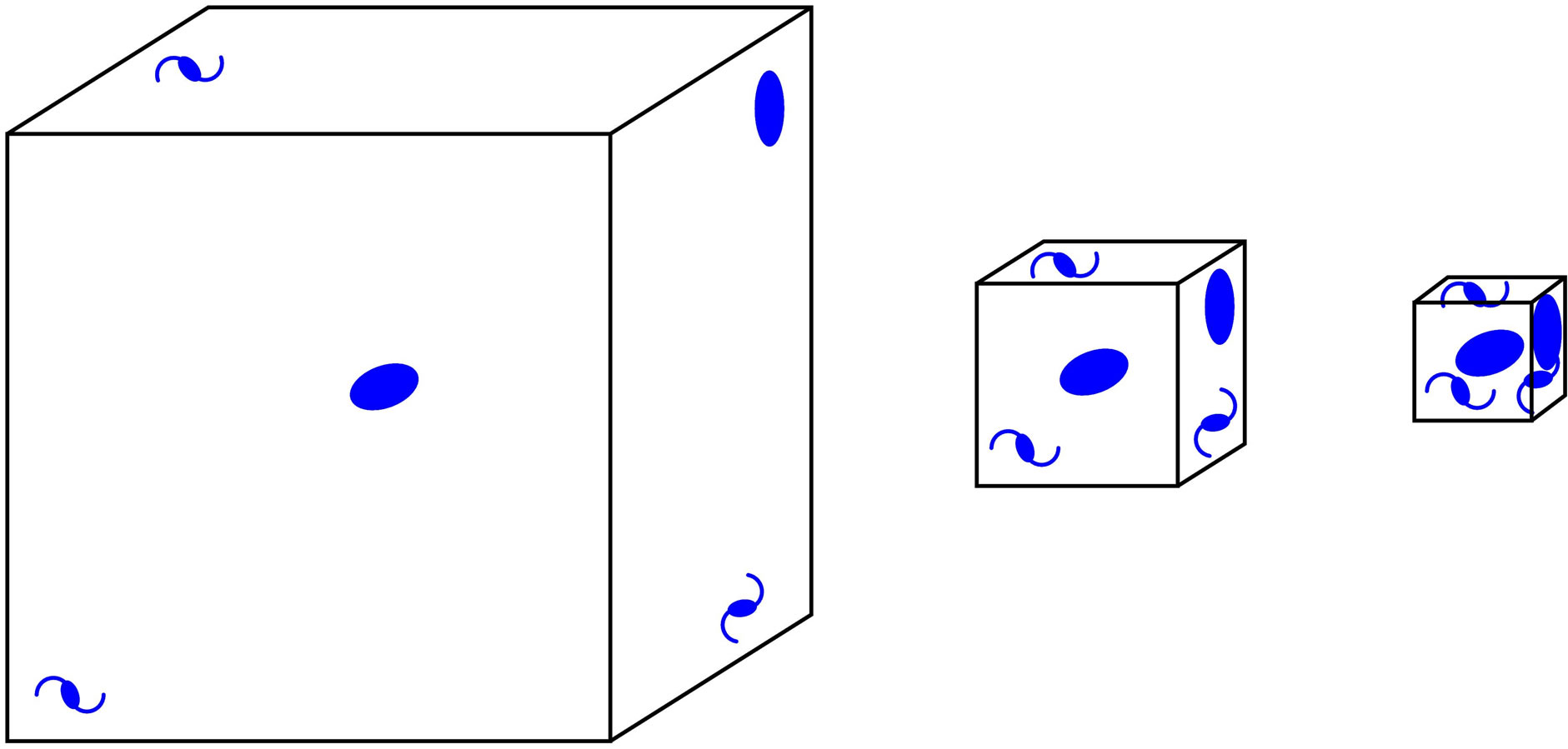
Figure 3. On the left: Schematic illustration of distribution of galaxies in our neighborhood for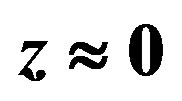 . If galaxies would not expand, then their distribution in cosmological distances for
. If galaxies would not expand, then their distribution in cosmological distances for 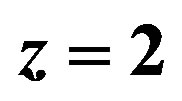 is sketched in the middle and for
is sketched in the middle and for 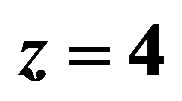 on the right. Such a picture is not observed.
on the right. Such a picture is not observed.
Consider now our Galaxy whose diameter is about 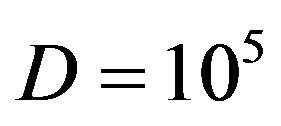 ly. Let us show that its current size
ly. Let us show that its current size  is attainable by the Hubble expansion rate. Assume that the Galaxy expanded from some smaller protogalaxy with diameter
is attainable by the Hubble expansion rate. Assume that the Galaxy expanded from some smaller protogalaxy with diameter  during the last
during the last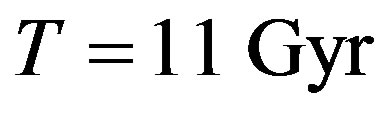 . From (3) we find that the present value of the Hubble constant recalibrated to
. From (3) we find that the present value of the Hubble constant recalibrated to 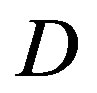 is
is . Then the present size of our Galaxy could be extrapolated as follows
. Then the present size of our Galaxy could be extrapolated as follows

which is indeed comparable with its actual diameter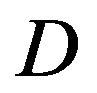 . Taking into account that the Hubble parameter H = H(t) was larger than
. Taking into account that the Hubble parameter H = H(t) was larger than , we could even get a size comparable with
, we could even get a size comparable with  at the rate
at the rate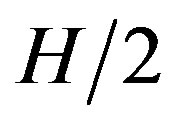 . The present expansion rate of our Galaxy is thus comparable with
. The present expansion rate of our Galaxy is thus comparable with 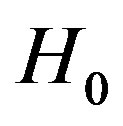 even though it is probably smaller.
even though it is probably smaller.
5) According to [12,22], the observed rate of star formation in galaxies at cosmological distances is proportional to . For instance, if
. For instance, if 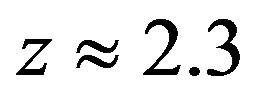 it is ten times higher than in our neighborhood. This extremely high rate can again be explained by higher mass density inside galaxies at large z than there is now for
it is ten times higher than in our neighborhood. This extremely high rate can again be explained by higher mass density inside galaxies at large z than there is now for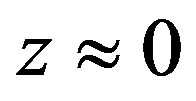 .
.
6) According to [23], the observed activity of galactic nuclei at cosmological distances is larger than in our neighborhood. This may again be explained by higher mass density inside galaxies for large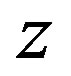 , even though central massive black holes were on average smaller.
, even though central massive black holes were on average smaller.
7) There exist several dwarf galaxies around our Galaxy (e.g. LEO IV) that were formed 13 Gyr ago. However, their star formation stopped after 300 Myr. Dark energy could again reduce the critical mass density necessary for star formation.
8) The mean radial component of velocities of all 150 globular clusters in our Galaxy indicates that globular clusters on average slowly move away from the Galactic center. This mean speed (normal or weighted by distances) is comparable with  (see [24]). It is even higher than
(see [24]). It is even higher than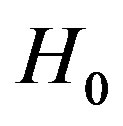 , but of the same order.
, but of the same order.
9) Almost all open or globular star clusters seem to be unstable as observed e.g. by [25]. It is again dark energy that very slowly, but continually increases the total energy (kinetic + potential) of each system of free bodies, and thus each star cluster slightly expands. Due to dark energy the frequency of escape of stars from clusters is higher than predicted by the classical Virial Theorem, which does not take into account the influence of dark energy. Dark energy thus contributes to the evaporation of star clusters and acts against the so-called gravothermal catastrophe (cf. [26]).
10) The exoplanet WASP-18b revolves around its mother star with mass 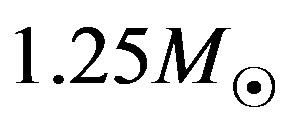 once per 0.94 day. Its orbit is almost circular with radius 3 million km. Since the rotational period of the star is 5.64 days, by Kepler’s third law the stationary orbit has radius 10 million km, i.e. the exoplanet is below the stationary orbit (cf. (9)). Due to tidal forces WASP-18b should approach its mother planet along a spiral trajectory within less than one million years. However, the star exists already for 700 Myr (see [27]). Astronomers do not know, how this exoplanet with 10 Jupiter masses could appear in this current position below the stationary orbit and why it would not fall down onto its mother planet in such a short geological period. This paradox can again be explained by antigravity forces. WASP-18 does not quickly spiral into its mother star, since the repulsive force due to dark energy acts in the opposite direction than the tidal forces for more than 700 Myr of its existence. From the evolution of all orbital parameters we could estimate within the next 10 years how large is the repulsive force that prevents the extrasolar planet from crashing onto its mother star.
once per 0.94 day. Its orbit is almost circular with radius 3 million km. Since the rotational period of the star is 5.64 days, by Kepler’s third law the stationary orbit has radius 10 million km, i.e. the exoplanet is below the stationary orbit (cf. (9)). Due to tidal forces WASP-18b should approach its mother planet along a spiral trajectory within less than one million years. However, the star exists already for 700 Myr (see [27]). Astronomers do not know, how this exoplanet with 10 Jupiter masses could appear in this current position below the stationary orbit and why it would not fall down onto its mother planet in such a short geological period. This paradox can again be explained by antigravity forces. WASP-18 does not quickly spiral into its mother star, since the repulsive force due to dark energy acts in the opposite direction than the tidal forces for more than 700 Myr of its existence. From the evolution of all orbital parameters we could estimate within the next 10 years how large is the repulsive force that prevents the extrasolar planet from crashing onto its mother star.
The points 1)-10) justify us in asserting that dark energy acts also inside galaxies (see Figure 4). Dark energy thus may slowly expand habitable zones (as in the case of the Earth) when the luminosity of the corresponding mother star increases. In this way habitable zones are more stable and exist for a longer time.
3. The Origin of Dark Energy
3.1. Dark Energy Mystery
In Section 2 we surveyed results showing that the influence of dark energy can be observed not only among galaxies, but also inside galaxies including our Galaxy and in the Solar System, too, i.e. dark energy acts not only globally, but also locally.
By [3] dark energy has an essential influence on the present value of the Hubble constant. To demonstrate its influence in the Solar System we must either measure very precisely (e.g. the Earth-Moon distance), or we have to consider extremely long time intervals, where all small deviations from the Newtonian theory of gravitation are usually not cancelled, but accumulated and then possibly
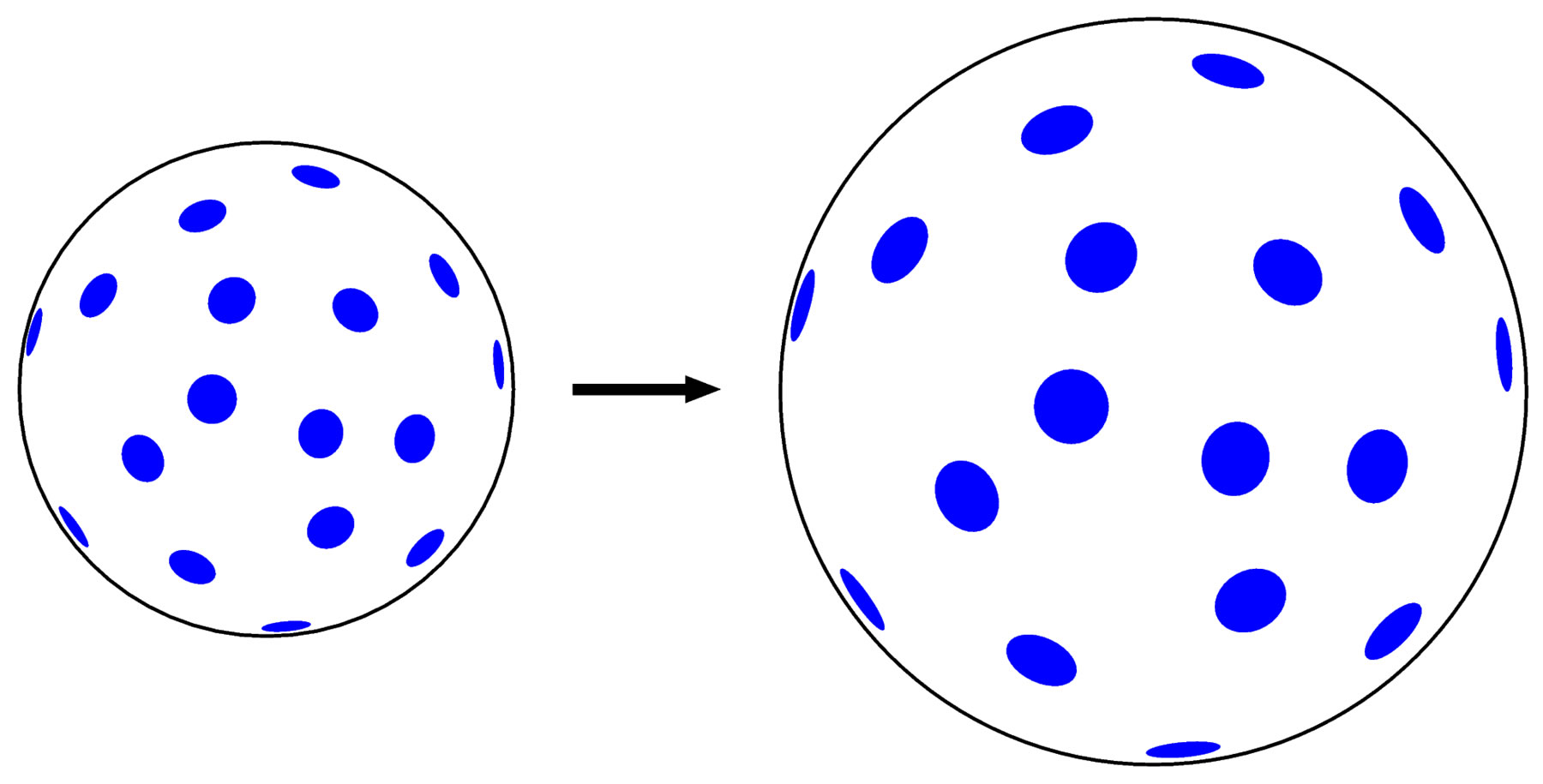
Figure 4. A two-dimensional model of an expanding Universe of positive curvature with expanding galaxies. In [20, p. 72] galaxies do not expand.
observed. An extremely small deviation  during one year may cause after one billion years a quite large and detectable value of
during one year may cause after one billion years a quite large and detectable value of  which is then interpreted as dark energy. For instance, in the case of our Moon,
which is then interpreted as dark energy. For instance, in the case of our Moon, 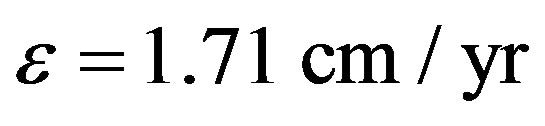 (see (8)) and in the case of our Earth
(see (8)) and in the case of our Earth 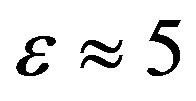 m/yr due to (2), (4), and (6). Thus, we should never identify any physical model with reality, since the above argument can be applied to any non-Newtonian model as well.
m/yr due to (2), (4), and (6). Thus, we should never identify any physical model with reality, since the above argument can be applied to any non-Newtonian model as well.
Let us estimate by means of classical physics how much dark energy is generated by the Earth-Sun system within one year. Assume for simplicity that the Earth has a circular orbit with radius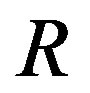 . From Kepler’s third law
. From Kepler’s third law 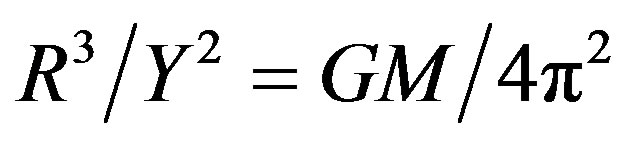 the total energy (kinetic + potential) of the Earth is equal to
the total energy (kinetic + potential) of the Earth is equal to

where 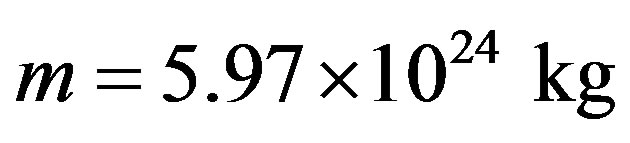 is the mass of the Earth,
is the mass of the Earth, 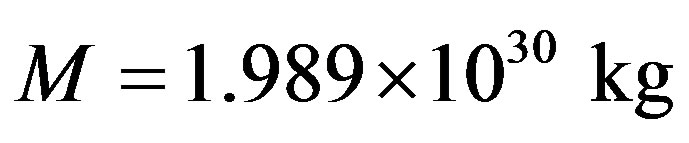 is the mass of the Sun,
is the mass of the Sun, 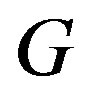 is the gravitational constant, and
is the gravitational constant, and  is the sidereal year as given in (5). Then for
is the sidereal year as given in (5). Then for  m (cf. (2)) we find that the annual increase of dark energy is
m (cf. (2)) we find that the annual increase of dark energy is

which is about a ten orders of magnitude lower value than the kinetic energy of the Earth, i.e.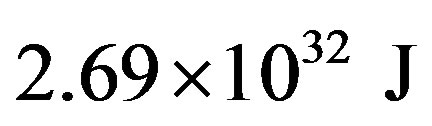
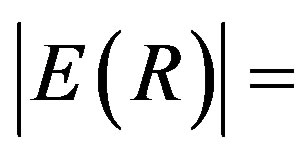 . By (5) this corresponds to a permanent power of almost 3000 TW for free. Therefore, the classical laws of conservation of energy and momentum do not hold.
. By (5) this corresponds to a permanent power of almost 3000 TW for free. Therefore, the classical laws of conservation of energy and momentum do not hold.
According to Krasinsky and Brumberg [28], the increase of the Earth-Sun distance is only 15 cm per year. However, their conclusion is derived under a nonrealistic supposition that the Newtonian theory of gravitation describes movements in the Solar System absolutely exactly. They solve an algebraic system for 62 unknown Keplerian elements of all planets and some large asteroids. No modeling error is assumed, no discretization error analysis is done, and the influence of dark energy is not taken into account.
It is said that the source of dark energy that accelerates the expansion of the Universe is unknown for the time being. This is often termed the Dark Energy Mystery. Several possible hypotheses of the origin of dark energy are surveyed in [29]. These hypotheses include quintessence, energy of the vacuum, variable fundamental constants, etc.
Another hypothesis was introduced in [2]. This is the hypothesis we will concentrate on in the next Subsection 3.2. Since the speed of gravitational interaction is finite, it causes aberration effects [30] between any two (or more) free bodies that interact gravitationally. In [2] we showed that gravitational aberration could contribute to dark energy and consequently to the accelerated expansion of the whole Universe. This hypothesis even has the potential to substantially explain the dark energy mystery.
3.2. Gravitational Aberration
Consider two bodies  and
and 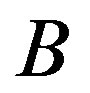 of equal masses that orbit symmetrically with respect to their midpoint. Since the speed of their mutual gravitational interaction is finite,
of equal masses that orbit symmetrically with respect to their midpoint. Since the speed of their mutual gravitational interaction is finite,  is attracted by
is attracted by  towards its previous position
towards its previous position 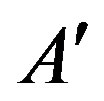 as indicated in Figure 5. Similarly
as indicated in Figure 5. Similarly  is attracted by
is attracted by 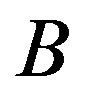 in the direction of its previous position
in the direction of its previous position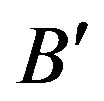 . Then a couple of non-equilibrium forces arises which acts permanently and thus, slowly increases the angular momentum and also the total energy of this system which is then interpreted as dark energy. This simple example indicates why the classical law of conservation of energy cannot be valid. If it would be valid, then the trajectories would be circles of constant radii for appropriate initial conditions.
. Then a couple of non-equilibrium forces arises which acts permanently and thus, slowly increases the angular momentum and also the total energy of this system which is then interpreted as dark energy. This simple example indicates why the classical law of conservation of energy cannot be valid. If it would be valid, then the trajectories would be circles of constant radii for appropriate initial conditions.
Our Galaxy and the Solar System provide us with a unique laboratory to study a finite speed of gravitational interaction and its product: dark energy. Gravitational waves were already predicted by Henri Poincaré. He conjectured that their speed is the same as the speed of light c (see [31]). However, by the results of Section 2 it seems that gravitational aberration angle is probably much smaller than that due to the aberration of light, but it is positive due to causality. Otherwise, the Solar System would be not so stable (see [3]).
According to Carlip [32], the gravitational interaction

Figure 5. Trajectories corresponding to two interacting bodies of equal masses constitute a double spiral. The aberration angles  and
and 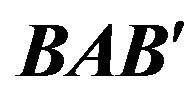 are extremely small but positive.
are extremely small but positive.
in general relativity produces almost no aberration effects contrary to known relatively large aberration effects in the electromagnetic interaction. However, Carlip assumes that the cosmological constant is zero and neglects some nonlinear terms to make calculations easier. He also assumes that the laws of conservation of energy and momentum are valid and thus he cannot get spiraling trajectories as schematically illustrated in Figure 5.
The gravitational aberration effects can be modeled by a nonautonomous system of differential equations with delay, where the aberration is a free parameter (see [2] and [30]). For the two-body problem the above system with delays yields slightly spiraling trajectories (see Figure 5) that describe reality (cf. Section 2) much better than the Newtonian theory of gravitation. As a result the two bodies are drifting apart. Also a system of N free bodies slightly expands on average due to gravitational aberration effects. This mechanism contributes to the expansion of the Universe and it can explain the Dark Energy Mystery.
3.3. Cosmological Constant
Is the cosmological constant a fundamental physical constant? We claim it is not. Since the gravitational aberration has a continual influence of the expansion rate of our Universe (at least partly), as shown in the previous subsection, the cosmological constant appearing in the standard cosmological model [20] should depend on time, i.e.,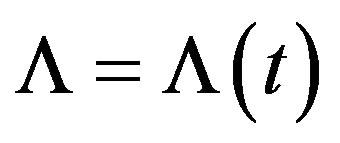 . It should also depend locally on many other quantities (mass distribution, velocities, distances, etc.). In other words,
. It should also depend locally on many other quantities (mass distribution, velocities, distances, etc.). In other words,  is probably not a fundamental physical constant like the speed of light
is probably not a fundamental physical constant like the speed of light  or the gravitational constant
or the gravitational constant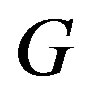 , but it represents only some average value due to gravitational aberration effects of all free bodies in the Universe. Its present value
, but it represents only some average value due to gravitational aberration effects of all free bodies in the Universe. Its present value 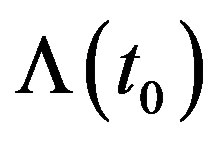 is roughly of order
is roughly of order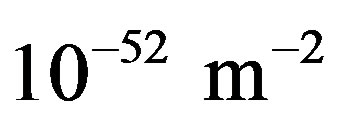 , but in the future it can became smaller. Note that the Hubble constant
, but in the future it can became smaller. Note that the Hubble constant  depends on time, too.
depends on time, too.
The corresponding expansion rate cca 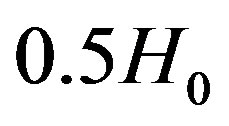 due to dark energy provides further support for the Anthropic Principle [3]. In other words, the amount of dark energy that is continually produced by the Earth-Sun system lies in a narrow interval that enabled the origin of intelligent life on the Earth. On the other hand, dark energy and the loss of atmosphere destroyed the habitable zone with liquid water on Mars (cf. (7)).
due to dark energy provides further support for the Anthropic Principle [3]. In other words, the amount of dark energy that is continually produced by the Earth-Sun system lies in a narrow interval that enabled the origin of intelligent life on the Earth. On the other hand, dark energy and the loss of atmosphere destroyed the habitable zone with liquid water on Mars (cf. (7)).
3.4. The Hubble Parameter
Knowledge of the effect of cosmological expansion on local systems (such as the Solar System) has a long history dating back to the paper [33]. At present we know that the expansion of our Universe accelerates. This fact is based on the 10% - 15% lower luminosity of very distant supernovae of type Ia that shine into a larger volume than if the expansion were to be decelerating, see [7, 8,34]. The observed acceleration is due to dark energy that is distributed almost uniformly in the Universe [35]. Therefore, dark energy has an essential influence on the present value of the Hubble constant (3) which characterizes the speed of this expansion.
For very distant cosmological objects with redshift 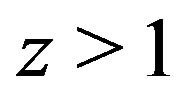 it was found by [35] that a decelerating expansion of the Universe turned into an accelerating one approximately eight billion years after the Big Bang. In [3], the Hubble parameter
it was found by [35] that a decelerating expansion of the Universe turned into an accelerating one approximately eight billion years after the Big Bang. In [3], the Hubble parameter 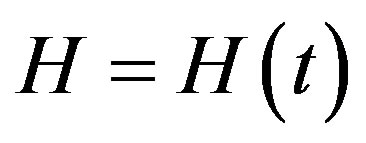 is split into two terms
is split into two terms , where
, where 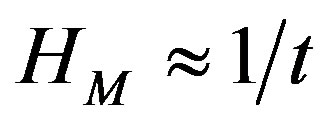 is a decreasing function due to the Big Bang and the subsequent gravitational interaction that slows the expansion of the Universe and
is a decreasing function due to the Big Bang and the subsequent gravitational interaction that slows the expansion of the Universe and 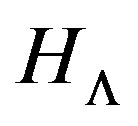 is a positive (and probably increasing) function that corresponds to dark energy which accelerates this expansion. The present value of
is a positive (and probably increasing) function that corresponds to dark energy which accelerates this expansion. The present value of 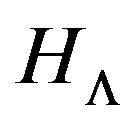 is so large that the impact of dark energy can also be detected in the Solar System as we have seen in Subsection 2.1.
is so large that the impact of dark energy can also be detected in the Solar System as we have seen in Subsection 2.1.
An extremely small time derivative of 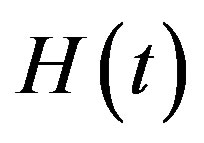 for the present time
for the present time 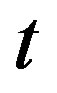 on the scale of the Solar System is derived in [5] yielding a tiny outward acceleration of
on the scale of the Solar System is derived in [5] yielding a tiny outward acceleration of 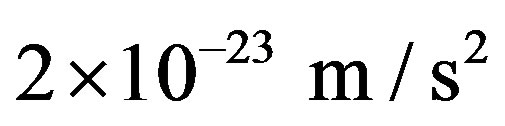 at Pluto’s distance of 40 au. Similar very small values are given in [6, p. 62] and [36, p. 5041]. However, the large value of the Hubble constant itself
at Pluto’s distance of 40 au. Similar very small values are given in [6, p. 62] and [36, p. 5041]. However, the large value of the Hubble constant itself  is surprisingly not considered in these papers. On the other hand, a more realistic expansion rate of
is surprisingly not considered in these papers. On the other hand, a more realistic expansion rate of  in the Solar System derived from growth patterns on fossil corals is proposed in [4].
in the Solar System derived from growth patterns on fossil corals is proposed in [4].
The Hubble parameter is usually defined by the relation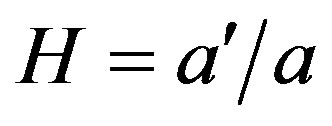 , where
, where  is the scaling parameter (for instance, if the Universe would have a constant positive curvature in all directions at time
is the scaling parameter (for instance, if the Universe would have a constant positive curvature in all directions at time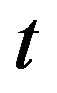 , then the scaling parameter
, then the scaling parameter  is equal to the radius of the Universe at time
is equal to the radius of the Universe at time ). Differentiating
). Differentiating 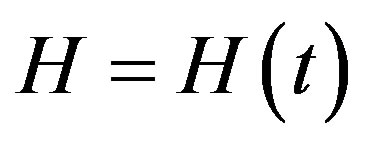 with respect to time, we find that
with respect to time, we find that
 (10)
(10)
where 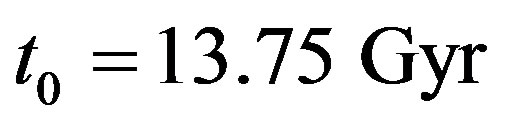 is the age of Universe and
is the age of Universe and 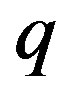 is the so-called deceleration parameter, which characterizes the expansion of the Universe. The Taylor expansion of the scaling parameter reads
is the so-called deceleration parameter, which characterizes the expansion of the Universe. The Taylor expansion of the scaling parameter reads
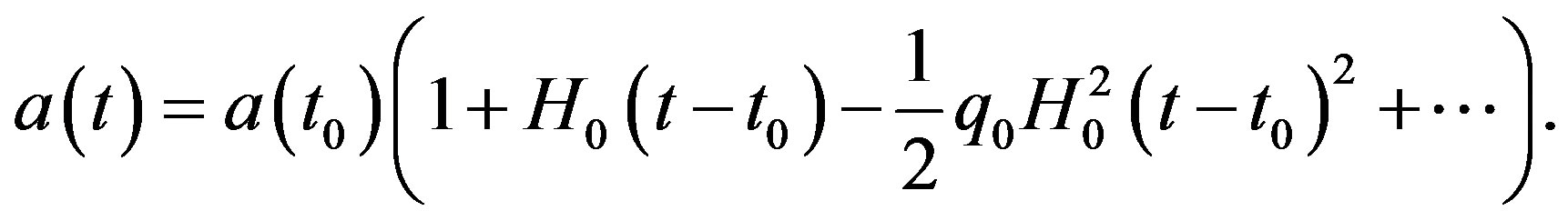 (11)
(11)
where 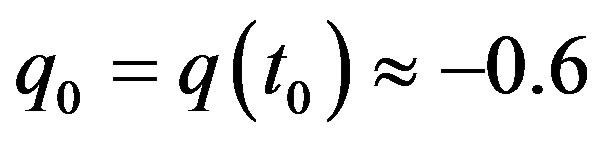 is the actual value of the scaling parameter. (Its negative value
is the actual value of the scaling parameter. (Its negative value 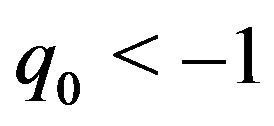 was predicted by Beatrice Tinsley already in 1978, see [37]. In this case,
was predicted by Beatrice Tinsley already in 1978, see [37]. In this case, 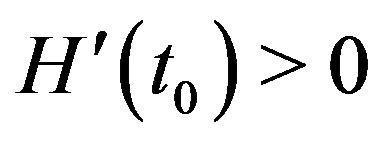 by (10).)
by (10).)
By [5,6], the effect of dark energy has no influence on the dynamics of the Solar System. Their authors claim that the quadratic term in the above Taylor expansion has almost no effect on the acceleration expansion of the Solar System which is true, but they do not take into account the large value of the Hubble constant (1) which appears in the linear term in (11).
4. Conclusions
Note that there exist close binary pulsars whose orbits do not expand with time, but decay. In this case, strong magnetic and gravitational fields are present and the system loses energy due to tidal forces, electromagnetic and gravitational waves. These effects are much stronger than weak effects coming from dark energy. Also various resonances may be significantly larger in comparison with dark energy effects.
The classical N-body problem is usually solved by symplectic methods that are designed in such a way that the energy is conserved. However, for numerical solution of long-term evolution problems (including aberration effects) these methods are not suitable, since they do not take into account dark energy and assume the infinite speed of gravitational interaction. Also various modifications of the Newtonian theory, known as MOND, assume the infinite speed of gravitational interaction, i.e., they do not produce aberration effects.
Dark energy is slightly, but continually generated by any system of free bodies that interact gravitationally. It increases its total (kinetic + potential) energy. Thus, it contributes to the migration of planets and their moons over long time periods, it causes that many star clusters dissipate [25], it helps reduce the frequency of collisions of galaxies and stars, etc. It stabilizes the Solar System and has also helped create suitable habitable conditions on the Earth for several billion years [3].
5. Acknowledgements
The authors thank Jan Brandts, Jiří Grygar, Filip Křížek, and Weijia Zhang for fruitful discussions. This paper was supported by Project RVO 67985840.
REFERENCES
- M. Křížek, J. Brandts and L. Somer, “Is Gravitational Aberration Responsible for the Origin of Dark Energy?” In: C. A. Del Valle and D. F. Longoria, Eds., Dark Energy: Theory, Implications and Roles in Cosmology, Nova Science Publishers, Inc., New York, 2012, pp. 29-57.
- M. Křížek, “Does a Gravitational Aberration Contribute to the Accelerated Expansion of the Universe?” Communications in Computational Physics, Vol. 5, No. 5, 2009, pp. 1030-1044.
- M. Křížek, “Dark Energy and Anthropic Principle,” New Astronomy, Vol. 17, No. 1, 2012, pp. 1-7. doi:10.1016/j.newast.2011.05.003
- W. J. Zhang, Z. B. Li and Y. Lei, “Experimental MeasUrements of Growth Patterns on Fossil Corals: Secular Variation in Ancient Earth-Sun Distance,” Chinese Science Bulletin, Vol. 55, No. 35, 2010, pp. 4010-4017. doi:10.1007/s11434-010-4197-x
- M. Carrera and D. Giulini, “Influence of Global CosmoLogical Expansion on Local Dynamics and Kinematics,” Reviews of Modern Physics, Vol. 82, No. 1, 2010, pp. 169-208. doi:10.1103/RevModPhys.82.169
- F. I. Cooperstock, V. Faraoni and D. N. Vollick, “The Influence of the Cosmological Expansion on Local Systems,” The Astrophysical Journal, Vol. 503, No. 1, 1998, pp. 61-66. doi:10.1086/305956
- S. Perlmutter, G. Aldering, et al., “Measurements of Omega and Lambda from 42 High-Redshift Supernovae,” The Astrophysical Journal, Vol. 517, No. 2, 1999, pp. 565- 586. doi:10.1086/307221
- A. G. Riess, A. V. Filippenko, et al., “Observational EviDence from Supernovae for an Accelerating Universe and a Cosmological Constant,” The Astrophysical Journal, Vol. 116, No. 3, 1998, pp. 1009-1038. doi:10.1086/300499
- M. Křížek and J. Brandts, “Manifestations of Dark Energy in the Dynamics of the Solar System,” In: A. G. Kosovichev, et al., Eds., Proceedings of the IAU Symposium No. 264, Solar and Stellar Variability: Impact on the Earth and Planets, Cambridge University Press, Cambridge, 2010, pp. 410-412.
- L. R. Kump, J. F. Kastings and R. G. Crane, “The Earth System,” Prentice Hall, New Jersey, 1999.
- K. Tsiganis, R. Gomes, A. Morbidelli and H. F. Levison, “Origin of the Orbital Architecture of the Giant Planets of the Solar System,” Nature, Vol. 435, No. 7041, pp. 459- 461. doi:10.1038/nature03539
- R. J. Bouwens, et al., “A Candidate Redshift z ≈ 10 Galaxy and Rapid Changes in That Population at an Age of 500 Myr,” Nature, Vol. 469, No. 7331, 2011, pp. 504-507. doi:10.1038/nature09717
- I. Trujillo, C. J. Conselice, et al., “Strong Size Evolution of the Most Massive Galaxies Since z ~ 2,” Monthly Notices of the Royal Astronomical Society, Vol. 382, No. 1, 2007, pp. 109-120.
- A. Ferré-Mateu and I. Trujillo, “Superdense Massive Galaxies in the Nearby Universe,” In: G. Bruzual and S. Charlot, Eds., Proceedings of the 27th General Assembly of IAU, S262, Kluwer, Dordrecht, 2010, pp. 331-332.
- J. van de Sande, et al., “The Stellar Velocity Dispersion of a Compact Massive Galaxy at z = 1.80 Using XShooter Confirmation of the Evolution in the Mass-Size and Mass-Dispersion Relations,” The Astrophysical Journal Letters, Vol. 736, 2011, 7 p.
- I. Damjanov, et al., “Red Nuggets at High Redshift: Structural Evolution of Quiescent Galaxies over 10 Gyr of Cosmic History,” The Astrophysical Journal Letters, Vol. 739, No. 2, 2011, p. L44. doi:10.1088/2041-8205/739/2/L44
- V. Gonzáles, I. Labbé, R. Bouwens, et al., “Evolution of Galaxy Stellar Mass Functions, Mass Densities, and Mass to Light Ratios from z ~ 7 to z ~ 4,” The Astrophysical Journal Letters, Vol. 735, No. 2, 2011, p. L34. doi:10.1088/2041-8205/735/2/L34
- I. Trujillo, “Origin and Fate of the Most Massive Galaxies,” In: M. R. Zapatero, et al., Eds., Highlights of Spanish Astrophysics VI, Proceedings of the 9th Scientific Meeting of the Spanish Astronomical Society, Madrid, 2010, pp. 120-130.
- F. Buitrago, et al., “Shaping Massive Galaxies: Their Morphology and Kinematics at z = 1 - 3,” In: M. R. Zapatero, et al., Eds., Highlights of Spanish Astrophysics VI, Proceedings of the 9th Scientific Meeting of the Spanish Astronomical Society, Madrid, 2010, pp. 154-160.
- P. J. E. Peebles, “Principles of Physical Cosmology,” Princeton University Press, New Jersey, 1993.
- G. Rudnick, et al., “Measuring the Average Evolution of Luminous Galaxies at z < 3: The Rest-Frame Optical Luminosity Density, Spectral Energy Distribution, and Stellar Mass Density,” The Astrophysical Journal, Vol. 650, No. 2, 2006, pp. 624-643. doi:10.1086/507123
- A. M. Swinbank, et al., “Intense Star Formation within Resolved Compact Regions in a Galaxy at z = 2.3,” Nature, Vol. 464, No. 7289, 2010, pp. 733-736. doi:10.1038/nature08880
- G. A. Shields, “A Brief History of Active Galactic Nuclei,” Publications—Astronomical Society of the Pacific, Vol. 111, No. 760, 1999, pp. 661-678. doi:10.1086/316378
- W. E. Harris, “Catalog of Parameters for Milky Way Globular Clusters: The Database,” The Astrophysical Journal, Vol. 112, No. 10, 1996, p. 1487.
- P. Kroupa, “Star-Cluster Formation and Evolution,” In: B. G. Elmegreen and J. Palous, Eds., IAU S 237, Triggered Star Formation in a Turbulent ISM, Cambridge University Press, Cambridge, 2007, pp. 230-237.
- E. N. Glass, “Gravothermal Catastrophe, an Example,” Physical Review D, Vol. 82, No. 4, 2010, Article ID: 044039. doi:10.1103/PhysRevD.82.044039
- J. Southworth, T. C. Hinse, et al., “Physical Properties of the 0.94-Day Period Transiting Planetary System WASP- 18,” Cornell University, Ithaca, 2009. arXiv:0910.4875v1.
- G. A. Krasinski and V. A. Brumberg, “Secular Increase of Astronomical Unit from Analysis of the Major Planet Motions, and Its Interpretation,” Celestial Mechanics and Dynamical Astronomy, Vol. 90, No. 3-4, 2004, pp. 267- 288. doi:10.1007/s10569-004-0633-z
- L. Amendola and S. Tsujikawa, “Dark Energy: Theory and Observations,” Cambridge University Press, Cambridge, 2010. doi:10.1017/CBO9780511750823
- M. Křížek, “Numerical Experience with the Finite Speed of Gravitational Interaction,” Mathematics and Computers in Simulation, Vol. 50, No. 1, 1999, pp. 237-245. doi:10.1016/S0378-4754(99)00085-3
- H. Poincaré, “Sur la Dynamique de l’Électron,” Comptes Rendus de l’Académie des Sciences, Vol. 140, 1905, pp. 1504-1508.
- S. Carlip, “Aberration and the Speed of Gravity,” Physics Letters A, Vol. 267, No. 2, 2000, pp. 81-87. doi:10.1016/S0375-9601(00)00101-8
- C. G. McVittie, “The Mass-Particle in Expanding Universe,” Monthly Notices of the Royal Astronomical Society, Vol. 93, 1933, pp. 325-339.
- S. Perlmutter, S. Gabi, et al., “Measurements of the Cosmological Parameters Ω and Λ from the First Seven Supernovae at z ≥ 0.35,” The Astrophysical Journal, Vol. 483, No. 2, 1997, pp. 565-581. doi:10.1086/304265
- A. G. Riess, L.-G. Strolger, et al., “New Hubble Space Telescope Discoveries of Type Ia Supernova at z ≥ 1: Narrowing Constraints on the Early Behavior of Dark Energy,” The Astrophysical Journal, Vol. 659, No. 1, 2007, pp. 98-121. doi:10.1086/510378
- B. Mashhoon, N. Mobed and D. Singh, “Tidal Dynamics in Cosmological Spacetimes,” Classical and Quantum Gravity, Vol. 24, No. 20, 2007, pp. 5031-5046. doi:10.1088/0264-9381/24/20/008
- B. Tinsley, “Accelerating Universe Revisited,” Nature, Vol. 273, 1978, pp. 208-211. doi:10.1038/273208a0

