International Journal of Astronomy and Astrophysics
Vol.1 No.2(2011), Article ID:5670,7 pages DOI:10.4236/ijaa.2011.12007
Model Atmosphere Analysis of Some B-Type Stars
1National Research Institute of Astronomy and Geophysics, Cairo, Egypt
2Physics Department, Faculty of Science, Northern Border University, Arar, Saudi Arabia
E-mail: somaya111@yahoo.com, abdo_nouh@hotmail.com
Received March 31, 2011; revised May 5, 2011; accepted May 17, 2011
Keywords: B-Type Stars, Model Atmosphere Analysis, Fundamental Parameters
Abstract
We present model atmosphere analysis for a sample of B-type stars in optical region to obtain their fundamental parameters e.g. effective temperature, surface gravities, and rotational velocities. Approximate masses for the sample of stars under study are obtained by comparing the resulted effective temperatures and surface gravities with the evolutionary tracks. Comparison between these masses and the empirical effective temperatures-mass relation revealed good agreement.
1. Introduction
B-type stars are hot stars defined by the presence of hydrogen (H) and neutral helium (HeI) in the optical spectra. H line strength increases over the B star subclasses while HeI decreases. There are a wide variety of subtypes, as B stars occur over a wide range of luminosity, many have companion stars, and many have circumstellar material.
Most of our knowledge about stellar atmospheres of B-type stars comes from basic physical parameters of individual stars such as effective temperature 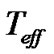 and surface gravity
and surface gravity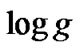 . Accurate
. Accurate 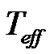 are needed for locating stars on the HR diagram, and for abundance determinations [1]. They can be derived by means of indirect methods based on the comparison of observed quantities (such as the color index, the flux distribution and the line profiles) with the corresponding computed ones, calculated by using model atmospheres. The effective temperature and the gravity of the model which gives the best representation of the observed data are said to be equivalent to the effective temperature and to the gravity of the star.
are needed for locating stars on the HR diagram, and for abundance determinations [1]. They can be derived by means of indirect methods based on the comparison of observed quantities (such as the color index, the flux distribution and the line profiles) with the corresponding computed ones, calculated by using model atmospheres. The effective temperature and the gravity of the model which gives the best representation of the observed data are said to be equivalent to the effective temperature and to the gravity of the star.
Due to the non-availability of non-LTE model atmospheres in a mass production, modeling the atmosphere of B stars was done basically using LTE approximation. Nowadays the situation is changed, non-LTE models for early type stars became partially available (e.g. BSTAR2006 grid [2], so it will be very important to reinvestigate the atmosphere of B stars using these models.
In the present paper, we present LTE/NLTE model atmosphere analysis for a sample of well known B-type stars. We derived their key stellar parameters, effective temperatures, surface gravities, rotational velocities and approximate masses.
The organization of the paper is as follows: Section 2 deals with the observations and model atmospheres used. In section 3 the result of investigations is discussed.
2. Observations, Model Atmospheres and Numerical Methods
2.1. Optical Spectra
The spectra of the stars under investigation were taken mostly from the HEROS spectra which was secured using Echell spectrograph HEROS ([3] and [4]) attached to cassegrain focus of the 2 m Telescope at Ondrejov observatory. All initial reduction of HEROS spectra (bias subtraction, flat-fielding and wavelength calibration) were carried out using modified MIDAS. The un-rectified, wavelength-calibrated spectra then imported into SPEFO (written by Dr. J. Horn (see [5] and [6] for details) where we rectified and extract the digital spectra. The spectrum covers the wavelength range 3450 A° - 8620A° the Balmer lines up to H15 as well as some infrared lines are seen. The resolving power is R = 20000 which analogue to FWHM = 0.25 A°. Table 1 represents the list of observed objects and their published parameters, for details we refer to [7] and reference there in.

Table 1. List of the program stars.
2.2. Theoretical Spectra
The present analysis will lie on LTE/NLTE grid of synthetic spectra. For LTE calculations, we adopted as input models, ATLAS9 grids [8] which consists of 409 models in total, assuming a solar metallicty and a microturblent velocity of 2 km/s and a mixing length to scale height ratio 1.25. Effective temperatures spans the range with a step in the model grid of 250 K for stars cooler than 10000 K, increasing up to 2500 K for hotter stars. Surface gravity span the range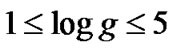 . The synthetic spectra were computed for the region λλ 1500 A° - 8000 A° and then smoothed using a Gaussian filter to a resolution of 1 A°.
. The synthetic spectra were computed for the region λλ 1500 A° - 8000 A° and then smoothed using a Gaussian filter to a resolution of 1 A°.
LTE spectra is synthesized ( for the region λλ 1500 A° - 8000 A° ) by using the LTE stellar spectral synthesis program SPECTRUM written by [9,10,11]. SPECTRUM inputs the columns for the mass depth points, the temperatures and the total pressure, then computes using a system of seven nonlinear equilibrium equations at each level in the atmosphere. The number densities of hydrogen, helium, carbon, oxygen and nitrogen, their relevant ions, all possible diatomic molecules that can be formed these species and the electron number densities.
We adopted for NLTE calculations the BSTAR2006 grid presented by [2]. The BSTAR2006 grid considers 16 values of effective temperatures, 15000 K ≤ Teff ≤ 30000 K with 1,000 K steps, 13 surface gravities, 1.75 ≤ logg ≤ 4.75 with 0.25 dex steps, 6 chemical compositions, and a microturbulent velocity of 2 km/s.
2.3. Determination of the Fundamental Parameters
Given a series of model spectra, it should possible to find the model that best fits the observed spectrum by a simple inspection. In practice when one has a set of over a thousand models whose differences are sometimes subtle, it was better to choose an automatic method for comparison. We do so using a computer program that can compare the flux values at every point of each spectrum and tabulate the differences into a single number that characterizes goodness of the fit.
So to determine the fundamental parameters of the observed spectra, by determining the best fit between the observed spectra and the grid, three algorithms should be developed, the first is to adjust the spectral resolution, and the second is to bring the two spectra to a common wavelength scale while the third is devoted to the method of fitting. Since the spectral resolution of the observed spectra is not the same as the grid, so in the first step the synthetic spectra are brought at the same resolution by convolution. A Gaussian profile with FWHM = 0.25 A° is used for this purpose. The second step is required to begin the comparison between the observed and grid spectra are to adjust the wavelength scale. Since, the radial velocity of the observed star being unknown so no valuable comparison can be made until the two spectra are properly shifted to be brought into the same reference system. We used the cross-correlation method to determine the line shifts and the radial velocities by computing the correlation coefficient which given by
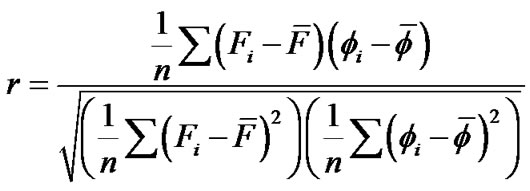 (1)
(1)
where 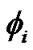 is the observed spectra and
is the observed spectra and 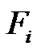 is the model, and
is the model, and 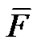 given by
given by
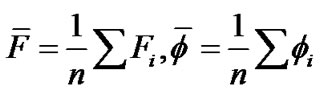 (2)
(2)
This step was performed by transforming the wavelengths  of both spectra into
of both spectra into  and finding the
and finding the  shift giving the highest correlation between the observed spectra and the spectra of the grid.
shift giving the highest correlation between the observed spectra and the spectra of the grid.
For the purpose of comparing the grid with the observed spectra, in the third step we have elaborated code which minimizes the Euclidan distance (D) between observed  and template
and template 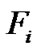 fluxes as explained by [12].
fluxes as explained by [12].
 (3)
(3)
where
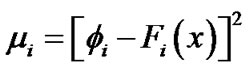 (4)
(4)
where x is the vector of the fundamental parameters i.e.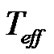 ,
, . The weight
. The weight 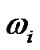 could be given by
could be given by
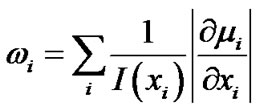 (5)
(5)
where
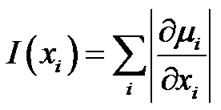 (6)
(6)
In the present calculations, we apply , this assumption is suitable for our purpose, where the information is distributed among most of the frequencies of the spectra (Allende Prieto, 2004), so we didn’t need the interpolation between the flux grid.
, this assumption is suitable for our purpose, where the information is distributed among most of the frequencies of the spectra (Allende Prieto, 2004), so we didn’t need the interpolation between the flux grid.
To determine the 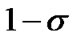 errors of the parameters, we follow the scheme of [13] which calculate the statistical error for a certain parameters (i) by
errors of the parameters, we follow the scheme of [13] which calculate the statistical error for a certain parameters (i) by
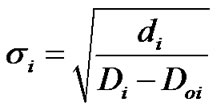 (7)
(7)
where 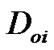 is the minimum distance of the best fit model,
is the minimum distance of the best fit model, 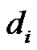 is a small change in the parameter (i) from the best fit value and
is a small change in the parameter (i) from the best fit value and 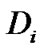 is the minimum distance for the parameter (i) with the new value.
is the minimum distance for the parameter (i) with the new value.
3. Results
Having built up the LTE/NLTE grid of synthetic spectra and the fitting algorithm we investigate the spectroscopic diagnostic tools developed from the grid. Instead of line profile fitting, we have chosen a global fit to the optical spectrum of each star.
We first used the algorithm described in Section 2.4 to compare the observed spectra with the theoretical one to determine the effective temperature and surface gravity of the best fitted models. In most cases the difference between the best fitted model obtained from the code and that of the closest one is very small, so visual inspection is applied for the final decision of the accepted model. With the best fitted model, we used the code ROTIN3 to calculate a grid of rotated spectra for 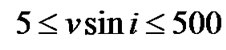 km/sec with step 10 km/sec. Then we applied the same algorithm again to determine the best rotational velocity. To do this, we used the spectral line Mg II 4481 (the recommended line to be free from the pressure broadening [14] in the fitting process.
km/sec with step 10 km/sec. Then we applied the same algorithm again to determine the best rotational velocity. To do this, we used the spectral line Mg II 4481 (the recommended line to be free from the pressure broadening [14] in the fitting process.
Table 3 summarizes the obtained physical parameters for the studied B-Type stars using LTE and/or NLTE model atmospheres. The first column is designed for the star’s name, the second, third, fourth, fifth and sixth columns are for the effective temperature, surface gravity, rotational velocity, methods of computations and masses respectively, while the last column is devoted to the reference of the fundamental parameters. Besides the fundamental parameters derived from the present calculations, we presented two values for each star collected from the literatures for the sake of comparison. As it well shown, there are some discrepancies between our result and those from the literatures. As the tools of calculations are different, we thus expect these discrepancies. Even one use two model atmospheres calculated by dif
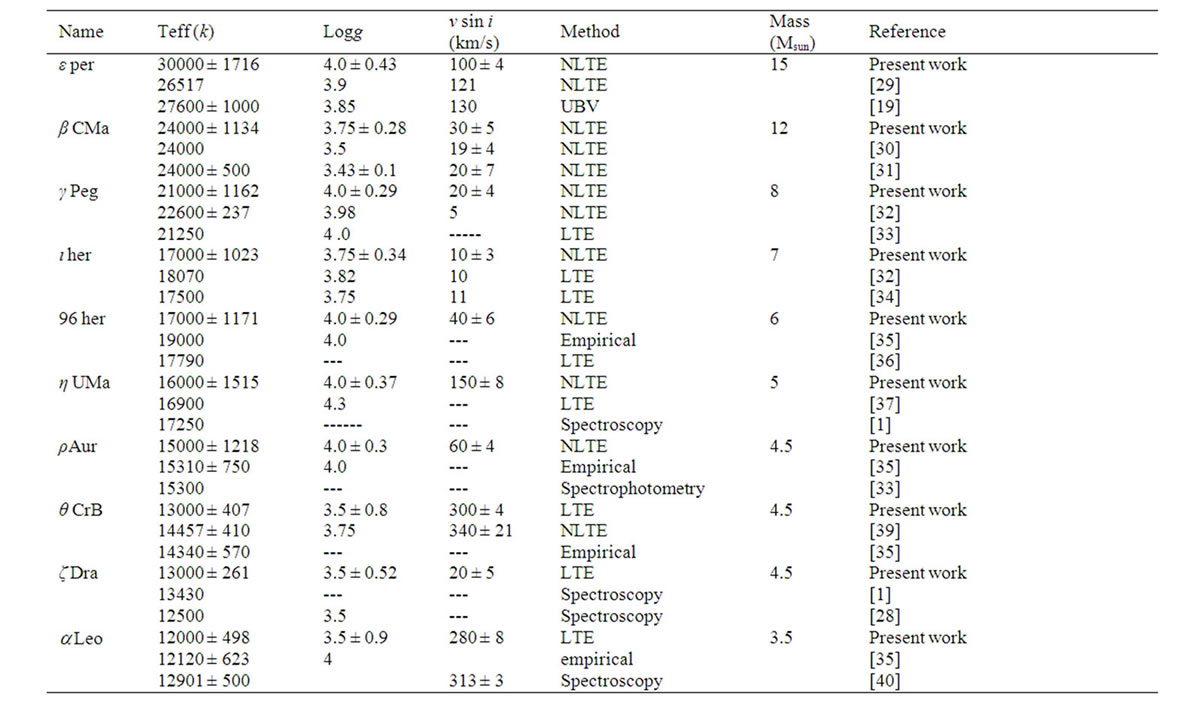
Table 3. Fundamental parameters of the program stars.
ferent codes, the results will not be identical.
In Figure 1, we plotted the optical spectra as well as the best fitted models. Three spectral regions are plotted, namely ll 4000 Aº - 4500 Aº, ll 4500 Aº - 5000 Aº and ll 6500 Aº - 7000 Aº. In general, the spectra are fitted well. For most stars, the Hg region match the observations quite well, but not perfectly.
To illustrate the reliability of the stellar parameters for our sample, we plotted the effective temperature versus surface gravity along with the evolutionary tracks of [15] with solar metalicity, this diagram is presented in Figure 2. From this figure we approximately determined the masses of stars, column 6 of Table 1. To check these masses, we used the empirical effective temperature mass relation. Figure 3 shows this comparison. As we see, good agreement for most of stars.
In the following we discuss the results for each individual object:
ε Per (HD 24760, 45 Per, HR 1220, ADS 2888A, HIP 18532; V = 2.9 m), is a well-known bright star, which has been used for a long time as a spectrophotometer and MKK classification standard for the spectral class B0.5 III [16], though it was also classified differently, e.g. B0.5 V [17]. This star was reported to be a double-lined spectroscopic binary [18]. [19] suggested it to be a triple system. In the present spectrum,  is in pure absorption, OI and FeII lines are not visible except the FeII 6516 Aº line, which shows a very weak absorption. Comparison between observed and theoretical spectra is good. Noticeable discrepancy is found between our result and that of the literatures. While, the present calculations give higher effective temperature and comparable surface gravity, the rotational velocity is lower. Further investigation of spectra with high resolution spectra may give more consistent result.
is in pure absorption, OI and FeII lines are not visible except the FeII 6516 Aº line, which shows a very weak absorption. Comparison between observed and theoretical spectra is good. Noticeable discrepancy is found between our result and that of the literatures. While, the present calculations give higher effective temperature and comparable surface gravity, the rotational velocity is lower. Further investigation of spectra with high resolution spectra may give more consistent result.
β CMa (HD44743, HR2294, Vmag = 1.97). Spectral type B1II [20]. Earlier photometric and spectroscopic data reveal that this object exhibits multiperiodicity with rather low frequencies. The variability of β CMa has been known for one century during which the star has been extensively studied. In the present spectrum, Ha shows a sharp absorption feature. Only the FeII 7462 Aº line is found in emission with a double peak structure.
γ Peg (HD 886, HR 39, Sp B2 IV), is listed as standard star of spectral type B2.5 IV in the Atlas of stellar spectra, by [21]. γ Peg is one of the so-called “classical” β cephei stars. It has been assigned to this group by [22] who demonstrated its variability in radial velocity with a single period of 0.1517 d and amplitude of 3.5 km/s. Hα is in sharp absorption [7]. Our spectrum for γ Peg cover only observations from 5850 A° to 8350 A° and we hope in future to collect observation for this star in a wider visible wavelengths to get more accurate results. The star
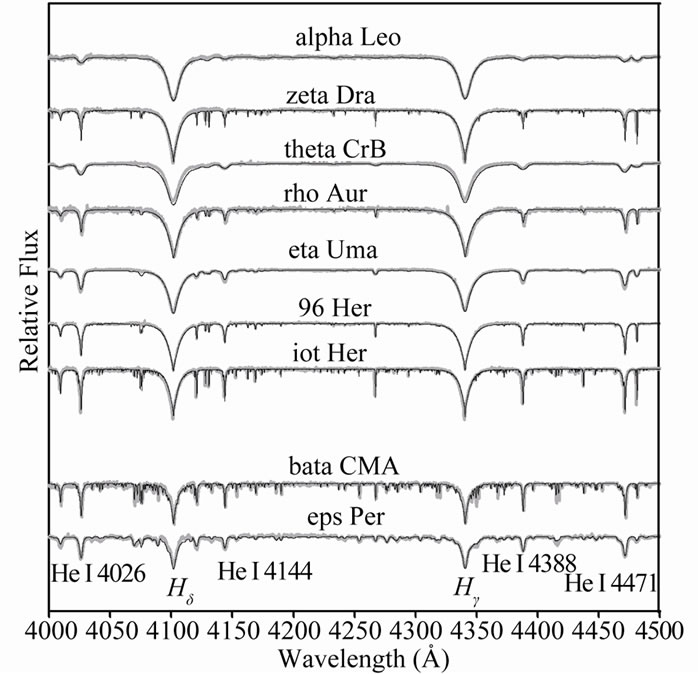

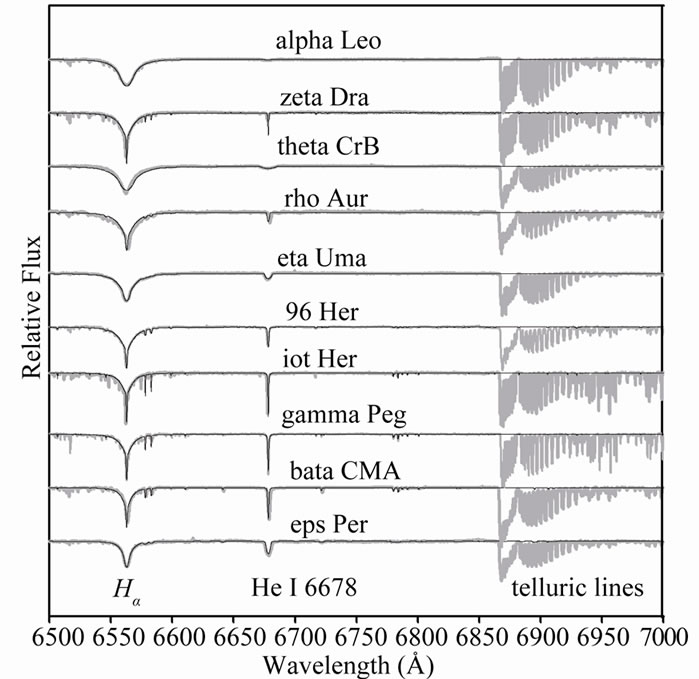
Figure 1. Comparison between observed optical spectra for 10 B-type stars (gray lines ) and synthetic spectra (black lines).
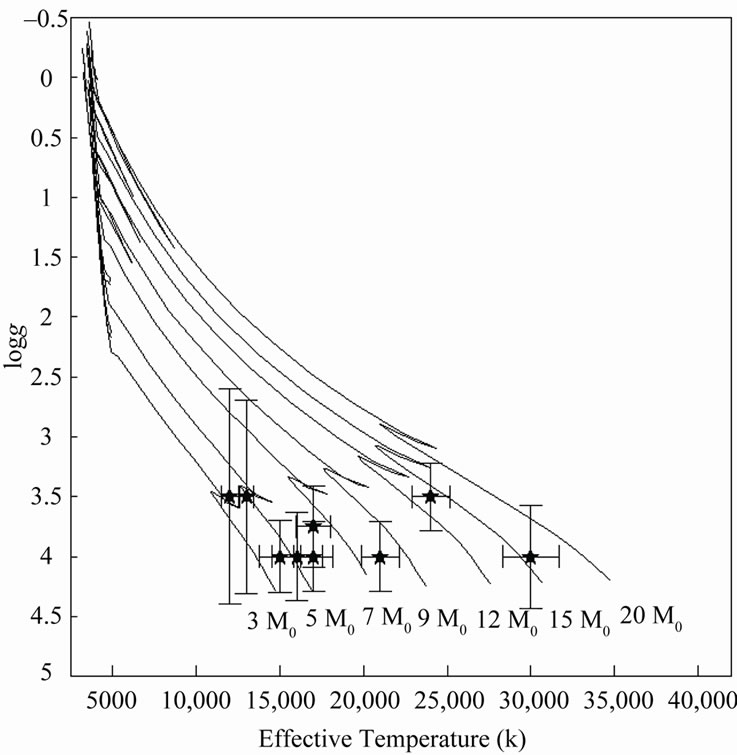
Figure 2. The distribution of the program stars in the temperature-gravity diagram. Evolutionary tracks for solar composition stars with masses 3 - 20 Msun from [15] are noted by continuous lines.
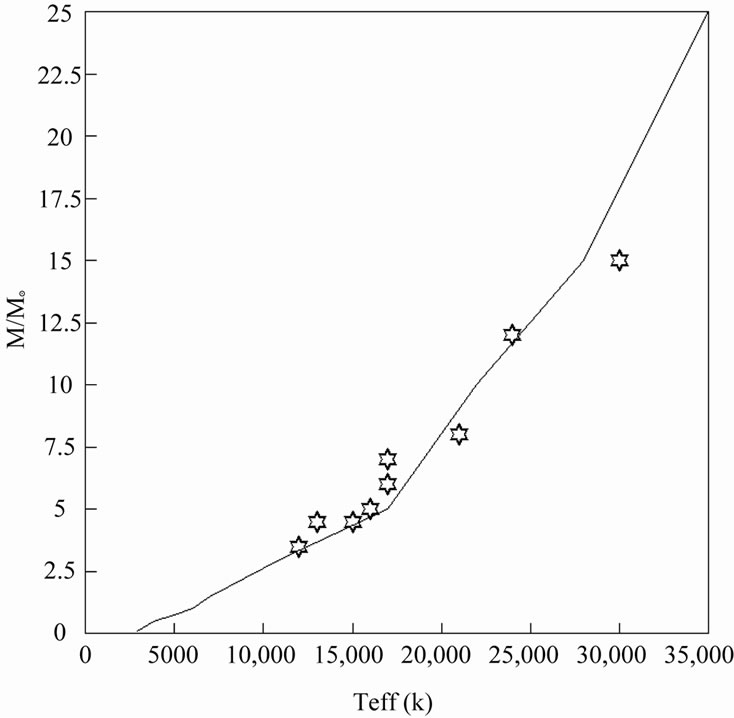
Figure 3. Comparison between the approximate masses of the program stars and the empirical effective temperature - mass formula (solid line).
possesses well expressed lines in its spectrum which may be attributed to its low rotational velocity (vsin i = 20 km/s).
ι Her (HD 160762, HR 6588, HIP 86414, V = 3.80 m). It is a single lined spectroscopic binary [23], and is considered as a good candidate for SPB stars i.e. (slowly pulsating B stars). The star shows a sharp absorption feature, and has a very low rotational velocity, which is confirmed by [24].
96 Her (HR 6738, HD 164852, HIP 88331), is a bright B star. Radial velocity variation of 96 Her were discovered by [25] on 25 Yerkes spectrograms. He found range from –98 to +74 km/s, The derived period was 50.2 days. [26] found this star to be spectroscopic binary.
η UMa (HR5191, HD120315, HIP67301). Spectral type B3 V [21]. The star is suspected to be a low amplitude photometric variable, and is listed as number 6450 in the new catalog of suspected variable stars. η UMa is frequently used as standard star for spectral classification. Morgan [21] establish η UMa as an “MK dagger type”, a star whose spectrum has been carefully examined and used to define the MK system.
ρ Aur (20 Aur = HR 1749 = HD 34759), is a bright single-lined spectroscopic binary from observations obtained at Mount Wilson, Victoria, Yerkes, McDonald and Kitt Peak Observatories [27] were the first to derive orbital elements. Both Hα and OI 7772 A° - 5 A° lines show absorption. FeII 6456, 7516, and 7712 A° lines are not visible, while both 6516 and 5169 A° lines are very weak [7].
θ CrB (HD 138794, HR 5778, HIP 76127). The star was originally defined as a Be star, however, in the present phase none of the concerned lines showed emission.
Hα and OI 7772 A° in absorption, FeII 5169 A° line shows weak absorption and FeII 7712 A°line is not visible [7].
ζ Dra (HR 6396, HD 155763, HIP 83895). The UV spectrum of which was studied by [28]. Hα shows a sharp absorption feature. OI 7772 A° - 5 A° in absorption with two resolved lines. FeII lines show sharp weak absorption features, the star has a low v sin i = 20 km/s.
a Leo (HD 87901, HR 3982). The present spectrum shows H in pure absorption feature, OI is in absorption, no visible FeII lines were found, except FeII 5169 A° in weak absorption. Comparison between optical spectra and best fitted model atmosphere is very good.
4. Conclusions
In summary, we presented model atmosphere analysis for a sample of B-type stars. We used LTE/NLTE to determine effective temperature, surface gravities, and rotational velocities for each star. We used the theoretical evolutionary track to test the reliability of derived fundamental parameters and to estimate the mass for each star. Comparison with the previous results is good in general, if we take into account that, they are computed with different methods. From the results obtained we can draw the following:
• Although the automatic methods are fast, the “by-eye” procedure is still which make the final decision.
• More accurate analysis of B-type stars could be drawn based on complete NLTE model atmosphere grid as well as a large sample of high S/N observed spectra. That’s will be done in the future.
• The difference remarked between the atmospheric parameters derived in the present investigation and that collected from the literatures, specially for hotter ones, may be attributed to the different methods of calculations.
5. Acknowledgements
This research has made use of the NASA’s Astrophysics Data System Abstract Service and Ondřejov observatory 2-meter HEROS spectra. S. M. Saad, would like to thank P. Skoda, M. Slechta, M. R. Sanad, A. Shokry, and much indebted to J. Kubat for his continuous support.
6. References
[1] N. A. Sokolov, “The Determination of T_eff_ of B, A and F Main Sequence Stars from the Continuum between 3200 A and 3600 A,” Astronomy and Astrophysics, Vol. 110, 1995, pp. 553-564.
[2] T. Lanz and I. Hubeny, “A Grid of NLTE Line-Blanketed Model Atmospheres of Early B-Type Stars,” The Astrophysical Journal Supplement Series, 2007, Vol. 169, No. 1, pp. 83-104. doi:10.1086/511270
[3] S. Stefl and T. Rivinius, “HEROS Be Star Campaigns,” ASP Conference Proceedings, Vol. 214, 2000, p. 356.
[4] P. Skoda and M. Slechta, “2-Meter Telescope Devices: Coudé Slit Spectrograph and HEROS,” Publications of the Astronomical Institute of the Academy of Sciences of the Czech Republic, No. 90, 2002, pp. 1-4.
[5] J. Horn, A. M. Hubert, H. Hubert, P. Koubsk'y and N. Bailloux, “CX Draconis—The Orbit Parameters for Both Components,” Astronomy and Astrophysics, 1992, Vol. 259, No. 1, pp. L5-L8.
[6] P. Skoda, “SPEFO—A Simple, Yet Powerful Program for One-Dimensional Spectra Processing,” ASP Conference Proceedings, Vol. 101, 1996, p. 187.
[7] S. M. Saad, J. Kubát, D. Korčáková, P. Koubský, P. Škoda, M. Šlechta, A. Kawka, A. Budovičová, V. Votruba, L. Šarounová and M. I. Nouh, “Observations of Hα, Iron, and Oxygen Lines in B, Be, and Shell Stars,” Astronomy and Astrophysics, Vol. 450, No. 1, 2006, pp. 427-430.
[8] R. L. Kurucz, “Synthetic Template Spectra,” Highlights of Astronomy, 1995, Vol. 10, p. 407.
[9] R. O. Gray, “The Calibration of Stromgren Photometry for A, F and Early G Supergiants. III—The A and Early F Supergiants,” Astronomy and Astrophysics, 1992, Vol. 265, No. 2, pp. 704-710.
[10] R. O. Gray, “Erratum: The Calibration of Stromgren Photometry for A, F and Early G Supergiants. III. The A and Early F Supergiants,” Astronomy and Astrophysics, Vol. 273, 1993, p. 349.
[11] R. O. Gray, “Precision Classification,” ASP Conference Series, Vol. 60, 1994, p. 75.
[12] C. Allende-Prieto, “Automated Analysis of Stellar Spectra,” Astronomische Nachrichten, Vol. 325, No. 6-8, 2004, pp. 604-609.
[13] Q. Z. Zhang and F. Cheng, “Application of the Complete Linearization Method to the Analysis of Solar Prominence Emission Spectrum,” Acta Astronomica Sinica, Vol. 27, 1986, pp. 30-37.
[14] D. F. Gray, “The Observation and Analysis of Stellar Photospheres,” John Wiley & Sons, New York, 1976.
[15] L. Girardi, A. Bressan, G. Bertelli and C. Chiosi, “Evolutionary Tracks and Isochrones for Lowand Intermediate-Mass Stars: From 0.15 to 7 Msun, and from Z=0.0004 to 0.03,” Astronomy and Astrophysics Supplement, Vol. 141, 2000, pp. 371-383.
[16] W. W. Morgan, P. C. Keenan and E. Kellman, “An Atlas of Stellar Spectra, with an Outline of Spectral Classification, Ill,” The University of Chicago Press, Chicago, 1943.
[17] H. L. Johnson and W. W. Morgan, “Fundamental Stellar Photometry for Standards of Spectral Type on the Revised System of the Yerkes Spectral Atlas,” The Astrophysical Journal, Vol. 117, 1953, p. 313. doi:10.1086/145697
[18] R. M. Petrie, “A Re-Examination of the Space Motions and Luminosities of the Stars of the Cassiopeia-Taurus Group Based upon New Radial Velocities,” Monthly Notices of the Royal Astronomical Society, Vol. 118, 1958, p. 80.
[19] A. E. Tarasov, P. Harmanec, J. Horn, L. S. Lyubimkov, S. I. Rostopchin, P. Koubsky, C. Blake, V. V. Kostunin, G. A. H. Walker and S. Yang, “The Archetype Line-Profile Variable ɛ 45 Persei Is a Spectroscopic Triple System,” Astronomy and Astrophysics Supplement, Vol. 110, 1995, p. 59.
[20] W. W. Morgan, A. C. Code and A. E. Whitford, “Studies in Galactic STRUCTURE.II.LUMINOSITY Classification for 1270 Blue Giant Stars,” Astrophysical Journal Supplement, Vol. 2, 1955, p. 41. doi:10.1086/190016
[21] W. W. Morgan and P. C. Keenan, “Spectral Classification,” Annual Review of Astronomy and Astrophysics, Vol. 11, 1973, p. 29. doi:10.1146/annurev.aa.11.090173.000333
[22] D. H. McNamara, “Periods and Absolute Magnitudes of the Beta Canis Majoris Stars,” Publications of the Astronomical Society of the Pacific, Vol. 65, No. 387, 1953, p. 286. doi:10.1086/126627
[23] H. A. Abt and S. G. Levy, “Binaries among B2-B5 IV, V Absorption and Emission Stars,” Astrophysical Journal Supplement Series, Vol. 36, 1978, pp. 241-258. doi:10.1086/190498
[24] H. A. Abt, H. Levato and M. Grosso, “Rotational Velocities of B Stars,” The Astrophysical Journal, Vol. 573, No. 1, 2002, pp. 359-365. doi:10.1086/340590
[25] E. R. Mitchell, “Treasurer’s Report,” Monthly Notices of the Royal Astronomical Society, Vol. 9, 1911, p. 26.
[26] P. Koubsky, J. Horn, P. Harmanec, L. H. Iliev, B. Z. Kovacev, C. T. Bolton, R. W. Lions, H. Bozic and K. Pavlovski, “96 Herculis: A Remarkable Early-Type Multiple System,” Information Bulletin on Variable Stars, No. 2778, 1985, p. 1.
[27] A. Blaauw and T. S. van Albada, “Radial Velocities of B-Type Stars in the Nearest Associations,” Astrophysical Journal, Vol. 137, 1963, p. 791. doi:10.1086/147556
[28] K. C. Smith and M. M. Dworetsky, “Elemental Abundances in Normal Late B-Stars and Hgmn-Stars from Co-Added IUE Spectra—Part One—Iron Peak Elements,” Astronomy and Astrophys, Vol. 274, No. 2, 1993, p. 335.
[29] W. Huang and D. R. Gies, “Stellar Rotation in Field and Cluster B Stars,” Astrophysical Journal, Vol. 683, No. 2, 2008, p. 1045. doi:10.1086/590106
[30] K. Lefever, J. Puls, T. Morel, C. Aerts, L. Decin and M. Briquet, “Spectroscopic Determination of the Fundamental Parameters of 66 B-Type Stars in the Field-of-View of the CoRoT Satellite,” Astronomy and Astrophysics, 2010, Vol. 515, p. 74.
[31] R. S. Levenhagen and N. V. Leister, “Spectroscopic Analysis of Southern B and Be Stars,” Monthly Notices of the Royal Astronomical Society, Vol. 371, No. 1, 2006, pp. 252-262. doi:10.1111/j.1365-2966.2006.10655.x
[32] E. L. Fitzpatrick and D. Massa, “Determining the Physical Properties of the B Stars. II. Calibration of Synthetic Photometry,” The Astronomical Journal, Vol. 129, No. 3, 2005, p. 1642.
[33] S. J. Adelman, “Spectrophotometry of B, A, and F stars,” Astrophysical Journal, Vol. 222, 1978, pp. 547-555. doi:10.1086/156168
[34] S. J. Adelman, “Elemental Abundance Analyses with DAO Spectrograms. VII—The Late Normal B Stars Pi Ceti, 134 Tauri, 21 Aquilae, and Nu Capricorni and the Use of RETICON Spectra,” Monthly Notices of the Royal Astronomical Society, Vol. 252, 1991, pp. 116-131.
[35] E. Theodossiou and E. Danezis, “The Stellar Temperature Scale for Stars of Spectral Types from O8 to F6 and the Standard Deviation of the MK Spectral Classification,” Astrophysics and Space Science, Vol. 183, No. 1, 1991, pp. 91-115.
[36] C. Morossi, M. L. Malagnini, “Observed and Computed Spectral Flux Distribution of Non-Supergiant O9-G8 Stars. III—Determination of T(eff) for the Stars in the Breger Catalogue,” Astronomy and Astrophysics Supplement Series, Vol. 60, 1985, pp. 365-372.
[37] J. S. Adelman, O. I. Pintado, M. F. Nieva, K. E. Rayle and S. E. Sanders Jr., “On the Effective Temperatures and Surface Gravities of Superficially Normal Main Sequence Band B and A Stars,” Astronomy and Astrophys, Vol. 392, 2002, pp. 1031-1037.
[38] Y. Frémat, J. Zorec, A.-M. Hubert and M. Floquet, “Effects of Gravitational Darkening on the Determination of Fundamental Parameters in Fast-Rotating B-Type Stars,” Astronomy and Astrophys, Vol. 440, No. 1, 2005, pp. 305-320.
[39] H. A. McAlister, T. A. Brummelaar, D. R. Gies, W. Huang, W. G. Bagnuolo Jr., M. A. Shure, J. Sturmann, L. Sturmann, N. H. Turner, S. F. Taylor, D. H. Berger, E. K. Baines, E. Grundstrom, C. Ogden, S. T. Ridgway and G. van Belle, “First Results from the CHARA Array. I. An Interferometric and Spectroscopic Study of the Fast Rotator α Leonis (Regulus),” Astrophysical Journal, 2005, Vol. 628, No. 1, pp. 439-452. doi:10.1086/430730

