Journal of Sensor Technology
Vol.3 No.4(2013), Article ID:40958,7 pages DOI:10.4236/jst.2013.34019
Clustering in Wireless Multimedia Sensor Networks
Department of Computer Science and Engineering, National Institute of Technology, Hamirpur, India
Email: pushpender.dhiman@gmail.com, nar.chand@gmail.com
Copyright © 2013 Pushpender Kumar, Narottam Chand. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 24, 2013; revised November 27, 2013; accepted December 4, 2013
Keywords: Wireless Multimedia Sensor Network; Clustering; Spectral Graph Partitioning; Eigenvector; Eigenvalue
ABSTRACT
Wireless Multimedia Sensor Networks (WMSNs) are comprised of small embedded audio/video motes capable of extracting the surrounding environmental information, locally processing it and then wirelessly transmitting it to sink/base station. Multimedia data such as image, audio and video is larger in volume than scalar data such as temperature, pressure and humidity. Thus to transmit multimedia information, more energy is required which reduces the lifetime of the network. Limitation of battery energy is a crucial problem in WMSN that needs to be addressed to prolong the lifetime of the network. In this paper we present a clustering approach based on Spectral Graph Partitioning (SGP) for WMSN that increases the lifetime of the network. The efficient strategies for cluster head selection and rotation are also proposed as part of clustering approach. Simulation results show that our strategy is better than existing strategies.
1. Introduction
Recent developments in wireless communication and embedded technology have made the wireless sensor network (WSN) possible. Wireless sensor networks are constituted of large number of low-cost, low-power and less communication bandwidth tiny sensor nodes. The sensors, which are randomly deployed in an environment, are required to collect data from their surroundings, process the data and finally send it to the sink through multi hops [1]. Traditional WSNs collects the scalar data such as temperature, pressure, etc. and transmit it to the sink. WSN has potential to design many new applications for handling emergency, military and disaster relief operations that require real time information for efficient coordination and planning [2].
Wireless multimedia sensor network (WMSN) uses cheap CMOS (Complementary Metal Oxide Semiconductor) camera and microphone sensors which can acquire multimedia information. WMSN consists of camera sensors as well as scalar sensors. Camera sensors can retrieve much richer information in the form of images or videos and hence provide more detailed and interesting data about the environment [3,4]. The multimedia content has the potential to enhance the level of information collected, compared with scalar data. Multimedia content produces immense amount of data to transmit over WMSN, which is limited in terms of power supply, communication bandwidth, memory, etc.
In a large scale network, if all the nodes have to communicate their data to their respective destination, it will deplete their energy quickly due to the long-distance, large volume of data and multi-hopnature of the communication. This will also lead to network contention. The clustering is a standard approach for achieving efficient and scalable control in these networks [5].
Clustering results in a number of benefits. It facilitates distribution of control over the network. It saves energy and reduces network contention by enabling locality of communication. Nodes communicate their data over shorter distances to their respective cluster head (CH). The cluster head aggregates these data into a smaller set of meaningful information. Not all nodes, but only the cluster heads need to communicate with their neighbouring cluster heads and sink/base station. Figure 1 shows the clustering of nodes in a general WSN.
In this paper, we have utilized spectral graph partitioning (SGP) technique based upon eigenvalues proposed by Fiedler to form clustering in WMSN [6]. SGP method has been used in many applications such as image segmentation, social networks, etc. [7].
The spectral graph partitioning (SGP) algorithm is based on second highest eigenvalues of particular graph.
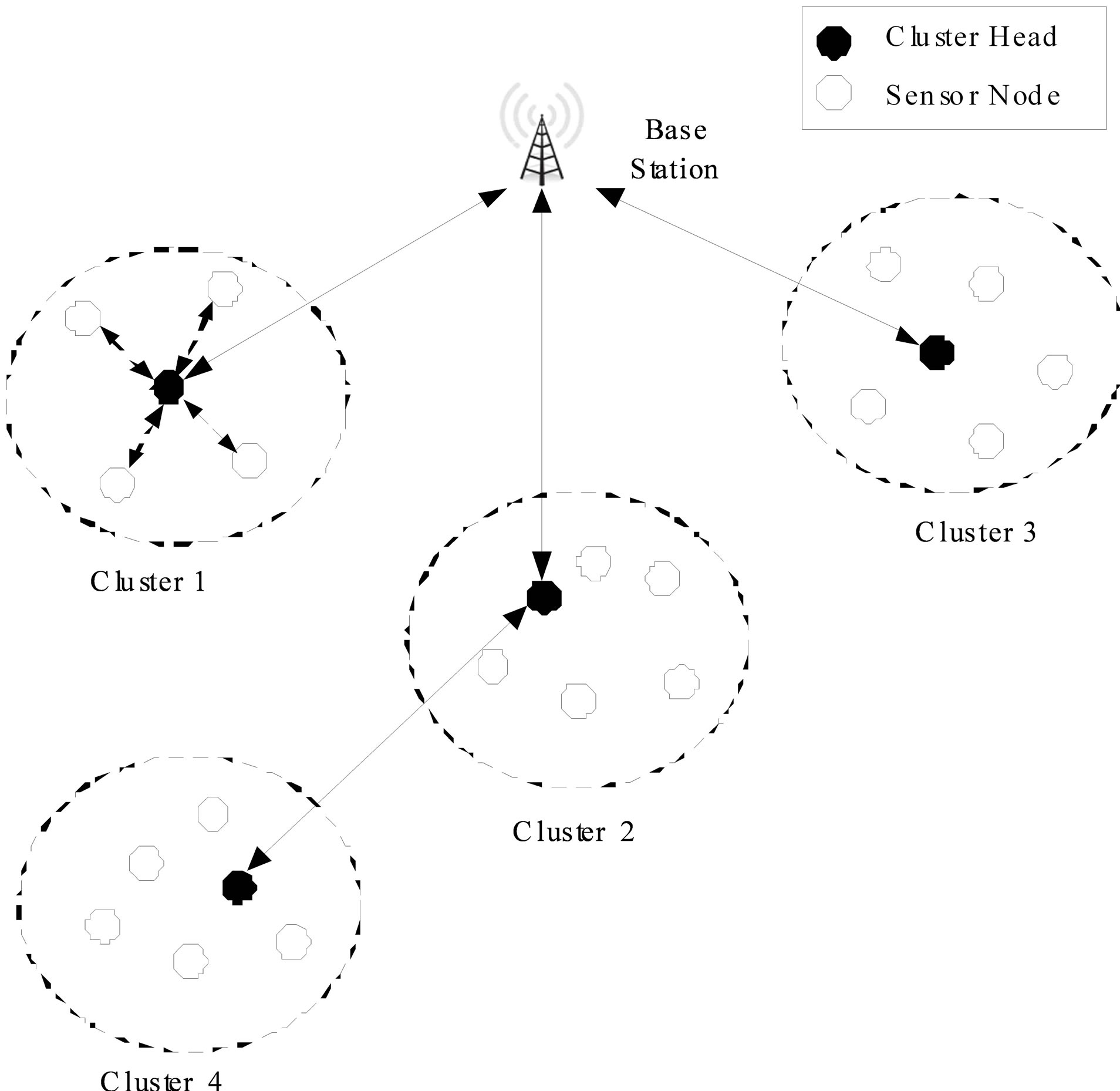
Figure 1. Clustering of SNs in WSN.
The second highest eigenvalue of the Laplacian matrix corresponding to different eigenvectors, is used to partition the graph into two parts. Within a cluster, a node with highest eigenvalue is selected as cluster head. In case of WMSN, large volume of sensed data is generated, therefore, such clustering can be utilized to reduce the volume and number of data transmissions through data aggregation. Simulation experiments have been performed to evaluate the performance of proposed method and compare it with the existing technique.
The rest of the paper is organized as follows. Section 2 reviews the related work. General SGP strategy for clustering has been presented in Section 3. Section 4 describes the use of SGP for WMSN. In Section 5 we present the results of performance evaluation of the method and Section 6 concludes the paper.
2. Related Work
The nodes are often grouped together into disjoint and mostly non-overlapping groups are called clusters. Clusters are used to minimize communication latency and improve energy efficiency. Leader of every cluster is often called the cluster head (CH) and generally has to perform more functions as compared to normal sensor node.
M. Qin et al. suggested voting-based clustering algorithm (VCA) [8] that enhances the criteria for cluster selection and combines load balancing consideration together with topology and energy information. VCA addresses inefficient cluster formation using a voting scheme, which enables the nodes to exchange information about their local network view. This method assumes synchronization among the nodes. Similar to WCA [9], the time required for the nodes to gather information about all other nodes depends on the network size and is not constant.
B. Elbhiri et al. [7] suggested spectral classification based on near optimal clustering in wireless sensor networks (SCNOPC-WSN) algorithm. This algorithm deals with the clustering problem in WSN. Energy aware adaptive clustering protocol is used for the bi-partitioning spectral classification and it guarantees robust clustering. SCNOPC-WSN also deals with the optimization of the energy dissipated in the network.
Banerjee and Khuller [10] suggested hierarchical clustering algorithm based on geometric properties of the wireless network. A number of cluster properties such as cluster size and the degree of overlap, which are useful for the management and scalability of the hierarchy, are also considered while grouping the nodes. In the proposed scheme, any node in the WSN can initiate the cluster formation process. Initiator with least node ID will take precedence, if multiple nodes started cluster formation process at the same time.
Bandyopadhyay and Coyle [11] proposed EEHC which is a distributed, randomized clustering algorithm for WSNs with the objective of maximizing the network lifetime. CHs collect the sensor reading in their individual clusters and send an aggregated report to the base station. Their technique is based on two stages—initial and extended.
In EEUC [12], the hot-spot problem in multihop networks is solved using cluster with unequal size. CHs that are closed to the base station tend to die faster, because they relay much more traffic than remote nodes. Setting smaller cluster sizes to the close CHs preserves their energy. Additional improvement for multihop networks is presented in [13], using a separation between the data gathering and aggregation task and the forwarding task.
Spectral graph partitioning algorithm partitions the graph using the eigenvectors of the matrix obtained from the graph. SGP obtains data representation in the low-dimensional space that can be easily clustered. Eigenvalues and eigenvectors provide a penetration into the connectivity of the graph.
3. SGP for Cluster Formation
Spectral graph partitioning technique is based on eigenvalues and eigenvector of the adjacency matrix of graph to partition the graph. The methods are called spectral, because they make use of the spectrum of the adjacency matrix of the data to cluster the points [14]. Spectral methods are widely applied for graph partitioning. Spectral graph partitioning is a powerful technique and also is being used in image segmentation and social network analysis. SGP divides the graph into two disjoint groups, based on eigenvectors corresponding to the second smallest eigenvalue of the Laplacian matrix [15].
Let G (V, E) is an undirected graph where V represents the set of vertices (sensor nodes) and E represents the set of edges connecting these vertices. Each vertex is identified by an index 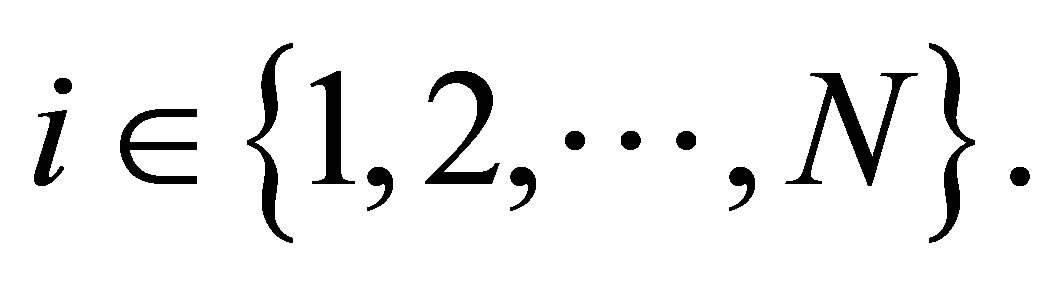 The edge between node i and node j is represented by eij. The graph can be represented as an adjacency matrix. The adjacency matrix A of graph G having N nodesis the N × N matrix where the non-diagonal entry aij is the number of edges from node i to node j, and the diagonal entry aii is the number of loops at node i. The adjacency matrix is symmetric for undirectedgraphs [16].
The edge between node i and node j is represented by eij. The graph can be represented as an adjacency matrix. The adjacency matrix A of graph G having N nodesis the N × N matrix where the non-diagonal entry aij is the number of edges from node i to node j, and the diagonal entry aii is the number of loops at node i. The adjacency matrix is symmetric for undirectedgraphs [16].
The adjacency matrix A is defined as
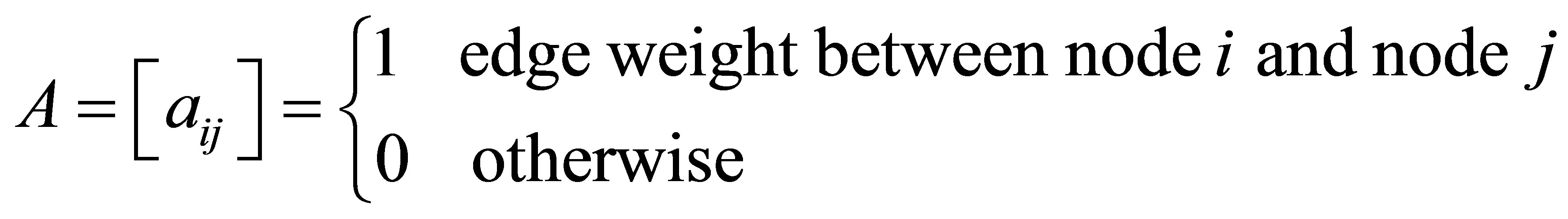
We also define degree matrix D for graph G. The degree matrix of a graph gives the number of edges between node i to another node [17]. The degree matrix is a diagonal matrix which contains information about the degree of each node. It is helpful to construct the Laplacian matrix of a graph. The degree matrix D for G is a N × N square matrix and is defined as

The Laplacian matrix is formed from adjacency matrix and the degree matrix. The Laplacian matrix of the graph G having N vertices is N × N square matrix and is represented as
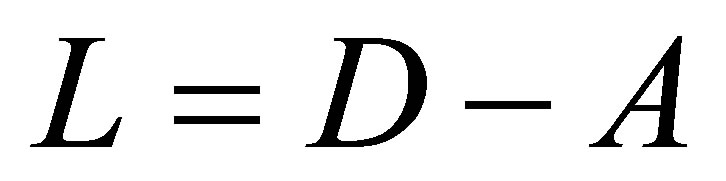
The normalized form of Laplacian matrix can be written as
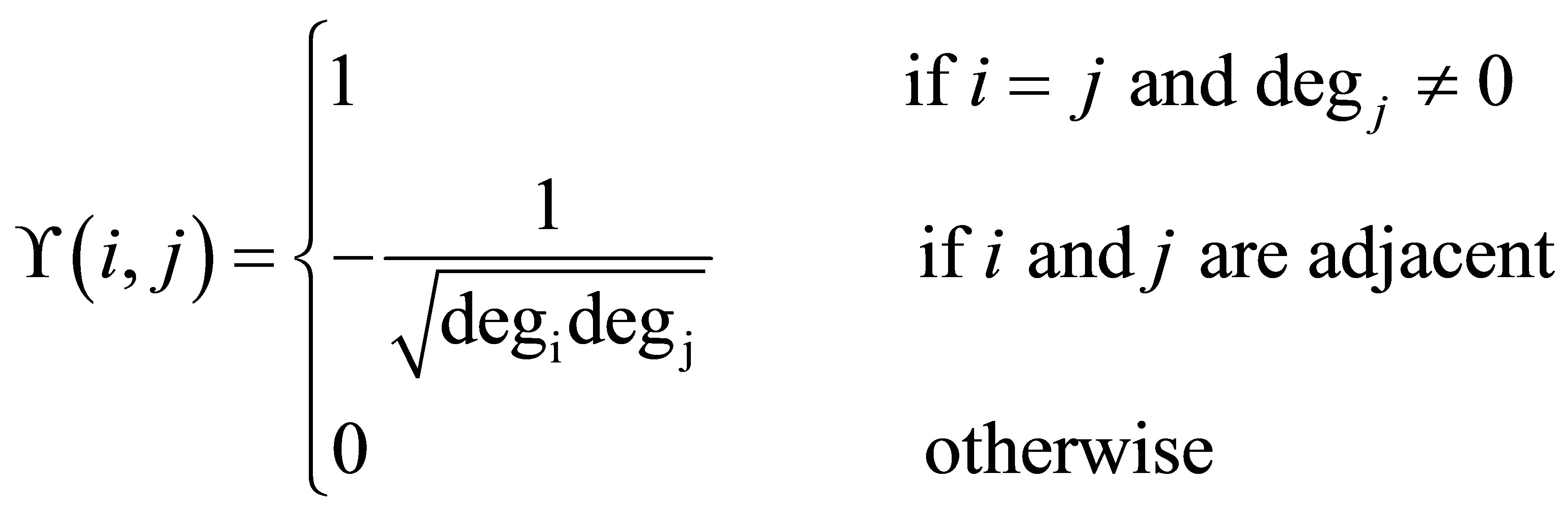
The eigenvalues of matrix  are denoted by
are denoted by 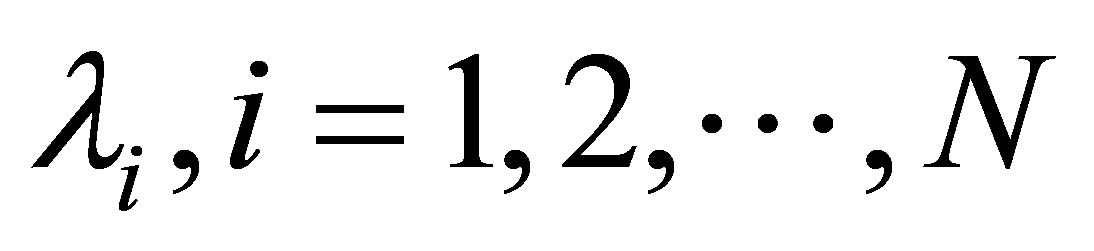 such that
such that 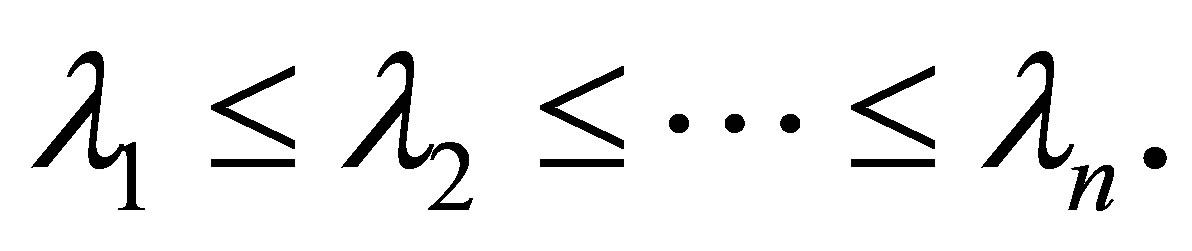 Laplacian matrix has the property
Laplacian matrix has the property 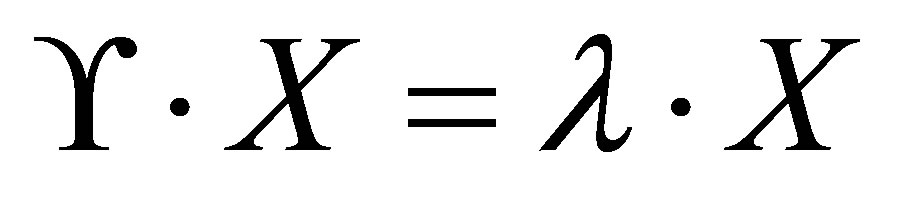 where X is the eigenvector of the matrix
where X is the eigenvector of the matrix  and λ is the eigenvalue of the matrix
and λ is the eigenvalue of the matrix . Laplacian matrix plays important role in spectral graph theory. λ1 represents the number of subgraphs in the network. The second smallest eigenvalue λ2 is referred to the algebraic connectivity and its corresponding eigenvector is usually referred to as the Fiedler Vector [14,18].
. Laplacian matrix plays important role in spectral graph theory. λ1 represents the number of subgraphs in the network. The second smallest eigenvalue λ2 is referred to the algebraic connectivity and its corresponding eigenvector is usually referred to as the Fiedler Vector [14,18].
We choose the eigenvector values corresponding to the second highest eigenvalue λ2. Second highest eigenvalue (λ2) divides the graph into two subgraphs. G is divided into two subgraphs 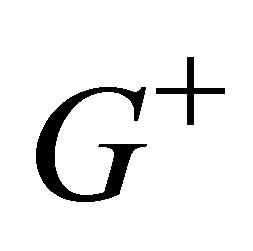 and
and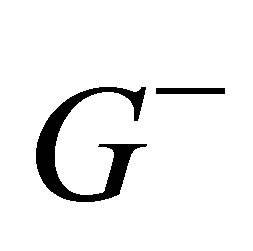 , where
, where 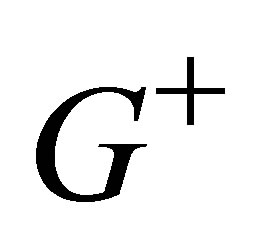 and
and 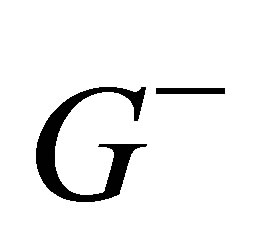 are the set of vertices related to the new subgraphs.
are the set of vertices related to the new subgraphs. 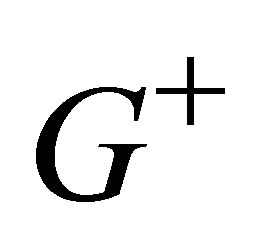 contains nodes corresponding to positive eigenvalues and
contains nodes corresponding to positive eigenvalues and 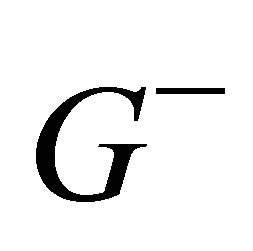 contains nodes corresponding to negative eigenvalues. The set of vertices is defined by
contains nodes corresponding to negative eigenvalues. The set of vertices is defined by
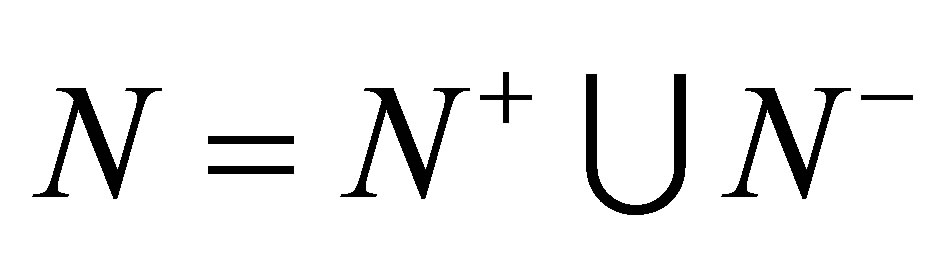
and
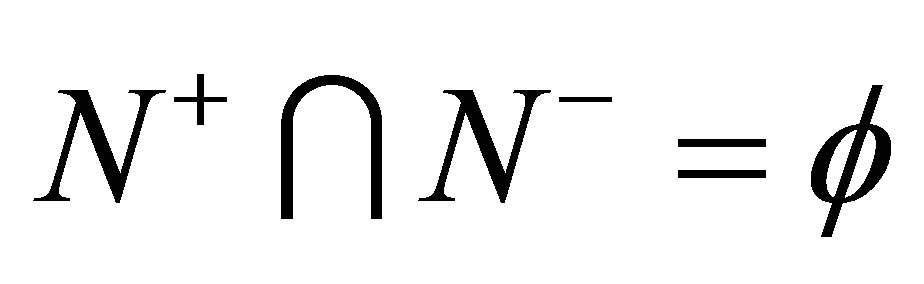
where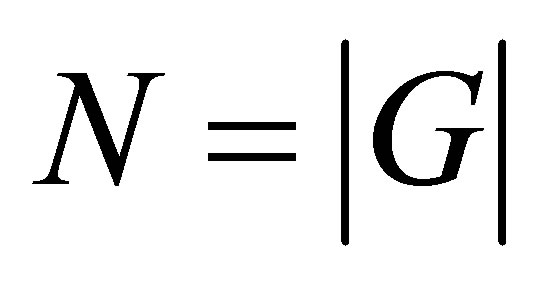 ,
, 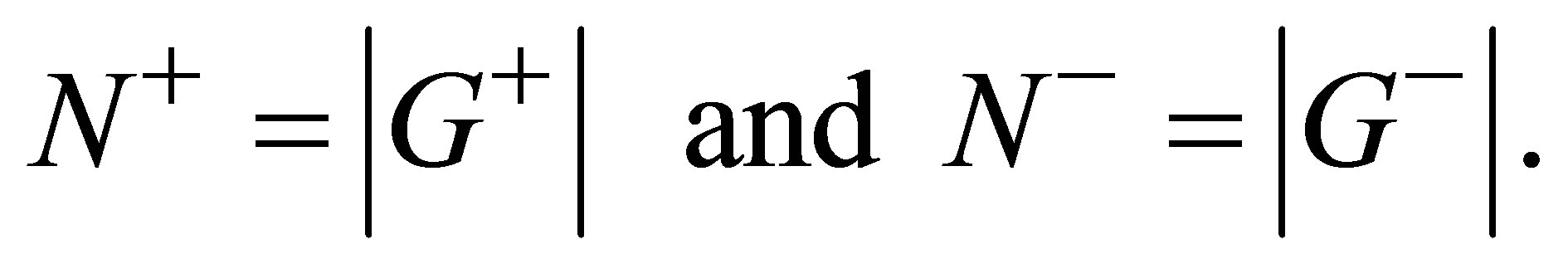
4. Cluster Formation in WMSN
SGP technique can be used for dividing the network into clusters. SGP has many advantages as compared to other clustering algorithms. SGP partitions the graph on the basis of eigenvalues and eigenvector adjacency matrix. If the graph is partitioned into more than two subgraphs, apply SGP technique recursively. These properties make SGP technique a better option for multimedia data clustering where large volume of data is transmitted between nodes and CH.
In our proposed method, clustering of WMSN has been done on the basis of Spectral Graph Partitioning technique [19]. Each node sends short message to sink which contains the location information of the node. On the basis of this information, the sink constructs the adjacency matrix and degree matrix and then constructs the Laplacian matrix. The eigenvector corresponding to second smallest eigenvalue (called Fiedler Vector) is used to partition the WMSN. The location of each node may be found by GPS or any other localization method [18,20].
4.1. Steps for Clustering
1) Construct a graph G of the given sensor network.
2) Construct the normalized Laplacian matrix as
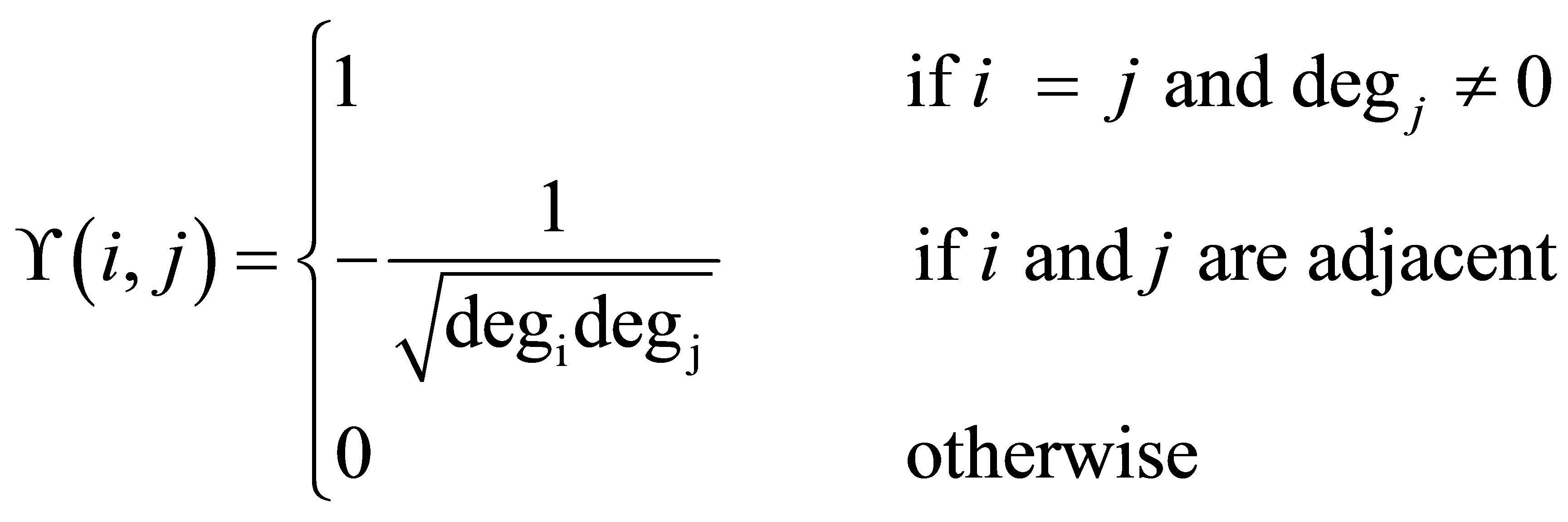
where 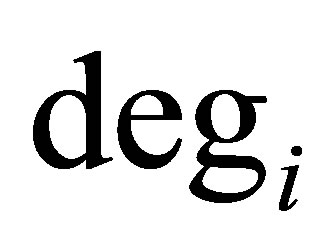 is the degree of node i 3) From the Laplacian matrix
is the degree of node i 3) From the Laplacian matrix 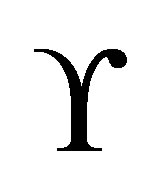 of the graph compute the eigenvalues and eigenvector of Laplacian matrix.
of the graph compute the eigenvalues and eigenvector of Laplacian matrix.
4) Select the second smallest eigenvalue λ2 of Laplacianmatrix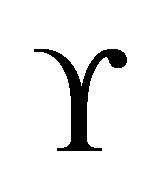 .
.
5) Choose eigenvector value corresponding to the eigenvalue λ2.
Divide the graph G into two subgraphs 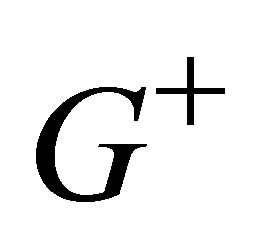 and
and 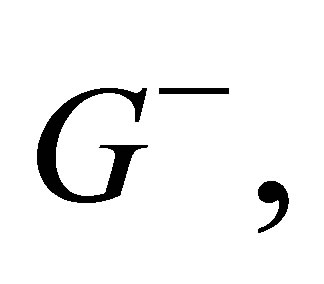 where
where 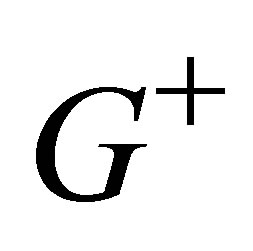 contains nodes corresponding to positive eigenvalues and
contains nodes corresponding to positive eigenvalues and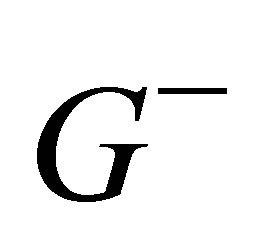 , contains nodes corresponding to negative eigenvalues.
, contains nodes corresponding to negative eigenvalues.
After the first iteration of above method, the whole network is divided into two clusters based on the eigenvalues of the nodes. Table 1 shows the two partitions/ clusters for a given graph shown in Figure 2. After first iteration cluster 1 contains all the nodes with positive eigenvector values and another cluster 2 contains nodes having negative eigenvector values. Cluster 1 has five nodes with positive value of eigenvector and the nodes are A, B, C, D and F. Cluster 2 has five nodes that have negative eigenvector values and the nodes are E, G, H, I and J.
Only two clusters are formed in first iteration. The larger size clusters can be further divided into two different clusters by applying the algorithm recursively. This process continues until maximum intra-node distance within a cluster is less than 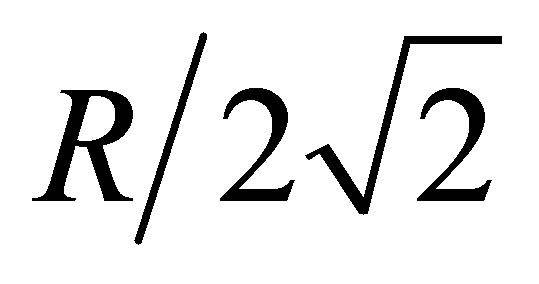 where R is the transmission range of the sensor node. When intranode distance is remaining
where R is the transmission range of the sensor node. When intranode distance is remaining 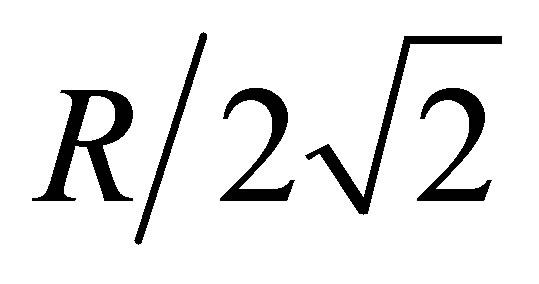 two nodes in neighbouring clusters can communicate in one hop. After applying the algorithm recursively, the given network is divided into four clusters as shown in Figure 3. Table 2 shows the formed cluster after first iteration.
two nodes in neighbouring clusters can communicate in one hop. After applying the algorithm recursively, the given network is divided into four clusters as shown in Figure 3. Table 2 shows the formed cluster after first iteration.
It has been observed that both the clusters have higher intra-node distance than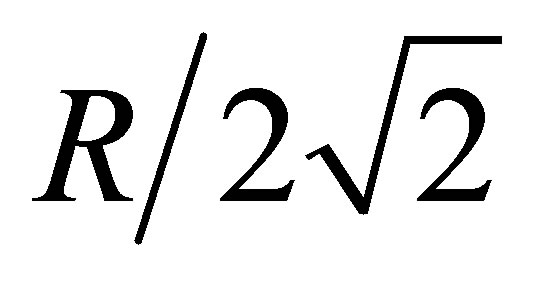 , so apply the algorithm to both the clusters. After applying the algorithm cluster 1 is portioned into two different clusters. This algorithm is also applied to cluster 2 of Figure 3.
, so apply the algorithm to both the clusters. After applying the algorithm cluster 1 is portioned into two different clusters. This algorithm is also applied to cluster 2 of Figure 3.
Thus the whole network is divided into four clusters as shown in Figure 4. Table 3 shows different nodes present in the each cluster
4.2. Cluster Head Election
The clustering algorithm divides the whole network into clusters. The next step is election of cluster head for each cluster. As per the property of SGP, the least eigenvector value of node signifies that the node is well connected to the other nodes within the cluster as well as it is connected to cluster [21].
For initial cluster head election, we chose the least eigenvector value among the nodes within cluster, Table 4 represents the eigenvector values of the cluster and Table 5 shows the elected cluster heads in different clusters on the basis of eigenvector values. Therefore, we compare the eigenvector values of the cluster and choose the
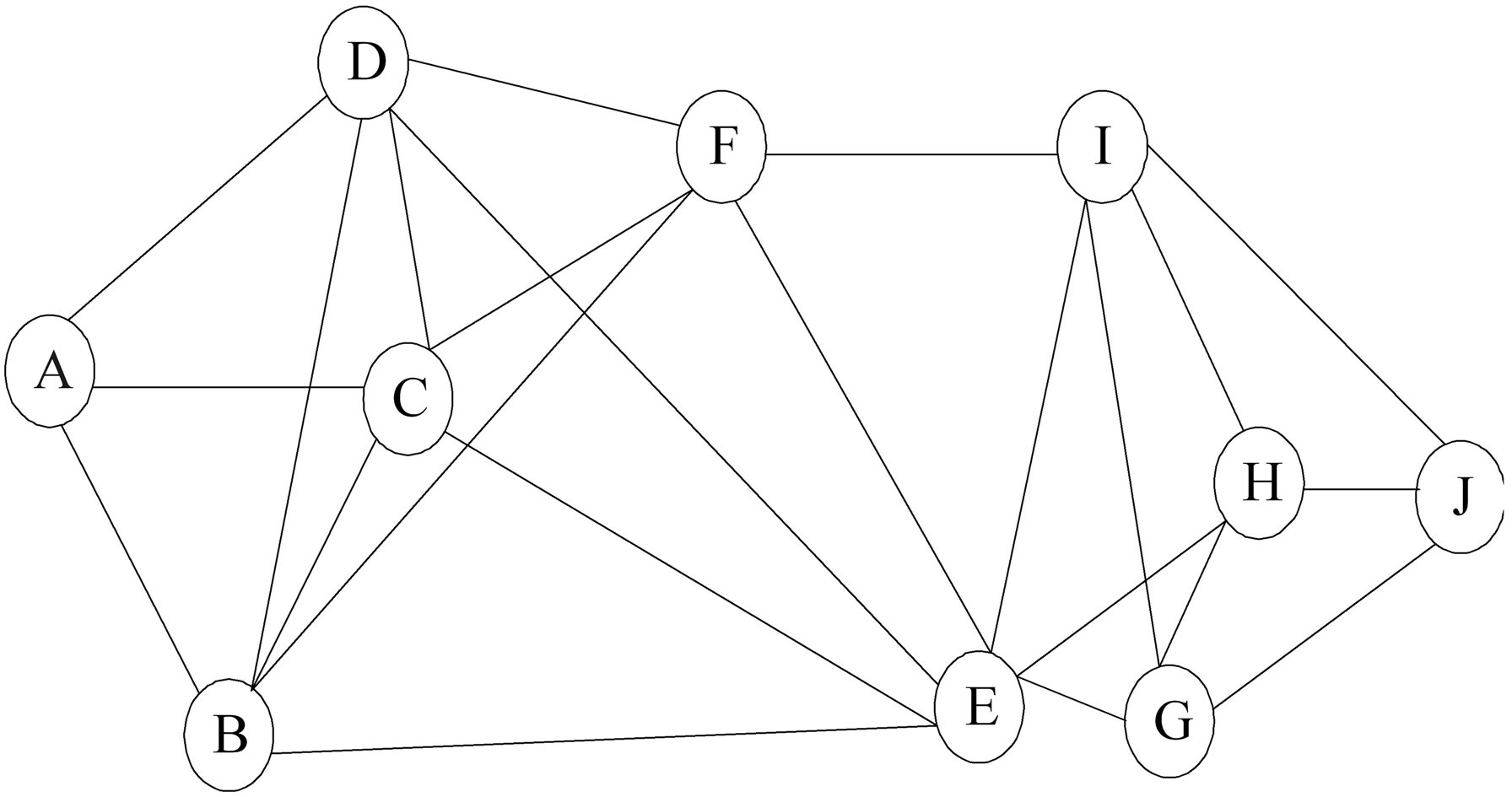
Figure 2. Given graph.
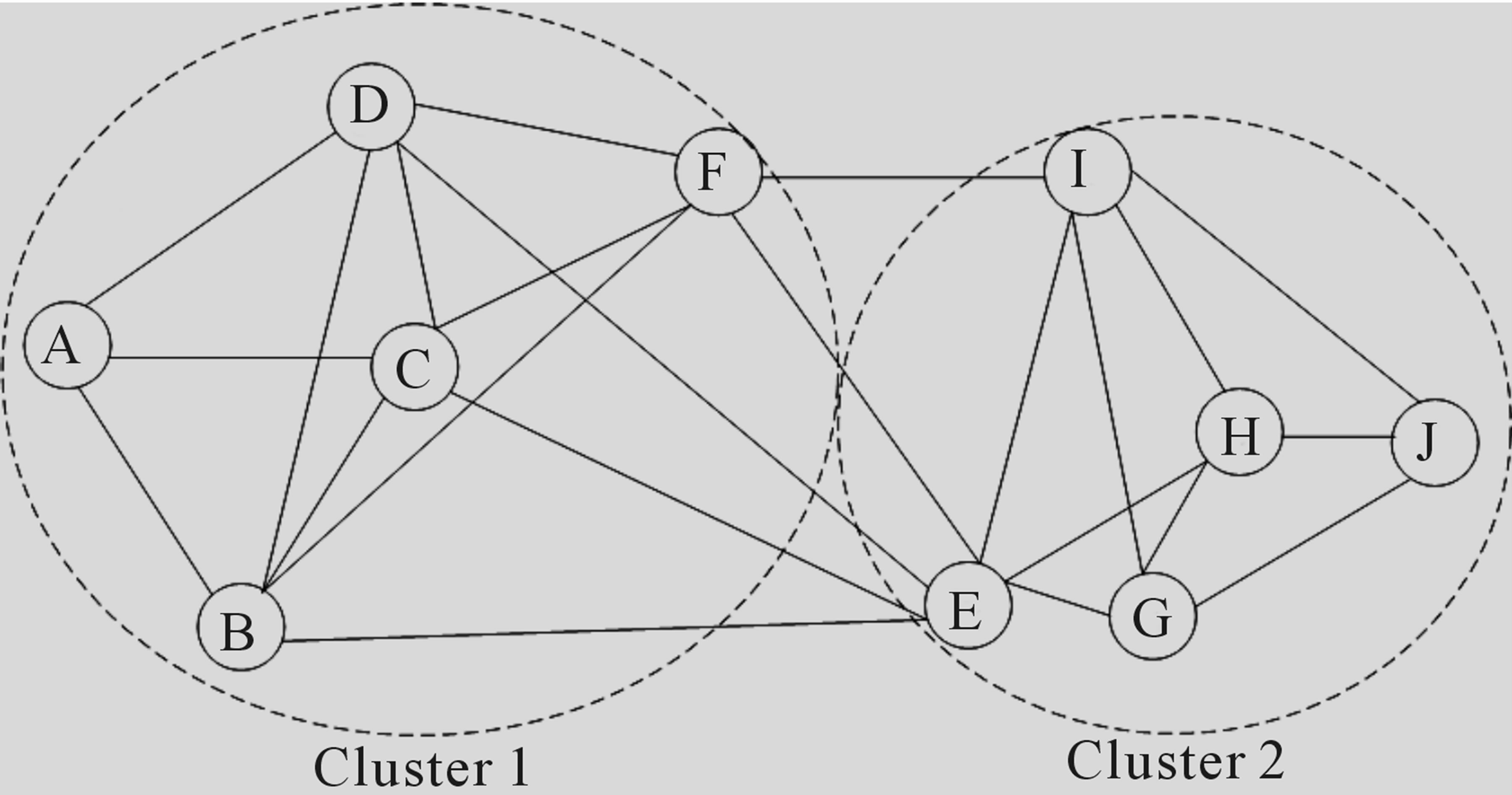
Figure 3. Clustering after first iteration.
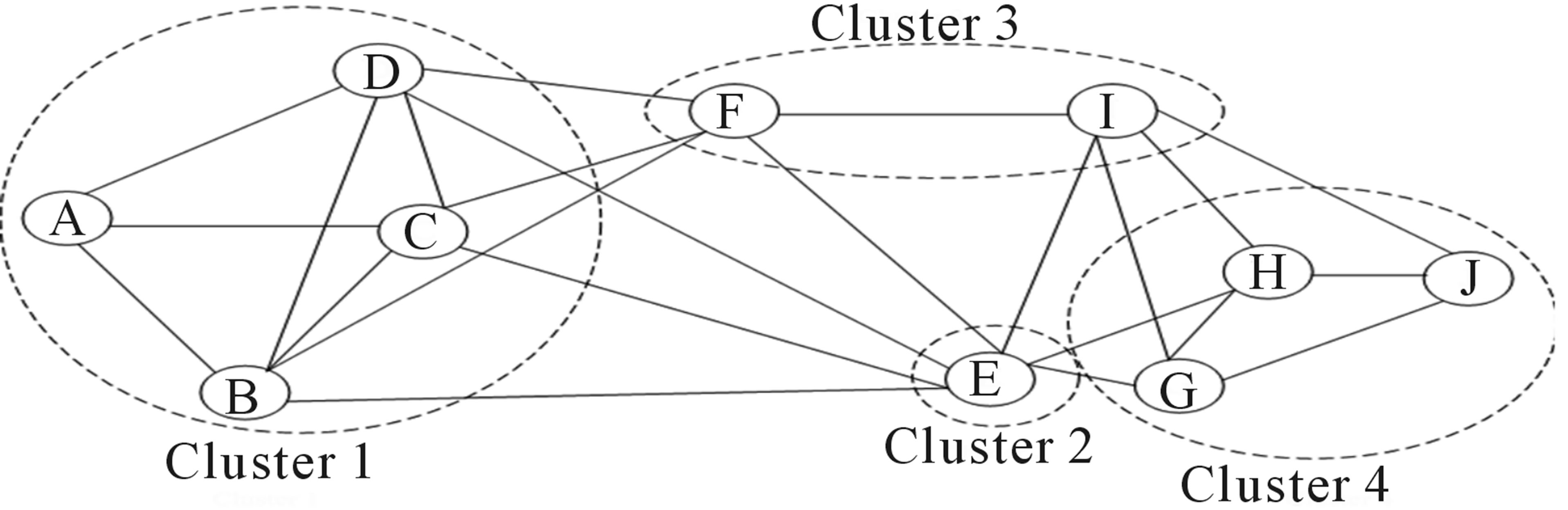
Figure 4. Network after clustering.
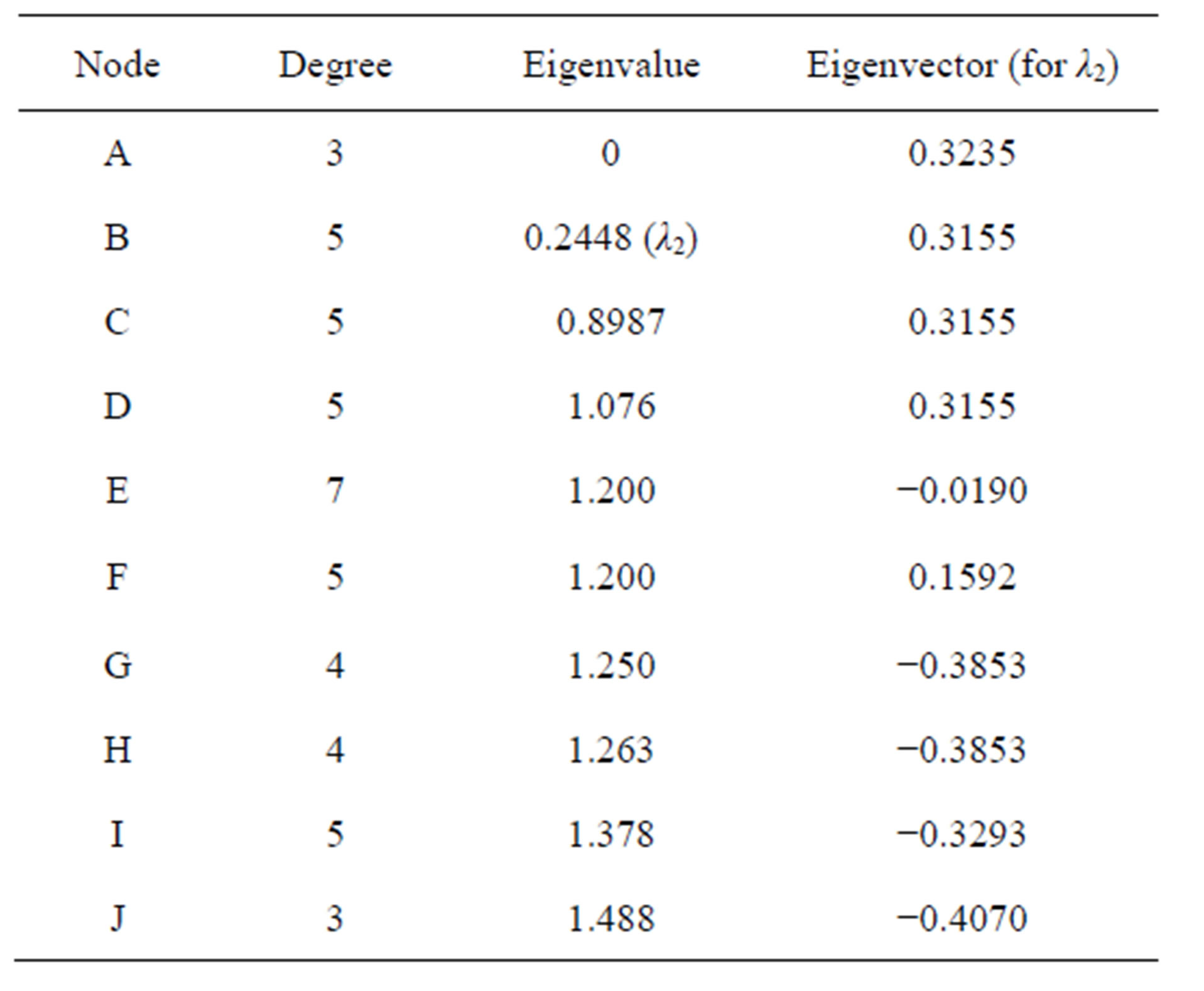
Table 1. Eigenvector table and clustering of given network.

Table 2. Initial clusters of network.

Table 3. Final clusters for the network.
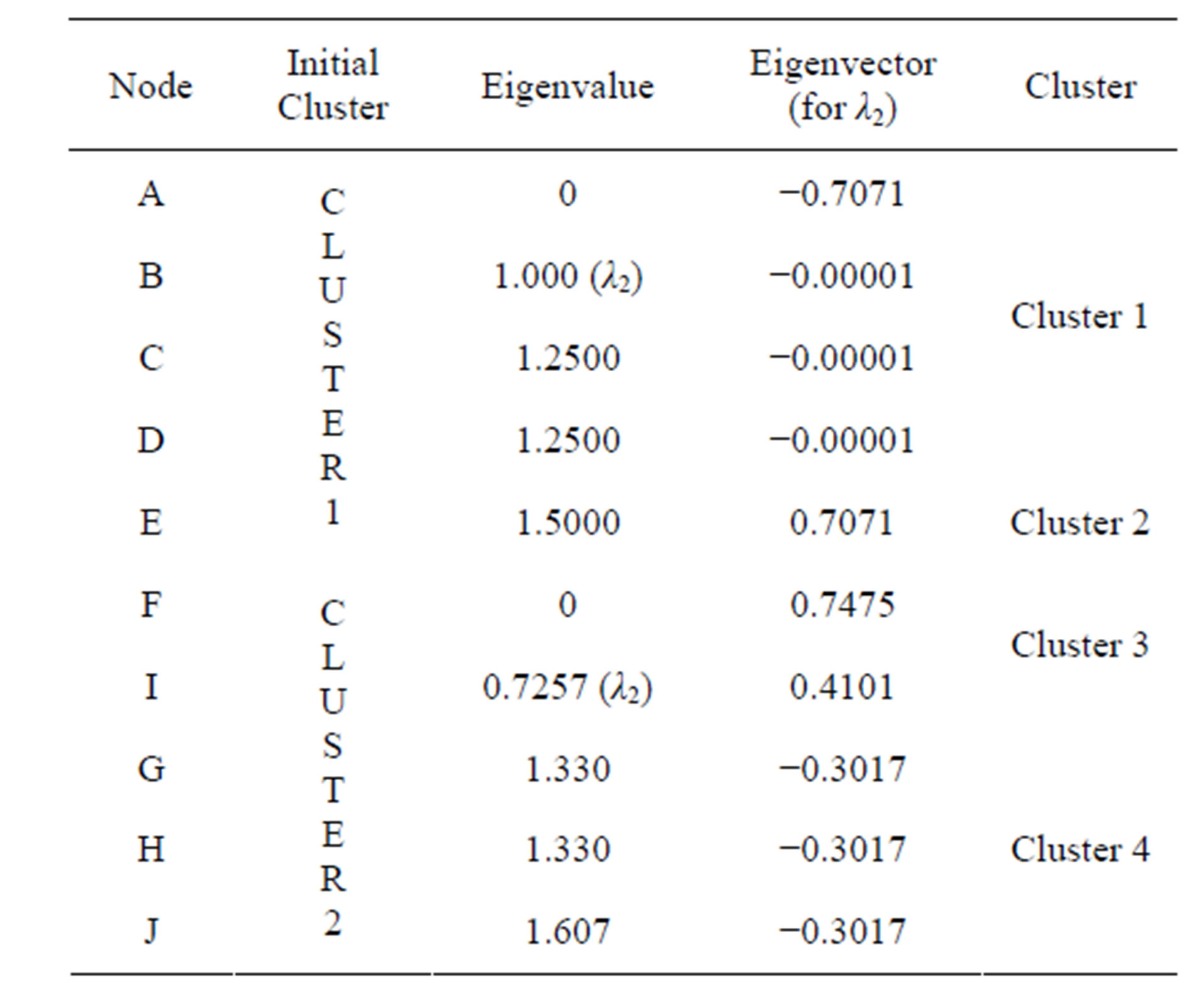
Table 4. Clustering after second iteration.
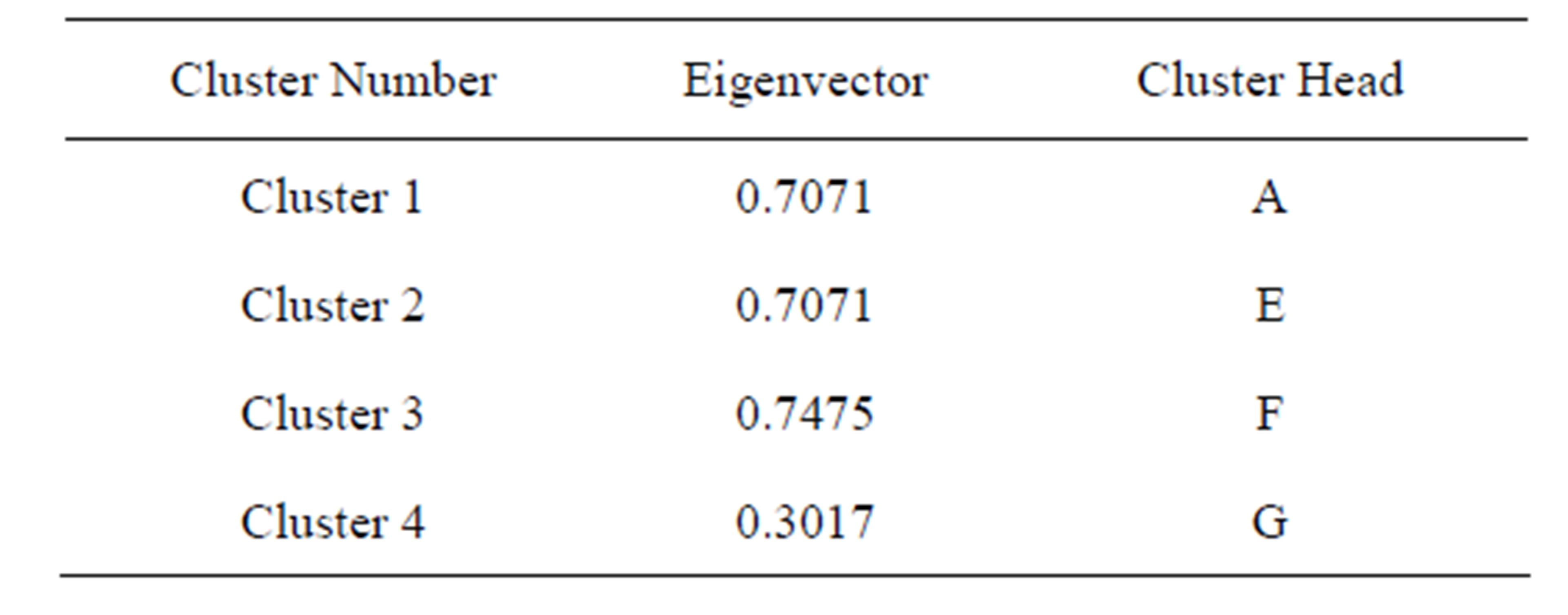
Table 5. Elected cluster heads.
least eigenvector node as a cluster head.

Figure 5 shows the flow chart for cluster head selection and rotation.
Figure 6 shows the elected cluster heads for different clusters.
Cluster head rotation must take place when residual energy (Eres) of the cluster head node falls below the threshold value (Eth). The present cluster head declares the election process by sending a message that contains its Eres to all the cluster members. The cluster members whose residual energy is greater than Eres responds to this message by sending the residual energy to the cluster head.
The new cluster head is elected based upon CH Candidacy Factor (CF) defined as
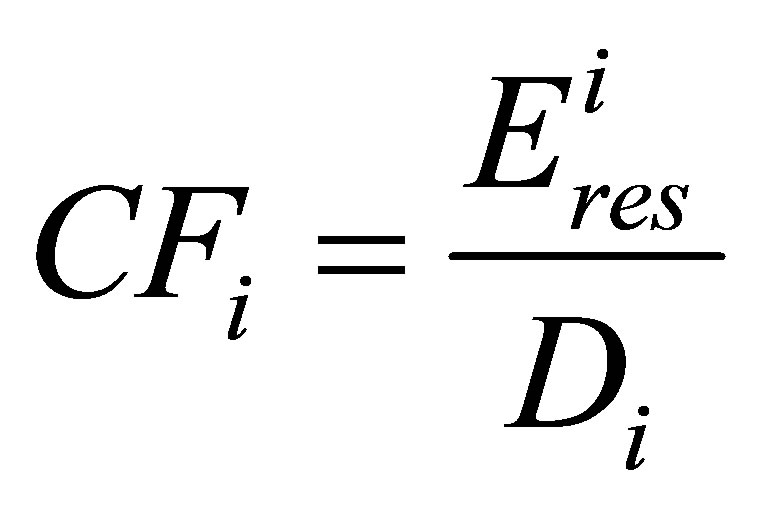
where  is the residual energy of node i, Di is the distance between node i and current cluster head. If
is the residual energy of node i, Di is the distance between node i and current cluster head. If 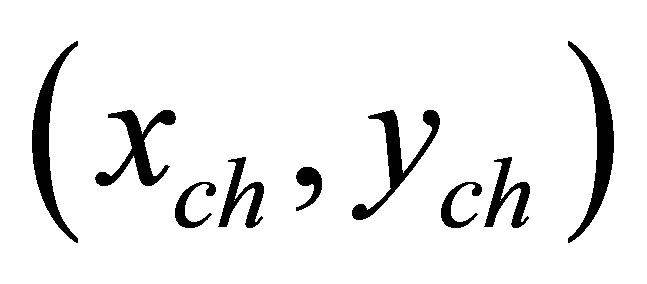 and
and 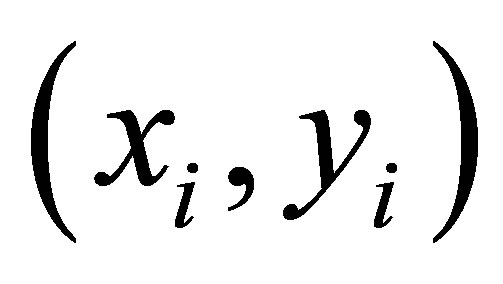 are the location coordinates of current cluster head and node i, respectably, then
are the location coordinates of current cluster head and node i, respectably, then
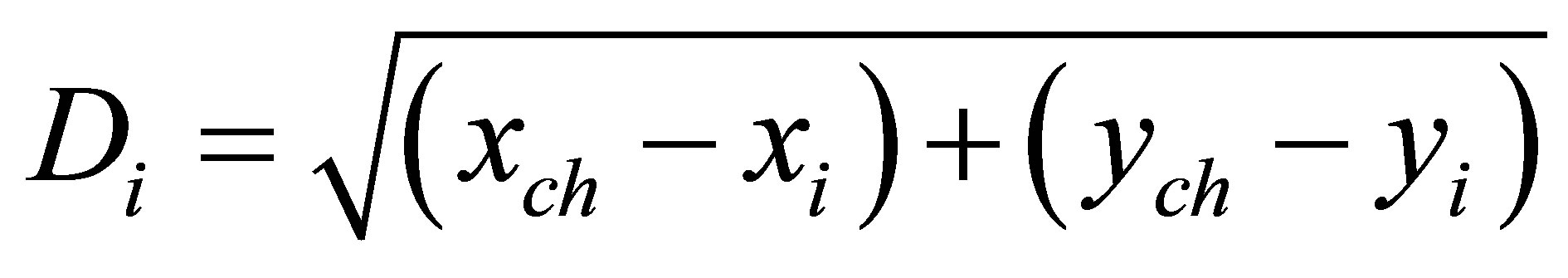
A node with highest value of CF is elected as next cluster head.
5. Performance Evaluation
In this section the performance of SGP has been evaluated through simulation. The simulation has been performed in Matlab2013a. The performance of SGP protocol is compared with HEED [22]. The performance metrics include percentage of nodes acting as cluster heads and ratio of single node cluster and network lifetime.
Ratio of single node cluster indicates that the ratio of number of clusters having single nodes to the total number of clusters. If the ratio of single node clusters in the network is high, it may lead to early energy dissipation.
Figure 7 illustrates the percentage of cluster with more than one node. High single node cluster (the cluster head) may lead to reduce the network lifetime. Single node cluster arise when a node is forced to represent itself. The figure shows that HEED produces a higher percentage of non-single node clusters than the SGP.
Percentage of nodes acting as cluster head describes the fraction of total sensor nodes in percentage, acting as cluster head in the sensing field. In WMSN, smaller percentage of nodes should act as CH, creating a cluster which has enough number of sensor nodes (cluster members). High values indicate that numbers of clusters are present in the network with small size of clusters.
Figure 8 shows the percentage of cluster heads selected by both HEED and SGP (for different number of nodes) are identical.
6. Conclusion
This paper has proposed an approach to deal with the
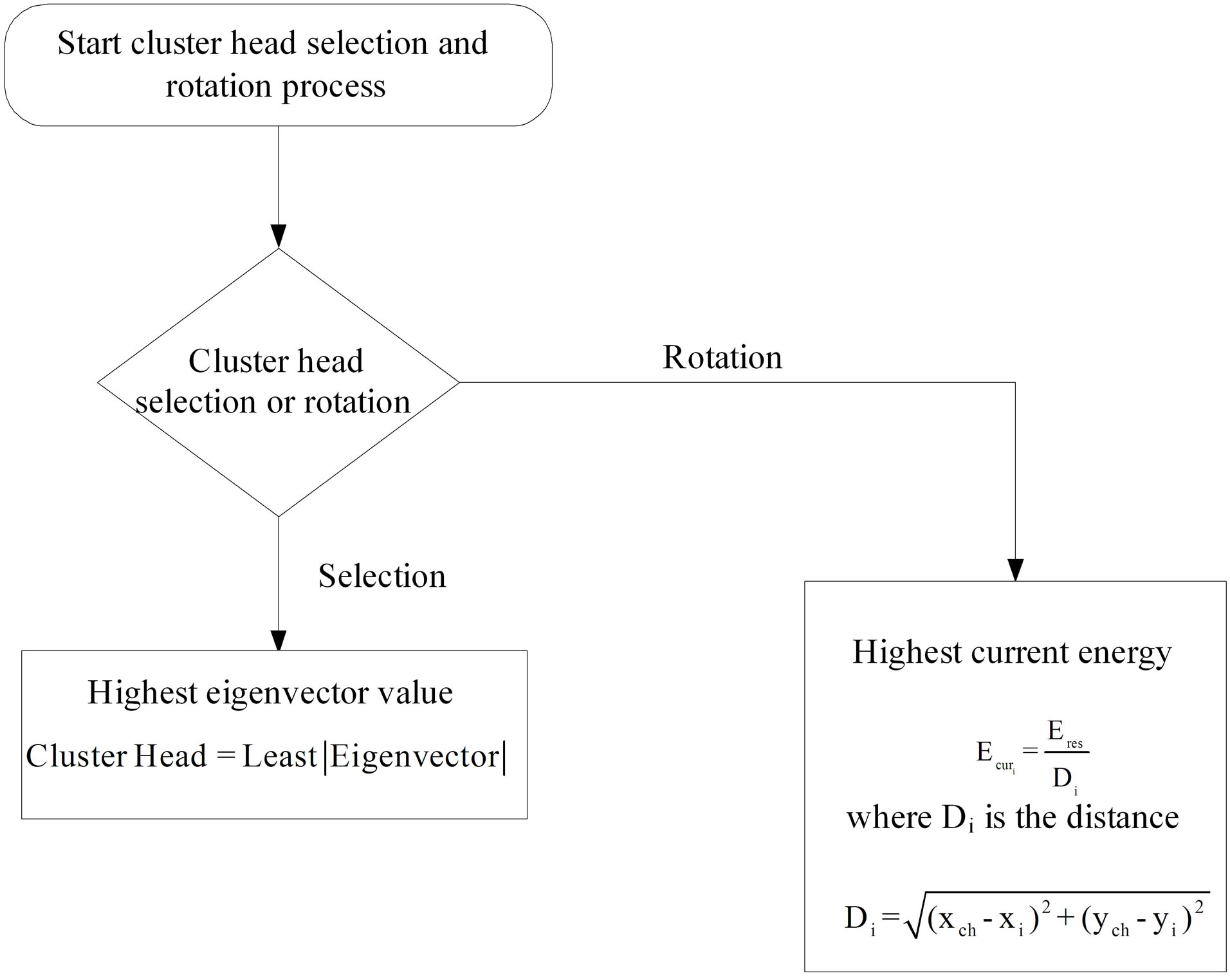
Figure 5. Flow chart for selection and election of cluster head.
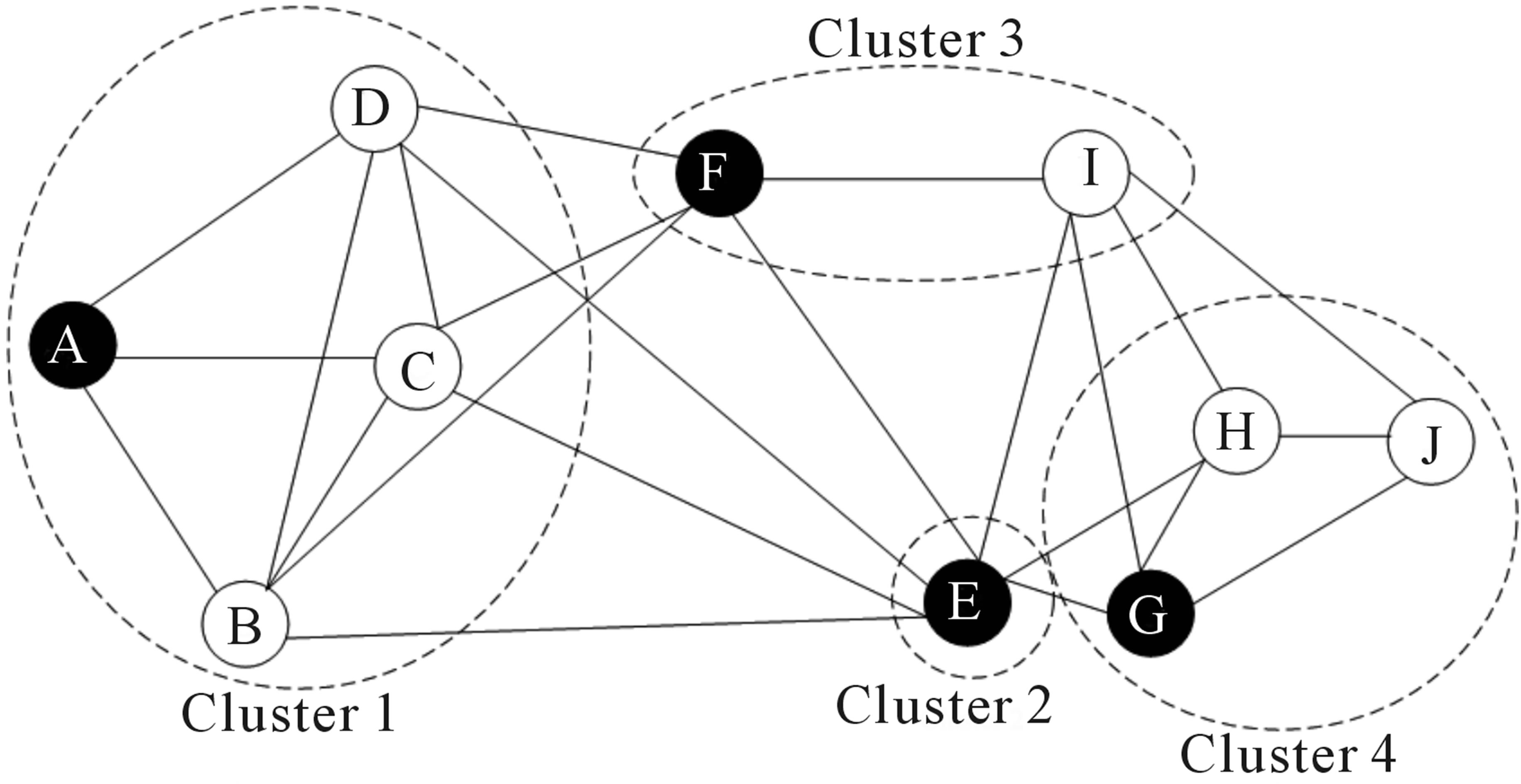
Figure 6. Election cluster heads of given graph.
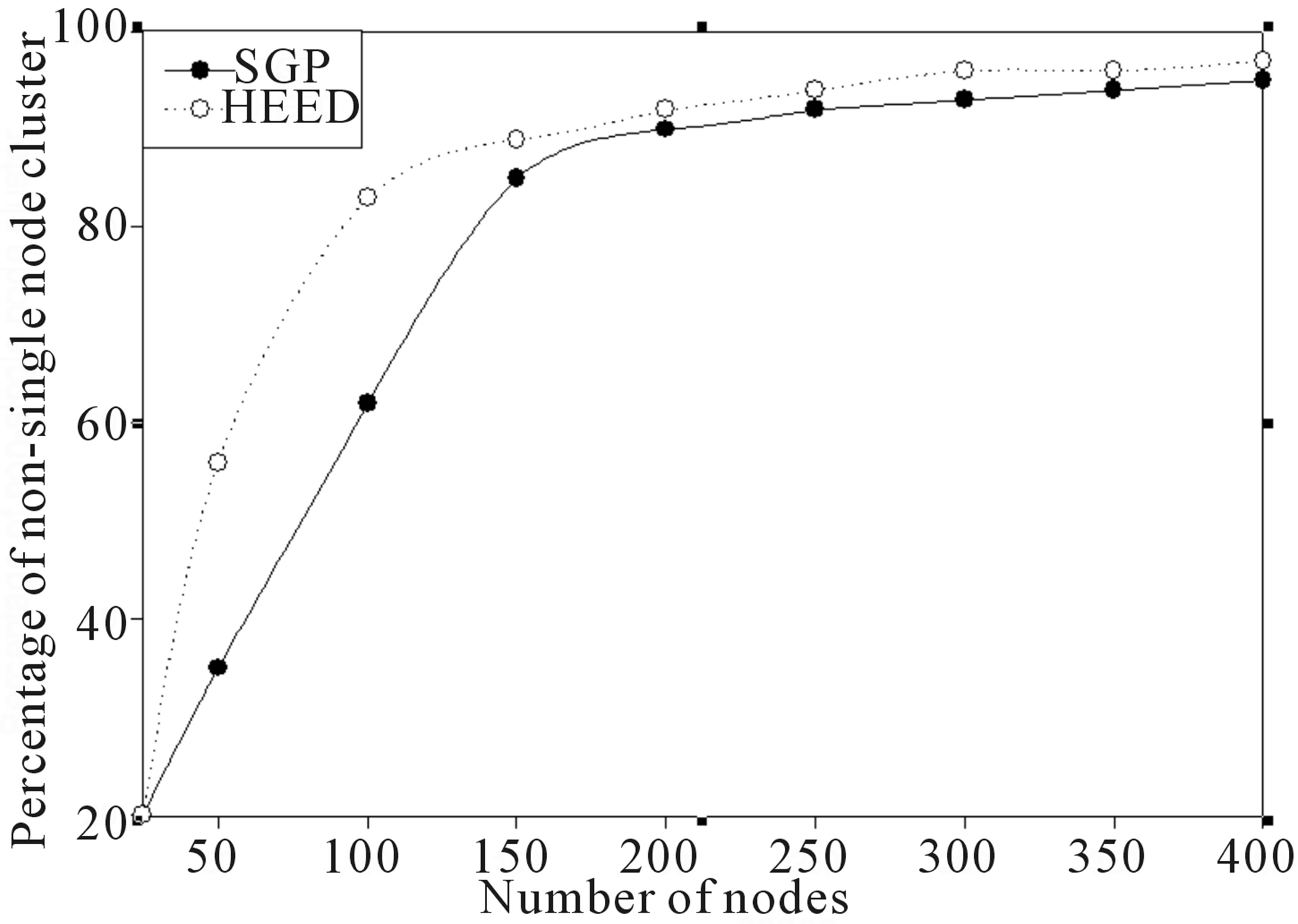
Figure 7. Percentage of non-single node cluster.
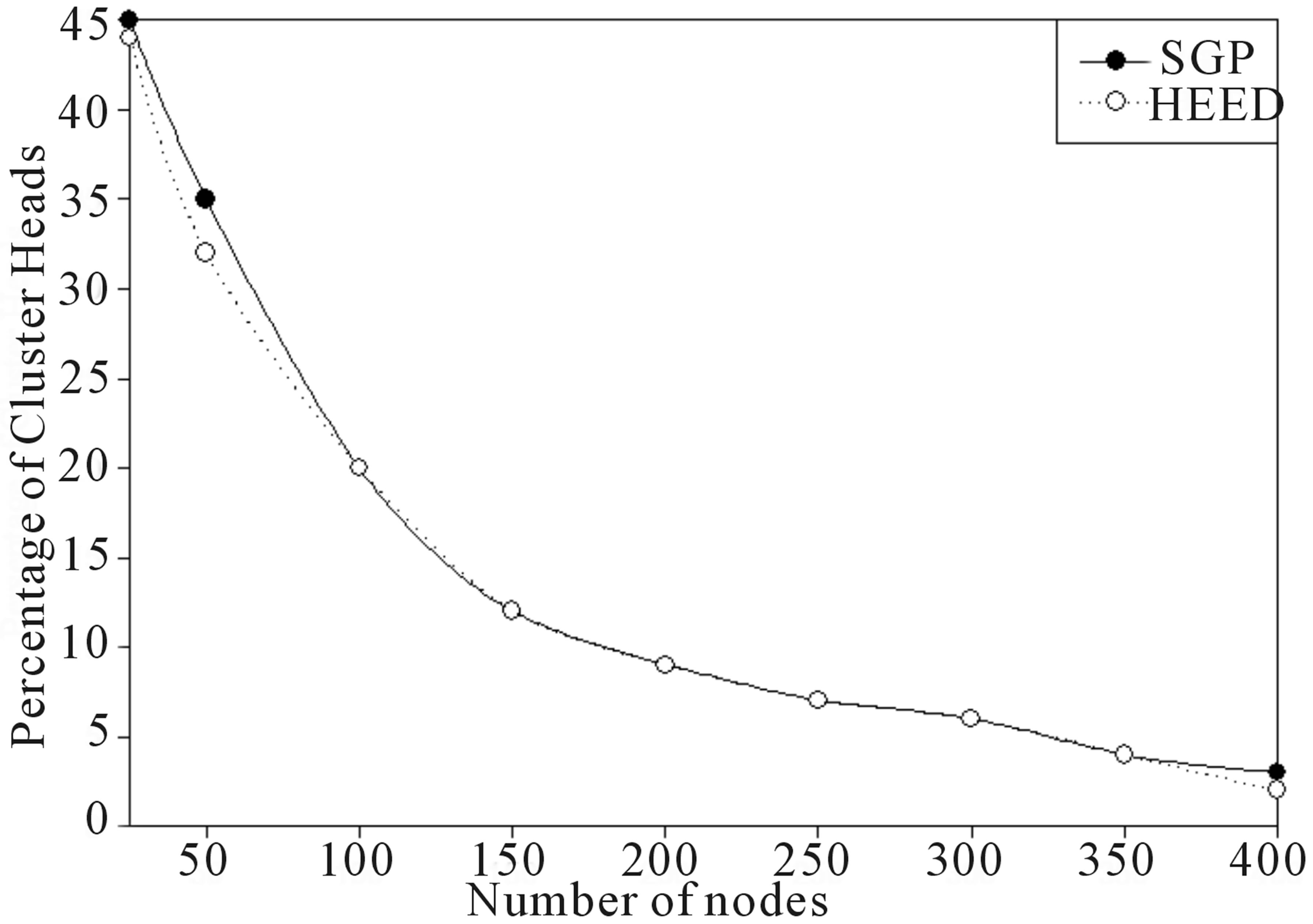
Figure 8. Percentage of selected cluster heads.
clustering problem in a given wireless multimedia sensor network. We have explained the details of the proposed clustering algorithm. It divides the network into two clusters and partitions the network till we get the clustering, where nodes in neighbouring clusters can communicate using single hop. A cluster head elections technique based on eigenvector has also been proposed. Simulation results show that our proposed algorithms perform better than those HEED algorithms.
REFERENCES
- F. Akyldiz, W. Su, Y. Sankarasubramaniam and E. Cayirci, “Wireless Sensor Networks: A Survey,” Computer Networks, Vol. 38, No. 4, 2002, pp. 393-422.
- S. Taruna and M. R. Tiwari, “An Event Driven Energy Efficient Data Reporting System for Wireless Sensor Networks,” Vol. 2, No. 2, 2013, pp. 70-75.
- I. F. Akyildiz, T. Melodia and K. R. Chowdhury, “A Survey on Wireless Multimedia Sensor Networks,” Computer Networks, Vol. 51, No. 4, 2007, pp. 921-960.
- P. Kumar and N. Chand, “Clustering in Wireless Multimedia Sensor Networks Using Spectral Graph Partitioning,” International Journal of Communication, Network and System Sciences, Vol. 6, No. 3, 2013, pp. 128-133.
- M. Demirbas, A. Arora, V. Mittal and V. Kulathumani, “A Fault-Local Self-Stabilizing Clustering Service for Wireless Ad Hoc Networks,” IEEE Transactions on Parallel and Distributed Systems, Vol. 17, No. 9, 2006, pp. 912- 922.
- B. Auffarth, “Spectral Graph Clustering,” Course Report. http://wwwlehre.inf.uos.de/~bauffart/spectral.pdf
- B. Elbhiri, S. El Fkihi, R. Saadane and D. Aboutajdine, “Clustering in Wireless Sensor Network Based on Near Optimal Bi-partitions,” 6th EURO-NF Conference on Next Generation Internet (NGI), 2010, pp. 1 -6.
- M. Qin and R. Zimmermann, “VCA: An Energy Efficient Voting Based Clustering Algorithm for Sensor Networks,” Journal of Universal Computer Science, Vol. 13, No. 1, 2007, pp. 87-109.
- M. Chatterjee, S. K. Das and D. Turgut, “WCA: A Weighted Clustering Algorithm for Mobile Ad hoc Networks,” Journal of Cluster Computing (Special Issue on Mobile Ad hoc Networks), Vol. 5, No. 2, 2002, pp. 193-204.
- S. Banerjee and S. Khuller, “A Clustering Scheme for Hierarchical Control in Multi-Hop Wireless Networks,” IEEE INFOCOM, 2001, pp. 1028-1037.
- S. Bandyopadhyay and E. Coyle, “An Energy Efficient Hierarchical Clustering Algorithmfor Wireless Sensor Networks,” 22nd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM), Vol. 3, 2003, pp. 1713-1723.
- C. Li, M. Ye, G. Chen and J. Wu, “An Energy Efficient Unequal Clustering Mechanism for Wireless Sensor Networks,” 2nd IEEE International Conference on Mobile Ad-hoc and Sensor Systems (MASS), 2005, pp. 125-132.
- Y. He, Y. Zhang, Y. Ji and S. X. Shen, “A New Energy Efficient Approach by Separating Data Collection and Data Report in Wireless Sensor Networks,” International Conference on Communications and Mobile Computing, 2006, pp. 180-192.
- A. Bertrand and M. Moonen, “Distributed Computation of the Fiedler Vector with Application to Topology Inference in Ad Hoc Networks,” Internal Report KU Leuven ESAT-SCD, 2012.
- Laplacian Matrix Wikipedia. http://en.wikipedia.org/wiki/Laplacian_matrix
- Adjacency Matrix Wikipedia. http://en.wikipedia.org/wiki/Adjacency_matrix
- Degree Matrix Wikipedia. http://en.wikipedia.org/wiki/Degree_matrix
- A. Savvides, C. Han and M. B. Srivastva, “Dynamic FineGrained Localization in Ad Hoc Networks of Sensors,” 7th International Conference on Mobile Computing and Networking (MOBICOM), 2001, pp. 166-179.
- D. Lu, N. Nan and X.-X. Huang, “Clustering Based Spectrum Allocation Scheme in Mobile Ad Hoc Networks,” Bulletin of Advanced Technology Research (BATR), Vol. 5, No. 12, 2011, pp. 37-41.
- N. Bulusu, J. Heidemann and D. Estrin, “GPS-Less Low Cost Outdoor Localization for Very Small Devices,” IEEE Personal Communication Magazine, Vol. 7, No. 5, 2000, pp. 28-34.
- A. Savvides, C. Han and M. B. Srivastva, “Dynamic FineGrained Localization in Ad Hoc Networks of Sensors,” 7th International Conference on Mobile Computing and Networking (MOBICOM), 2001, pp. 166-179.
- O. Younis and S. Fahmy, “Distributed Clustering in AdHoc Sensor Networks: A Hybrid, Energy Efficient Approach,” IEEE Transactions on Mobile Computing, Vol. 3, No. 4, 2004, pp. 366-379.

