Journal of Sensor Technology
Vol.2 No.3(2012), Article ID:22870,11 pages DOI:10.4236/jst.2012.23017
Design and Development of an Electronic Sensor to Detect and Measure Curvature of Spaces Using Curvature Energy
1Department of Research in Mathematics and Engineering, Technological Institute of High Studies of Chalco, Chalco, Mexico
2Headquarters of Electronic Engineering, Technological Institute of High Studies of Chalco, Chalco, México
Email: francisco.bulnes@tesch.edu.mx, isaias@kolob.com.mx, ton-0210@hotmail.com, tescha_calidad@hotmail.com
Received June 8, 2012; revised July 8, 2012; accepted August 13, 2012
Keywords: Sensor of Curvature; Curvature Detection; Curvature Accelerometer; Electronic Curvature Perception; Sensor-Perception Curve; Curvature Energy
ABSTRACT
Using fine electromagnetic signals to measure observables of other fields like curvature and torsion of a space, and the corresponding value of their integrals of the action of perception of curvature through electronic signals that detect curvature on a curved surface, it is designed and constructed a sensor of curvature of accelerometer type that detects and curvature measures in 2 and 3-dimensional spaces using the programming of shape operators on spheres and the value of their integrals along the curves and geodesics in their principal directions.
1. Introduction
The construction of an electronic sensor with base in accelerometers as transducer is an instrument that makes possible to measure curvatures of solid bodies in the space [1,2]. This promotes the development of systems applied to provide automatons with intelligence to execute accurate movements, between other technological and scientific applications that will be mentioned soon after. The design and construction of this sensor needs the recognition on the part of the accelerometer of the property of roundness of a surface or body, their perception of this roundness from the point of view of the signals of the sensor that the accelerometer will involve in their advance, and their aptitude to cause information in real-time, according to this perception as curvature of the surface or body (reading of the sensor). In our design analysis, we will consider like model of curvature, the obtained one by the Gaussian curvature, which involves from the mathematical point of view curvatures along geodesic, curves on surfaces and space, sections of curved surfaces and bodies in the space, considering the design of an operator of shape based at the beginning in the geometry of the sphere S2.
Due to this there are no electronic instruments for detection and direct measurement of curvature, we can suggest the design of an indirect detector based on the concept of roundness sensor to detect curvature in regions near a curved surface or curved body. As the mobile moves on the solid surface, the device sensor of the accelerometer will perceive an angle between nearby points (with a step qn (= mm)), doing that, the curvature could be measured in angles. This establishes certain advantages as for the handling of the interface of programming of the information that throws the sensor and the demodulation of the proper electronic signals of the sensor to recognise angles according to frequencies corresponding to micro-voltages given in Mv [3-5].
In fact the frequencies range is designed to record in information electronically codified the range of curvature established by the principal curvatures on a surface. In case of 2-surfaces, there are two principal directions on which there measures itself the maximum and minimal value of curvature of the surface determining their shape [6]. These maximum and minimal values for the curvature k, determine the interval k1 £ k £ k2 [6], on which we design the programming of our sensor.
The previous interval re-interpreted from the point of view of the energy of the sensor to detect these values considers the domineering energy condition (using the eigen-values k1, and k2, of the corresponding shape operator [6-8]):
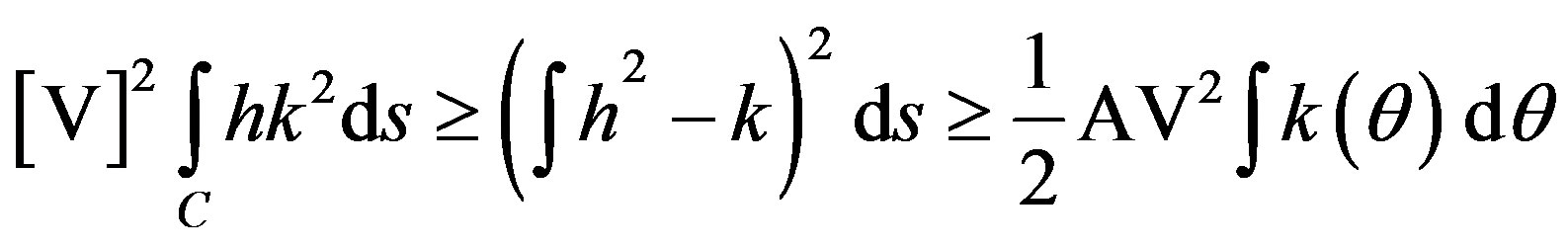 , (1)
, (1)
where V, is the applied voltage in the sensor to detect curvature, A, is the area of the plate inside the accelerometer that detect curvature through their deviation, h, their mean curvature and the last integral correspond to the curvature energy employed by the accelerometer in their detection of curvature along the principal direction.
Also we can use certain studies of the models of Gaussian and normal curvatures to determine through Hilbert inequality and based on certain bound of roundness obtained through the implementation of the spherical operator [9], and using one particular case given by measurement for light waves contemplate in the Bulnes theorem published in ASME 2009 [10,11], the possible integral expression of the total Hamiltonian of electromagnetic energy, establishing a condition of domineering energy [11], when there is curvature in the 3-dimensional space (that means, if the energy is given by this roundness censor, there is curvature measured like energy that makes the censoring appear and measured directly using positioned of the sensor device). This makes possible to us to obtain a curve of perception of curvature that measures the condition of domineering energy in the sensor to establish its position in the surface [12], and this way to measure in every point of the surface their curvature.
The latter condition is somehow in a certain sense, in the mathematical context to the property of obstruction to the integrability of the field equations studied in theoretical physics but in a practical form (similar of engineering) who can serve to us to design a detector and curvature meter in the space, using theoretical hypotheses [9,11].
To realise curvature detection it is necessary to be sure, that the above mentioned property or observable comes from an intrinsic property of the shape of body in geometry, as a matter of fact, this is more important geometrical invariant and let us know all of a space or body.
2. Experimental Section
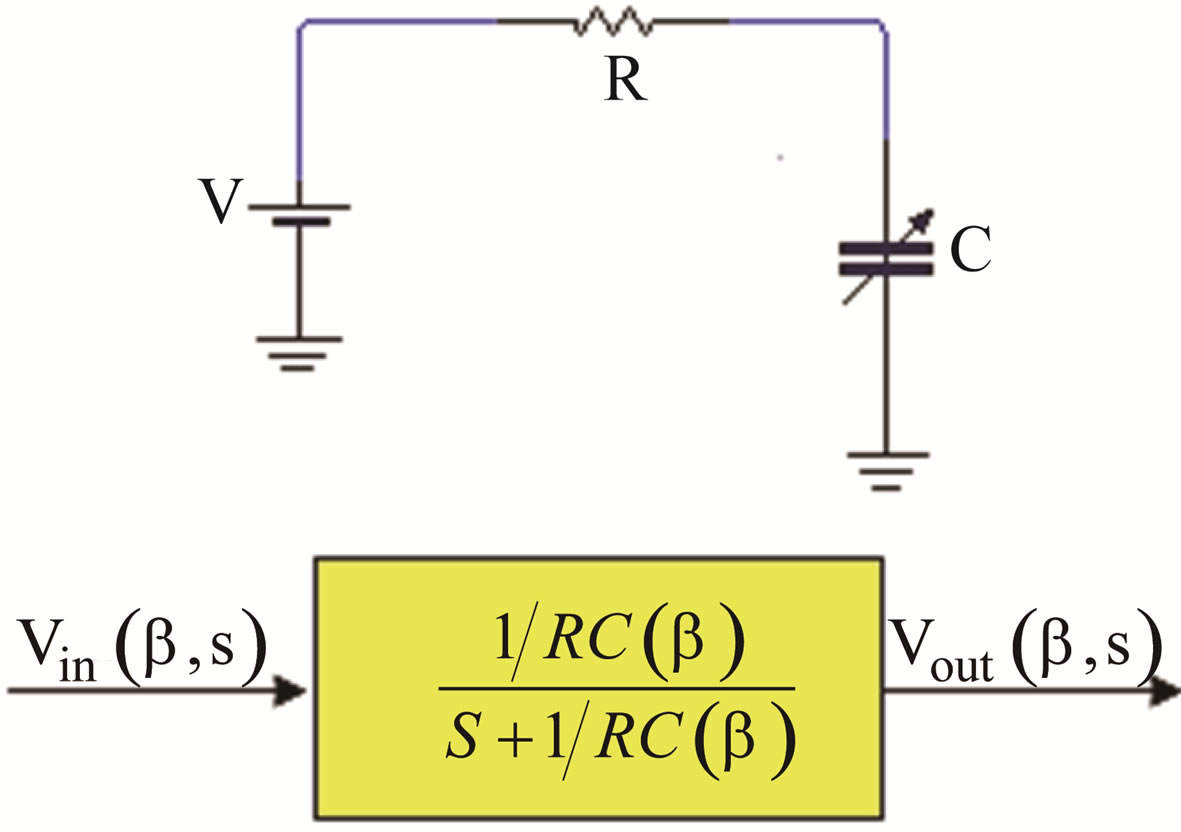
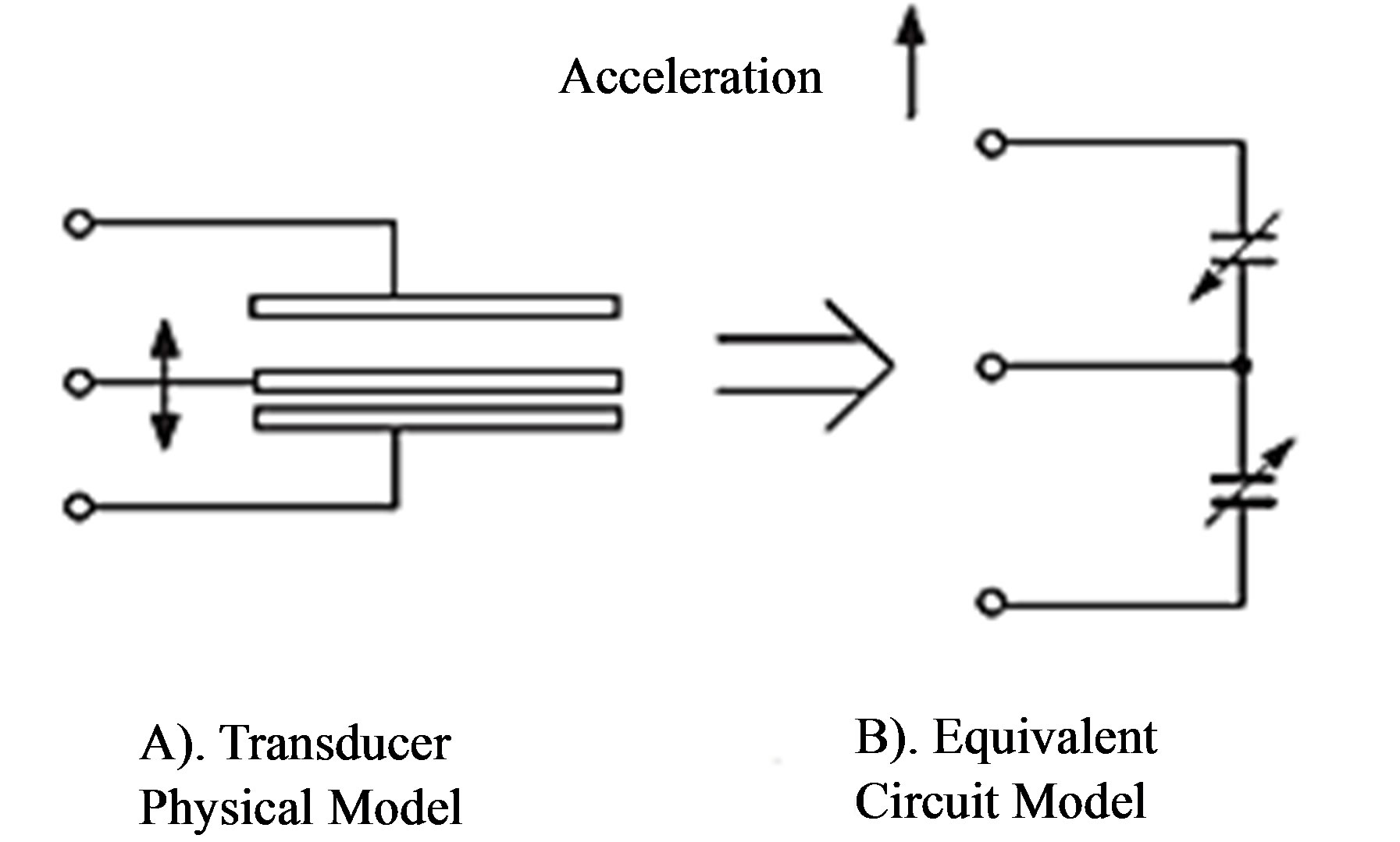
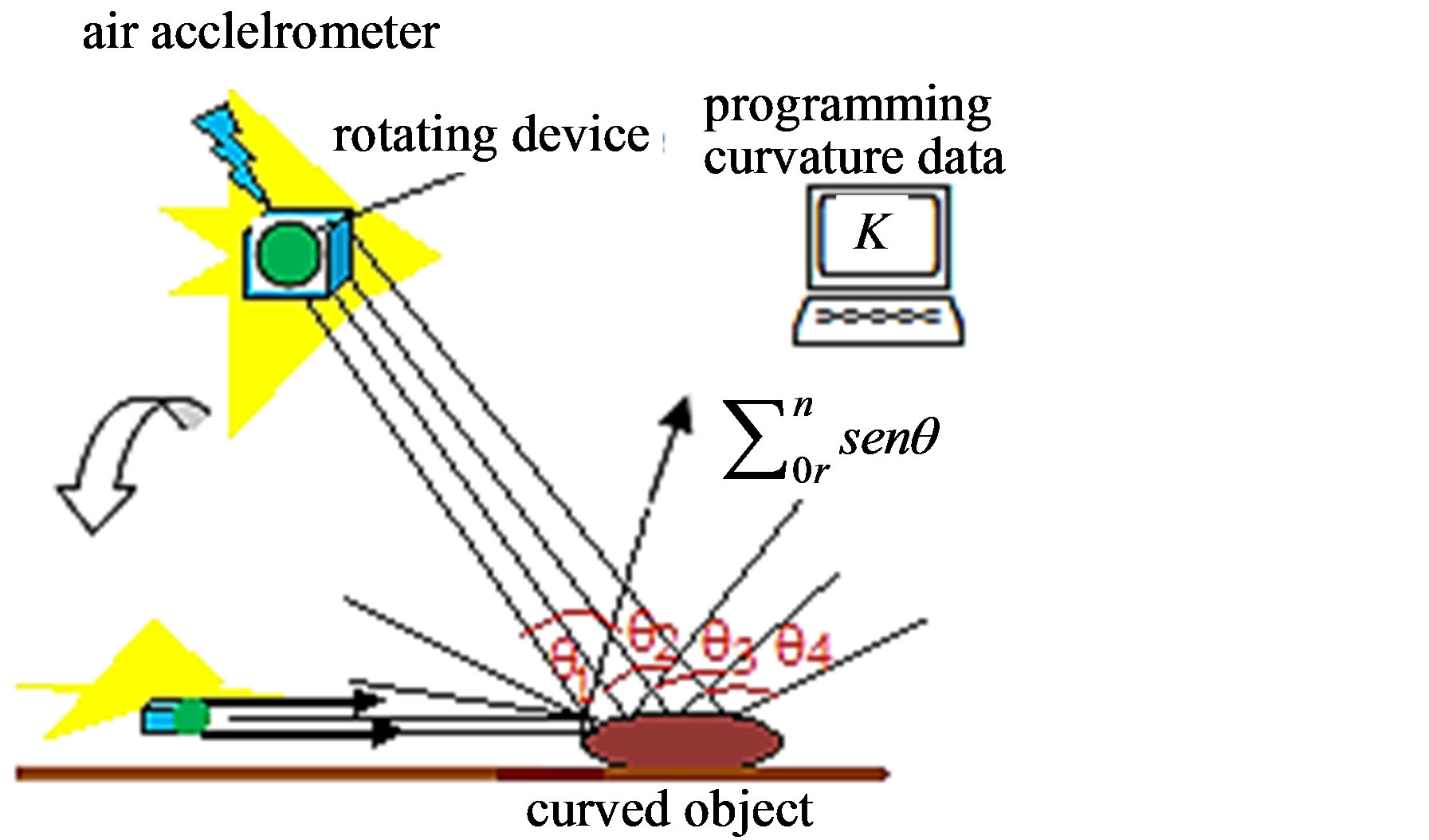
The experimental problem will consist in designing and developing a sensitive device to recognise curvature in round surfaces measuring the magnitude of roundness of these and their data encoding from voltage to curvature. Thus our device must be of type of accelerometer to recover in deviation information, the dynamic movements that cause the variations of round surfaces. We also wish that the signal of voltage keeps in the signaling process, doing that our system is of type LTI (Linear Time Invariant). In Figure 1, we establish the corresponding circuit of our accelerometer.
The electrical resistance is considered to be a constant, without nevertheless the capacitance is variable and it is according to the angular position β, (inside the device) and of the time t. With base in the Kirchoff law for voltage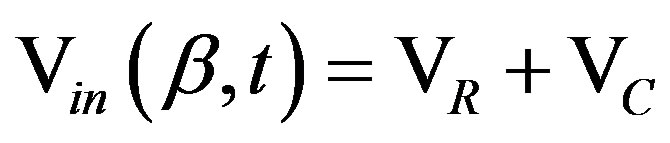 , the integral equation is [13]:
, the integral equation is [13]:
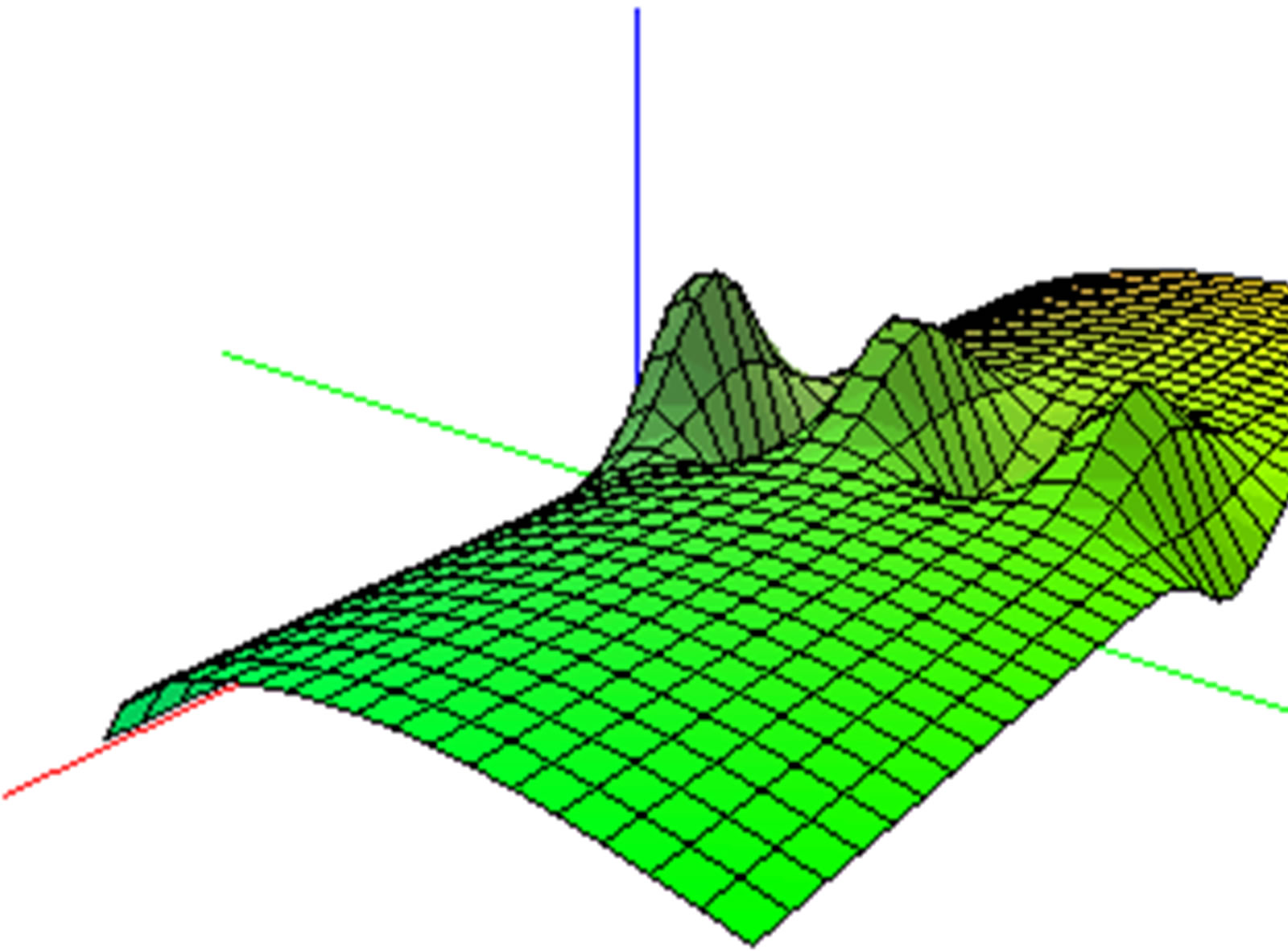

Figure 1. In general, the accelerometers contain an onboard 2-pole switched capacitor filter [5]. A Bessel implementation is used because it provides a maximally flat delay response (linear phase) thus preserving pulse shape integrity [5,8]. Because the filter is realised using switched capacitor techniques, there is no requirement for external passive components (resistors and capacitors) to set the cut-off frequency [5]. The surface z(x, y) = 1 + exp(–2y2)(2J1- r, p(x, y)) + Y1 – r, 1 – r(x, 2x), shows a 2-dimensional model of the filter that we use. This surface represents the domineering energy.
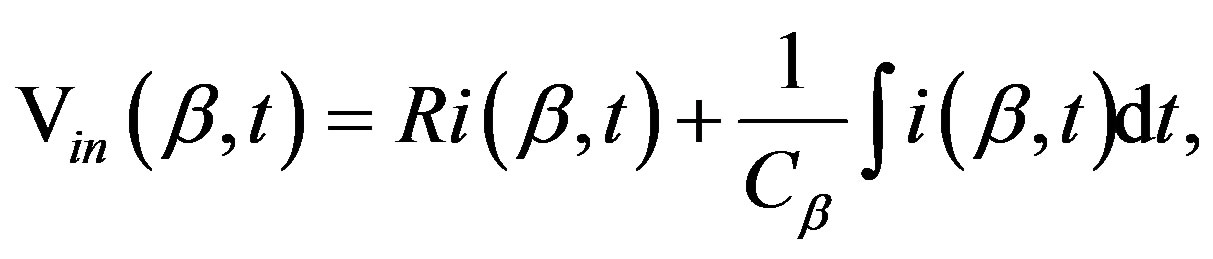
One considers β, constantly in a time t0. For effect of obtaining an output and an input variable, the transference function is obtained [13]. Thus applying the Laplace transform we have
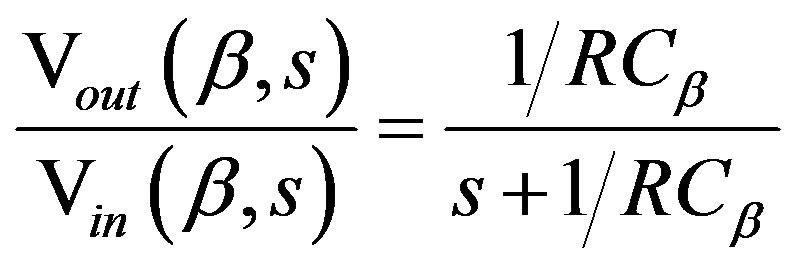 In the domain of the time through the inverse Laplace transform it is had that:
In the domain of the time through the inverse Laplace transform it is had that:
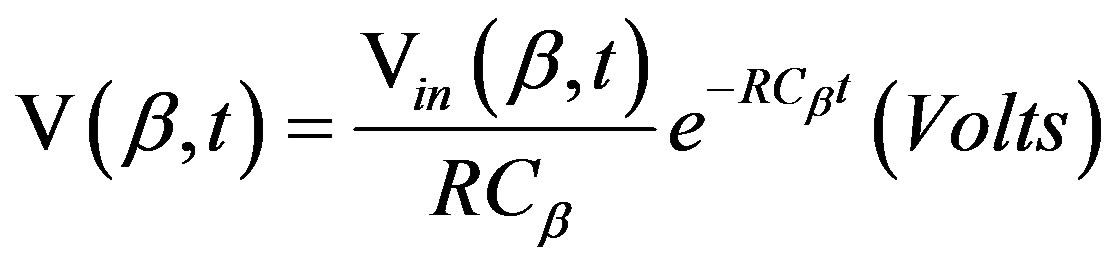 .
.
In Figure 2(e), it shows the time of sudden discharge of a capacitor, this must be like that since the variations must be instantaneous to be able to have electrical
(a)
(b)

(c) (d)
 (e)
(e)
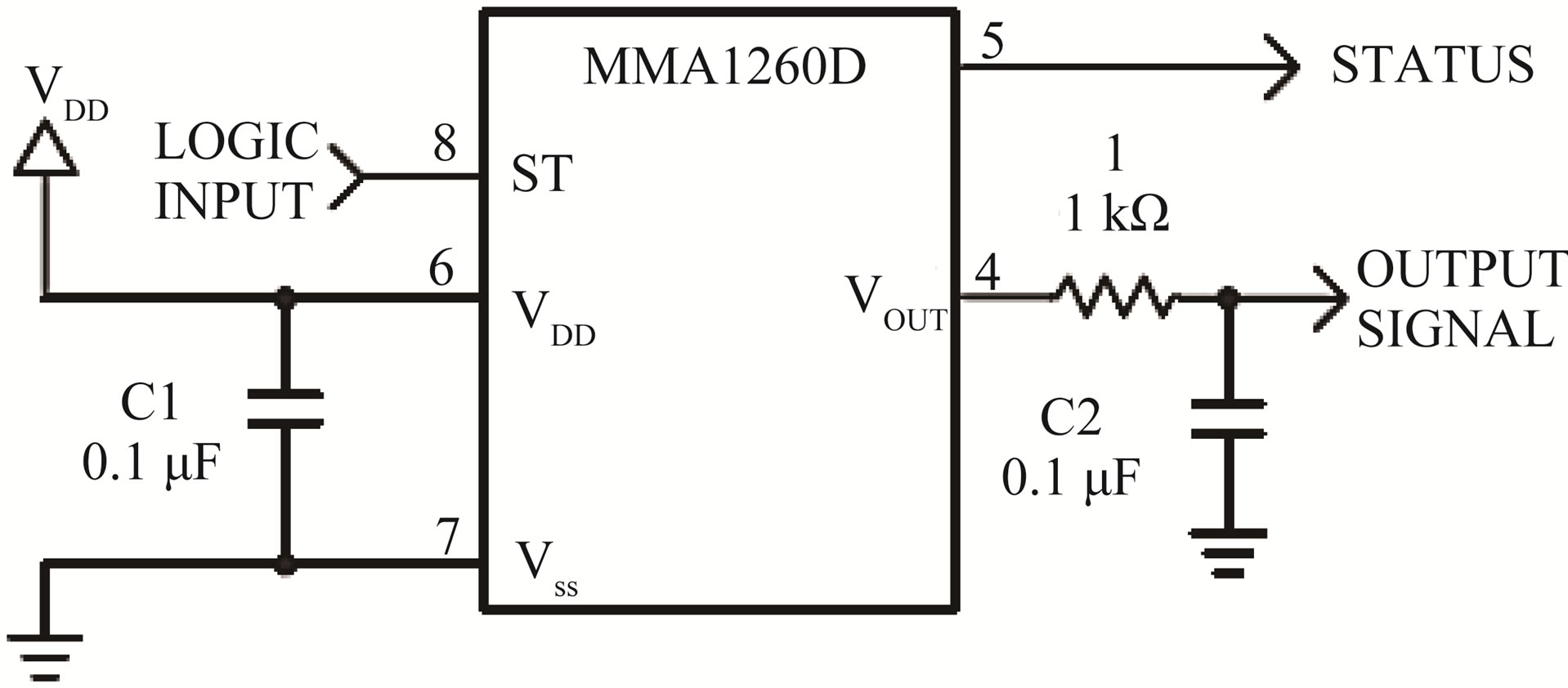
Figure 2. (a) Impress circuit to accelerometer; (b) SOIC accelerometer with recommended connection diagram; (c) Template designed to put the different components of the transduction [1,13]; (d) Our analog system is a RC-circuit and their transference function; (e) In the mathematical modeling of the analog system it is despised R, for effect of bringing the real accelerometer behavior near. This measurement was realised to little counts of micro-volts [1,5].
signals that are processed to an analog or digital electronic system.
Since we want to measure curvature through the energy transduction in mV, using the condition of domineering energy that exists in curvature given by Equation (1), we can consider the following equivalence table between the deviation measured on the curved surface and the output of domineering energy in mV (see Table 1).
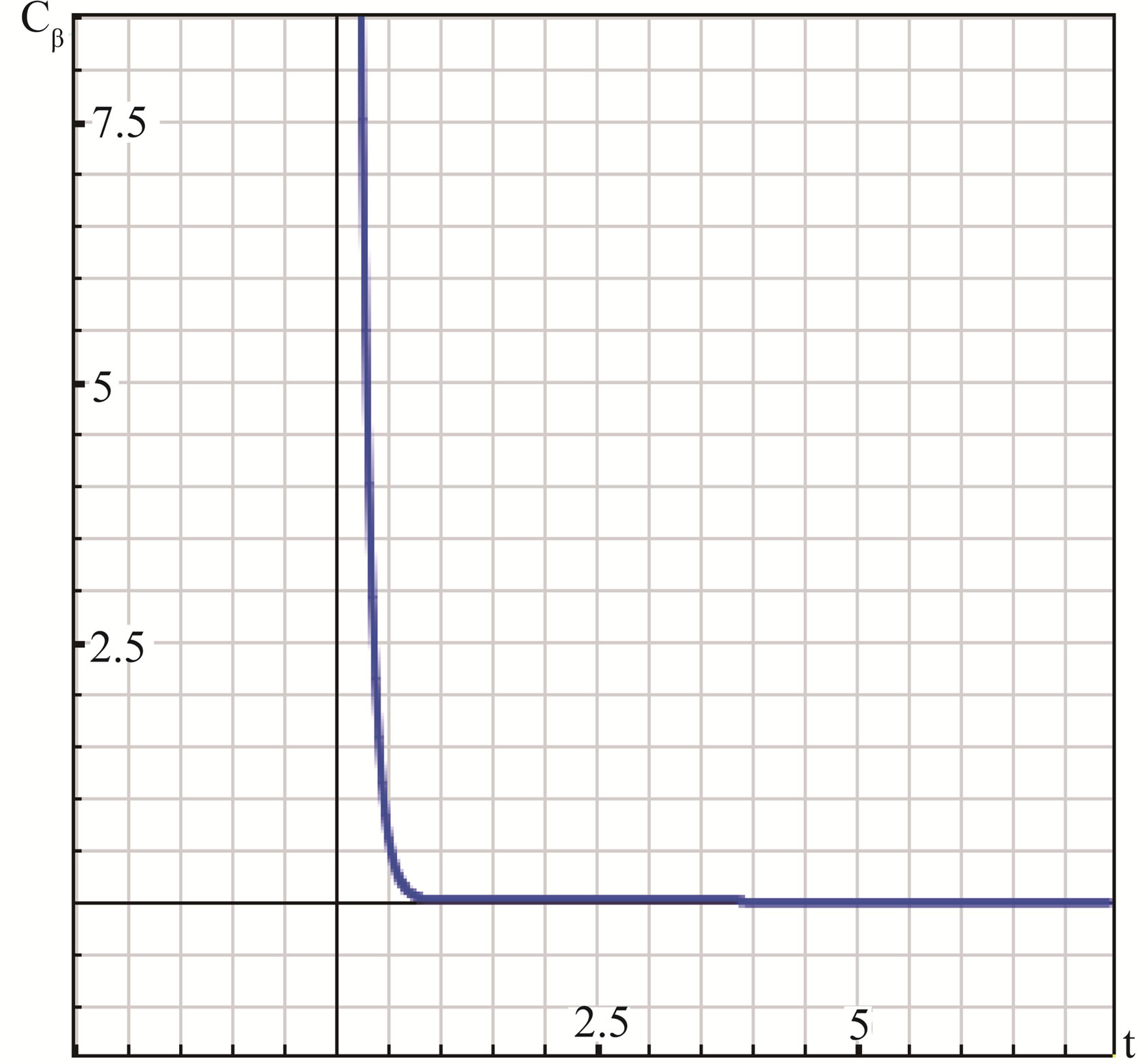
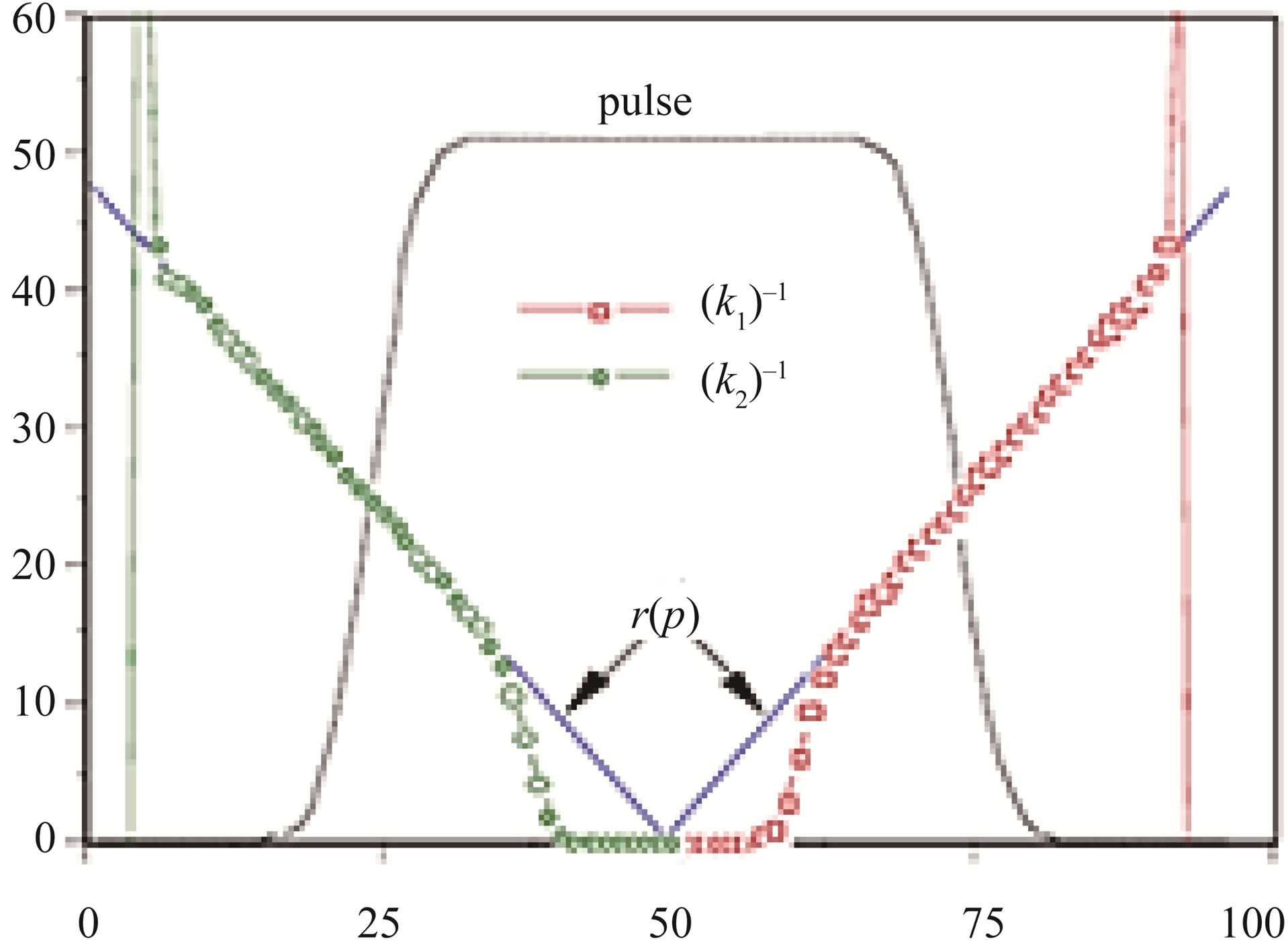
Considering experiments in laboratory a continuous sign of voltage is had according to the time. This variation of continuous voltage allows to relate in real-time the position of the mobile system (see Figure 3).
This analogical signal is digitalised for effect of treating by means of digital system position information in any application. Considering the sectional curvature on one geodesic of the curved surface, we have than in a point P, this is defined as:
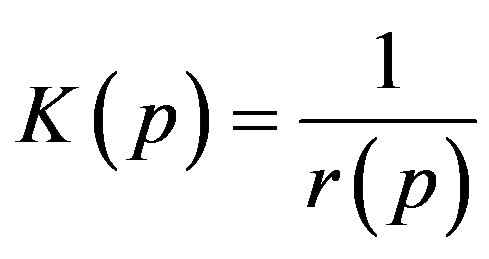 , (4)
, (4)
where K, is the curvature and r, the radius of the osculating circumference in the point p. Let’s consider an arbitrary direction where we realize a curvature measurement. The sensor advances on the geodesic correspondent in this direction. The circular section or corresponding osculating circumference is a section of the sphere S2, that we will program for the securing of other curvatures when it changes r. But thinking that the Gaussian curvature is the product of its principal curvatures we have that:
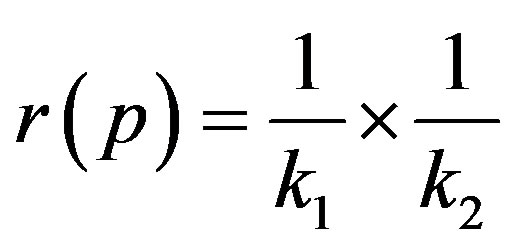 . (5)
. (5)
Considering the output voltage with pulse
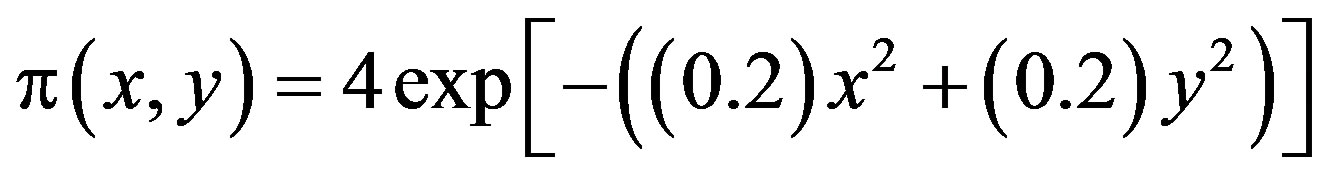 we observe, that there is an osculatriz circular section in the point p, such that the product of principal curvatures k1k2, corresponds within a radius of the sphere that is detected, depending on the roundness perceived by the sensor, which we confirm in the graph for a point p, with
we observe, that there is an osculatriz circular section in the point p, such that the product of principal curvatures k1k2, corresponds within a radius of the sphere that is detected, depending on the roundness perceived by the sensor, which we confirm in the graph for a point p, with
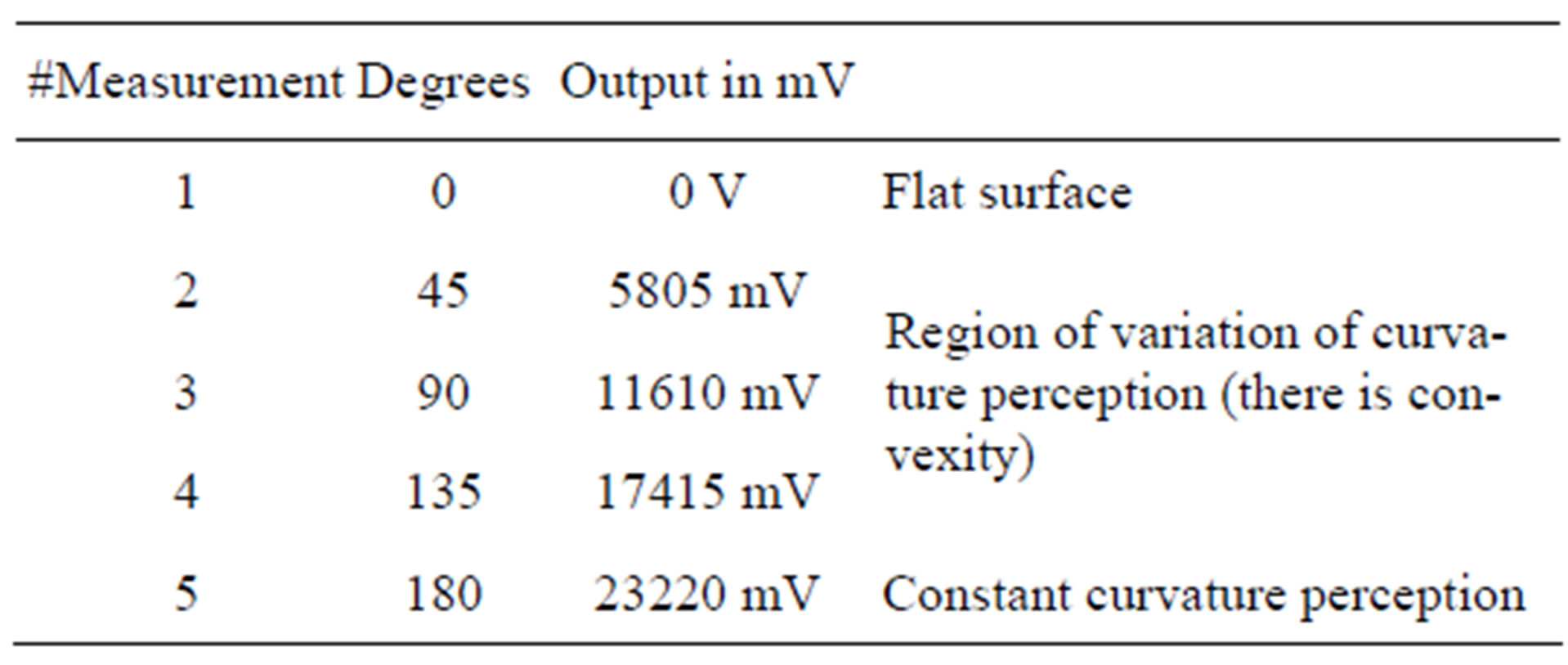
Table 1. Standard table of measurements of the accelerometer for different inclination angles. The perception in our accelerometer is designed in base to the formula of sensibility s = g*V, where g, is the factor of gravity and V, is the voltage measured in mV. Likewise 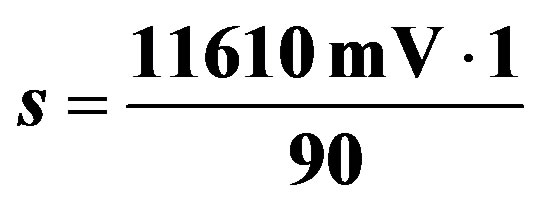 and the sensibility s = 129 mV/g [8].
and the sensibility s = 129 mV/g [8].
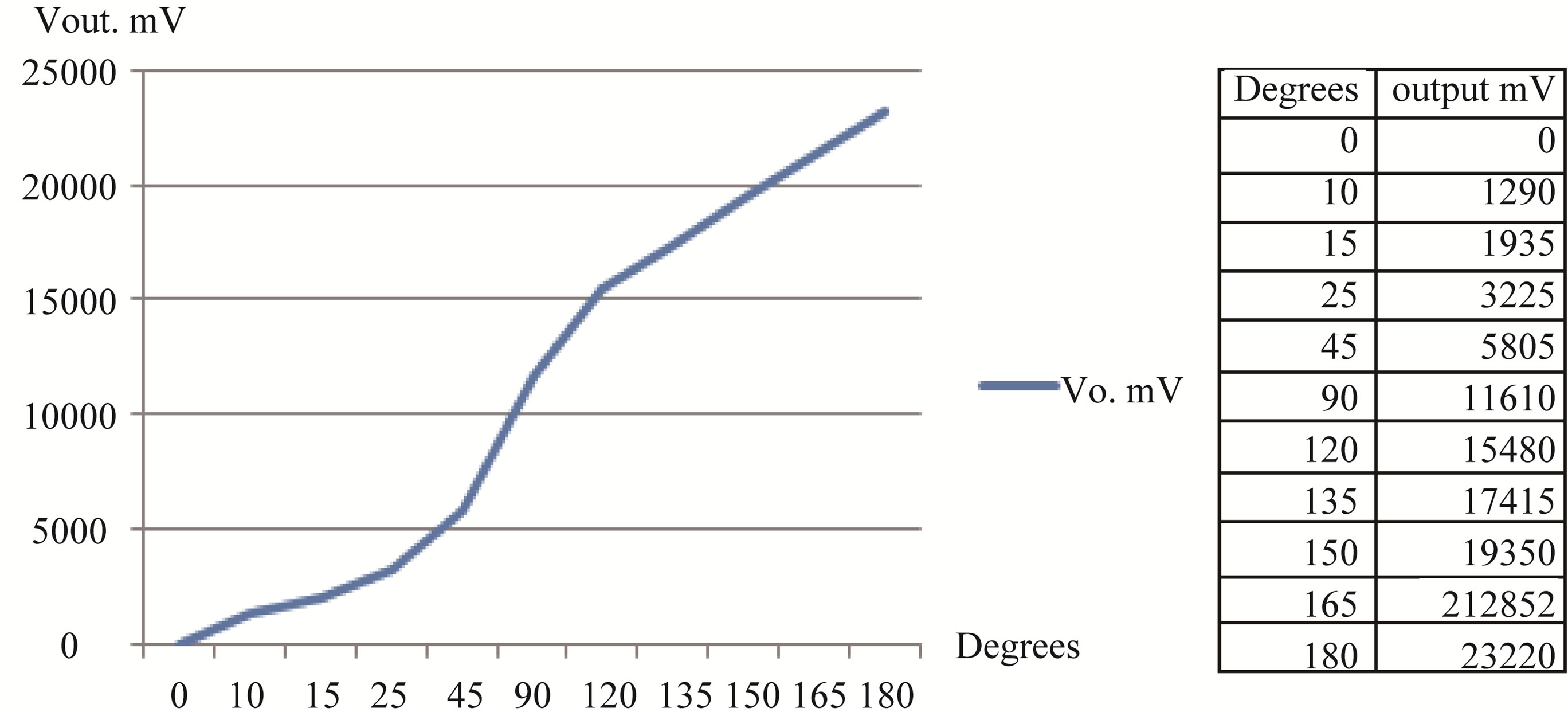
Figure 3. Graph of degrees vs output voltage. Sensor-perception curve. The curvature is detected through the deviations in angles perceived. The second column measures the electronic perception of this curvature through exits of the accelerometer given in mV.
ω = 50 cycles/second. In this case, in the field of the frequencies, said radius of sectional curvature is recognized by two directions of the principal curvatures through their Fourier transform
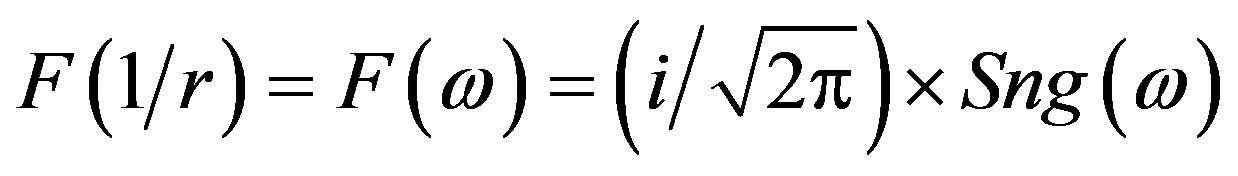
[5] (see Figure 4).
As the mobile moves on the solid surface, so that watching it in a transverse way that is a semi-circumference, the radius at the point p, and to any other pn, the measure is 10 centimeters, according to the designed pulse and given in the Equation (4), it is had that k(pn) = 0.1.
With base in the Figure 5, if the radius is a constant then it is possible to calculate total curvature in function of energy [12]. For this case is established degree angular displacements in degree, where the curvature length between the points q and p is given for (Figures 5 and 6):
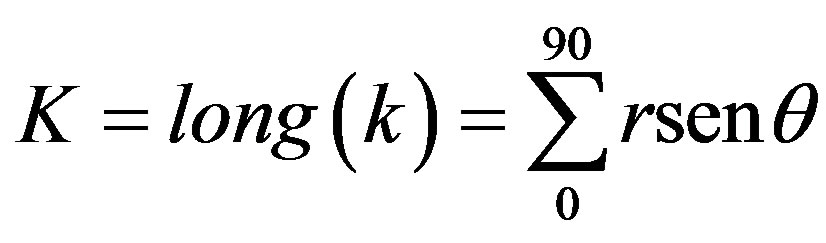 (6)
(6)
Considering that for every value of θ, a sign of voltage is proposed the block diagram of an electronic circuit that realises the sum to obtain the total curvature indicated in the Equation (6).
3. Results and Discussion
The detection and measurement of curvature using the value of the integrals of a field interacting on the geometric pattern along their geodesic ones will be made on the signals of finite energy defined in [11], and that they will code the information of curvature in a spectral space 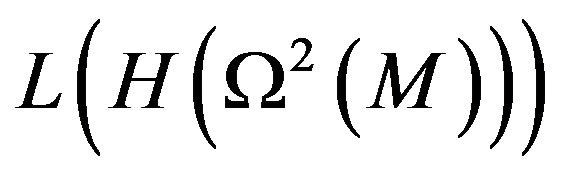 (spectral range of frequencies) though the signals given in the frequency ω, that detects and measures curvature.
(spectral range of frequencies) though the signals given in the frequency ω, that detects and measures curvature.
The corresponding design to our sensor obeys the standards of design of accelerometers with capacity of dynamic perception given by the electrostatic force
 (a)
(a)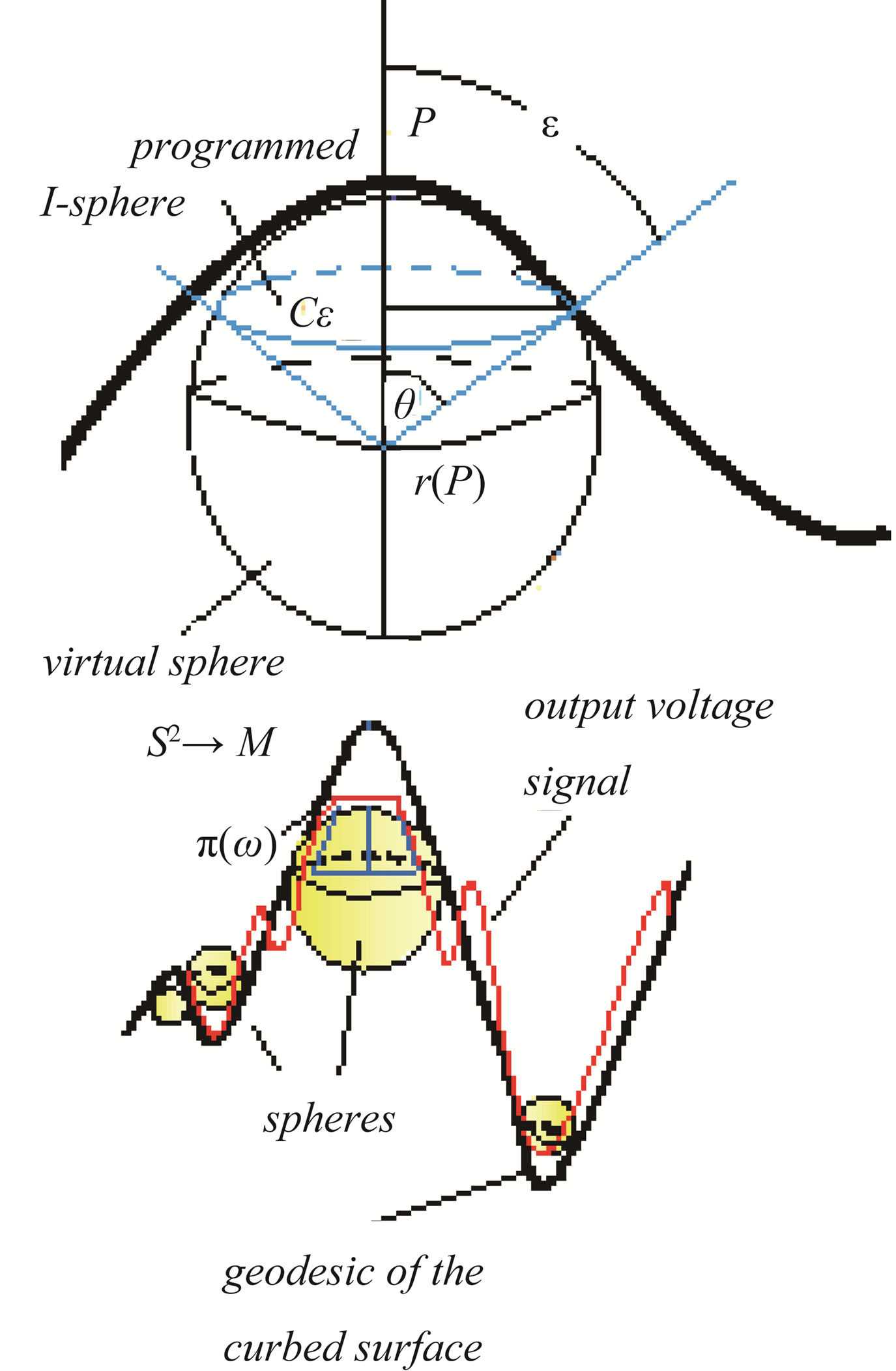 (b)
(b)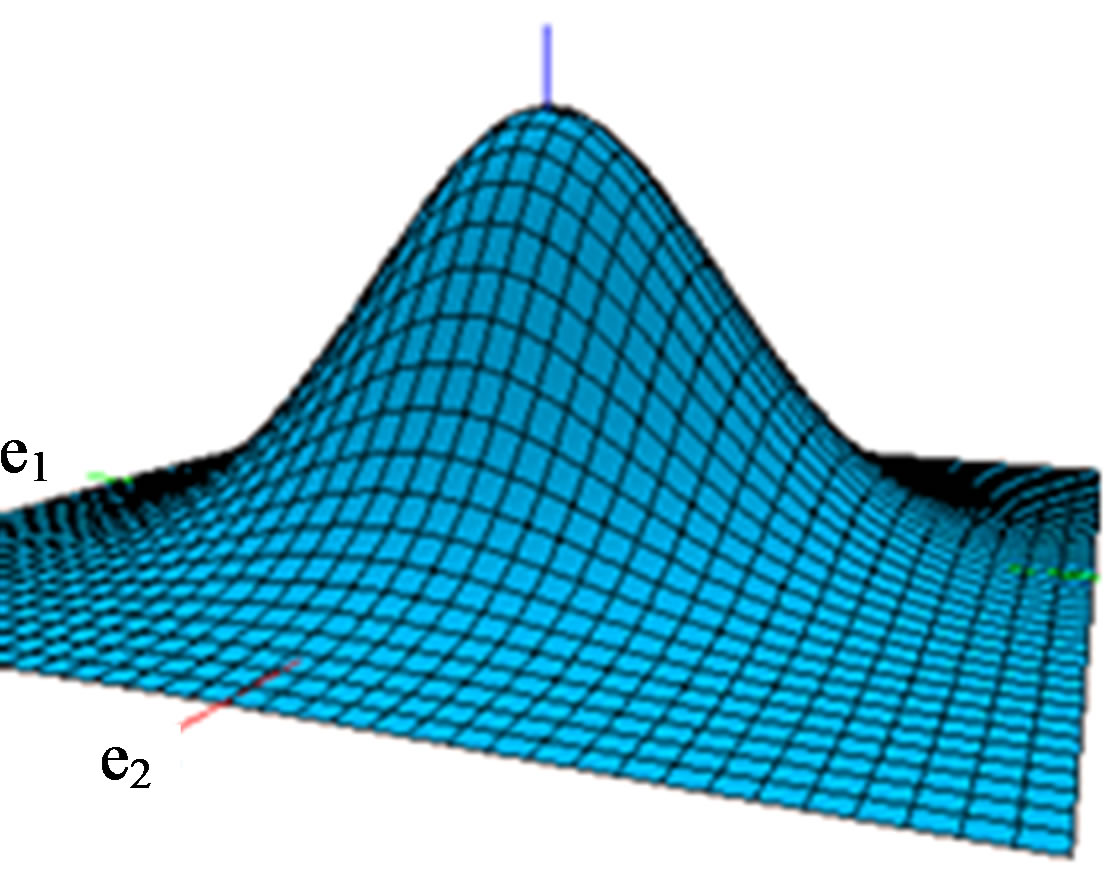 (c)
(c)
Figure 4. (a) The Fourier transform of k1k2, shows through the function Sng(w), the directions of the principal curvatures on the sphere S2. Sensor-perception curve [8]; (b) The curvature is detected through the deviations in angles perceived; (c) The showed surface establishes the detectable curvature range in two directions (e1, and e2) on 2-dimensional surfaces.
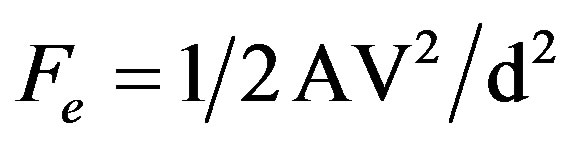 , that the deflection causes in g-cell component. This force is designed in our sensor by the basic isotopic component of Gaussian factor to lectures of curvature defined as α(–1)2 × 1 × (4π2), where (–1)2, is the basic charge given in function of the milimetric potential V, the factor A = 4p2, that there is the surface of the sphere of radius the unit S2(1), α, is the degree of the spherical map used in the transduction of the physical model to measure, which comes like a factor of electromagnetic adjustment of the sensor on the curved surface and the factor 1, is the positive charge generated inside the sensor (see Figure 7(a)). This is equivalent to the product of the force for the square of the distance of separation between the plates sensors of the nucleus of the sensor, where one gathers the change of the load according to the surface (negative load), and other gathers the charge invested in the process of detection (positive charge). The resultant deflection is measured by the accelerometer’s control ASIC and a proportional output voltage results [1]. This procedure assures that both the mechanical (g-cell) and electronic sections of the accelerometer are functioning.
, that the deflection causes in g-cell component. This force is designed in our sensor by the basic isotopic component of Gaussian factor to lectures of curvature defined as α(–1)2 × 1 × (4π2), where (–1)2, is the basic charge given in function of the milimetric potential V, the factor A = 4p2, that there is the surface of the sphere of radius the unit S2(1), α, is the degree of the spherical map used in the transduction of the physical model to measure, which comes like a factor of electromagnetic adjustment of the sensor on the curved surface and the factor 1, is the positive charge generated inside the sensor (see Figure 7(a)). This is equivalent to the product of the force for the square of the distance of separation between the plates sensors of the nucleus of the sensor, where one gathers the change of the load according to the surface (negative load), and other gathers the charge invested in the process of detection (positive charge). The resultant deflection is measured by the accelerometer’s control ASIC and a proportional output voltage results [1]. This procedure assures that both the mechanical (g-cell) and electronic sections of the accelerometer are functioning.
The EDMC-sensor is based on the emission of signals in two directions for the register of their g-cell curvatures of 2-dimensional surfaces. This way, the total curvature will come given by the information of the areas of shades and the geodesic information that sends the accelerometer (integral of line) to the computer (see Figure 7(b)).
Theorem (F. Bulnes). Let an accelerometer given by the device D, defined for their g-cell whose curvature energy to the case 2-dimensional is the bounded by the integral
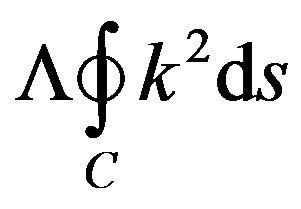
[12,14], where Λ, is an output electromagnetic factor from D, (to obtain curvature). Let S, the corresponding shape operator on S2 (and their contours), that is to say, is that whose normal curvature is given for 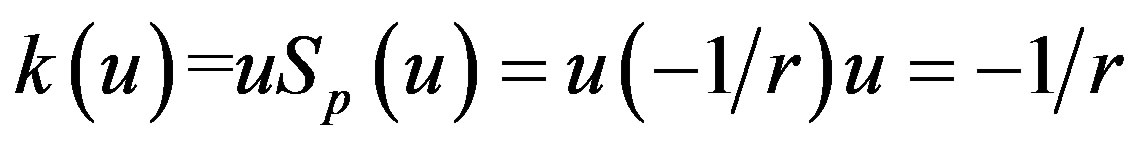 . Then our curvature is defined for the inequality of voltage-curvature energy given by (1) whose energy is Ek = (1/2)V2Asen2θ.
. Then our curvature is defined for the inequality of voltage-curvature energy given by (1) whose energy is Ek = (1/2)V2Asen2θ.
Proof. Considering the condition of minimization of a geodesic segment on the length of a position p, up to a position arch q, of our sensor D, we have that of the osculating sphere (Figure 4(b)) exists a polar circumference Cε, sufficiently near the geodesic γ, where the curvature measurement is realised in a principal direction [9].

Figure 5. Schematic that describes the experimentation.
 (a)
(a) (b)
(b)
Figure 6. (a) Block diagram to our circuit of interface; (b) Checking interface on curved surface.
 (a)
(a)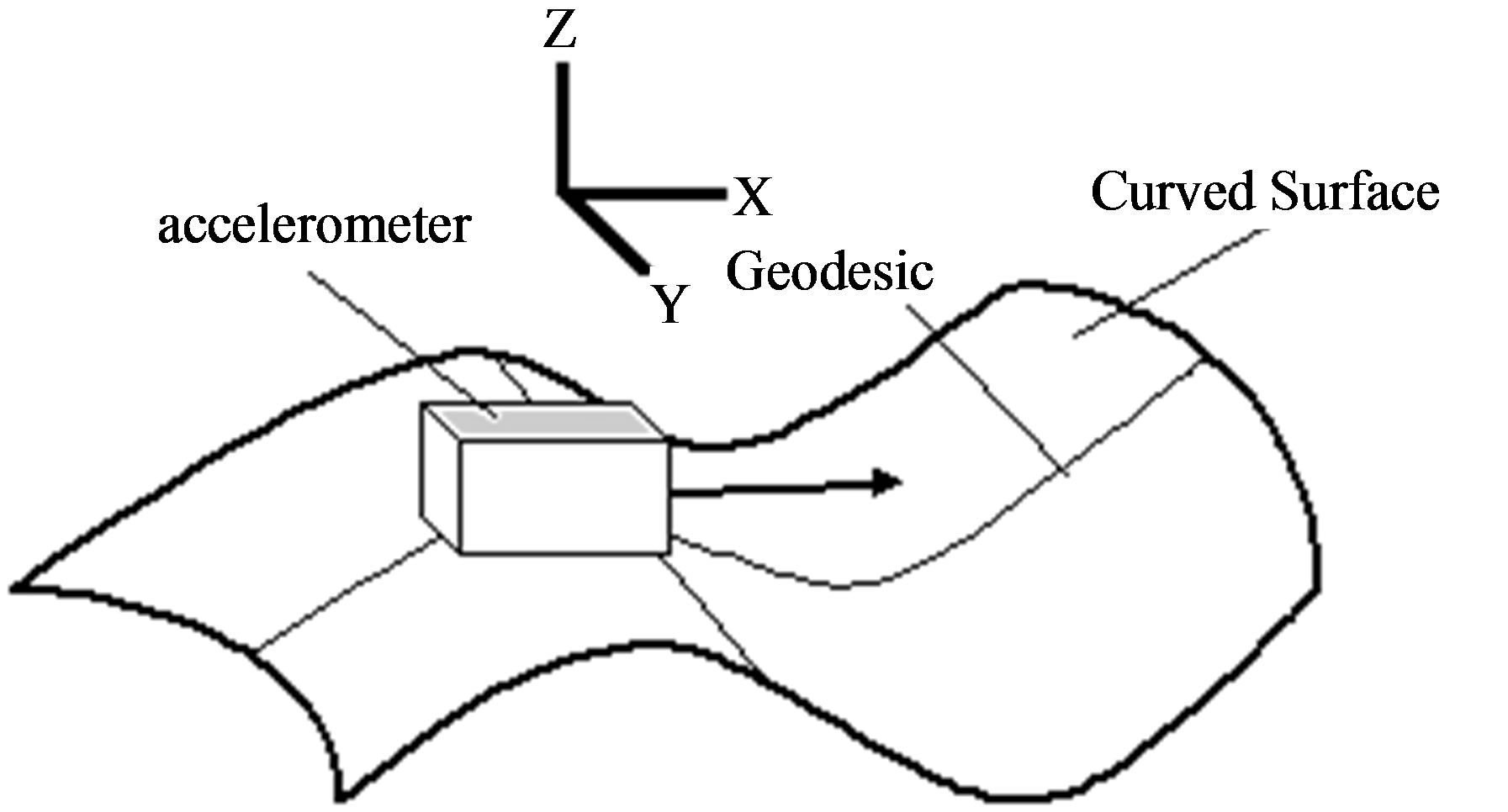 (b)
(b) (c)
(c)
Figure 7. (a) Diagram of transduction to the g-cell component; (b) Schematic in the 2-dimensional surface of the accelerometer action; (c) Equipment to prove the accelerometer: test surface, multi-meter.
Then it is necessary to satisfy that L(Cε) ³ L(γ), where the Equation (6) is their particular case to the design of our sensor.
But whose polar circumference Cε, with center in the point p, it is in fact an ordinary circumference of Euclidean radio r senθ, where the angle θ, it is the negligible arch length between the radio of the osculating sphere. We consider the bound given by the integral
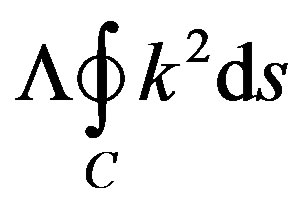 where Λ, to our sensor accelerometer type according to our experiments is a voltage factor [2,14]. Then one integral that establishes our maximum of energy used in the detection and curvature measurement [2] (using the fact of that Work = Energy = Fe ´ L) is:
where Λ, to our sensor accelerometer type according to our experiments is a voltage factor [2,14]. Then one integral that establishes our maximum of energy used in the detection and curvature measurement [2] (using the fact of that Work = Energy = Fe ´ L) is:
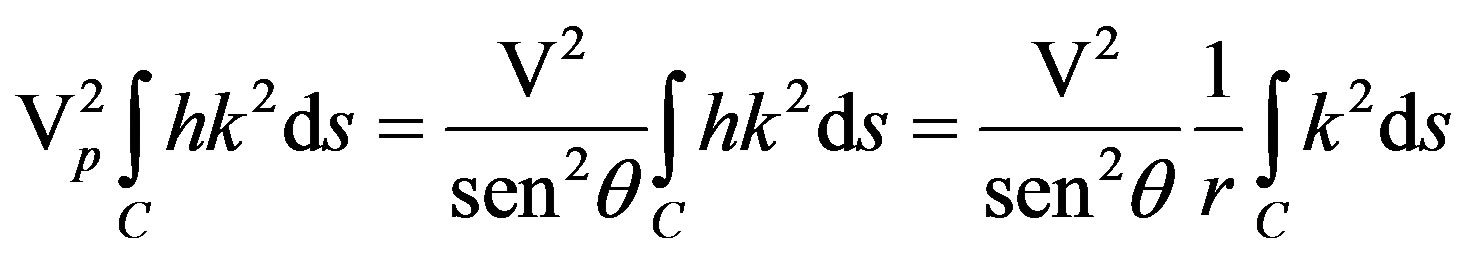 , (7)
, (7)
where Vp, is their peak-voltage or output maximum voltage. On the other side, applying the inequality L(Cε) ³ L(γ), we can establish that the superior extreme given in the Equation (7) is a condition of curvature energy of majoring curvature given on a geodesic γ, if their longitude of curvature is the given by the Equation (6), to know:
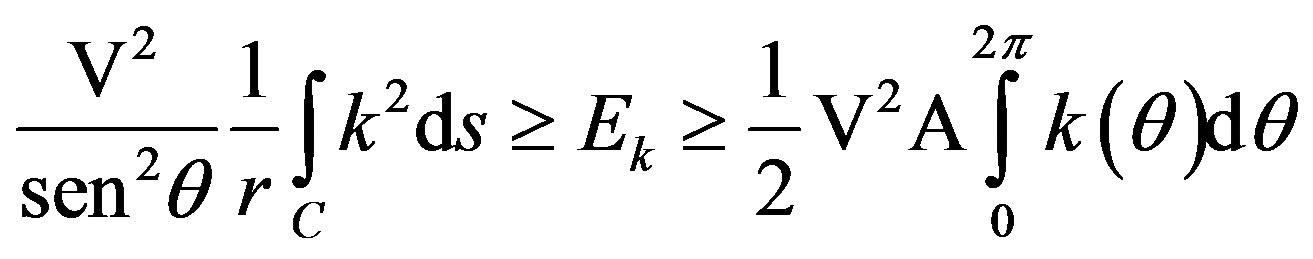 (8)
(8)
where Ek, is the curvature energy that is bounded for the energies originated from its geodesic and normal curvatures. In effect, considering that k(θ), is their normal curvature (this one is given for the polar circumference Cε, as the function 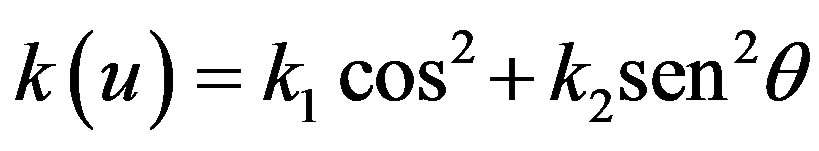 and calculating says k(u), on the sphere S2, given in the Figure 4(b) (that is to say, k1 = k2 = k, and
and calculating says k(u), on the sphere S2, given in the Figure 4(b) (that is to say, k1 = k2 = k, and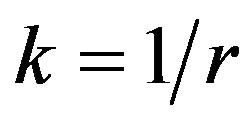 ) we have that the Inequation (8) takes the form:
) we have that the Inequation (8) takes the form:
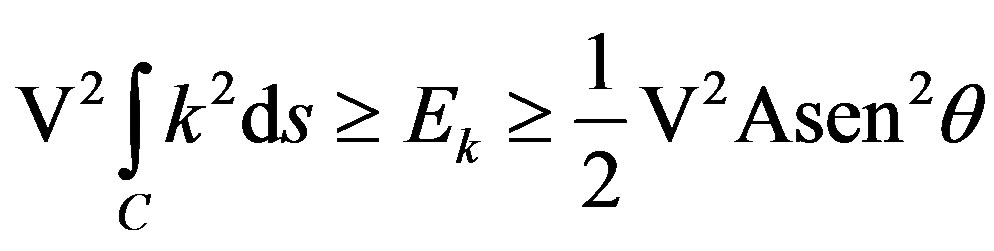 . (9)
. (9)
On the other side, if we consider the intermediate energy E, like the originated in voltage V2, then we obtain
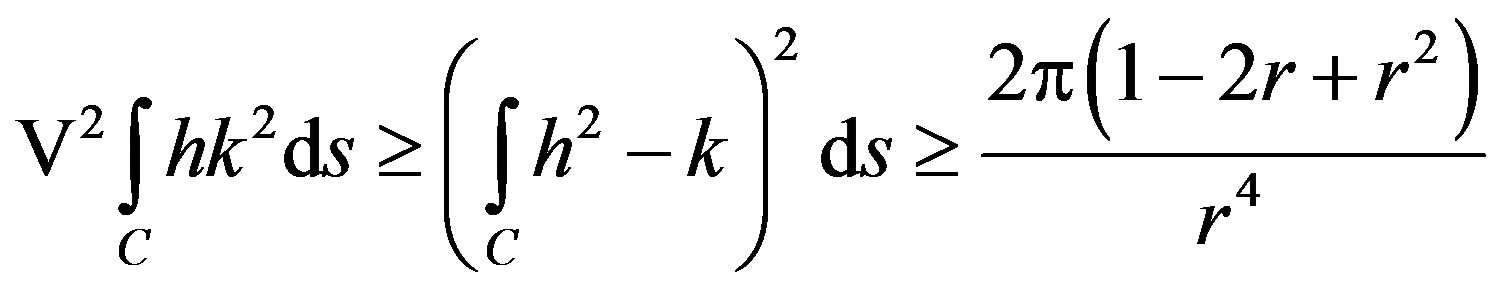 . (10)
. (10)
We have to Little contours resulting of the variations of position inside from Daccelerometer, (and in fidelity to their programming in S2) that
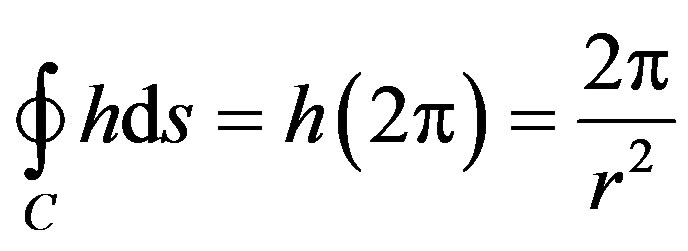 .
.
Then the inferior extreme of E, is entirely subordinated to this studied level since
 which gives us the integral
which gives us the integral
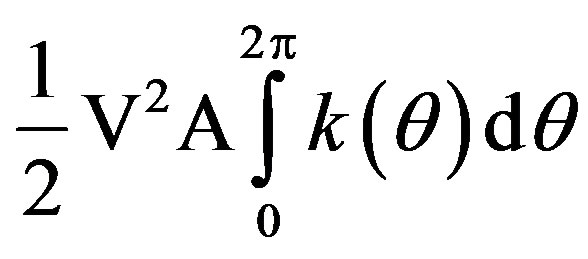 .
.
Observe that the intermediate term in last inequality is a function f(r), that can be deduced by the bound designed for Bessel functions in the energy of the g-cell device. Finally Ek ³ E. This complete our demonstration.
In the case n = 3 (curvature to objects in the space or solid objects) the shades projected by the object are 2-dimensional, useful to calculated curvature for 3-dimensional objects through plane images in the two main directions as the one shown (two accelerometers). You can use a rotating system for obtaining of 3-dimensional image through a type accelerometer that sends the data directly to the microprocessor computational of the surface of the body or object like spectral signals
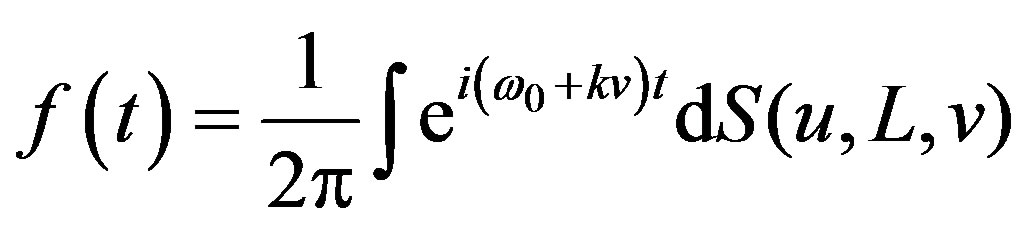 (11)
(11)
The Equation (11) encoded in curvature data (see Figure 8). The accelerometer will have a curvature sensor given for
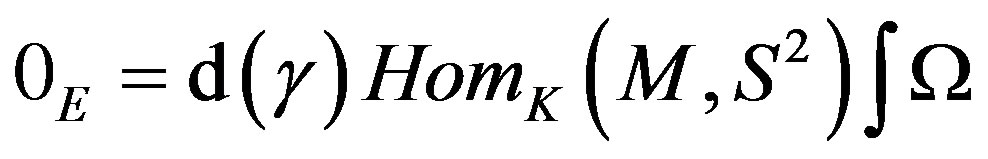 (12)
(12)
 (d)
(d)
Figure 8. Device of measurement of curvature that uses light waves to measure curvature of 2-dimensional and 3-dimensional objects (presented in ASME, 2009 [11]): (a) Photosensitive grill with complexes phases. The grills are two, which receive the reflexes of the incidental waves of light in the object or body to measure their curvature; (b) Device of rotation and control of wave emission under a constant electromagnetic field; (c) Shades of main directions of emission only for control of position of the body. These get connected to a computer with a program that it transforms the sheen intensities in angles though the phases of the photosensitive grills [4,11]; (d) The same principle that before device using the flight automaton equipped with rotating device to send light waves and angular lectures to computer monitor. The theoretical support was given in [11].
Then sensor have the constant Gaussian factor 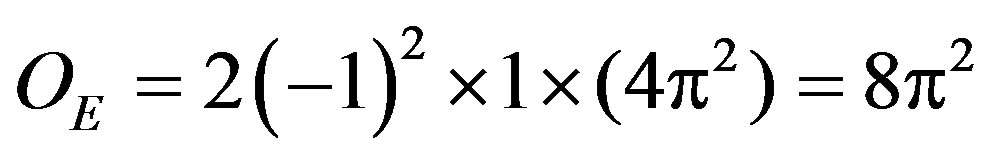 . The measure obtaining is very nearly to the factor of gravity considered in the design of the g-cell system in our sensor through S3. Also observe that the Equation (12), is the minimum part of energy in the inequality given by the Inequation (1). A study related with optimization proves that the optimal surface in the development of an informatics detector (in this case informatics curvature detector) is an ellipsoid tending to sphere, this last as exceptional case.
. The measure obtaining is very nearly to the factor of gravity considered in the design of the g-cell system in our sensor through S3. Also observe that the Equation (12), is the minimum part of energy in the inequality given by the Inequation (1). A study related with optimization proves that the optimal surface in the development of an informatics detector (in this case informatics curvature detector) is an ellipsoid tending to sphere, this last as exceptional case.
The such according to our curvature studies comes from a theoretical sensor of curvature in presence of the incurve and detected by a wave of light [9,11]
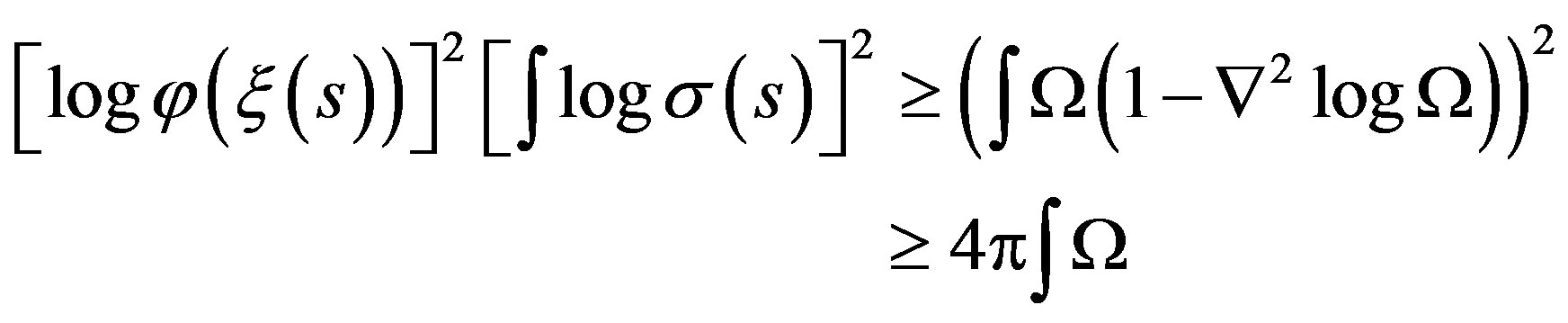 (13)
(13)
The adjournment effect and the information of deviations that detects the accelerometer can be obtained of equal forms for the installation of a rotating base with a device that reads the incidences of the rays reflected in the surface of the body (see Figures 8(a)-(d)).
The recovering of all data given by the Equation (11) and re-interpreted by the Equation (12) in the space (for example a 3-dimensional space) realizes through the integral transform [14] (which reconstruct all space through of values of light geodesics (cycles)):
 (14)
(14)
All the processed data will be gathered by a computer to process them, giving 2-dimensional planes as a result. Using the integrals given by the Equation (14), we recover the total curvature of the object through all those data gathered in those planes and lines (see Figure 9(c)).
A second idea that can substitute the accelerometer system in the device, is the evaluation of derivation suffered by these rays when impacting in the curved surface and code these data like spectral signals given for the Equation (11) for those different deviations.
The deviations can be coded by the Doppler effects of the reflected signals [15] (Figure 8(b)). The consistency of the summary of data and their code in curvature values, is given by the following result [1], applying the Gaussian curvature sensor given in spherical operator in the Equation (12) and the property given by voltages and light signals used for its measurement.
4. Other Developments in the Study of Curvature from Gravity: One Proposal of Ultra-Sensitive Interstellar Accelerometer
The curvature perception in the space is associated increasingly with their interpretation as a distortion of the
 (a)
(a) (b)
(b)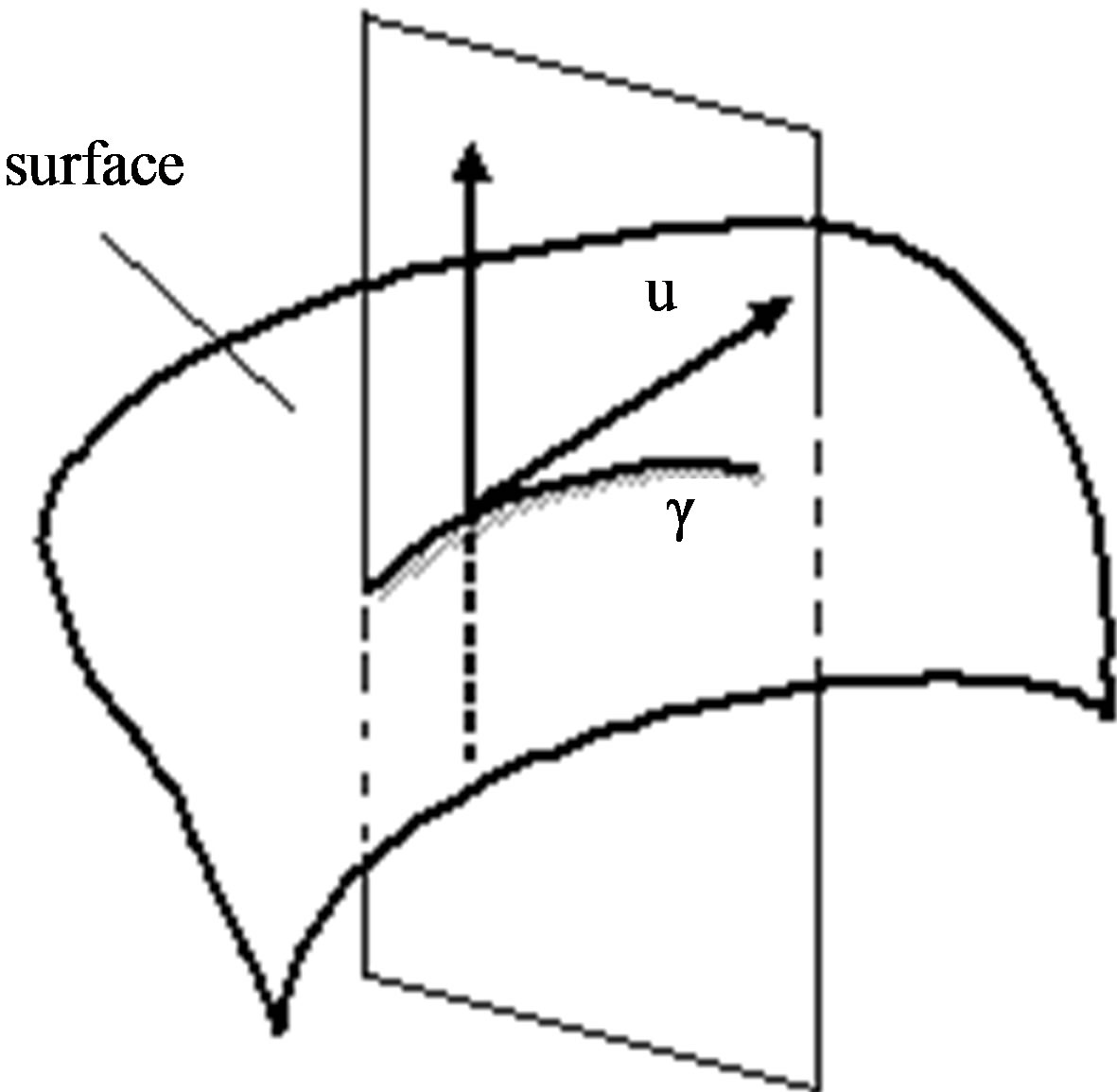 (c)
(c)
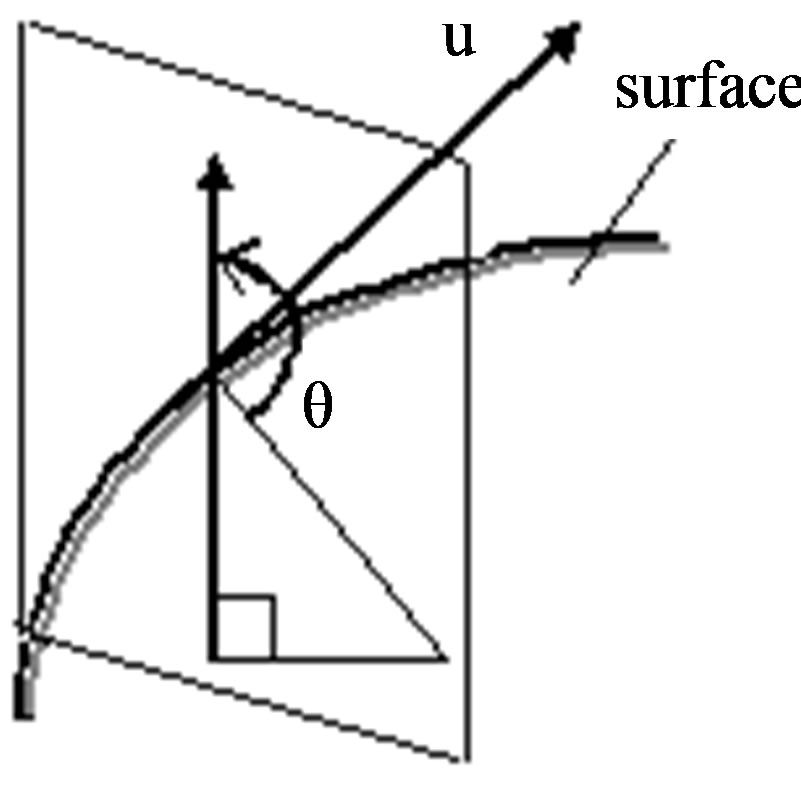
Figure 9. (a) Normal curvature concept; (b) Accelerometer measuring curvature using normal curvature on geodesic in the curved surface; (c) Geodesic used to measure curvature on surface.
micro-local structure of the space-time due to the interaction of particles of the matter and energy with diverse field manifestations. The matter is shaped by hypothetical particles that take as basic the background radiation of the space, which in the last studies due to QFT, SUSYtheory [16] and brane theory [16], the strings are organised and tacked to form spaces of major dimensions represented by diverse particles of the matter as they are gravitons, barions, fermions of three generations, etc., shaping the gravity at quantum level, obtaining representations of the same one for classes of cohomology of the QFT, like for example the FRW-cohomology, which considers diverse symmetries of cylindrical and spherical type for the gravity modeling like a wave of gravitational energy “quasi-locally”. Their integrals of action define a energy density (Hamiltonian) given for the gravitational case like [17]:
 (11)
(11)
where Lα is the Lagrangian, Tαβ, is the corresponding tensor of matter and energy, Γ, is a Hamiltonian density and Xβ, is the corresponding field of displacement of the particles in the space moving for action of Lα, influenced by the tensor one of matter and energy Tαβ. It is necessary to indicate that Lα has component that is invariant yet under movements influenced by the tensor Tαβ, which is their electromagnetic component LMAX, (Maxwell Lagrangian).
One of the important ideas inside the study of the microscopic space-time there are the group representations of SU(2), where one of which considering the supersymmetry is S3 (sphere of dimension 3) [14]. In r the topological invariant of their 2-form ω3, given in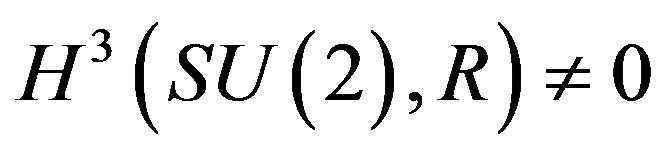 , and whose cohomology in not null [14], shows clearly that the gravity presence can be warned at least on the surface of this sphere, which can be considered to be a mini-twistor in the presence of gravity considering a ambitwistor space of couples (Zα, Wα), to the microscopic space-time, where Zα, are the fields of gauge nature (in this case electromagnetic fields) and the fields of particles of the gravity (gravitons), (that in this case is the background).
, and whose cohomology in not null [14], shows clearly that the gravity presence can be warned at least on the surface of this sphere, which can be considered to be a mini-twistor in the presence of gravity considering a ambitwistor space of couples (Zα, Wα), to the microscopic space-time, where Zα, are the fields of gauge nature (in this case electromagnetic fields) and the fields of particles of the gravity (gravitons), (that in this case is the background).
Based on it, and considering the value of curvature to be the contour deformation on a surface (initial idea created by relativity to understand curvature in a space-time surface [10,14]), at the same time that a field distortion created like an undulation in the space time for backreaction for photon propagation in the presence of gravity (see Figures 10(a) and (b) (using string theory)), we can extrapolate this idea to the design of a type of accelerometer that can be connected to the devices of navigation of a traveling satellite by the space, where said accelerometer involves in their interior a sensor of ultrasensitive gravity based on a solid sphere S3, of material similar to a colloid, captured the changes of the weight of a liquid also of colloid type (perhaps of major density that of the ball S3) due to the universal factor G.
We are basing in the design of a classical accelerometer, respect to their g-cell component, to establish a sensor of dynamical movements designed and proposed on a solid ball of colloid material inside other colloid media in the box of device (with more density than ball) such due to little variations of movements the colloid that make a detour to the ball inside the device provokes stretch marks and waves on the surface of the ball, having the twistor model S3. The above mentioned undulations can be codified like curvatures of quantum level, since our ultra-sensitive sensor will be designed to detect quantum gravity (Figures 11(a) and (b)).
5. Curvature Application like Light Natural Obstacle
A simple application (of ordinary type) on the curvature measurement through electromagnetic fields can happen in the design and construction of sensors of natural lighting to distribute the lamps light in ideal form arranged inside a building or house room. Likewise the curvature concept in this case appears like the obstacle of darkness that it wants to eliminate in an area of the building under a sensor of perception of lighting, which
 (a)
(a)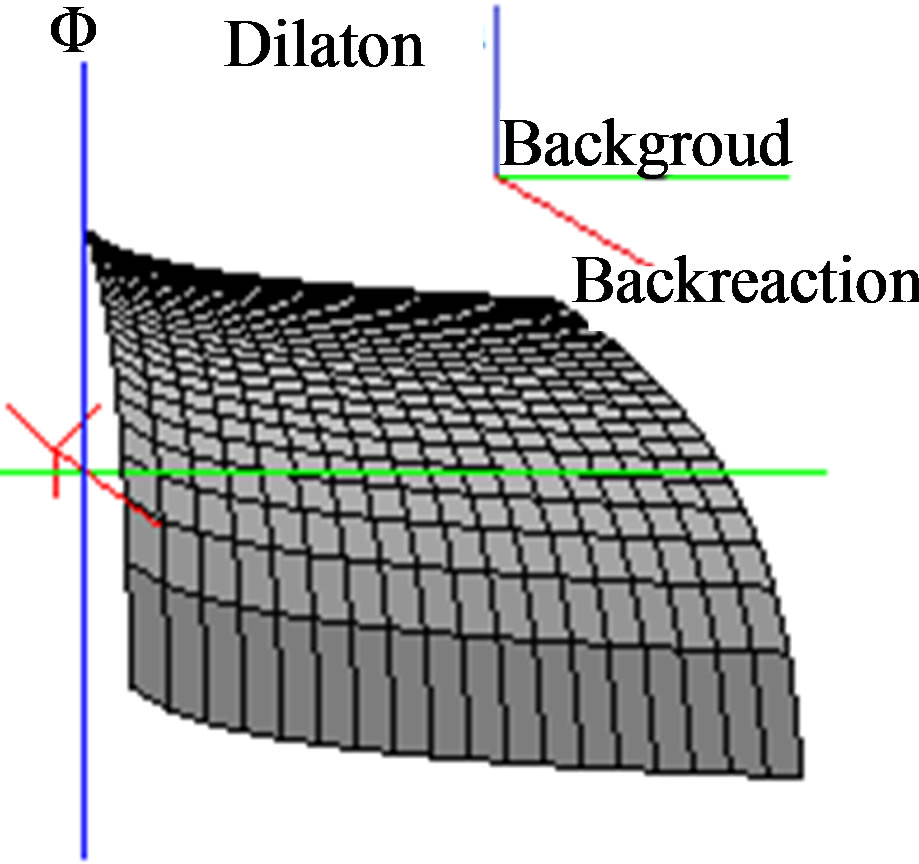 (b)
(b)
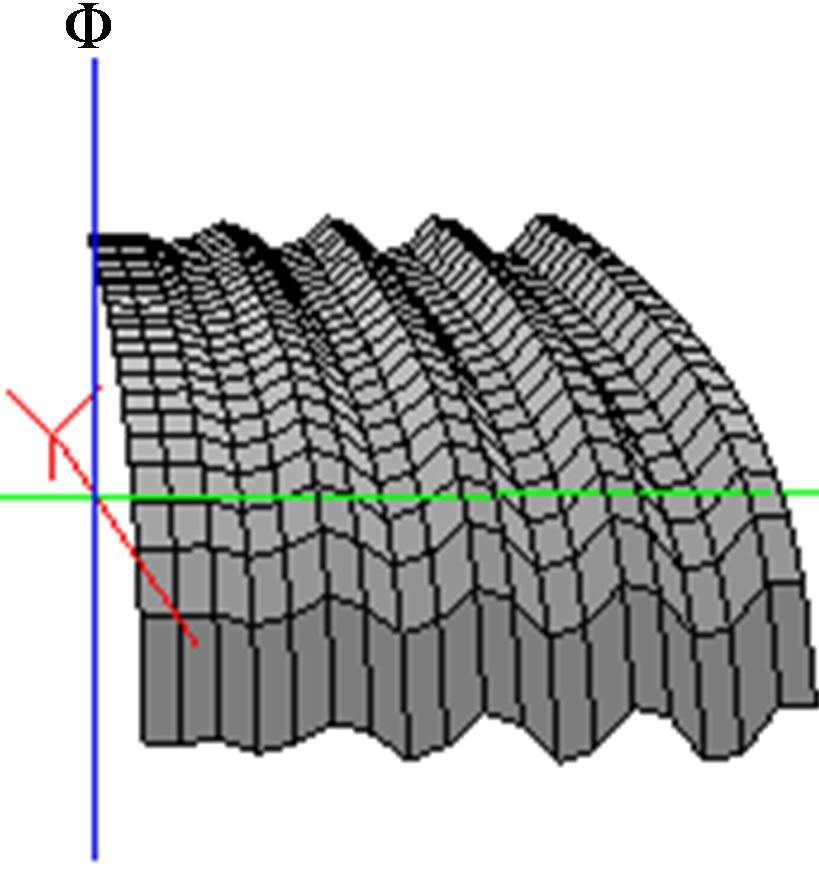
Figure 10. (a) We have the wave propagation of the background radiation (green), propagation of quantum electromagnetic waves, without background radiation (black) and propagation of quantum electromagnetic waves distorted with background radiation (blue). The stripe in brown represents the flat space with the corresponding distortions that create the angle θ, in the Figure (a). The difference between the two waves come reflected in the corresponding hollows of the (a). Also this Figure (a) gives us the microlocal aspect of the space-time in Max Planck dimension; (b) Dilaton measuring distortion due to quantum gravity, according to the model computational magnetic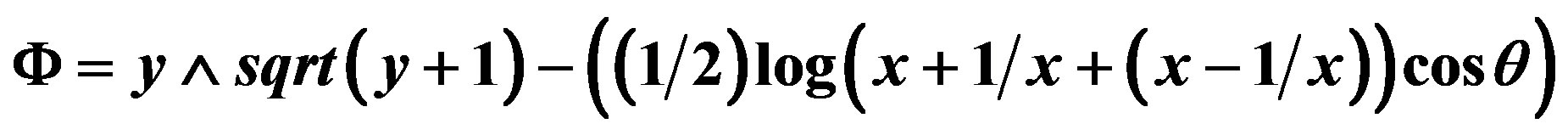 . In the case when θ = 0, (there is not photon backreaction).
. In the case when θ = 0, (there is not photon backreaction).
discards the grade of high lighting (areas where it will not be necessary to illuminate for the existence of light of the exterior to the building) and that applies the lighting in the obscure areas (places where there are shades projected by obstacles that generate darkness).
6. Conclusions
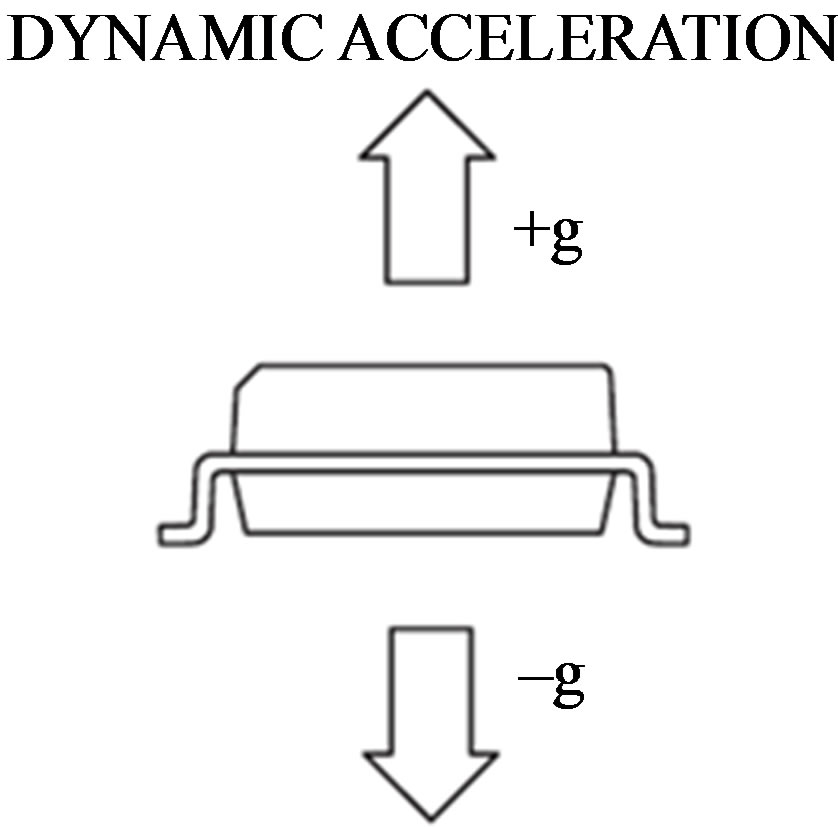
The curvature is a geometrical and of field observable very difficult to define and therefore measuring in direct form. Nevertheless, it is the most important invariant of the form of a geometric body. The methods that we propose are based on the idea of measuring this one observable of field and geometric form through energy that can be defined by voltages of output calibrated in microvolts and generated from an interface that relates grades of angular deviation to output voltages of a sensor with a
 (a)
(a)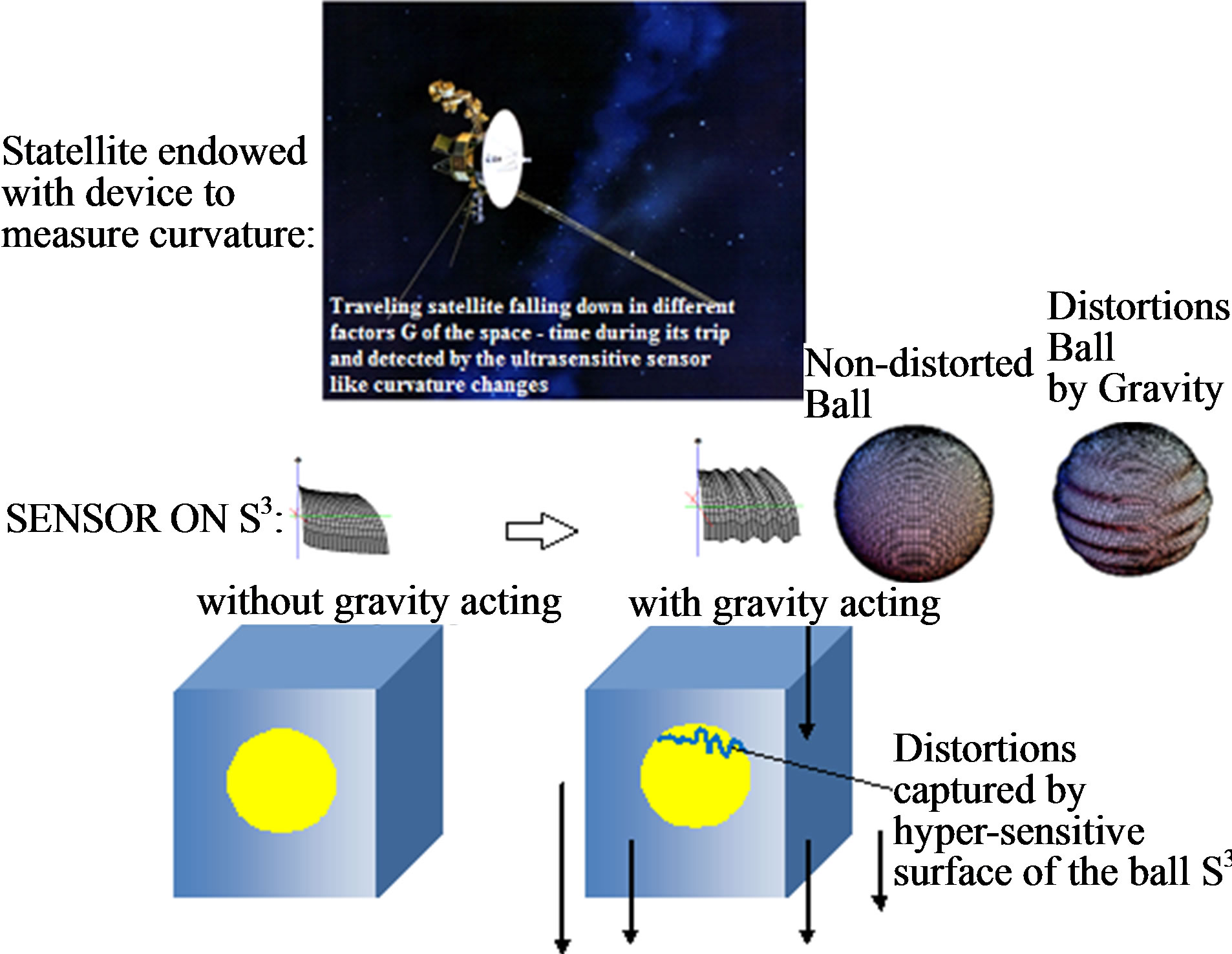 (b)
(b)
Figure 11. (a) Classical accelerometer in the earth’s gravity; (b) The curvature will be able to express itself like a Gaussian curvature according to spherical harmonics given by Legendre polynomials. The sensor is a sensor of free fall that can register different force factors G. The actions of change can be reprogrammed by the proper device considering these to be a Lagrangian action given for [10,14].
type transducer accelerometer (see Figure 12).
Nevertheless we coincide that the development of this type of sensors must be improved as for its sensibility of curvature perception which will have to be obtained through thinner and better signals calibrated in order to diminish problems of dispersion, directional adjustment of the accelerometer, process of transference of information of voltage recorded in curvature and the manipulation of the sensor to measure and to detect curvature. Also their application way: along this work we have
 (a)
(a) (b)
(b)
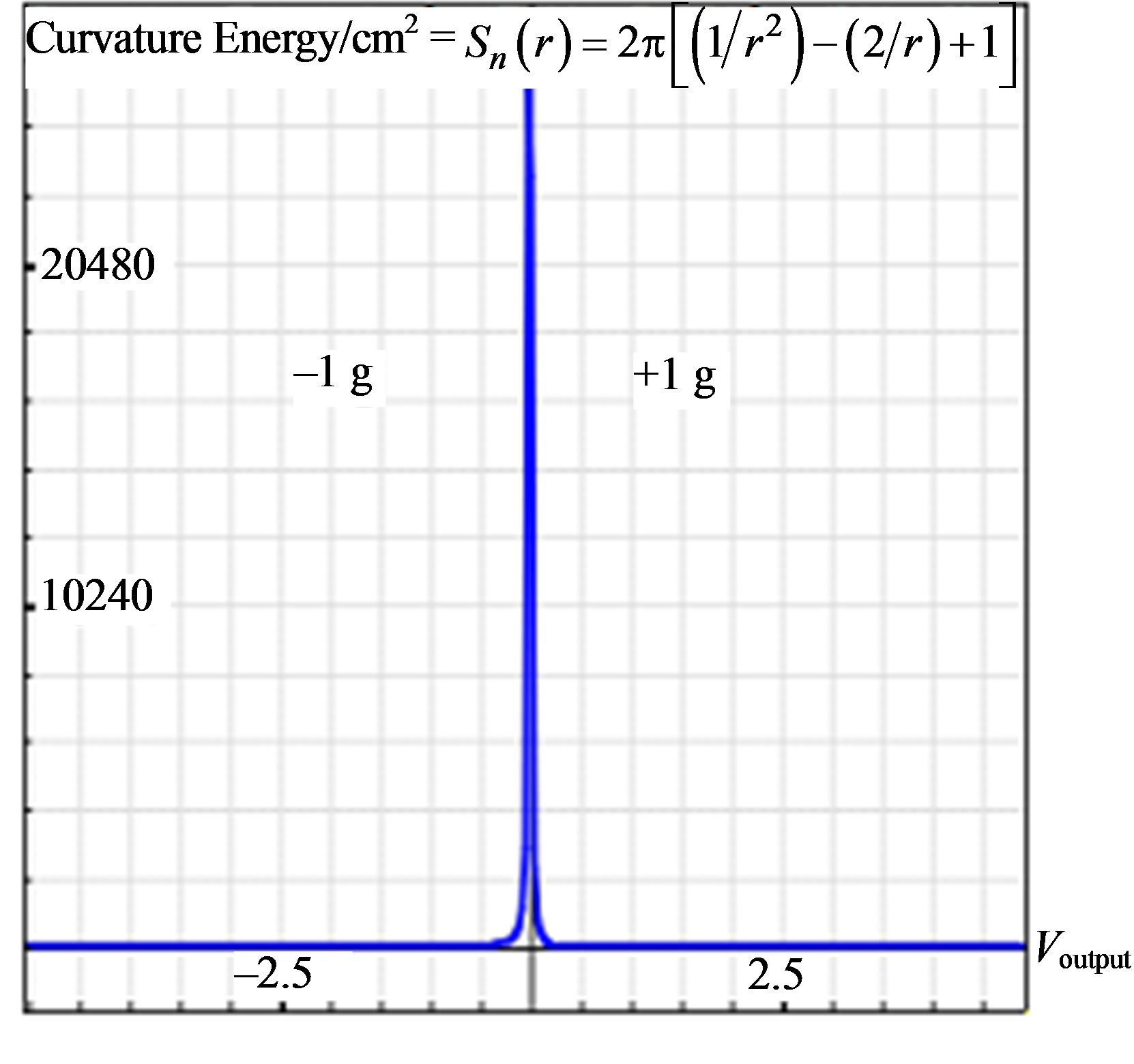
Figure 12. (a) Curve of curvature energy estimated and used in the theorem (F. Bulnes) to design our accelerometer device with relation voltage-curvature energy (Curvature Energy/cm = k(r) = ). Its similar one observes with the form of pulse for a sphere (Figure 4(a)). In this case and using developments of cylindrical functions (Bessel functions) the pulse is thinner. A small calculation on the output voltages in the g-cell: 3.7V – 2.5V = 1.2V, they verify the standard design for accelerometers considering the earth gravity (Figure 10(a)); (b) To calculate curvatures on 3-dimensional objects only there are considered to be two principal directions on the surface that bound it, in the case 4-dimensional, there are considered to be three principal directions, and this way successively. To an n-dimensional body the curvature is calculated on (n – 1) principal directions. This is because our design is based on Gaussian curvature.
). Its similar one observes with the form of pulse for a sphere (Figure 4(a)). In this case and using developments of cylindrical functions (Bessel functions) the pulse is thinner. A small calculation on the output voltages in the g-cell: 3.7V – 2.5V = 1.2V, they verify the standard design for accelerometers considering the earth gravity (Figure 10(a)); (b) To calculate curvatures on 3-dimensional objects only there are considered to be two principal directions on the surface that bound it, in the case 4-dimensional, there are considered to be three principal directions, and this way successively. To an n-dimensional body the curvature is calculated on (n – 1) principal directions. This is because our design is based on Gaussian curvature.
proposed some ideas of the way of application of sensors with different types of accelerometers (at least in idea, design and possibilities). With the development and improving of these sensors it will allow us to measure observable of field more complexes as the torsion and that have to do with the particles interaction in the physical case as well as the measurement of involution of the curvature in a body for the geometric case, that is to say, measure fields directly. For this geometric case the torsion measurement will be able to be applied to bodies charged with fields of diverse nature where in this case their torsion will be their geometric image of the proper field as well as the effects that this one produces in the matter.
7. Acknowledgements
We are grateful for the support offered to the division of electronic engineering, their laboratory of digital electronics and the department of research in mathematics and engineering of the Technological Institute of High Studies of Chalco. One grateful to engineering Carlos Sotero for the quality characteristics of the figures.
REFERENCES
- V. Kaajakari, “Closed Form Expressions for RF MEMS Switch Actuation and Release Time,” Electronics Letters, Vol. 43, No. 3, 2009, pp. 149-150. doi:10.1049/el:20093281
- V. Kaajakari, A. T. Alastalo and T. Mattila, “Electrostatic Transducers for Micromechanical Resonators: Free Space and Solid Dielectric,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 53, No. 12, 2006, pp. 2484-2489.
- O. Holmgren, K. Kokkonen, T. Veijola, T. Mattila, V. Kaajakari, A. Oja, J. V. Knuuttila and M. Kaivola, “Analysis of Vibration Modes in a Micromechanical SquarePlate Resonator,” Journal of Micromechanics and Microengineering, Vol. 19, No. 1, 2009, Article ID: 015028.
- V. Kaajakari and A. Lal, “Micromachined Ultrasonic Motor Based on Parametric Polycrystalline Silicon Plate Excitation,” Sensors and Actuators A: Physical, Vol. 137, No. 1, 2007, pp. 120-128. doi:10.1016/j.sna.20
- A. T. Alastalo and V. Kaajakari, “Intermodulation in Capacitively Coupled Microelectromechanical Filters,” IEEE Electron Device Letters, Vol. 26, 2005, pp. 189-191.
- S. Kobayashi and K. Nomizu, “Foundations of Differential Geometry,” Wiley and Sons, New York, 1969.
- J. Lau, C. Lee, C. Premachandran and Y. Aibin, “Advanced MEMS Packaging (Electronic Enginnering),” Kindle Editon, USA, 2010.
- R. Pallás and J. G. Webster, “Sensors and Signal Conditioning,” 2nd Edition, John Wiley & Sons, New York, 2001.
- F. Bulnes, “Research on Curvature of Homogeneous Spaces,” TESCHA, Mexico, 2010, pp. 44-66. http://www.tesch.edu.mx
- F. Bulnes, “Electromagnetic Gauges and Maxwell Lagrangians Applied to the Determination of Curvature in the Space-Time and Their Applications,” Journal of Electromagnetic Analysis and Applications, Vol. 4, No. 6, 2012, pp. 252-266. doi:10.4236/jemaa.2012.46035
- F. Bulnes, E. Hernandez and J. Maya, “Design of Measurement and Detection Devices of Curvature through of the Synergic Integral Operators of the Mechanics on Light Waves,” Proceedings of International Mechanics Engineering Conference and Exposition, Orlando Florida, 16 November 2009, pp. 91-102. doi:10.1115/IMECE2009-10038
- L. J. Van Vliet and P. W. Verbeek, “Curvature and Bending Energy in Digitized 2D and 3D Images,” Proceedings of 8th Scandinavian Conference on Image Analysis, Tromso, 25-28 May 1993, pp. 1403-1410.
- B. Nashelky, “Electronics: Circuit Theory and Electronic Devices,” Pearson Prentice Hall, Upper Saddle River, 2003.
- F. Bulnes, “Doctoral Course of Mathematical Electrodynamics,” International Proceedings of 2nd Appliedmath SEPI-IPN and IM-UNAM, Vol. 1, No. 2, 2006, pp. 398- 447.
- G. Sparr, K. Strȧhlen, K. Lindström and H. W. Persson, “Doppler Tomography for Vector Fields,” Inverse Problems, Vol. 11, No. 5, 1995, p. 1051. doi:10.1088/0266-5611/11/5/009
- J. Król, “Quantum Gravity Insights from Smooth 4-Geometries on Trivial R4, Quantum Gravity,” Intech, Austria, 2012, pp. 53-78.
- L. Mason, “A Hamiltonian Interpretation of Penrose’s Quasi-Local Mass,” Classical and Quantum Gravity, Vol. 6, No. 2, 1989, p. L7. doi:10.1088/0264-9381/6/2/001
Notation and Abbreviators
K—Curvature as general concept of roundness property. Also used in the paper as Gaussian curvature in a point p;
k—Gaussian curvature along of the geodesic or surface;
OE—Spherical operator which related;
ki—Principal curvature in the principal ith-direction. In our research i = 1, 2, only;
V—Voltage;
A—Area;
L(H(Ω2(M))—Space of spectral transformations on curvature 2-forms given in space Ω2(M);
M—Space whose curvature is measured. In our study M, represent 2-dimensional surfaces or 3-dimensional bodies;
S2—2-dimensinal sphere. Also is the 2-dimensional sphere used in the spherical map to design our curvature sensor;
r(P)—Evaluation of curvature radius from the product from their inverse principal curvatures;
Ω—Curvature form in the 4 and 4-dimensional spaces;
J1 – r, p —Bessel function of first specie;
Y1 – r, 1 – r—Bessel function of second specie;
(Zα, Wα)—Ambitwistor element whose elements are invariant-covariant fields;
R—Set of real numbers;
SU(2)—group that defines the finite actions through unitary anti-Hermitians matrix of range 2.
Abbreviations SOIC—Small-outline integrated circuit;
mV—Micro-volts;
EDMC—Electromagnetic device to measure curvature;
ASIC—Application-specific integrated circuit;
QFT—Quantum field theory;
SUSY—Super-symmetry theory;
FRW—cohomology-Friedman-Robertson-Walker metrics. The cosmological principle (principle of homogeneity and isotropy of the universe to great scale). The cohomology are the relations of similarity in dual spaces.

