Journal of Sensor Technology
Vol.2 No.1(2012), Article ID:17933,4 pages DOI:10.4236/jst.2012.21004
Influence of Magnetic Field Inhomogeneity on a Magneto-Optical Current Sensor
1Electrical Engineering Department, Islamic University of Gaza, Gaza, Palestine
2Measurements and Sensor Technology, Technical University Munich, Munich, Germany
3Physics Department, Al-Aqsa University, Gaza, Palestine
Email: hkhozondar@iugaza.edu
Received August 14, 2011; revised September 6, 2011; accepted October 1, 2011
Keywords: Fiber Optic Sensors; Magneto-Optical Sensor; Faraday Rotation
ABSTRACT
The growth in the capacity of electric power system creates a demand for the protection of relaying systems. Optical current transducers—OCT that are mainly made up of single mode optical fibers which are subjected to Faraday rotation are used as a replacement for electromagnetic transducers due to their immunity to electromagnetic interference. However, the principal parameter in this system, the sensitivity to magnetic fields or current, depends on the Verdet constant, which is low in the case of optical fibers. However, the optical path length can be increased to compensate for it by winding the fiber around a current carrying element a large number of turns. In this work, we study a current sensor, which is made up of a conductor coil with a fiber inside, thus increasing sensitivity. We study the effect of the inhomogeneity of the magnetic field induced by the current on the sensitivity of the optical fiber sensor.
1. Introduction
The protection of relaying systems is a prominent task for optical current sensors. These sensors can recognize sudden failures, such as surges, and identify the failure parts in the power systems. These relaying systems require current sensors, which are mostly electromagnetic devices that suffer from magnetic saturation effects and residual field effects. Recently several studies use optical current sensors as replacement for these established systems. Optical current sensors with mainly optical fibers do not suffer from electromagnetic interference, has light-weight and small size, and possess a low susceptibility to environmental influences [1].
The concept of the optical sensors is the magnetooptical principle. Thus, it is named magneto-optical sensor (MO). The magneto-optical sensor is based on the Faraday rotation effect [2], which states that the polarization of light waves is rotated with the propagation of the light along (or opposite to) a magnetic field inside some material. This rotation depends on the Verdet constant which a property of the material as well as the strength of the magnetic field and the optical path. Several studies have been performed to modify the performance of MO sensors, see for example [3,4]. In contrary to some bulk materials, the Verdet constant of optical fibers is quite small [5]. However, this can be compensated for by introduced magneto-optical fiber gratings based on magnetooptical materials [6] and [7] or by increasing the optical path by winding the fiber around a current conducting element a large number of turns. A different possibility is to wind the conductor several times around the straight fiber, thus creating a coil like configuration.
In optical fiber sensors, linearly polarized optical waves are input to the optical fiber. The linear polarization can be expressed mathematically as a superposition of two circular polarizations (right-hand and left-hand). The magnetic field induced around a current carrying element induces a circular birefringence inside the optical fiber coil. Hence, after passing through the coil, a relative phase difference between two circular polarization components is generated, which results in the rotation of the linear polarization angle in proportion to the enclosed current and the number of fiber turns.
Figure 1 shows an example of MO sensor system where the fiber is passing through the axis of a solenoid of radius R and possessing N coils. In Figure 1, the unpolarized light from a light source in this case a SLD passes through a linear fiber polarizer. The output light of the polarizer passes through a polarization controller and then into a fiber placed in the axis of the solenoid. The current passes through the coils of the solenoid from the current sources and produces a magnetic field, which will

Figure 1. Setup of a possible fiber based magneto-optical current measurement system.
rotate the polarization of the light passing through the fiber. The output polarization is measured using a polarization measurement system and the results are transmitted to a personal computer.
In current calculations, the magnetic field inside the solenoid is assumed to be constant. This approximation is true in the case of an infinitely long solenoid. However, the solenoid, which is used in MO sensors, has a finite length. As a result, this might lead to a discrepancy between the theory and the measurement. The purpose of this work is to show this discrepancy for the short solenoid. The next Section 2 is dedicated to review Faraday rotation. Section 3 introduces the system and Section 4 represents the main principles of the MO sensors. A summary and conclusion is given in Section 5.
2. Faraday Rotation
The Faraday effect describes the rotation if the plane of polarization of a light wave as it propagates through a medium subjected to a magnetic field parallel to the direction of propagation of the light. The Faraday effect in single mode fibers permits a fast response for current sensing on hight-voltage transmission lines if sufficiently long fibers can be used [8-10]. In an ideal nonbirefringent fiber of length LF, wound in NF turns of radius r around a conductor carrying a current I, the Faraday effect will rotate the plane of polarization for an incident linearly polaized light beam through an angle θF which is proportional to the magnetic field strength , and the Verdet constant V.
, and the Verdet constant V.
 (1)
(1)
The Verdet constant can be utilized as an indicator for the suitability of a magnetic material for its use as Faraday rotator. It is defined as the rotation per unit path, per unit field strength [11].
3. System Architecture
The magnetic field strength 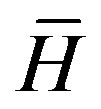 induced by an electrical current in a conductor can be calculated by the BiotSavart law
induced by an electrical current in a conductor can be calculated by the BiotSavart law
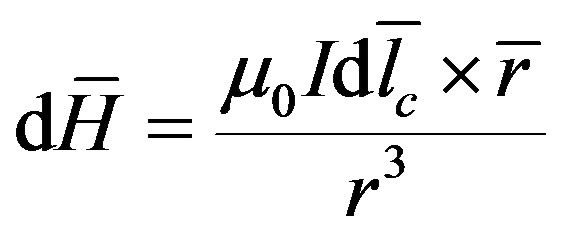 (2)
(2)
where μ0 is permeability of vacuum, lc is the length element of the conductor, and r the displacement vector from the element to the field point.
The configuration we have is that the fiber is passing along the axis of a solenoid, named the z-axis. The solenoid have length LS and NS turns of radius R. The center of the coordinate axis is chosen to be the center of the solenoid. The magnetic field strength 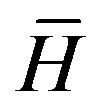 is calculated at a point (X, 0, Z) from the solenoid center to be
is calculated at a point (X, 0, Z) from the solenoid center to be
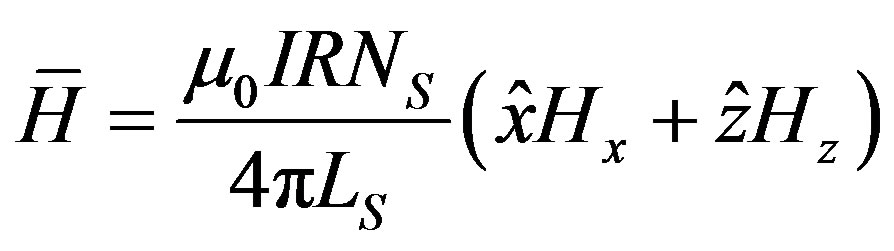 (3)
(3)
where NS is defined as the length of the solenoid LS divided by the thickness of the constructing wire of the solenoid WS,
 (4)
(4)
 (5)
(5)
and
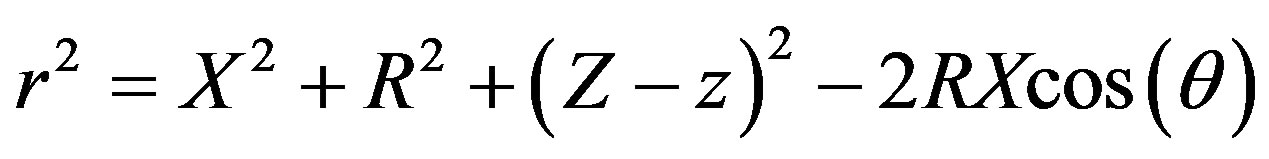 (6)
(6)
In the calculation of the magnetic field the y component is equal to zero due to the symmetry of the problem.
Equation (3) can be formulated in terms of Elliptic functions E(m) and K(m)
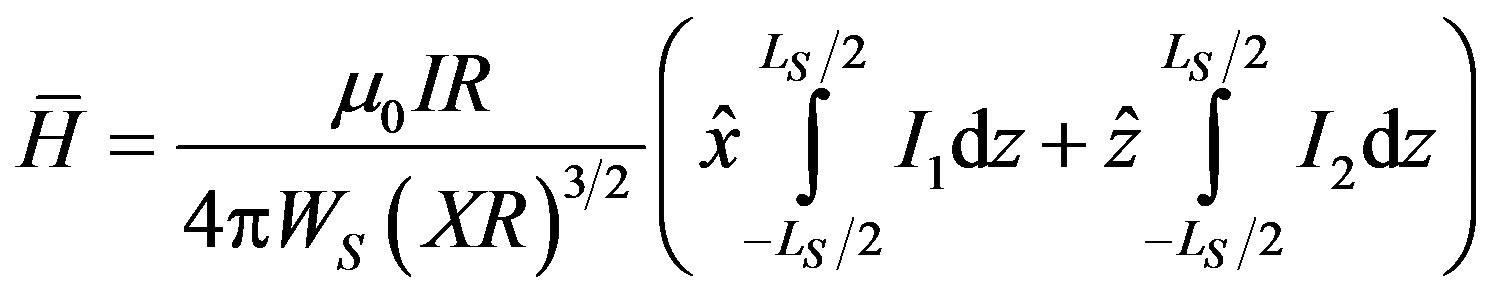 (7)
(7)
where
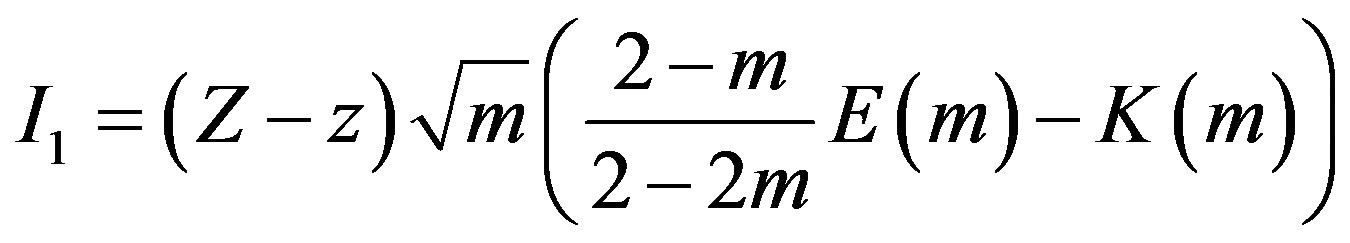 (8)
(8)
 (9)
(9)
and m is
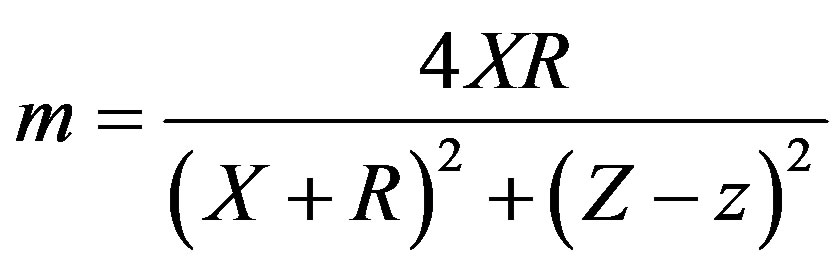 (10)
(10)
The sensitivity S = dθ/dI is calculated as follows,
 (11)
(11)
In Equation (11) the length of the fiber is limited by the length of the solenoid. Here the length of the solenoid is introduced as a variable such that we can calculate the sensitivity for different solenoids’ lengths.
4. MO Sensor with the Fiber Passing through the Center of the Solenoid
In this section, we consider a special case where the fiber is passing through the center of the solenoid. In this case the magnetic field at a point along the z axis can simply calculated from Equation (3) or Equation (7) by simply define X = 0
 (12)
(12)
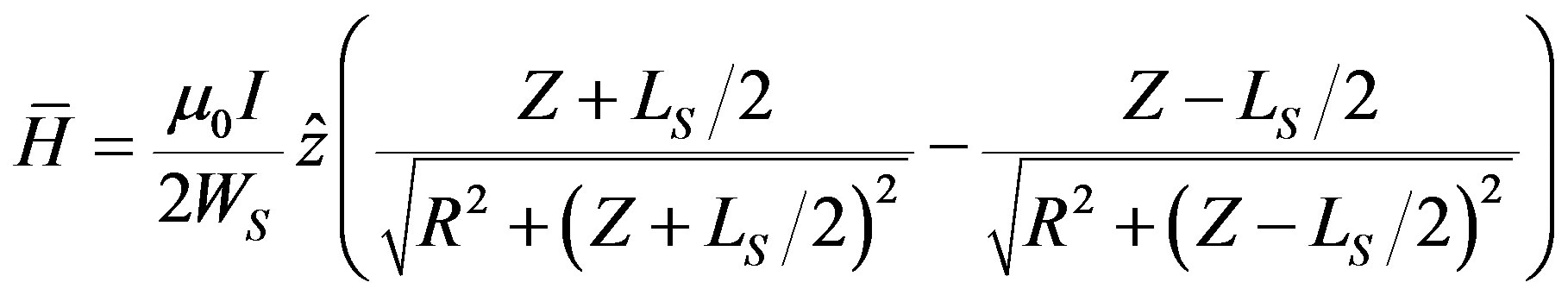 (13)
(13)
Equation (13) is simplified for a very long solenoid to be
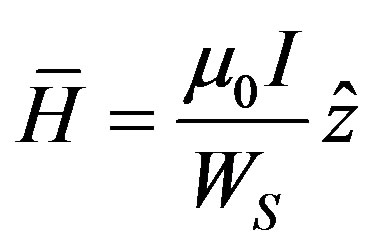 (14)
(14)
The sensitivity can be calculated from Equations (11) and (12) yielding
 (15)
(15)
while the approximated sensitivity Sa as calculated using Equation (14) is
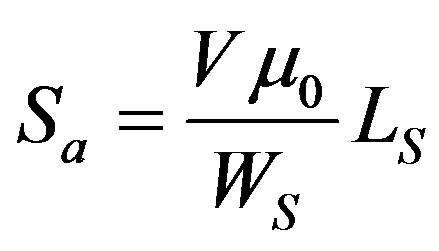 (16)
(16)
Figure 2 shows the magnetic field at the center of the solenoid as calculated from the exact formula 14 and the approximated formula 15. It is clear that the field extended at the ends of the solenoid in the exact calculation as compared to the approximated calculation.
Figure 3 and Figure 4 illustrate the sensitivity as a
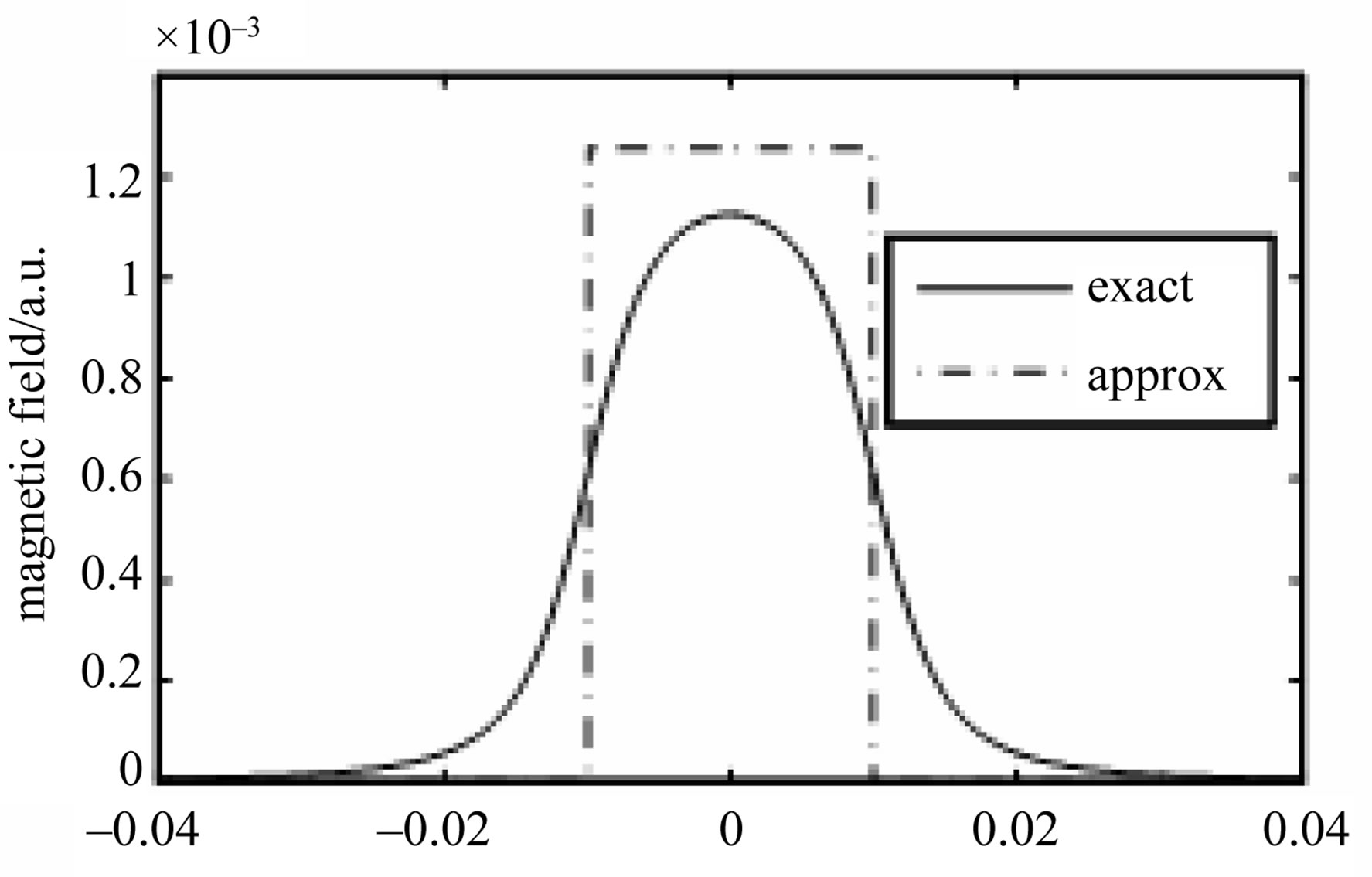
Figure 2. Magnetic field projected on the fiber from the exact and the approximate formula.
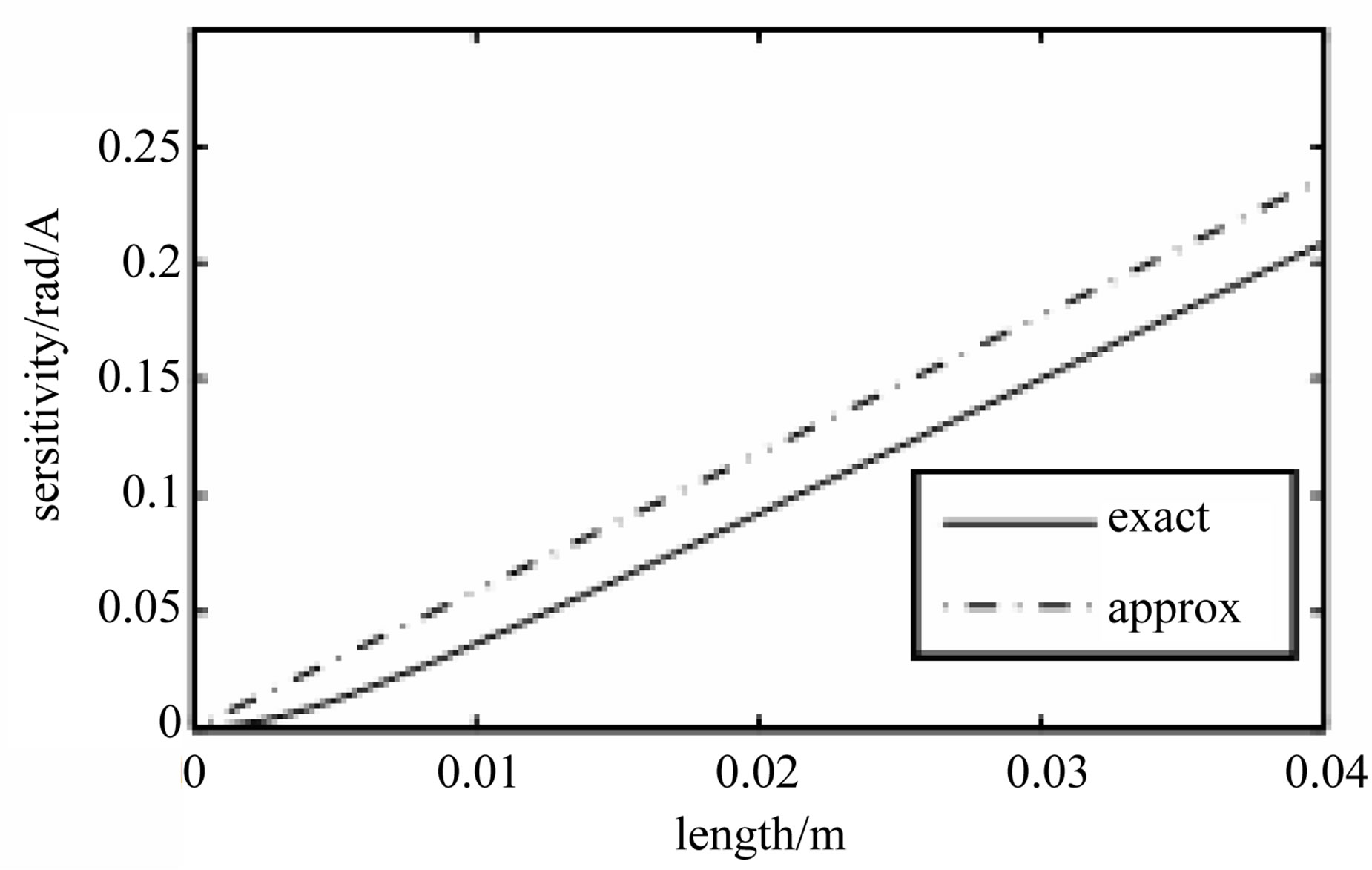
Figure 3. Sensitivities of short solenoids as function of the solenoid length as measured using exact field and approximate field formulas for small solenoid length.
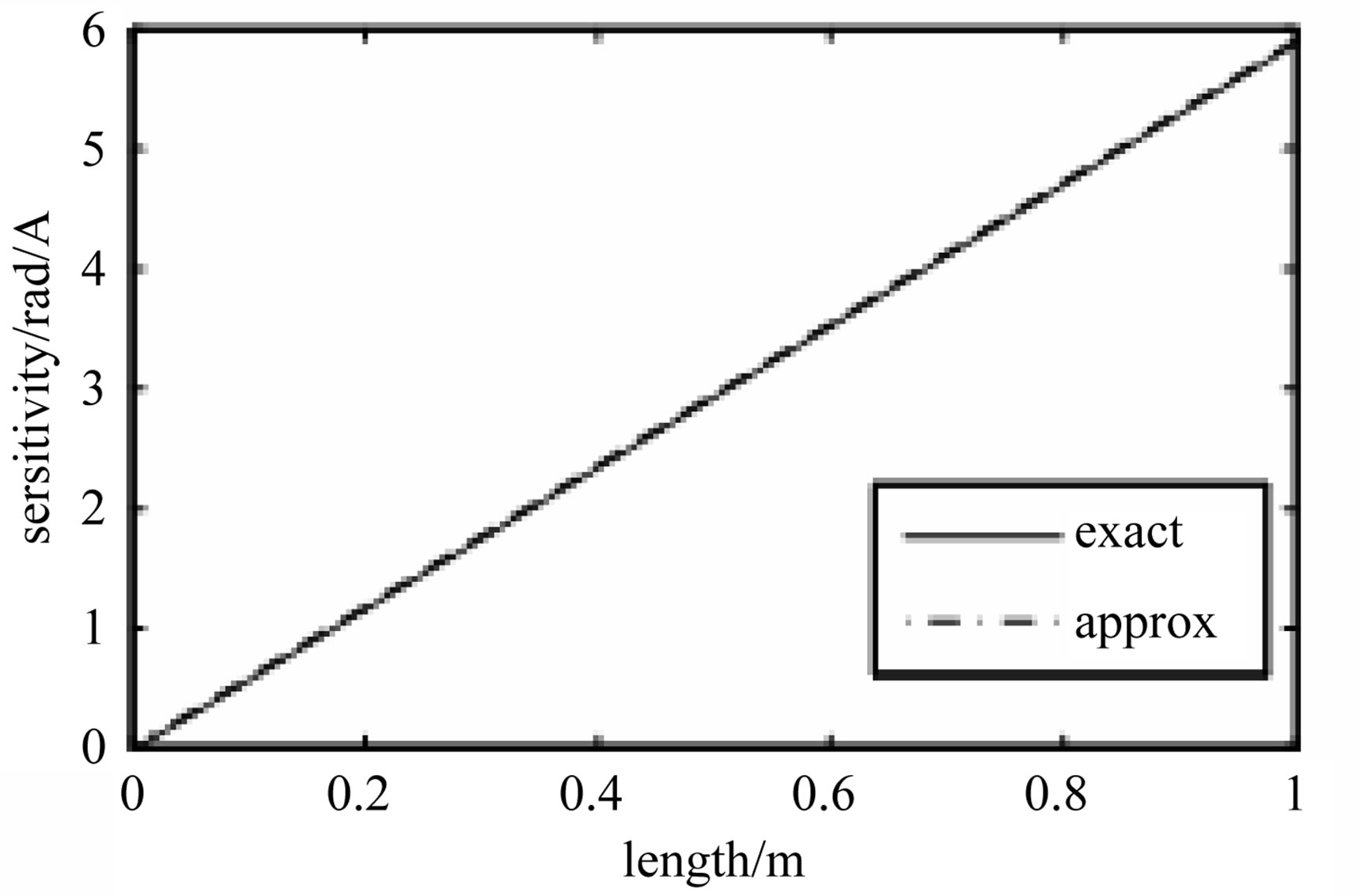
Figure 4. Sensitivities of long solenoids as function of the solenoid length as measured using exact field and approximate field formulas for small solenoid length.
function of the length of the solenoid. In Figure 3, which represents the sensitivity for short solenoids, illustrates that the calculated sensitivity from the exact formula is different from the sensitivity as calculated from the approximate formula. However, the two values of the sensitivity match for long solenoids as represented by Figure 4.
5. Summary and Conclusion
The effect of an inhomogeneous magnetic field on the sensitivity of an optical current sensor is studied in this work. The sensor consists of an optical fiber situated at the longitudinal axis of the solenoid. The results show that the sensitivity as calculated from exact calculation of the magnetic field differs from the sensitivity calculated using an approximate calculation of the magnetic field for short solenoids. For long solenoids the two values coincides.
REFERENCES
- F. Rahmatian and J. N. Blake, “Applications of High Voltage Fiber Optic Current Sensors,” 2006 IEEE Power Engineering Society General Meeting, Montreal, 18-22 June 2006.
- M. J. Freiser, “A Survey of Magneto-Optic Effects,” IEEE Transactions on Magnetics, Vol. 4, No. 2, 1968, pp. 152-161. doi:10.1109/TMAG.1968.1066210
- J. G. Bai, G. Lua and T. Lin, “Magneto-Optical Current Sensing for Applications in Integrated Power Electronics Modules,” Sensors and Actuators A, Vol. 109, 2003, pp. 9-16.
- H. J. El-Khozondar, R. J. El-Khozondar, M. S. Mueller and A. W. Koch, “Sensitivity of TM Nonlinear Magnetooptical Integrated Optical Sensor,” Multidicipline Modeling in Materials and Structures (MMMS), accepted, 2011.
- B. Lee, “Review of Present Status of Optical Fiber Sensors,” Optical Fiber Technology, Vol. 9, No. 2, 2003, pp. 57-79.
- B. Wu, Y. Yang, and K. Qiu, “Magneto-Optic Fiber Bragg Gratings with Application to High-Resolution Magnetic Field Sensors,” 1st Asia-Pacific Optical Fiber Sensors Conference, Chengdu, 7-9 November 2008.
- L. Shao, C. L. W. Liu and D. Xu, “A Passive Optical Fiber Current Sensor Based on YIG,” 1st Asia-Pacific Optical Fiber Sensors Conference, Chengdu, 7-9 November 2008, pp. 1-4.
- A. M. Smith, “Polarization and Magnetooptic Properties of Single-Mode Optical Fiber,” Applied Optics, Vol. 17, No. 1, 1978, pp. 52-56. doi:10.1364/AO.17.000052
- A. Papp and H. Harms, “Polarization Optics of Liquid Core Optical Fibers,” Applied Optics, Vol. 16, No. 5, 1977, pp. 1315-1319. doi:10.1364/AO.16.001315
- H. Schneider, H. Harms, A. Papp and H. Aulich, “LowBirefringence Single-Mode Optical Fibers: Preparation and Polarization Characteristics,” Optical Society of America, Vol. 17, 1978, pp. 3035-3037.
- A. K. Zvezdin and V. A. Kotov, “Modern Magnetooptics and Magnetooptical Materials,” CRC Press, Boca Raton, 1997. doi:10.1887/075030362X

