Journal of Sensor Technology
Vol.1 No.3(2011), Article ID:7662,4 pages DOI:10.4236/jst.2011.13011
The Effect of Magnetic Field-Tuned Resonance on the Capacitance of Laminate Composites
Magnetoelectronic Lab, Nanjing Normal University, Nanjing, China
E-mail: *zhangning@njnu.edu.cn
Received June 1, 2011; revised July 15, 2011; accepted July 26, 2011
Keywords: Composite Materials, Laminates, Functional, Magnetoelectric Coupling, Magneto-Capacitance Effects
Abstract
The magneto-electric coupling and magneto-capacitance effect of a layer composite ferromagnet/ piezoelectric/ferromagnet was investigated. Several resonant peaks were observed on the curves of the capacitance versus frequency. The resonant peaks were found to shift under an applied magnetic field, and the impedance of the sample can be changed from capacitive to inductive ones with changing the field. Thus, giant negative and positive magneto-capacitance effects can be observed simultaneously under a magnetic field less than 1 k Oe near the resonant points. Experimental and theoretical analysis showed that such magnetically tuned variation in impedance originates from the magnetic field-induced change of the compliances of the magnetic phase of the composite.
1. Introduction
The magnetic field-induced change of capacitance, which is known as magneto-capacitance (MC) effects, is currently attracting much interest of study for new applications in microwave field, magnetic detection in broad band of frequency and electronic devices, such as magnetic sensors, tunable spin filter, storage devices, etc. Compared to Hall detector, MC sensors have higher accuracy, simpler structure and much cheaper cost [1-6]. There are two kinds of materials that can show MC effects. One is single phase material and the other is laminate composites. However, the multiferroic single-phase material shows a very low MC effect and often need to be operated under very strong magnetic field [7]. For example, a 2% room-temperature MC effect in nanocomposites of BaTiO3-CoFe2O4 with a magnetic field of 8 T has reported recently [8]. Since Suchtelen suggested magnetoelectric effects in composites, extensive studies have also been performed on MC effect in the magnetoelectric composites [9]. On the other hand, there was report to point out that the resonance frequency of the layered magnetostrictive/piezoelectric composites can be tuned by external magnetic field [10-13]. Thus, huge MC effect can be expected near the resonant frequency of a laminate composite since any small change in frequency near the resonance points will cause a dramatic change in the capacitance.
In this work, we present an observation of the magnetic field-induced shift of the resonance-frequency of a trilayer composite at room temperature.
2. Sample Characterization
The magnetoelectric (ME) laminate under investigation was a trilayer composite of Terfenol-D/Pb(Zr, Ti)O3/ Terfenol-D. Terfenol-D is a rare earth alloy and famous for its performance in magnetostriction. Pb(Zr, Ti)O3 (PZT) is a most often used piezoelectrics for its mature techniques of preparation and larger pezioelectric coefficients. Both were cut into strips in size of (20 × 7 × 2) mm3 and of (30 × 8 × 2) mm3, respectively. The layer of PZT was made a little longer than Terfenol-D in order to make electrodes. The cut strips were glued into sandwich-like trilayers by nonconductive epoxy adhesives, as shown in Figure 1. Two magnetic fields were used for the magnetoelectric measurements, a bias field and an alternative filed. Both fields were paralell each other. The sample was placed in the fields with its length parallel to the fields. The capacitance along the direction of the thickness of the PZT was measured with a high frequency LCR Meter (TH2826, Tonghui Electronic Co.,

Figure 1. Configuration of the magnetoelectric laminates.
LTD, Changzhou, China).
3. Experimental Results and Discussion
Figure 2 shows the frequency dependence of capacitance under different external magnetic fields. Firstly, three resonance peaks are observed in the range of the frequencies manipulated with zero magnetic field. They locate at 175.5 kHz, 187.1 kHz and 194.0 kHz, respectively. Huge variation of capacitance can be found in the areas around the resonance frequencies ( ). But the value reveals to be relatively stable in other areas. Secondly, the resonance frequencies change distinctly with increasing magnetic field. Take the second peak as an example, the resonant frequency decreases from
). But the value reveals to be relatively stable in other areas. Secondly, the resonance frequencies change distinctly with increasing magnetic field. Take the second peak as an example, the resonant frequency decreases from 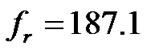 to 184.4 kHz with increasing the field from 0 to 150 Oe, then increases from fr = 184.4 to 189.3 kHz with increasing the field from 150 to 300 Oe.
to 184.4 kHz with increasing the field from 0 to 150 Oe, then increases from fr = 184.4 to 189.3 kHz with increasing the field from 150 to 300 Oe.
To reveal the magnetic field effect on the resonance
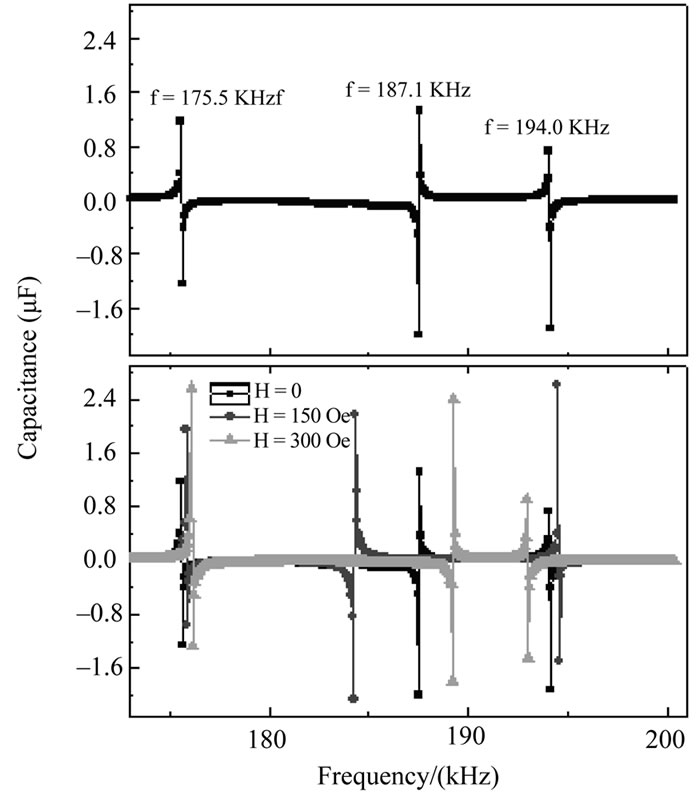
Figure 2. Upper panel: the frequency dependence of capacitance under zero field. Lower panel: the frequency dependence of capacitance under different external magnetic fields.
frequency, field dependent shift of frequency at different resonant points were investigated. Defined the frequency shift as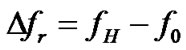 , where
, where 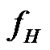 and
and 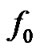 are the frequencies with and without field, respectively, the relation between
are the frequencies with and without field, respectively, the relation between 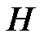 and
and 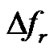 is shown in Figure 3. It is found that the shifts undergo a peak at first then a valley as the field is increased from zero to about 1500 Oe. Then all the shifts maintain stable at different final states.
is shown in Figure 3. It is found that the shifts undergo a peak at first then a valley as the field is increased from zero to about 1500 Oe. Then all the shifts maintain stable at different final states.
Just as the frequency shifts, giant magneto-capacitance can be observed near the resonant frequencies, as shown in Figure 4. It can be seen that the capacitances at different resonant points also experience a peak and a valley with increasing the field. It means that the impedance of the sample can be changed from capacitive to inductive ones with changing the field. Thus, giant negative and positive magneto-capacitance effects can be observed simultaneously under a magnetic field less than 1 k Oe near the resonant points.
According to the theory of multilayer composites [10, 14], the sound speed in the present laminate composite can be expressed as
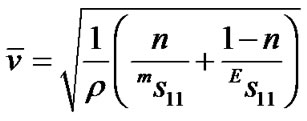 (1)
(1)
where 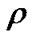 is the average density of the composite,
is the average density of the composite,  and
and  are the compliances of PZT and Terfenol-D respectively,
are the compliances of PZT and Terfenol-D respectively, 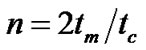 ,
,  is the thickness of Terfenol-D,
is the thickness of Terfenol-D,  is the total thickness of the laminate. When under a magnetic field,
is the total thickness of the laminate. When under a magnetic field, 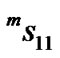 in Equation (1) should be replaced with [10]
in Equation (1) should be replaced with [10]
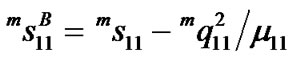 (2)
(2)
where 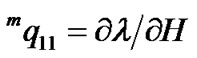 is the piezomagnetic coefficient, l is the magnetostrictive coefficient, and μ11 is magnetic permeability of Terfenol-D. Since
is the piezomagnetic coefficient, l is the magnetostrictive coefficient, and μ11 is magnetic permeability of Terfenol-D. Since  is generally positive,
is generally positive, 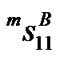 should be less than
should be less than 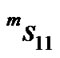 under an applied field, leading to increase the sound speed in Ter-
under an applied field, leading to increase the sound speed in Ter-

Figure 3. Applied magnetic field dependence of the frequency shifts at different resonant points of the sample.
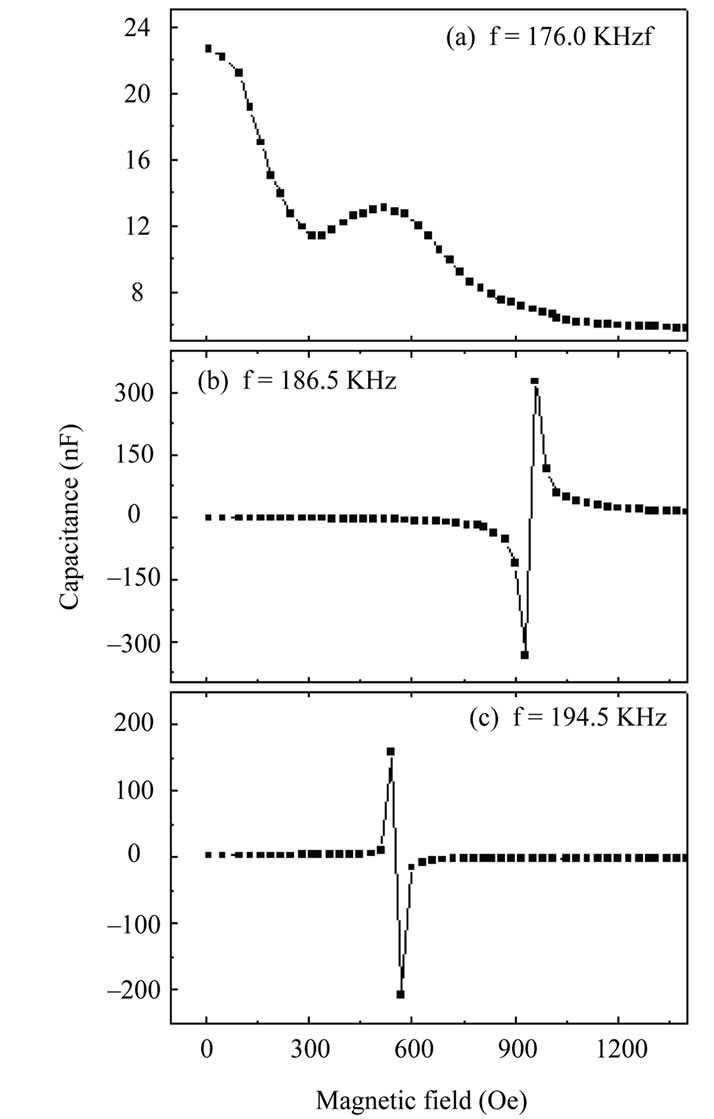
Figure 4. Applied magnetic field dependence of the capacitances near different frequencies.
fenol-D with presence of a magnetic field. Therefore, the sound speed in laminate composite can be magnetically tuned. On the other hand, the resonant frequency of longitudinal vibration mode of a piezoelectric is given as [15]
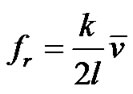 ,
, (3)
(3)
where l is the length of the PZT. So we have the conclusion that the magnetic field-controlled compliances of the ferromagnet are responsible for the magneto-frequency. Equation (3) refers only to the vibration in longitudinal direction of the sample. It means that Equation (3) can be set up only in the case that the couplings between the longitudinal vibration and the vibrations in both transverse directions can be ignored. It requires, in this ideal case, the thickness and the width of the sample are much smaller than the length. But this condition can not be satisfied completely for practical samples. So the values measured in Figure 2 can not fully coincide with that calculated from Equation (3).
According to the constitutive equations of the piezoelectric and magnetostrictive phases and the interlayer elastic coupling [10], as well as considering the capacitance with two plain plates is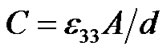 , where A is the area of a plate and d is the PZT thickness, and
, where A is the area of a plate and d is the PZT thickness, and 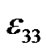 can be expressed as
can be expressed as
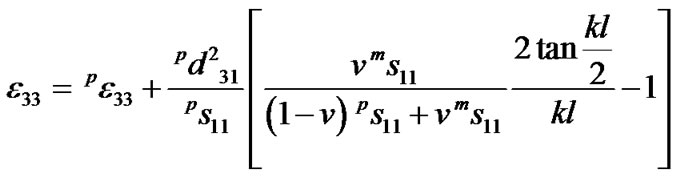
so the expression of the capacitance for the composite can be written as

(4)
where
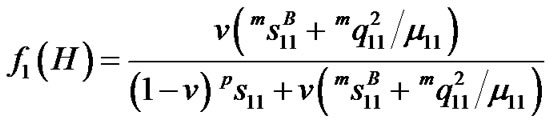 ,
,
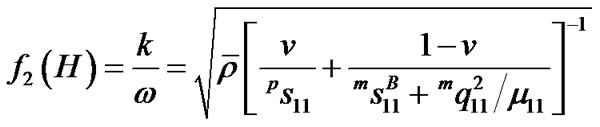 ,
, 
is angular frequency, 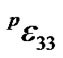 and
and 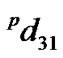 are the permittivity and piezoelectric coefficient of PZT, respectively,
are the permittivity and piezoelectric coefficient of PZT, respectively, 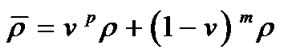 is the average mass density, n is the PZT volume fraction, and
is the average mass density, n is the PZT volume fraction, and 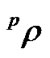 and
and 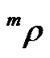 are the densities of PZT and Terfenol-D, respectively. Equation (4) shows that the capacitance of the composite is closely relative to the signal frequency, the size of the sample and the physical parameteres of the materials used. Since the compliances of PZT and Terfenol-D are influenced by the applied field (Equation (2)), the capacitance of the composite is also the function of magnetic field. In accordance with Equation (3), the resonant condition should be
are the densities of PZT and Terfenol-D, respectively. Equation (4) shows that the capacitance of the composite is closely relative to the signal frequency, the size of the sample and the physical parameteres of the materials used. Since the compliances of PZT and Terfenol-D are influenced by the applied field (Equation (2)), the capacitance of the composite is also the function of magnetic field. In accordance with Equation (3), the resonant condition should be
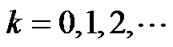
 (5)
(5)
Thus, collecting the results from Equation (1)-(4), we obtain the relation between resonant frequency and external magnetic field as
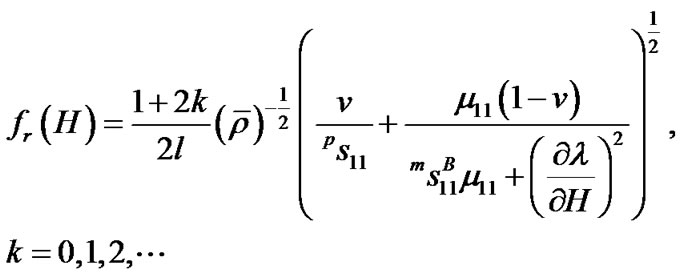
(6)
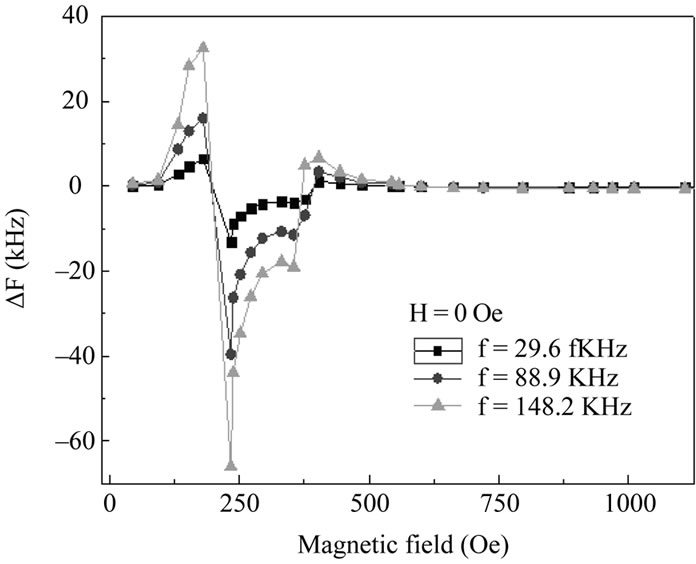
Figure 5. Calculated frequency shifts as functions of applied magnetic field.
Using Equation (6), the resonance frequencies under zero field and the shifts of the resonance frequencies with changing magnetic field can be worked out, respectively. The results are shown in Figure 5. The material parameters used in the calculation are
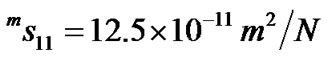 ,
,
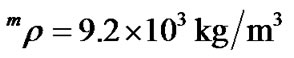
(for Terfenol-D),
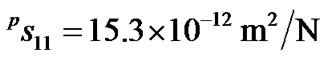 ,
,
 ,
,
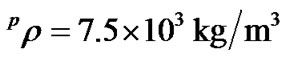
(for PZT), respectively [16-17], and the volume fraction of PZT is taken as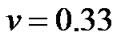 . As can be seen, the results shown in Figure 5 are in agreement with that observed in experiments (in Figure 3), suggesting that the theoretical model discussed above is reasonable.
. As can be seen, the results shown in Figure 5 are in agreement with that observed in experiments (in Figure 3), suggesting that the theoretical model discussed above is reasonable.
Equation (6) suggests that there are several capacitive resonant frequencies fr for the present composite, and the resonant points appear periodically. However, it is worthy of noticing that Equation (6) was derived on the base of Equation (3). So the vibration of single direction is also one of the assumptions of Equation (6). Thus, the experimental data of 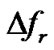 seems deviate from those of the calculated data. Nevertheless, Equation (6) is also helpful in understanding the origination of
seems deviate from those of the calculated data. Nevertheless, Equation (6) is also helpful in understanding the origination of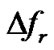 .
.
4. Conclusions
The impedance of layered magnetoelectric composites can be changed from capacitive to inductive ones with changing applied field near their magnetoelectric resonant points. Thus, giant negative and positive magnetocapacitance effects can be observed simultaneously around the resonant frequencies. Magnetic field-induced change of the compliances of the ferromagnetic phase results in the variation of the sound speed, then in the resonant frequencies and the capacity of the layered composite. Because of high sensitivity and low applied magnetic field, the present magnetocapacitive effect can be widely used in magnetic sensors, state transducers and actuators for relays.
5. Acknowledgements
This work was supported by the National Science Foundation of China under grand number 50977046.
6. References
[1] M. A. Subramanian, T. He, J. Z. Chen, N. S. Rogado, T. G. Calvarese and A. W. Sleight, “Giant Room— Temperature Magnetodielectric Response in the Electronic Ferroelectric LuFe2O4,” Advanced Materials, Vol. 18, No. 13, 2006, pp. 1737-1739. doi:10.1002/adma.200600071
[2] H. Kaiju, S. Fujita, T. Morozumi and K. Shiiki, “Magnetocapacitance Effect of Spin Tunneling Junctions,” Journal of Applied Physics, Vol. 91, No. 10, 2002, p. 7430. doi:10.1063/1.1451754
[3] M. P. Singh, K. D. Truong and P. Fournier, “Magnetodielectric Effect in Double Perovskite La2CoMnO6 Thin Films,” Applied Physics Letters, Vol. 91, No. 4, 2007, Article ID: 042504. doi:10.1063/1.2762292
[4] N. Hur, S. Park, S. Guha, A. Borissov, V. Kiryukhin and S.-W. Cheong, “Low-Field Magnetodielectric Effect in Terbium Iron Garnets,” Applied Physics Letters, Vol. 87, No. 4, 2005, Article ID: 042901. doi:10.1063/1.1997272
[5] M. P. Singh, W. Prellier, C. Simon and B. Raveau, “Magnetocapacitance Effect in Perovskite-Superlattice Based Multiferroics,” Applied Physics Letters, Vol. 87, No. 2, 2005, Article ID: 022505. doi:10.1063/1.1988979
[6] M. Gich, C. Frontera, A. Roig, J. Fontcuberta, E. Molins, N. Bellido, C. Simon and C. Fleta, “Magnetoelectric Coupling in ε-Fe2O3 Nanoparticles,” Nanotechnology, Vol. 17, No. 3, 2006, p. 687. doi:10.1088/0957-4484/17/3/012
[7] J. G. Wan, Q. Lu, B. Chen, F. Q. Song, J. M. Liu, J. B. Dong and G. H. Wang, “Giant Room-Temperature Magnetocapacitance in Co2+ Doped SnO2 Dielectric Films,” Applied Physics Letters, Vol. 95, No. 15, 2009, Article ID: 152901. doi:10.1063/1.3249584
[8] I. Fina, N. Dix, L. Fàbrega, F. Sánchez and J. Fontcuberta, “Magnetocapacitance in BaTiO3-CoFe2O4 Nanocomposites,” Thin Solid Films, Vol. 518, No. 16, 2010, pp. 4634-4636. doi:10.1016/j.tsf.2009.12.048
[9] J. V. Suchtelen, “Product Properties: A New Application of Composite Materials,” Philips Research Reports, Vol. 27, 1972, pp. 28-37.
[10] C. Israel, V. M. Petrov, G. Srinivasan and N. D. Mathur, “Magnetically Tuned Mechanical Resonances in Magnetoelectric Multilayer Capacitors,” Applied Physics Letters, Vol. 95, No. 7, 2009, Article ID: 072505. doi:10.1063/1.3205477
[11] Y. J. Chen, X. Y. Zhang, C. Vittoria and V. G. Harris, “Giant Magnetodielectric Effect and Magnetic Field Tunable Dielectric Resonance in Spinel MnZn Ferrite,” Applied Physics Letters, Vol. 94, No. 10, 2009, p.102906. doi:10.1063/1.3095498
[12] G. Srinivasan, C. P. De Vreugd, V. M. Laletin, N. Paddubnaya, M. I. Bichurin, V. M. Petrov and D. A. Filippov, “Resonant Magnetoelectric Coupling in Trilayers of Ferromagnetic Alloys and Piezoelectric Lead Zirconate Titanate: The Influence of Bias Magnetic Field,” Physical Review B, Vol. 71, No. 18, 2005, Article ID: 184423. doi:10.1103/PhysRevB.71.184423
[13] V. Castel and C. Brosseau, “Magnetic Field Dependence of the Effective Permittivity in BaTiO3/Ni Nanocomposites Observed via Microwave Spectroscopy,” Applied Physics Letters, Vol. 92, No. 23, 2008, Article ID: 233 110. doi:10.1063/1.2943153
[14] S. X. Dong, J. F. Li and D. Viehland, “Longitudinal and Transverse Magnetoelectric Voltage Coefficients of Magnetostrictive/Piezoelectric Laminate Composite: Theory,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 50, 2003, p.1253.
[15] J. G. Wan, Z. Y. Li, Y. Wang, M. Zeng, G. H. Wang and J.-M. Liu, “Strong Flexural Resonant Magnetoelectric Effect in Terfenol-D∕Epoxy-Pb(Zr,Ti)O3 Bilayer,” Applied Physics Letters, Vol. 86, No. 20, 2005, Article ID: 202504. doi:10.1063/1.1935040
[16] A Bayrashev,W. P. Robbins and B. Ziaie, “Low Frequency Wireless Powering of Microsystems Using Piezoelectric-Magnetostrictive Laminate Composites,” Sensors and Actuators A, Vol. 114, No. 2-3, 2004, pp. 244-249. doi:10.1016/j.sna.2004.01.007
[17] M. I. Bichurin,V. M. Petrov and G. Srinivasan, “Theory of Low-Frequency Magnetoelectric Coupling in Magnetostrictive-Piezoelectric Bilayers,” Physical Review B, Vol. 68, No. 5, 2003, Article ID: 054402. doi:10.1103/PhysRevB.68.054402

