Journal of Behavioral and Brain Science
Vol.4 No.7(2014), Article
ID:47993,17
pages
DOI:10.4236/jbbs.2014.47032
EEGbands: A Computer Program to Statistically Analyze Parameters of Electroencephalographic Signals
Miguel Angel Guevara, Araceli Sanz-Martin, Marisela Hernández-González
Instituto de Neurociencias, CUCBA, Universidad de Guadalajara, Guadalajara, Jalisco, México
Email: mariselh@cencar.udg.mx
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 May 2014; revised 30 June 2014; accepted 12 July 2014
ABSTRACT
The quantitative analysis of electroencephalographic activity (EEG) is a useful tool for the study of changes in brain electrical activity during cognitive and behavioral functions in several experimental conditions. Their recording and analysis are currently carried out primarily through the use of computer programs. This paper presents a computerized program (EEGbands) created for Windows operating systems using the Delphi language, and designed to analyze EEG signals and facilitate their quantitative exploration. EEGbands applies Rapid Fourier Transformation to the EEG signals of one or more groups of subjects to obtain absolute and relative power spectra. It also calculates both interhemispheric and intrahemispheric correlation and coherence spectra and, finally, applies parametrical statistical analysis to these spectral parameters calculated for wide frequency EEG bands. Unlike other programs, EEGbands is simple and inexpensive, and rapidly and precisely generates results files with the corresponding statistical significances. The efficacy and versatility of EEGbands allow it to be easily adapted to different experimental and clinical needs.
Keywords:EEG Correlation, EEG Coherence, Relative Power, Absolute Power, EEG Software, EEG Signal Analysis

1. Introduction
The electroencephalographic (EEG) activity makes it possible to study the relationship between behavior and the nervous system without an invasive intervention. EEGs can be defined as voltage fluctuations caused by intra and extraneuronal ionic currents in a population of pyramidal cortical neurons, arranged radially to the surface, which are activated synchronously. Although generated in the cortex, EEGs are modulated by the activity of subcortical regions [1] . As EEGs have a high temporal resolution, they can produce recordings that last from milliseconds to hours or even days.
Although qualitative EEG analysis is still used in medicine, quantitative analysis of EEGs has become even more common due to the advances offered by personal computers. The recording and quantitative analysis of electroencephalographic data have been used for many years to examine changes in brain electrical activity associated with different physiological states; for example, sleep and wakefulness [2] ; hormonal changes [3] ; pharmacological manipulations [4] [5] ; during different behaviors [6] -[8] ; and while performing cognitive tasks [9] -[13] . In the clinical setting, quantitative EEGs have proven useful in investigating alterations in the functional relations among cortical regions in several pathologies, including cerebral tumors [14] , epilepsy [15] , schizophrenia [16] , Asperger syndrome [17] , autism [18] , Alzheimer’s disease [19] [20] , sleep apnea [21] [22] , and child abuse [23] among others.
Quantitative analysis of EEGs requires the digitization of analogical signals, for which it is desirable to use time series methods, such as spectral analysis of amplitudes. All spectral analyses decompose the complex wave forms of a linear sum of components of elementary waves. Fourier analysis allows the signal to be changed lineally from the time domain to the frequency domain using sine and cosine as elementary waves [24] . The Fast Fourier Transform (FFT) makes it possible to break an EEG signal down into its frequency components, calculate the amplitude of each component, and then group them into specific frequency bands. These amplitudes (grouped in individual frequencies or bands) constitute the amplitude spectrum of the signal under study, and the square of this amplitude spectrum is the absolute power (i.e., the amplitude at each frequency is squared). The sum of all the absolute power values that make up the spectrum is called total absolute power, and this can be considered graphically as the area comprised between the spectral curve and the abscissa axis. The relative power spectrum is obtained from the absolute powers by calculating the proportion of each frequency (or frequency band) with respect to total absolute power.
In addition to FFT, the quantitative analysis of EEG has also often used coherence and correlation, two mathematical indexes that make it possible to determine the degree of similarity between two electroencephalographic signals, and to establish a possible functional relation among different brain regions [25] -[28] . The use of coherence and correlation is based on the assumption that electroencephalographic similarity between two cortical areas reflects similarity in the underlying neurophysiological processes, such as the same inputs, similar information processing, or broad connections between them. In the opposite case, when the underlying neurophysiologic processes of two cortical areas are different, the EEG signals from the two areas differ as well [29] - [32] . In other words: the greater the functional relation between the two areas, the greater the similarity in their respective activity [31] [33] .
Though these two methods have traditionally been considered equivalent, there are some important differences in the procedures used to calculate them and in the results that they provide. Coherence is calculated by dividing the numerical square of the cross-spectrum by the product of the autospectra; therefore, it is sensitive to changes in power as well as to alterations in phase relationships. For this reason, if either power or phase changes in one of the signals, the coherence value is affected. Another important distinction is that the coherence value for a single epoch or segment is always 1, regardless of the true phase relationship and the power differences between the two signals. Over successive epochs, the measure of coherence is dependent on the power and phase of the two signals through the epochs. If there is no variation over time in the original relationship between the two signals, then the coherence value will equal 1 [34] [35] . This means that coherence does not give direct information on the true relationship between the two signals, but only on the stability of this relationship with respect to power asymmetry and phase relationships [35] . Correlation, in contrast, may be calculated over one single, or several, epochs, and is sensitive to both phase and polarity, regardless of amplitude. Calculating coherence involves squaring the signal, which results in coherence values of 0 to 1, and a loss of polarity information. Unlike coherence, correlation is sensitive to polarity; hence its values rank from −1 to 1 [35] .
At present, the quantitative study of cerebral electrical activity and its functions remains a slow and cumbersome process because, in order to complete and interpret results, the researcher has to use computer programs to analyze the digitized signals and then a different software for the statistical analysis of the data processed (for example, absolute power of coherence) spatially when group analysis is required. Considering this problem and the great utility of quantitative EEG analysis, this paper describes the EEGbands program, which is designed to obtain, rapidly and simultaneously, both the spectral analysis of EEG signals and the statistical (parametric) comparisons among groups or conditions of the signals involved. This program represents an improvement over its predecessors—EEGmagic [36] and EEGcorco [37] —because the former does not analyze coherence, and the latter does not obtain absolute and relative power. Unlike its predecessors that can only work with 2 or 4 channels of EEG signals, EEGbands can simultaneously analyze up to six EEG signals. The objective of this article is to describe the operation and characteristics of EEGbands as well as its practical advantages and disadvantages.
2. Method
2.1. Main Functions
EEGbands is a computer program designed to analyze EEG signals. The program applies Fast Fourier Transform to EEG signals to obtain the values of absolute power (AP) and relative power (RP) of each wide frequency band. In addition, it calculates the correlation spectra (Pearson’s product-moment) and coherence spectra to determine quantitatively the degree of EEG similarity between homologous areas of the right and left hemispheres, and between areas localized in a single hemisphere (interhemispheric and intrahemispheric correlation, respectively). All the above calculations are performed using the standard data required to apply parametric statistics. This means that AP and RP values are transformed into natural logarithms, and correlation and coherence values to Fisher’s Z scores [38] [39] . Finally, EEGbands applies parametric statistics to the values obtained from the spectral analysis.
2.2. Features of EEGbands
EEGbands is a flexible program since it works with EEG signals transformed to ASCII format. Most commercial computer programs designed to acquire EEG signals (i.e. Neuroscan Scan IV, Grass Technology Poly VIEW or Medicit Track Waker) allow their data to be exported to ASCII format. EEGbands is written in Delphi and will run in the Windows environment in any PC-compatible computer that has at least a Pentium processor and 1 Mb of RAM memory. The program requires little space on the hard drive because both the signals to be analyzed and the exit files are in text format (ASCII) and thus occupy only a small amount of disk space. Memory requirements or limitations are determined by the amount of data to be processed.
2.3. Formulas for Calculating EEG Parameters
Figure 1 shows the sequence of steps for computing absolute and relative power, coherence and, correlation.
2.3.1. Power Spectra
Formula (1) represents the Continuous Fourier Transform, while Formulas (2) and (3), respectively, represent the real and imaginary parts of the transform [40] . The instantaneous spectrum of a signal can be obtained by applying Formula (6). Formulas (4) and (5), respectively, show how to obtain the real and imaginary parts of the direct Discrete Fourier Transformation. The absolute power spectra, through the frequency of an EEG signal, can be obtained using Diagram I in Figure 1. The instantaneous spectra of the digitized signals are obtained by calculating the real and imaginary parts of the Direct Fourier transform [40] .
 (1)
(1)
 (2)
(2)
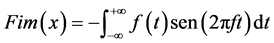 (3)
(3)
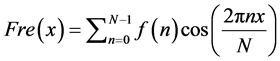 (4)
(4)
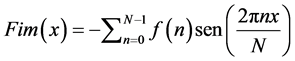 (5)
(5)
 (6)
(6)
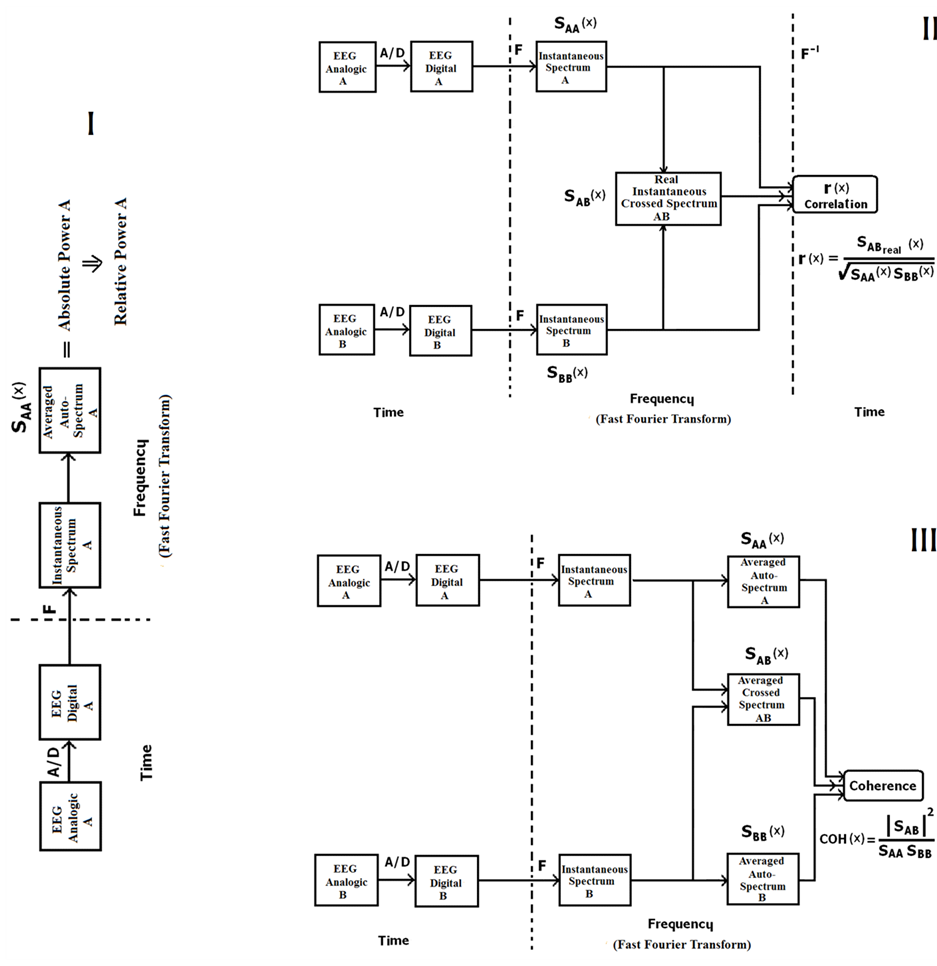
Figure 1. Flowchart indicating the steps to be followed to obtain the values of the parameters analyzed by EEGbands: I = Power; II = Correlation (r); III = Coherence (coh). SAA, SBB = autopower spectra; F = Direct Fourier Transform; F−1 = Inverse Fourier Transform; A/D = Analog-to-Digital Converter; EEG = electroencephalographic activity.
where:
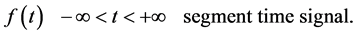
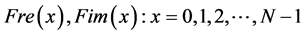 (The N frequencies at which the signals are decomposed).
(The N frequencies at which the signals are decomposed).
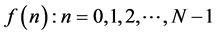 (N samples that make up the signals in the time).
(N samples that make up the signals in the time).
The autopower spectra (average) of signals A and B are obtained from Formulas (7) to (12). Thereafter, the absolute power spectra at frequencies may be grouped in to specific bands. Mean while, relative power is the proportion of each band with respect to total power. The cross-spectrum (average) of the digitized A and B signals are calculated by Formulas (13) to (16):
A autospectrum signal:
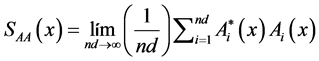 (7)
(7)
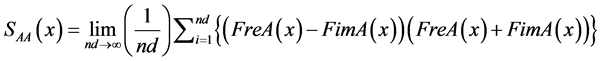 (8)
(8)
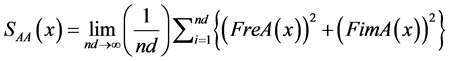 (9)
(9)
B autospectrum signal:
 (10)
(10)
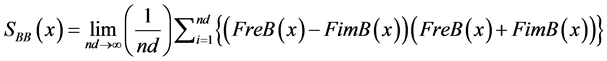 (11)
(11)
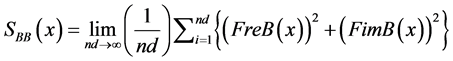 (12)
(12)
Cross-spectrum between signals A and B:
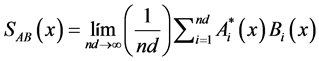 (13)
(13)
 (14)
(14)
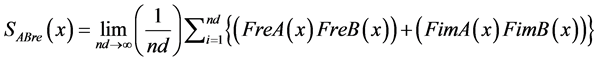 (15)
(15)
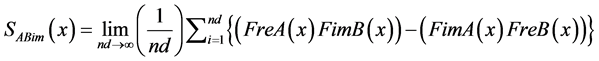 (16)
(16)
where:
nd = number of segments.
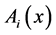 ,
, 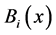 = instantaneous spectra of signals A and B in frequency x.
= instantaneous spectra of signals A and B in frequency x.
 ,
,  = complex conjugates of the instant spectra of signals A and B in frequency x (the conjugate of a complex number is obtained by inverting the sign of the imaginary part).
= complex conjugates of the instant spectra of signals A and B in frequency x (the conjugate of a complex number is obtained by inverting the sign of the imaginary part).
2.3.2. Coherence Spectrum
According to the algorithm illustrated in Figure 1 (III), coherence can be calculated incorporating formulas 7, 10 and 13 into formula 17; that is, the values of the coherence spectrum can be obtained from the autospectra and cross-spectra of signals A and B (Formulas (17)-(19)):
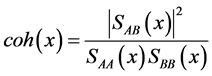 (17)
(17)
where: 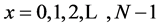 (N frequencies at which the A and B signals are decomposed)
(N frequencies at which the A and B signals are decomposed)
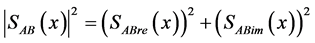 (18)
(18)
By substituting Formulas (9), (12) and (14) in Formula (17), Formula (19) is obtained:
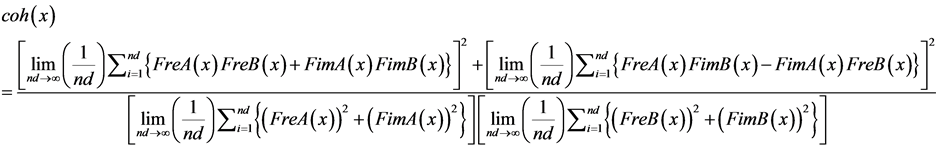 (19)
(19)
2.3.3. Correlation Spectrum
The punctual correlation between two signals, A and B for example, can be calculated using Formula (20). However, as Guevara et al. [26] [37] report, Formula (21) can be applied to obtain the correlation spectrum using the autospectra and cross-spectrum of signals A and B (Figure 1 (II)):
 (20)
(20)
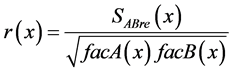 (21)
(21)
where:  (N frequencies at which the A and B signals are decomposed).
(N frequencies at which the A and B signals are decomposed).
Equations (22)-(29) explain the components of Equation (21).
By applying the Fourier Inverse Transformation to the cross-spectrum of a signal, the crossed-correlation function is obtained; as expressed in Equation (22):
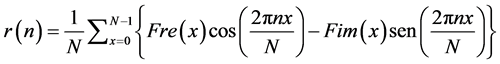 (22)
(22)
r(n), 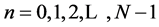 (correlation at each time).
(correlation at each time).
Fre(x) = real part of the cross-spectrum at frequency X.
Fim(x) = imaginary part of the cross-spectrum at frequency X.
The point of correlation that is of interest is the correlation at time zero (for each x frequency); in other words, the only factor of interest is the first place (correlation at time zero) of the correlation function.
Where: n = 0; cos(0) = 1.0, sen(0) = 0; the equation is (23):
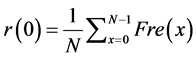 (23)
(23)
It is clear that calculating the first place of the correlation function does not require the use of the imaginary part of the cross-spectrum. Moreover, if it is assumed that for each x frequency all others are zero (as in an ideal filter, where the signals contain only one frequency), then for each x frequency the correlation function at time zero will be calculated by Equation (24):
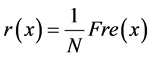 (24)
(24)
where 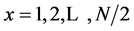 (
(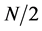 frequencies into which the signals are decomposed) (x initiates at one because the “DC” component is not considered).
frequencies into which the signals are decomposed) (x initiates at one because the “DC” component is not considered).
Since we know that in the previous equation Fre(x) is equal to the real part of the cross-spectrum, 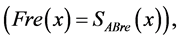 Equation (15):
Equation (15):
Upon considering a single segment (nd = 1, which is possible for the correlation), we obtain Equation (25):
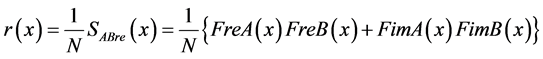 (25)
(25)
To obtain correlations in the range −1 to +1, the values of every r(x) must be divided by the square root of the product of place zero of the inverse transformation of the autospectra signals for the same x frequency; i.e., the autocorrelation at time zero of each A and B signal (FacA(x) and facB(x)), as indicated in Equation (21):
Where facA(x) and facB(x) are defined by Equations (26) and (27):
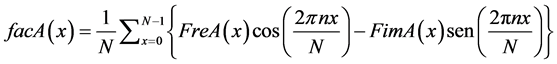 (26)
(26)
 (27)
(27)
However, considering that the only point of interest is the place zero of the Inverse Transformation (n = 0), that the autospectra do not contain an imaginary part, and a value of 0 for all the different frequencies of X, then FreA(x) and FreB(x) are equivalent to the autospectra of the A and B signals. Therefore, for one segment (nd = 1), Equations (28) and (29) are developed:
 (28)
(28)
 (29)
(29)
Upon substituting Equations (25), (28) and (29) in Equation (21), we obtain Equation (30):
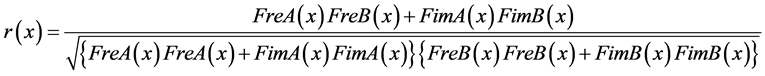 (30)
(30)
In this way, it becomes possible to calculate the correlation spectrum (correlation values for every frequency into which the signal is decomposed) between two cerebral areas.
2.4. Program Performance
To run EEGbands, the analog signals (continuous in amplitude and time) must be digitized (discretized in amplitude and time). For this purpose, “n” points (samples), equally spaced in time, must be taken for each signal segment, and several of these segments must be taken in order to represent the condition of interest. Signals will be stored in text format in individual files (one file for each channel recorded). In these files, each row is assigned only one type of data. Before being transferred to the program, all signals must be reviewed in order to eliminate possible artifacts and coherent noise.
Although the program runs in Windows, it is convenient to assign the signal files an 8-digit name; for example, the file name 21HABAF3.RE2 indicates: two digits for the name of the subject (21), four digits for condition (HABA), and two digits for the derivation (F3). It is also convenient to have 3 digits that identify the type of file (this is arbitrary; RE2 in this example).
Figure 2 shows the Home screen of EEGbands. As can be seen, EEGbands requires a file with names (data files). The program requires at least 2 groups of subjects (independent groups) or one group of subjects with at least 2 conditions (correlated groups). Each separate group or repetition of the same group, occupies a cell; that is, one site in the statistical design. In all cases there must be at least 2 cells. The maximum number of cells that can be occupied by conditions (or groups) is 20.
The user must indicate whether the program will be working with 2, 4 or 6 channels (i.e., if it will analyze 2, 4 or 6 per subject), and whether sampling was reordered at 256, 512, or 1024 Hz (the only sampling frequencies allowed in the program).
By default, the program determines the limits of the EEG bands recorded: band 1, 1 - 3 Hz; band 2, 4 - 7 Hz; band 3, 8 - 10 Hz; band 4, 11 - 13 Hz; band 5, 14 - 19 Hz; band 6, 20 - 30 Hz; and band 7 31 - 50 Hz. However, on the Home screen the user can modify the first 6 analysis bands (band 7 cannot be changed). The user must also indicate whether she/he wants band 7 (gamma) to be considered. Finally, if the program is operating with correlated or mixed designs, the user can choose to subtract the first cell as baseline.
Also on the Home screen, the user must choose whether the statistical design is for independent groups, correlated groups, or mixed groups (also known as split-plot) [41] , and indicate if the design has one or two factors (treatments) and the level numbers of each one. Here, she/he must respect the maximum limit of 20 cells (total groups and/or conditions) and have the same number of subjects in each group (or condition). The maximum number of subjects per group is 30. The mixed design (split-plot) always has two factors: first, the independent groups (plots); and second, the repeated measurements made with each group. In general, all factorial designs may have only two factors, each with a maximum of 10 levels. If the design has 2 groups (or 2 conditions in the same group), t-tests (for independent or correlated groups, as appropriate) are applied to the results. However, if there are more than 2 groups (or conditions), the program automatically applies analysis of variance (ANOVA) and the corresponding post hoc tests (Tukey and Duncan). Figure 3 describes graphically several different designs in which data can be analyzed. As can be seen, the cells are sequentially numbered from left to right and from top to bottom.
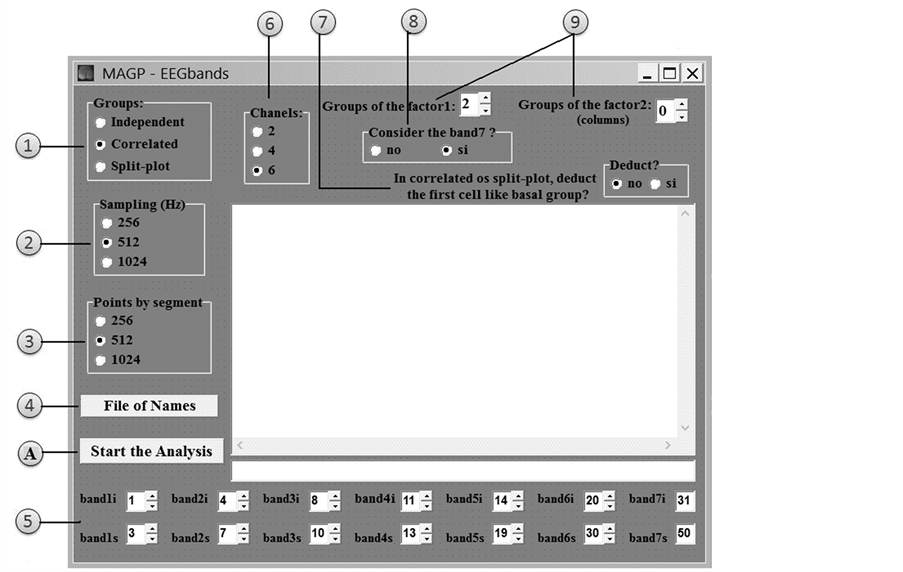
Figure 2. On the Home screen, the user can select all the options of EEGbands: (1) The kind of statistical design (independent groups, correlated groups, or mixed); (2) and (3) Sampling frequency and signal segment points; (4) Name of the text file containing the names of the files of the digitized signals that will be analyzed; (5) The lower (1) and upper value(s) of each band (except band 7, which cannot be modified); (6) The number of channels to be analyzed; (7) The option to subtract the first cell as baseline (only in correlated or mixed designs); (8) The option to consider band 7 (gamma) in the analyses or omit it; (9) Factor levels of statistical design; (A) Start the analysis.
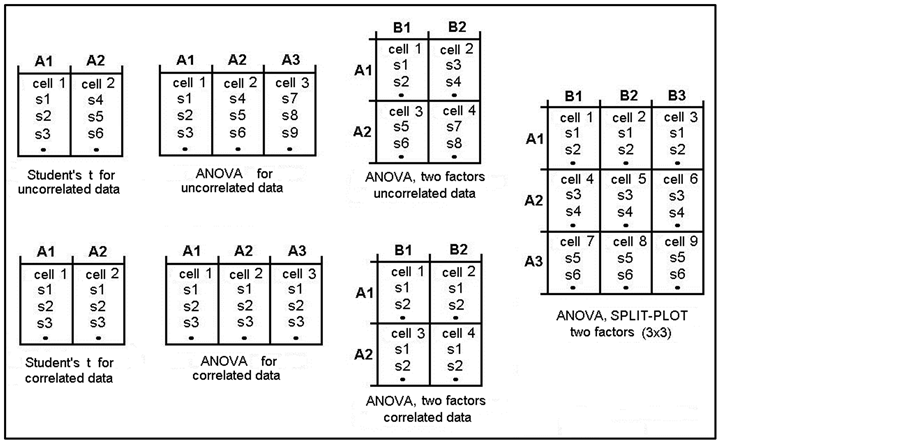
Figure 3. Schematic representation of different statistical designs that can be applied by means of the EEGbands program. The statistical test used for each design is indicated. All must have an equal number of subjects in each cell. A indicates factor or treatment 1, and B indicates factor or treatment 2.
Figure 4 shows how to construct the names file (OAHA3GPS.TXT in the example). While this Figure has only 2 subjects in each group, 2 conditions with 6 derivations are shown, and the complete file contains 2 groups with 12 subjects each. In turn, each group (CG, EG) has 2 conditions (OA, HA). Each subject was recorded at 6 brain regions (derivations F1, F2, F3, F4, P3 and P4). All files have the REV termination, but this can be changed to any other ending (the file must be created in a text editor or Windows Notepad, not in a word processor). This compete file will be used to illustrate the implementation of the program.
All subjects in the first cell must be listed in the names file; each one with all the derivations recorded (from the left channel first, then from the right one). Subsequently, all subjects in the second cell must be listed in the file, and so on until all the cells that make up the design are filled. In the example, the “names file” contains data from a two-factor mixed design (2 × 2). First, the names of the files that constitute the first cell (Group 1 in the first condition) appear, followed by cell 2 (Group 1 in the second condition), cell 3 (Group 2 in the first condition) and, finally, cell 4 (Group 2 in the second condition). EEGbands will not function if any of these files are missing; that is, all files for all subjects must be in the same folder (and all must appear in the “names file”).

Figure 4. Names file with 4 cells that correspond to a 2-factor mixed design (2 × 2). Each cell contains only 2 subjects, each one recorded at 6 derivations. The lines and comments to the right of the names of the files have been added only to illustrate the order of cells. In the example, subjects 02 and 03 belong to the first group, and subjects 23 and 26 to the second. Each group (CG, EG) was recorded in 2 conditions, OA and HA; and the EEG activity of each subject was recorded at 6 scalp regions, F1, F2, F3, F4, P3 and P4. The file extension is REV (but this is arbitrary). It is important to mention that there can be no blank lines at the end of the last names file (in the example, the cursor appears under the last name).
Upon pressing the “Start Analysis” button, the program begins to make calculations and the following output files (text files) are obtained (Table 1):
EEGbands provides 12 output files, all of which have the same name as the “names file”, but a different ending (last 3 characters). The terminated file ABS has both untransformed and transformed values of the absolute power spectrum of the 7 selected bands. REL contains the transformed and untransformed values of the relative power spectrum of the 7 selected bands. TER has both untransformed and transformed values of the interhemispheric correlation spectrum of the 7 bands. TRR contains the untransformed and transformed values of the intrahemispheric correlation spectrum of the 7 bands. TEH shows the untransformed and transformed values of the interhemispheric coherence spectrum in the 7 bands. In TRH we see the untransformed and transformed values of the intrahemispheric coherence spectrum in the 7 bands. All these files, except REL, also have a column for the total band. The RES file contains the untransformed results of all the spectra calculated by band; while RET contains the transformed values. When the program operates with a design that involves 6 channels (6 recorded brain areas), 210 variables (columns) are obtained in the RET and RES files. Table 2 describes the position of these variables. If the program works with only 4 channels, the file contains 112 columns (corresponding to the first 112 columns in Table 2); and if it works with only 2 channels, then the file has 42 columns (first 42 columns of Table 2).
Figure 5 shows parts of the RES and RET files, where we can see that the lines are grouped into the different cells that make up the statistical design. The appropriate statistical test will be applied to each column of these results files and the output files will be obtained from the remaining results. If the statistical design has only two cells, EEGbands will apply a Student t test to either independent or correlated groups. Figure 6 shows part of the output files obtained from the application of the Student t test for independent groups: TES (for untransformed data) and TET (for transformed data).
EEGbands applies an ANOVA when the design has more than two cells. If there is only one factor (independent variable or treatment), the program applies a one-factor ANOVA for separate or correlated groups. If there is more than one factor (i.e., more than one independent variable or treatment), a factorial ANOVA will be applied. EEGbands can only work with 2-factor designs in 3 modes: independent groups, correlated groups and mixed designs (split-plot). In all cases, the program can only run when the same numbers of subjects are included in each cell. The ANOVA results expressed as transformed data are contained in an AVT file.
Figure 7 shows the results of the application of a mixed ANOVA (split-plot) to each variable (columns) in the output file, AVT. Significant comparisons (p < 0.05) are indicated with an asterisk.
In addition to the AVT file, EEGbands always generates TET and TES files after conducting an ANOVA; these files are identical to those obtained in 2-cell designs. In mixed designs, Student t tests for independent groups and a Student t test for correlated groups are provided (as appropriate). When EEGbands runs an ANOVA, it also does the post hoc comparisons among cells using Tukey and Duncan tests to determine the
Table 1 . Names of EEGbands’ exit files. The middle column contains the names of the output files without transformation; on the right, the names of the equivalent files with the transformed results are shown (powers to logarithms, correlations and coherences to Fisher Z).
Table 2. Distribution of the variables analyzed with EEGbands in the RES and RET files, when 6 channels are analyzed.
significant differences among groups or conditions. These data are reported in TUK and TUT files, which contain the untransformed and transformed data, respectively (Figure 8).
2.5. Considerations
If the user chooses the option of subtracting the first cell (as baseline), it will not be considered in the number of cells in the result (the new cell 1 is the subtraction of original cell 2 from original cell 1). If the design has two
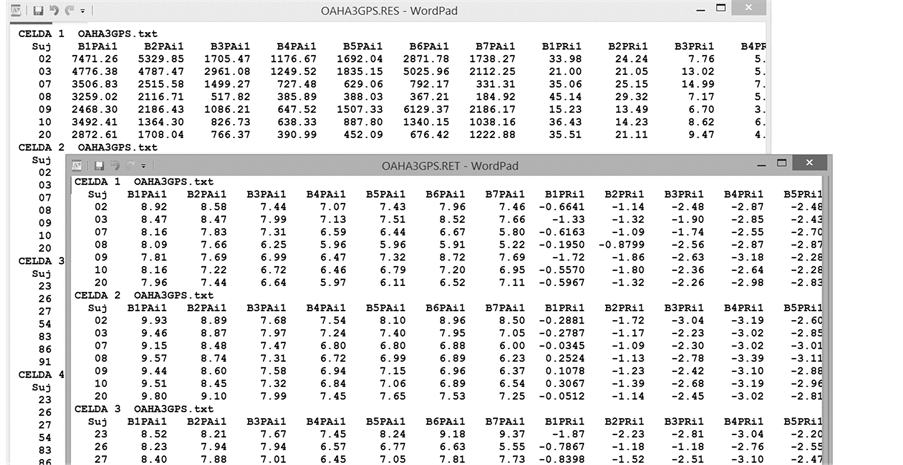
Figure 5. Part of the RES and RET output files. In this example, the program worked with 6 channels in a 2 ´ 2 mixed design. In the first column, “suj” is the identification of each subject. In the following columns, B1PAi1, B2PAi1... are the values of all variables calculated by the program for each subject (see Table 2).
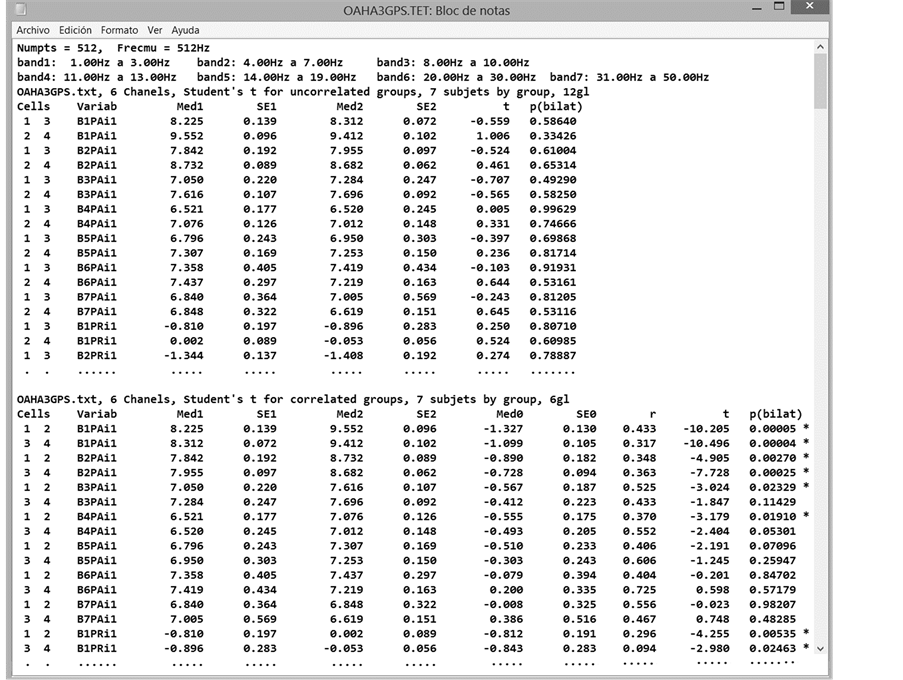
Figure 6. Part of the output files, TET. The initial part of the comparisons between groups (Student t test for independent groups) appears first, followed by the initial part of the intra-group comparisons (Student’s t test for correlated groups).
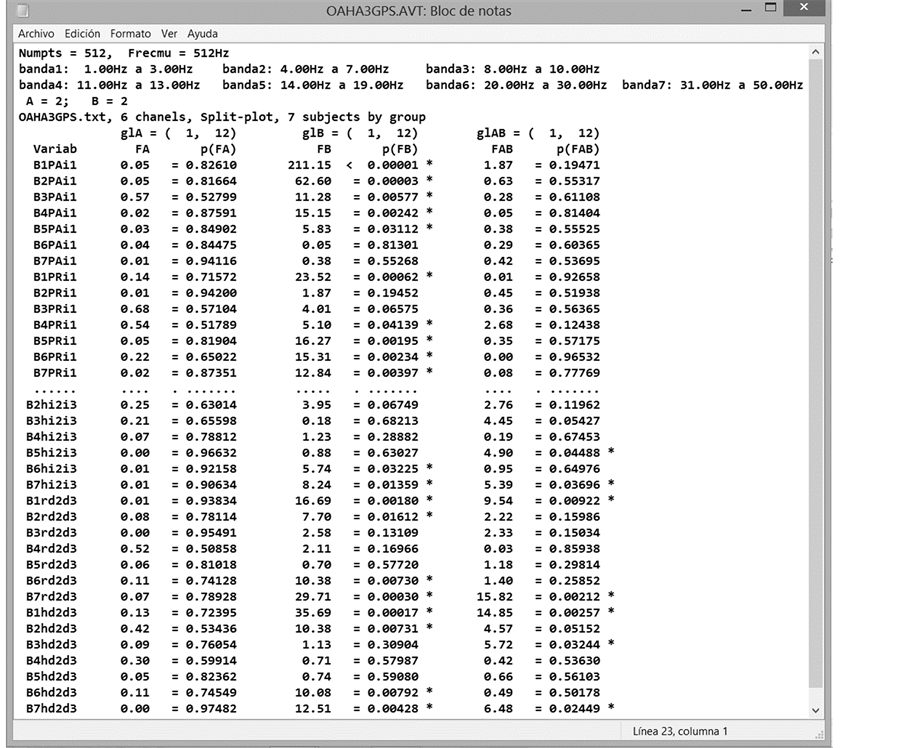
Figure 7. Initial and final parts of the output file, AVT. EEGbands ran with 6 channels and a mixed 2 ´ 2 design. The columns contain the significance for factor A [p(FA)], factor B [p(FB)] and the interaction A ´ B [p(FAB)].
factors, the first cell of each level of factor A is subtracted; i.e., the first cell of factor B is taken as baseline. Thus, for example, if the user chooses to subtract baseline and she/he has a 2-factor mixed design with 2 levels in each factor (i.e., 4 cells: A1B1, A1B2, A2B1, A2B2), the program will analyze only two cells (A1B2-A1B1 and A2B2-A2B1), since the first level of factor B will be subtracted from the second level. In this case, EEGbands automatically applies a Student t test for independent groups instead of a mixed ANOVA.
If the first cell is subtracted, then the RET file (with the transformed variables) will hold the transformations of the differences; i.e., the subtractions are made with untransformed data and the difference is then transformed. The only exception is relative power, whose differences are not transformed. Also, the absolute difference in absolute power is not processed if it has a negative value (in real numbers there are no logarithms of negative numbers); that is, the absolute value of the difference is transformed such that subsequent statistical comparisons with transformed absolute power are made using the absolute values of the differences.
3. Discussion and Conclusions
In the present article, we have described the computer program EEGbands, which offers an easy and novel way to obtain complex quantitative analyses of EEGs recorded in 6 derivations; one that combines the simultaneous analysis of the frequency domain (power and coherence) and time (correlation). This program allows one to calculate―quickly and simultaneously―absolute power, relative power, and the correlation and coherence spectra of EEG signals, as well as their respective statistical parametric analyses. All these calculations can be
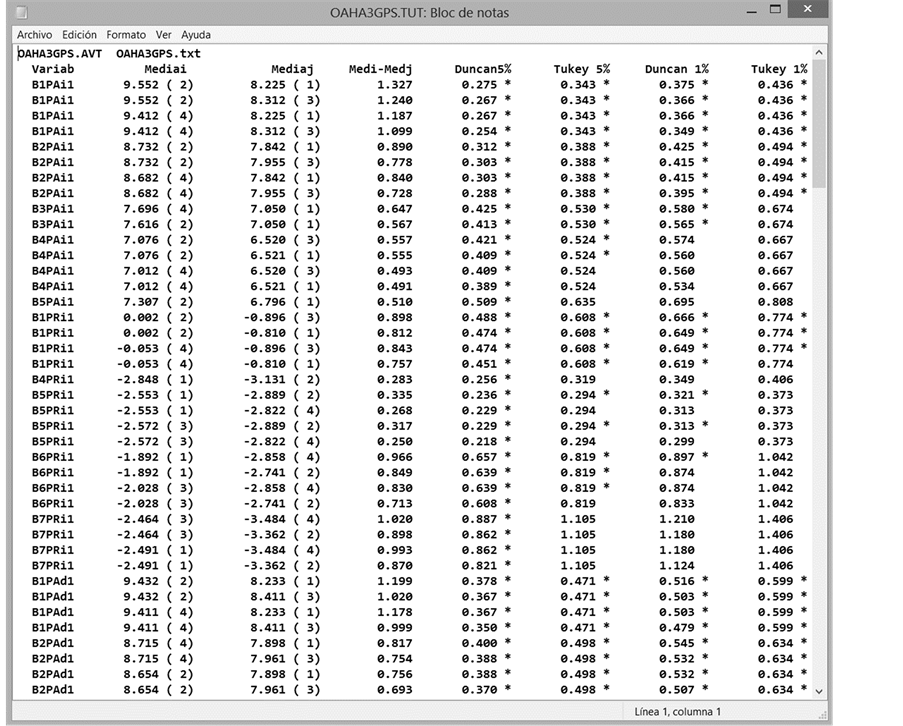
Figure 8. Fragment of the output file, TUT. In this example, Tukey and Duncan post hoc test have been applied to the results of the ANOVA. This analysis was performed with transformed data.
obtained for broad bands in a very short time by applying several parametric statistical tests. Unlike most commercial programs designed to analyze EEGs, EEGbands makes it possible to extract coherence and correlation.
The main contribution of EEGbands is that it permits the simultaneous calculation of absolute power, relative power, inter and intrahemispheric correlation and coherence spectra, and the application of adequate parametric statistical analyses. To the best of our knowledge, no commercially available programs offer all these possibilities.
EEGbands thus provides numerous advantages: it runs on any PC, requires no complex equipment, and its output files take up little memory space on the hard drive. The versatility and flexibility of this program make it easily adaptable to diverse experimental and clinical needs. Moreover, the fact that EEGbands can also be easily adapted to portable computers means that it can solve problems that may arise when analyzing signals in locations outside the laboratory; for example, in hospitals or schools.
Although EEGbands offers several advantages, it has some limitations. One very important condition is that the data from the different derivations and conditions of each subject must be very well organized in their respective files. However, if adequate care is taken to assure this condition, the program will run the statistical test(s) required with no problems whatsoever. Another limitation of this program is that it cannot analyze more than six derivations simultaneously, though for studies that require more than six derivations, it can simply be run several times, until all the comparisons of interest have been carried out.
Finally, EEGbands is a program that makes it possible the quantitative analysis of spectral power, coherence and correlation during different cognitive tasks, behaviors and physiological stages in both humans and animals. Right now this program is been used by different laboratories to study the brain electrical activity during sexual and maternal behavior (the last in human and rats), cognitive changes during pregnancy and the EEG correlation in children and adolescents survivors of child abuse or neglect.
For purposes of scientific research, EEGbands is available upon request and can be installed free of charge. The only requirement is to cite this paper when results obtained with the program are published.
References
- Niedermeyer, E. (1999) The Normal EEG of the Waking Adult. Electroencephalography. Lippincott Williams y Wilkins, Baltimore.
- Corsi-Cabrera, M., Guevara, M.A., Del Río-Portilla, Y., Arce, C. and Villanueva-Hernández, Y. (2000) EEG Bands during Wakefulness, Slow-Wave and Paradoxical Sleep as a Result of Principal Component Analysis in Man. Sleep, 23, 738-744.
- Solís-Ortiz, S., Ramos, J., Arce, C., Guevara, M.A. and Corsi-Cabrera, M. (1994) EEG Oscillations during Menstrual Cycle. International journal of neuroscience, 76, 279-292. http://dx.doi.org/10.3109/00207459408986010
- Sanz-Martin, A., Guevara, M.A., Amezcua, C., Santana, G. and Hernández-González, M. (2011) Effects of Red Wine on the Electrical Activity and Functional Coupling between Prefrontal-Parietal Cortices in Young Men. Appetite, 57, 84-93. http://dx.doi.org/10.1016/j.appet.2011.04.004
- Hernández-González, M., Martínez-Pelayo, M., Arteaga Silva, M., Bonilla-Jaime, H. and Guevara, M.A. (2009) Ethanol Changes the Electroencephalographic Correlation of the Ventral Tegmental Area and Nucleus Accumbens, Components of the Mesoaccumbens System in Rats. Pharmacology Biochemistry and Behavior, 92, 124-130.http://dx.doi.org/10.1016/j.pbb.2008.10.020
- Hernández-González, M., Guevara, M.A., Cervantes, M., Moralí, G. and Corsi-Cabrera, M. (1998) Characteristic Frequency Bands of the Cortico-Frontal EEG during the Sexual Interaction of the Male Rat as a Result of Factorial Analysis. Journal of Physiology-Paris, 92, 43-50. http://dx.doi.org/10.1016/S0928-4257(98)80022-3
- Guevara, M.A., Martinez-Pelayo, M., Arteaga Silva, M., Bonilla-Jaime, H. and Hernández-González, M. (2008) Electrophysiological Correlates of the Mesoaccumbens System during Male Rat Sexual Behaviour. Physiology & Behavior, 95, 545-552. http://dx.doi.org/10.1016/j.physbeh.2008.07.025
- Hernandez-Gonzalez, M., Navarro-Meza, M., Prieto-Beracoechea, C.A. and Guevara, M.A. (2005) Electrical Activity of Prefrontal Cortex and Ventral Tegmental Area during Rat Maternal Behavior. Behavioural Processes, 70, 132-143.http://dx.doi.org/10.1016/j.beproc.2005.06.002
- Guevara, M.A., Rizo Martínez, L.E., Robles Aguirre, F.A. and Hernández González, M. (2012) Prefrontal-Parietal Correlation during Performance of the Towers of Hanoi Task in Male Children, Adolescents and Young Adults. Developmental Cognitive Neuroscience, 2, 129-138.
- Guevara, M.á., González, M.H., Martínez, L.E.R. and Aguirre, F.A.R. (2013) Performance of the Towers of Hanoi task and Cortical Electroencephalographic Power Changes Associated with Infancy, Adolescence, and Early Adulthood. Experimental brain research, 231, 315-324. http://dx.doi.org/10.1007/s00221-013-3693-z
- Sanz-Martin, A., Hernández-González, M., Guevara, M.A., Santana, G., Gumá-Díaz, E. and Amezcua, C. (2012) Effects of Alcohol on the Performance of the Tower of London Task in Relation to the Menstrual Cycle: An Electroencephalographic Study. Behavioural pharmacology, 23, 637-649. http://dx.doi.org/10.1097/FBP.0b013e3283584748
- Sanz-Martin, A., Hernandez-Gonzalez, M., Guevara, M.A., Santana, G. and Guma-Diaz, E. (2014) Effect of Alcohol on Electrical Organisation in the Brain during a Visuospatial Working Memory Task and Its Relationship with the Menstrual Cycle. Revista de Neurologia, 58, 103-112.
- Ruiz-Díaz, M., Hernández-González, M., Guevara, M.A., Amezcua, C. and Ågmo, A. (2012) Prefrontal EEG Correlation during Tower of Hanoi and WCST Performance: Effect of Emotional Visual Stimuli. Journal of Sexual Medicine, 9, 2631-2640. http://dx.doi.org/10.1111/j.1743-6109.2012.02782.x
- Grindel, O.M., Koptelov, I.M., Masherov, E.L. and Pronin, I.N. (1998) Foci of Pathological Activity in the Human Brain and Their Influence on the Spatial-Temporal Relationships of the EEG. Zhurnal Vysshei Nervoi Deiatelnosti Imeni I P Pavlova, 48, 671-686.
- Cespedes-Garcia, Y., González-Hernández, J.A., García-Fidalgo, J., Begueria-Santos, R.A. and Figueredo-Rodríguez, P. (2003) Interictal EEG Coherence in Patients with Partial Temporal Lobe Epilepsy. Revista de Neurología, 37, 1107-1111.
- Cerdan, L.F., Guevara, M.A., Sanz, A., Amezcua, C. and Ramos-Loyo, J. (2005) Brain Electrical Activity Changes in Treatment Refractory Schizophrenics after Olanzapine Treatment. International Journal of Psychophysiology, 56, 237-247. http://dx.doi.org/10.1016/j.ijpsycho.2004.12.008
- Lazar, A.S., Lazar, Z.I., Biro, A., Gyori, M., Tarnok, Z., Prekop, C., Keszei, A, Stefanik, K., Gadoros, J., Halasz, P. and Bodizs, R. (2010) Reduced Fronto-Cortical Brain Connectivity during NREM Sleep in Asperger Syndrome: An EEG Spectral and Phase Coherence Study. Clinical Neurophysiology, 121, 1844-1854. http://dx.doi.org/10.1016/j.clinph.2010.03.054
- Leveille, C., Barbeau, E.B., Bolduc, C., Limoges, E., Berthiaume, C., Chevrier, E., Mottron, L. and Godbout, R. (2010) Enhanced Connectivity between Visual Cortex and Other Regions of the Brain in Autism: A REM Sleep EEG Coherence Study. Autism Research, 3, 280-285. http://dx.doi.org/10.1002/aur.155
- Adler, G., Brassen, S. and Jajcevic, A. (2003) EEG Coherence in Alzheimer’s Dementia. Journal of Neural Transmission, 110, 1051-1058. http://dx.doi.org/10.1007/s00702-003-0024-8
- Pogarell, O., Teipel, S.J., Juckel, G., Gootjes, L., Moller, T., Burger, K., Leinsinger, G., Moller, H.J., Hegerl, U. and Hampel, H. (2005) EEG Coherence Reflects Regional Corpus Callosum Area in Alzheimer’s Disease. Journal of Neurology, Neurosurgery and Psychiatry, 76, 109-111. http://dx.doi.org/10.1136/jnnp.2004.036566
- Abdullah, H., Maddage, N.C., Cosic, I. and Cvetkovic, D. (2010) Cross-Correlation of EEG Frequency Bands and Heart Rate Variability for Sleep Apnoea Classification. Medical and Biological Engineering and Computing, 48, 1261-1269. http://dx.doi.org/10.1007/s11517-010-0696-9
- Aksahin, M., Aydin, S., Firat, H. and Erogul, O. (2010) Artificial Apnea Classification with Quantitative Sleep EEG Synchronization. Journal of Medical Systems, 36, 139-144.
- Teicher, M.H., Ito, Y., Glod, C.A., Andersen, S.L., Dumont, N. and Ackerman, E. (1997) Preliminary Evidence for Abnormal Cortical Development in Physically and Sexually Abused Children Using EEG Coherence and MRIa. Annals of the New York Academy of Sciences, 821, 160-175. http://dx.doi.org/10.1111/j.1749-6632.1997.tb48277.x
- Thatcher, R.W. (1998) Normative EEG Databases and EEG Biofeedback. Journal of Neurotherapy, 2, 8-39. http://www.tandfonline.com/doi/abs/10.1300/J184v02n04_02#.U1xaLNEU-TM
- Guevara, M.A., Lorenzo, I., Arce, C., Ramos, J. and Corsi-Cabrera, M. (1995) Inter and Intrahemispheric EEG Correlation during Sleep and Wakefulness. Sleep, 18, 257-265.
- Guevara, M.A., Ramos, J. and Corsi-Cabrera, M. (1997) Un Método Práctico para el Espectro de Correlación entre Señales Electroencefalográficas para Evaluar Relaciones Funcionales entre áreas Cerebrales. Revista Mexicana de Psicología, 14, 5-12. http://www.sociedadmexicanadepsicologia.org/index.php/revista-mexicana-de-psicologia
- Shibasaki, H. and Nagamine, T. (2003) EEG (MEG)/EMG Correlation. In: Hallett, M., Ed., Movement Disorders: Handbook of Clinical Neurophysiology, Volume 1, Elsevier, 15-29.
- Byring, R.F., Haapasalo, S. and Salmi, T. (2004) Adolescents with Learning Disorders Have Atypical EEG Correlation Indices. II. Correlation Indices during Reading. Clinical Neurophysiology, 115, 2584-2592. http://www.clinph-journal.com/article/S1388-2457(04)00226-3/abstract
- Brazier, M.A. and Casby, J.U. (1952) Cross-Correlation and Autocorrelation Studies of Electroencephalographic Potentials. Electroencephalography and Clinical Neurophysiology, 4, 201-211. http://dx.doi.org/10.1016/0013-4694(52)90010-2
- French, C.C. and Beaumont, J.G. (1984) A Critical Review of EEG Coherence Studies of Hemisphere Function. International Journal of Psychophysiology, 1, 241-254. http://dx.doi.org/10.1016/0167-8760(84)90044-8
- Grindel, O.M. (1965) The Significance of Correlation Analysis for Evaluation of the EEG in Man Mathematical Analysis of the Electrical Activity of the Brain. Harvard University Press, Cambridge.
- Thatcher, R.W. and Walker, R.A. (1980) EEG Coherence and Intelligence in Children. Electroencephalography & Clinical Neurophysiology, 49, S161.
- Shaw, J.C. (1981) An Introduction to the Coherence Function and Its Use in EEG Signal Analysis. Journal of Medical Engineering&Technology, 6, 279-288. http://dx.doi.org/10.3109/03091908109009362
- Bendat, J.S. (1980) Engineering Applications of Correlation and Spectral Analysis. John Wiley & Sons, New York.
- Guevara, M.A. and Corsi-Cabrera, M. (1996) EEG Coherence or EEG Correlation? International Journal of Psycho-physiology, 23, 145-153. http://www.sciencedirect.com/science/article/pii/S0167876096000384
- Guevara, M.A. and Hernández-González, M. (2009) EEGmagic: programa para analizar señales electroencefalográficas. Revista Mexicana de Ingeniería Biomédica, 30, 41-53. http://www.rmib.somib.org.mx/Vol30No1.html
- Guevara, M.A., Hernández-González, M., Sanz-Martin, A. and Amezcua, C. (2011) EEGcorco: A Computer Program to Simultaneously Calculate and Statistically Analyze EEG Coherence and Correlation. Journal of Biomedical Science and Engineering, 4, 774-787. http://www.scirp.org/journal/PaperInformation.aspx?paperID=9174
- Sánchez-Bruno, A. and Borges del Rosal, A. (2005)Transformación Z de Fisher para la determinación de intervalos de confianza del coeficiente de correlación de Pearson, Psicothema, 17, 148-153. http://www.psicothema.com/pdf/3079.pdf
- Deeny, S.P., Hillman, C.H., Janelle, C.M. and Hatfield, B.D. (2003) Cortico-Cortical Communication and Superior Performance in Skilled Marksmen: An EEG coherence Analysis. Journal of Sport & Exercise Psychology, 25, 188-204.
- Brigham, E.O. (1974) The Fast Fourier Transform. Prentice-Hall, Inc., Englewood Cliffs.
- Kirk, R. (1968) Experimental Design: Procedures for the Behavioral Sciences. Brooks/Cole, Belmont.


