Advances in Chemical Engineering and Science
Vol.07 No.02(2017), Article ID:74579,17 pages
10.4236/aces.2017.72011
The Effects of Oxidation States, Spin States and Solvents on Molecular Structure, Stability and Spectroscopic Properties of Fe-Catechol Complexes: A Theoretical Study
Mohammad A. Matin1, Mazharul M. Islam2,3*, Thomas Bredow2,3, Mohammed Abdul Aziz4
1Centre for Advanced Studies in Sciences (CARS), Dhaka University, Dhaka, Bangladesh
2Mulliken Center for Theoretical Chemistry, Institut für Physikalische und Theoretische Chemie, Universität Bonn, Bonn, Germany
3ZFM-Center for Solid State Chemistry and New Materials, Leibniz Universität Hannover, Hannover, Germany
4Department of Chemistry, Dhaka University, Dhaka, Bangladesh

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 31, 2016; Accepted: March 4, 2017; Published: March 7, 2017
ABSTRACT
In this study, in order to explain the solvent and spin state effects on the mole- cular structure of catechol-Fe complex [Fe(cat)3]n− where n = 2 and 3, Hartree Fock (HF)-Density Functional Theory (DFT) hybrid calculations are performed at the B3LYP/6-311g(d,p) level of theory. The binding energies of Fe2+ and Fe3+ in high-spin state are higher than intermediate and low-spin states which show that the complex formation in a high spin state is more favorable. The calculated binding energies at different solvents indicate that the binding energies in polar solvents are lower than non-polar solvents. Furthermore, spectroscopic studies including FTIR and Raman spectrum in various solvents reveal that the formation of intermolecular bonds between the oxygen atom of carbonyl group and the hydrogen atom of solvent causes a spectral red shift. The calculated FTIR and geometry parameters are in good agreement with previous experimental data. Donor-acceptor interaction energies are evaluated due to the importance of the charge transfer in the complex formation. It is observed that the free electrons of oxygen atom interact with the antibonding orbitals of the iron. Finally, some correlations between the quantum chemical reactivity indices of the complexes and solvent polarity are considered. The study indicates a linear correlation between chemical hardness and binding energies of [Fe(cat)3]3− complex.
Keywords:
Transition Metal, Iron-Catechol, HF/DFT Hybrid Method, Solvent, Reactivity Indices

1. Introduction
Iron is a pivotal nutrient for life which is one of the most abundant elements on the earth. It plays an important role in biological processes such as oxygen transport, energy generation, electron transfer and DNA synthesis [1] . Iron- containing enzymes make up a large number of the O2-activating enzymes, because of the bioavailability of iron in Nature [2] . A sufficient supply of Fe is necessary for optimal plant productivity and agricultural product quality [3] . In one hand, iron is essential for the correct functioning of all living cells. On the other hand, it becomes toxic when presents in excess. The excess of iron may cause iron overload which is a condition that originates from the aggregation of iron in the body. This problem can be minimized by the iron chelating agents as a chelator prevents to catalyze redox reactions [4] [5] .
Catechol, which is a phenolic compound known as pyrocatechol or 1,2-dihy- droxybenzene with the molecular formula C6H4(OH)2, acts as iron chelating agent [6] [7] . Basic solutions of catechol react with iron to form [Fe(cat)3]n− complexes which have been widely used for the development of satisfactory chelating agents for the treatment of human metal intoxication [7] . Because of multiple redox states of iron and a number of open shell spin states in its different common oxidation states, the binding of iron with catechol and other chelating agents has opened up a wide variety of research activities in recent years. The redox chemistry and strong chelating abilities of Fe in the bulk aqueous phase are well established at the fundamental level [8] and recently were utilized in functionalizing surfaces and nanoparticles for applications in green chemistry [9] and in the development of biomedical and sensing devices [10] [11] [12] . Several researchers have attempted for the fabrication of synthetic materials inspired by mussel byssal threads, in order to elucidate the Fe3+-catechol interaction mechanisms [13] [14] . The coordination between Fe3+ and catechols is strongly dependent on the pH, and Fe3+ does not affect a significant covalent crosslinking via oxidation of catechols, in a pH-controlled catechol-Fe3+ cross-linking polymer [15] . However, spectroscopic evidence has linked the presence of Fe3+ to catechol oxidation for decades [16] [17] [18] . It has been reported that catechol- modified polyethylene glycol (PEG) polymers could be covalently cross-linked under acidic pH conditions in the presence of Fe3+ [19] [20] . Therefore, the mechanism of interactions between Fe3+ and catechols must be extensively investigated.
Recent theoretical study based on HF/DFT hybrid functional has considered the ferric complexes of catecholic ligands which are close to the complexes of the present study [21] . The simulations of the Raman spectra of the [Fe(cat2−)3]3− model compound and the enzyme-difference spectra in catechol 1,2-dioxygenase (C12O) at B3LYP level were in agreement with experimental results [22] . The simulated Raman spectra of the DOPA-modified polyethylene glycol (DOPA- PEG) polymer and Fe3+ induced complexes of adsorbed Mefp-1 protein film on iron substrate at the B3LYP level were also in agreement with experimental spectra [23] [24] . Liu et al. have simulated the Fe3+-DOPA mediated bridging at both wet(water) and gas phase conditions [25] at the B3LYP/LACVP* level of theory. They calculated the entropy, Gibbs free energy and cohesion force for mechanical strength.
In the present study, we have performed a theoretical investigation on the structure, binding energies, stability and spectroscopic properties of the [Fe(cat)3]n− complexes (for Fe(II) and Fe(III) oxidation states) in the gas phase and different solvents using the first principles HF/DFT hybrid approach. The thermodynamic stability of all the possible spin states for both oxidation states is verified. The natural bond orbital (NBO) analysis [26] on [Fe(cat)3]3− complex is reported, as we have predicted the second-order interaction energies. We have also studied the chemical reactivity indices such as chemical hardness (η) [27] and electronic chemical potential (μ) [28] , as determined by using the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energy gap. These findings help us understand the thermody- namic behavior of such systems as a function of the quantum chemistry descriptors.
2. Computational Details
The model compounds were subjected to geometry optimizations followed by computations of time dependent density functional theory (TD-DFT) electronic absorption spectra, IR spectra, and pre-resonance Raman spectra. The geome- tries of the complexes were optimized at the HF/DFT hybrid B3LYP [29] level using the 6 - 311 g (d, p) basis set and the stability were confirmed by checking no imaginary frequency. In order to produce reliable resonance in Raman spectra, computation needs to reproduce any electronic absorption band that lies in the vicinity of the excitation wavelength used in the experiment. We tested different exchange correlation functionals and found that the long range corrected CAM-B3LYP [30] functional is the best suited to reproduce the charge transfer bands found in complexes between Fe3+ and catechols. We examined high-spin (HS), intermediate-spin (IS) and low-spin (LS) states which stands for 4, 2 and 0 unpaired electrons and 5, 3 and 1 unpaired electrons for ferrous and ferric complexes respectively. All quantum chemical calculations were performed using the Gaussian 09 [31] simulation package. The Gauss View 5.0.8 was used for visualization of the structures and simulated vibrational spectra.
In order to estimate the zero-point vibrational energies (ZPVEs), frequency calculations were performed for all structures in the different spin states. All minimum structures were verified with the real frequencies. Geometry optimization was taken to be converged if the maximum atomic force was smaller than 0.00045 Hartree/Bohr. No symmetry was imposed in all the calculations. The raw vibrational frequencies were scaled by a factor of 0.9668, which produced good agreement with the experiment for a wide range of systems [32] .
Solvent effects were taken into account by the conductor like polarizable continuum model (CPCM) [33] . Natural bond orbital analysis was performed to provide the appropriate scheme for the metal-ligand interactions [34] [35] . Molecular orbital analysis was also done to calculate the HOMO-LUMO energy gap and the chemical reactivity indices (η and μ), on the basis of Koopmans [36] theorem at the same level of theory.
3. Results and Discussion
3.1. Spin State and Structural Analysis
After the full optimization, the total energy of the considered spin states for both Fe2+ and Fe3+ oxidation states for [Fe(cat)3]n− complexes are calculated and the relative energy values for all the states are compared in Table 1. The corresponding calculations were done in the gas phase at high-spin (HS), intermediate-spin (IS) and low-spin (LS) states. In case of Fe2+ complexes, the relative energies of intermediate-spin and low-spin states are higher than high-spin state by 9.29 and 12.15 kcal∙mol−1 respectively (see Table 1). Similarly, for Fe3+ complexes, the relative energies at intermediate and low spin states are higher than high-spin states by 6.57 and 7.4 kcal∙mol−1 respectively. It is observed that the stability of the complexes increase in the order of HS > IS > LS for both Fe2+ and Fe3+ tris-catechol complexes. Due to the increase in the amount of the exact exchange energy, higher spin state with a larger number of unpaired electrons is strongly stabilized compared to the lower spin states [37] [38] .
The metal-ligand binding energies were computed according to Equation (1) [10] .
 (1)
(1)
Here Ecomplex, Emetal and Eligand is the energy of [Fe(cat)3]n− complex, metal and ligand respectively. The calculated binding energy values are compared in Table 1. Based on the calculated binding energies both for Fe2+ and Fe3+ complexes, it
Table 1. Calculated relative energy, binding energy and enthalpy (kcalmol−1) of the [Fe (cat) 3]n− complexes for different spin states in gas phase.
is observed that Fe3+ complexes are more stable than Fe2+ complexes. In both cases, the values of the binding energy of the high-spin and intermediate-spin state complexes are more negative than the low-spin state complex. In case of Fe2+, the low-spin and intermediate spin complexes are less stable than the high-spin state by approximately 12.15 and 9.29 kcal∙mol−1 respectively. In case of Fe3+, the low-spin and intermediate spin complexes are less stable than the high-spin state by approximately 7.4 and 6.57 kcal∙mol−1 respectively. Compar- ing all the calculated binding energy values, it is concluded that Fe3+ at high-spin state is the most preferable to form the iron-catecolate complex. According to Boys-Bernardi counterpoise (CP) correction method [39] we have checked the basis set superposition error (BSSE) for the [Fe(cat)3]3− complex of high spin
state only. The BSSE-corrected energy 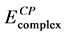 (−2408.41 au) is compared with the uncorrected energy
(−2408.41 au) is compared with the uncorrected energy 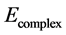 (−2408.48 au). The relative deviation defined as
(−2408.48 au). The relative deviation defined as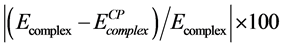 . The BSSE was within 0.003% of the complex energy which is in the range of computational error [40] .
. The BSSE was within 0.003% of the complex energy which is in the range of computational error [40] .
The effects of temperature and contributions from zero point energy on the calculated formation energies of the [Fe(cat)3]n− are explicitly taken into account by additional frequency calculations (at 298.15 K and 1atm pressure). The enthalpy of formation is calculated according to the Equation (1). Based on the calculated enthalpy, it is observed that the correction terms range upto 4.5 kcal∙mol−1 which is in the acceptable range as observed in previous theoretical studies [41] [42] . The correction terms do not change the stability of the [Fe(cat)3]n− complexes. Therefore the [Fe(cat)3]3− complex at high-spin state is the most stable among all the considered complexes and employed for further investigation in gas phase and different solvents.
The geometrical parameters at different spin states for Fe3+ complexes in gas phase are given in Table 2 which include the average and standard deviations of the metal−oxygen distances,  , C-O distances,
, C-O distances,  , the angles of O− metal−O triplets,
, the angles of O− metal−O triplets, 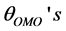 , the C-C-O angles,
, the C-C-O angles, 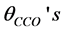 and the angles of metal-O-C,
and the angles of metal-O-C, 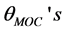 respectively. The atomic labels are depicted for a [Fe(cat)3]3− complex in Figure 1. All the
respectively. The atomic labels are depicted for a [Fe(cat)3]3− complex in Figure 1. All the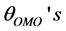 , however, fluctuate significantly from
, however, fluctuate significantly from
Table 2. Geometry parameters of the [Fe(cat)3]3− complex. The metal-O bond lengths (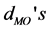 ), C-O bond lengths (
), C-O bond lengths (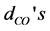 ), the O-metal-O bending angles (
), the O-metal-O bending angles ( ), the C-C-O bending angles (
), the C-C-O bending angles (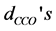 ) and metal-O-C bending angles (
) and metal-O-C bending angles (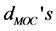 ) are shown for trivalent metal ion for [Fe (cat) 3]3−. The average values are listed with the standard deviations in parentheses.
) are shown for trivalent metal ion for [Fe (cat) 3]3−. The average values are listed with the standard deviations in parentheses.
aX-ray analysis on a tris-catecholato Fe(III) crystal gave 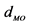 = 2.015 Å and
= 2.015 Å and 


Figure 1. Metal binding to catechol, optimized geometry of the [Fe(cat)3]3− complex.
their average values of approximately 90˚. The present 
3.2. Solvent Effects on the Binding Energies of [Fe(cat)3]3−
In order to study the solvent effects on the iron binding with catechol, we have studied [Fe(cat)3]3− complex at the HS state in various solvents with the increasing dielectric constant including chloroform, acetone, ethanol, methanol, acetonitrile, DMSO and water (as shown in Table 3). The changes in binding energies in terms of dielectric constants are presented in Figure 2. It is observed that the binding energies decrease as the dielectric constants increase, which is in well
Figure 2. The relationship between the binding energy values and solvent dielectric constants.
Table 3. Calculated binding energy Ebind (kcal∙mol−1), carbonyl and carbon-carbon stretching frequency of the [Fe(cat)3]3− complex in gas phase and different solvents.
agreement with a recent theoretical investigation [47] . It is due to the fact that, in presence of the solvents the solvation of the complex prevents their effective interactions.
3.3. Solvent Effect on the Carbonyl and Carbon-Carbon Stretching Frequency of [Fe(cat)3]3−
The IR spectra of [Fe(cat)3]3− complex in gas phase as well as solvents are calculated. The C-O and C-C vibrational modes are given in Table 3. It is observed that both these modes shift to a lower frequency (red shift) when the solvent polarity increases. Figure 3(a) shows the FTIR spectra of the [Fe(cat)3]3− complex at gas phase and solvents (acetone, ethanol and water). We have also checked the FTIR spectra in chloroform, acetonitrile, methanol and DMSO solvents. Two intense peaks appeared at 1260 and 1470 cm−1 in gas phase and almost near 1226

Figure 3. (a) FTIR spectrum of [Fe(cat)3]3− complex. (b) Carbonyl stretching and (c) C-C vibrational frequency as a function of the solvent dielectric constant.
and 1449 cm−1 at those solvents. Each of these two major peaks have originated from the in-plane deformation mode involving the C-C and C-O stretching and the C-H bending of catecholate. These two major IR peaks are close in frequency to those previously observed for mefp-1 adsorbed on an iron substrate at 1258 and 1485 cm−1 [48] and at 1265 and 1487 cm−1 of DOPA modified tris (DOPA- PEG) Fe(III) complex [15] . The high intensities of the present IR peaks arise from the large charge polarization due to the highly positive Fe(III) being surrounded by three negatively charged catecholate ligands. Because of the charge polarization, the vibrations that result in unsymmetrical distortions of the complex induce large dipole moment changes and large IR intensities.
Figure 3(b) indicates the relationship between the C-O stretching vibrational frequency and solvent dielectric constant. The differences in the vibrational frequency between the gas phase and the solutions are attributed to the intermolecular bonding between the oxygen atom of the carbonyl group and a hydrogen atom of the solvent [49] [50] . The catecholic ring C-C vibrational modes have also shifted to a lower frequency (red shift) when the solvent polarity increases (as shown in Figure 3(c)). In most of the cases, the C-C vibrations occur in two rings out of three rings of the complex.
3.4. Solvent Effects on the Pre-Resonance Raman Shifts of [Fe(cat)3]3− Complex
In order to study the effect of solvents on the preresonance Raman intensities, a wide variety of solvents with increasing dielectric constants were used. Using the optimized geometry for every solvent, the excitation wavelength was calculated with TD-DFT method. Using those wavelengths, we calculated preresonance raman with Raman Optical Activity (ROA). Figure 4 shows the pre-resonance Raman spectra of [Fe(cat)3]3− in three different solvents (water, ethanol and chloroform) along with the gas phase. It clearly indicates that, in presence of solvents, the Raman peaks shifted (blue shifts). We have also checked Raman shifts in acetone, methanol, acetonitrile and DMSO solvents. Table 4 lists the Raman peaks with nine strongest intensities. As observed (Table 4), the vibrational modes have shifted to a higher frequency (blue shift) when the solvent
Table 4. Pre-resonance Raman shifts (cm−1) for the present Tris-catecholato [Fe(cat)3]3− complex along with the Resonance Raman peaks previously measured for the synthetic and natural cross-linked structures.
aSynthetic tris(DOPA-PEG) Fe(III) complex formed at pH ≈ 12 [15] . bSynthetic tris-catecholato Fe(III) complex [48] . cSynthetic pink form of MAP cross-linked by forming complexes with Fe(III) [51] . dMussel cuticle cross-linked by forming complexes with Fe(III) [16] .
Figure 4. Pre-resonance Raman spectra of the [Fe(cat)3]3− complex calculated using an electronic excitation wavelength of 521 nm.
polarity has increased. The present calculation agrees reasonably with the previous Raman experiments on the synthetic and natural cross-linked MAPs, where the low-frequency (512 - 614 cm−1) modes arose from the chelation of Fe by catecholate [15] .
3.5. Solvent Effect on the UV-Visible Spectra
Figure 5 shows the UV-vis absorption spectrum of the [Fe(cat)3]3− complex. The strongest peak was observed at 521 nm in gas phase. The absorption maximum
Figure 5. UV-vis absorption spectrum of [Fe(cat)3]3− complex.
was located at 521 nm, agreeing with the experimental wavelength (492 nm) of the maximum peak found for the tris(DOPA-PEG) Fe(III) [15] and 490 nm for tris catechol-iron complex [52] . We have also checked the absorption maximum at different solvents including chloroform, acetone, ethanol, acetonitrile, methanol, DMSO and water. In all cases, the maximum transition wavelength is obtained at 523 nm.
To characterize the electronic transitions, five frontier MOs were pictorized ranging from the highest occupied MO-2(HOMO-2) to the lowest unoccupied MO + 1(LUMO + 1) (Figure 6). The absorption maximum at 521 nm originated mostly (96%) from HOMO to LUMO transition in gas phase. In HOMO transition, the electron density existed mostly over three catecholate ligands. In the LUMO (as shown in Figure 6), the electron density has largely moved out of the catecholates into the Fe ion. Therefore the strongest peak in the UV-vis spectra has originated clearly from ligand-to-metal charge transfer.
4. NBO Analysis
In the natural bond orbital (NBO) analysis, the electronic wave function is elucidated in terms of occupied Lewis and unoccupied Lewis localized orbitals. The strength of donor-acceptor interactions, E(2), are evaluated by second-order perturbation theory [53] . Table 5 summarizes the E(2) values of the [Fe(cat)3]3− in different solvents for the important NBO interactions. The most important interaction energies of these complexes are due to the interactions between the lone pair electrons of the O atom (LPO) and antibonding orbital of the Fe3+(LP*Fe). According to Table 5, E(2) values increase with an increase in the solvent polarity. Therefore, donor-acceptor interaction energies are the greatest values in the water solvent.
Figure 6. Frontier MOs of the [Fe(cat)3]3− complex. The H, C, and O atoms are shown as white, gray, and red spheres, respectively. The orbital lobes shown in green and red represent the opposite phases.
Table 5. Significant donor-acceptor interaction energies of [Fe(cat)3]3− complex in different solvent media.
5. Quantum Chemistry Reactivity Indices
The HOMO-LUMO energy gap (Eg) is an important factor for the evaluation of polarizability of a molecule [54] . The chemical stability assessment requires the knowledge of quantum chemistry reactivity indices such that a high HOMO- LUMO gap indicates a large chemical stability [55] . According to the frontier molecular orbital (FMO) theory, reactivity indices can be defined on the basis of the energy gap between the HOMO and LUMO. Hard molecules have a large energy gap while soft molecules have a small one. Soft molecules are more polarizable than hard type due to their small energy of excitation.
Quantum reactivity indices such as the HOMO-LUMO gap (Eg), chemical hardness (η) and electronic chemical potential (μ) are reported in Table 6. It is observed that Eg in the gas phase is lower than other solvents which indicates that charge transfer is higher in solvents than in gas phase. The correlation between the chemical hardness and solvent dielectric constant is shown in Figure 7. It is observed that the chemical hardness in the gas phase is lower than in the solvents. This indicates that the stability of [Fe(cat)3]3− in the gas phase is lower than in solution.
Figure 7. The correlation of electronic potential and solvent dielectric constant.
Table 6. Energy gap and quantum reactivity indices of the catecholate and [Fe(cat)3]3− complex in different solvent media
6. Conclusions
The effect of oxidation states and spin states of iron for the binding in [Fe(cat)3]n− complexes are studied theoretically using quantum chemical approach based on the B3LYP/6-311G (d,p) level of the theory. Our study shows that Fe3+ in high spin state is the most preferable oxidation state to form the iron-catechol complex. The effects of various solvents with increasing dielectric constants on the structure, binding energy, FT-IR, preresonance Raman and UV-vis spectra of the [Fe(cat)3]3− complex were investigated. The binding energies in polar solvents are lower than those in non-polar ones.
The simulated FT-IR showed that both the C-O and C-C vibrational modes have shifted to a lower frequency (red shift) when the solvent polarity increases. The preresonance Raman spectra of [Fe(cat)3]3− clearly indicated that, in presence of solvents, the Raman peaks shifted (blue shifts). The simulated UV-vis spectra of the [Fe(cat)3]3− complex were also consistent with the previous measurements and calculations. Furthermore, through the NBO analysis, the metal-ligand interactions were studied and verified that charge transfer occurs from the oxygen atoms of the ligand to the Fe (III). Also, based on this analysis it is concluded that the charge transfer in the gas phase is higher than in solution.
Finally, according to quantum chemical reactivity indices, the correlations between the electronic potential and binding energy of the [Fe(cat)3]3− complex as well as the solvent dielectric constant were obtained, respectively. The present metal−ligand binding energies, structures, and atomic charges of the metal-ca- techolate complexes will serve as a keystone for such modeling using molecular dynamics or Monte Carlo simulations.
Acknowledgements
The Regional Scientific Computing Center for Lower Saxony (RRZN) of the University of Hannover is acknowledged for high performance computing facilities to perform this research activity.
Cite this paper
Matin, M.A., Islam, M.M., Bredow, T. and Aziz, M.A. (2017) The Effects of Oxidation States, Spin States and Solvents on Molecular Structure, Stability and Spectroscopic Properties of Fe-Catechol Complexes: A Theoretical Stu- dy. Advances in Chemical Engineering and Science, 7, 137-153. https://doi.org/10.4236/aces.2017.72011
References
- 1. Crichton, R. (2016) Iron Metabolism: From Molecular Mechanisms to Clinical Consequences. John Wiley & Sons, Hoboken.
https://doi.org/10.1002/9781118925645 - 2. Sahu, S. and Goldberg, D.P. (2016) Activation of Dioxygen by Iron and Manganese Complexes: A Heme and Nonheme Perspective. Journal of American Chemical Society, 138, 11410-11428.
https://doi.org/10.1021/jacs.6b05251 - 3. Briat, J.F., Dubos, C. and Gaymard, F. (2015) Iron Nutrition, Biomass Production, and Plant Product Quality. Trends Plant Science, 20, 33-40.
https://doi.org/10.1016/j.tplants.2014.07.005 - 4. Ma, Y., Zhou, T., Kong, X. and Hider, R. C. (2012) Chelating Agents for the Treatment of Systemic Iron Overload. Current Medicinal Chemistry, 19, 2816-2827.
https://doi.org/10.2174/092986712800609724 - 5. Timoshnikov, V.A., Kobzeva, T.V., Polyakov, N.E. and Kontoghiorghes, G.J. (2015) Inhibition of Fe2+- and Fe3+- Induced Hydroxyl Radical Production by the Iron-Chelating Drug Deferiprone. Free Radical Biological Medicine, 78, 118-122.
https://doi.org/10.1016/j.freeradbiomed.2014.10.513 - 6. Katoh, S., Toyama, J., Kodama, I., Kamiya, K., Akita, T. and Abe, T. (1992) Protective Action of Iron-Chelating Agents (Catechol, Mimosine, Deferoxamine, and Kojic Acid) against Ischemia-Reperfusion Injury of Isolated Neonatal Rabbit Hearts. European Surgical Research, 24, 349-355.
https://doi.org/10.1159/000129227 - 7. Xu, G., Yang, C., Liu, B., Wu, X. and Xie, Y. (2004) Synthesis of New Potential Chelating Agents: Catechol-Bisphosphonate Conjugates for Metal Intoxication Therapy. Heteroatom Chemistry, 15, 251-257.
https://doi.org/10.1002/hc.20013 - 8. Al-Abadleh, H.A. (2015) Review on the Bulk and Surface Chemistry of Iron in Atmospherically-Relevant Systems Containing Humic like Substances. RSC Advance, 5, 45785-45811.
https://doi.org/10.1039/C5RA03132J - 9. Kobayashi, S. and Makino, A. (2009) Enzymatic Polymer Synthesis: An Opportunity for Green Polymer Chemistry. Chemical Review, 109, 5288-5353.
https://doi.org/10.1021/cr900165z - 10. Xu, C., Xu, K., Gu, H., Zheng, R., Liu, H., Zhang, X., Guo, Z. and Xu, B. (2004) Dopamine as a Robust Anchor to Immobilize Functional Molecules on the Iron Oxide Shell of Magnetic Nanoparticles. Journal of American Chemical Society, 126, 9938-9939.
https://doi.org/10.1021/ja0464802 - 11. Zurcher, S., Wackerlin, D., Bethuel, Y., Malisova, B., Textor, M., Tosatti, S. and Gademann, K. (2009) Biomimetic Surface Modifications Based on the Cyanobacterial Iron Chelator Anachelin. Journal of American Chemical Society, 128, 1064-1065.
https://doi.org/10.1021/ja056256s - 12. Statz, A.R., Meagher, R.J., Barron, A.E. and Messersmith, P.B. (2005) New Peptidomimetic Polymers for Antifouling Surfaces. Journal of American Chemical Society, 127, 7972-7973.
https://doi.org/10.1021/ja0522534 - 13. Krogsgaard, M., Behrens, M.A., Pedersen, J.S. and Birkedal, H. (2013) Self-Healing Mussel-Inspired Multi-pHresponsive Hydrogels. Biomacromolecules, 14, 297-301.
https://doi.org/10.1021/bm301844u - 14. Brubaker, C.E., Kissler, H., Wang, L.J., Kaufman, D.B. and Messersmith, P.B. (2010) Biological Performance of Musselinspired Adhesive in Extrahepatic Islet Transplantation. Biomaterials, 31, 420-427.
https://doi.org/10.1016/j.biomaterials.2009.09.062 - 15. Holten-Andersen, N., Harrington, M.J., Birkedal, H., Lee, B.P., Messersmith, P.B., Lee, K.Y.C. and Waite, J.H. (2011) PH-Induced Metal-Ligand Cross-Links Inspired by Mussel Yield Self-Healing Polymer Networks with near-Covalent Elastic Moduli. Proceedings of the National Academy of Sciences of the United States of America, 108, 2651-2655.
https://doi.org/10.1073/pnas.1015862108 - 16. Harrington, M.J. and Waite, J.H. (2007) Holdfast Heroics: Comparing the Molecular and Mechanical Properties of Mytilus Californianus Byssal Threads. Journal of Experimental Biology, 210, 4307-4318.
https://doi.org/10.1242/jeb.009753 - 17. Mentasi, E. and Pelizzetti, E. (1973) Reactions between Iron(III) and Catechol (O-Dihydroxybenzene). Part I. Equilibria and Kinetics of Complex Formation in Aqueous Acid Solution. Journal of Chemical Society, Dalton Transaction, 23, 2605-2608.
https://doi.org/10.1039/dt9730002605 - 18. Mentasi, E., Pelizzetti, E. and Saini, G. (1973) Reactions between Iron(III) and Catechol (O-Dihydroxybenzene). Part II. Equilibria and Kinetics of the Redox Reaction in Aqueous Acid Solution. Journal of Chemical Society, Dalton Transaction, 23, 2609-2614.
https://doi.org/10.1039/dt9730002609 - 19. Barrett, D.G., Fullenkamp, D.E., He, L., Holten-Andersen, N., Lee, K.Y.C. and Messersmith, P.B. (2013) PH-Based Regulation of Hydrogel Mechanical Properties through Mussel-Inspired Chemistry and Processing. Advanced Functional Materials, 23, 1111-1119.
https://doi.org/10.1002/adfm.201201922 - 20. Fullenkamp, D.E., Barrett, D.G., Miller, D.R., Kurutz, J.W. and Messersmith P.B. (2014) PH-Dependent Cross-Linking of Catechols through Oxidation via Fe3+ and Potential Implications for Mussel Adhesion. RSC Advances, 4, 25127-25134.
https://doi.org/10.1039/C4RA03178D - 21. Sebestík, J., Safarík, M. and Bour, P. (2012) Ferric Complexes of 3-Hydroxy-4-Pyridinones Characterized by Density Functional Theory and Raman and Uv-Vis Spectroscopies. Inorganic Chemistry, 51, 4473-4481.
https://doi.org/10.1021/ic202004d - 22. Horsman, G.P., Jirasek, A., Vaillancourt, F.H., Barbosa, C.J., Jarzecki, A.A., Xu, C., Mekmouche, Y., Spiro, T.G., Lipscomb, J.D., Blades, M.W., et al. (2005) Spectroscopic Studies of the Anaerobic Enzyme-Substrate Complex of Catechol 1,2-Dioxy-genase. Journal of American Chemical Society, 127, 16882-16891.
https://doi.org/10.1021/ja053800o - 23. Matin, M.A., Chitumalla, R.K., Lim, M., Gao, X. and Jang, J.K. (2015) Density Functional Theory Study on the Cross-Linking of Mussel Adhesive Proteins. Journal of Physical Chemistry B, 119, 5496-5504.
https://doi.org/10.1021/acs.jpcb.5b01152 - 24. Zhang, F., Sababi, M., Brinck, T., Persson, D., Pan, J. and Claesson, P. M. (2013) In Situ Investigations of Fe3+ Induced Complexation of Adsorbed Mefp-1 Protein Film on Iron Substrate. Journal of Colloid and Interface Science, 404, 62-71.
https://doi.org/10.1016/j.jcis.2013.05.016 - 25. Liu, Q., Lu, X., Zhang, H., Liu, G., Zhong, H. and Zeng, H. (2016) Probing the Reversible Fe3+-DOPA-Mediated Bridging Interaction in Mussel Foot Protein-1. Journal of Physical Chemistry C, 120, 21670-21677.
https://doi.org/10.1021/acs.jpcc.6b07482 - 26. Weinhold, F. and Landis, C.R. (2001) Natural Bond Orbitals and Extensions of Localized Bonding Concepts. Chemical Education Research, 2, 91-104.
https://doi.org/10.1039/B1RP90011K - 27. Pearson, R. (1997) Chemical Hardness-Applications from Molecules to Solids. Wiley, Weinheim.
- 28. Pearson, R.G. (1992) The Electronic Chemical Potential and Chemical Hardness. Journal of Molecular Structure, 255, 261-270.
https://doi.org/10.1016/0166-1280(92)85014-C - 29. Becke, A.D. (1993) Density-Functional Thermochemistry. III. The Role of Exact Exchange. Journal of Chemical Physics, 98, 5648-5652.
https://doi.org/10.1063/1.464913 - 30. Yanai, T., Tew, D.P. and Handy, N.C.A. (2004) New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chemical Physics Letter, 393, 51-57.
https://doi.org/10.1016/j.cplett.2004.06.011 - 31. Frisch, M.J., Trucks, G.W., Schlegel, H.B., Scuseria, G.E., Robb, M.A., Cheeseman, J.R., Scalmani, G., Barone, V., Mennucci, B., Petersson, G.A., Nakatsuji, H., Caricato, M., Li, X., Hratchian, H.P., Izmaylov, A.F., Bloino, J., Zheng, G., Sonnenberg, J.L., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Vreven, T., Montgomery Jr., J.A., Peralta, J.E., Ogliaro, F., Bearpark, M., Heyd, J.J., Brothers, E., Kudin, K.N., Staroverov, V.N., Kobayashi, R., Normand, J., Raghavachari, K., Rendell, A., Burant, J.C., Iyengar, S.S., Tomasi, J., Cossi, M., Rega, N., Millam, J.M., Klene, M., Knox, J.E., Cross, J.B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R.E., Yazyev, O., Austin, A.J., Cammi, R., Pomelli, C., Ochterski, J.W., Martin, R.L., Morokuma, K., Zakrzewski, V.G., Voth, G.A., Salvador, P., Dannenberg, J.J., Dapprich, S., Daniels, A.D., Farkas, O., Foresman, J.B., Ortiz, J.V., Cioslowski, J. and Fox, D.J. (2010) Gaussian 09, Revision B.01. Gaussian Inc., Wallingford.
- 32. Merrick, J.P., Moran, D. and Radom, L. (2007) An Evaluation of Harmonic Vibrational Frequency Scale Factors. Journal of Physical Chemistry A, 111, 11683-11700.
https://doi.org/10.1021/jp073974n - 33. Cossi, M., Barone, V., Cammi, R. and Tomasi, J. (1996) Ab Initio Study of Solvated Molecules: A New Implementation of the Polarizable Continuum Model. Chemical Physics Letter, 255, 327-335.
https://doi.org/10.1016/0009-2614(96)00349-1 - 34. Glendening, E.D., Landis, C.R. and Weinhold, F. (2012) Natural Bond Orbital Methods. Computational Molecular Science, 2, 1-42.
https://doi.org/10.1002/wcms.51 - 35. Reed, A.E., Curtiss, L.A. and Weinhold, F. (1988) Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chemical Review, 88, 899-926.
https://doi.org/10.1021/cr00088a005 - 36. Koopmans, T. (1934) über Die Zuordnung Von Wellenfunktionen Und Eigenwerten Zu Den Einzelnen Elektronen Eines Atoms. Physica, 1, 104-113.
https://doi.org/10.1016/S0031-8914(34)90011-2 - 37. Swart, M. (2013) Spin States of (Bio) Inorganic Systems: Successes and Pitfalls. International Journal of Quantum Chemistry, 113, 2-7.
https://doi.org/10.1002/qua.24255 - 38. Harvey, J.N. (2004) Dft Computation of Relative Spin-State Energetics of Transition Metal Compounds. In: Kaltsoyannis, N. and McGrady, J.E., Eds., Principles and Applications of Density Functional Theory in Inorganic Chemistry II, Springer, Berlin, 151-184.
https://doi.org/10.1007/b97939 - 39. Boys, S.F. and Bernardi, F. (1970) The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Molecular Physics, 19, 553-566.
https://doi.org/10.1080/00268977000101561 - 40. Daza,a, M.C., Dobado, J.A. and Jose, M.M. (1999) Basis Set Superposition Error-Counterpoise Corrected Potential Energy Surfaces. Application to Hydrogen PeroxideX (X=F2,Cl2,Br2,Li+,Na+) Complexes. Journal of Chemical Physics, 110, 11806-11813.
https://doi.org/10.1063/1.479166 - 41. Islam, M.M. and Bredow, T. (2015) Rutile Band-Gap States Induced by Doping with Manganese in Various Oxidation States. Journal of Physical Chemistry C, 119, 5534-5541.
https://doi.org/10.1021/acs.jpcc.5b00023 - 42. Islam, M.M., Bredow, T. and Gerson, A. (2011) Electronic Properties of Vanadium-Doped TiO2. ChemPhysChem, 12, 3467-3473.
https://doi.org/10.1002/cphc.201100557 - 43. Aakesson, R., Pettersson, L.G.M., Sandstroem, M. and Wahlgren, U. (1994) Ligand Field Effects in the Hydrated Divalent and Trivalent Metal Ions of the First and Second Transition Periods. Journal of American Chemical Society, 116, 8691-8704.
https://doi.org/10.1021/ja00098a032 - 44. Yang, Y., Ratner, M.A. and Schatz, G.C. (2014) Multireference Ab Initio Study of Ligand Field D-D Transitions in Octahedral Transition-Metal Oxide Clusters. Journal of Physical Chemistry C, 118, 29196-29208.
https://doi.org/10.1021/jp5052672 - 45. Raymond, K.N., Isied, S.S., Brown, L.D., Fronczek, F.R. and Nibert, J.H. (1976) Coordination Isomers of Biological Iron Transport Compounds. VI. Models of the Enterobactin Coordination Site. A Crystal Field Effect in the Structure of Potassium Tris(Catecholato)Chromate(Iii) and -Ferrate(Iii) Sesquihydrates, K3[M(O2C6H4)3]. Cntdot.1.5H2O, M=Chromium, Iron. Journal of American Chemical Society, 98, 1767-1774.
https://doi.org/10.1021/ja00423a022 - 46. Hay, B.P., Dixon, D.A., Vargas, R., Garza, J. and Raymond, K.N. (2001) Structural Criteria for the Rational Design of Selective Ligands. 3. Quantitative Structure-Stability Relationship for Iron(III) Complexation by Tris-Catecholamide Siderophores. Inorganic Chemistry, 40, 3922-3935.
https://doi.org/10.1021/ic001380s - 47. Yoosefian, M. and Adeleh, M. (2015) Solvent Effects on Binding Energy, Stability order and Hydrogen Bonding of Guanine-Cytosine Base Pair. Journal of Molecular Liquids, 209, 526-530.
https://doi.org/10.1016/j.molliq.2015.06.029 - 48. Salama, S., Stong, J.D., Neilands, J.B. and Spiro, T.G. (1978) Electronic and Resonance Raman Spectra of Iron(III) Complexes of Enterobactin, Catechol, and N-Methyl-2,3-Dihydroxybenzamide. Biochemistry, 17, 3781-3785.
https://doi.org/10.1021/bi00611a017 - 49. Kavian, S., Izadyar, M. and Housaindokht, M.R. (2016) Solvent and Spin State Effects on Molecular Structure, IR Spectra, Binding Energies and Quantum Chemical Reactivity Indices of Deferiprone-Ferric Complex: DFT Study. Polyhedron, 117, 623-627.
https://doi.org/10.1016/j.poly.2016.06.041 - 50. Wang, H., Wang, L., Shen, S., Zhang, W., Li, M., Du, L., Zheng, X. and Phillips, D. L. (2012) Effects of Hydrogen Bond and Solvent Polarity on the C=O Stretching of Bis(2-Thienyl)Ketone in Solution. Journal of Chemical Physics, 136, Article ID: 124509.
https://doi.org/10.1063/1.3697482 - 51. Taylor, S.W., Chase, D.B., Emptage, M.H., Nelson, M.J. and Waite, J.H. (1996) Ferric Ion Complexes of a Dopa-Containing Adhesive Protein from Mytilus Edulis. Inorganic Chemistry, 35, 7572-7577.
https://doi.org/10.1021/ic960514s - 52. Sever, M.J. and Wilker, J.J. (2004) Visible Absorption Spectra of Metal-Catecholate and Metal-Tironate Complexes. Dalton Transition, 7, 1061-1072.
https://doi.org/10.1039/B315811J - 53. Andersson, K., Malmqvist, P.A. and Roos, B.O. (1992) Second-Order Perturbation Theory with a Complete Active Space Self-Consistent Field Reference Function. Journal of Chemical Physics, 96, 1218-1226.
https://doi.org/10.1063/1.462209 - 54. Fukui, K. (1982) The Role of Frontier Orbitals in Chemical Reactions (Nobel Lecture). Angew Chemistry International Edition, 21, 801-809.
https://doi.org/10.1002/anie.198208013 - 55. Zhou, Z. and Parr, R.G. (1990) Activation Hardness: New Index for Describing the Orientation of Electrophilic Aromatic Substitution. Journal of American Chemical Society, 112, 5720-5724.
https://doi.org/10.1021/ja00171a007








