ABSTRACT

Temporal autocorrelation (also called serial correlation) refers to the relation- ship between successive values (i.e. lags) of the same variable. Although it has long been a major concern in time series models, however, in-depth treatments of temporal autocorrelation in modeling vehicle crash data are lacking. This paper presents several test statistics to detect the amount of temporal autocorrelation and its level of significance in crash data. The tests employed are: 1) the Durbin-Watson (DW); 2) the Breusch-Godfrey (LM); and 3) the Ljung-Box Q (LBQ). When temporal autocorrelation is statistically significant in crash data, it could adversely bias the parameter estimates. As such, if present, temporal autocorrelation should be removed prior to use the data in crash modeling. Two procedures are presented in this paper to remove the temporal autocorrelation: 1) Differencing; and 2) the Cochrane-Orcutt method.

Keywords:

Serial Correlation, Durbin-Watson, Breusch-Godfrey, Ljung-Box, Differencing, Cochrane-Orcutt

1. Introduction

Temporal autocorrelation (i.e. serial correlation) is a special case of correlation, and refers not to the relationship between two or more variables, but to the relationship between successive values of the same variable. Temporal autocorrelation is closely related to the correlation coefficient between two or more varia- bles, except that in this case we do not deal with variables X and Y, but with lagged values of the same variable. Most regression methods that are used in crash modeling assume that the error terms are independent from one another, and they are uncorrelated. This assumption is formally expressed [1] as:

(1)

where,

E: the expected value of all pair-wise products of error terms,

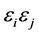: error terms of the i and j observations respectively,

which means that the expected value of all pair-wise products of error terms is zero, and when the error terms are uncorrelated, the positive products will cancel those that are negative leaving an expected value of 0.0 [1] . If this assumption is violated, the standard errors of the estimates of the regression parameters are significantly underestimated which leads to erroneously inflated coefficients values, and incorrect confidence intervals. The presence of correlated error terms means that these types of inferences cannot be made reliably [2] . The violation of this assumption occurs because of some temporal (time) component (i.e. heterogeneity due to time) that can affect the observations drawn across the time, such as time series data, panel data in the form of serial correlation, and any other dataset that might be collected over a period of time. In this context, the error in a first time period influences the error in a subsequent time period (either the previous period, or the next period or beyond) [3] . For example, we might expect the disturbance (i.e. error term) in year t to be correlated with the disturbance in year t − 1 and with the disturbance in year t + 1, t + 2, and so on. If there are factors responsible for inflating the observation at some point in time to an extent larger than expected (i.e. a positive error), then it is reasonable to expect that the effects of those same factors linger creating an upward (positive) bias in the error term of a subsequent period. This phenomenon is called positive first-order autocorrelation, which is the most common manner in which the assumption of independence of errors is violated. For instance, if a dataset influenced by quarterly seasonal factors, then a resulting model that ignores the seasonal factors will have correlated error terms with a lag of four periods. There are different structure types of temporal autocorrelation: 1^st order, 2^nd order, and so on. The form of temporal autocorrelation that is encountered most often is called the first order temporal autocorrelation in the first autoregressive term, which is denoted by AR (1). The AR (1) autocorrelation assumes that the disturbance in time period t (current period) depends upon the disturbance in time period t − 1 (previous period) plus some additional amount, which is an error, and can be modeled as [3] :

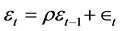(2)

where,

ε_t :the disturbance in time period t,

ε_{t − 1}: the disturbance in time period t − 1,

ρ: the autocorrelation coefficient,

: the model error term.

The parameter ρ can take any value between negative one and positive one. If ρ > 0, then the disturbances in period t are positively correlated with the disturbances in period t − 1. In this case, positive autocorrelation exists which means that when disturbances in period t − 1 are positive disturbances, then disturbances in period t tend to be positive. When disturbances in period t − 1 are negative disturbances, then disturbances in period t tend to be negative. Temporal datasets are usually characterized by positive autocorrelation. If ρ < 0, then the disturbances in period t are negatively correlated with the disturbances in period t − 1. In this case there is negative autocorrelation. This means that when disturbances in period t − 1 are positive disturbances, then disturbances in period t tend to be negative. When disturbances in period t − 1 are negative disturbances, then disturbances in period t tend to be positive.

The second order temporal auto correlation is called the second-order autoregressive process or AR (2). The AR (2) autocorrelation assumes that the disturbance in period t is related to both the disturbance in period t − 1 and the disturbance in period t - 2, and can be modeled as [3] :

(3)

where,

ρ₁: the autocorrelation coefficient in time period t − 1.

ρ_1: the autocorrelation coefficient in time period t - 2.

The disturbance in period t depends upon the disturbance in period t − 1, the disturbance in period t - 2, and some additional amount, which is an error (∈_t). In a similar manner, the temporal autocorrelation can be extended to the ρth order autocorrelation AR (ρ). However, the most often used temporal autocorrelation is the first-order autoregressive process [3] . If the temporal autocorrelation is found to be significant in crash data, then it must be removed before using the data in the modeling process [4] [5] [6] .

1.1. Sources of Temporal Autocorrelation

Temporal autocorrelation can arise from the following sources:

・ Omitted Explanatory Variables: Omitting some important explanatory variables from the modeling process can create temporal autocorrelation that can produce biased parameter estimates and incorrect inferences, especially if the omitted variable is correlated with variables included in the model [1] [7] [8] [9] .

・ Misspecification of the Mathematical Form of the model can create temporal autocorrelation. For example, if a linear form of the model is specified when the true form of the model is non-linear, the resulting errors may reflect some temporal autocorrelation [10] [11] [12] [13] .

・ Misspecification of The Error Terms of the model due to some purely random factors, such as changes in weather conditions, economic factors, and other unaccounted for variables, which could have changing effects over successive periods. In such instances, the value of the error terms in the model could be miss pecified [3] .

1.2. Detection of Temporal Autocorrelation

Several methods are available to detect the existence of the temporal autocorrelation in the crash dataset, including the residuals scatter plots, the Durbin-Watson test, the Durbin h test, the Breusch-Godfrey test, the Ljung-Box Q test, and correlograms. These will be described in detail below:

・ Scatter Plot of Residuals

The error for the i^th observation in the dataset is usually unknown and unobservable. However, the residual for this observation can be used as an estimate of the error, then the residuals can be plotted against the variables that may be related to time. The residual would be measured on the vertical axis. The temporal variables such as, years, months, or days would be measured on the horizontal axis. Next, the residual plot can be examined to determine if the residuals appear to exhibit a pattern of temporal autocorrelation. If the data are independent, then the residuals should be randomly scattered about 0.0. However, if a noticeable pattern emerges (particularly one that is cyclical or seasonal) then temporal autocorrelation is likely an issue. It must be emphasized that this is not a formal test of serial correlation. It would only suggest whether temporal autocorrelation may exist. We should not substitute a residual plot for a formal test [1] [13] .

・ The Durbin-Watson (DW) Test

The most often used test for first order temporal autocorrelation is the Durbin-Watson DW test [13] . The DW test is a measure of the first order autocorrelation and it cannot be used to test for higher order temporal autocorrelation. The DW test is constructed to test the null and alternative hypotheses regarding the temporal autocorrelation coefficient (ρ):

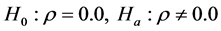(4)

The null hypothesis of ρ = 0.0 means that the error term in one period is not correlated with the error term in the previous period, while the alternative hypothesis of ρ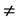0.0 means the error term in one period is either positively or negatively correlated with the error term in the previous period. To test the hypothesis, the DW test statistic on a dataset of size n is formulated as [1] :

(5)

where,

DW: the Durbin-Watson statistic,

e_t: the residual error term in time period t,

e_{t ?1}: the residual error term in the previous time period t − 1.

The DW statistics ranges from 0.0 to 4.0, and it can be shown that:

(6)

where,

ρ^: the residual temporal autocorrelation coefficient.

When ρ^ = 0.0, (i.e. no autocorrelation), then DW = 2.0.

When ρ^ tends to 1.0, then DW = 0.0.

When ρ^ tends to −1.0, then DW = 4.0.

The critical values of DW for a given level of significance, sample size and number of independent variables can be obtained from published tables that are tabulated as pairs of values: DL (lower limit of DW) and DU (upper limit of DW). To evaluate DW [3] :

1) Locate values of DL and DU in Durbin-Watson statistic table.

2) For positive temporal autocorrelation:

a) If DW < DL then there is positive autocorrelation.

b) If DW > DU then there is no positive autocorrelation.

c) If DL < DW < DU then the test is inconclusive.

3) For negative temporal autocorrelation:

a) If DW < (4.0 ? DU) then there is no negative autocorrelation.

b) If DW > (4.0 ? DL) then there is negative autocorrelation.

c) If (4.0 ? DU) < DW < (4.0 ? DL) then the test is inconclusive.

A rule of thumb that is sometimes used is to conclude that there is no first order temporal autocorrelation if the DW statistic is between 1.5 and 2.5. A DW statistic below 1.5 indicates positive first order autocorrelation. A DW statistic of greater than 2.5 indicates negative first order autocorrelation [3] . Alternatively, a significant p-value for the DW statistic would suggest rejecting the null hypothesis and concluding that there is first order autocorrelation in the residuals, and a non-significant p-value would suggest accepting the null hypothesis and concluding that there is no evidence of first order autocorrelation in the residuals.

・ The Durbin h Test

When one or more lagged dependent variables are present in the data, the DW statistic will be biased towards 2.0, this means that even if temporal autocorrelation is present it may be close to 2.0, and hence it cannot detect it. Durbin suggests a test for temporal autocorrelation when there is a lagged dependent variable in the dataset, and it is based on the h statistics. The Durbin h statistics is defined as:

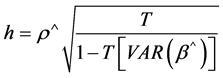(7)

where,

T: the number of observations in the dataset,

ρ^: the temporal autocorrelation coefficient of the residuals,

VAR (β^): the variance of the coefficient on the lagged dependent variable.

Durbin has shown that the h statistics is approximately normally distributed with a unit variance, hence the test for first order autocorrelation can be done using the standard normal distribution. If Durbin h statistic is equal to or greater than 1.96, it is likely that temporal autocorrelation exists [1] .

・ The Breusch-Godfrey Lagrange Multiplier (LM) Test

The Breusch-Godfrey test is a general test of serial correlation and can be used to test for first order temporal autocorrelation or higher order autocorrelation. This test is a specific type of Lagrange Multiplier test. The LM test is particularly useful because it is not only suitable for testing for temporal autocorrelation of any order, but also suitable for models with or without lagged dependent variables [14] . The null and alternative hypotheses used with this test for a second order autocorrelation are:

(8)

The LM test statistic is given by:

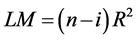(9)

where,

LM: the Lagrange multiplier test statistic,

n: the number of observations in the dataset,

i: the order of the autocorrelation,

R²: the unadjusted R² statistic (coefficient of determination) of the model.

The LM statistic has a chi-square distribution with two degrees of freedom, χ² (2) [15] .

・ The Ljung-Box Q (LBQ) Test

The Ljung-Box Q test (sometimes called the Portmanteau test) is used to test whether or not observations taken over time are random and independent for any order of temporal autocorrelation. It is based on asymptotic Chi-Square distribution χ². In particular, for a given i lag, it tests the following hypotheses [16] :

H₀: the autocorrelations up to i lags are all zero (10)

H_a: the autocorrelations of one or more lags differ from zero (11)

The test statistic is determined as follows [16] :

(12)

where,

LBQ_i: the Ljung-Box Q statistic,

n: the number of observations in the data,

j: the lag being considered,

i: the autocorrelation order,

r: the residual error term in lag j.

・ Correlograms

Correlograms are autocorrelation plots that can show the presence of temporal autocorrelation. The autocorrelation would appear in lag 1.0 and progress for n lags then disappear. In these plots the residual autocorrelation coefficient (ρ^) is plotted against n lags to develop a correlogram. This will give a visual look at a range of autocorrelation coefficients at relevant time lags so that significant values may be seen [17] . In most software packages, two types of autocorrelation functions are presented: the autocorrelation function (ACF), and the partial autocorrelation function (PACF). The ACF is the amount of autocorrelation between a variable and a lag that is not explained by correlations at all lower-order- lags, and the PACF is the difference between the actual correlation at specific lag and the expected correlation due to propagation of correlation at the previous lag. If the PACF displays a sharp cutoff while the ACF decays more slowly we conclude that the data displays an autoregressive model (AR), and the lag at which the PACF cuts off is the indicated number of AR terms. If the ACF of the data displays a sharp cutoff and/or the lag-1 autocorrelation is negative then we have to consider adding a moving average term (MA) to the model, and the lag at which the ACF cuts off is the indicated number of MA terms. In general, the diagnostic patterns of ACF and PACF for an AR (1) term [18] are:

ACF: declines in geometric progression from its highest value at lag 1.0.

PACF: cuts off abruptly after lag 1.0.

If the ACF of a specific variable shows a declining geometric progression from the highest value at lag 1.0, and the PACF shows an abrupt cut off after lag 1.0., this would indicate that this variable has not encountered temporal autocorrelation.

1.3. Remedies for Temporal Autocorrelation

When temporal autocorrelation is determined to be present in the dataset, then one of the first remedial measures should be to investigate the omission of one or more of the key explanatory variables, especially variables that are related to time. If such a variable does not aid in reducing or eliminating temporal autocorrelation of the error terms, then a differencing procedure should be applied to all temporal independent variables in the dataset to convert them into their differences values, and rerun the regression model by deleting the intercept from the model [17] . If this remedy does not help in eliminating temporal autocorrelation, then certain transformations on all variables can be performed for the AR (1) term. These transformations aim at performing repeated iterative steps to minimize the squared sum of errors in the regression model. Examples of such transformations are: Cochrane-Orcutt procedure; and Hildreth-Lu procedure. More advanced methods can also be used for big datasets such as: Fourier series analysis; and the spectral analysis [17] [18] .

2. Data

Missouri crash data for three years (2013-2015) for the Interstate I-70, MO, USA are used in this paper as reported by the Missouri State Highway Patrol (MSHP) and recorded in the Missouri Statewide Traffic Accident Records System (STARS). The data included a wide range of independent variables (i.e. risk factors) in the analysis:

・ Road geometry (grade or level; number of lanes)

・ Road classification (rural or urban; existing of construction zones)

・ Environment (light conditions)

・ Traffic operation (annual average daily traffic, AADT)

・ Driver factors (driver’s age; speeding; aggressive driving; driver intoxicated conditions; the use of cell phone or texting)

・ Vehicle type (passenger car; motorcycles; truck)

・ Number of vehicles involved in the crash

・ Time factors (hour of crash occurrence; weekday; month)

・ Accident type (animal; fixed object; overturn; pedestrian; vehicle in transport).

3. Methodology

In this paper, three of the most widely used tests to detect the existence of temporal autocorrelation in the crash data are investigated, namely: The Durbin- Watson (DW), the Breusch-Godfrey (LM), and the Ljung-Box Q (LBQ) tests. The three temporal independent variables in the dataset (i.e. month, weekday, hour) are used in the application of each test.

The tests can be applied at different levels of temporal aggregation (i.e. over one year, over two years, three years, etc.) to help identify any hidden effects of the temporal autocorrelation that might exist within a timeframe. In this paper, the JMP12 software package is used to compute the DW statistics, the associated residual temporal autocorrelation coefficients, and their significance at the 95% confidence level (i.e. p-values). JMP requires that the input format of the crash data be in either excel spreadsheet (i.e. *.xlsx) or in text (i.e. delimited or *.csv) and then the output is produced as excel spreadsheet or delimited text. The Eviews 9 software is used to compute the LM statistics, and their significance at the 95% confidence level (i.e. p-values). The software requires that the input format of the crash data be in either excel spreadsheet (i.e. *.xlsx) or in text (i.e. delimited or *.csv) and then the output is produced as excel spreadsheet or delimited text. The Stata 14 software is used to compute the Box-Ljung Q statistic (LBQ) at each lag separately with the autocorrelation function (ACF) and the partial autocorrelation function (PACF) at each lag as well, and their significance at the 95% confidence level (i.e. p-values). The software requires that the input format of the crash data be in either excel spreadsheet (i.e. *.xlsx) or in text (i.e. delimited or *.csv) and then the output is produced as excel spreadsheet or delimited text.

The Durbin Watson (DW) test is applied to the I-70 data at two temporal levels; aggregation by year, and aggregation over all three years. Data for each year in aggregate is separately tested using (month, weekday, and hour) as the independent temporal variables, and then the aggregate three-year period is tested using the same independent variables.

The Breusch-Godfrey (LM) test is applied to the I-70 data for the first 36 lags at two temporal levels; aggregation by year, and aggregation over all three years. Data for each year in aggregate is separately tested using (month, weekday, and hour) as the independent temporal variables, and then the aggregate three-year period is tested. The LM test is applied with degrees of freedom equal to the number of lags (i.e. 36 degrees of freedom). The minimum recommended number of lags that should be considered for the LM and LBQ tests is roughly taken as the natural logarithm of the number of observations within the dataset [19] , and larger values are recommended to detect the existence of temporal autocorrelation. For the I-70 dataset, the number of observations of the aggregated three years (2013-2015) is 5869, and the minimum recommended number of lags = ln (5869) = 8.7. This paper uses 36 lags in both the LM and LBQ tests instead of the minimum recommended number.

The Box-LjungQ statistic (LBQ) is applied to the I-70 data for the aggregated three-year period (2013-2015) using the time independent variables (month, weekday, and hour) and for the first 36 lags. In addition, correlograms of the autocorrelation function (ACF) and partial autocorrelation function (PACF) for the I-70 data for the aggregated three-year period (2013-2015) are presented.

3.1. The Durbin-Watson Test Results

Table 1 shows the results of the Durbin-Watson (DW) test for the I-70 at the one-year aggregate level. It can be seen that the temporal autocorrelation of the I-70 dataset for the year 2013 is found to be 3.64% with p value of 0.0512 (which is non-significant at alpha of 0.05); for the year 2014 year is found to be 7.19% with p-value of 0.0002 (which is significant at alpha of 0.01); and for the year 2015 is found to be 2.38% with p-value of 0.1371 (non-significant at alpha of 0.05). So, the only significant temporal autocorrelation is existed within the I-70 (2014) data, which should be removed before using this dataset in any modeling process.

3.2. The Breusch-Godfrey Test Results

Table 2 shows the results of the LM test for the I-70 crash data at the one-year aggregate level. The LM value (using 36 lags or 36 degrees of freedom) of the I-70 dataset for the year 2013 is found to be 31.022 with p-value of 0.7042 (non- significant at alpha of 0.05); for the year 2014 is found to be 60.129 with p-value of 0.0071 (significant at alpha of 0.01); and for the year 2015 is found to be 50.876 with p-value of 0.0512 (non-significant at alpha of 0.05). The results of the LM test confirm the results of the DW test that the I-70 dataset for the year 2014 contains a significant temporal autocorrelation as shown in Table 2.

3.3. Removal of the Temporal Autocorrelation from Crash Data

Since both the DW and the LM tests have shown the existence of temporal autocorrelation in the I-70 (2014) crash data, the next step is to remove it before using the data in any modeling process. Two approaches are investigated in this paper for the removal of temporal autocorrelation, the differencing procedure, and the Cochrane-Orcutt procedure.

3.4. The Differencing Procedure

Since a significant temporal autocorrelation is found to be existed within the I- 70 (2014) data, then this should be removed before using the dataset in any potential modeling process [4] [5] [6] . In order to remove any significant temporal autocorrelation that may be existed in a dataset, one of the first remedial measures should be to investigate the omission of one or more of the explanatory variables, especially variables that are related to time. Assuming that, the three time variables in the datasets (month, weekday, hour) have potential influence on the dependent variable, then they are unlikely to be removed from the analysis. Hence, the next step is to apply a differencing procedure to all time independent variables in the dataset to convert them into their differences values. The differencing procedure can be applied by subtracting the previous observation from the current observation, as shown in Equation (13) [20] :

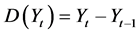(13)

where,

D (Y): the difference of variable Y at lag t,

Y_t: the value of Y at lag t,

Y _{t − 1}: the value of Y at lag t − 1.

The rho (i.e. the residual autocorrelation coefficient) is assumed to be (1.0) in the differencing procedure, which could overestimate the true rho value [21] . The first order differencing is applied to the I-70 (2014) dataset, and the ordinary least square residuals were obtained, then the Durbin-Watson (DW) test is calculated to check for the temporal autocorrelation. The result of the DW statistic showed that the temporal autocorrelation was still existed even after applying the first order differencing. Although the first order differencing is enough to show whether the differencing procedure can be used to remove the serial (temporal) correlation or not [21] , however, more differencing orders (up to 7 orders) are applied to the I-70 (2014) dataset, and the Durbin-Watson test (DW statistic) is calculated each time to check for the temporal autocorrelation. The results showed that the temporal autocorrelation was not removed by this method. Table 3 shows seven differencing orders that were applied to the data and their DW statistics.

3.5. The Cochrane-Orcutt Procedure

When the differencing procedure cannot eliminate the temporal autocorrelation in a dataset, then the Cochrane-Orcutt procedure should be applied for the Autoregressive AR (1) term of this dataset [20] . The procedure uses the ordinary least square residuals to obtain the value of rho which minimizes the sum of squared residuals. Rho is then used to transform the observations of the varia- bles. The process continues until convergence is reached [20] [22] . Considering the general ordinary least squared regression model:

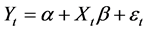(14)

where,

Y_t: the dependent variable at time (lag) t,

α: the intercept,

β: the vector of regression coefficients,

X_t: the vector of explanatory variables at time (lag) t,

ε_t: the error term of the model at time (lag) t.

When applying the DW test, if the (DW) statistic revealed that the temporal autocorrelation exists among the model error terms, then the residuals must be modeled for the first order autoregressive term AR (1) such that:

(15)

where,

ρ: the temporal autocorrelation coefficient (rho) between pairs of observations, 0 < ρ < 1,

e_t: the error term of the residuals at time (lag) t.

The Cochrane-Orcutt procedure is obtained by taking a quasi-differencing or generalized differencing, such that the sum of squared residuals is minimized [20] [22] :

(16)

The Cochrane-Orcutt iterative procedure starts by obtaining parameter estimates by the ordinary least square regression (OLS). Applying Equation (15), the OLS residuals are then used to obtain an estimate of rho from the OLS regression. This estimate of rho is then used to produce transformed observations, and parameter estimates are obtained again by applying OLS to the transformed model. A new estimate of rho is computed and another round of parameter estimates is obtained. The iterations stop when successive parameter estimates differ by less than 0.001 [20] .

The iterative Cochrane-Orcutt procedure was applied to the I-70 (2014) dataset, and an optimized rho (i.e. the residual autocorrelation coefficient) value of 0.07333 was obtained using the Stata 14 software that minimizes the estimated sum of squared residuals (ESS), then the DW statistic was calculated for the transformed residuals. The results showed that the temporal autocorrelation was removed from the I-70 (2014) dataset, as shown in Table 4. The DW statistic for the I-70 (2014) dataset is changed after applying the Cochrane-Orcutt procedure from 1.843 (with a significant p-value of 0.0002) to 1.992 (with a non-significant p-value of 0.7167).

After removing the temporal autocorrelation from the I-70 (2014) dataset, the DW test and the LM test were applied for the aggregated three years’ period (2013-2015) for the I-70 dataset. The DW statistic for the three years’ period (2013-2015) is 1.971 with temporal autocorrelation of 1.47% for the I-70 dataset, which is non-significant, as shown in Table 5.

The LM value for the aggregated three years’ period (2013-2015) using 36 lags is 41.203 for the I-70 dataset, which is non-significant, as shown in Table 6. The results from the DW test and the LM test indicate that there is no significant temporal autocorrelation among each of the temporal independent variables (i.e. month, weekday, and hour) in the (2013-2015) dataset.

3.6. The LBQ Test Results

The Box-Ljung Q statistic (LBQ) is applied to the aggregated three-year period (2013-2015). Table 7 shows the Box-Ljung Q statistic, the auto correlation function (ACF) and the partial autocorrelation function (PACF) with their p-values for the I-70 dataset for the first 36 lags. It can be seen that the LBQ statistic, the ACF, and the PACF for all 36 lags are non-significant for the I-70 crash data. The LBQ statistic increases with the lag progress, indicating no temporal autocorrelation within the dataset and confirming the results of the DW test and the LM test.

4. Conclusion

Temporal autocorrelation (also called serial correlation) refers to the relationship between successive values (i.e. lags) of the same variable. Although it is a major concern in time series models, however, it is very important to be checked in crash data modeling as well. The results of crash data modeling can be improved

when several years of crash data are utilized in the analysis, such as a period of three years instead of one year. However, this means that the same roadway will generate multiple observations over time, which could be correlated due to some temporal (time) component and could adversely affect the precision of parameter estimates. There are several methods that can be used to detect the existence of the temporal autocorrelation in the crash dataset, such as: 1) the residuals scatter plots; 2) the Durbin-Watson (DW) test; 3) the Durbin h test; 4) the Breusch-Godfrey (LM) test; 5) the Ljung-Box Q (LBQ) test; and 6) correlograms. The residuals scatter plots and correlograms are not formal tests, and they would only suggest whether temporal autocorrelation may exist within crash data. The Durbin h test can only be used when there is a lagged dependent variable in the data. This paper used the Durbin-Watson (DW), Breusch-Godfrey (LM), and the LBQ tests to detect the temporal autocorrelation among the temporal independent variables in the crash data (i.e. hour, weekday, month) for the interstate I-70 in Missouri for the years (2013-2015). Although the applications of these tests can be found in time series models, they have not been addressed in modeling crash data. As such, this paper thoroughly investigated the applicability of these tests to crash data.

Cite this paper

Abdulhafedh, A. (2017) How to Detect and Remove Temporal Autocorrelation in Vehicular Crash Data. Journal of Transportation Technologies, 7, 133-147. https://doi.org/10.4236/jtts.2017.72010

References

NOTES

*PhD in Civil Engineering.