Journal of Transportation Technologies
Vol.05 No.02(2015), Article ID:55273,13 pages
10.4236/jtts.2015.52009
The Relation between Freeway Average Speed and Speed Noise
Bahar Zarin1, Siamak Ardekani2
1Department of Civil & Environmental Engineering, The University of Maryland, College Park, MD, USA
2Department of Civil Engineering, The University of Texas at Arlington, Arlington, TX, USA
Email: bzarin@umd.edu, ardekani@uta.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 January 2015; accepted 27 March 2015; published 31 March 2015
ABSTRACT
Many factors affect the vehicular fuel consumption rate. The most significant traffic-related ones are speed, number of stops, speed noise, and acceleration noise (acceleration standard deviation). Fuel consumption models for both urban and highway traffic are used to evaluate the effect of these factors. Previous literature shows the speed and the acceleration of vehicles as well as the aerodynamic effects are the most commonly used variables in the highway fuel consumption mo- dels. However, most existing models are based on the average or cruising speed and the effect of speed variation is by-and-large ignored. Incorporating the speed noise as a variable in the prediction models seems impractical because measuring it is cumbersome. However, knowing the relation between speed and speed noise may allow including the effect of speed noise in the model indirectly. To that end, this study examines the relation between speed and speed noise. The resulting mathematical relation is used to incorporate the speed noise effects in the fuel consumption model.
Keywords:
Speed Noise, Average Speed, Fuel Consumption Models, Regression Model

1. Introduction
The US transportation sector is a major consumer of fossil fuels (Consumption of Oil for Transportation, 2013). In fact, the transportation sector in the US accounts for about two-thirds of the liquid petroleum fuels consumed each year in the US. This energy use is concentrated primarily in the highway mode [1] . The factors that affect variation in the fuel consumption rate include traffic characteristics, vehicle performance characteristics, driver characteristics, environment conditions, pavement conditions, etc. [2] . Among them, traffic-related factors are studied in this research. The studies show the traffic-related factors include but are not limited to variables such as speed, number of stops, speed noise, and acceleration noise.
The significance of this issue is emphasized when it is realized that all modes of transportation that consume fossil fuels contribute to air and water pollution through the burning and the refueling cycle (Consumption of Oil for Transportation). In the US, transportation-related emissions account for about 60% of carbon monoxide, 40% of nitrogen oxides and about 40% of volatile organic compounds―including hydrocarbons emissions (Consumption of Oil for Transportation).
The primary objective of this research is to find a relation between speed and the speed noise (standard deviation of speed along time) to be incorporated into a new fuel consumption model for highway traffic. Most of the existing models offer simplified expressions to compute fuel consumption based on average link speeds without much regard to the transient effects of speed. However, this study addresses this issue, presenting the new parameter in the existing model to consider speed noise as an explanatory variable.
Addressing the above mentioned purposes of the study, the main questions are stated below:
・ Is there any relation between speed and speed noise in highway traffic?
・ Does this relation differ based on the number of lanes in the highway?
・ How could this relationship be used to modify the current highway fuel consumption models?
2. Literature
2.1. Overview of Existing Fuel Consumption Models
Many models have been developed considering some of the influential variables in fuel consumption. Most of the time, a study’s specific objectives define which variables to be included and which not. The study by Evans et al. shows that the speed alone accounts for more than 70% of the variability in fuel consumption for a given vehicle [3] . Later, other research introduces other explanatory variables such as acceleration and deceleration. An example could be entering and exiting at a toll station where the average speeds may be the same, but the fuel consumption in those situations is substantially different [4] . Akcelik considers the fuel consumption as a function of three explanatory variables: the cruising speed, the delay time, and the number of stops [5] . Song and Yu consider the parameter of vehicle-specific power (VSP) as a measurement for vehicle activities in the fuel consumption model [4] .
Ahn et al. introduce a model that uses instantaneous speed and acceleration. Their proposed model includes a combination of linear, quadratic, and cubic speed and acceleration terms [6] . Chang and Morlok show there is a linear relation between fuel consumption and travel time [7] . Herman and Ardekani have shown the influence of stops on vehicle fuel consumption in urban traffic [8] . Other studies have attempted to quantify the impact of vehicle stops and speed on vehicle fuel-consumption and emission rates in a wider range [9] .
Evans et al. investigate the relationship between the fuel consumption rate and different explanatory variables including speed noise [3] . Based on this article’s findings, the fuel consumption rate and speed noise are highly correlated, but this variable is not included in their proposed model since they found that about 80 percent of the variability in fuel consumption can be accounted for by the average trip time, the distance, and the work per unit distance to accelerate.
In some fuel consumption studies, models are categorized into two traffic conditions as urban (speed less than 40 mph) versus highway (speed greater than 40 mph). The highway condition, which is of interest in this study is the condition under which average speed is so high (more than 40 mph) that the aero-dynamic effects on fuel consumption become important [2] .
The two well-known highway steady-state speed models are the models introduced by Vincent et al. and Post et al. Vincent et al. introduce the following model for highway traffic condition [10] :
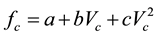 (1)
(1)
where:
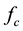 : Steady-state fuel consumption rate at cruising speed (ml/km);
: Steady-state fuel consumption rate at cruising speed (ml/km);
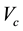 : Steady-state cruising speed (km/hr);
: Steady-state cruising speed (km/hr);
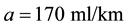 ;
;
 ;
;
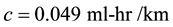 .
.
Vincent et al. uses TRANSYT/8 to provide an approximate estimate of the fuel consumption in a network when a particular set of signal timings is operating. Their proposed equation for fuel consumption is valid at constant cruise speed [10] .
Post et al. include the aero-dynamic effects in their proposed model [2] :
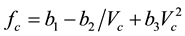 (2)
(2)
where:
 ;
;
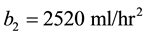 ;
;
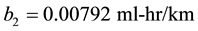 .
.
Among these two, the Vincent et al. model is considered in this research because it is valid at any speed range. Also, this model is used in several simulation packages such as TRANSYT. The speed in this model is the cruising speed, and the aim of this study is to revise it to also incorporate the speed variation in the model.
2.2. Effects of Speed Variation on Fuel Consumption
Hopkins, Hazel and McGrath in their research, report that a non-uniform velocity profile can result in 5% - 15% more fuel consumption than a constant speed profile [11] . In another study by Chang and Morlok, the effect of increasing standard deviation of speed on fuel consumption is evaluated for land transport vehicles (road or rail). The simulated result indicates a positive linear relation between the speed standard deviation and the fuel consumption rate [7] .
Speed standard deviation is a measure of speed fluctuation. There are rarely any studies focused on finding the relation between speed and speed deviation (standard deviation of speed). Shankar and Mannering evaluate the relation between lane-mean speed and lane-speed deviation. Based on their findings, the relationship between lane-mean speed and lane-speed deviation is statistically valid [12] . However, the aim of their research is providing a better understanding of mean speeds and speed deviations across the lanes of a multilane highway rather than finding this relation along the time axis which is the focus of this study.
Usually, average speed is the flow-weighted speed calculated based on the formula below:
 (3)
(3)
where:
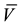 is the flow-weighted speed in the minute of interest;
is the flow-weighted speed in the minute of interest;
 is the average speed of vehicles on lane i on the minute of interest;
is the average speed of vehicles on lane i on the minute of interest;
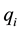 is the flow on lane i in the minute of interest.
is the flow on lane i in the minute of interest.
In the process of evaluating the relationship postulated to exist between speed variance and speed, two different types of speed variances could be considered. They are defined below in more detail:
The variance over time of the aggregate speed is the variance of the flow-weighted speed in every time interval of t minutes [13] . Usually the time interval depends on the objective of the study and the availability of the associated data. However, the time interval should be long enough to have sufficient values of speed for computing the variance and short enough to satisfy the consistency of the assumption of a stationary traffic state [14] .
This variance is computed according to the following equation:
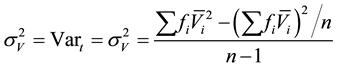 (4)
(4)
Speed standard deviation is computed according to the following equation:
 (5)
(5)
where:




Variance over flow of the speed calculates the variance of average speed across the lanes. In other words, this is the variance between average speeds on each of the lanes i during the time interval of interest.
Finally, the total variance incorporates both of the components involved, more explicitly the variance over time of the aggregated (individual) speed in each unique lane and also the variance over the average speed among lanes during the time interval of interest.
The provided review of the literature has shown the complex nature of factors that affect the vehicle fuel consumption. These factors include traffic-related factors, roadway-related factors, environmental conditions, vehicle characteristics, and driver behavior, especially, factors such as vehicle speed and acceleration, start-up emissions, and engine characteristics. Several models that predict the fuel consumption rate and are based on different groups of factors are highlighted. The few studies on the relation between the speed standard deviation and the fuel consumption indicate there is a significant and direct relation. The next section describes the methodology used to mathematically model such relation and the associated data sources used.
3. Methodology
The first group of data used for assessing the relation between speed and speed noise (speed standard deviation) is derived from the Texas Department of Transportation (TxDOT) traffic data. The data is in the form of daily traffic counts data, which is filed for all Dallas-Fort Worth (DFW) highway detector stations. The data includes speed and volume counts for each highway lane in five-minute intervals. For the purpose of this research, different highways have been considered, and the traffic speed data for highways with two, three, and four lanes (in each direction) have been gathered. In order to have more observations, more than one day for each type of highway is analyzed [15] .
The raw data includes aggregated traffic data (date and time, detector status, speed, volume, and occupancy) for five-minute intervals and for the entire day. The data are converted to 30-minute interval data. In each 30-minute interval, the average speed of the six five-minute aggregate-speeds, and the speed standard deviation of these six five-minute aggregate-speeds are calculated. It should be noted that because of using the aggregated data some of the micro level characteristics might be lost.
The other set of data is derived from the research by Ardekani and Sumitsawan [16] . This data is used to find the correlation coefficient between speed standard deviation and fuel consumption rate. In this research two different driving modes (cruise and varying speed) are used. In the constant speed mode, the test car maintains a cruise speed of 30 mph. In the other case, the test car speeds up from zero to 30 mph in 10 seconds. For both cases the fuel consumption data are collected [16] .
The approach for conducting this research from a methodological perspective is quantitative. Regression models and statistical analysis are used to find the relation between speed and speed noise. Later, a mathematical approach is used to incorporate the effect of speed noise into the fuel consumption model.
The F-test and t-test are used to identify whether or not the model and the coefficients in the model are statistically significant. Later, to formulate the final model, a semi-standardized residuals test is used to define the outliers and remove them from the data set. The initial assumption of this analysis is that the residuals are normally distributed and have a constant variance.
4. Results
A regression model is developed to model the relationship between speed and speed-noise. The conventional method of finding any correlation is based on a linear regression. Data is collected for both speed and speed standard deviation. The initial assumption is that speed noise decreases as the speed increases. In this modeling effort, the speed is the independent variable and speed noise is the dependent variable. Also, the regression allows the estimation of the coefficients of the following model:

where:




Regression analysis is applied to three highways (from 2 lanes per direction to 4 lanes per direction). Later, the reliability of the results and the significance of the model are tested using different methods including the generalized F-test and evaluation of the p-values. To formulate the final model, the statistical outliers are defined by using the natural version of Cook’s D Statistic techniques. The final model includes all the observations excluding the outliers.
In Figures 1-9, the speed standard deviation in miles-per-hour is plotted versus speed in miles-per-hour for each of the lanes of all highways. The first highway is the two-lane per direction highway of eastbound SH 114 at O’Connor which is located in Dallas County, Texas.
The speed varies between 40 (mph) and 65 (mph), and the linear relation is fairly strong and similar in both lanes. The second highway is the three-lane per direction highway of Northbound US 175 at Pine St. US 17 is located in Dallas County, Texas.
Figure 1. Speed variation and speed relation for a two-lane per direction highway (lane 1).
Figure 2. Speed variation and speed relation for a two-lane per direction highway (lane 2).
Figure 3. Speed variation and speed relation for a three-lane per direction highway (lane 1).
Figure 4. Speed variation and speed relation for a three-lane per direction highway (lane 2).
Figure 5. Speed variation and speed relation for a three-lane per direction highway (lane 3).
Figure 6. Speed variation and speed relation for a four-lane per direction highway (lane 1).
Figure 7. Speed variation and speed relation for a four-lane per direction highway (lane 2).
Figure 8. Speed variation and speed relation for a four-lane per direction highway (lane 3).
The speed varies between 35 (mph) and 70 (mph) in this segment of the highway. The linear relation is strong in all of the lanes. The middle lane shows a slightly stronger linear relation.
Finally, the third highway is the four-lane per direction highway of Southbound US75 at Mockingbird. This point at US75 includes four lanes in each direction and is located in Dallas County, Texas.
The speed varies between 35 (mph) and 70 (mph) in this segment of the highway. The linear relation is strong in all of the lanes. The middle lanes and the right lane show slightly stronger linear relation.
Finally, all of the highways’ data are combined to come up with an average formula for the relation between speed standard deviation and speed. The result shows that there is a strong negative relation between speed standard deviation and speed. The outcome is shown in Figure 10. The equation between standard deviation of speed and speed shows there is a negative relation between standard deviation of speed and speed. In addition, this equation indicates the correlation between speed standard deviation and speed. The correlation coefficient as shown in Figure 10 and Table 1 is −0.18, meaning that at speeds above 20 mph, and keeping all the other conditions unchanged, an increase in average speed by one mph causes the standard deviation of speed to decrease by 0.18 mph.
Figure 9. Speed variation and speed relation for a four-lane per direction highway (lane 4).
Figure 10. Speed variation and speed relation for all the highway sections studied.
Table 1. Speed variation models for various highway sections in Dallas, TX.
The result indicates that there is a strong relation between speed standard deviation and speed. The coefficient of determination in all the four models is above 0.70, which shows a large amount of variability in speed noise could be explained by the variability in speed. This relation seems to be stronger in right lanes rather than left lanes, and that could be attributed to the wider range of speed variation in the right lanes.
The results of the regression analysis along with the regression model for each lane and for all the highways are summarized in Table 1.
An overview of all the regression analyses and plots reveals there is a high correlation between the speed and the speed standard deviation. Based on the results, it could be concluded that at higher speeds, the speed variation is lower. This relation is stronger in the right lanes compared to the left lanes. Almost all the R-squared values are above 0.70, which indicates a large amount of variability in speed noise could be explained by variability in speed.
The final model derived from a combination of all the data is shown below.

where:


As noted before, the speed variance in the above model denotes the variance over time of the aggregate speeds and the speed variable represents the five-minute aggregate speeds. The model is derived from the data gathered from the two-lane, three-lane, and four-lane per direction highways in Dallas area. The same model could also be used in other areas; but may need re-calibration due to potential regional differences in driver behavior.
The next section discusses how the findings could be used to modify an existing steady-state fuel consumption model to reflect the impact of the variation in speed in the model and reflect more precisely the actual fuel consumption rates.
4.1. Sample Model Application
In the previous section, a model was developed to show the relation between the speed standard deviation and the speed. In this section, one of the applications of this finding is introduced. This derived model is implemented in an existing well-known fuel consumption model to improve it by taking the speed noise into consideration. In other words, the modified model reflects the influence of the speed noise in fuel consumption models.
There are a few studies that postulate a positive relation between the speed variation and fuel consumption, but there is no study that presents an analytical model to capture this influence. Therefore, in this section, an analysis is performed to mathematically formulate this correlation.
The data used to determine the correlation coefficient between fuel consumption rate and the standard deviation of speed is derived from the research by Ardekani and Sumitsawan [16] . In this study, the fuel consumption rate is measured once for the steady-state speed of 30 mph and once for the increasing speed from 0 to 30 mph. The value of change in fuel consumption over speed standard deviation is considered to be the correlation coefficient between fuel consumption and the speed standard deviation.
The below formula is used to calculate the coefficient:

In this study there are two main scenarios, one with constant speed of 30 (mph) and the other one with speed varying from 0 to 30 mph. Since we have the data for two points, the speed standard deviation is calculated as below.

Knowing the speed standard deviation and average change in fuel consumption, the coefficient between fuel consumption and the speed standard deviation could be calculated. Table 2 shows the average change in fuel condition for different road condition and calculated associated coefficient.
The final correlation coefficient is calculated as below:
Figure 11 also demonstrates the final correlation coefficient between fuel consumption and the standard deviation.
Table 2. Correlation coefficient between fuel consumption and speed standard deviation.
Figure 11. The correlation between fuel consumption and the speed standard deviation.
4.2. Modifying the Vincent Steady-State Speed Model
As noted earlier, one of the well-known average speed models (steady-statespeed models) is the Vincent model [10] . This model is valid at any speed range, so if the relatively constant speed can be maintained, this model could be used [2] . Also, The Vincent model is used in several simulation packages such as TRANSYT.
The Vincent model for the highway traffic condition is as follows:

where:





The reason for choosing a steady-state speed model is its simplicity, generality, and applicability. The other advantage of this model is that just cruising speed of the vehicle needs to be available for calculations and the model will still be relatively accurate in predicting the fuel consumption rate. The greatest shortcoming of this type of model is that it does not account for speed variation, which in reality makes a difference in the fuel consumption rate. The reason for not including the impact of the speed variation in these models might be the difficulty of measuring speed variation for model calibration purpose.
The proposed model is the Vincent model which is modified by adding another term. The added term reflects the impact of standard deviation of the speed on fuel consumption since the standard deviation of speed is found to be influential in fuel consumption rate.
The proposed model is as follows:

where:







The original Vincent model is in metric units, the conversion from original formula done by applying the kilometer to mile conversion of 1 km = 0.621371 miles.
Now that the relation between the speed standard deviation and speed has been formulated, the corresponding term can be substituted in the equation, as follows:
Putting all the variables and their coefficients together in the formula, the final formulation is obtained as below:
where:


In the above proposed model, the impact of speed variation is captured in the fuel consumption model. It should be noted that the final fuel consumption model is valid for all highways with four or fewer lanes per direction.
5. Conclusions
The primary aim of this research has been to use field data to formulate a relation between the speed standard deviation and speed. In doing so, the speed and volume count data are extracted from the TxDOT detector data website. This relation is investigated by applying a linear regression model to the speed standard deviation against the average speed in different highways and for each lane separately. The results for all of the highways sections studied demonstrate a strong relation between speed standard deviation and speed. The final model is formulated using the entire data for all the highways with four or fewer lanes per direction. The final model also indicates a strong relation between speed standard deviation and speed.
The established model between speed and its standard deviation could be used for different purposes. One of the key applications, though, is in fuel consumption modeling. The existing steady-state speed models for highways do not account for the impact of speed variation in estimating the fuel consumption. Therefore, the only needed speed profile is the cursing speed. This is mainly because measuring the speed standard deviation is difficult.
Based on the findings of this study, a new term could be added to the fuel consumption model to overcome that deficiency. Now that the relation between speed standard deviation and speed is established, the equivalent speed term could substitute the speed standard deviation term in the proposed model. The initial model that is considered is the Vincent model for highways. The final proposed model has similar terms as the Vincent model; however, the coefficients are modified to reflect the variation in speed impact on fuel consumption.
As is always the case with any mathematical model, there are some limitations in applying the proposed model. Addressing each of these limitations could be a direction for future research on this topic. Some of the limitations include:
・ The established model between speed and its standard deviation might not be applicable in regions outside the study area due to specific highway conditions (number of lanes, design speeds, lane and shoulder widths, etc.). So further studies might be needed to establish a generic model applicable to a variety of highway geometries.
・ Another model limitation was the lack of adequate data to compute the correlation coefficient between fuel consumption and speed standard deviation. A More systematic field study could be conducted to get a more accurate correlation coefficient.
・ The initial assumption for developing regression model between speed and its standard deviation and identifying outliers is that the residuals are normally distributed and have a constant variance. If further analysis shows that the variance of residuals is not constant, a weighted regression should be used to correct the deficiency.
・ The developed model between speed and its standard deviation in this study was based on data from highways in one county (Dallas County, Texas). This model could be applied in different regions to see if it applies to other regions regardless of regional differences in driving behavior.
・ The primary model for modification in this research was the Vincent fuel consumption model, but the new speed standard deviation term could be considered in any steady-state speed or average speed model to reflect the speed variation in estimating fuel consumption.
・ The correlation between speed variation and fuel consumption could further be examined using fuel consumption data obtained directly from an instrumented vehicle.
・ In this study, the aggregated data as an input was used to develop a macro model between speed and speed standard deviation. The non-aggregated data for individual vehicles could be used to examine the extent to which the micro level characteristics are lost by using aggregated data.
・ The final proposed model for fuel consumption with the re-calibrated coefficients could be used in a case study with different scenarios in cruising speed and varying speeds to further validate the model.
References
- Schipper, L., Saengerand, C. and Sudardshan, A. (2010) Retrieved July 2013, from http://academia.edu/368027/Transport_and_Carbon_Emissions_in_the_United_States_The_Long_View
- Ardekani, S., Hauer, E. and Jamei, B. (1992) Traffic Impact Models. Chapter 7 in Traffic Flow Theory, Oak Ridge National Laboratory Report.
- Evans, L., Herman, R. and Lam, T. (1976) Multivariate Analysis of Traffic Factors Related to Fuel Consumption in Urban Driving. Transportation Science, 10, 205-215. http://dx.doi.org/10.1287/trsc.10.2.205
- Song, G. and Yu, L. (2009) Estimation of Fuel Efficiency of Road Traffic by Characterization of Vehicle-Specific Power and Speed Based on Floating Car Data. Transportation Research Record: Journal of the Transportation Research Board, 2139, 11-20. http://dx.doi.org/10.3141/2139-02
- Akcelik, R. (1981) Fuel Efficiency and Other Objectives in Traffic System Management. Traffic Engineering and Con- trol, 22, 54-65.
- Ahn, K., Rakha, H., Trani, A. and Van Aerde, M. (2002) Estimating Vehicle Fuel Consumption and Emissions Based on Instantaneous Speed and Acceleration Levels. Journal of Transportation Engineering, 128, 182-190. http://dx.doi.org/10.1061/(ASCE)0733-947X(2002)128:2(182)
- Chang, D.J. and Morlok, K.M. (2005) Vehicle Speed Profiles to Minimize Work and Fuel Consumption. Journal of Transportation Engineering © ASCE.
- Herman, R. and Ardekani, S. (1985) The influence of Stops on Vehicle Fuel Consumption in Urban Traffic. Transportation Science, 19, 1-12. http://dx.doi.org/10.1287/trsc.19.1.1
- Rakha, H. and Ding, Y. (2003) Impact of Stops on Vehicle Fuel Consumption and Emissions. Journal of Transportation Engineering, 129, 23-32. Technical Papers. http://dx.doi.org/10.1061/(ASCE)0733-947X(2003)129:1(23)
- Vincent, R.A., Mitchell, A. and Robertson, D. (1980) User Guide to TRANSYT Version 8. Transport and Road Research Lab Report No 8. LR888.
- Hopkins, J.B., Hazel, M.E. and McGrath, T. (1978) Railroads and the Environment―Estimation of Fuel Consumption in Rail Transportation Volume III: Comparison of Computer Simulations with Field Measurements. Final Rep. No. FRA-OR&D-75-74. III to U.S. Federal Railroad Administration, Rep. No. PB-288866, National Technical Information Service, Springfield, Va.
- Shankar, V. and Mannering, F. (1998) Modeling the Endogeneity of Lane-Mean Speeds and Lane-Mean Speed Deviations: A Structural Equations Approach. In Transportation Research - Part A, 32, 311-322. http://dx.doi.org/10.1016/S0965-8564(98)00003-2
- Blandin, S., Salam, A. and Bayen, A. (2011) Individual Speed Variance in Traffic Flow: Analysis of Bay Area16 Radar Measurements. 91th Annual Meeting of the Transportation Research Board, Washington DC.
- Bulteau, E., Leblanc, R., Blandin, S. and Bayen, A. (2013) Fconsumption Ratlow Estimation Using Higher-Order Speed Statistics, Individual Speed Variance in Traffic Flow: Analysis of Bay Area16 Radar Measurements. 93th Annual Meeting of the Transportation Research Board, Washington DC.
- DFW Traffic Data, Retrieved January, 2013, http://dfwtraffic.dot.state.tx.us/#showContent%28%27/DfwTrafficData/%27%29%3B
- Ardekani, S.A. and Sumitsawan, P. (2010) Effect of Pavement Type on Fuel Consumption and Emissions in City Driving. Final Report to the Ready Mixed Concrete Research & Education Foundation.




























