Journal of Signal and Information Processing
Vol.07 No.04(2016), Article ID:72166,25 pages
10.4236/jsip.2016.74020
Inspection of the Output of a Convolution and Deconvolution Process from the Leading Digit Point of View―Benford’s Law
Monika Pinchas
Department of Electrical and Electronic Engineering Ariel University, Ariel, Israel

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 8, 2016; Accepted: November 19, 2016; Published: November 22, 2016
ABSTRACT
In the communication field, during transmission, a source signal undergoes a convolutive distortion between its symbols and the channel impulse response. This distortion is referred to as Intersymbol Interference (ISI) and can be reduced significantly by applying a blind adaptive deconvolution process (blind adaptive equalizer) on the distorted received symbols. But, since the entire blind deconvolution process is carried out with no training symbols and the channel’s coefficients are obviously unknown to the receiver, no actual indication can be given (via the mean square error (MSE) or ISI expression) during the deconvolution process whether the blind adaptive equalizer succeeded to remove the heavy ISI from the transmitted symbols or not. Up to now, the output of a convolution and deconvolution process was mainly investigated from the ISI point of view. In this paper, the output of a convolution and deconvolution process is inspected from the leading digit point of view. Simulation results indicate that for the 4PAM (Pulse Amplitude Modulation) and 16QAM (Quadrature Amplitude Modulation) input case, the number “1” is the leading digit at the output of a convolution and deconvolution process respectively as long as heavy ISI exists. However, this leading digit does not follow exactly Benford’s Law but follows approximately the leading digit (digit 1) of a Gaussian process for independent identically distributed input symbols and a channel with many coefficients.
Keywords:
Blind Adaptive Equalizers, Blind Adaptive Deconvolution, Leading Digit Theory, Benford’s Law

1. Introduction
We consider a blind deconvolution problem in which we observe the output of an unknown, possibly nonminimum phase, linear system (single-input-single-output (SISO) finite impulse response (FIR) system) from which we want to recover its input (source) using an adjustable linear filter (equalizer). During transmission, a source signal undergoes a convolutive distortion between its symbols and the channel impulse response. This distortion is referred to as ISI [1] [2] [3] . It is well known that ISI is a limiting factor in many communication environments where it causes an irreducible degradation of the bit error rate thus imposing an upper limit on the data symbol rate [1] [4] . In order to overcome the ISI problem, a blind adaptive equalizer can be implemented in those systems [2] - [26] . But, since no training symbols are used in the deconvolution process and the channel coefficients are unknown to the receiver, no indication can be made (via the ISI or MSE expressions) during the deconvolution process whether the blind adaptive equalizer succeeded to remove the heavy ISI from the transmitted symbols or not. Such an information can be very useful to those systems involving the variable step-size parameter technique to get on one hand a fast removal of the heavy ISI by applying initially a relative high valued step-size parameter and then continuing with another step-size parameter which is lower compared to the first one in order to achieve on the other hand a very low residual ISI at the latter stages of the deconvolution process [27] - [30] .
According to [31] , Benfords law (also known as the first-digit law) defines a peculiar distribution of the leading digits of a set of numbers. The behavior is logarithmic, with the leading digit 1 reflecting largest probability of occurrence and the remaining ones showing decreasing probabilities of appearance following a logarithmic trend. According to [31] , Benfords law has been widely proposed as a discriminating tool for naturally-shaped datasets [32] and even employed [33] or criticized [34] as a somewhat reliable diagnostic tool to detect a large variety of frauds. In [31] , Benfords law was evaluated as a discriminator for audio signals. In particular it was employed to detect differences between natural and artificially created chords and real music.
In the communication field, the transmitted symbols may belong to a squared constellation input such as the 16QAM or to a PAM constellation where the transmitted symbols are statistically independent and have the same probability to appear for transmission. Thus, the recovered symbols should also appear approximately with equal probability. Up to now, the output of a convolution process such as the output of a channel was mainly investigated from the ISI point of view. In this paper, the output of a convolution and deconvolution process is inspected from the leading digit point of view. Simulation results will indicate that for the 4PAM and 16QAM constellation input, the number 1 is the leading digit at the output of a convolution and deconvolution process respectively as long as heavy ISI exists. However, this leading digit does not follow exactly Benford’s Law but follows approximately the leading digit (digit 1) of a Gaussian process for independent identically distributed input symbols and a channel with many coefficients.
The paper is organized as follows: After having described the system under consideration in Section 2, the inspection of the output of a convolution and deconvolution process from the leading digit point of view is given via simulation results in Section 3. Section 4 is our conclusion.
2. System Description
The system under consideration is illustrated in Figure 1, where we make the following assumptions:
1) The input sequence 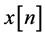 belongs to a 16QAM input constellation (a modulation using ± {1, 3} levels for in-phase and quadrature components) or a 4PAM case (a modulation using ± {1, 3} levels for the symbols) with variance
belongs to a 16QAM input constellation (a modulation using ± {1, 3} levels for in-phase and quadrature components) or a 4PAM case (a modulation using ± {1, 3} levels for the symbols) with variance 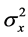 where
where  and
and 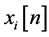 are the real and imaginary parts of
are the real and imaginary parts of 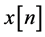 respectively. The input symbols are independent and identically distributed.
respectively. The input symbols are independent and identically distributed.
2) The unknown channel 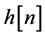 is a possibly nonminimum phase linear time-in- variant filter in which the transfer function has no “deep zeros”, namely, the zeros lie sufficiently far from the unit circle.
is a possibly nonminimum phase linear time-in- variant filter in which the transfer function has no “deep zeros”, namely, the zeros lie sufficiently far from the unit circle.
3) The equalizer 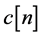 is a tap-delay line.
is a tap-delay line.
4) The noise 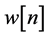 is an additive Gaussian white noise with zero mean and variance
is an additive Gaussian white noise with zero mean and variance 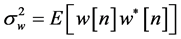 where
where 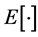 is the expectation operator and
is the expectation operator and 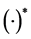 is the conju- gate operation on
is the conju- gate operation on .
.
The transmitted sequence 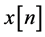 is sent via the channel
is sent via the channel 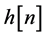 where it is also cor- rupted with noise
where it is also cor- rupted with noise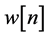 . Thus, the equalizer’s input sequence
. Thus, the equalizer’s input sequence 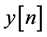 may be written as:
may be written as:
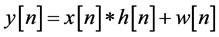 (1)
(1)
where “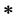 ” denotes the convolution operation. The equalized output sequence is defined by:
” denotes the convolution operation. The equalized output sequence is defined by:

where 



where 


Figure 1. Block diagram of a baseband communication system.

where 




where d is the digit number.
3. The Output of a Convolution and Deconvolution Process from the Leading Digit Point of View
In this section we first start to inspect the output of the convolution process from the leading digit point of view for the noiseless case. After that, we turn to inspect the output of the deconvolution process considering also the noisy situation.
In the following we use the 4PAM constellation input with three different channel cases having real valued coefficients:
Case I: Rayleigh fading channel with variance equal to 0.2.
Case II: Gaussian channel with zero mean and variance equal to 1.
Case III: A channel where the coefficients are uniformly distributed within
Figures 2-8 show the averaged value for the leading-digit distribution for 9000 symbols
Figure 2. The leading-digit distribution for 9000 symbols (4PAM constellation) sent via a Rayleigh channel compared to Benford’s law. The channel length was set to 13. The averaged results were obtained in 100 Monte Carlo trials for the noiseless case.
Figure 3. The leading-digit distribution for 9000 symbols (4PAM constellation) sent via a Rayleigh channel compared to Benford’s law. The channel length was set to 23. The averaged results were obtained in 100 Monte Carlo trials for the noiseless case.
Figure 4. The leading-digit distribution for 9000 symbols (4PAM constellation) sent via a Rayleigh channel compared to Benford’s law. The channel length was set to 33. The averaged results were obtained in 100 Monte Carlo trials for the noiseless case.
Figure 5. The leading-digit distribution for 9000 symbols (4PAM constellation) sent via a Rayleigh channel compared to Benford’s law. The channel length was set to 53. The averaged results were obtained in 100 Monte Carlo trials for the noiseless case.
Figure 6. The leading-digit distribution for 9000 symbols (4PAM constellation) sent via a gaussian channel compared to Benford’s law. The channel length was set to 13. The averaged results were obtained in 100 Monte Carlo trials for the noiseless case.
Figure 7. The leading-digit distribution for 9000 symbols (4PAM constellation) sent via the channel compared to Benford’s law. The channel’s coefficients were uniformly distributed within
Figure 8. The leading-digit distribution for 9000 symbols (4PAM constellation) sent via the channel compared to Benford’s law. The channel’s coefficients were uniformly distributed within
(belonging to a 4PAM constellation) sent via the above mentioned channel cases with different values for the channel length, compared with Benford’s law. 100 Monte Carlo trials were used to get the averaged results for the leading-digit distribution for each channel case and channel length, where for each trial, the channel coefficients were randomly selected from the predefined channel case. According to Figures 2-8, the leading digit at the output channel is the number 1. This phenomenon becomes even more evident for higher values for the channel length (Figure 5, Figure 8). Although the number 1 is the leading digit at the output channel (Figures 2-8), this leading digit (number 1) does not follow Benford’s law as it can be seen according to Figures 2-8. Figure 9 shows the averaged value for the leading-digit distribution for 9000 numbers belonging to a Gaussian distribution with zero mean and variance 1 compared to Benford’s law. According to Figure 9, the number 1 is the leading digit but it does not follow Benford’s law. Based on the central limit theorem [35] , the output channel can be approximately considered as Gaussian for a high valued channel length. Therefore, the leading digit (number 1) behavior in Figure 5 and Figure 8 is similar to that obtained in Figure 9. Figures 2-8 show averaged results of the leading digit distribution. Therefore, in order to show that the leading number is 1 for each simulation trial out of the 100 Monte Carlo trials, further simulation was set up. Figures 10-16 show the probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where
Figure 9. The leading-digit distribution for 9000 numbers belonging to a gaussian distribution with zero mean and variance 1 compared to Benford’s law. The averaged results were obtained in 100 Monte Carlo trials.
Figure 10. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where
Figure 11. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where
Figure 12. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where
Figure 13. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where
Figure 14. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where
Figure 15. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where
Figure 16. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where
number 1 minus the probability of occurrence of the number “i” (where

Now, we turn to the deconvolution case where the equalized output is of our interest. 9000 symbols belonging to a 16QAM input constellation were sent via the channel used in [20] :

Usually, the equalizer’s coefficients are updated constantly. However, in order to see the behaviour of the leading digit at the equalized output during the deconvolution process, the updating mechanism of the equalizer’s coefficients was stopped at several places during the deconvolution process. Namely, the equalizer’s coefficients were updated as long as we have not reached the desired iteration number. For example, if the desired iteration number was set to 10, then the equalizer’s coefficients were not updated anymore after 10 iterations. Thus, the residual ISI level at the equalizer’s output remained fixed. Figures 17-20 show the averaged value for the leading-digit distribution at the equalized output for SNR of 30 dB compared with Benford’s law. Based on the obtained results for the convolution case described earlier in this section, it was quite expected to get the number 1 as the leading digit at the equalized output at the early stages of the deconvolution process (Figure 17, Figure 18). In addition, as it was for the convolution case, the leading digit (number 1) at the equalized output does
Figure 17. The leading-digit distribution at the equalized output compared to Benford’s law. The channel length as well as the equalizer’s tap length were set to 13. The step-size parameter was set to 0.00008. The averaged results were obtained in 100 Monte Carlo trials for
Figure 18. The leading-digit distribution at the equalized output compared to Benford’s law. The channel length as well as the equalizer’s tap length were set to 13. The step-size parameter was set to 0.00008. The averaged results were obtained in 100 Monte Carlo trials for
Figure 19. The leading-digit distribution at the equalized output compared to Benford’s law. The channel length as well as the equalizer’s tap length were set to 13. The step-size parameter was set to 0.00008. The averaged results were obtained in 100 Monte Carlo trials for
Figure 20. The leading-digit distribution at the equalized output compared to Benford’s law. The channel length as well as the equalizer’s tap length were set to 13. The step-size parameter was set to 0.00008. The averaged results were obtained in 100 Monte Carlo trials for
not follow Benford’s law. According to Figure 19 and Figure 20 the number 1 is no more the leading digit at the equalized output. Thus, this may indicate that most of the ISI is already removed by the equalizer which is confirmed in our case with Figure 21 and Figure 22. Figures 23-26 show the probability of occurrence of the number 1
Figure 21. The real part of the equalized output for
Figure 22. The real part of the equalized output for
Figure 23. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where

Figure 24. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where

Figure 25. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where

Figure 26. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where

minus the probability of occurrence of the number “i” (where



Figure 27. The leading-digit distribution at the equalized output compared to Benford’s law. The channel length as well as the equalizer’s tap length were set to 13. The step-size parameter was set to 0.00008. The averaged results were obtained in 100 Monte Carlo trials for
Figure 28. The leading-digit distribution at the equalized output compared to Benford’s law. The channel length as well as the equalizer’s tap length were set to 13. The step-size parameter was set to 0.00008. The averaged results were obtained in 100 Monte Carlo trials for
Figure 29. The leading-digit distribution at the equalized output compared to Benford’s law. The channel length as well as the equalizer’s tap length were set to 13. The step-size parameter was set to 0.00008. The averaged results were obtained in 100 Monte Carlo trials for
Figure 30. The real part of the equalized output for
Figure 31. The real part of the equalized output for
Figure 32. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where

Figure 33. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where

Figure 34. Probability of occurrence of the number 1 minus the probability of occurrence of the number “i” (where

output for SNR of 20 dB. According to Figures 32-34, the probability of occurrence of the number 1 minus the probability of occurrence of the number 3 is approximately zero only at the latter stages of the deconvolution process (Figure 34) while this is not the case at the earlier stages of the deconvolution process (Figure 32).
4. Conclusion
In this paper, we have shown via simulation results that the number 1 is the leading digit at the output of a convolution and deconvolution process for a 4PAM and 16QAM input constellation respectively, as long as heavy ISI exists. In addition, simulation results have shown that the behaviour of this leading digit does not follow exactly Benford’s Law but follows approximately the leading digit (digit 1) of a Gaussian process for independent identically distributed input symbols and a channel with many coefficients.
Acknowledgements
We thank the Editor and the referee for their comments.
Cite this paper
Pinchas, M. (2016) Inspection of the Output of a Convolution and Deconvolution Process from the Leading Digit Point of View―Benford’s Law. Journal of Signal and Information Processing, 7, 227-251. http://dx.doi.org/10.4236/jsip.2016.74020
References
- 1. Pinchas, M. (2013) Residual ISI Obtained by Nonblind Adaptive Equalizers and Fractional Noise. Mathematical Problems in Engineering, 2013, Article ID: 830517.
http://dx.doi.org/10.1155/2013/830517 - 2. Pinchas, M. (2013) Two Blind Adaptive Equalizers Connected in Series for Equalization Performance Improvement. Journal of Signal and Information Processing, 4, 64-71.
http://dx.doi.org/10.4236/jsip.2013.41008 - 3. Pinchas, M. (2013) Residual ISI Obtained by Blind Adaptive Equalizers and Fractional Noise. Mathematical Problems in Engineering, 2013, Article ID: 972174.
http://dx.doi.org/10.1155/2013/972174 - 4. Pinchas, M. and Bobrovsky, B.Z. (2006) A Maximum Entropy Approach for Blind Deconvolution. Signal Processing, 86, 2913-2931.
http://dx.doi.org/10.1016/j.sigpro.2005.12.009 - 5. Godard, D.N. (1980) Self Recovering Equalization and Carrier Tracking in Two-Dimenional Data Communication System. IEEE Transactions on Communications, 28, 1867- 1875.
http://dx.doi.org/10.1109/TCOM.1980.1094608 - 6. Lazaro, M., Santamaria, I., Erdogmus, D., Hild, K.E., Pantaleon, C. and Principe, J.C. (2005) Stochastic Blind Equalization Based on PDF Fitting Using Parzen Estimator. IEEE Transactions on Signal Processing, 53, 696-704.
http://dx.doi.org/10.1109/TSP.2004.840767 - 7. Sato, Y. (1975) A Method of Self-Recovering Equalization for Multilevel Amplitude-Modulation Systems. IEEE Transactions on Communications, 23, 679-682.
http://dx.doi.org/10.1109/TCOM.1975.1092854 - 8. Beasley, A. and Cole-Rhodes, A. (2005) Performance of an Adaptive Blind Equalizer for QAM Signals. IEEE Military Communications Conference, Atlantic City, 17-20 October 2005, 2373-2377.
http://dx.doi.org/10.1109/milcom.2005.1606023 - 9. Alaghbari, K.A.A., Tan, A.W.C. and Lim, H.S. (2012) Cost Function of Blind Channel Equalization. 4th International Conference on Intelligent and Advanced Systems (ICIAS), Kuala Lumpur, 12-14 June 2012, 665-669.
http://dx.doi.org/10.1109/icias.2012.6306097 - 10. Daas, A., Hadef, M. and Weiss, S. (2009) Adaptive Blind Multiuser Equalizer Based on PDF Matching. International Conference on Telecommunications (ICT), Marrakech, 25-27 May 2009, 213-216.
http://dx.doi.org/10.1109/ictel.2009.5158646 - 11. Giunta, G. and Benedetto, F. (2013) A Signal Processing Algorithm for Multi-Constant Modulus Equalization. 36th International Conference on Telecommunications and Signal Processing (TSP), Rome, 2-4 July 2013, 52-56.
http://dx.doi.org/10.1109/TSP.2013.6613890 - 12. Daas, A. and Weiss, S. (2010) Blind adaptive Equalizer Based on PDF Matching for Rayleigh Time-Varying Channels. Conference Record of the 44th Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, 7-10 November 2010, 456- 460.
http://dx.doi.org/10.1109/acssc.2010.5757600 - 13. Abrar, S. (2005) A New Cost Function for the Blind Equalization of Cross-QAM Signals. 17th International Conference on Microelectronics (ICM 2005), Islamabad, 13-15 December 2005, 290-295.
http://dx.doi.org/10.1109/icm.2005.1590087 - 14. Blom, K.C.H., Gerards, M.E.T., Kokkeler, A.B.J. and Smit, G.J.M. (2013) Nonminimum- Phase Channel Equalization Using All-Pass CMA. 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC), London, 8-9 September 2013, 1467-1471.
http://dx.doi.org/10.1109/pimrc.2013.6666373 - 15. Nikias, C.L. and Petropulu, A.P. (Eds.) (1993) Higher-Order Spectra Analysis: A Nonlinear Signal Processing Framework. Prentice-Hall, Upper Saddle River, Chapter 9, 419-425.
- 16. Bellini, S. (1986) Bussgang Techniques for Blind Equalization. IEEE Global Telecommunication Conference Records, Houston, 1-4 December 1986, 1634-1640.
- 17. Fiori, S. (2001) A Contribution to (Neuromorphic) Blind Deconvolution by Flexible Approximated Bayesian Estimation. Signal Processing, 81, 2131-2153.
http://dx.doi.org/10.1016/S0165-1684(01)00108-6 - 18. Haykin, S. (1991) Blind Deconvolution. In: Haykin, S., Ed., Adaptive Filter Theory, Prentice-Hall, Englewood Cliffs, Chapter 20.
- 19. Pinchas, M. (2010) A Closed Approximated Formed Expression for the Achievable Residual Intersymbol Interference Obtained by Blind Equalizers. Signal Processing Journal, 90, 1940-1962.
http://dx.doi.org/10.1016/j.sigpro.2009.12.014 - 20. Shalvi, O. and Weinstein, E. (1990) New Criteria for Blind Deconvolution of Nonminimum Phase Systems (Channels). IEEE Transactions on Information Theory, 36, 312-321.
http://dx.doi.org/10.1109/18.52478 - 21. Pinchas, M. (2011) 16QAM Blind Equalization Method via Maximum Entropy Density Approximation Technique. International Conference on Signal and Information Processing (CSIP), Shanghai, 28-30 October 2011, 700-703.
http://wenku.baidu.com/view/30d075b569dc5022aaea002a.html - 22. Pinchas, M. and Bobrovsky, B.Z. (2007) A Novel HOS Approach for Blind Channel Equalization. IEEE Transactions on Wireless Communications, 6, 875-886.
http://dx.doi.org/10.1109/TWC.2007.04404 - 23. Gitlin, R.D., Hayes, J.F. and Weinstein, S.B. (1992) Automatic and Adaptive Equalization. In: Gitlin, R.D., Hayes, J.F. and Weinstein, S.B., Eds., Data Communications Principles, Plenum, New York, 517-605.
http://dx.doi.org/10.1007/978-1-4615-3292-7 - 24. Pinchas, M. (2011) A MSE Optimized Polynomial Equalizer for 16QAM and 64QAM Constellation. Signal, Image and Video Processing, 5, 29-37.
http://dx.doi.org/10.1007/s11760-009-0138-z - 25. Im, G.-H., Park, C.J. and Won, H.C. (2001) A Blind Equalization with the Sign Algorithm for Broadband Access. IEEE Communications Letters, 5, 70-72.
http://dx.doi.org/10.1109/4234.905939 - 26. Pinchas, M. (2016) New Lagrange Multipliers for the Blind Adaptive Deconvolution Problem Applicable for the Noisy Case. Entropy, 18, 65.
http://dx.doi.org/10.3390/e18030065 - 27. Demir, M.A. and Ozen, A. (2012) A Novel Variable Step Size Adjustment Method Based on Autocorrelation of Error Signal for the Constant Modulus Blind Equalization Algorithm. Radioengineering, 21, 37-45.
- 28. Hamzehyan, R., Dianat, R. and Shirazi, N.C. (2012) New Variable Step-Size Blind Equalization Based on Modified Constant Modulus Algorithm. International Journal of Machine Learning and Computing, 2, 30-34.
http://dx.doi.org/10.7763/IJMLC.2012.V2.85 - 29. Xiong, Z., Li, L., Zhuo, D., Dong, Z. and Zhang, L. (2004) A New Adaptive Step-Size Blind Equalization Based on Autocorrelation of Error Signal. 7th International Conference on Signal Processing, 2, 1719-1722.
- 30. Iyi, Z., Lei, C. and Yunshan, S. (2009) Variable Step-Size CMA Blind Equalization Based on Non-Linear Function of Error Signal. International Conference on Communications and Mobile Computing, 1, 396-399.
- 31. Barbancho, I., Tardon, L.J., Barbancho, A.M. and Sbert, M. (2015) Benford’s Law for Music Analysis. Proceedings of the 16th ISMIR Conference, Malaga, Spain, 26-30 October 2015, 735-741.
- 32. Del Acebo, E. and Sbert, M. (2005) Benford’s Law for Natural and Synthetic Images. Proceedings of the 1st Eurographics Conference on Computational Aesthetics in Graphics, Visualization and Imaging, Girona, 18-20 May 2005, 169-176.
- 33. Jacob, B.A. and Levitt, S.D. (2003) Rotten Apples: An Investigation of the Prevalence and Predictors of Teacher Cheating. The Quarterly Journal of Economics, 118, 843-877.
http://dx.doi.org/10.1162/00335530360698441 - 34. Deckert, J., Myagkov, M. and Ordeshook, P.C. (2010) The Irrelevance of Benford’s Law for Detecting Fraud in Elections. Caltech/MIT Voting Technology Project, Working Paper.
- 35. Papoulis, A. (1965) Probability, Random Variables, and Stochastic Processes. International Student Edition, McGraw-Hill, New York, Chapter 8, 266.
Abbreviations
ISI: Intersymbol Interference
SNR: Signal to Noise Ratio
SISO: Single Input Single Output
FIR: Finite Impulse Response
QAM: Quadrature Amplitude Modulation
PAM: Pulse Amplitude Modulation
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jsip@scirp.org




































