Received 16 June 2015; accepted 18 August 2015; published 21 August 2015

ABSTRACT

This paper investigates the generalized uncertainty principles of fractional Fourier transform (FRFT) for concentrated data in limited supports. The continuous and discrete generalized uncertainty relations, whose bounds are related to FRFT parameters and signal lengths, were derived in theory. These uncertainty principles disclose that the data in FRFT domains may have much higher concentration than that in traditional time-frequency domains, which will enrich the ensemble of generalized uncertainty principles.

Keywords:

Discrete Fractional Fourier Transform (DFRFT), Uncertainty Principle, Frequency-Limiting Operator

1. Introduction

In information processing, the uncertainty principle plays an important role in elementary fields, and data concentration is often considered carefully via the uncertainty principle [1] - [8] . In continuous signals, the supports are assumed to be infinite, based on which various uncertainty relations [1] [2] [9] - [21] [22] have been presented. However, in practice, both the supports of time and frequency are often limited for N-point discrete signals. In such case, the infinite support fails to hold true. In limited supports, some papers such as [23] - [26] have discussed the uncertainty principle in conventional time-frequency domains for continuous and discrete cases and some conclusions are achieved that can be taken as our special cases in the following sections. However, none of them has covered the FRFT in terms of Heisenberg uncertainty principles that have been widely used in various fields [4] - [6] . Therefore, there has a great need to discuss the uncertainty relations in FRFT domains. As the rotation of the traditional FT [27] , FRFT [5] [6] [28] - [30] has some special properties with its transform parameter and sometimes yields the better results such as the detection of LFM signal [31] . Readers can see more details on FRFT in [6] and [32] and so on.

In this paper, we extend the Heisenberg uncertainty principle in FRFT domain for both discrete and continuous cases for the ε-concentrated signals or the signals with finite supports. It is shown that these bounds are connected with lengths of the supports and FRFT parameters. In a word, there have been no reported papers covering these results and conclusions, and most of them are new or novel.

2. Preliminaries

2.1. Definition of DFRFT

Here, we first briefly review the definition of FRFT. For given continuous signal 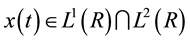and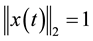, its FRFT [6] is defined as

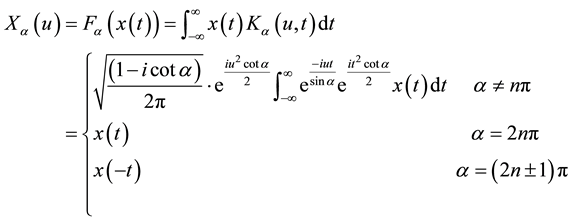(1)

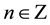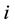where and is the complex unit, 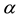is the transform parameter defined as that in [6] . In addition,

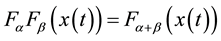. If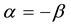, , i.e., the inverse FRFT.

However, unlike the discrete FT, there are a few definitions for the DFRFT [32] , but not only one. In this paper, we will employ the definition defined as follows [6] [32] :

(2)

Clearly, if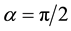, (2) reduces to the traditional discrete FT [6] [32] . Also, we can rewrite definition (2) as

,

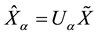where,.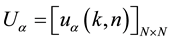

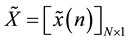For DFRFT, we have the following property [5] [6] [32] :

.

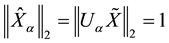More details on DFRFT can be found in [6] and [32] .

2.2. Frequency-Limiting Operators

Definition 1: Let be a complex-valued signal with and its FRFT, if there is a function vanishing outside (is a measurable set) such that (

is a small value with), then is -concentrated.

Specially, if, then definition 1 reduces to the case in time domain [23] [24] . If, then definition 1 reduces to the case in traditional frequency domain [23] [24] . The can be calculated after the is

fixed because and. Therefore,

Definition 2: Generalized frequency-limiting operator is defined as

(3)

If, then definition 2 is the time-limiting operator [23] [24] . If, then definition 2 is the traditional frequency-limiting operator [23] [24] . Definitions 1 and 2 disclose the relation between and. For the discrete case, we have the following definitions.

Definition 3: Let (with) be a discrete sequence with and its DFRFT, if there is a sequence satisfying such that (is a small value with), then is -concentrated.

Here, is the 0-norm operator that counts the non-zero elements.

Definition 4: Generalized discrete frequency-limiting operator is defined as

with is the DFRFT of and is the character function

on.

Clearly, definitions 3 and 4 are the discrete extensions of definitions 1 and 2. They have the similar physical meaning. These definitions are introduced for the first time, the traditional cases [23] [24] are only their special cases. Definition 3 and 4 disclose the relation between and.

2.3. The Continuous Heisenberg Uncertainty Principles

As shown in introduction, the existed continuous generalized uncertainty relations [9] - [21] are mainly for the infinite supports. Here, we discuss the case of finite support. First we introduce the following lemma.

Lemma 1: , where denotes the Frobenius norm operator.

Proof: From the definition of the operator in definition 2, we have

Exchange the locations of the integral operators, we obtain

,

so that

.

Set, we have

.

Now, we know that [see the proof of (3.1) in 25]

.

Let, then

where is the character function of the set. Therefore, via Parseval’s theorem [6] and the definition of

FRFT in (1) we have

Hence, we obtain the final result

Now we give the first theorem.

Theorem 1: Let be a measurable set and suppose is the FRFT of for transform parameter , such that is ?concentrated on . Then

. (4)

Proof: Since, therefore we can find such that makes.

Meanwhile, via triangle inequality and the definitions of concentration we have

At the same time, we know,

so that

,

i.e.,.

Therefore,.

From [24] [27] , we know that.

Use the above two results, we obtain

,

i.e.,.

Hence,. The special case is trivial. Here, we find that when, (4) reduce to the traditional case in Theorem 2 [(3.1), 25].

Obviously, this bound is different from that [20] of infinite case. In [20] , the main involved objects are the variances of the signal in infinite supports. Here the measurable sets (,) are involved, which is instructive

for the discrete case in the next section. If, what will happen? Clearly, it is impossible. From the conclusion [33] , if, then, otherwise, which is in conflict with that is measurable and limited. Therefore, in the continuous case, cannot hold true. However, what about

the discrete case? The next section will answer.

3. The Discrete Heisenberg Uncertainty Principles

3.1. The Uncertainty Relation

First let us introduce a lemma.

Lemma 3:, where is the Frobenius matrix norm.

Proof: From the definition of the operator in definition 4, we have

.

Exchange the locations of the sum operators, we obtain

Hence, according to the definition of the Frobenius matrix norm [27] [34] and the definition of DFRFT, we have

.

In the similar manner with the continuous case, we can obtain. Since, we have

, thus, we get. Therefore, we can obtain the following theorem 2.

Theorem 2: Let be the DFRFT of the time sequence for transform parameter , with -concentrated on index set . Let be the numbers of nonzero entries in (respectively). Then

. (5)

Here, we find that when, (5) reduce to the traditional case in Theorem 3 [(3.9), 25].

3.2. The Extensions

Set in theorem 2, we can obtain the following theorem 3 directly.

Theorem 3: Let be the DFRFT of the time sequence with length N. counts the numbers of nonzero entries in (respectively). Then

. (6)

Clearly, theorem 3 is a special case of theorem 2. Also, this theorem can be derived via theorem 1 in [26] .

Differently, we obtain this result in a different way. Here we note that since, there is at least one non-zero element in every FRFT domain for. Therefore, for.

Through setting special value for in theorem 3, we have

Corollary 1:

. (7)

Proof: Now we prove corollary 1 in the sense of sampling and mathematical solution for better understanding these relations. Without loss of generality, we often assume that the continuous signal (the continuous version of) is band-limited, then is obtained through sampling. From the sequence length N in the definition of DFRFT in (2), we know the sampling period defined as: (implies this result). We assume there is no aliasing after sampling in the FRFT domain, then from the sampling

Theorem, we know that all the energy of are limited within the scope [32] [35] , i.e., all the energy of must be within . Without

loss of generality, we assume based on the shifting property of FRFT [6] [32] , i.e., all the energy of

must be within. Let be the sites where is nonzero, and

be the corresponding nonzero elements of. Accordingly, from the definition of DFRFT

[6] [32] , we have

and. (8)

We rewrite (8) in terms of matrices and vectors. Define the matrix, where, then we obtain

,

where, and.

Clearly, is a matrix, which includes matrixes with dimensions of

so that we can rewrite matrix as

and, where.

From the definition of DFRFT, we know that the bases (for different

ks and) are mutually orthogonal [6] [32] . Therefore, the different rows are not correlated so that

is nonsingular and can be rewritten as. Since every ele-

ment in is not zero and is nonsingular, then there must be a non-zero element in at least. Other

wise, , which is in conflict with. Therefore, in every there is at least one non-zero element. Therefore, there are at least non-zero elements in the DFRFT

domain in total. Thus, theorem 3 is verified.

Furthermore, we can obtain the following more general uncertainty relation associated with DFRFT.

Clearly, if and, then the generalized uncertainty bounds are lower than the tradi-

tional cases. Therefore, the generalized uncertainty principles show that the resolution will be higher.

Theorem 4: Let be the DFRFT of the time sequence (and) with length N and. counts the number of nonzero elements in. Then

, where. (9)

Proof: From the assumption and the definition of DFRFT [6] [32] , we know

for.

where,.

Therefore, let, we have [26]

where and with and with.

Hence, we obtain

.

Set, then

Using the triangle inequality, we have

, hence

From and Parseval’s principle [6] , we obtain

.

Hence

.

Therefore, we obtain

Adding all the above inequalities, we have

with.

Similarly, from and Parseval’s principle [6] , we obtain, hence

.

From the definition and property of DFRFT [6] [32] we have

with.

Hence, we finally obtain the proof

with.

4. The Simulation

In this section we give an example to show that the data in FRFT domains may have much higher concentration than that in traditional time-frequency domains.

Now considering the chirp signal with and sampling period, (see Figure 1(a)).

Clearly, we can obtain from Figure 1 that, ,. Therefore, we have. This verifies that the data in FRFT domains may have much higher concentration than that in traditional time-frequency domains. (Note here that if the transformed coefficient is less than 0.1, then we take it as zero value. See Figure 1(b) and Figure 1(c)).

5. Conclusion

In practice, we often process the data with limited lengths for both the continuous (ε-concentrated) and discrete signals. Especially for the discrete data, not only the supports are limited, but also they are sequences of data

points whose number of non-zero elements is countable accurately. This paper discussed the generalized uncertainty relations on FRFT in term of data concentration. We show that the uncertainty bounds are related to the FRFT parameters and the support lengths. These uncertainty relations will enrich the ensemble of FRFT. Moreover, these uncertainty relations will help finding the optimal filtering parameters [31] such as [6] [34] [36] . Our simulation also shows that the data in FRFT domains may have much higher concentration than that in traditional time-frequency domains.

Acknowledgements

We will thank Professor R. Tao very much for his valuable suggestions in improving our work. This work was fully supported by the NSFCs (61002052 and 61471412) and partly supported by the NSFC (61250006) and Third Term of 2110 in Dalian Navy Academy.

Cite this paper

XiaotongWang,GuanleiXu, (2015) Support-Limited Generalized Uncertainty Relations on Fractional Fourier Transform. Journal of Signal and Information Processing,06,227-237. doi: 10.4236/jsip.2015.63021

References

NOTES

^*Corresponding author.