Journal of Signal and Information Processing
Vol.05 No.04(2014), Article ID:50479,11 pages
10.4236/jsip.2014.54015
Edge Detection with a Preprocessing Approach
Mohamed Abo-Zahhad1, Reda Ragab Gharieb1, Sabah M. Ahmed1, Ahmed Abd El-Baset Donkol2
1Department of Electrical Engineering Communication and Electronics, Assuit University, Assiut, Egypt
2Department of Electrical Engineering and Computer Sciences, Nahda University, Beni-Suef, Egypt
Email: zahhad@yahoo.com, rrgharieb@gmail.com, sabahma@yahoo.com, eng_ahmeddonkol@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 August 2014; revised 15 September 2014; accepted 7 October 2014
ABSTRACT
Edge detection is the process of determining where boundaries of objects fall within an image. So far, several standard operators-based methods have been widely used for edge detection. However, due to inherent quality of images, these methods prove ineffective if they are applied without any preprocessing. In this paper, an image preprocessing approach has been adopted in order to get certain parameters that are useful to perform better edge detection with the standard operators-based edge detection methods. The proposed preprocessing approach involves computation of the histogram, finding out the total number of peaks and suppressing irrelevant peaks. From the intensity values corresponding to relevant peaks, threshold values are obtained. From these threshold values, optimal multilevel thresholds are calculated using the Otsu method, then multilevel image segmentation is carried out. Finally, a standard edge detection method can be applied to the resultant segmented image. Simulation results are presented to show that our preprocessed approach when used with a standard edge detection method enhances its performance. It has been also shown that applying wavelet edge detection method to the segmented images, generated through our preprocessing approach, yields the superior performance among other standard edge detection methods.
Keywords:
Discrete Wavelet Transform, Image Edge Detection, Robert, Prewitt, Sobel, Canny Techniques

1. Introduction
Edge detection is basically an image segmentation technique that divides spatial domain, on which the image is defined into meaningful parts or regions [1] . Edges characterize boundaries of objects in an image and object recognition is of fundamental importance in image processing. Edges typically occur on the boundary between two different regions in an image, where there is a more or less abrupt change in gray level or texture indicating the end of one region and the beginning of another. Edge detection allows user to observe those boundaries. Edge detection therefore finds practical applications in medical imaging, computer-guided surgery, locate object in satellite images, face recognition, and finger print recognition, automatic traffic controlling systems, study of anatomical structure etc. Several edge detection techniques have been developed such as gradient based standard operators like Robert, Prewitt, Sobel. However, they have not given sharp edges and have been highly sensitive and provided poor performance in noisy images [1] . Laplacian based Marr Hildrith operators also suffers from two limitations: high probability of detecting false edges and the localization error may be severe at curved edges but the algorithm proposed by Canny in 1986 is considered as the ideal edge detection algorithm for images that are corrupted with noise [2] . Canny’s aim is to discover the optimal edge detection algorithm which reduces the probability of detecting false edges, and gives sharp edges.
Wavelet analysis is an efficient tool for edge detection. Deterministic methods are inappropriate when noise models are applied. In images with low SNR, the noise must be accounted with a noise model, multiplicative or additive [3] . An important issue in edge detection is the scale of detection filter. Small-scaled filters are sensitive to edge signals but also proneto noise, whereas large-scaled filters are robust to noise but could filter out fine details. As suggested by Marr and Hildreth [4] , multiple scales could be employed to describe and synthesize the varieties of edge structures. The idea of scale multiplication was first exploited in [5] , where it was shown that the scale products could improve the edge localization. Mallat [6] illustrated mathematically that signals and noise had different singularities and edge structures present observable magnitudes along the scales, while noise decreased rapidly. With this observation, Xu et al. [7] proposed a wavelet-based spatially selective filtering technique by multiplying the adjacent scales. Sadler and Swami [8] applied the wavelet-multiscale-products to step detection and estimation and Bao and Zhang [9] presented a denoising scheme by thresholding the multiscale products.
This paper presents a preprocessing approach to enhance the performance of standard operators-base edge detection methods. The approach consists of computation of the image histogram, finding out the total number of peaks and suppressing irrelevant peaks. From the intensity values corresponding to relevant peaks, threshold values are obtained. From these threshold values, optimal multilevel thresholds are calculated using the Otsu method, then multilevel image segmentation is carried out. Finally, a standard edge detection method is applied to the resultant segmented image. The rest of the paper is organized as follows: In Section 2, a review of standard operator-based edge detection methods are described, advantage and disadvantage of these methods are summarized and standard wavelet edge detection method is also explained. In Section 3, the edge detection with the proposed preprocessing approach is introduced. Section 4 presents simulation results and shows a quantitative comparison between several preprocessed standard edge detection methods and these standard methods without the preprocessing. We draw the conclusion in Section 5.
2. Previous Work
Edge detection is the process of determining where edges of objects fall within an image. Figure 1 shows schematic diagram for the standard edge detection method. To sense and detect abrupt change at edges, several operators have been constructed based on different ideas. In the following section, a brief review of some operators is presented.
2.1. First Order Edge Detector
The gradient method detects the edges by looking for the maximum and minimum in the first derivative of the
image. Thus, consider the two dimensional function 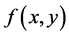 to represent the input image then image gradient is given by the following formula [1] :
to represent the input image then image gradient is given by the following formula [1] :
Figure 1. Standard edge detector.
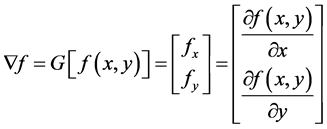 (1)
(1)
The gradient magnitude can be computed by the formula:
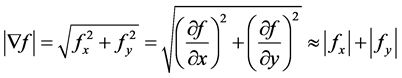 (2)
(2)
The gradient direction can be computed by the formula:
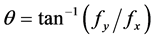 (3)
(3)
The magnitude of the gradient computed by Equation (2) gives edge strength and the gradient direction is always perpendicular to the direction of the edge. Robert, Sobel, and Prewitt operators are classified as standardfirst order derivative operators which are easy to operate but highly sensitive to noise [1] .
2.1.1. Robert Operator
The input image is convolved with the default kernels of operator and gradient magnitude and directions are computed. It uses the following 2 × 2 two kernels [10] :
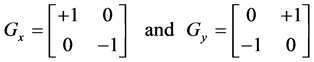 (4)
(4)
The plus factor of this operator is its simplicity but having small kernel it is highly sensitive to noiseand not compatible with today’s technology [10] .
2.1.2. Sobel Operator
It convolves the input image with kernel and computes the gradient magnitude and direction. It uses the following 3 × 3 two kernels:
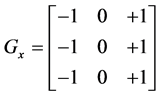 and (5)
and (5)
As compared to Robert operator, Sobel operator has slow computation. However it is less sensitive to noise as compared to Robert operator.
2.1.3. Prewitt Operator
Prewitt edge operator gives better performance than that of Sobel operator. The function of Prewitt edge detector is almost the same as Sobel detector but have different kernels:
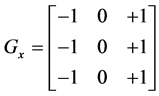 and (6)
and (6)
2.2. Second Order Edge Detector
Any definition of a second derivate 1) must be zero in flat areas; 2) must be nonzero at the onset and end of a gray level step and ramp; and 3) must be zero along ramps of constant slope [11] . The Laplacian operator 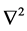 for a 2D image f(x, y) is defined by the following formula [10] :
for a 2D image f(x, y) is defined by the following formula [10] :
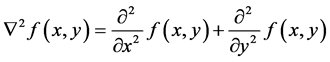 (7)
(7)
There are several ways to define digital Laplacian using neighborhoods. Whatever the definition, it has to satisfy the properties of a second derivate outlined in Equation (11). The following notation is used for second order derivative in the x and y directions [11]
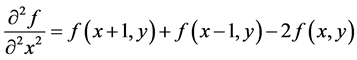 (8)
(8)
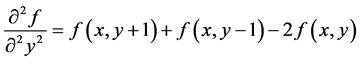 (9)
(9)
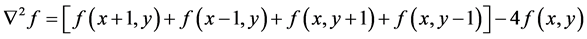 (10)
(10)
Furthermore, when the first derivative is at a maximum, the second derivative is zero [12] .
2.2.1. Laplacian
Laplacian of an image 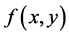 is defined by:
is defined by:
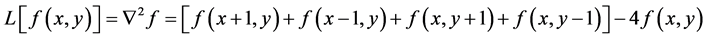 (11)
(11)
In this case, Laplacian kernel given by the following equation is adopted.
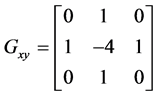 (12)
(12)
2.2.2. Laplacian of Gaussian (Marr-Hildreth Edge Detector)
The Laplacian of Gaussian (LoG) follows the following four steps [12] :
1) Smooth the image using Gaussian filter which is defined by:

2) Enhance the edges using Laplacian operator which given by this equation [12] :

3) Estimate the zero crossings denote the edge location.
4) Use linear interpolation to determine the sub-pixel location of the edge.
Greater the value of σ, broader the Gaussian filter, more is the smoothing. Too much smoothing may make the detection of edges difficult; also called the Maxican Hat operator.
2.2.3. Difference of Gaussian
To reduce the computational requirements, the LoG is approximated by the DoG. The width of the edge can be adjusted by changing 



LoG requires large computation time for a large edge detector mask. Second Order Derivative Methods Properties. The following are the three most important properties of the second order derivatives:
1) Second order derivative methods especially Laplacian, are very sensitive to noise.
2) Probability of false and missing edges remains.
3) Localization is better than gradient operators.
2.3. Canny Edge Detector
The Canny edge detection algorithm is known to many as the optimal edge detector. Canny’s intentions were to enhance the many edge detectors already out at the time he started his work. He was very successful in achieving his goal and his ideas and methods can be found [2] . In his paper, he followed a list of criteria to improve current methods of edge detection. The first and most obvious is low error rate. It is important that edges occurring in images should not be missed and that there be no responses to non-edges. The second criterion is that the edge points be well localized. In other words, the distance between the edge pixels as found by the detector and the actual edge is to be at a minimum. A third criterion is to have only one response to a single edge. This was implemented because the first two were not substantial enough to completely eliminate the possibility of multiple responses to an edge.
Based on these criteria, the Canny edge detector first smoothies the image to eliminate the noise. It then finds the image gradient to highlight regions with high spatial derivatives. The algorithm then tracks along these regions and suppresses any pixel that is not at the maximum (non-maximum suppression). The gradient array is now further reduced by hysteresis. Hysteresis is used to track along the remaining pixels that have not been suppressed. Hysteresis uses two thresholds and if the magnitude is below the first threshold T1, it is set to zero (made a non-edge). If the magnitude is above the high threshold T2, it is made an edge. And if the magnitude is between the two thresholds, then it is set to zero unless there is a path from this pixel to a pixel with a gradient above the second threshold T2. In order to implement the canny edge detector algorithm, a series of steps must be followed [13] .
Step 1: Smooth the image with a two dimensional Gaussian filters.
Step 2: Take the gradient of the image.
Step 3: The direction of the edge is computed using the gradient in the x and y directions.
Step 4: relate the edge direction to a direction that can be traced in an image.
Step 5: Non-maximum suppression.
Step 6: Hysteresis.
2.4. Advantages and Disadvantages of Standard Edge Detection Methods
Each edge detection method has its advantages and disadvantages. Table 1 summarize the main advantages and disadvantages of each method [12] .
2.5. Edge Detection Using Wavelets
2.5.1. 2D Discrete Wavelet Transform Edge Detection
First we define a Gaussian equation in two dimensions as [14] [15]

Table 1. Advantages and disadvantages of edge detector ion methods.
where, σ is standard deviation of the signal, and we assume that





The wavelet transform of f(x, y) at the scale s has two components defined by


2.5.2. Wavelet Edge Detector Implementation
Wavelet edge detection can be demonstrated as in Figure 2. Each process and the corresponding output will be discussed in the following sections.
2.5.3. The Smoothing
We smooth the image and detect the sharp variation points from their first order derivative. The smoothing function is any function whose integral is equal to 1 and that converges to 0 at infinity. One can choose smoothing function equal to a Gaussian.

We assume

By convolving the image with smoothing function we removes small signal fluctuation, then sharp variations will only be detected. The value of σ can be changed from image to image according to the amount of edges and detail. Linear filtering of an image is accomplished through an operation called convolution. In convolution, the value of an output pixel is computed as a weighted sum of neighboring pixels. The matrix of weights is called the convolution kernel, also known as the filter. In general case the wavelet domain in 2-dimension has R4 (Four dimensions) namely (x, y, scale and rotation). At each step, the image is convolved with a wavelet to obtain the coefficients. It is then smoothed with a Gaussian. Both the wavelet and Gaussian filtering are done using separate 1-D filters vertically and horizontally.
Figure 2. Standard wavelet edge detection method.
2.5.4. Local Modulus Maxima
In order to compute the local maxima of the modulus of the image in DWT we need to find: 1—the modulus and 2—the angle of the DWT at each scale. The modulus maxima are then defined as the points of the modulus images that are larger than the two neighbors whose positions are in the direction indicated by the angle value at the corresponding location. Now let’s know how we can get first the modulus of the image:

Then we get the angle of the DWT. There are only four possible directions when describing the surrounding pixels: 0 degree (in the horizontal direction), 45 degree (along the positive diagonal), 90 degree (in the vertical direction), or 135 degree (along the negative diagonal). Now from the modulus image and the angular DWT we can find the local modulus maxima.
2.5.5. Chain the Edge
The edge points can then be gathered together into chains. For point that is a maximum, we can join it with the point closest to it if they have similar angles. They thus define the multi-scale image edges.
2.5.6. Thresholding
Although the maxima of the modulus of the discrete wavelet transform are a good approximation of the edges in an image, even in the absence of noise often there are many false edges as can be seen. Therefore a criterion such as thresholding must be determined to separate the “true” edges from the “false” edges.
3. A Preprocessed Edge Detection Approach
Figure 3 shows schematic diagram for the proposed preprocessed edge detection method. In this method the image is processed and the resulting one is applied to standard edge detection method for the objective to enhance the final edge detection method performance.
The proposed preprocessing involves computation of the histogram, finding out the total number of peaks and suppressing irrelevant peaks. From the intensity values corresponding to peaks, threshold values are obtained. From these threshold values, optimal thresholds are calculated using the Otsu method for multilevel image thresholds [16] . This preprocessing can be implemented in the following steps demonstrated by an image example:
1. Filter the original image Figure 4 using a Gaussian filter as shown in Figure 5.
2. Convert the image to grayscale as shown in Figure 6.
3. Use an averaging mask over the image and resize the image. To limit computation time, we resize the image to have 256 rows and columns that are proportion to it i.e. the original aspect ratio is maintained as shown in Figure 7.
4. A histogram of the image is generated. Thus, the result is of the form [intensity level, number of pixels with that intensity level] as shown in Figure 8.
Figure 3. Proposed technique for edge detection.
Figure 4. Original image.
Figure 5. Gaussian filtered image.
Figure 6. Gray image.
Figure 7. Resized image.
Figure 8. Image histogram.
5. From the histogram data, create a set of values from which the local peaks are counted 58 elements.
6. From the above set, create a set where the peaks that are within 1% of the maximum value (of the number of pixels corresponding to the same intensity level) are counted and others are discarded 57 elements. This factor has been statistically obtained from assessing many images [17] .
7. From the set created in the previous step, remove the peaks that correspond to intensities that are within 20 levels of each other 7 elements. The number 20 is again found effective after experiments by [17] . Now, we have the number of peaks which are thresholds that we can consider from the image. They represent the significant peaks in the histograms shown in Figure 9.
8. Using the threshold values above, find out the optimal threshold using Otsu’s method; Thresh = [53 74 98 128 162 190 218].
9. Based in the thresholds obtained from Otsu’s method, segment the resized image as shown in Figure 10.
4. Simulation Results
This section presents a comparison between different edge detection models. For this purpose MATLAB 8.1 (R2013a) program has been adopted to investigate the difference between edge detection models. Namely, BSD (Berkeley Segmentation Dataset) images [18] and respective ground truths are used for experimentation. It has been found that the best model is wavelet edge detection model. This comparison between Roberts, Prewitt, LoG, Canny and Wavelet edge detection methods is done using ground truth of images. The performance para- meters used are Performance Ratio (PR), Peak Signal to Noise Ratio (PSNR), False Alarm Count (FAC), Miss Count (MSC), and Figure of Merit (FoM). PR is defined as the ratio of true to false edges [19] .

The FoM is defined by

where, false edges are the non-edge pixels identified as edges, 


As shown in Table 2, the preprocessed edge detection methods provide better performance measures than the standard ones. However, the preprocessed edge detection methods take more computation time due to the preprocessing. Figure 11 shows the original image used in simulation and its ground truth and the output of standard and preprocessed methods mentioned in Table 2.
Figure 9. Otsu threshold.
Figure 10. Otsu image.






Figure 11. Comparison between various edge detection models (a) Original image; (b) Ground truth; (c) Robert; (d) Proposed Robert; (e) Prewitt; (f) Proposed Prewitt; (g) LoG; (h) Proposed LoG; (i) Canny; (j) Proposed Canny; (k) Wavelet; (l) Proposed wavelet.
Table 2. Comparison between the proposed preprocessed and standard edge detection methods.
5. Conclusion
In this paper, we have presented a preprocessing approach in order to enhance the performance of commonly used edge detection methods. The preprocessing approach consists of computation of the image histogram, finding out the total number of peaks and suppressing irrelevant peaks. From the intensity values corresponding to relevant peaks, threshold values are obtained. From these threshold values, optimal multilevel thresholds are calculated using the Otsu method, then multilevel image segmentation is carried out. Finally, a standard edge detection method can be applied to the resultant segmented image. The preprocessing approach has been summarized in steps and demonstrated by an image example. Simulation results have shown that the preprocessing approach is used with standard edge detection methods to enhance their performance. Results have also shown that wavelet edge detection with the preprocessing approach provides the superior performance among other standard methods with and without preprocessing approach.
References
- Mukesh, K. and Rohini, S. (2013) Algorithm and Technique on Various Edge Detection: A Survey. International Journal (SIPIJ), 4, 65-75.
- Canny, J. (1986) A Computational Approach to Edge Detection. Transactions on Pattern Analysis and Machine Intellgence, 3, 679-697.
- Rufeil, E., Gimenez, J. and Flesia, G. (2012) Comparison of Edge Detection Algorithms on the Undecimated Wavelet Transform. CLAM 2012, Latin American Congress in Mathematics, Argentina.
- Marr, D. and Hildreth, E. (1980) Theory of Edge Detection. Proceedings of the Royal Society of London. Series B, Biological Sciences, 207, 187-217. http://dx.doi.org/10.1098/rspb.1980.0020
- Urkowitz, M. (1969) A Nonlinear Edge-Detection Technique. Proceedings of IEEE, 814-815.
- Mallat, S. (1998) Wavelet Tour of Signal Processing. Academic Press.
- Xu, Y., Weaver, J.B., Healy, D.M. and Lu, J. (1994) Wavelet Transform Domain Filters: A Spatially Selective Noise Filtration Technique. IEEE Transaction on Image Processing, 3, 747-758. http://dx.doi.org/10.1109/83.336245
- Brian, M. and Swami, A. (1999) Analysis of Multiscale Products for Step Detection and Estimation. IEEE Transaction on Information Theory, 45, 1043-1051.
- Bao, P. and Zhang, L. (2003) Noise Reduction for Magnetic Resonance Images via Adaptive Multiscale Products Thresholding. IEEE Transaction on Medical Imaging, 22, 1089-1099. http://dx.doi.org/10.1109/TMI.2003.816958
- Rani, V. and Sharma, D. (2012) A Study of Edge-Detection Methods. International Journal of Science, Engineering and Technology Research (IJSETR), 1, 62-65.
- Gonzalez, R.C. and Woods, R.E. (2002) Digital Image Processing. 2nd Edition, Prentice Hall, Upper Saddle River.
- Saluja, S., Singh, A.K. and Agrawal, S. (2013) A Study of Edge-Detection Methods. International Journal of Advanced Research in Computer and Communication Engineering (IJARCCE), 2, 994-999.
- Raman, M. and Aggarwal, H. (2009) Study and Comparison of Various Image Edge Detection Techniques. International Journal of Image Processing (IJIP), 3, 1-12.
- Bella, B., Tawfik, S. and EL-Gazzar, M.M. (2013) Multiscale Edge Detection Using Wavelet Transform Compared to Other Methodologies. International Journal of Mathematics and Computer Applications Research (IJMCAR), 3, 103- 114.
- Seema, B.K. (2013) An Edge Detection Approach Based on Wavelets. International Journal of Engineering Research & Technology (IJERT), 2, 2836-2840.
- Otsu, N. (1979) A Threshold Selection Method from Gray Level Histograms. IEEE Transactions on Systems Man Cybernet, SMC-9, 62-66.
- Nain, N., Jindal, G. and Jain, A. (2008) Dynamic Thresholding Based Edge Detection. Proceedings of the World Congress on Engineering, London, 2-4 July 2008.
- Martin, D., Fowlkes, C. and Tal, D. (2001) A Database of Human Segmented Natural Images and Its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics. ICCV Vancouver, 1-8.
- Khaire, P.A. and Thakur, N.V. (2012) A Fuzzy Set Approach for Edge Detection. International Journal of Image Processing (IJIP), 6, 403-412.


















