ABSTRACT

This paper proposes a novel implementation of the level set method that achieves real-time level-set-based object tracking. In the proposed algorithm, the evolution of the curve is realized by simple operations such as switching values of the level set functions and there is no need to solve any partial differential equations (PDEs). The object contour could change due to the change in the location, orientation or due to the changeable nature of the object shape itself. Knowing the contour, the average color value for the pixels within the contour could be found. The estimated object color and contour in one frame are the bases for locating the object in the consecutive one. The color is used to segment the object pixels and the estimated contour is used to initialize the deformation process. Thus, the algorithm works in a closed cycle in which the color is used to segment the object pixels to get the object contour and the contour is used to get the typical-color of the object. With our fast algorithm, a real-time system has been implemented on a standard PC. Results from standard test sequences and our real time system are presented.

1. Introduction

Tracking is the problem of generating an inference about the motion of an object given a sequence of images. Good solutions to this problem have a variety of applications areas including surveillance ‎[1-7], human-computer interfaces ‎[3,4], and medical imaging ‎[8,9].

Deformable models have been used in tracking tasks ‎[8] and ‎[10-12]. Deformable model is appealing for object tracking because the object in the image sequence can vary from frame to frame due to a change in the view point, the motion of the object, or its nonrigid nature. The principal challenges for object tracking using deformable models are to develop accurate deformable model of image variability and to design computationally efficient tracking algorithms which use this model. Also parametric deformable models have some difficulties in handling topological changes such as the merging and splitting of object regions. For these reasons, the level set method ‎[13,14] is a more powerful technique. But the high computational cost of the level set method has limited its popularity in real-time scenarios.

Tracking using level set methods can be classified as edge based or region based. Edge based models can be traced back to the snake model in ‎[15]. Using the difference between the current frame and a reference background, a region based model was proposed in ‎[16]. Considerable work has been done to improve the speed of level-set-based curve evolution. The basic idea has been to limit the solution of the level set PDE to a narrow band around the zero level set ‎[17,18], but issues such as narrow band construction, reinitialization and step size control still make existing level set methods computationally too expensive for real-time tracking. In ‎[19] the authors proposed a region based level set model for tracking. They used an energy functionality that contains two terms, fidelity term and smoothness term. The resultant evolution equation contains two speeds. The speed represents the competition between two regions, and the speed makes the curve smooth. For implementation of their evolution equation they defined two lists of neighboring pixels 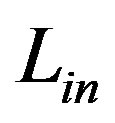and 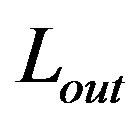of the contour. Their level set is evolved by switching the neighboring pixels between the two lists 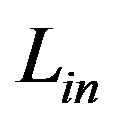and.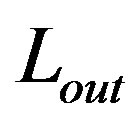

In this paper, we propose a novel approach to tracking using the level set methods. Our approach is based on that the implicitly represented curves can be moved by changing the sign of values of the level set function inside and outside the curve. Our approach requires simple addition operation and then changes the sign of some values inside or outside the curve to achieve the tracking. Our method does not contain any functional energy, so it does not need to solve any partial differential equations (PDEs), thus reducing the computation dramatically compared with other techniques proposed before. The proposed tracking technique tries to trace both contour and color variations in order to locate the object in the consecutive frames. With our approach, real-time levelset-based video tracking can be achieved by using a conventional PC.

The rest of the paper is organized as follows. In Section 2 we give a brief review of the level set methods. Section 3 presents the new level set technique for tracking. In Section 4 the proposed technique for object tracking is described. The experimental results are presented in the Section 5. The paper is concluded in Section 6.

2. Level Set Methods

The main idea behind the level set formulation is to represent an interface 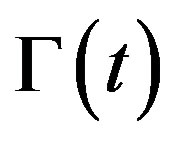bounding a possibly multiply connected region in 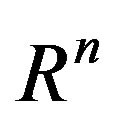by a Lipschitz continuous function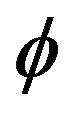, changing sign at the interface, i.e.

(1)

In numerical implementations, often regularity is imposed on to prevent the level set function of being too steep or flat near the interface. This is normally done by requiring to be the signed distance function to the interface

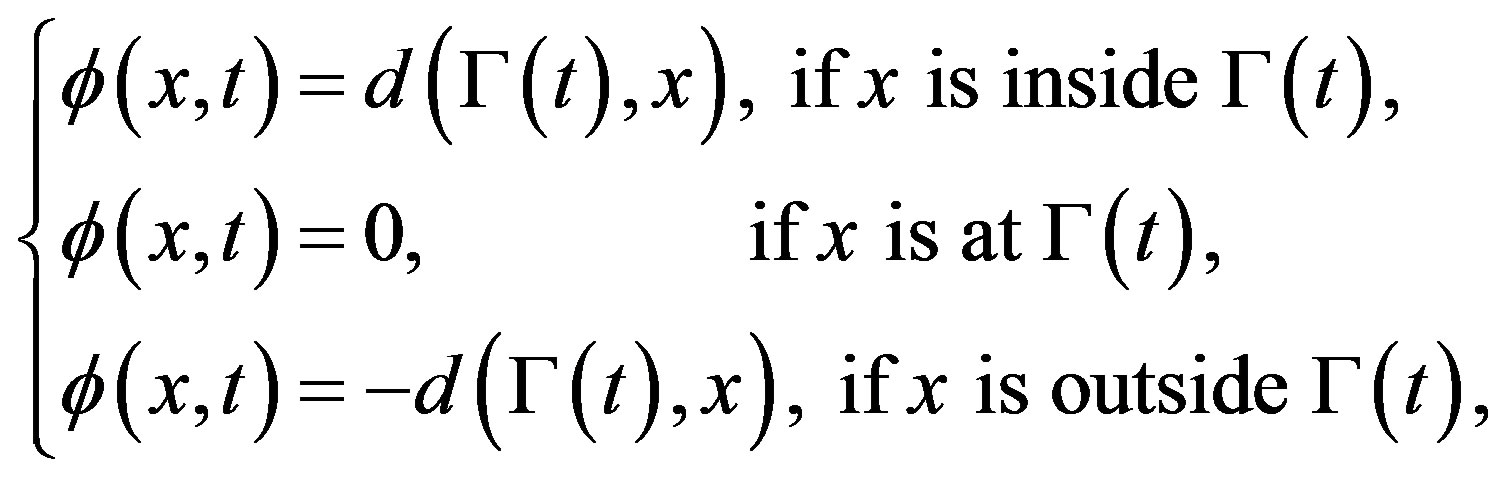(2)

where denotes Euclidian distance between x and. We emphasize that requiring (2) is a technicality to prevent instabilities in numerical implementations.

The interface 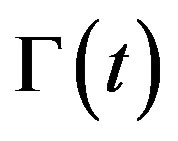is implicitly moved according to the nonlinear PDE

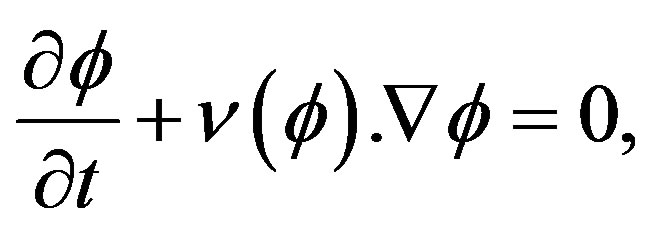(3)

where is a given velocity field. This vector field can depend on geometry, position, time and internal or external physics. Usually only the velocity normal to the interface 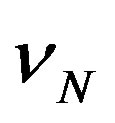is needed, and 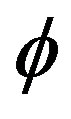is then moved according to the modified equation

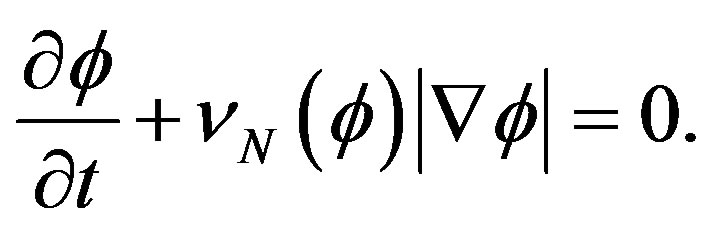(4)

3. Tracking Level Set Model

In this paper, we use a region-based level set model for the object tracking. The tracking process is depending on the quality of the matching between the object contour and the interface of the level set function,. The tracked object is segmented then the tracking process is started.

The used level set function, 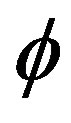is be given by:

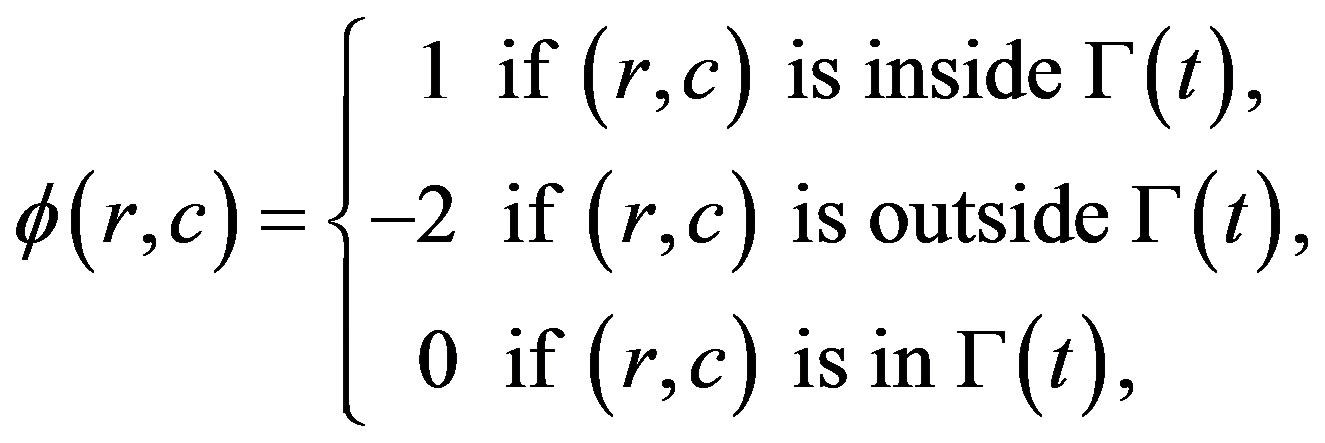(5)

where (r,c) are the row and column coordinates of the current point. From (5) we can conclude that contains two regions, inside region with value “+1” and outside region with value “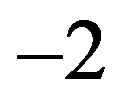”, see Figure 1.

Our method does not need to solve any PDE, so regularity is not important. Therefore 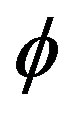is not required to be a distance function. The tracked object is segmented and given the value “1”, the value “0” is reserved for the background, see Figure 2.

Deformation

The deformation process is started by adding both the segmented image, I, see Figure 2, and the current level set function, see Figure 1. The result is put in a new image called,

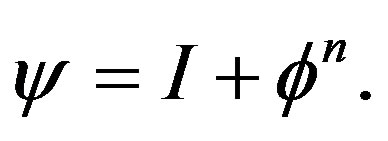(6)

Every intersection between the object region, and level set regions has a unique value in the resultant image,. It is clear that any point in ψ will take its value based on the following:

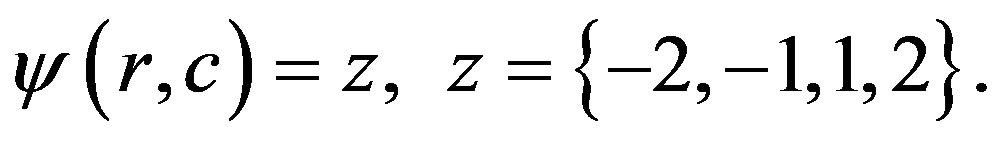(7)

The number of points carrying any value, 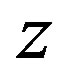, in 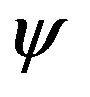gives information about the amount of overlap between the level set function and the object, we have four states, see Figure 3:

1) The number of occurrence of the value “” in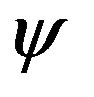, results from addition of the object and the exterior region

of, represents the area in which the object misses the interior region of.

2) The number of occurrence of the value “2” represents the area in which the object hits the interior region of.

3) The number of occurrence of the value “1”, results from the addition of  the background and the interior region of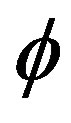, represents the area in which the interior region of 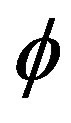misses the object.

4) The number of occurrence of the value “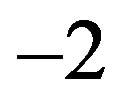”, results from addition of the background and exterior region of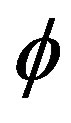, represents the area in which the exterior region of 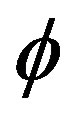hits the background.

The next step is the deformation process which is done by simply changing some values in the resultant image,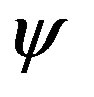. The values are changed to force the interface contour, , to catch the object’s boundary. By considering the object-mask arrangement shown in Figure 3, we can observe that to force to catch the object the values of 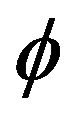should be changed based on the following rules, see Figure 4:

1) The pixels of values “−2” and “2” remain without change2) the pixels of value “1” is regarded as outside region so it should be changed to the value “−2”3) the pixels of value “−1” is regarded as inside region

so it should be changed to the value “2”. The above steps can be achieved by:

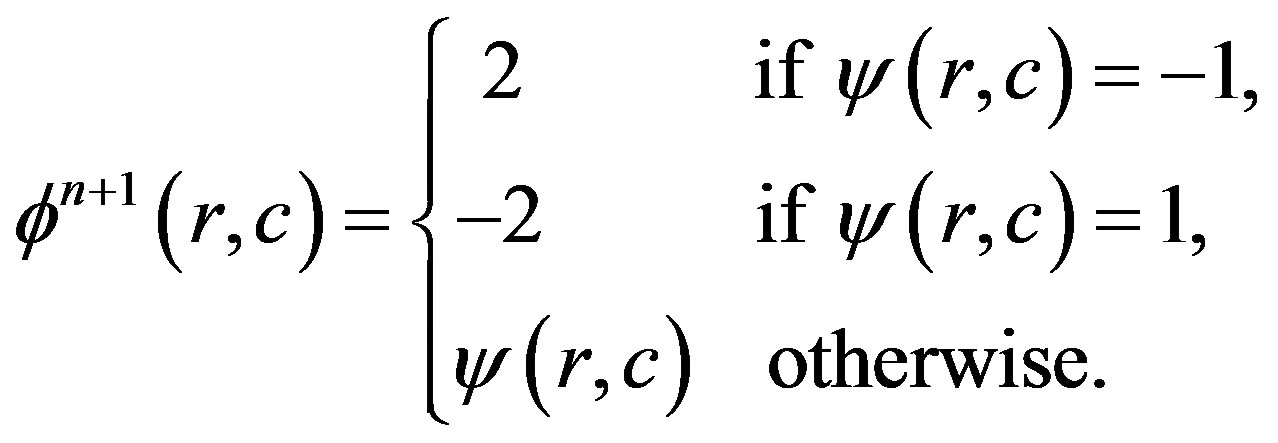(8)

4) Finally, to get the level set model in (5) the pixels of the exterior region are changed to the value “−1”,

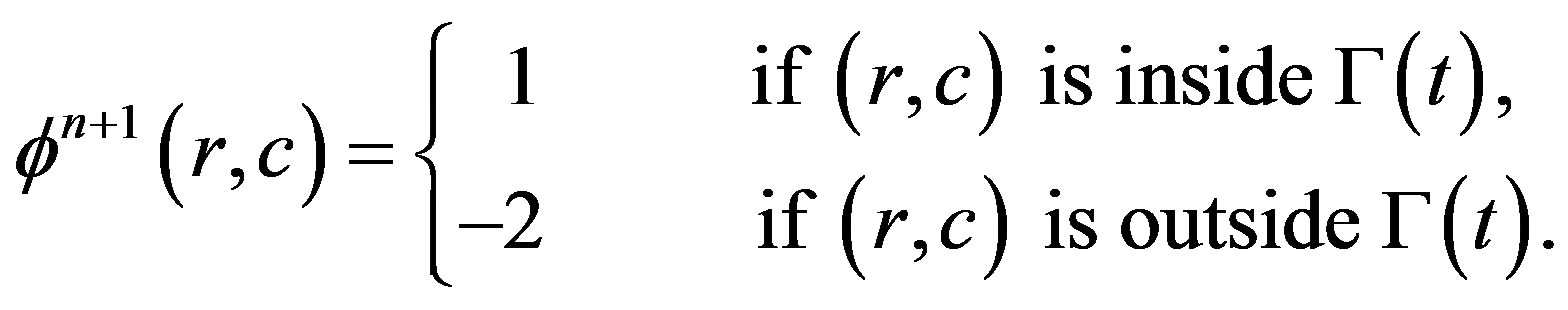(9)

4. Proposed System

In this section our algorithm for object tracking is described. Before the start of tracking process there are two necessary steps. The first step, Display, is to select the object for tracking. Second step, Initialization, is carried out to locate the object contour.

4.1. Display

The captured images are previewed and the initial level set function, ϕ, is created by hand and given values as shown in Figure 1. The process is done by putting the interface 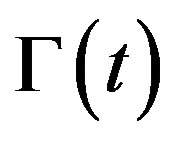over the object needed to be tracked, see Figure 5 in the experimental result section.

4.2. Initialization

The current frame is converted from RGB color system into HSI color space that decouples the brightness information from the color information. Under this represent-

tation we could easily segment the object by assuming that the changes of the object hue or saturation are much smaller than the expected changes in the intensity. Thus the object is a blob in the image with limited variation in hue and saturation and slightly larger variation in the intensity. The object segmentation is performed in two steps: 1) get the typical-color of the object, see Algorithm 1, and 2) use the typical-color to threshold the current frame to extract the object, see Algorithm 2, the resultant image, I, is binary image with object and background values as shown in Figure 2.

Now we have 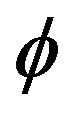and so (6) can be used to find the new image,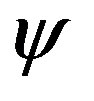. The new, which catches the object, is then found by (7) and (8).

4.3. Tracking-Target

The tracking is a sequence of operations; the first step is to use the level set function, , from the previous frame,

in order to get the typical-color in the current frame. The second step is to use this color for object segmentation, i.e. getting the image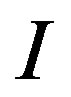. Finally we use and to deform the model towards a better fit using the steps in Section 3.A. By this the interface of the level set will move to catch the moved target.

4.4. Advantages and Disadvantages

Some of methods presented in the literature have a matching problem in which the systems mistake the object. This is because the objects may change color due to environmental or camera changes. Kinematics-based algorithms may not work properly when the objects abruptly change their motion from one frame to the next ‎[20,21]. Such situations can be due to collisions or sharp turns. Also the algorithms that detect motion in a sequence of frames by extracting tokens such as edges, corners, interest points, etc. ‎[22,23] mistake objects when there is a change in their 2-dimensional shape ‎[24,25]. The solution of the above problems is to use high frame rate. By maintaining the interframe time small, we maintain both shape and color variation to minimum. High frame rate requires a high speed tracking algorithm to segment and track the object in the small interframe time.

The proposed method does not contain any PDE and the tracking process is done by simple addition and change values operations, see (6) and (8). Thus, the speed of deformation is the strongest point in the proposed system. It is capable of tracking objects at 30 frames/sec on regular PC (CORE 2 Duo). Each of the frames is 480 × 640 RGB 24-bit pixels. This speed keeps the color position and shape variation in the interframe time small. Consequently the reliability of the tracking process increases.

The most important limitation of the proposed system is that it loses track of the object when the object is partially occluded by similar color object. In this case the deformation algorithm tends to combine both similar color objects within a single contour. As one of the object moves away from the other the algorithm will follow both objects. Also, the algorithm gives poor results if there is no color difference or intensity contrast between the object and the background as with all tracking algorithms.

5. Experimental Results

In this section two examples are given to demonstrate the system capability for real time tracking. In all experiments we used CORE 2 Duo Laptop with 2.2 GHz speed and 4 GB memory.

5.1. Example 1

The used video is taken using a webcam at 30 frames per second. The sequence consists of frames each of (480 × 640 pixels). As shown in Figure 5, frame 0 shows the object (blue paper) with the initial model being place on it. The initial contour is determined manually using the mouse. In the initialization the deformation process is used to get the contour of the object. As can be clearly shown in some subsequent frames in Figure 5, the proposed system is able to continuously track the object real time. The motion of the contour is due to the change of the location of the object.

6.2. Example 2

The proposed system is applied to track an object in a video downloaded from the internet. The downloaded video has 30 frames per second each is 480 × 640 pixels. Figure 6 shows the tracking results of the object. The object color and contour are used for tracking. Despite the motion and shape changes of the object, the deformable model reasonably delineates the contour of the object throughout the whole sequence.

6. Conclusion

This paper introduced a new tracking algorithm that is fast enough to track an object in real time. The used definition of an object is any connected area in the captured frame which has a consistent feature. Although arbitrary complex feature could be used, the one selected is the HSI representation of color which practically fits a wide range of applications. A deformable model which depends on the level set methods has been pursued because

of its speed and simplicity. The deformation requires only two-image addition to obtain the contour of the target object. Using this algorithm, a real time system was constructed using a standard CORE 2 Duo Laptop. Many experiments are made on real videos with frame rate of 30 frames/sec. The result showed that the proposed technique can track an object in real time.

REFERENCES