Journal of Signal and Information Processing
Vol.5 No.2(2014), Article ID:45992,9 pages DOI:10.4236/jsip.2014.52008
Quantum Inspired Shape Representation for Content Based Image Retrieval
Rahmeh Jobay, Azzam Sleit
Computer Science Department, University of Jordan, Amman, Jordan
Email: rahmeh.jobay@yahoo.com, azzam.sleit@ju.edu.jo
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 30 December 2013; revised 20 January 2014; accepted 20 February 2014
ABSTRACT
Content Based Image Retrieval (CBIR) is a technique in which images are indexed based on their visual contents and retrieving is only based upon these indexed images contents. Among the visual contents to describe the image details is shape. Shape of object, is considered as the most important distinguishable feature which living things can easily recognize, which is also a fact while this line is being written, and large efforts are currently underway in describing image contents by their shapes. Inspired by the core foundation of quantum mechanics, a new easy shape representation for content based image retrieval is proposed by borrowing the concept of quantum superposition into the basis of distance histogram. Results show better retrieval accuracy of the proposed method when compared with distance histogram.
Keywords:CBIR, Shape, Qubit, Quantum Superposition

1. Introduction
In shape-based content image retrieval, a good retrieval accuracy requires an effective shape descriptor to perceptually find similar shapes from a database, this means that the descriptor should also retrieve the rotated, scaled and translated shapes which are known as the robustness requirements. Another important requirement is that the ability of shape descriptor to hierarchaly represent image content which can achieve a high level of matching efficiency. This is because shapes can be compared at coarse level of detail thus eliminating large amount of dissimilar shape and then compared at finer level of detail. There are many important application areas of shape-based content image retrieval, and it can be used in medical diagnosis for medical image by identifying similar past cases [1] -[5] . Another important application is in crime investigation to retrieve the most similar suspects owing similar face shapes with target one, moreover, shape-based content image retrieval is important in security check for finger print or retina scanning for access privileges. Doing this research in this field can also help chemists, biologists, geologists in their fields too, thus, making shape-based content image retrieval [6] -[14] more adequate than other visual content based image retrieval systems.
Distance histograms based methods [15] -[19] are an effective contour based shape representation methods, which contain statistical information about the shape of object that can be used to describe shape of target. Distance histograms have the ability to be invariable to translation, rotation and normalization, making it invariant to scaling. However, these distance histograms only reflect the statistical characteristic information of the shape rather than spatial information. Therefore, many alternative approaches have been proposed to reflect spatial information and most of these methods use the total number pixels with same centroidal distance as a measure, hence, these traditional distance-based histograms lack the ability to extract spatial relationship effectively.
In recent years, quantum mechanics concepts and theories have been cooperated into computer science [20] [21] , information theory, signal processing, the employment of physical quantum systems and the realization of the information they convey are considered as the break down debate in the classical world at present. Furthermore, there has been some work done using a quantum information theory approach for classical problems by Eldar and Oppenheim [22] .
Oppenheim and Eldar are the first to bring forward the concepts and theories of quantum signal processing (Quantum Signal Processing, QSP). QSP applies the math foundations of quantum mechanics to signal processing, which is aimed at first developing new or modifying existing signal processing algorithms by borrowing from the principles of quantum mechanics. Since then QSP has attracted a lot of researcher to research it. Tseng and Hwang [23] proposed a quantum image edge detection algorithm which takes advantage of quantum superposition and quantum state collapse theories by means of random observation. These methods depend on mapping pixel gray level from image space into quantum space. Nӧell, Ӧmer and Suda [24] proposed a new representation for HSI color space by mapping hue and saturation into quantum space. These researches provided us with some digital image processing methods based on quantum theory and opened up the thought to develop a new quantum inspired a shape representation method.
2. Background
2.1. CBIR Components
A classical CBIR system consists of the following three main stages which are shown in Figure 1:
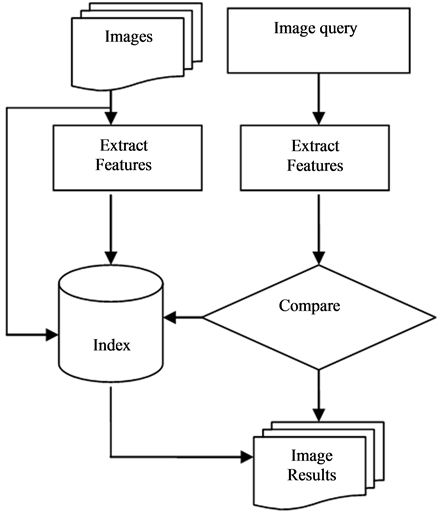
Figure 1. Components of CBIR (image from [3] ).
a) Feature extraction: image is processed to extract features in order to represent image content as numeric values which are called feature vectors.
b) Image indexing: image database are indexed and represented by their feature vectors.
c) Compare and retrieval: in this stage a query image is compared with database images according to their extracted feature vectors in order to retrieve the most relevant ones in ranked order.
Image feature extraction plays an important role in the image retrieval process and the most common extracted features are color, texture and shape. Among them, shape is considered the most powerful important feature for image indexing and retrieval. Shape feature extraction from a given image is called shape representation. Shape representation methods tend to effectively find perceptually important shape features based on boundary information or interior content and these features are evaluated by how accurately they retrieve similar shapes from a designated database.
2.2. Shape Representation Methods
Shape representation methods are generally classified into two main categories: contour-based or region-based [6] [7] , which mean the shape feature is either extracted from contour only or shape whole region. Under each category, different methods are further classified into global and structural which correspond to whether a shape is represented as a whole or represented by segments (primitives).
Contour shape representation methods exploit the boundary information and tend to contain critical information about the shape of object they are divided to global and structural approaches. In global approaches, the shape boundary is not divided into subparts and treated as a whole and a feature vector is derived for the whole boundary. The matching between two shapes is performed by finding the distance between their corresponding feature vectors which is usually conducted by Euclidian distance or city block distance [25] .
Among contour based shape representation methods is shape signature which result in one dimensional function derived from shape boundary points. Many shape signatures have been proposed such as, centroidal profile, complex coordinates, centroidal distance signature as shown in Figure 2, tangent angle, cumulative angle, curvature, area and chord-length. Shape signature tend to be scale and translation invariant when normalized, however, shift matching is needed in order compensate orientation requirements which is considered time consuming during comparison. Therefore, most shape signatures are quantized into signature histogram which is rotationally invariant.
Centroidal distances histogram is an effective contour shape representation method which is invariable to translation and rotation. Normalization makes distances histogram invariable to scaling. During feature extraction centroidal distances are computed between points on the shape boundary and the centroid of shape, these distances contain information about the shape of target. Fan [18] used distance histogram (DH) to describe the shape of target by sampling the centroidal distances into buckets resulting in a histogram denoted as:
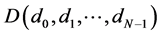 (1)
(1)
where N is the number of buckets in the histogramand di is the total number of centroidal distances which were discretized into bucket i.
However, the consideration of spatial relationship is neglected in centroidal distance histogram and two different shapes may have the same distance histogram several methods were proposed to solve this problem, for example, a shape feature vector called distance coherence is proposed in [17] , and the main idea is divide pixel in each interval of histogram into coherent and incoherent. This approach takes the advantages of the spatial information of contour effectively.
3. Theory of QSP
In classical information processing, the state 0 or 1 is used to represent the binary bit. In QSP the bit is called
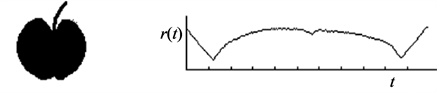
Figure 2. An apple shape and its centroidal distance signature.
qubit (pronounced q bit) and its state is represented as the superposition of two quantum states |0> and |1> as follow:
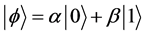 (2)
(2)
where α and β are probability amplitudes of states |0> and |1>, and |α|², |β|² are the measurement probability of state |0> and |1> respectively. In single qubit system, |0> and |1> are the two ground states such that |α|² + |β|² = 1 must be satisfied. In quantum world, this means the state of qubit can be found in state |0> and state |1> simultaneously but with different probabilities and once a measurement is carried out it will collapse into classical bit which can be found either in state |0> or |1>.
For digital images, a pixel grey level value is mapped from image space into pixel qubit in quantum system space by imitating the mathematical expression in Equation (2). Let f(m,n) be a normalized input image, f(m,n) Î [0,1] is the grey level value of the (m,n) pixel, Statically The (m,n) pixel qubit can be defined as:
 (3)
(3)
Such that 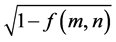 and
and 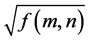 are the appearance probabilities for pixel grey level being at state 0 and 1 simultaneously.
are the appearance probabilities for pixel grey level being at state 0 and 1 simultaneously.
4. Quantum Distance Histogram Shape Representation
In this section we introduce the structure of quantum distance histogram (QDH) by incorporating the principle of quantum superposition from quantum mechanics into distance into the basis of distance histogram
4.1. Pixel Centroidal Distance Qubit
Pixel centroidal distance qubit is the basis for the new method and computed by transforming centroidal distances of pixels along shape contour from 2D space into quantum space. Let C2 be a given a 2D shape contour and ![]() is point along the contour. Then
is point along the contour. Then 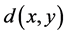 is the normalized centroidal distance in the range [0,1]. The transformation of point distance
is the normalized centroidal distance in the range [0,1]. The transformation of point distance 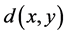 into quantum bit
into quantum bit  is the superposition of two quantum states |0> and |1> which is expressed by the following equation:
is the superposition of two quantum states |0> and |1> which is expressed by the following equation:
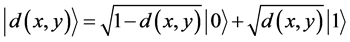 (4)
(4)
For certain point centroidal distance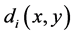 , its correlative characteristic with neighboring pre-post points centroidal distances along shape boundary is made up by superpositioning their state in bi-qubits system defined as:
, its correlative characteristic with neighboring pre-post points centroidal distances along shape boundary is made up by superpositioning their state in bi-qubits system defined as:
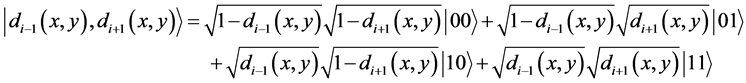 (5)
(5)
Thinking at the quantum level, we made a kind of blending among neighboring points centroidal distances on the ith point location such that it will constitute all states of the built up bi-qubits system simultaneously with different probabilities. Thus, the state of point location fluctuates among |00>, |01>, |10> and |11> states until it collapse into definite state by measurement, thereby, existing this action exhibited from the quantum level.
4.2. Quantum Distance Histogram (QDH)
The proposed QDH is a feature vector shape representation which combines DH and quantum superposition. Firstly, points centroidal distance are transformed into quantum space, then a measurement is performed per each point to find its state. QDH is expressed as follows:
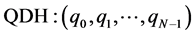 (6)
(6)
where qi is the total number of points possessing the ith state in n-qubits system.
QDH possess the invariability to translation and rotation, since points centroidal distance is not influenced by translation on the other side rotation has no influence on the distribution of points states, hence QDH posses the invariability to rotation. However, scaling invariability can be solved by dividing each total number of points in the ith state in QDH by the total number of points for the whole states of QDH. Therefore the elements of QDH will be normalized in the range between 0 and 1.
5. Experimental Results
5.1. Similarity Measure
Once the designated database is indexed based on the extracted shape features, querying for most relevant images to a given image shape feature is performed by comparing the extracted shape representation with the designated database. In most CBIR, the distance between two images features is used to measure their similarity. The smaller the distance value, the smaller the difference between images, therefore, the more similar of images. One of the most used distance methods to measure the similarity between compared images is the Minkowsky distance. Minkowsky distance is based on Lp norm which is expressed as:
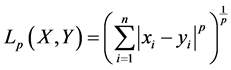 (7)
(7)
when p = 1 or p = 2, it is called the city block distance and Euclidean distance respectively as expressed below in Equation (8) and Equation (9) accordingly:
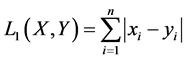 (8)
(8)
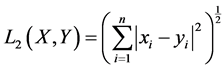 (9)
(9)
In this paper, Equation (8) is employed as a measure to find the similarity between compared image’s feature vectors.
5.2. Performance Evaluation
Precision and recall are the most common used metrics to evaluate the performance of image retrieval algorithms. Where precision is the percent of relevant images retrieved in the answer set, while recall is the percent of relevant images retrieved to the all relevant images in the designated database and they are defined as below:
 (10)
(10)
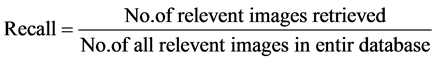 (11)
(11)
In the experiment, we use precision and recall measures for the first N images retrieved as an evaluation criteria for the proposed method. In addition, the average precision and average recall measures are used to analyze the effectiveness of the QDH. The performance of QDH was compared with DH.
5.3. Experiments
In the forthcoming experiments, 4-qubits representation (16 states) is used to create the feature vector for the QDH method. For DH, the number of total bins for the feature vector is adjusted to 20 bins.
For results shown in both Figure 3 and Figure 4, we randomly selected 400 images from different classes of MPEG-7 shape database as our test images for the first 10 and 20 answers respectively. QDH was able to achieve a precision rate of 60% and recall rate of 30% for the first 10 retrieved answers while DH achieved a precision rate of 42% and recall rate of 20%. In Addition,the precision and recall rates achieved by QDH for the first 20 retrieved answers were 46%, while DH has performed a recall and precision rate of 29%.
In Figure 5 we have also performed another comparative experiment between DH and QDH by randomly selecting 100 different images from MPEG-7 database and computed precision and recall answer after answer for the first 10 retrievals in order to obtain the average recall and average precision. Results indicate, for the first 2 retrieved answers, both DH and QDH have accurately retrieved correct answers with precision rate of 100% and 80%. For the rest 8 answers QDH has performed better precision rate which means more similar images retrieved. This is contributed to the fact that, QDH not only consider the statistical information about the shape of object, it also has the ability to reflect the relationship between centroidal distances by superpositioing their states in 4- qubits system which led to more precise representation, hence more accurate retrieval.
In Figure 6 and Figure 7, we show the top 10 retrievals for six sample images obtained by the proposed QDH and DH respectively. The first image in the answer set is the query image itself, since the computed distance between their feature vectors is exactly zero. The rest 9 images are the most similar ones. Crystal clear, QDH representation achieves better retrievals when compared with those retrieved by DH. Thanks to quantum superposition, more shape details are retained and confined into one dimensional vector during feature extraction, therefore, more precise representation and consequently better retrieval results.
Figure 3. Precision vs. Recall for the first 10 retrieved images.
Figure 4. Precision vs. Recall for the first 20 retrieved images.
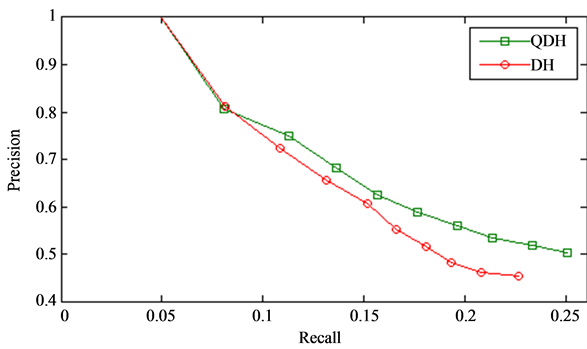
Figure 5. Average Precision and Recall for first 10 retrievals.
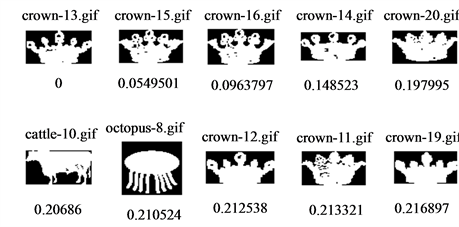
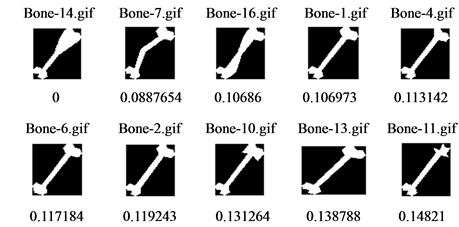
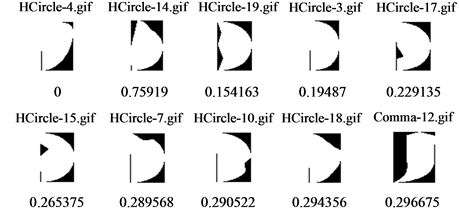
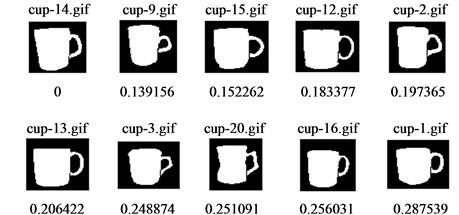


Figure 6. Sample retrievals by proposed method (QDH).

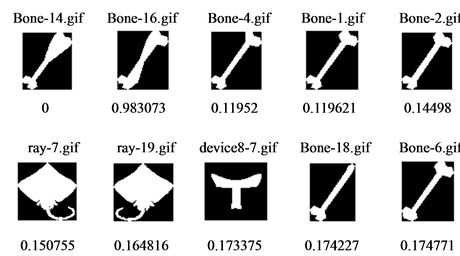



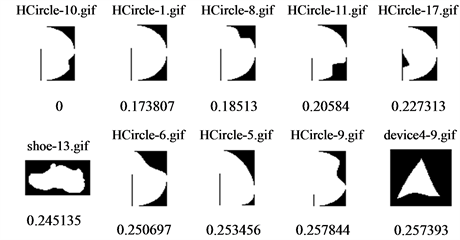
Figure 7. Sample retrievals by distance histogram (DH).
6. Conclusions and Future Work
In this paper, quantum inspired shape-based image retrieval is proposed on the basis of distance histogram and the concept of quantum superposition. The proposed algorithm was able to correlate the centroidal distances information of pixels on the contour with its neighboring pixels, thus compensating spatial information consideration lackness in distance histogram when describing shape. Experimental results demonstrate that the proposed approach has better precision and recall compared with distance histogram For future work, we suggest conducting an experiment by tuning the number of points in building the i-qubits system during feature extraction. For example, a system of 6-qubits is constructed for each pixel along shape boundary by transforming the centroidal distances of its three consecutive post and previous neighbor pixels into 6-qubits system which has 64 states. Hence, each pixel is represented by 6-qubits in order to reveal more details about the correlative relationship for this pixel with its neighbor ones, therefore, finer representation. At the first stage of retrieval, a coarse retrieval using 4-qubits QDH is employed to filter images from database to reduce the search space and then perform retrieval based on 6-qubits system.
References
- Rui, Y., Huang, T.S. and Chang, S.F. (1997) Image Retrieval: Past, Present and Future. In: Liao, M., Ed., Proceedings of the International Symposiumon Multimedia Information Processing, Taipei, 11-13 December 1997.
- del Bimbo, A. (1999) Visual Information Retrieval. Academic Press, London.
- Smeulders, A.W.M., Worring, M., Santini, S., Gupta, A. and Jain, R. (2000) Content-Based Image Retrieval at the End of the Early Years. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22, 1349-1380.
- Kuo, W.-J., Chang, R.-F., Lee, C.C., Moon, W.K. and Chen, D.-R. (2002) Retrieval Technique for the Diagnosis of Solid Breast Tumors on Sonogram. Ultrasound in Medicine and Biology, 28, 903-909. http://dx.doi.org/10.1016/S0301-5629(02)00541-0.
- Antani, S., Long, L.R. and Thoma, G.R. (2004) Content-Based Image Retrieval for Large Biomedical Image Archives. In: Proceedings of 11th World Cong Medical Informatics, San Francisco, 7-11 September 2004, 829-833.
- Rauber, T.W. (1994) Two-Dimensional Shape Description. Technical Report: GRUNINOVA-RT-10-94, Universidade Nova de Lisboa, Lisoba, Portugal.
- Loncaric, S. (1998) A Survey of Shape Analysis Techniques. Pattern Recognition, 31, 983-1001. http://dx.doi.org/10.1016/S0031-2023(97)00122-2
- Zhang, D. and Lu, G. (2004) Review of Shape Representation and Description Techniques. Pattern Recognition, 37, 1- 19. http://dx.doi.org/10.1016/j.patcog.2003.07.008.
- Safar, M., Shahabi, C. and Sun, X. (2000) Image Retrieval by Shape: A Comparative Study. In: Proceedings of IEEE International Conference on Multimedia and Expo, New York, 30 July-2 August 2000, 141-144.
- Zhang, G., Ma, Z.M., Tong, Q., He, Y. and Zhao, T.N. (2008) Shape Feature Extraction Using Fourier Descriptors with Brightness in Content-Based Medical Image Retrieval. International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Harbin, 15-17 August 2008, 71-74. http://dx.doi.org/10.1109/IIH-MSP.2008.16
- Wu, Y.Y. and Wu, Y.Q. (2009) Shape-Based Image Retrieval Using Combining Global and Local Shape Features. CISP 2nd International Congress on Image and Signal Processing, Tianjin, 17-19 October 2009, 1-5.
- Sleit, A., Salah, I. and Jabay, R. (2008) Approximating Images Using Minimum Bounding Rectangles. In: The First International Conference on the Applications of Digital Information and Web Technologies (ICADIWT 2008), Ostrava, 4-6 August 2008, 394-396.
- Sleit, A., Abu-Areda, A. and Al-Hasan, H. (2010) Shape Approximation Using Circular Grids. WSEAS Transactions on Information Science and Applications, 7, 542-551.
- Zhang, W., Dickinson, S., Sclaroff, S., Feldman, J. and Dunn, S. (1998) Shape-Based Indexing in a Medical Image Database. IEEE Workshop on Biomedical Image Analysis, Santa Barbara, 26-27 June 1998, 221-230.
- Sajjanhar, A. and Lu, G. (1997) A Grid Based Shape Indexing and Retrieval Method. The Australian Computer Journal, 29, 131-140.
- Sajjanhar, A. (2003) Spatial Information in Histograms for Shape Representation. In: Intelligent Data Engineering and Automated Learning. Lecture Notes in Computer Science, Vol. 2690, Springer, Berlin, 855-859. http://dx.doi.org/10.1007/978-3-540-45080-1_118
- Sajjanhar, A., Lu, G. and Zhang, D.S. (2004) Coherence Based Histograms for Shape Retrieval. Proceedings of International Conference on Computer Science, Software Engineering Information Technology, E-Business and Applications (CSITeA04), Cairo, 27-29 December 2004, 27-29.
- Fan, S. (2001) Shape Representation and Retrieval Using Distance Histograms. Technical Report, University of Alberta, Alberta.
- Super, B.J. (2004) Fast Correspondence-Based System for Shape Retrieval. Pattern Recognition Letters, 25, 217-225. http://dx.doi.org/10.1016/j.patrec.2003.10.003
- Lo, H.K., Popescu, S. and Spiller, T. (1998) Introduction in Quantum Information and Computation. World Scientific, Singapore.
- Brooks, M. (1999) Quantum Computing and Communication. Springer Verlag, London. http://dx.doi.org/10.1007/978-1-4471-0839-9
- Eldar, Y.C. and Oppenheim, A.V. (2002) Quantum Signal Processing. IEEE Signal Processing Magazine, 19, 12-32. http://dx.doi.org/10.1109/MSP.2002.1043298
- Tseng, C.C. and Hwang, T.M. (2003) Quantum Digital Image Processing Algorithms. 16th IPPR Conference on Computer Vision, Graphics and Image Processing, Kinmen, 17-19 August 2003, 827-834.
- Nӧell, M., Ӧmer, B. and Suda, M. (2007) Quantum Information Algorithms—New Solutions for Known Problems. e & i Elektrotechnik und Informationstechnik, 124, 154-157. http://dx.doi.org/10.1007/s00502-007-0434-7
- Veltkamp, R.C. and Hagedoorn, M. (2000) State of the Art in Shape Matching. In: Lew, M.S., Ed., Principles of Visual Information Retrieval, Springer-Verlag, London, 87-119.

