Journal of Signal and Information Processing
Vol.3 No.4(2012), Article ID:24960,8 pages DOI:10.4236/jsip.2012.34058
Union Resolution Performance of Frequency Modulation Parameter Based on RWT for LFM Signals
![]()
1National Major Laboratory of Complex Electromagnetic Environmental Effects for Electronic Information System, Luoyang, China; 2School of Electronic Science and Engineering, National University of Defense Technology, Changsha, China.
Email: leewench@yahoo.com.cn
Received July 22nd, 2012; revised August 24th, 2012; accepted September 7th, 2012
Keywords: Multi-Component LFM Signals; Radon-Wigner Transform (RWT); Resolution Ellipse; Union Resolution of FM Parameter; Half-Power Lobe Width
ABSTRACT
Union resolution performance of FM (frequency modulation) parameter based on Radon-Wigner transform (RWT) for multi-component LFM (linear frequency modulation) signals is studied. Firstly, the RWT output expression is offered, and the independent resolution performances of initial frequency and chirp rate are analyzed. Secondly, the RWT output approximate analytic expression is given based on quadratic Taylor’s series expansion, and the contour property is analyzed. Contour can be used to picture the union resolution performance of FM parameter, and 2-D resolution performance is studied based on approximate analytic expression, and the union resolution expression of FM parameter and resolution ellipse are offered. The simulation results validate the union resolution expression, and show that the union resolution can improve the resolution performance of multi-component LFM signals, contrasted with absolute resolution performance. The paper can help the study of LFM parameter estimation and resolution performance.
1. Introduction
The LFM signal is widely applied in domains such as radar, correspondence and sound navigation. LFM signal’s parameter estimation is an important research subject in the electronic intelligence system, target motive parameter estimation and ISAR image. There are many literatures about LFM signal parameter estimation method, such as estimation performance, the operating speed and the application, for example ML (Maximum Likelihood) method [1], polynomial phase transform (PPT) [2,3], Radon-Wigner transform (RWT) or the Wigner-Hough transform (WHT) [4-6], Radon-Ambiguity transform (RAT) [7,8], Fractional Fourier transform (FrFT) [9]. RWT or WHT are the commonly used LFM signal parameter estimation methods. RWT method searches the straight line in the Wigner-Ville time-frequency distribution plane. The cross term can be suppressed effectively through the line integral in RWT, which is used to estimate the initial frequency and chirp rate of LFM signals, ulteriorly, the amplitude and phase information can be estimated.
The research of RWT resolution for LFM signal is the foundation for multi-component signal separation. And there are quite a few literatures about the RWT resolution. Simulation results in literature [8] show that the RAT chirp rate resolution is  and
and 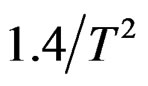 for the square-law and enveloping ambiguity respectively. Literature [10] defines the nominal resolution with the main lobe of 3 dB width (half-power width), Literature [11] indicates the range-velocity union resolution with the ambiguity diagram’s 3/4 interception area. In summary, the resolution definition is disparate in different literatures, and the nominal resolution can reflect the resolution performance on a certain extent, but not accurately.
for the square-law and enveloping ambiguity respectively. Literature [10] defines the nominal resolution with the main lobe of 3 dB width (half-power width), Literature [11] indicates the range-velocity union resolution with the ambiguity diagram’s 3/4 interception area. In summary, the resolution definition is disparate in different literatures, and the nominal resolution can reflect the resolution performance on a certain extent, but not accurately.
The unite resolution of RWT FM parameter (initial frequency and chirp rate) for the multi-component signal is related with SNR (signal to noise ratio), signal form and processing method. Generally the system resolution performance is analyzed under the condition of great SNR and best signal processing, therefore this article analyzes the RWT resolution performance for signal with great SNR. Firstly, the RWT output expression is given, and the independent resolutions of initial frequency and chirp rate are analyzed. Secondly, the RWT output approximate analytic expression is given by Taylor series expansion. The contour line nature is analyzed and the contour line deviation caused by approximation in Taylor expansion is revised. The contour line and two-dimensional resolution have been studied based on the analytic expression. The mathematical expression of FM parameter union resolution and the resolution ellipse area are obtained. Finally, the simulation results indicate that the union resolution of FM parameter is higher than independent resolution.
2. RWT FM Parameter Estimation
2.1. LFM Signal Model
Single LFM signal model is expressed by:
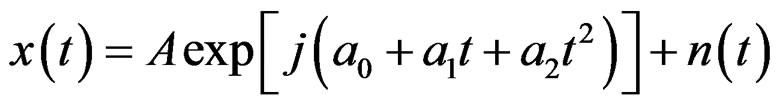 (1)
(1)
where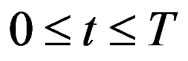 ,
, are the signal scope, the phase, the initial angular frequency (or initial frequency) and the angle FM rate (or chirp rate) respectively.
are the signal scope, the phase, the initial angular frequency (or initial frequency) and the angle FM rate (or chirp rate) respectively. 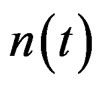 is gauss white noise, whose mean is zero and variance is
is gauss white noise, whose mean is zero and variance is .
.
2.2. RWT of LFM Signal
The essence of Radon transformation is to transform the straight line to the point in plane through the rotation axis projection integral, and a point coordinate corresponds the straight line slope and the slant range, then the detection and estimation are carried in this parameter spatial domain. RWT method transform the LFM signal from the time domain to the parameter spatial domain including the initial frequency and the FM rate.
The Wigner-Ville distribution [5] of 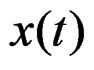 is
is
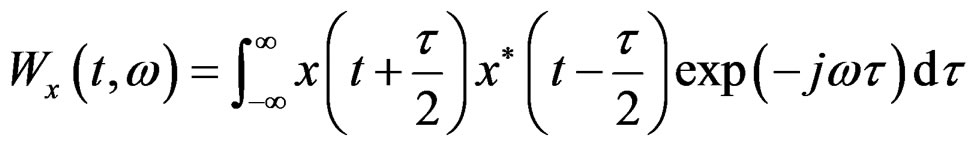 (2)
(2)
LFM signal chirp rate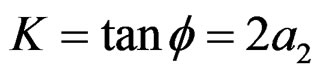 ,
,  axis intercept
axis intercept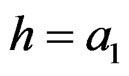 , viz. initial frequency of
, viz. initial frequency of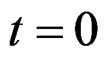 .
.
According to the Wigner-Ville distribution characteristic of LFM signal, Radon straight line integral transformation is expressed by the straight line slope  and the axis intercept
and the axis intercept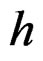 , the integral is done along the line
, the integral is done along the line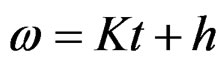 . Then the signal is transformed from time domain to the parameter spatial domain composed by initial frequency h and chirp rate K. The scheme of Radon transformation is shown in Figure 1. The RWT formula is expressed by:
. Then the signal is transformed from time domain to the parameter spatial domain composed by initial frequency h and chirp rate K. The scheme of Radon transformation is shown in Figure 1. The RWT formula is expressed by:
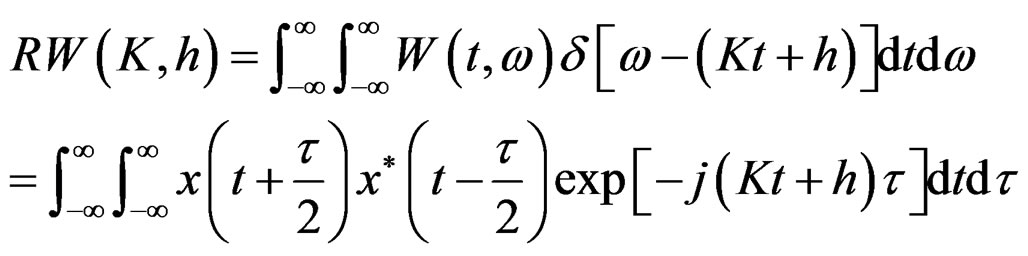 (3)
(3)
Using the integration variable replacement [12], the formula can be transformed into:
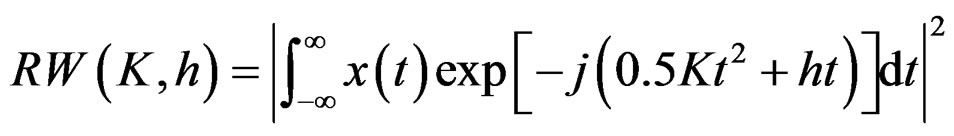 (4)
(4)
Namely the two-dimensional integral of RWT modeling can be transformed to the power spectrum estimation
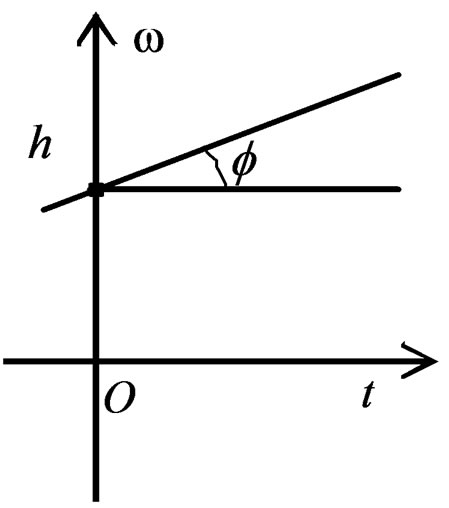
Figure 1. Scheme of radon transform.
of the time domain dechirp signal [13]. And the best estimation of  may be determined by the maximum value position of
may be determined by the maximum value position of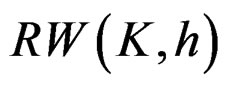 , and obtain the estimation value
, and obtain the estimation value  of
of  by the
by the  parameter estimation.
parameter estimation.
3. RWT Resolution of Initial Frequency and Chirp Rate
From formula (4), the RWT output of the noise-free LFM signal model  is expressed by:
is expressed by:
 (5)
(5)
where
 (6)
(6)
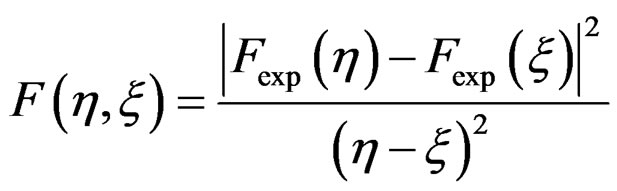 (7)
(7)
 (8)
(8)
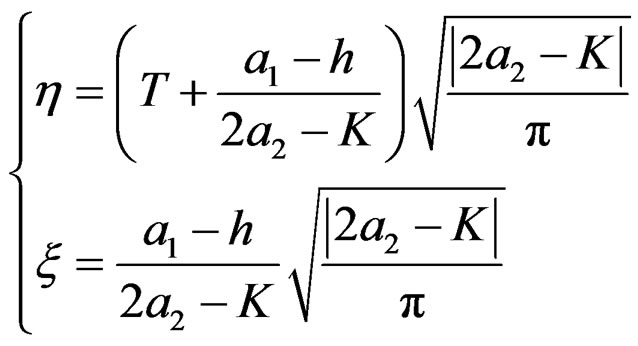 (9)
(9)
where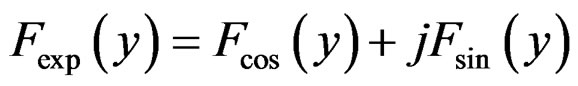 ,
,  is Fresnel cosine integral and
is Fresnel cosine integral and  is Fresnel sine integral [12].
is Fresnel sine integral [12]. 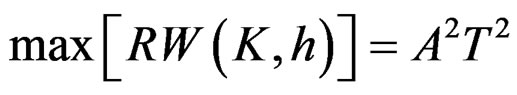 when
when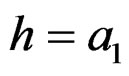 ,
,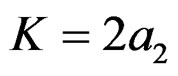 . The half-power lobe width of the RWT output function, that is
. The half-power lobe width of the RWT output function, that is , is shown in Figure 2.
, is shown in Figure 2.
• When 
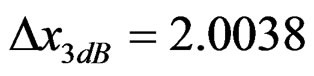 is obtained via interpolation method from
is obtained via interpolation method from 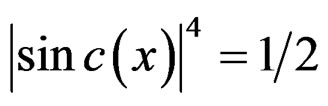 in Figure 2(a). The half-power lobe width of
in Figure 2(a). The half-power lobe width of  is:
is:
 (10)
(10)
• When 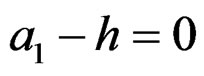
Using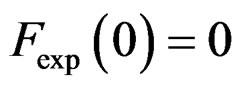 , obtains:
, obtains:
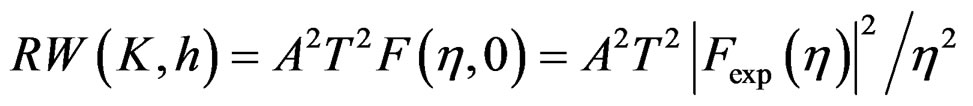 (11)
(11)
where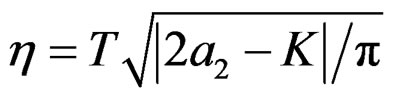 .
.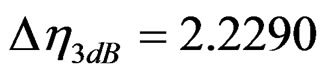 is obtained via interpolation method from
is obtained via interpolation method from 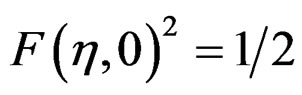 in Figure 2(b). The half-power lobe width of
in Figure 2(b). The half-power lobe width of 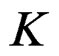 is:
is:
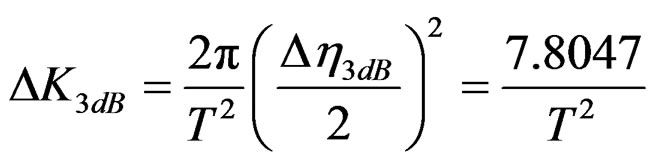 (12)
(12)
4. Taylor Formula and Character of the RWT Function
4.1. Taylor Formula of the RWT Function
The RWT function’s main lobe reflects the RWT union resolution of initial frequency and chirp rate. In order to
 (a)
(a)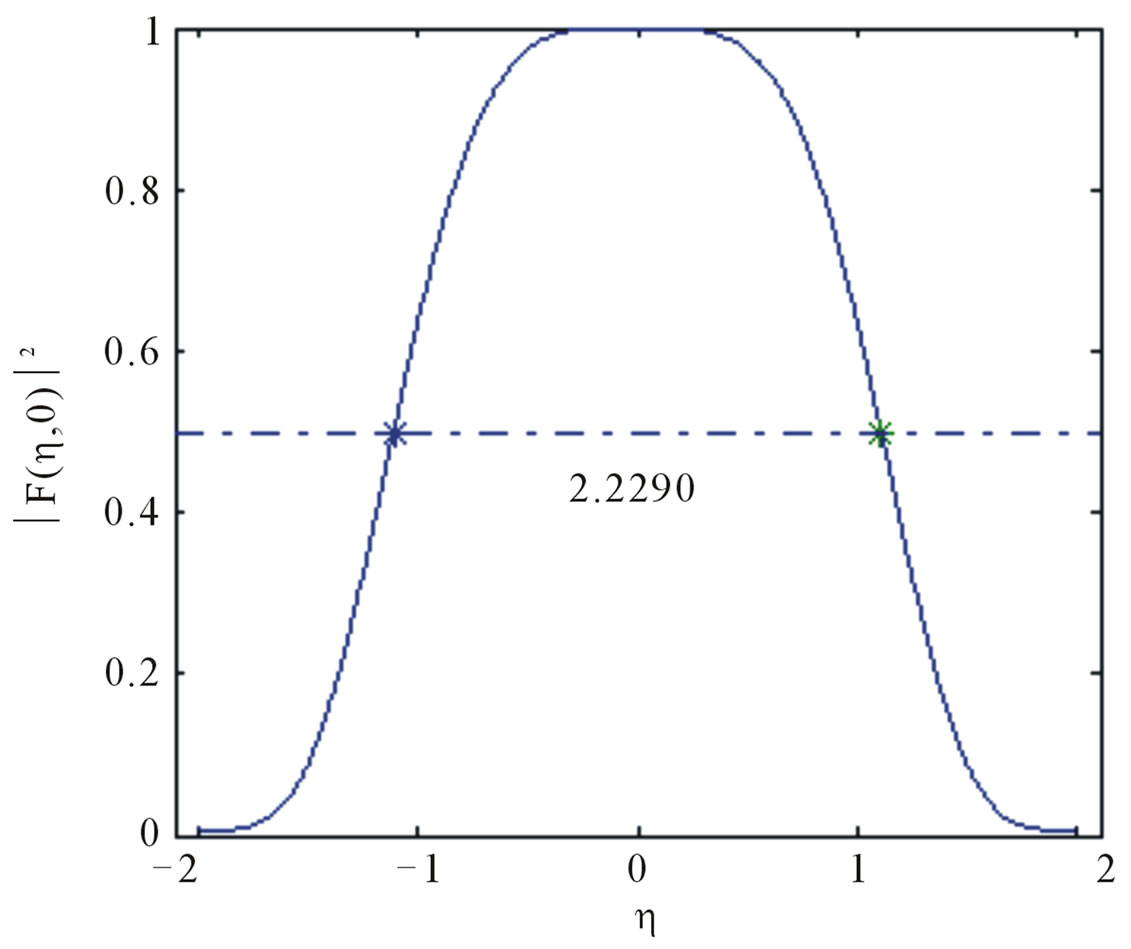 (b)
(b)
Figure 2. Tangential plane of RWT function. (a)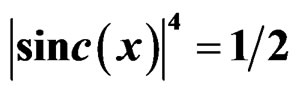 ; (b)
; (b)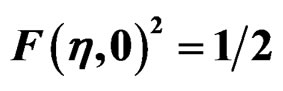 .
.
obtain the main lobe analytic expression in the different high, the RWT function is indicated with the quadratic Taylor series expansion on the point with maximum value, which is 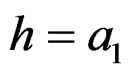 and
and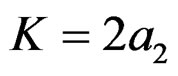 . The Taylor expansion of
. The Taylor expansion of  is quite complex, so this article directly calculates the quadratic Taylor series of RWT output on the maximum value using the expression of
is quite complex, so this article directly calculates the quadratic Taylor series of RWT output on the maximum value using the expression of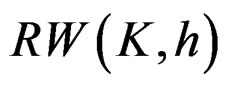 . The quadratic Taylor formula is expressed by [12]:
. The quadratic Taylor formula is expressed by [12]:
 (13)
(13)
From formula (4), when the noise-free input signal model is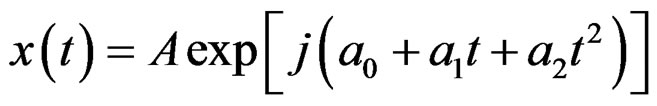 ,
, 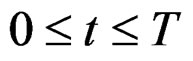 , the RWT function is:
, the RWT function is:
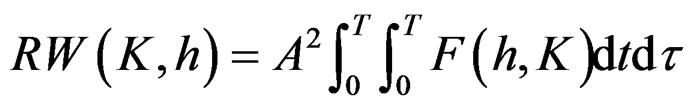 (14)
(14)
where
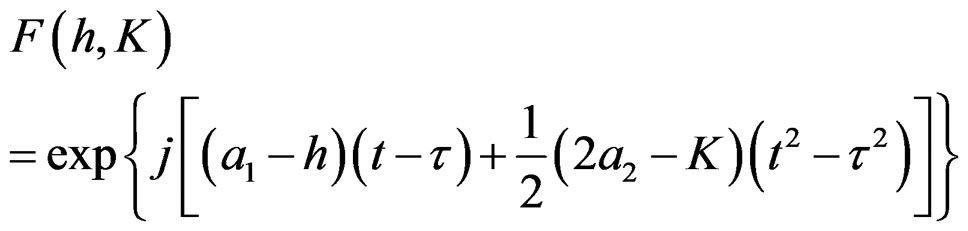 (15)
(15)
Via ,
,
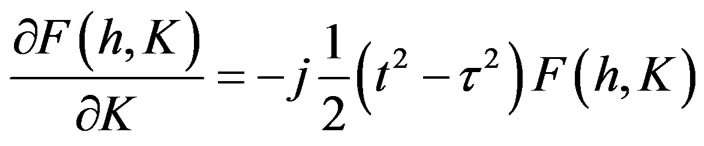 ,
,
 ,
,
 ,
,
 ,
,
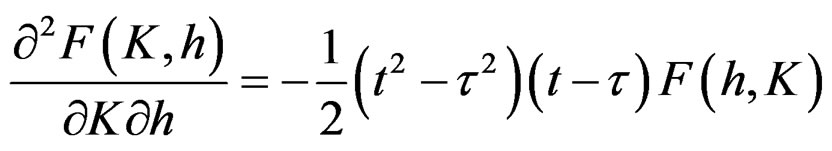 obtains these item in formula (13) as follows:
obtains these item in formula (13) as follows:
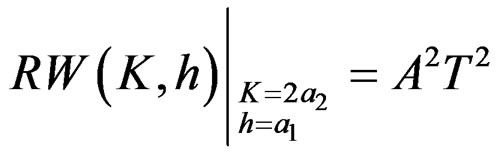 (16)
(16)
 (17)
(17)
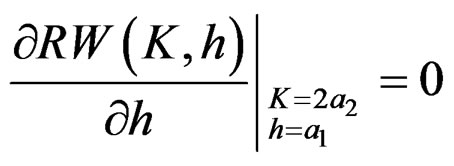 (18)
(18)
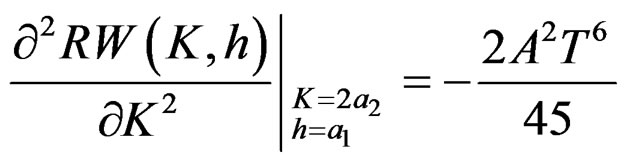 (19)
(19)
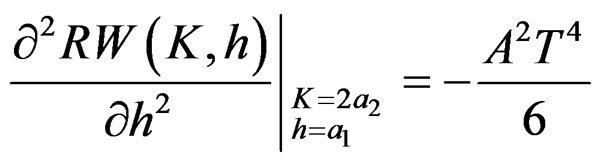 (20)
(20)
 (21)
(21)
Taylor formula (13) is transformed into:
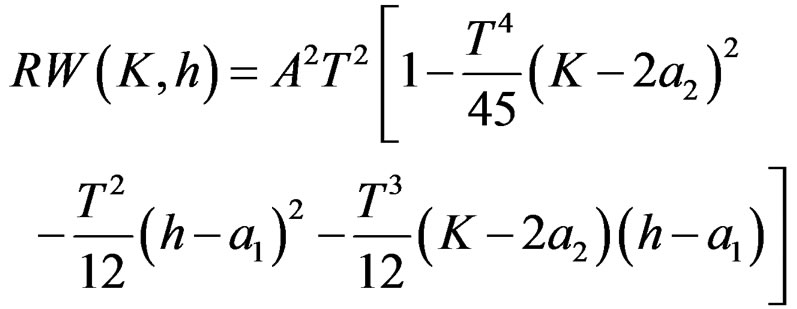 (22)
(22)
Obviously the RWT output is nonstandard quadratic surface, which can be proved to be nonstandard ellipse paraboloid.
4.2. The Contour Line Parameter Analysis of the Quadratic Taylor Formula
The RWT output is two-dimensional function of initial frequency and chirp rate, and the greatest value is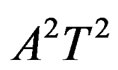 . The lobe characteristic of the RWT output function is reflected by the contour line along
. The lobe characteristic of the RWT output function is reflected by the contour line along  and the cutting coefficient of contour line is
and the cutting coefficient of contour line is . The output result is not the standard analytic expression, therefore the RWT cutting contour line is indicated by the quadratic Taylor formula, as follows:
. The output result is not the standard analytic expression, therefore the RWT cutting contour line is indicated by the quadratic Taylor formula, as follows:
 (23)
(23)
Substitutes the quadratic Taylor formula, obtains:
 (24)
(24)
where
 (25)
(25)
Using  as the center, and prescribing counterclockwise is positive, the coordinate system
as the center, and prescribing counterclockwise is positive, the coordinate system
 is counter-clockwise rotated with angle
is counter-clockwise rotated with angle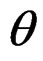 , and the coordinate system
, and the coordinate system  is obtained, shown in Figure 3.
is obtained, shown in Figure 3.
 (26)
(26)
 (27)
(27)
In the coordinate system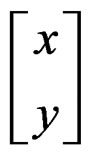 , Equation (24) transforms into:
, Equation (24) transforms into:
 (28)
(28)
when the item of 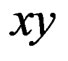 is zero, the equation is standard ellipse, and obtains
is zero, the equation is standard ellipse, and obtains
 (29)
(29)
And formula (28) is simplified to
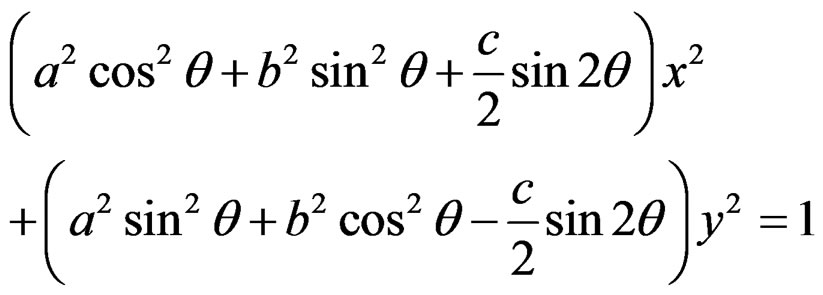 (30)
(30)
It can be proved that the equation coefficient is more than zero, that is
 (31)
(31)
Therefore, the equation is the elliptic equation, the RWT quadratic surface is nonstandard ellipse paraboloid.
4.3. Contrastive Analysis of Quadratic Taylor Formula and Actual Contour Line
In order to analyze conveniently, the performance of
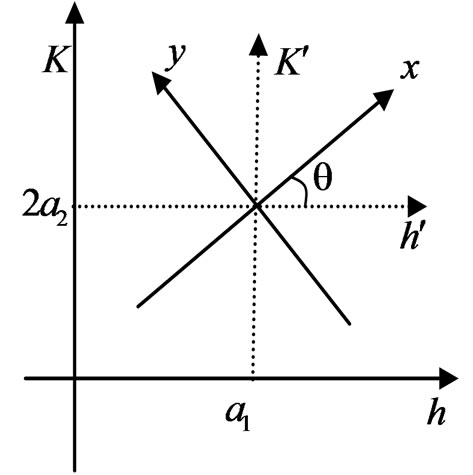
Figure 3. Coordinate system conversion.
RWT resolution is characterized by half-power lobe width in this article. The half-power lobe contour line, which is obtained by quadratic Taylor formula, is the RWT output amplitude . By
. By
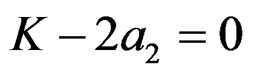 , the half-power lobe width of
, the half-power lobe width of 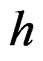 is:
is:
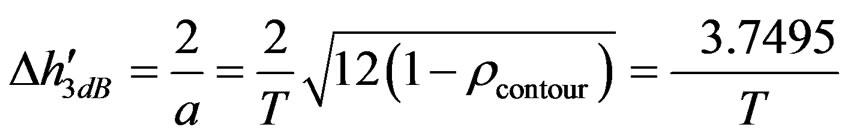 (32)
(32)
By , the half-power lobe width of
, the half-power lobe width of  is:
is:
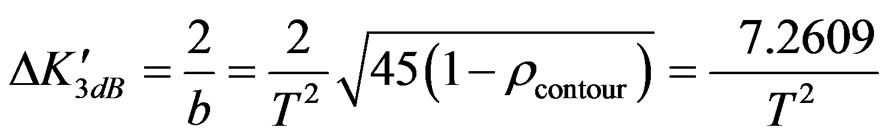 (33)
(33)
The result is close with the half-power lobe width 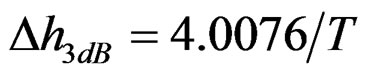 and
and , which is obtained directly by curve simulation and interpolation. There are two main error sources: The one is abbreviate of higher item, the other is cutting departure from the spot with maximum value. The half-power lobe width of the actual RWT output can be approached by adjustment the parameter
, which is obtained directly by curve simulation and interpolation. There are two main error sources: The one is abbreviate of higher item, the other is cutting departure from the spot with maximum value. The half-power lobe width of the actual RWT output can be approached by adjustment the parameter , and the best revision interception coefficient
, and the best revision interception coefficient  is:
is:
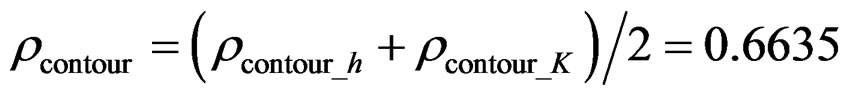 (34)
(34)
where 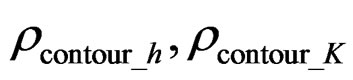 are obtained separately by the half-power lobe width of h, K, the expression is expressed as follows:
are obtained separately by the half-power lobe width of h, K, the expression is expressed as follows:
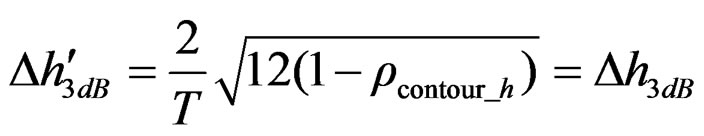 (35)
(35)
 (36)
(36)
Namely, when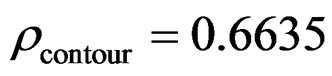 , the lobe width using the quadratic Taylor formula is able to approach the actual RWT output half-power lobe width, which is proved by the simulation result.
, the lobe width using the quadratic Taylor formula is able to approach the actual RWT output half-power lobe width, which is proved by the simulation result.
5. RWT Union Resolution of Initial Frequency and Chirp Rate
The signal resolution is analyzed usually by two signals with equi-signal length, amplitude and initial time. The multi-component signal amplitude is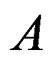 , the length is
, the length is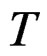 , namely
, namely 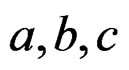 are the constants, the signal position is
are the constants, the signal position is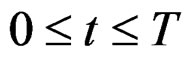 , the
, the 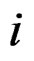 th component signal’s initial frequency is
th component signal’s initial frequency is  and chirp rate respectively is
and chirp rate respectively is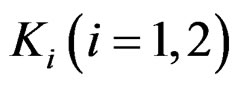 , its half-power cutting contour line is:
, its half-power cutting contour line is:
 (37)
(37)
This formula can be reduced to:
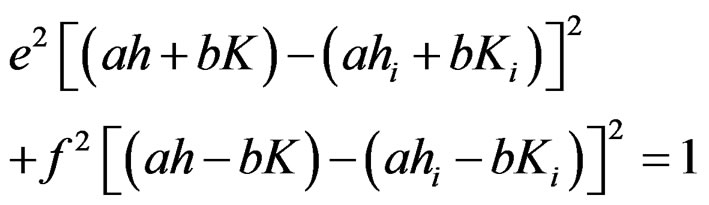 (38)
(38)
where
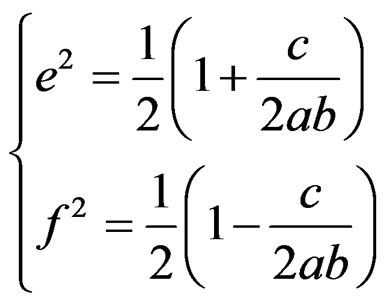 (39)
(39)
Defines
 (40)
(40)
Obtains
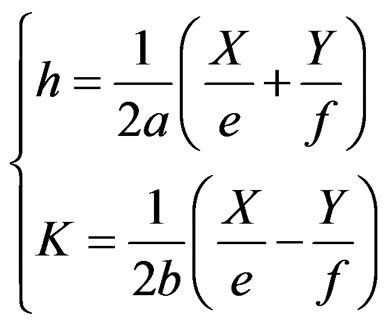 (41)
(41)
Therefore 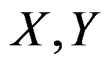 and
and 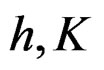 both have corresponding relationships, formula (37) in coordinate system
both have corresponding relationships, formula (37) in coordinate system 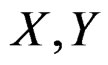 is circle equation.
is circle equation.
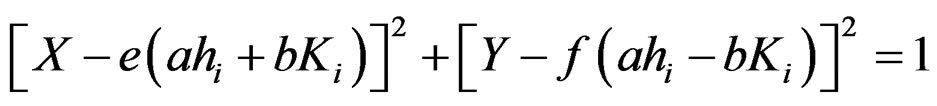 (42)
(42)
where, the circle point of the  th component signal in coordinate system
th component signal in coordinate system 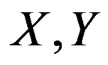 is
is ,
, 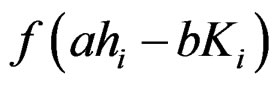 , and the circle track data can be generated by the circle equation, from which, we can get the corresponding contour line data
, and the circle track data can be generated by the circle equation, from which, we can get the corresponding contour line data  after the coordinate system conversion.
after the coordinate system conversion.
The two component signal’s FM parameters are ,
, 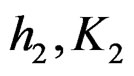 respectively. According to the nominal resolution, two signals can not be distinguished if half-power contour lines have the intersection point in the coordinate system
respectively. According to the nominal resolution, two signals can not be distinguished if half-power contour lines have the intersection point in the coordinate system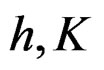 , otherwise two signals are distinguishable. In the coordinate system
, otherwise two signals are distinguishable. In the coordinate system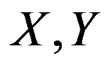 , the contour line is circle. So long as the central distances of two circles are more than 2, the two LFM signals can be distinguished. The condition is described by:
, the contour line is circle. So long as the central distances of two circles are more than 2, the two LFM signals can be distinguished. The condition is described by:
 (43)
(43)
Inputting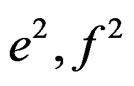 , the formula can be reduced to:
, the formula can be reduced to:
 (44)
(44)
Inputting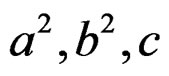 , the resolution expression based on parameter is
, the resolution expression based on parameter is
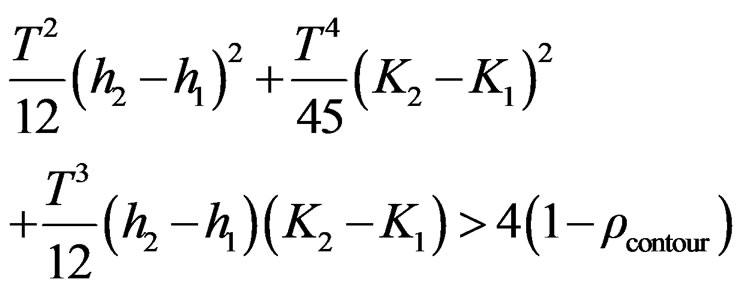 (45)
(45)
where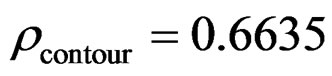 , and multi-component signal is able to be resolved, so long as the position of FM parameter
, and multi-component signal is able to be resolved, so long as the position of FM parameter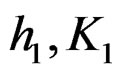 ,
,  satisfies the above equation. Obviously in order to achieve the high resolution of initial frequency and chirp rate, the time length must be increased.
satisfies the above equation. Obviously in order to achieve the high resolution of initial frequency and chirp rate, the time length must be increased.
The union resolution of initial frequency and chirp rate may be indicated by the interception ellipse area.
 (46)
(46)
Obviously the resolution ellipse’s area is in reverse proportion with , related with the interception coefficient
, related with the interception coefficient .
.
6. Simulation Results
6.1. The RWT Output of Single Component LFM Signal
The signal model is:
 (47)
(47)
The digital simulation result is given in Figure 4, where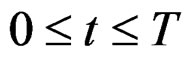 ,
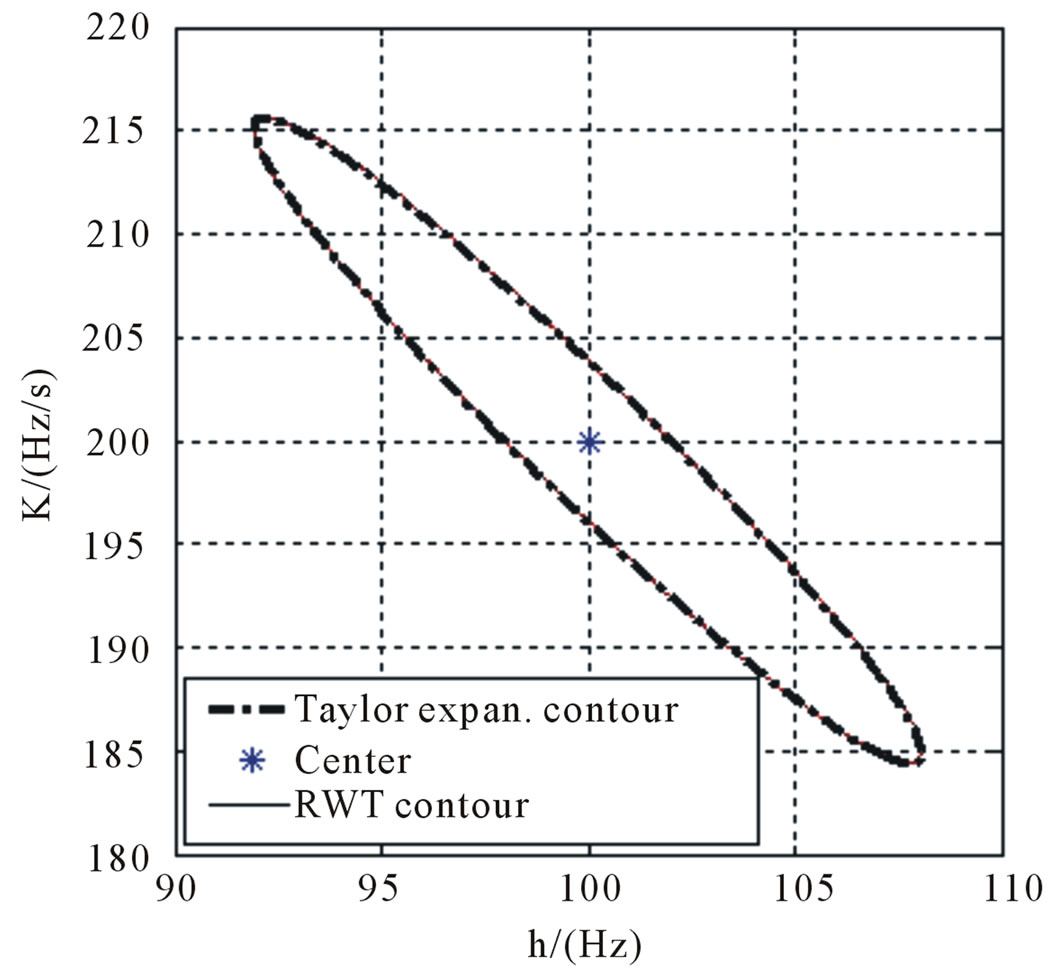
, 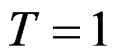 , namely a = 0.5334, b = 0.2754, c = 0.2845, and the FM parameter sampling interval is quite small in order to study the fine characteristic of RWT output. Figure 4(a) is the contrast of RWT half-power contour line and the Taylor’s expansion contour line in
, namely a = 0.5334, b = 0.2754, c = 0.2845, and the FM parameter sampling interval is quite small in order to study the fine characteristic of RWT output. Figure 4(a) is the contrast of RWT half-power contour line and the Taylor’s expansion contour line in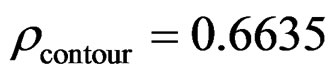 . Figure 4(b) is the contour line view. It is indicated that the contour line two-dimensional superposition is very good for the two methods, therefore the RWT output half-power contour line is described well by the contour line equation in
. Figure 4(b) is the contour line view. It is indicated that the contour line two-dimensional superposition is very good for the two methods, therefore the RWT output half-power contour line is described well by the contour line equation in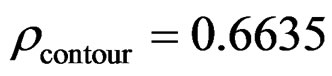 . The results indicate simultaneously that the FM parameter estimation error is very small for a single component noise-free LFM signal.
. The results indicate simultaneously that the FM parameter estimation error is very small for a single component noise-free LFM signal.
6.2. The RWT of Multi Component LFM Signal
The signal model is:
 (48)
(48)
The signal length is 1s, initial frequency independent resolution is , chirp rate independent resolution is
, chirp rate independent resolution is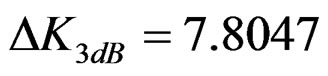 . The first component is:
. The first component is:
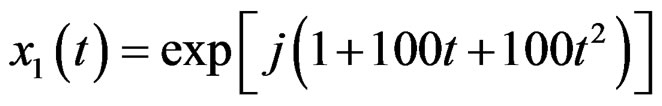 (49)
(49)
The second component is:
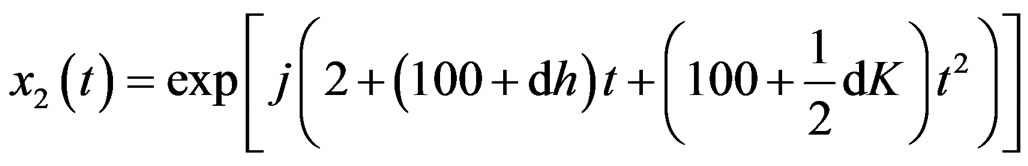 (50)
(50)
The RWT resolution performance of two component LFM signals is studied by changing the initial frequency and chirp rate of the second component separately in
 (a)
(a)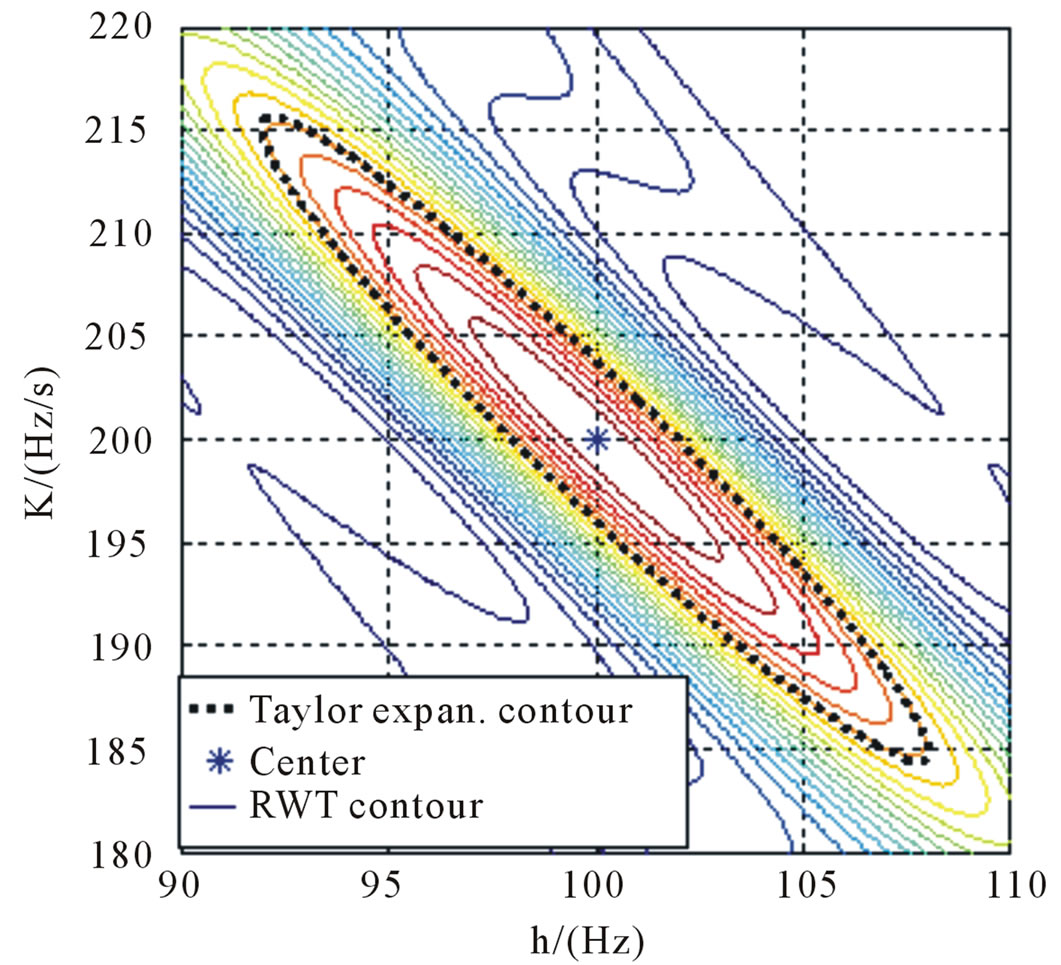 (b)
(b)
Figure 4. Contrast of Taylor formula and actual contour line of single component LFM signal. (a) Is the contrast of RWT half-power contour line and the Taylor’s expansion contour line in ; (b) Is the contour line view.
; (b) Is the contour line view.
what follows.
6.2.1. Independent Resolution of Initial Frequency and Chirp Rate
The simulation results of initial frequency and chirp rate independent resolution are shown in Figure 5, including contour map and projection view. Two LFM signals with same chirp rate and different initial frequency ( ,
, ) are shown in Figure 5(a). Two LFM signals with same initial frequency and different chirp rate (
) are shown in Figure 5(a). Two LFM signals with same initial frequency and different chirp rate (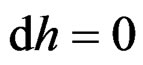 ,
, ) are shown in Figure 5(b). Obviously in the RWT output two-dimensional surface of initial frequency and chirp rate, the mutual
) are shown in Figure 5(b). Obviously in the RWT output two-dimensional surface of initial frequency and chirp rate, the mutual
 (a)
(a)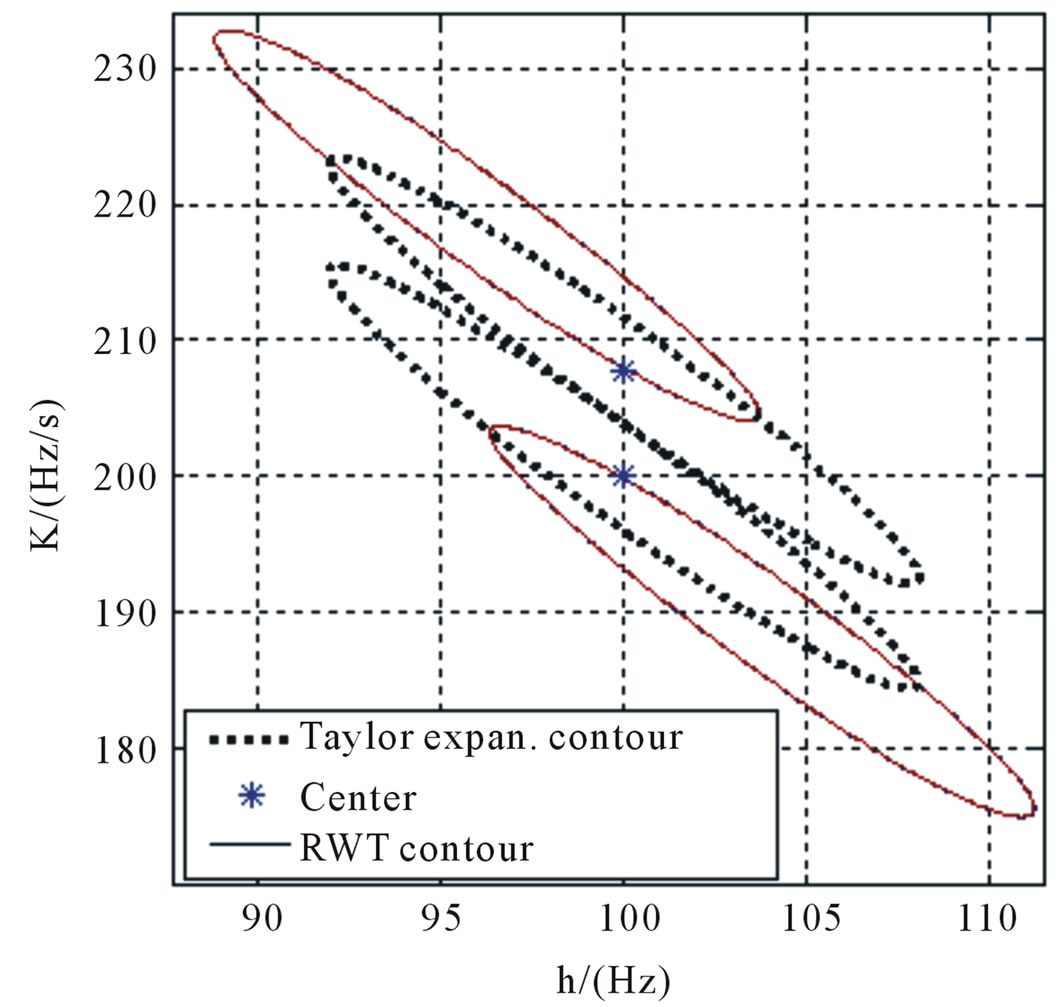 (b)
(b)
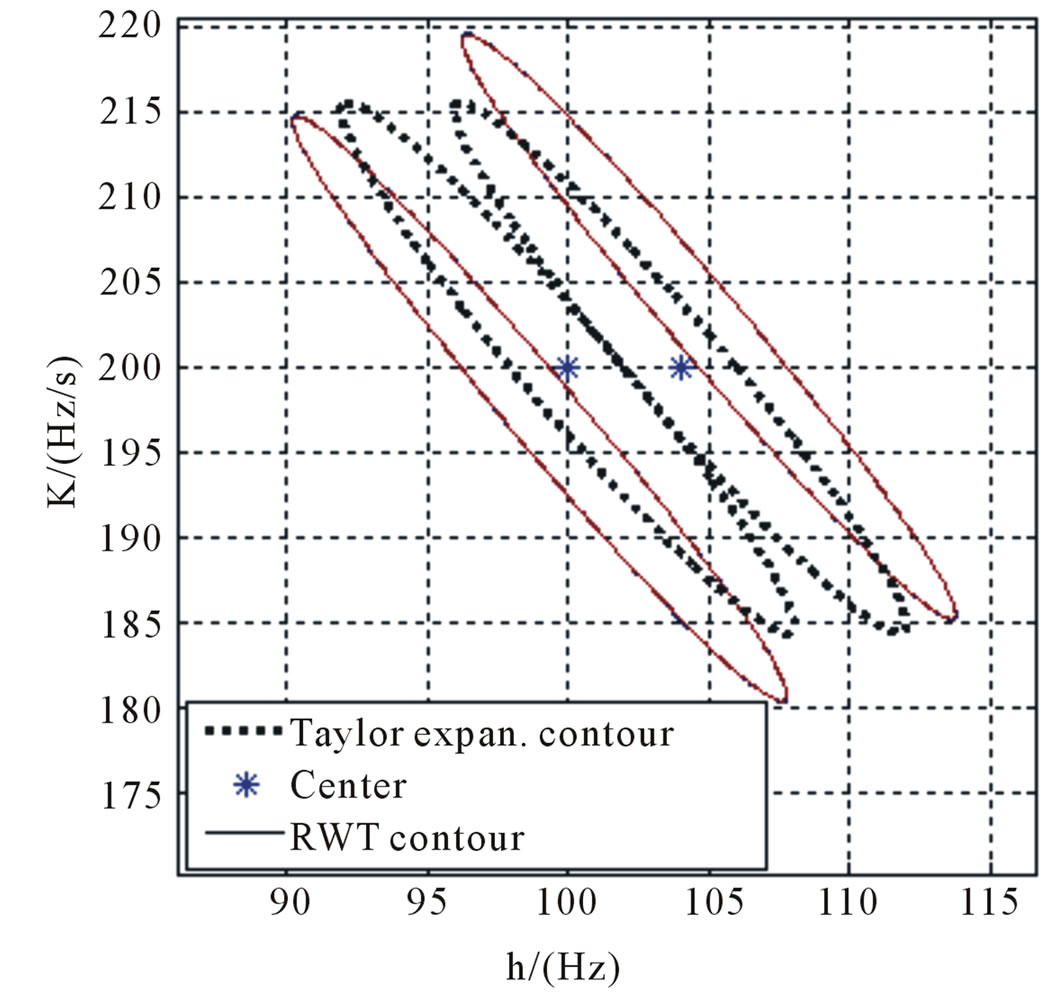
Figure 5. Contrast of Taylor formula and actual contour line of multi component LFM signal. The second component in formula (50) is (a) dh = ∆h3dB, dK = 0; (b) dh = 0, dK = ∆K3dB.
coupling of the very near two LFM signals cause the RWT output peak position to be away from the primary position, which incurs FM parameter estimation deviation. Simultaneously the further simulation results indicate that the different phase item 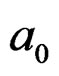 in the two LFM signals causes the different peak position errors, and the starting phase items of the two LFM signals affect the parameter estimation errors, but the LFM signals are distinguishable if the distinguishing condition is satisfied. Therefore the nominal resolution reflects the resolution performance to a certain extent. For single component LFM signal or multi-component LFM signal with the great FM parameter space interval in RWT, the RWT
in the two LFM signals causes the different peak position errors, and the starting phase items of the two LFM signals affect the parameter estimation errors, but the LFM signals are distinguishable if the distinguishing condition is satisfied. Therefore the nominal resolution reflects the resolution performance to a certain extent. For single component LFM signal or multi-component LFM signal with the great FM parameter space interval in RWT, the RWT
 (a)
(a) (b)
(b)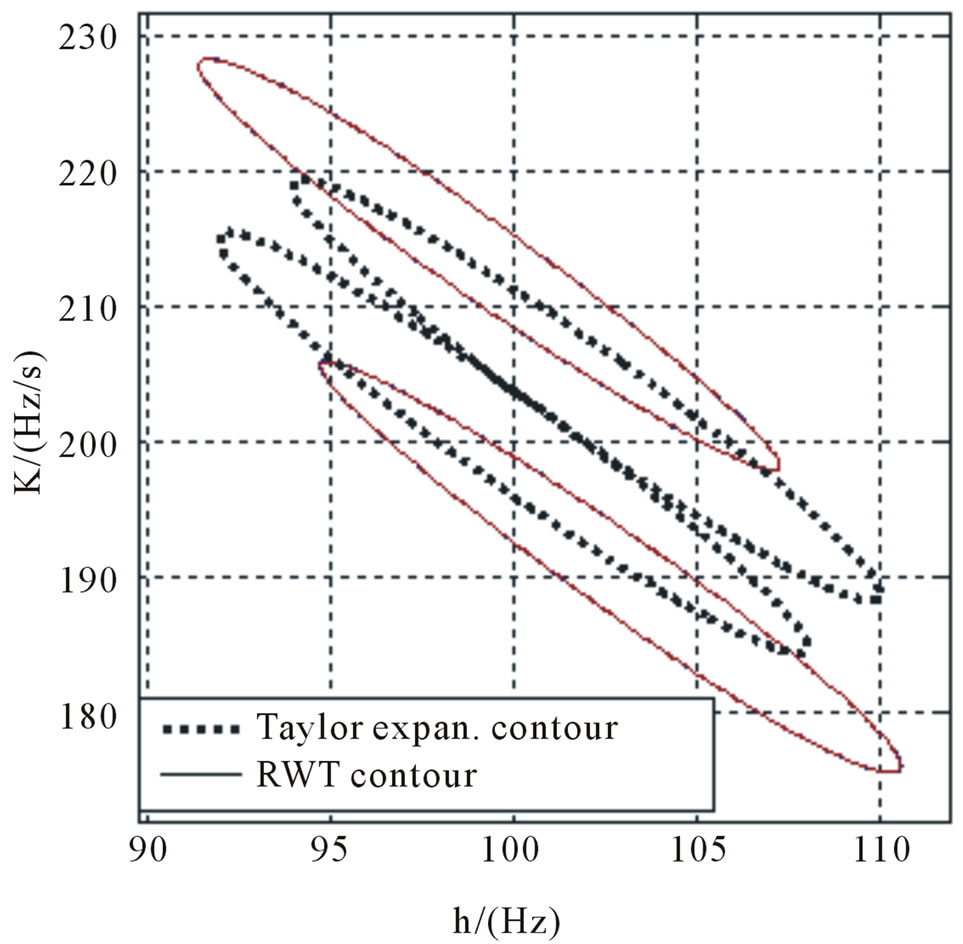 (c)
(c)
Figure 6. Union resolution of initial frequency and chirp rate of multi component LFM signal. The second component in formula (50) is (a) dh = ∆h3dB/2, dK = 0; (b) dh = 0, dK = ∆K3dB/2; (c) dh = ∆h3dB/2, dK = ∆K3dB/2.
parameter estimation error is related with SNR input. On the other hand, for the distinguishable multi-component LFM signal with the close FM parameter space interval, FM parameter estimation error is related with both SNR and other component signal’s parameter.
6.2.2. Union Resolution of Initial Frequency and Chirp Rate
Union resolution of multi-component LFM signal is studied and simulation results are shown in Figure 6, including contour map and projection view. (a) The second component ,
, 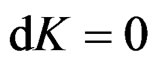 , and the signals cannot be distinguished by RWT method; (b) The second component
, and the signals cannot be distinguished by RWT method; (b) The second component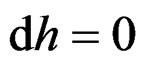 ,
, 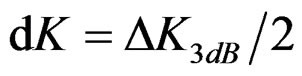 , and the signals cannot be distinguished by RWT method; (c) The second components with the initial frequency and chirp rate are all half of independent resolution, namely
, and the signals cannot be distinguished by RWT method; (c) The second components with the initial frequency and chirp rate are all half of independent resolution, namely 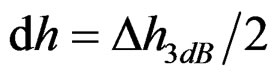 and
and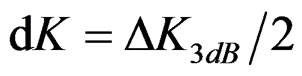 . It is obviously the two LFM signals are distinguishable by RWT method. The simulation results confirm the superiority of the FM parameter union resolution.
. It is obviously the two LFM signals are distinguishable by RWT method. The simulation results confirm the superiority of the FM parameter union resolution.
As to two multi-component signals with close FM parameter space, the estimation error is big when the amplitudes are similar, and the optimum parameter estimation of various components can be obtained by Relax iteration method [14]. On the other hand, if the intensity difference of two signals is distinct, the strong signal suppresses the weak signal, therefore the CLEAN technology must be used to extract the signals [15].
7. Conclusion
Union resolution performance of FM parameter based on RWT for multi-component LFM signals is studied in this paper. Firstly, the RWT output expression is given, and the independent resolutions of initial frequency and chirp rate are analyzed. Secondly, the RWT output approximate analytic expression is given by Taylor series expansion. The contour line property is analyzed and the contour line is deviation, which caused by approximation in Taylor expansion, is revised. Contour can be used to picture the union resolution performance of FM parameter of RWT, and 2-D resolution performance is studied based on approximate analytic expression. The union resolution expression of FM parameter and resolution ellipse area is offered. Finally the simulation results indicate that the union resolution of FM parameter is higher than independent resolution. The research in this paper can help the study of LFM parameter estimation and resolution performance.
REFERENCES
- T. J. Abatzoglou, “Fast Maximum Likelihood Joint Estimation of Frequency and Frequency Rate,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 22, No. 6, 1986, pp. 708-715.
- S. Peleg and B. Porat, “Linear FM Signal Parameter Estimation from Discrete-Time Observations,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 27, No. 4, 1991, pp. 607-615. doi:10.1109/7.85033
- S. Peleg and B. Porat, “Estimation and Classification of Polynomial Phase Signals,” IEEE Transactions on Information Theory, Vol. 37, No. 2, 1991, pp. 423-430. doi:10.1109/18.75269
- J. C. Wood and D. T. Barry, “Radon Transformation of Time-Frequency Distributions for Analysis of Multi-Component Signals,” IEEE Transactions on Signal Processing, Vol. 42, No. 11, 1994, pp. 3166-3177. doi:10.1109/78.330375
- J. C. Wood and D. T. Barry, “Linear Signal Synthesis Using the Radon-Wigner Transform,” IEEE Transactions on Signal Processing, Vol. 42, No. 8, 1994, pp. 2105- 2111. doi:10.1109/78.301845
- S. Barbarossa, “Analysis of Multi-Component LFM Signals by a Combined Wigner-Hough Transform,” IEEE Transactions on Signal Processing, Vol. 43, No. 6, 1995, pp. 1511-1515. doi:10.1109/78.388866
- M. S. Wang, A. K. Chan and C. K. Chui, “Linear Frequency-Modulated Signal Detection Using Radon-Ambiguity Transform,” IEEE Transactions on Signal Processing, Vol. 46, No. 3, 1998, pp. 571-586. doi:10.1109/78.661326
- W. C. Li, M. Dan, X. S. Wang, D. Li and G. Y. Wang, “Fast Estimation Method and Performance Analysis of Frequency Modulation Rate via RAT,” International Conference on Information and Automation, Changsha, China, 20-23 June 2008, pp. 144-147. doi:10.1109/ICINFA.2008.4607984
- L. B. Almeida, “The Fractional Fourier Transforms and Time-Frequency Representations,” IEEE Transactions on Signal Processing, Vol. 42, No. 11, 1994, pp. 3084-3091. doi:10.1109/78.330368
- M. I. Skolnik, “Radar Handbook,” 2nd Edition, McGrawHill Publishing Company, New York, 1990.
- A. W. Rihaczek, “Principles of High-Resolution Radar,” McGraw-Hill Publishing Company, New York, 1969.
- L. X. Wang, D. Z. Fang, M. Y. Zhang, et al., “Mathematics Handbook,” Higher Education Publishing Company, Beijing, 2004.
- W. P. Li, “Wigner Distribution Method Equivalent to Dechirp Method for Detecting a Chirp Signal,” IEEE Transactions on Acoustics, Speech, Signal Processing, Vol. 35, No. 8, 1987, pp. 1210-1211.
- Y. M. Zheng and Z. Bao, “Autofocusing of SAR Images Based on Relax,” IEEE International Radar Conference, Alexandria, 7-12 May 2000, pp. 533-538. doi:10.1109/RADAR.2000.851890
- J. Tsao and B. D. Steinberg, “Reduction of Side Lobe and Speckle Artifacts in Microwave Imaging: The CLEAN Technique,” IEEE Transactions on Antennas and Propagation, Vol. 36, No. 4, 1988, pp. 543-556. doi:10.1109/8.1144

