Journal of Signal and Information Processing
Vol. 3 No. 3 (2012) , Article ID: 22115 , 8 pages DOI:10.4236/jsip.2012.33040
Continuously Variable Bandwidth Sharp FIR Filters with Low Complexity
![]()
Department of Electronics and Communication Engineering, National Institute of Technology, Calicut, India.
Email: jamestgeorge@yahoo.com, elizabeth@nitc.ac.in
Received May 15th, 2012; revised June 23rd, 2012; accepted July 1st, 2012
Keywords: Variable Bandwidth Filter; Frequency-Response Masking; Low Complexity; Finite Impulse Response Filter; Re-Sampling
ABSTRACT
In software defined radio (SDR), sharp filters of different bandwidth are required to fine tune the desired channel. This requires different computational resources and large number of filter coefficients. This paper proposes a continuously variable bandwidth sharp finite impulse response (FIR) filter with low distortion and low complexity. For this, a fixed length FIR filter is used with two arbitrary sampling rate converters. This system can be used for both the continuous increase as well as decrease of the effective bandwidth of a filter. The low complexity and sharpness are achieved by using the frequency-response masking (FRM) approach for the design of the fixed length FIR filter. The sharp transition width leads to maximum rejection to channel interference in SDR.
1. Introduction
Real time variable frequency response characteristics are required in various telecommunication applications including the software defined radio (SDR). SDR implies that important radio characteristics can be defined by software. In every radio receiver, one of the important characteristics is the bandwidth of the filter that selects the desired channel.
Several methods exist [1-8] for realizing the discretely variable bandwidth filter. The usual method to change the frequency response of a digital filter is to increase the number of taps or the order of the finite impulse response (FIR) filter to reduce the bandwidth and to decrease the number of taps to increase the bandwidth.
This can be implemented in SDR by modifiable software or firmware operating on programmable devices having constraints in resources as well as power. In the hardware implementation of a variable bandwidth filter, we must use a variable length data array, coefficient array, adders, multipliers etc. along with the filter design algorithm operating in the background to compute the new coefficients for each desired bandwidth.
The number of taps in a FIR filter is known to be proportional to the ratio of sample rate to transition bandwidth i.e. fs/∆f. When the bandwidth of a filter is reduced or increased by a factor, the transition width is also reduced or increased respectively by the same factor i.e., the spectral shape scales with bandwidth. Hence as the number of taps varies, the transition bandwidth and hence the overall bandwidth will also vary.
Now, if the number of taps is fixed, then to obtain a continuously variable bandwidth FIR filter, a new technique was proposed by Fred Harris [9] where a filter design algorithm is not needed to operate in the background to compute new coefficients for each desired bandwidth. Here, the principle used is that the absolute bandwidth of a filter is reduced by operating it at a reduced sample rate. This is accomplished [9] by efficiently shifting the frequency spectrum of the input signal by using an arbitrary down sampler. The down-sampled signal is then processed with a fixed length, fixed bandwidth FIR filter and then shifted back to the original spectrum by using an up-sampler. The combined technique gives the effect of reducing the effective bandwidth of the filter. This method can only decrease the bandwidth. However, many applications may require a bandwidth greater than the bandwidth of the fixed length filter. But this may lead to distortion in the output signal response. The main cause for this distortion is the non-zero transition bandwidth of the fixed length filter. The length of the FIR filter is inversely proportional to the transition bandwidth.
In this paper, the technique of obtaining a continuously variable bandwidth filter using re-sampling, is modified in such a way that, we get a bandwidth increase as well as decrease. At the same time, the distortion in the output response is reduced to a minimum. Hence, the variable bandwidth filter proposed in this paper has the property of fine tuning, i.e., continuous variation of the bandwidth is possible with minimum distortion, which includes both decrease and increase of bandwidth. The fixed length FIR filter is designed by frequency-response masking (FRM) technique. This leads to a sharp transition width and hence less distortion in the output spectrum as well as reduction in the computational complexity.
The next section reviews the variable bandwidth filter. Section 3 presents the design procedure for the arbitrary sample rate converter. The principle and structure of the low complexity technique on the design of the fixed length FIR filter, more specifically, the FRM is presented in Section 4. Section 5 gives the implementation as well as the detailed performance analysis and in Section 6, the computational complexity analysis is done. Section 7 concludes the paper.
2. Review of Variable Bandwidth Filter
Figure 1 shows the concept of a variable bandwidth filter. In the case of a constant form factor FIR filter, the length of the filter is inversely proportional to the transition width, which is proportional to the bandwidth of the filter. Thus, if the bandwidth of the filter is changed by a factor, the length of the filter is also changed by the same factor.
In order to realize a variable bandwidth filter without changing the number of coefficients or coefficient values, we can utilize the relationship between the sample rate and bandwidth [9-11]. This can be further elaborated that the interval between the main lobe peak and the first zero crossing of the impulse response is the reciprocal of the filter bandwidth. Also the interval between the samples is the reciprocal of the sample rate.
The number of taps of the filter (TP) is given by 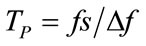 , where “fs” is the sampling frequency and “∆f” is the transition bandwidth. If the bandwidth is changed, the transition bandwidth is also changed by the same factor. Hence if the number of taps of the filter is fixed, one method of changing the bandwidth is to change the sampling rate. The absolute bandwidth is proportional to the sampling rate [9]. So we can change the absolute bandwidth of a filter by operating it at a different sampling rate. The technique used in [9] reduces the absolute bandwidth of a filter by operating it at a reduced sample rate. In this paper, we have modified the implementation in such a way that the bandwidth of the filter can also be increased by increasing the sample rate. The use of an FRM based FIR filter, makes the transition bandwidth sharp and reduces the complexity and distortion.
, where “fs” is the sampling frequency and “∆f” is the transition bandwidth. If the bandwidth is changed, the transition bandwidth is also changed by the same factor. Hence if the number of taps of the filter is fixed, one method of changing the bandwidth is to change the sampling rate. The absolute bandwidth is proportional to the sampling rate [9]. So we can change the absolute bandwidth of a filter by operating it at a different sampling rate. The technique used in [9] reduces the absolute bandwidth of a filter by operating it at a reduced sample rate. In this paper, we have modified the implementation in such a way that the bandwidth of the filter can also be increased by increasing the sample rate. The use of an FRM based FIR filter, makes the transition bandwidth sharp and reduces the complexity and distortion.
The implementation of the process is represented in Figure 2. An input signal which is initially oversampled is applied to an arbitrary sample rate converter (up or down) that preserves the dynamic range and still satisfies
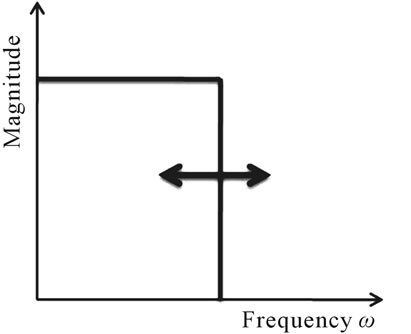
Figure 1. Magnitude response of variable bandwidth filter.

Figure 2. Functional block diagram of variable bandwidth filter [9].
the Nyquist criterion. The modified signal is processed by the fixed length, fixed bandwidth FRM based FIR filter. The output of the filter is then converted back to the original input sampling rate by using another arbitrary sample rate converter (down or up).
3. Arbitrary Sample Rate Converter
Figure 3 shows the interpolation indexing. This gives the method of forming a sample value at a location “y” that does not correspond to an available location of a M-path polyphase interpolator. The value of M is taken as 5 for illustration.
Figure 4 shows the implementation of an arbitrary ratio interpolator [9]. Three M-path polyphase filters are used for calculating the sample values of the interpolant and the sample derivatives at the offset position  from the interpolating output phase centre. The computed output is formed from a local Taylor series as given by Equation (1).
from the interpolating output phase centre. The computed output is formed from a local Taylor series as given by Equation (1).
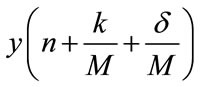
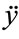


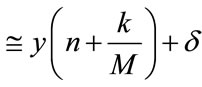 (1)
(1)
The increment d_acc satisfies the following relation shown in Equation (2) and the required bandwidth can be achieved by just changing the parameter d_acc as shown in Equation (3).
 (2)
(2)
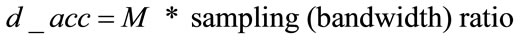 (3)
(3)
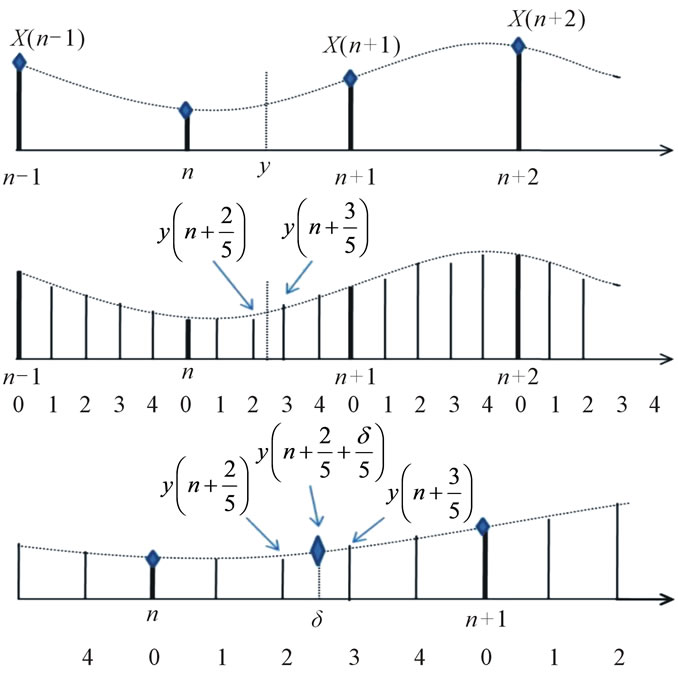
Figure 3. Interpolation indexing [10].
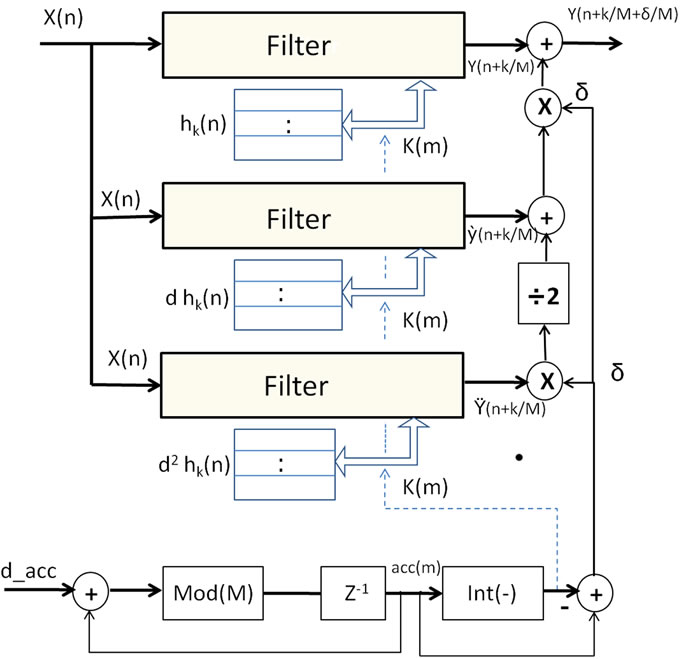
Figure 4. Implementation of arbitrary sampling rate converter [9].
where M: number of polyphase filters fsin: input sampling rate to interpolate fsout: output sampling rate of interpolator
4. Review of FRM Technique
In this section, we provide a brief review of FRM technique [12-14], which is one of the most efficient techniques for the synthesis of sharp linear phase digital filters using several wide transition band sub filters. Compared to the conventional direct-form realization, it gives a large reduction in the computational complexity because of the large number of sparse coefficients.
Figure 5 shows the basic realization structure of the FRM technique.  is an M-fold version of a given prototype with symmetrical impulse response, linear phase low pass filter. “θ” and “φ” are the pass band and stop band edges respectively and the transition width of
is an M-fold version of a given prototype with symmetrical impulse response, linear phase low pass filter. “θ” and “φ” are the pass band and stop band edges respectively and the transition width of  is
is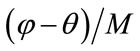 , which is a factor of M narrower than the transition width of the prototype filter. The complementary filter of
, which is a factor of M narrower than the transition width of the prototype filter. The complementary filter of , denoted by
, denoted by , can be expressed as
, can be expressed as 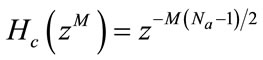
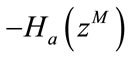 , where Na is the length of the impulse response of
, where Na is the length of the impulse response of 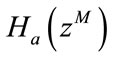 which has to be odd. Two masking filters
which has to be odd. Two masking filters  and
and 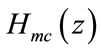 are cascaded to
are cascaded to 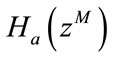 and
and  respectively and added together to form the FRM filter with an overall transfer function as given in Equation (4). The FRM based filter responses are illustrated in Figure 6 [12].
respectively and added together to form the FRM filter with an overall transfer function as given in Equation (4). The FRM based filter responses are illustrated in Figure 6 [12].
 (4)
(4)
In this paper, the design specifications for the conventional FIR filter is chosen as ωp = 0.266, ωs = 0.273, minimum stop band attenuation = 60 dB and maximum pass band ripple = 0.1 dB, for illustration. Frequency response of the conventional FIR filter is shown in Figure 7(a). The required length of the FIR filter is 570, and the number of multipliers required is 285 and Figure 7(b) shows the frequency response of the FRM based FIR filter, both designed for the above specifications. The total length of the FRM filter is 645, which is obtained as the sum of the lengths of the prototype filter 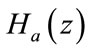 and two masking filters
and two masking filters 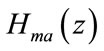 and
and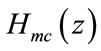 . But here, the number of multipliers required is only 101, which is very much less than that of the conventional FIR filters for getting the same transition bandwidth.
. But here, the number of multipliers required is only 101, which is very much less than that of the conventional FIR filters for getting the same transition bandwidth.
5. Simulation of Variable Bandwidth Filter Using Re-Sampling
In order to illustrate the performance of the variable bandwidth filter using re-sampling technique, the input signal is formed as a sum of 18 sinusoids spanning the input bandwidth for simulation using MatLAB. This is chosen such that, it covers approximately twice the fixed bandwidth of the conventional FIR filter (for validation). It should be sampled by at least four times the Nyquist
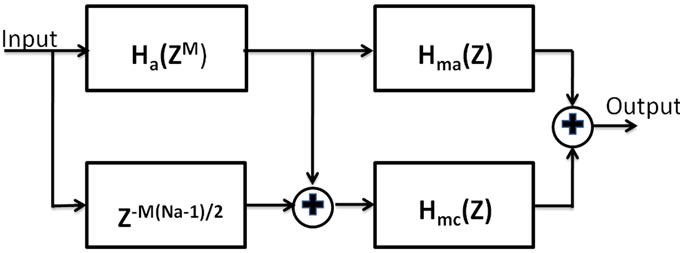
Figure 5. Realization structure of FRM filter [12].

Figure 6. Illustration of FRM approach [12].
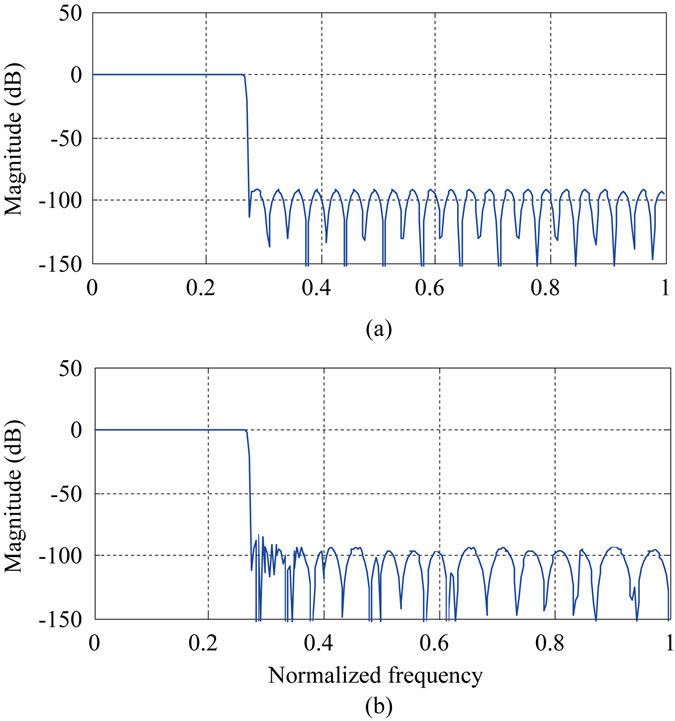
Figure 7. Performance comparison of the conventional FIR filter and FRM based filter. (a) Frequency response of conventional FIR filter with order = 570; (b) Frequency response of FRM based filter with less complexity.
rate in order to get a bandwidth reduction of 40% without distortion. The arbitrary sample rate converter is designed to operate with signals sampled at two times the two sided bandwidth. The number of stages required in the converter is controlled by the excess sample rate. Here we use a 64 path polyphase partition with 10 tap filter per path for getting a minimum attenuation of 60 dB in the stop band. For getting the precise values, three such polyphase filters are used for implementing the first three terms of the Taylor series expansion as given in the Equation (1). One arbitrary sample rate converter is used at the input and a similar one is used at the output of the fixed length, low pass filter of Figure 2, for converting back to the original input sampling rate with a new d_acc, which is the reciprocal of the initial d_acc as represented in Figure 4. The simulation of the variable bandwidth filter using MatLAB is presented in the following subsections as bandwidth reduction as well as bandwidth enhancement using conventional FIR filter and both the cases using FRM based FIR low pass filter.
5.1. Bandwidth Reduction
For reducing the bandwidth, (which is referred as case-1 in this paper) the first converter in Figure 2 is chosen to be a down-sampler and the last block is an up-sampler. For the design of the variable bandwidth filter, first a conventional FIR filter is designed with an appropriate set of specifications. Figure 8(a) shows the input spectrum as well as the frequency response of the FIR filter, if the filter is operated at the same sampling rate as that of the input signal. Figure 8(b) is the spectrum of the output of the decimator which is operated as a 1 to 0.8 (effective sampling ratio) down-sampler. The downsampled but not bandwidth reduced input spectrum is seen expanded. More portion of the signal bandwidth is now seen to extend beyond the filter pass band. Figure 8(c) is the spectrum at the output of the fixed length low pass filter. Figure 8(d) is the spectrum obtained at the output of the second sampling rate converter, which is an interpolator in case-1. Here a 0.8 to 1 up-sampler is used. Hence the signal is converted back to the original sampling rate. It can be seen that the output spectrum and the corresponding frequency response are the same, if we had increased the number of taps of the fixed length FIR filter (570 to 712), to get the reduced bandwidth. Figure 8(d) also shows the approximate effective bandwidth of the overall system for visualization.
5.2. Bandwidth Enhancement
In order to increase the bandwidth, the first converter in Figure 2 is used as an up-sampler and the second converter as a down-sampler. This is referred to as case-2 with a conventional FIR filter. The first converter is a 1 to 1.4 up-sampler and the second one is a 1.4 to 1 down-sampler. The input signal used in case-2 is the same as in case-1. The waveforms in Figure 9 for case-2 are also arranged in a way similar to those in Figure 8. The output spectrum in Figure 9(d) shows a bandwidth enhancement. When the bandwidth is enhanced, the transition bandwidth is also enhanced. This leads to a distortion of the spectrum as is evident in Figure 9(d). This is
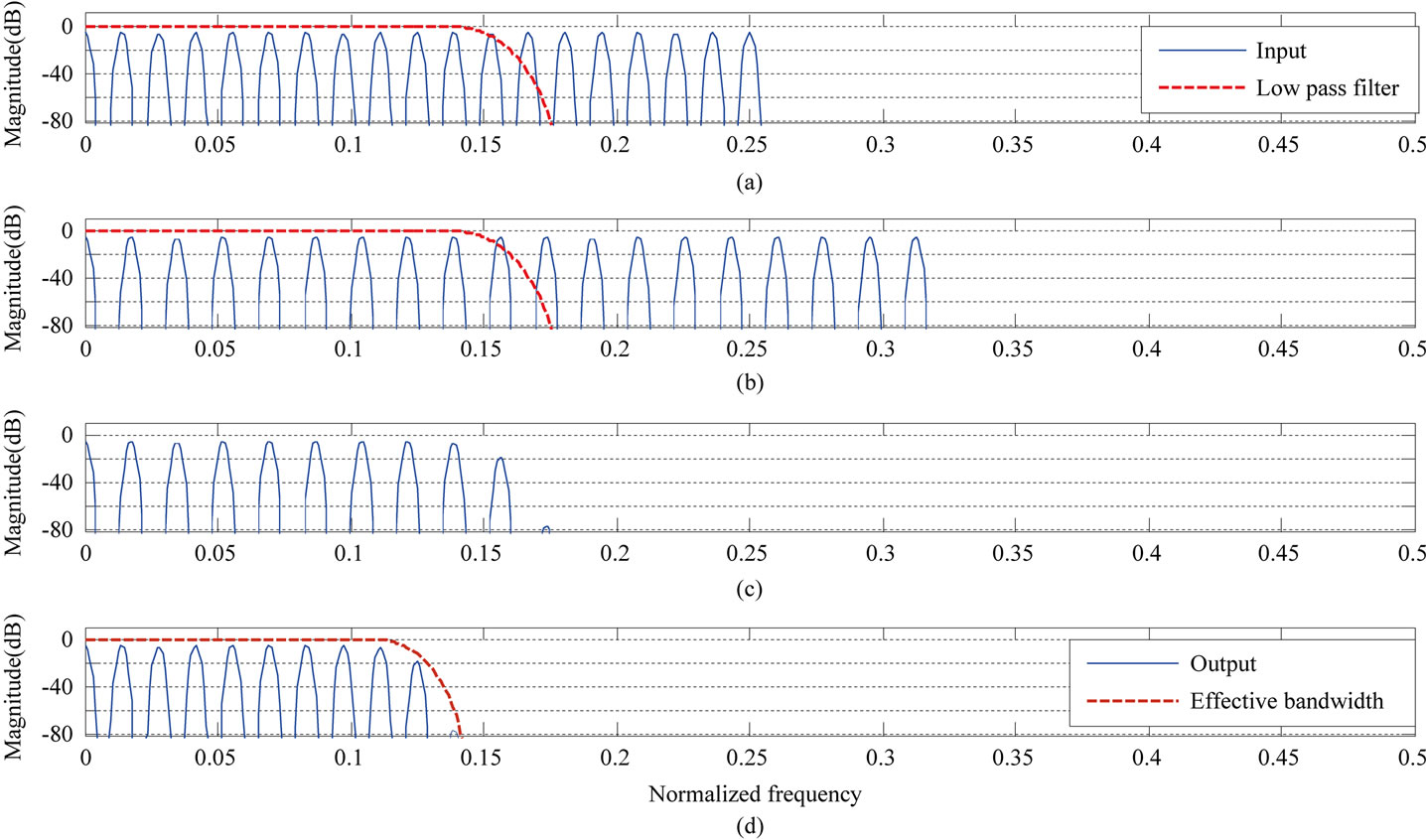
Figure 8. Input and output of the three processing blocks of Figure 2 with conventional FIR filter for case-1. (a) Spectrum of the input and response of low pass filter; (b) Spectrum of the output of 1 to 0.8 down-sampler; (c) Spectrum of the output of low pass filter; (d) Spectrum of the output of 0.8 to 1 up-sampler and effective bandwidth.
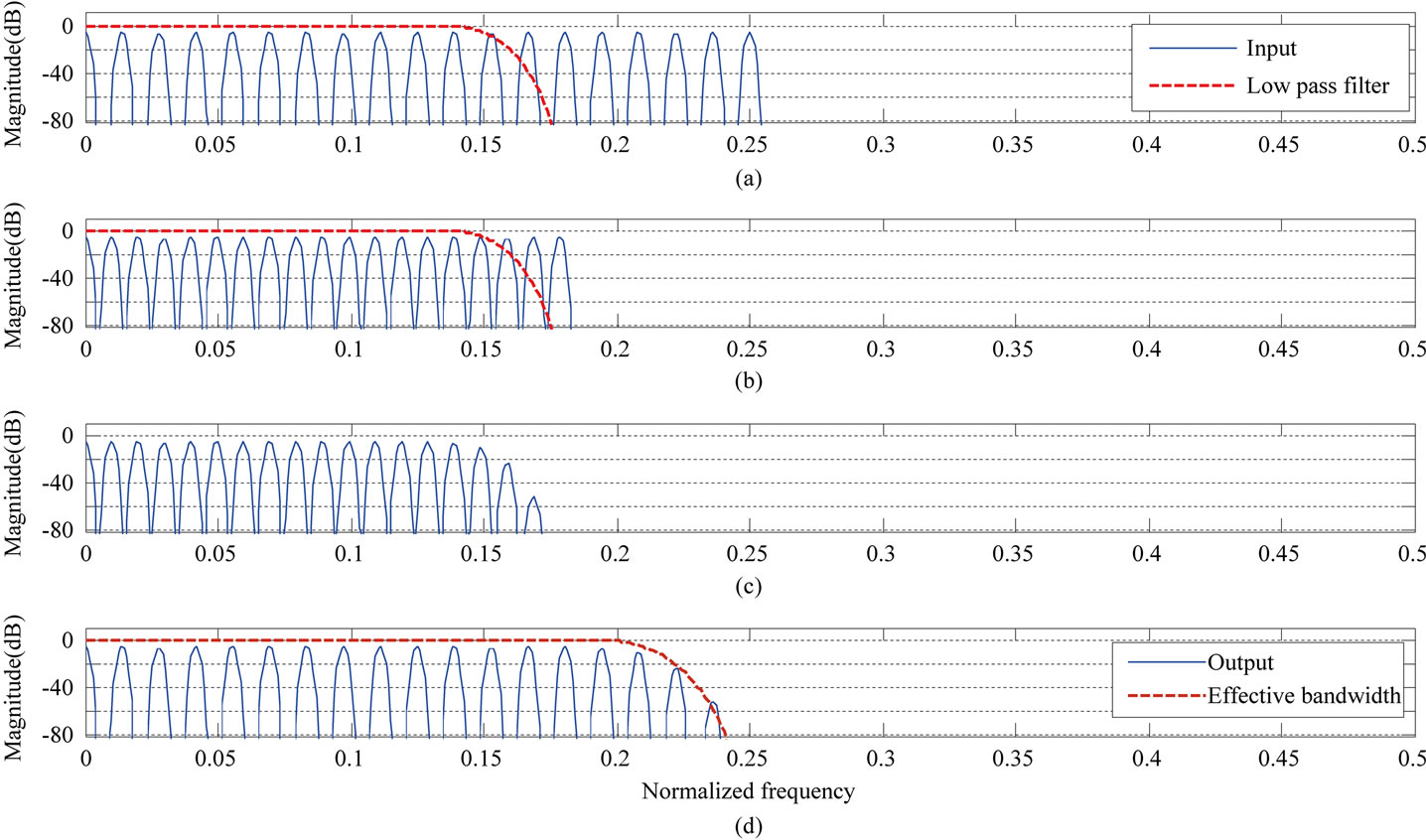
Figure 9. Input and output of the three processing blocks of Figure 2 with conventional FIR filter for case-2. (a) Spectrum of the input and response of low pass filter; (b) Spectrum of the output of 1 to 1.4 up-sampler; (c) Spectrum of the output of low pass filter; (d) Spectrum of the output of 1.4 to 1 down-sampler and effective bandwidth.
seen to be more evident in case-2 than in case-1.
5.3. FRM Based Variable Bandwidth Filter
The stretching of the transition bandwidth in case-2 can be eliminated to a high degree, if we use FRM technique for the design of the FIR filter. Hence we have designed a low complexity FRM based FIR low pass filter with smaller transition bandwidth by selecting ωp = 0.12 and ωs = 0.13 and keeping all other specifications, the same.
The corresponding spectra for case-1 and case-2 with FRM based FIR filter are shown in Figure 10 and Figure 11 respectively. Hence by using FRM technique for the design of the FIR filter for variable bandwidth application using re-sampling, the shape of the output spectra is improved and the complexity is reduced as well. Selecting case-1 or case-2 through d_acc (Figure 4) together with FRM based FIR filter, sharp band edge tuning can be achieved.
6. Complexity Analysis
In this section, the computational complexity is analyzed. Computational complexity is quantified using the number of multipliers needed for the realization of various filters. Here the bandwidth of the filter for the comparison is taken as the ratio of input and output bandwidth and the values are taken as same as in section 4 for comparison. Table 1 gives the complexity comparison in terms of the multipliers for various filters. We can see that the number of multipliers needed is very less in the case of the variable bandwidth filter with FRM than the variable bandwidth filter with conventional FIR filter as well as the equivalent fixed bandwidth, fixed length FIR filter. In addition to this, a set of multipliers (20 for the two terms and 30 for the three terms implementation of the Taylor series terms for better approximation) together with a set of memory locations with pre-stored polyphase filter coefficients are only needed for realizing the arbitrary sample rate converter. Increased number of polyphase stages does not increase the computational complexity, but it will improve the granularity. The reduction in the complexity is achieved for both case-1 and case-2.
7. Conclusion
We have presented a technique to obtain a continuously variable bandwidth filter as a combination of two arbitrary sample rate converters and a fixed length, low complexity, sharp transition-band filter designed using FRM technique. The first sample rate converter either increases or decreases the sample rate according to the proportional requirement of the effective bandwidth. This
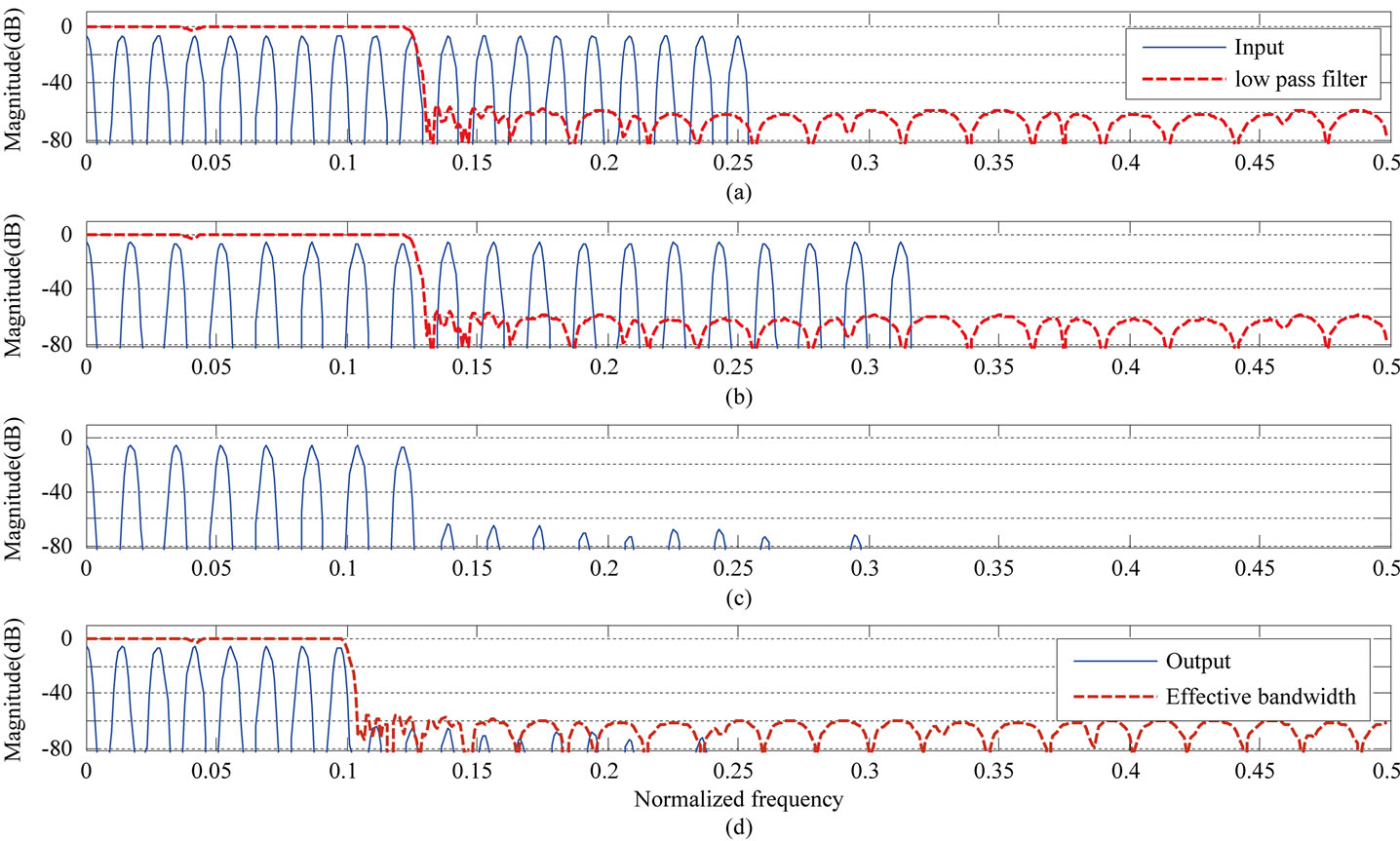
Figure 10. Input and output of the three processing blocks of Figure 2 with FRM filter for case-1. (a) Spectrum of the input and response of low pass filter; (b) Spectrum of the output of 1 to 0.8 down-sampler; (c) Spectrum of the output of low pass filter; (d) Spectrum of the output of 0.8 to 1 up-sampler and effective bandwidth.

Figure 11. Input and output of the three processing blocks of Figure 2 with FRM filter for case-2. (a) Spectrum of the input and response of low pass filter; (b) Spectrum of the output of 1 to 1.4 up-sampler; (c) Spectrum of the output of low pass filter; (d) Spectrum of the output of 1.4 to 1 down-sampler and effective bandwidth.
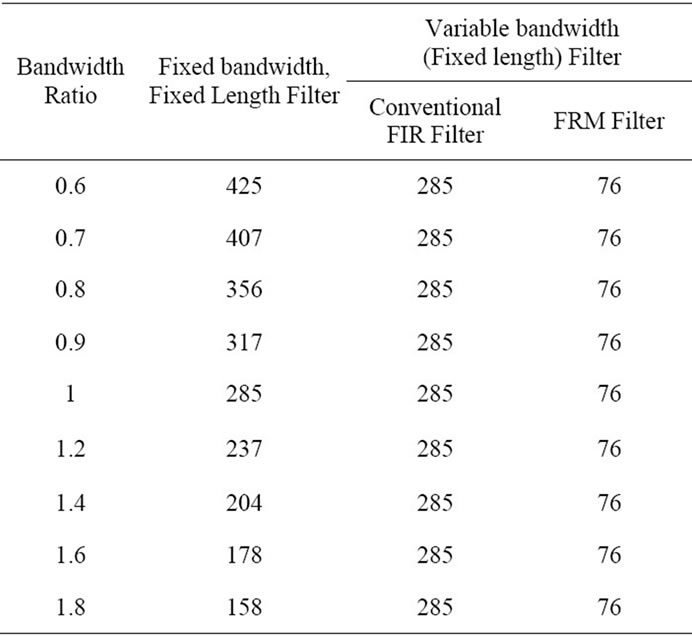
Table 1. Complexity comparison in terms of multipliers, for various filters.
signal is processed with the fixed length, fixed bandwidth filter and the output of the filter is given to a second sample rate converter for converting back to the original input sample rate. This effectively changes the bandwidth of the filter.
Arbitrary sampling rate is achieved by using a polyphase interpolator and the fixed length filter is implemented by FRM technique for reducing the complexity. Sharp transition band is achieved and this helps in reducing the inter-channel interference. Computational complexity of the whole system is same for the entire range of operating bandwidth. The rejection of adjacent bands with continuous variation up to 40% decrease and 200% enhancement in effective bandwidth is better than 60 dB.
REFERENCES
- Y. J. Yn, Y. C. Lim and D. Shi, “Low-Complexity Design of variable bandedge linear phase FIR filters with sharp transition band,” IEEE Transactions on Signal Processing, Vol. 57, No. 4, 2009, pp. 1328-1338.
- H. Johansson, “On linear phase FIR filters with variable bandwidth,” IEEE Transactions on Circuits and Systems II: Express Briefs, Vol. 51, No. 4, 2004, pp. 181-184.
- R. Mahesh and A. P. Vinod, “Reconfigurable Frequency Response Masking Filters for Software Radio channelization,” IEEE Transactions on Circuits and Systems II: Express Briefs, Vol. 55, No. 3, 2008, pp. 274-278.
- C. W. Farrow, “A continuously variable digital delay element,” IEEE International Symposium on Circuits and Systems, Espoo, 7-9 June 1988, pp. 2641-2645.
- A. V. Oppenheim, W. F. G. Mecklenbrauker and R. M. Mersereau, “Variable cutoff linear phase digital filter,” IEEE Transactions on Circuits and Systems, vol. 23, no. 4, 1976, pp. 199-203.
- S. Roy and S. S. Ahuja, “Frequency Transformations for linear-phase variable-cutoff digital filters,” IEEE Transactions on Circuits and Systems, vol. 26, no. 1, 1979, pp. 73-75.
- F. Harris, “Selectable Bandwidth Filter formed from Perfect Reconstruction Polyphase Filter Bank,” 2010 Conference Record of the Forty fourth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, 5-7 November 2010, pp. 1292-1296. doi:10.1109/ACSSC.2010.5757740
- R. Mahesh and A. P. Vinod, “Reconfigurable low area complexity filter bank architecture based on frequency response masking for nonuniform channelization in software radio receivers,” IEEE Transactions on Aerospace and Electronic Systems, vol. 47, no. 2, 2011, pp. 1241-1255. doi:10.1109/TAES.2011.5751255
- F. Harris, “Fixed Length FIR Filters with Continuously Variable Bandwidth,” 1st International Conference on Wireless Communication, Vehicular Technology, Information Theory and Aerospace & Electronic Systems Technology, Aalborg, 17-20 May 2009, pp. 931-935.
- F. J. Harris, “Multirate Signal Processing for Communication Systems,” Prentice Hall, Upper Saddle River, 2004.
- P. P. Vaidyanathan, “Multirate Systems and Filter Banks,” Englewood Cliffs, Prentice Hall, 1993.
- Y. Lim, “Frequency-response masking approach for the synthesis of sharp linear phase digital filters,” IEEE Transactions on Circuits and Systems, Vol. 33, No. 4, 1986, pp. 357-364.
- T. Saramaki and Y. C. Lim, “Use of the Remez Algorithm for Designing FRM Based FIRr Filters,” Circuits, Systems, and Signal Processing, Vol. 22, No. 2, 2003, pp. 77-97. doi:10.1007/s00034-004-7021-5
- Y. Wei and Y. Lian, “Frequency-Response Masking Filters Based on Serial Masking Schemes,” Circuits, Systems, and Signal Processing, Vol. 29, No. 1, 2010, pp. 7- 24.

