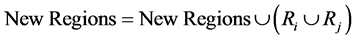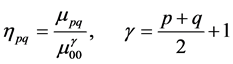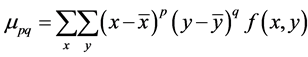Journal of Data Analysis and Information Processing
Vol.02 No.04(2014), Article ID:51858,19 pages
10.4236/jdaip.2014.24014
Hierarchical Image Segmentation Using a Combined Geometrical and Feature Based Approach
Melissa Cote, Parvaneh Saeedi
School of Engineering Science, Simon Fraser University, Burnaby, Canada
Email: melissa_cote@sfu.ca, psaeedi@sfu.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 August 2014; revised 30 October 2014; accepted 20 November 2014
ABSTRACT
This paper presents a fully automatic segmentation algorithm based on geometrical and local attributes of color images. This method incorporates a hierarchical assessment scheme into any general segmentation algorithm for which the segmentation sensitivity can be changed through parameters. The parameters are varied to create different segmentation levels in the hierarchy. The algorithm examines the consistency of segments based on local features and their relation- ships with each other, and selects segments at different levels to generate a final segmentation. This adaptive parameter variation scheme provides an automatic way to set segmentation sensiti- vity parameters locally according to each region's characteristics instead of the entire image. The algorithm does not require any training dataset. The geometrical attributes can be defined by a shape prior for specific applications, i.e. targeting objects of interest, or by one or more general constraint(s) such as boundaries between regions for non-specific applications. Using mean shift as the general segmentation algorithm, we show that our hierarchical approach generates segments that satisfy geometrical properties while conforming with local properties. In the case of using a shape prior, the algorithm can cope with partial occlusions. Evaluation is carried out on the Berkeley Segmentation Dataset and Benchmark (BSDS300) (general natural images) and on geo-spatial images (with specific shapes of interest). The F-measure for our proposed algorithm, i.e. the harmonic mean between precision and recall rates, is 64.2% on BSDS300, outperforming the same segmentation algorithm in its standard non-hierarchical variant.
Keywords:
Image segmentation, adaptive color analysis, shape analysis, prior model, image processing, split-and-merge segmentation, perceptual grouping

1. Introduction
Image segmentation is one of the most commonly used processes in applications of computer vision. It is also one of the most challenging problems and has a wide range of computer vision and machine learning applica- tions in areas such as geo-spatial, biomedical, security, surveillance, and inspection. These applications general- ly require matching, correspondence establishing, and identification of image regions. Segmentation algorithms that deliver robust and consistent results under different conditions such as scene and viewpoint variations, shading, specularities and illumination change have key roles in the success of their machine vision applications. The task of segmentation is often complicated by various factors such as unclear boundaries, color/intensity si- milarities of adjacent structures, and variations in shape or other characteristics of image segments. In the past few decades numerous algorithms have been developed to address the need for robust and reliable segmenta- tions. Due to issues such as complexity and diversity of data and image sources, the quest for a good segmenta- tion algorithm that performs equally well for different images and applications is somehow still not fully satis- fied.
This work presents a computational approach to the problem of image segmentation. Our proposed method can be broadly used in applications for indoor and outdoor scenes as well as for regions with specific shapes. The paper is structured in the following way. Related work regarding image segmentation is reviewed next, fol- lowed by the contributions of the proposed approach. Section 2 details the methodology, while Section 3 de- scribes how to modify it to accommodate shape-specific segmentation. Experimental results on varied imageries (state-of-the-art color dataset and benchmark, geo-spatial), as well as their qualitative and quantitative evalua- tions are provided in Section 4. Finally, Section 5 presents conclusions and future works.
1.1. Related Work
1.1.1. Feature Based Segmentation
Early works in image segmentation were based on featural and low level information such as intensity value, color, texture, edge, etc. Feature based methods cluster image pixels into homogeneous regions that have high probability of arising from a similar physical property. Chen et al. [1] proposed a color based image segmenta- tion algorithm using contrast information. They utilized four directional operators to extract directional color contrast information. A single-threshold scheme was used to detect directional boundaries. These directional boundaries were merged together via a verification process to form 2-D boundaries of segments. Felzenszwalb and Huttenlocher [2] utilized the intensity differences across the boundary of regions and the intensity differ- ences between neighboring pixels within a region to make a graph based representation of an image which was used in the segmentation process by finding the minimal spanning tree of the graph. In more recent work, Lo et al. [3] introduced a texture-based segmentation algorithm that performed feature extraction using the Dual-Tree Complex Wavelet Transform (DT-CWT). They first transferred all image pixels into a spatial-texture space and then used a clustering method to cluster pixel vectors (created for all pixels). Tan and Isa [4] used histograms for image segmentation. They presented a novel histogram thresholding algorithm also known as fuzzy C-means hybrid (HTFCM). Their method could obtain regions with uniform colors.
Feature based methods are simple and intuitive to implement. However, most of them require tuning of sever- al control parameters, and generally the performance of these methods is subjected to proper setting of such parameters. Also, since these methods rely on texture, region homogeneity, intensity, etc. their performance could be highly affected by noise, illumination condition, variation in the view point and sometimes specific properties of objects.
1.1.2. Model Based Segmentation
In recent years, model based image segmentation algorithms have attracted more attention. Model based image segmentation aims to recover predefined shapes or structures from an image using shape properties and con- straints. States of the art on model based segmentation are mostly based on active shape and appearance models, active contours and deformable templates, and level set methods.
Active shape and appearance models incorporate statistical or parametric models of shapes (using training data) in the segmentation process. Cootes et al. [5] described point distribution models based on Principal Com- ponent Analysis (PCA) to parameterize variations of active contours in a training dataset. They exploited a linear formulation of the shape model (active shape model) to iteratively search for the shape in an image. Staib and Duncan [6] proposed a parametric model based on an elliptic Fourier decomposition of the shape boundaries. The segmentation problem was addressed as an optimization problem that found the best match between the model and the image gradient. Wang and Staib [7] used shape parameters derived from statistical variations of object boundary points in a training set to model an object. A Bayesian formulation, based on this model and the gradient of the image, was employed to identify the object’s boundaries in the image.
In general, active shape model based approaches use an off-line learning process. Processing the training dataset is commonly performed via manual segmentation and the shape model cannot be extended as new seg- mentation results become available [8] . Perhaps the main disadvantage associated with these methods is the lack of robustness in the recognition and training phases. For instance, often there is a poor performance under partial occlusion and imperfect training datasets cannot be utilized.
Combining prior shape information with active contours and deformable templates is also used in model based segmentation. In these approaches, the active contour’s energy function is modified such that it incorpo- rates a representation of the reference shape within it. Therefore, the contour converges to the boundaries that are more similar to the prior shape boundary. Tsai et al. [9] [10] proposed a model based curve evolution tech- nique using a parametric model of the segmenting curve by applying principal analysis component to a collec- tion of signed distance representations of the training data. Foulonneau et al. [11] presented a new way of con- straining the evolution of a region based active contour with respect to a reference shape. Minimizing a shape prior was achieved through a distance between shape descriptors based on the Legendre moments of the charac- teristic function. Using the level set method for finding specific shapes in an image has also been reported by many researchers. Chen et al. [12] modified the energy function so that it depends on the image gradient and the prior shape. In this approach the level set formulation could find boundaries that were similar in shape to the prior, even under partial occlusions. Leventon et al. [13] incorporated prior shape information into the geodesic active contour method by introducing model representation of deformable shapes and probability distribution over the variances of a set of training shapes. The segmentation process embedded an initial curve as the zero level set of a higher dimensional surface, and evolved the surface such that the zero level set converged on the boundaries of the object to be segmented. The main advantage of the Leventon method was on intrinsically representing active contours by the level set function. This feature made it possible to construct a parameterization free shape model. Rousson and Paragios [14] proposed a level set based approach for shape-driven object extraction using a voxel-wise probabilistic level set formulation. Constraints on the segmentation process were imposed by seeking a projection of the prior model onto the image plane using a similarity transformation. Rik- lin-Raviv et al. [15] introduced a variational approach for model based segmentation, using a single reference object. They proposed a shape-similarity measure by generalizing the Chan-Vese [16] level set framework and embedding the projective homography between the prior shape and the image to segment.
The advantage of methods based on active contours and level sets is that they can handle topological changes of the contour in a natural way. For instance, the contour may split and/or merge during evolution without any special considerations. For shape modeling, this property allows constructing shape similarity measures that can handle variant shape topologies. But like many other level set based methods, these methods can suffer from numerical instabilities and sensitivity to noise. They are also prone to getting caught in local minima.
1.1.3. Hierarchical Segmentation
Recently, many hierarchical approaches have been proposed for image segmentation purposes. Sharon et al. [17] presented a fast segmentation by a weighted aggregation (SWA) method that determined salient regions of an image and built them into a hierarchical structure. Their algorithm consisted of an adaptive process in which pixels were recursively aggregated into increasingly large-scale aggregates of coherent properties: intensity, texture and boundary integrity. Paris and Durand [18] presented a hierarchical segmentation approach using mean shift segments [19] for segmenting color images and videos. They used Mores theory to topologically de- compose mean shift segments into density modes. Their method is fast and requires no training. They reported an F-measure, i.e. the harmonic mean between precision and recall rates, of 0.61 on average on the Berkeley Segmentation Dataset and Benchmark (BSDS300). Alpert et al. [20] presented a probabilistic aggregation based method that utilized local intensity, texture of regions along with the length of common boundaries between neighboring regions to segment grayscale images. In their method they merged pixels according to the above cues to generate larger regions as the aggregation advances. They trained their system parameters using a large number of patches and hold those parameters unchanged for the entire tested image subjects. To verify their al- gorithm they had chosen a set of images with clear distinction between the object in the foreground from back- ground. They compared their results against manually created ground truth and showed an F-measure of 0.87. Such high F-measure was due to the fact that the image test subjects were handpicked with the above criteria making comparison of this method with other methods, where the input data is not biased, impossible. Corso et al. [21] introduced an image labeling method based on a graph-shift algorithm (an energy minimization algo- rithm) for natural image labeling. They decomposed the image into multiple layers and adaptively manipulated (shifted) the parent-child relationship. They efficiently computed all possible shifts (which lead to the change of energy) for all of the nodes in the image graph and assessed the energy function. Using the energy value, they coarsened the image adaptively. While they showed some visual labeling results, they have presented no F- measure for their method.
Here, we propose a fully automatic, non-training-based segmentation method for color images based on geo- metrical and local features. First, we create a hierarchical composition of all potential segments of the image us- ing a multi-layer approach in which segments can partially or fully overlap with other segments at different lay- ers. In this approach, a general segmentation method (such as mean shift [19] , graph-based [2] , etc.) is utilized. The segmentation algorithm is run using a range of parameter settings that leads to results from under to over segmentation outcomes. Then, starting both from the finest level (most over-segmented layer) and the coarsest level (most under-segmented layer), the algorithm examines various local properties of the segments and com- pare those properties between parent and children segments along the hierarchical direction. These properties include color, texture and distinctiveness of the boundaries. The proposed algorithm is a general approach; however we show that with the addition of complementary shape constraints, it can be used to bias the detection of objects with specific shapes.
1.2. Contributions
The main contributions of this paper are as following:
1) A new adaptive parameter manipulation that in general can be incorporated with any algorithm where the quality of results on different input images is dependent on adjusting some control parameters. The adaptive parameter variation scheme provides an automatic way to set control parameters locally according to each sub-re- gion’s quality instead of the entire image.
2) A novel segmentation algorithm based on local image features and geometrical properties of regions. Through a hierarchical approach, mean shift segmentation is applied on the image several times using different settings that drive segmentation results from under to over segmentation. By inspecting the relationship between parents-children in two directions of bottom-up and top-down, segments conforming best with local and geometrical constraints are chosen from different levels of the hierarchy.
2. Methodology
This section describes the proposed approach to image segmentation. General segmentation problems are first illustrated, followed by the description of the proposed hierarchical feature-based segmentation method, divided into several processes: general hierarchical segmentation, definition of region comparison constraints, segment tree creation, search and identification of segments, and segment post-processing. Shape-specific geometrical aspects are presented in Section 3.
2.1. General Segmentation Problems
The performance of image segmentation algorithms often depends on various elements such as the skill of the user (if manual or semi-automatic), the compatibility of the method with the nature of the application, and the image quality. There is no algorithm that has established itself as the definitive solution to the image segmen- tation problem.
Often segmentation algorithms are parameter dependent which adds to the applicability of such algorithms. Examples of such cases can be seen for mean shift segmentation algorithm [19] , fuzzy 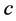 -means clustering [22] , and Gaussian mixture model [23] . For instance, fuzzy
-means clustering [22] , and Gaussian mixture model [23] . For instance, fuzzy 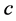 -means clustering requires that three parameters (number of iterations, termination threshold, and number of clusters) be set according to the application. As another example, the quality of segmentation in mean shift is controlled by three parameters: the spatial resolution
-means clustering requires that three parameters (number of iterations, termination threshold, and number of clusters) be set according to the application. As another example, the quality of segmentation in mean shift is controlled by three parameters: the spatial resolution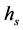 , the range (or color) resolution
, the range (or color) resolution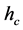 , and the minimum segment size
, and the minimum segment size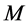 . These parameters are usually set manually and often a single setting will not be sufficient for a complete segmentation. Figure 1 depicts an example of a segmentation process using the mean shift algorithm where
. These parameters are usually set manually and often a single setting will not be sufficient for a complete segmentation. Figure 1 depicts an example of a segmentation process using the mean shift algorithm where 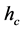 was set to two different values. In these two examples, a variation in
was set to two different values. In these two examples, a variation in 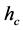 has caused the segmentation results to be improved for some regions but deteriorated for others. It is a challenge (if ever possible) to find one value for
has caused the segmentation results to be improved for some regions but deteriorated for others. It is a challenge (if ever possible) to find one value for 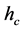 to segment all building regions correctly, which is why we propose a local adaptive parameter manipulation scheme.
to segment all building regions correctly, which is why we propose a local adaptive parameter manipulation scheme.
2.2. Proposed Hierarchical Feature-Based Segmentation
In this paper we propose a segmentation algorithm for segmenting color images based on distinctiveness in color and region boundaries. The algorithm includes four main processes as depicted in Figure 2. Details of each process along with quality assessment constraints are described in this section.
2.2.1. General Hierarchical Segmentation
In this section, we define a general hierarchical segmentation process to generate a large number of potential segmentation outcomes. Here, any common segmentation algorithm could be utilized as long as the quality control parameters are identified and changed in between the layers. The results of these segmentations must cover all potential outcomes from under to over segmentation.
In this work, we have used the mean shift segmentation method [19] . The idea behind the mean shift algorithm is, for a set of discrete data, to locate the stationary points of the underlying density function, allowing the detection of the modes of the density. For an image segmentation application, the input space is defined by a joint domain (location and color of pixels), with each pixel iteratively associated with a significant mode of the density, located in its neighborhood, thus delineating clusters in the joint domain. An image region (segment) is therefore defined by all the pixels associated with the same mode in the joint domain. From our experiments, the main control parameter for this method is the range resolution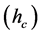 . The input image
. The input image 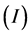 is segmented multiple times for the range resolutions of:
is segmented multiple times for the range resolutions of:
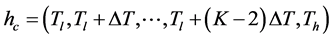
For each value of 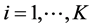 where
where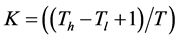 , a segmented image
, a segmented image 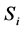 is generated that includes regions
is generated that includes regions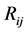 :
:
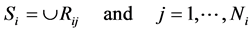 (1)
(1)
Figure 1. Mean shift algorithm on aerial imagery. (a) Low ran- ge resolution (hc) value; (b) High range resolution (hc) value.
Figure 2. Algorithm’s main components.
Here 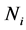
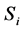
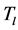


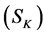

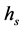
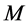
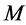
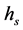
similar manner to 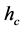
this paper. An additional segmented image 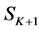
single region.
This hierarchical segmentation scheme generates a large number of segments based on a range of various parameter settings. Clearly the collections of these segments include redundant, overlapping, divided and merged segments and only a few of these segments will conform to valid/intended segments. The tendency of each segmented region for splitting or merging based on the color range (in the consecutive layers) are measured using two constraints that are explained next.
2.2.2. Region Comparison Constraints
For non-specific applications (generic segmentation), the proposed algorithm is based on two sets of constraints that measure the quality of potential segments. When segmenting an image based on its pixels’ colors, the color resolution can affect the sensitivity of the segmentation results. Therefore, since the hierarchical multi-layer segmentation generates region components by varying the range (color) resolution, the neighboring segments in one level might be merged together in the next level, if their color values fall into one color range interval. A similar reasoning can be done if using another segmentation algorithm.
The color constraint in this section implies selecting regions according to their color stability across hierarchical segmentation layers. Here we define the color stability of a region by its reluctantness in splitting into two or more regions or merging with its neighboring regions. Therefore, we are after the most distinctive regions across all hierarchical segmentation levels. In the hierarchical segmentation process, the highest level is the least sensitive layer (includes the lowest number of segments) and the lowest level (with minimum range resolution value) is the most sensitive layer (includes the highest number of segments). Here we introduce two constraints: Dividability and Distinctiveness.
1) Dividability: Dividability indicates the tendency of a region to break into two or more parts color-wise. It is a reflection of the entropy computed from the distribution of the regions’ colors. Many color based segmentation approaches use a color reduction process in which the amount of the information presented by color is reduced drastically. An example of a reduction process is the color quantization in which only a certain number of colors are used to represent an image. The association of each color with the representative quantized color is usually based on the minimum distance constraint. The HSV color model has been used in many applications. Since the hue component of this model holds the color information, this model is very useful for processing color images. Unfortunately, the hue component is unstable near the chromatic axis. That is, with low saturation, the error within hue measurements is high. As saturation is a radial dimension, it has a linear relationship with the certainty in the hue measurement. Also, when it comes to natural scenes, often regions that are identified by a human as being similar in color indeed have different hue values. For the two above reasons we created a color reduction scheme in which 219 colors are grouped into 22 groups. Each group includes similar colors that cover various shades and tones of that color. The similarity of each pixel is measured with all individual colors of each group. For each pixel, both the reduced color value (the most similar color using Euclidean distance) as well as its group will be maintained. The concept of grouping colors allows us to correctly associate together those neighboring regions that include various shades of the same color usually due to illumination or reflection variation. Figure 3 represents five groups of the above 22 groups of colors.
The dividability of a region is high when its tendency to break into different colors is high, which is reflected
by high entropy. The dividability measure 

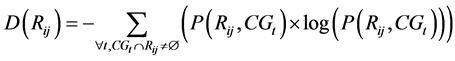
Figure 3. Five representative groups of colors along with their colors.

Here, 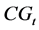
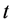
2) Distinctiveness: The distinctiveness of a region is measured according to the quality of its boundary points. Distinctive regions tend to have clear and solid boundaries. For this, the input image is first edge detected (Canny) and then the edges are linked together, as the Canny edge detector rarely produces closed boundaries. The linking is achieved by analyzing pixels in a 9 × 9 pixel neighborhood at each edge point. For each edge point two measures are calculated:
· Magnitude of the gradient vector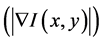
· Direction of the gradient vector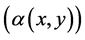
Using the two above measures, points with similarities in both magnitude and direction will be added to the edge point and the algorithm progresses until there is no point in the neighborhood that can be added to the current edge point. The similarity constraints are defined by:
a) An edge pixel with coordinates 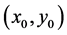
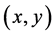

b) An edge pixel with coordinates 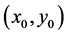
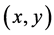

Once all edge points are linked, a minimum length constraint of 20 pixels is applied and any edge with a length smaller than that will be removed from the edge map. The final edge map is referred by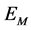
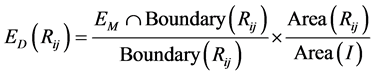
where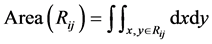


boundary pixels of region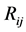
2.2.3. Segment Tree Creation
Tree 


In this tree, a node (region) 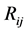
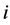
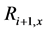
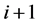

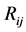
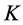
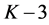
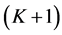
2.2.4. Tree Search (Segment Selection)
To extract all regions that best conform to the geometrical and color constraints, an iterative algorithm is designed. Two different searches are performed: a bottom-up search and a top-down search.
The bottom-up search starts at the lowest level of the tree (leaves of the tree) and goes up iteratively, always assessing two consecutive levels against each other (Figure 4(b)). The assessment is invoked by comparing each child with its parent. If a child is found to be better than its parent, the selected child is added to the set 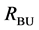


A child 

In Figure 4, the lowest level 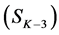


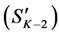


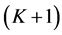
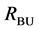
The top-down approach is similar to the bottom-up one in the sense that two consecutive levels are assessed against each other, comparing children and parent. However it differs twofold, in the order in which the levels are visited (from the root of the tree going down to the leaves), and in the segments that are selected to put in the set 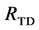

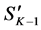


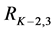

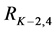
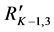
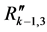
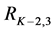
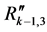
Figure 4. Graphical presentation of the search segmentation tree.
the set 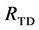
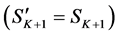
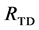
Results from the bottom-up and the top-down searches typically differ from each other, thus sets 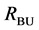



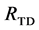
2.2.5. Post-processing of Segments
A post-processing merging algorithm may be applied on the segments of sets 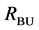
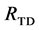
The idea is to merge in passes, starting with the most similar pairs of neighboring segments and updating the segments before the next pass, stopping when no more pairs can be merged. The algorithm works as follows:
1) Put all the segments in the initial set Regions (Regions = 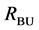

2) Create a new empty set of segments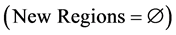
3) For every segment 
a) Color: normalized color group histogram 
b) Texture: gradient magnitude mean and standard deviation values.
4) For every segment
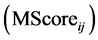




The color similarity 
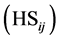

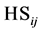
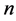

The texture similarity 

The flag NoEdge is utilized in a way that if the common boundary between two neighboring segments 
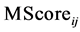
5) For every segment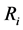
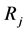

6) Once all segments have been assessed for merging, replace the working set Regions by the updated one:
7) Repeat steps 3 to 6 until no pair of neighboring segments can be merged (the set New Regions remains equal to the set Regions).
8) Replace all the segments from New Regions in the initial set (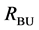
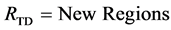
post-processing merging algorithm can be repeated once more on the combined segments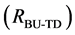
3. Shape Specific Segmentation
For specific applications, a geometrical constraint via a shape prior can be added to the system to bias the segmentation towards a particular shape. This section shows how to integrate such a constraint into the proposed methodology (see Section 2) with minimal modifications.
Here we assume that the knowledge of the prior shape is provided via vector
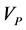
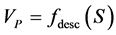
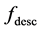
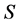


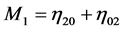



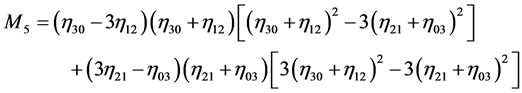

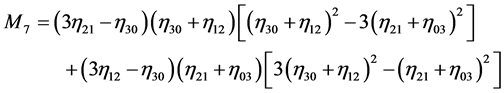
where
and,
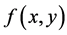



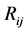

The shape similarity of a region 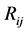
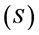
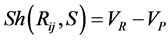
Clearly the shape similarity of the regions 

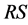
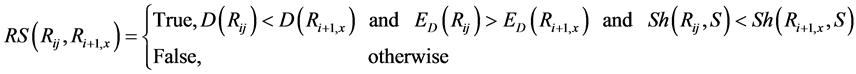
We will present the results of the addition of the shape constraint in the next section for geo-spatial aerial images.
4. Experimental Results
In this section, experimental results for various image types are presented: firstly for the general segmentation problem using the Berkeley Segmentation Dataset and Benchmark (BSDS300), and secondly for the specific application of geo-spatial aerial imagery segmentation and rooftop detection. We also demonstrate that our hierarchical segmentation scheme is applicable to other general segmentation methods.
4.1. Berkeley Dataset (BSDS300)
We tested our proposed algorithm on the publicly available Berkeley Segmentation Dataset and Benchmark (BSDS300) [25] , which consists of human segmented natural images and a benchmark that assesses the quality of a boundary detection or segmentation algorithm based on the F-measure (harmonic mean between precision and recall rates).
4.1.1. Parameter Setting
The range resolution 
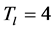


4.1.2. Benchmark Results
Figure 6 presents typical results for the BSDS300 dataset. Our method successfully finds most of the objects in a given image. However, using the mean shift algorithm for the initial hierarchical segmentation has some shortcomings when it comes to natural scenes. Because it relies on color information and the distance relationship of pixels of similar color only, the segments may not correspond to what humans would define as different objects, different textures, or parts of the same object or same texture. Incorporating cues from edge distinctiveness improves the segment selection but cannot make up for real missed edges by the mean shift algorithm.
Figure 5. Mean shift segments of a typical BSDS300 image for a range resolution (hc) of Tl = 4, Th = 16 and T = 2. Original image shown top left.
Figure 6. Sample images from BSDS300 dataset along with segmentation results of the proposed algorithm.
The algorithm has an overall F-measure of 0.642, which is similar to other recent algorithms as reported on the website of the benchmark (between 0.57 and 0.70). Methods that have achieved a higher score include an approximation of the weighted min-cover problem that extracts salient smooth curves [26] , a method based on local changes in brightness, color, and texture cues [27] , and an improvement of [27] coupling the local cues with global information obtained from spectral partitioning [28] . However, these algorithms are in fact boundary detection algorithms, and as such do not necessarily find closed segments representing objects. Our method has the advantages of being automatic, producing closed segments (true segmentation), and not requiring any parameter tuning nor training phase. Moreover, the benchmark is designed to accommodate soft boundary maps, with higher values signifying greater confidence in the existence of the boundary. Our method is penalized for producing closed binary boundaries, which may be more common for computer vision applications. Another aspect affecting the performance of any algorithm on the benchmark is related to the lack of consistency in human segmentations: the reported level of details varies from one image to another. An example would be for distinctive clouds in a sky that are sometimes segmented as different objects, sometimes completely merged as one large object with the blue sky.
4.1.3. Effect of the Different Stages
In this section, we illustrate the effect of the different stages of the hierarchical segmentation algorithm. Figure 7 shows, for a typical image, selected segments from the bottom-up and the top-down searches both before and after post-processing (


The selected segments differ according to the direction of traversal of the tree and complement each other. For instance, the bottom-up search failed to find the proper boundaries of the animal’s tail end, which were better defined through the top-down search. Combining the results allowed for a more accurate segmentation of the tail. The post-processing merging scheme was successful in removing some of the inaccurate boundaries, for instance on the animal’s body. For the bottom-up search, the post-processing reduced the number of segments from 106 to 44, and from 68 to 37 for the top-down search (there were 136 mean shift segments at 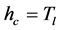

Table 1 presents the overall F-measure, recall and precision rates of the entire dataset for the different stages. The best results come from the combination of bottom-up and top-down searches after post-processing (F-measure of 0.642), which justifies the usefulness of combining the two approaches. The bottom-up search has a higher recall rate than the top-down search, but a lower precision. This observation is consistent with the expectations as the bottom-up search, starting from the most sensitive level, has a tendency to find more segments, i.e. more true boundary pixels which increases the recall rate, but also more false boundary pixels at the same time, which decreases the precision rate. The top-down search, starting from the least sensitive level, has a tendency to find less segments, i.e. less true boundary pixels, which decreases the recall rate, but less false boundary pixels, which increases the precision rate.
4.1.4. Comparison with Non-Hierarchical Version
We also have compared our hierarchical segmentation approach, using mean shift as the general segmentation method, with the standard non-hierarchical mean shift segmentation algorithm. Table 2 presents the overall F-measure, recall and precision rates of the entire dataset for values of 

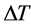
4.1.5. Applicability to Another General Segmentation Algorithm
In order to show that our hierarchical segmentation scheme can be integrated with other general segmentation algorithms that can produce segmentation outcomes at different granularities (from under to over segmentation) by varying their parameters’ values, we substituted the mean shift segmentation algorithm [19] with the graph- based image segmentation algorithm [2] . This algorithm segments images based on a predicate that measures the evidence of a boundary between two regions using a graph-based representation of the image. Its main control parameter k sets the scale of observation. It was defined as Tl = 100, Th = 1300 and T = 200 for the entire dataset. These values were selected in a way that the graph-based segments would cover from under to over segmentation for 90% of the dataset. Figure 8 shows the graph-based segments of a typical image (same as in Figure 5) for all values of k.
Table 3 presents the overall F-measure, recall and precision rates of the entire dataset for the different stages, with the best results again coming from the combination of bottom-up and top-down searches after post-pro- cessing (F-measure of 0.628).
Figure 7. Results after different stages of the proposed algorithm for a typical BSDS300 image. Segments from bottom-up search (RBU) before (a) and after (b) post-processing, segments from top-down search (RTD) before (c) and after (d) post- processing, combination of the bottom-up and top-down results (RBU-TD) before (e) and after (f) post-processing.
Table 1. F-measure, recall and precision rates for the different stages of the proposed algorithm.
Table 2. F-measure, recall and precision rates for non-hierarchical mean shift segmentations for different hc values and our proposed method.
Table 3. F-measure, recall and precision rates for the different algorithm’s stages using graph-based segmentation [2] .
4.2. Geo-Spatial Aerial Images
To test the proposed algorithm in a practical and specific application, we utilized the proposed algorithm for the segmentation of aerial geo-spatial images (Pictometry Int. Corp.’s, resolution of 0.15 meter/pixel). The test images are from suburban regions of Vancouver, BC, Canada. The parent application for this case is a rooftop detection system. Since we are interested in selecting segments from the hierarchical tree that conform better to a rooftop profile, a square model was added as the shape prior to the geometrical constraint (equation (23)).
As for the BSDS300, the range resolution 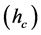


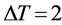
1) Light morphological cleaning (opening with a squared structural element of 9 × 9 pixels) is carried out on each segment to remove small protrusions and separate objects that could be linked by a small isthmus.
2) All segments connected to the image border are discarded since we are looking only for rooftops that are fully contained within the image.
3) Segments corresponding to vegetation are removed. An analysis of several hundred objects (rooftops and non-rooftops) has shown that green vegetation (be it grass or trees) can be distinguished from rooftops based on the saturation component of the HSV color space. A vegetation mask 



here, 


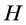
4) Segments smaller than a specific size are removed. For aerial images the minimum size of a rooftop was defined at 1000 pixels (22.5 m2).
Quantitative assessment of the results is done through four metrics which have become standard for the evaluation of man-made structure extraction [29] : shape accuracy, correctness, completeness and overall quality. The results are compared with manually delimitated ground truth data. The shape accuracy [30] , based on the overlap between the segmented rooftop and its ground truth, is estimated by:

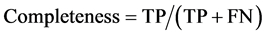

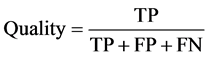
here 

Here, TP represents true positives (correctly extracted building pixels), FP false positives (incorrectly extracted building pixels), and FN false negatives (missed building pixels). When computing these results, all missing and falsely detected rooftops in Figure 9 are accounted for. When one rooftop is detected as several segments, the system is penalized accordingly, considering only the largest segment as true positives. Optimal values for the four metrics are 1 (or 100%), and the overall quality cannot be higher than neither correctness nor completeness. The mean shape accuracy is computed rooftop-wise whereas the mean values of the other three metrics are computed pixel-wise across all images.
The proposed method (Table 4) holds a shape accuracy of 84.6%, correctness of 84.2%, completeness of
Figure 8. Graph-based segments of a typical BSDS300 image for a scale of observation (k) of Tl = 100, Th = 1300 and T = 200. Original image shown on the top left.
Figure 9. Examples of aerial images that are processed by the proposed algorithm to identify rooftops. Segmentation results are shown on the second row, and results after filtering on the third and the ground truth on the last row.
Table 4. Quantitative results for geo-spatial images.
92.1% and overall quality of 78.5%. Its shape accuracy is comparable to that reported in other works (81% in [31] , 83.6% in [32] ). It performs better with the shape constraint (equation (23)) than without it. The number of buildings in the ground truth data for the first image (Figure 9, first column) was 44 out of which 43 were detected by the proposed system. 10 false positives were also detected in this case. The second image (Figure 9, second column) included 11 rooftops, which were all detected. 33 false positives were also detected. The third image (Figure 9, third column) had 10 rooftops and all of them were identified correctly but the system also identified 15 false positives. The high completeness rate reflects that most of the rooftop pixels are detected as such. Because the method was developed mainly as a general segmentation approach, in its current state it detects a substantial number of non-rooftop objects.
A simple filtering scheme was applied to discard some of the background segments. One way to increase the performance and get higher correctness and overall quality would be to filter out segments with no evident shadows. By using the image acquisition parameters in estimating the direction of the sun and the expected shadows of each segment (rooftop candidate), flat ground structures such as roads and fields could be removed, impacting the quantitative assessment metrics significantly.
5. Conclusion
An automatic segmentation approach was introduced in this paper. The proposed approach uses a hierarchical multi-layer segmentation scheme with a tree-based search mechanism to inspect the consistency of segmented regions and their relationship with each other, providing automatic adaptive parameter selection. Performance of the algorithm was showcased by applying it on different types of images including natural scenes through the Berkeley Segmentation Dataset and Benchmark (BSDS300) and geo-spatial imageries. The proposed hierarchical scheme displayed comparable performance with recent algorithms on the BSDS300 dataset, and outperformed the original non-hierarchical segmentation algorithm for the same range of parameter values. While the mean shift algorithm was used as a general segmentation algorithm to demonstrate the feasibility and usefulness of our hierarchical segmentation scheme for most results, we have also shown the applicability of the approach to other general segmentation algorithms that can produce segmentations at several granularities, such as the graph-based image segmentation algorithm. Future works include the analysis of the applicability to soft and/or stochastic segmentation environments.
Acknowledgements
The authors would like to acknowledge with gratitude NSERC Canada and MacDonald Dettwiler and Associates Ltd. for support through the NSERC Discovery Grant Program.
References
- Chen, H., Chien, W. and Wang, S. (2004) Contrast-Based Color Image Segmentation. IEEE Signal Processing Letters, 11, 641-644. http://dx.doi.org/10.1109/LSP.2004.830116
- Felzenszwalb, P. and Huttenlocher, D. (2004) Efficient Graph-Based Image Segmentation. International Journal of Computer Vision, 59, 167-181. http://dx.doi.org/10.1023/B:VISI.0000022288.19776.77
- Lo, E.H., Pickering, M.R., Frater, M.R. and Arnold, J.F. (2011) Image Segmentation from Scale and Rotation Invariant Texture Features from the Double Dyadic Dual-Tree Complex Wavelet Transform. Image and Vision Computing, 29, 15-28. http://dx.doi.org/10.1016/j.imavis.2010.08.004
- Tan, K.S. and Isa N.A.M. (2011) Color Image Segmentation Using Histogram Thresholding—Fuzzy C-Means Hybrid Approach. Pattern Recognition, 44, 1-15. http://dx.doi.org/10.1016/j.patcog.2010.07.013
- Cootes, T.F., Taylor, C.J., Cooper, D.H. and Graham, J. (1995) Active Shape Models—Their Training and Application. Computer Vision and Image Understanding, 61, 38-59. http://dx.doi.org/10.1006/cviu.1995.1004
- Staib, L.H. and Duncan, J.S. (1992) Boundary Finding with Parametrically Deformable Models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14, 1061-1075. http://dx.doi.org/10.1109/34.166621
- Wang, Y. and Staib, L.H. (1998) Boundary Finding with Correspondence Using Statistical Shape Models. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Santa Barbara, 23-25 June 1998, 338-345.
- Fussenegger, M., Roth, P.M., Bischof, H. and Pinz, A. (2006) On-Line, Incremental Learning of a Robust Active Shape Model. DAGM-Symposium, 122-131.
- Tsai, A., Yezzi, A., Wells, W., Tempany, C., Tucker, D., Fan, A., Grimson, W. and Willsky, A. (2001) Model-Based Curve Evolution Techniques for Image Segmentation. Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Kauai, 8-14 December 2001, I-463-I-468.
- Tsai, A., Yezzi, A., Wells, W., Tempany, C., Tucker, D., Fan, A., Grimson, W. and Willsky, A. (2003) A Shape-Based Approach to the Segmentation of Medical Imagery Using Level Sets. IEEE Transactions on Medical Imaging, 22, 137- 154. http://dx.doi.org/10.1109/TMI.2002.808355
- Foulonneau, A., Charbonnier, P. and Heitz, F. (2006) Affine-Invariant Geometric Shape Priors for Region-Based Active Contours. IEEE Transactions on Pattern Analysis and Machine Intelligence, 28, 1352-1357. http://dx.doi.org/10.1109/TPAMI.2006.154
- Chen, Y., Tagare, H., Thiruvenkadam, S., Huang, F., Wilson, D., Gopinath, K.S., Briggs, R.W. and Geiser, E. (2002) Using Shape Priors in Geometric Active Contours in a Variational Framework. International Journal of Computer Vision, 50, 315-328. http://dx.doi.org/10.1023/A:1020878408985
- Leventon, M.E., Grimson, W.E.L. and Faugeras, O. (2000) Statistical Shape Influence in Geodesic Active Contours. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head Island, 13-15 June 2000, 316-323.
- Rousson, M. and Paragios, N. (2008) Prior Knowledge, Level Set Representations & Visual Grouping. International Journal of Computer Vision, 76, 231-243. http://dx.doi.org/10.1007/s11263-007-0054-z
- Riklin-Raviv, T., Kiryati, N. and Sochen, N. (2007) Prior-Based Segmentation and Shape Registration in the Presence of Perspective Distortion. International Journal of Computer Vision, 72, 309-328. http://dx.doi.org/10.1007/s11263-006-9042-y
- Chan, T.F. and Vese, L.A. (2001) Active Contours without Edges. IEEE Transactions on Image Processing, 10, 266-277. http://dx.doi.org/10.1109/83.902291
- Sharon, E., Galun, M., Sharon, D., Basri, R. and Brandt, A. (2006) Hierarchy and Adaptivity in Segmenting Visual Scenes. Nature, 442, 810-813. http://dx.doi.org/10.1038/nature04977
- Paris, S. and Durand, F. (2007) A Topological Approach to Hierarchical Segmentation Using Mean Shift. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, 17-22 June 2007, 1-8.
- Comaniciu, D. and Meer, P. (2002) Mean Shift: A Robust Approach toward Feature Space Analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24, 603-619. http://dx.doi.org/10.1109/34.1000236
- Alpert, S., Galun, M., Brandt, A. and Basri, R. (2012) Image Segmentation by Probabilistic Bottom-Up Aggregation and Cue Integration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 34, 315-327. http://dx.doi.org/10.1109/TPAMI.2011.130
- Corso, J.J., Yuille, A. and Tu, Z. (2008) Graph-Shifts: Natural Image Labeling by Dynamic Hierarchical Computing. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, 23-28 June 2008, 1-8.
- Bezdek, J.C. (1981) Pattern Recognition with Fuzzy Objective Function Algorithms. Plenum Press, New York. http://dx.doi.org/10.1007/978-1-4757-0450-1
- Duda, R., Hart, P. and Stork, D. (2001) Pattern Classification. John Wiley & Sons, New York.
- Hu, M.K. (1962) Visual Pattern Recognition by Moment Invariants. IRE Transactions on Information Theory, 8, 179- 187. http://dx.doi.org/10.1109/TIT.1962.1057692
- Martin, D.R., Fowlkes, C., Tal, D. and Malik, J. (2001) A Database of Human Segmented Natural Images and Its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics. Tech. Rep. UCB/CSD-01-1133, EECS Department, University of California, Berkeley.
- Felzenszwalb, P. and McAllester, D. (2006) A Min-Cover Approach for Finding Salient Curves. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshop, New York, 17-22 June 2006, 185.
- Martin, D.R., Fowlkes, C.C. and Malik, J. (2004) Learning to Detect Natural Image Boundaries Using Local Brightness, Color, and Texture Cues. IEEE Transactions on Pattern Analysis and Machine Intelligence, 26, 530-549. http://dx.doi.org/10.1109/TPAMI.2004.1273918
- Maire, M., Arbeláez, P., Fowlkes, C. and Malik, J. (2008) Using Contours to Detect and Localize Junctions in Natural Images. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, 23-28 June 2008, 1-8.
- Agouris, P., Doucette, P. and Stefanidis, A. (2004) Automation and Digital Photogrammetric Workstations. In: Manual of Photogrammetry, 5th Edition, American Society for Photogrammetry and Remote Sensing, Bethesda, 949-981.
- McKeown, D., Bulwinkle, T., Cochran, S., Harvey, W., McGlone, C. and Shufelt, J. (2000) Performance Evaluation for Automatic Feature Extraction. International Archives of Photogrammetry and Remote Sensing, 33, 379-394.
- Ruther, H., Martine, H.M. and Mtalo, E.G. (2002) Application of Snakes and Dynamic Programming Optimization Technique in Modeling of Buildings in Informal Settlement Areas. ISPRS Journal of Photogrammetry and Remote Sensing, 56, 269-282. http://dx.doi.org/10.1016/S0924-2716(02)00062-X
- Peng, J. and Liu, Y.C. (2005) Model and Context-Driven Building Extraction in Dense Urban Aerial Images. International Journal of Remote Sensing, 26, 1289-1307. http://dx.doi.org/10.1080/01431160512331326675