Open Journal of Modelling and Simulation
Vol.02 No.02(2014), Article ID:44458,9 pages
10.4236/ojmsi.2014.22008
Predicting Traffic Congestion: A Queuing Perspective
Jojo Desmond Lartey
Department of Information Technology, Methodist University College Ghana, Accra, Ghana
Email: jlartey@mucg.edu.gh
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 January 2014; received 1 March 2014; accepted 10 March 2014
ABSTRACT
Mobility is an indispensable activity of our daily lives and road transport is one popular approach to mobility. However road congestion occurrence can be irritating and costly. This work contributes to the modeling and therefore predicting road congestion of a Ghanaian urban road by way of queuing theory using stochastic process and initial value problem framework. The approach is used to describe performance measure parameters, allowing the prediction of the level of queue built up at a signalized intersection as an insight into road vehicular congestion there and how such congestion occurrence can be efficiently managed.
Keywords:
Road Traffic; Congestion; Queues; Stochastic Process; Markov Chain

1. Introduction
Being the capital of Ghana, socio-economic factors in Accra are influencing rapid growth in vehicular population. Human population growth in the capital coupled with increased road vehicle ownership is the main factor fueling vehicular population increases. Human population growth in the capital is 4.4% above national average, and presently road vehicle ownership is increasing at 83.9% per annum [1] . Accra is one of the most populous cities in the country, and the levels of road vehicular traffic congestion now observed in Dansoman, a suburb of Accra, is a reflection of worsening urban traffic congestion experiences emanating from increased vehicular population. The volume of vehicular traffic on these roads increases during rush hours to and from work, during which a journey could take much longer time. Also there are certain odd times, outside the rush hours, when this congestion phenomenon had occurred unexpected.
Road traffic management (RTM) in Ghana, like most developing countries, has been very challenging and most attempts to address the problem have yielded little results [2] . This includes arterial routes expansion to accommodate increased vehicular traffic volume, mass transport facility and road junction control measures among others. Given the factors fuelling vehicular population in the capital, Accra roads appear woefully inade- quate to match present vehicular population on our roads. This disparity is causing road traffic congestion, which is crippling mobility in the capital and gradually grinding economic activities in the city to a halt. Road traffic signal used as a road junction control measure to minimize congestion currently is inadequate. This is evi- dent from the observation that although the majority of the signal lights have been revamped, they are being augmented currently by human traffic wardens (TW) to manage the situation. On countless occasions have I observed activities of these wardens on traffic flow rates at signalized junctions during peak hours and their interventions amazingly make positive impact on the congestion problem. Clearly automatic signal control approach to traffic management is not working as expected and delays due to road congestion and its accompanying cost is weakening the economic impact of urban road transport. Given that roads are constantly used by vehicles at all times, human intervention for optimal road vehicular traffic control by TW cannot be avoided, especially for developing economies like Ghana. Also given that the disparity in road expansion and road vehicular population increases, the positive impact of TW on road traffic congestions is likely to be inefficient if traffic flow and evolution, especially for the unexpected congestions, is not accurately predicted.
However relatively little attention, by way of research, has been given to this congestion problem in the urban towns of Ghana. A scientific approach investigation of the problem could encourage the improvement of transport policies and strategies in place to mitigate this economic debilitating spate of congestion on our roads. For instance as a first step towards prescribing a solution to the problem, the ability to forecast traffic volumes for any time period, especially those critical periods, cannot be over emphasized. This forecast approach also has the capacity to directly support proactive traffic control, including educated deployment of TW to critical areas as well as accurate travel time estimations.
The primary contribution of this paper is to demonstrate a modeling of traffic evolution on an arterial road to Malam highway that serves surrounding suburbs and communities. Other possible benefit of this work is that it serves as a basis to other interesting investigations to characterize traffic congestion and the results obtained may serve as vital inputs to decisions that seek to improve traffic control and management. The objective therefore is to investigate the problem of congestion on the road segment and subsequently build upon this investigation to develop efficient tools capable of predicting and providing intelligent information on vehicular traffic flow.
Queues are waiting lines which occur whenever units must wait for a facility because the facility may be busy and therefore it is unavailable to render service required. The study of queues describes this phenomenon and since Erlang’s pioneering work for queuing theory, a number of authors have applied the theory in many areas (see [3] - [7] and reference therein) including its extensive practical application in most performance analysis. This work contributes to the application of queuing theory, to model the traffic congestion problem identified, using stochastic processes framework, to a signalized road intersection. We solve the model’s system of differential equations by initial value problem method. We then attempt to give a performance measure analysis to describe traffic intensity variations. The next section gives a theoretical background to model the traffic flow at the road intersection. Section 3 focuses on application of the theory to data obtained from Dansoman signalized junction, on the Malam-Kaneshiee Road while Section 4 serves as the concluding section, giving insights gained from the results as well as suggestions to overcome the undesirable descriptions that the results indicate.
2. Theoretical Background
This section gives the theory used in this work including brief general features of a queuing systems as well as the concept of stochastic process description of a Markovian queuing system from which time dependent transi- tions obtained using initial value problem approach and various performance measure characteristics deduced.
2.1. Features of a Queuing System
Typically any queuing system is composed of units, referred to as customers, needing some kind of service and who arrive at a service facility, join a queue if service is not immediately available, and eventually leave after receiving the service. A server refrerrs to mechanism that delivers service(s) to the customer. If upon arrival a “customer” finds the server busy, then s/he may form a queue, join it or leave the system without receiving any service even after waiting for some time [8] [9] . This therefore permits a number of different possible con- figurations such as the following, used in this work, to describe vehicular traffic flow as a queuing system:
1) Customers are vehicles using the road infrastruction at the signalized intersection for which the traffic light in use to regulate vehicular flow through the intersection is the server.
2) Vehicles arrive randomly as units and form a single file of waiting line until they are served by a server.
3) Vehicles are served individually in parallel, according to the order in which they arrived.
4) The Arival Pattern: This is the manner in which arrivals occur, indicted by the inter-arrival time between any two consecutive arrivals. For our stochastic modelling framework, the inter-arrival time may vary and may be described by a specific probability distribution that best describes the arrival pattern observed.
5) Arrival Rate : This is the average number of vehicles arriving per unit time.
: This is the average number of vehicles arriving per unit time.
6) The Service Pattern: This is the manner in which the service is rendered and is specified by the time taken to complete a service. Similar to the arrival pattern, distribution of the service time must be specified under sto- chastic modelling considerations.
7) Service Time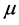 : This gives the average number of vehicles served per unit time.
: This gives the average number of vehicles served per unit time.
8) Server Utilization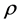 : This gives the average utilisation of the server, given by
: This gives the average utilisation of the server, given by 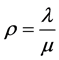
9) Mean Service Time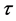 : The time to serve a designated customer.
: The time to serve a designated customer.
10) Mean Waiting Time T: The average time spent in the queue by a customer who receives a service.
11) Mean Queue Size N: The Average number of customers in the system for service
The quality of service one receives could be judged, at least in part, by the length of time one waits in the queue for service and this is very much influenced by what constitutes the configurations of the syetem. We can indicate this configuration as A/B/C/X/Y/Z, [10] - [12] , according to Kendall-Lee notation, where the symbols A, B, C, X, Y, and Z respectively indicating the inter-arrival time distribution, the service time distribution, the number of servers, the system capacity, the population size and the queue discipline. For instance M/M/2/FCFS/ 6/∞ refers to a queuing system that possesses a Markovian Poisson arrivals, Markovian exponential service, two servers, first come first served (FCFS) queue discipline, a limit of six customers in the queue and an unlimited source of customers in the population.
2.2. Stochastic Processes
We let 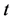 be a parameter that assumes values in a set
be a parameter that assumes values in a set , and let
, and let  represent a random variable for every
represent a random variable for every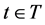 . Then
. Then 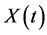 gives the rule describing the observed non-deterministic behaviour of the traffic system being modelled and any collection of
gives the rule describing the observed non-deterministic behaviour of the traffic system being modelled and any collection of  constitutes a stochastic process [13] whose index
constitutes a stochastic process [13] whose index 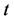 interprets the time element of the physical evolution of the system.
interprets the time element of the physical evolution of the system.  describes the state of the process at time t while the elements of T indicate time epochs. In this case
describes the state of the process at time t while the elements of T indicate time epochs. In this case 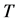 is a linear set and may result in a discrete- time process or a continuous-time process. For example,
is a linear set and may result in a discrete- time process or a continuous-time process. For example,  can be described as discrete-time process while that
can be described as discrete-time process while that  can also be described as a continuous-time process. The set of all possible values that the random variable
can also be described as a continuous-time process. The set of all possible values that the random variable 




1) Distribution of the number of vehicles 

2) Distribution of the waiting time in the queue, the time that an arrival has to wait in the queue. Suppose 

3) Distribution of the virtual waiting time 
4) Distribution of the busy period being the length (or duration) of time during which the server remains busy. The busy period is the interval from the moment of arrival of a unit vehicle at an empty system to the moment that the channel becomes free for the first time. This therefore constitutes a random variable.
2.3. Markov Chain
Suppose that we observe the state of the vehicular traffic at discrete time points t = 0, 1, 2,… for which suc- cessive time points define a set of random variables (RVs)










Equation (1) indicates a relation of dependence between the RVs 


Given that the state space 





have a time homogeneous continuous Markov Chain. A discrete time Markov chain in which transitions can happen at any time is known as continuous time Markov chain [13] . Now given the non-deterministic nature of the observed vehicular traffic, such stochastic description of the queuing build-up is realistic and appropriate for dynamics of the traffic congestion as a queuing system.

2.4. Time Dependent Transitions for M/M/1 Queue
Suppose that 



where







miting probability that there are 






If we consider two sets of limiting probabilities 










For a queuing system of many vehicles and one server, suppose 




time-dependent transition probabilities for this Markov chain, let 
tion vector for the states “being served” and “finished being served” so that 



distribution vector becomes
If we let 

time step is given by 

the corresponding matrix equation in (6).

Performing matrix multiplication then we have 

Applying differential calculus and taking limits so that 


and whose solution using Initial Value Prblem approach, is given by Equation (8b).


Since we assumed that there is an individual initially being served, then for initial conditions 




Also since 

2.4.1. Service Time
Let T denote the time at which service is completed. This is considered to be the time taken for making a transi- tion from one state to another, then T is a continuous random variable with range












Thus the reciprocal of Equation (10f) gives 
2.4.2. Unbounded Queue
Suppose at each instant of time, the queue is in a certain state 






















If we let the traffic intensity 




rate increases and approaches the mean service rate, the






Therefore substituting Equations (13b) into Equation (12), gives Equation (14) the probability that the queue is in state 

2.4.3. Computing the Mean Queue Size N
Now to compute the mean queue size



2.4.4. Computing the Mean Wait Time T
Suppose the queue is empty (state 0) when an item arrives, then the server will begin processing the item im-
mediately, and the item will spend the mean service time 
queue is in State 1 when an item arrives, the item will spend twice the mean service time in the queue before de-
parting and this will have a value of






3. Application
In this section, we apply the theory to data we collected for the traffic flow through Dansoman junction, on Malam-Kaneshie urban road. The junction is signalised with traffic lights and so constitutes a queuing system. We consider the application to traffic stream of vehicular movement and in this case the road vehicles constitute our arrivals process, the traffic light signal at the intersection is the server and the controlled passage gives the service process, with the green light as the service mechanism. The population in this case is of the infinite type. Table 1 gives the number of vehicles arriving at the queue in the Dansoman intersection for six days during which the arrivals were noted every 5 minutes from 07:30 hours to 08:00 hours. We also observed the green
Table 1. Six day-week vehicle traffic count for dansoman junction intersection.
light duration when vehicles flow through the intersection, given by Table 2 and this allows the service time to be obtained.
We also found out from observation that each vehicle spends an average of 240 second to traverse a distance of 0.6 kilometres which accommodates 65 vehicles on the average. We therefore have the waiting time and the queue length as 240 seconds and 65 vehicles respectively.
Accordingly we obtained the average arrival rate for the period as
Figure 1, observe the random nature of the arrival counts and thus we assume Markovian arrival rate.
We then determine the service rate

served that the average service time 






queue length and therefore waiting time that can spelling catastrophic condition such as those perpetual con- gestions observed during the morning rash hour period. Also note the observed queue size of 65 vehicles as well as an average waiting time of 240 seconds. These values respectively compares with the theoretical values of 



For a fixed mean service rate, when 


most of the time. Also the mean wait time
the queue is empty, the item will wait in the queue for one mean service time. As the load on the queue increases, the mean queue size and the mean wait time will increase. When items arrive in the queue as fast as there are departing ones then 



4. Conclusion
We have in this work, measured the traffic flow at the Dansoman Junction of Malam-Kaneshie urban road during the morning rush hours and have demonstrated features of the queue built up at the signalised inter- section with data and modeled the traffic flow there as a M/M/1. We have shown that the current queue system will continue to develop heavy traffic, evident by the growing queue length and waiting time, during the peak hours. This obviously has quality of service (QoS) implications for the system at the moment evident from the traffic intensity estimates from the data collected. This work therefore gives insight into possible undesirable le- vels of vehicular traffic congestion and the obvious question is how to minimise or at least contain these unde- sirable levels in order to optimise waiting time at the intersection. Possible line of attack includes the use of
Table 2. Observed green light duration for vehicles served.
Figure 1. Plots of Dansoman junction sampled morning rush hour traffic count.
signal time adjustments or increase in the road infrastructure. We explore this in our further work from which we report on realistic approach of mitigating the problem thereby improving the QoS performance.
References
- The Ministry of Information Ghana (2011) Meet the Press Series. www.ghana.gov.gh/index.php/information/meet-the-press/3786-meet-the-press
- Abane, A.M. (1993) Tackling Traffic Congestion in Accra, Ghana: A Road User’s Perspective. Journal of Advanced Transportation, 27, 193-206. http://dx.doi.org/10.1002/atr.5670270205
- Cox, D.R. and Smith, W.L. (1961) Queues. John Wiley, New York.
- Kleinrock, L. (1976) Queueing Systems. John Wiley & Sons, New York.
- Kelly, F.P. (1979) Reversibility and Stochastic Networks. John Wiley & Sons, New York.
- Daduna, H. (2001) Queueing Networks with Discrete Time Scale. Lecture Notes in Computer Science. 2046 Volumes. Springer-Verlag, Berlin Heidelberg, 1-7.
- Kothari, C.R. (2007) Quantitative Techniques. Vigas, Bnagalore.
- Waters, D. (2008) Quantitative Methods for Business. Printice Hall, Essex.
- Gupta, M.P. and Khanna, R.B. (2007) Quantitative Techniques for Decision Making. Prentice Hall, New Delhi.
- Gross, D. and Harris, C. (1998) Fundamentals of Queuing Theory. 3rd Edition, John Wiley, Chichester.
- Forbs, C., Evans, M., Hasting, N. and Peacock, B. (2011) Statistical Distribution. John Wiley & Sons Inc., New York.
- Castañda, L.B., Arunachalam, V. and Dharmaraja, D.D. (2012) Introduction to Probability and Stochastic Processes with Applications. John Wiley, New York. http://dx.doi.org/10.1002/9781118344972
- Medhi, J. (2003) Stochastic Models in Queueing Theory. 2nd Edition, Esevier Inc., Berlin.
- Calvert, J. and Voxman, W. (1994) Finite Mathematics. McGraw-Hill, New York.
- Weisstein, W. (1984) CRC Concise Encyclopedia of Mathematics. Chapman and Hall, New York.
- Cox, D.R. (1955) A Use of Complex Probabilities in the Theory of Stochastic Processes. Mathematical Proceedings of the Cambridge Philosophical Society, 51, 313-319.
- Krajewski, L.J., Ritzman, L.P. and Malhotra, M.K. (2007) Operations Management: Process and Value Chains. 8th Edition, Printice Hall, New York.
- ONeil, P.V. (1993) Advabced Engineering Mathematics. 3rd Edition, PWS, Boston.
- Boyce, W.E. and Di Prima, R.C. (1992) Elementary Differential Equations and Boundary Value Problems. 5th Edition, John Wiley & Sons, New York.










