International Journal of Geosciences
Vol.06 No.11(2015), Article ID:61343,12 pages
10.4236/ijg.2015.611096
Comparison and Validation of the Recent Freely Available DEMs over Parts of the Earth’s Lowest Elevation Area: Dead Sea, Jordan
A’kif Al-Fugara
Department of Surveying Engineering, Faculty of Engineering, Al al-Bayt University, Mafraq, Jordan

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 12 October 2015; accepted 20 November 2015; published 23 November 2015

ABSTRACT
The present research study assesses the accuracy of two recent freely available ASTER-GDEM ver.2, SRTM ver.4.1 digital elevation models for parts of the lowest area on the earth on the shores of the Dead Sea, the site located over areas with high variation in topography within the “humratessahan” watershed, where the elevation varies between 700 m above sea level in the north east of the watershed to 210 meter below sea level. The reference elevation data used in this study are topographical points extracted from existing digital vector topographical map published by Royal Jordanian Geographical Center (RJGC). However, the contour lines do not cover the whole area especially in the flat areas where elevation is less than the contour line interval. Therefore, the second reference data created with photogrammetric techniques from stereoscopic pairs of aerial photos had been used for the surface to surface comparison and elevation profiles assessment purpose. It is demonstrated that the vertical accuracy of ASTER-GDEM ver.2 is 22.223 m (Root Mean Square Error (RMSE)) against reference elevation data, while the SRTM ver.4.1 has an RMSE of 15.858 m; the statistics results indicate that the theoretical accuracy is achievable and meets the expected accuracy specification. Furthermore, as for its unprecedented detail, it is believed that the photogrammetric derived DEM offers an alternative in accessibility to high-quality elevation data with vertical accuracy of 0.78 m (Root Mean Square Error (RMSE)).
Keywords:
ASTER-GDEM ver.2, SRTM ver.4.1, Aerial Photos, Vertical Accuracy, Dead Sea

1. Introduction
A digital elevation model (DEM) is a three-dimensional (3D) digital representation of ground surface topology or relief using two-dimensional (2D) raster file consisting of terrain elevations for ground positions at regularly- spaced horizontal intervals [1] [2] . DEM-derived topographic parameters such as slope, aspect, and curvature are the most vital and elementary data source to a variety of earth observation platforms which provide the basic information required to characterize the topographic attributes of terrain [3] . DEM data have been becoming more popular with the invention of Geospatial Information Systems (GIS) and spatial numerical computer-based models [4] . DEMs have become very significant and efficient tool in geo-hazard mapping and prediction: flood inundation mapping and modeling [5] ; landslide susceptibility mapping and land subsidence mapping [6] . Review of DEM applications in hydrological modeling, geomorphologic analysis, and biological applications can be found in [7] .
Currently, a variety of different methods are being used for DEMs generation. It can be interpolated from contour lines obtained from topographic maps [8] , or from irregularly spaced three-dimensional spot heights points collected from terrestrial surveying measurements [9] , digital aerial and terrestrial photogrammetry with stereo aerial photogrammetric method using stereo data [10] , optical satellite sensor images from space [11] , active airborne laser scanning technique [12] , and interferometric synthetic aperture radar [13] . DEMs generated using these techniques are available at multiple resolutions in digital format. In particular, digital aerial photogrammetry is a powerful tool in surface model generation and extracting of high resolution DEMs by means of using stereo photos data. However, in many developing countries, the only sources of DEMs are the freely ones on the web. In this study, three techniques and their results will be compared against accurate heights obtained from topographic maps and spot heights points collected from terrestrial surveying measurements. The DEM extracted based on digital aerial photogrammetry, the latest release of the Advanced Space-borne Thermal Emission Reflectometer DEM (ASTER GDEM2) and DEMs based on the Shuttle Radar Topography Mission (SRTM) as released by the United States Geological Survey (SRTM3 USGS version 2.1) and by the Consortium for Spatial Information (SRTM CGIAR-CSI version 4.1).
The Shuttle Radar Topography Mission (SRTM) generated one of the most-complete high-resolution digital topographic data sets of the world to date [14] . SRTM collected synthetic aperture radar (SAR) interferometry (InSAR) using two antenna pairs operating in C- and X-bands, simultaneously illuminating the earth’s surface and recording backscattered radar signals onboard the Shuttle Endeavour, which has been used by the Jet Propulsion Laboratory (JPL) to generate a near-global topography data product for earth’s surface between latitudes 60N and 57S. Since the initial release in 2003, the SRTM DEM (hereafter called SRTM) has been improved several times, culminating most recently with Version 4. SRTM Version 4, which has a 3 arcsec (approximately 90 m × 90 m) ground resolution, is reported to have a vertical error of less than 16 m at a 90% confidence level scale [15] . When SRTM data were released, and due to its vertical accuracy of approximately 15 m or better on 30 m geographic cells, they quickly became attractive for various applications [16] .
The ASTER GDEM version 2 (GDEM2) was released globally for free of charge by National Aeronautics and Space Administration of United States (NASA) and the Ministry of Economy, Trade and Industry of Japan (METI) on October 2011. The ASTER GDEM covers land surfaces between 83˚N and 83˚S at a spatial resolution of 1 arc-second (approximately 30 m at the equator. Improvements in the GDEM2 result from acquiring 260,000 additional scenes to improve coverage. A validation study carried out by joint US-Japan ASTER GDEM v.2 has demonstrated an absolute average vertical accuracy within −0.20 meters with reference to 18,000 geodetic control points over the CONUS, with an accuracy of 17 meters at the 95% confidence level [17] . So it will be a practical product for many applications, such as radar interferometry, topographical analysis, hydrological studies, disaster and environmental monitoring.
Numerous studies were carried out for external validation of SRTM and ASTER elevation data using various kinds of reference data and reference DEMs [18] -[23] . Some of these studies have focused mainly on their preliminary or other releases, covering different continental areas, but not the lowest point on the earth at area below sea level. For this reason, the present study was undertaken to assess the vertical accuracy of ASTER GDEM2, SRTM version 4.1 by comparing them with two reference data generated from aerial photogrammetry and topographical maps over part of the lowest area on the earth on Dead Sea shore, Jordan.
2. Material and Methods
2.1. Study Area
The study area is located in Western Jordan to the South-East of the Dead Sea. It extends from the Western part of Salt city near Kufur Huda to Dead Sea shoreline covers an area of 45.9 km2. The survey are located between E longitudes 35˚36'50" to 35˚42'16" and N latitudes 32˚4'44" to 32˚7'31". Terrain elevation varies from −210 metres below mean sea level close to the Dead Sea, earth’s lowest elevation on land, and increases towards the east to 700 meters at west of Salt city. The relief of the study area varies from completely flat areas to mountainous regions with steep slopes. This region presents great interest and has attracted attention from various scientific research disciplines where DEMs have a significant contribution, including geological and geomorphological applications, land subsidence and other geophysical or environmental studies. Many dendrites Wades are also present in the area. The flow direction of these Wades is directed from northeast to southwest (NE-SW). Figure 1 shows the location map of the study area.
2.2. Available DEMs
Two open source DEMs with different precision and coverage were used for the study: 1) the Consultative Group for International Agriculture Research Consortium for Spatial Information Shuttle Radar Topographic Mission version 4.1 (CGIAR-CSI-SRTM v4.1); 2) Advanced Space-borne Thermal Emission and Reflection Radiometer-Global Digital Elevation Model version 2 (ASTER GDEM v.2).
2.2.1. SRTM
The most recent SRTM 3-arc-second product (90 m resolution) product has been treated by Consultative Group for International Agriculture Research Consortium for Spatial Information (CGIAR-CSI) and is available online through the CGIAR-CSI download database [24] . The SRTM digital elevation data provided by CGIAR-CSI has been processed to fill data voids, and to facilitate their ease of use in a variety geospatial and GIS applications. The DEM files are available for download as 5 degree × 5 degree tiles, in geographic coordinate system- WGS84 datum, from which tiles No. 4406 was downloaded. These files are available for download in both Arc-Info ASCII format, and as GeoTiff. The file was uncompressed at first, then ArcGIS is used to convert it to UTM projection and written to “geotiff” format, then the data was referenced to/UTM 36N, WGS84.
2.2.2. The ASTER GDEM V.2 Dataset
The ASTER GDEM V2 dataset is available from multiple websites (e.g. Japan Space Systems ASTER GDEM webpage) as 1˚ × 1˚ tiles, with 30 m cell size. ASTER GDEM was downloaded on the official distribution site (http://www.gdem.aster.ersdac.or.jp). GDEM is in a geographic coordinate system, with the World Geodetic System 1984 (WGS84) horizontal datum and the Earth Gravitational Model 1996 (EGM96) vertical datum.
2.2.3. Reference Elevation Data
The accuracy evaluation of SRTM and ASTER height models was carried out by comparison over the study area with two reference data sets, provided respectively by topographical map and a DSM generated by aerial stereo pair photos.
1) Reference data extracted from topographical map
The accuracy assessment of the DEMs requires a huge number of checkpoints with high accuracy to obtain reliable measures [25] . For the purpose, in this study, the reference elevation data used are topographical points extracted from existing digital vector topographical map published by Royal Jordanian Geographical center (RJGC) in 2007, including contour lines with 10 m intervals and spot height elevation data. Contour lines were derived from aerial photos of the study area captured on 2004, and additionally Spot height elevation data were surveyed and modified during 2010. The data are projected in WGS 1984 (UTM). All the 430,240 points extracted from the topographical map through conversion of the contour lines into XYZ points were compared with their corresponding points in the examined DEMs (Figure 2). However, the contour lines do not cover the whole area. In flat areas with elevation less than 10 m, there are no contour lines. Therefore, the second reference data was used.
2) DEM generation from aerial photo stereo pairs
Figure 1. Location of the test site plotted on photogrammetric-derived DEM.
Figure 2. Subset of the study site and the distributions of reference points extracted from contour lines.
The digital elevation model have been developed from stereo pairs of colour aerial photographs were acquired from the aerial photo archives at the Jordanian Royal Geographical Jordanian Centre (JRGC). These images were acquired using a Leica RC 30 Aerial Camera Systems of focal length 153.28 at a 1:25000 nominal scale along 2 strips with an approximate image overlap of 70% in flight. The photo negatives were scanned with a photogrammetric precision scanner at resolution of 20 μm resulting in an approximate ground pixel resolution of 0.50 m and later were compressed in a TIFF format. Each frame has associated with camera calibration report including information relating to the focal length, lens type and acquisition date. An integrated geo-referencing exploiting 10 ground control points was conducted in the reference system WGS84 UTM Zone 36N, which was used for all further investigations. The images orientation and point extraction procedures were carried out using SOCET SET software packages. The standard procedure to generate a DEM using automated stereo-correlation process is based on fundamental steps that consist in interior orientation, exterior orientation (registration into a defined reference system) and point extraction [11] . SOCET SET provides translators converting digital terrain data and feature data into several standard international formats, which are DTED, ASCI DTM, ARC Grid, DGN Post, and SDTS. Shape file format was selected for this project implementation. Figure 3 illustrates the final resulted elevation points generated with photogrammetric SOCET SET software.
2.3. Data Preparation and Geo-Referencing
The two DEMs were converted into square tiles of identical binary data format but with different spatial coverage (SRTM: 3 degrees × 3 degrees, ASTER: 1 degree × 1 degree) and stored in a 16 bit integer format, which is a sufficiently precise digital representation of the elevations. In order to compare the elevation models, all DEMs and reference data of the study sites were transformed into the same projection system―Universal Transverse Mercator (UTM) zone 36 north. WGS 1984 was selected as both datum and spheroid. The original 90 m resolution of the SRTM was resembled to 30 m to enable comparison with the ASTER GEODEM data. A cubic convolution method is used for the re-sampling process with the resulting grid size of 30 × 30 m. Then, the data were cut to create the largest rectangle possible shaped dataset by clipping SRTM and ASTER DEMs over Photogrammetric DEM. Finally, no misalignment between DEMs was assured.


Figure 3. (a) The final resulted elevation points generated with photogrammetric SOCET SET software; (b) DTM as Shape File shown in ARCGIS software; (c) 3D perspective view of the study area. DEM was draped by the mosaic image.
2.4. Validation Methods
In order to describe and compare the Accuracy of elevation values of each DEM, DEM differencing was performed at first to derive elevation error maps. From a statistical point of view, the vertical accuracy of the three elevation data was assessed by computing the differences between the DEM pixel value and the corresponding reference elevation points. For each point, an elevation error was computed as the difference between explored and reference data Equation (1):
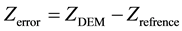 (1)
(1)
In Equation (1), Zerror is the elevation error, ZDEM is the elevation value of the DEM being explored, and Zrefrence is the corresponding reference elevation point value. Positive differences represent locations where the DEM elevation exceeded the reference elevation points; and, conversely, negative errors occur at locations where the DEM elevation was below the reverence elevation points.
After that, a common measure of quantifying vertical accuracy in DEMs, was calculated for each DEM’s errors. among them the mean error (Meanerror), maximum error (Meanerror), minimum error (Minimumerror) error, standard deviation error (STD), Sample Variance (σ2), and root mean square error (RMSE) values were calculated as follows in Equations (2)-(5) [26] .
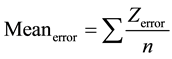 (2)
(2)
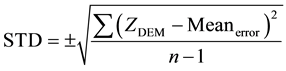 (3)
(3)
 (4)
(4)
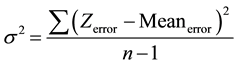 (5)
(5)
Correlation scatter plots were performed to assess the level of correlation between the DEMs values and reference elevation values. Three scatter plots were produced and correlation coefficient determined. correlation coefficient represents the association between two variables or the degree of co-variation of the two variables or the tendency of variable to vary together in the sense that one increases as the other increases (positive co-variation) or in the sense that one variable increases as the other decreases (negative co-variation). Finally, longitudinal Profiles were extracted on the DEMs using the 3-analyst extension in ArcGIS at 30 m interval, along the longest study area dimension, and the data exported to excel for comparison, taking into account, the profile path to pass through various elevation, slopes, and aspect. Profiles of the three DEMs were plotted and compared.
3. Results and Discussion
Table 1 shows the summary statistics for elevation errors of ASTER-GDEM ver.2, SRTM ver.4.1, and aerial photo-derived elevation errors over the study area. The difference of the mean value (mean elevation difference) for the SRTM, ASTER, and aerial photogrammetric elevations are +3.7 m, −4.7 m, and +0.87 m respectively. The difference in the maximum values (highest elevation difference) for the SRTM, ASTER, and aerial photo- grammetric elevations are +49 m, +54 m, and +13 m respectively, where the minimum values (lowest difference) for the SRTM, ASTER, and Aerial photogrammetric elevations are −52 m, −58 m, and −12 m respectively. The overall absolute vertical accuracy expressed as the vertical RMSE, which is the standard measure of DEM’s vertical accuracy taking into account both random and systematic errors introduced during the data generation process. It measures the difference between the values of the DEM elevations and the values of corresponding reference elevations. It is currently widely adopted mostly because it is a comprehensive statistic and because it is easy to implement [27] . In this study, the RMSE of SRTM DEM in relation to a reference DEM (ASTER DEM) was calculated. It is demonstrated that the vertical accuracy of ASTER GDEM2 in term of RMSE against reference elevation is 22.223 m, while for the SRTM v4.1 DEM the RMSE is 15.858 m against reference
Table 1. The summary statistics for ASTER, SRTM, aerial photo-derived elevation over the study area.
elevation. Results are in agreement with the expected theoretical values achieved in previous studies. It was confirmed that the vertical accuracy of ASTER GDEM is 26 m (root mean square error (RMSE) against GPS-GCPs [28] [29] . [30] have attained the same estimated accuracy of GDEM for two different regions in western Germany and the Eastern Desert of Egypt. Further, [31] investigated the total RMSE values of GDEM evaluated by over Istanbul are 20 m or better compared with the reference DEM generated from 1:5000 scaled topographic maps. On other hand, SRTM mission specifications [32] , SRTM was estimated to generate DEMs with a vertical RMSE of 16 m equivalent vertical accuracy requirements for topographic data at scale 1:250,000 that meet the USA map accuracy standards [33] . Further, the statistics shows that the vertical accuracy of photogrammetric DEM is RMSE of 0.78 m which is close to the previous studies reported that the vertical accuracy of the DEM is a function of photo scale and is estimated as 1/9000th of the flying height of the aircraft carrying the camera system [25] [34] . In this study, the average flying height of the photographs was about 4000 m and which resulted in a vertical error of 0.55 m.
The relative vertical accuracy is expressed as the standard deviation of the vertical error [34] . It is especially important for derivative products that make use of the local differences among adjacent elevation values, such as slope and aspect [19] [23] [35] . The values of standard deviation of SRTM, ASTER, and aerial photo derived DEM difference are ±6.349 m, ±9.897 m, and ±1.35 m respectively. Standard deviation value illustrates the spread of elevation difference values around the mean error value for each study. The statistics show that ASTER error is more variable (wider spread) than for SRTM and aerial photo which characterized by longer right tail data, the variance is sensitive to unusually high or low values, and smaller standard deviation and consequently smaller variance and consequently smaller variability. It is generally believed that ASTER is inconsistent comparing to SRTM and aerial photogrammetric DEM, the higher the st.dev value, the more vertical accuracy diverse from place to another and it is affected by the stack number of stereo images and slope [36] .
The histograms of the differences between DEMs and the reference elevation data (Figure 4) are closely follow a normal distribution. However, for the SRTM difference histogram present a positive mean error of 3.2 m (Mean ERROR), Which is illustrated in the histograms (Figure 4(a)) with positive bias observed, indicating that the SRTM Elevation Modem of positive errors greater than those of the negative errors (overestimated the terrain elevation). A general overestimation of terrain elevation of SRTM observations were further confirmed in many previous studies [20] -[22] . While the photogrammetric elevation model errors present a slight positive mean error close to zero (mean error of 0.82 m). A value of St. Dev. close to zero indicates that the tails on both sides of the mean are balance out, which is the case for a typical symmetric distribution (Figure 4(b)). The basic statistics of errors in ASTER show a negative mean error of −4.7 m. The histograms of elevation differences (Figure 4) present a slightly negative skew, indicating a clear negative bias for ASTER with respect to reference elevation data, where the ASTER model underestimates the spatial distribution of terrain elevation, this underestimation of ASTER was noted in previous studies [22] [23] [37] .
The correlation plots between reference elevation data and each of the three DEMs obtained are shown in Figure 4(e) and Figure 4(f). As mentioned earlier, these plots are based on a selection of 430239 reference elevation points. Results illustrate that SRTM v4.1 and photogrammetric elevation data elevation values are slightly better correlated to the reference than ASTER. The correlation coefficients are 0.999, 0.985 and 0.999 for ASTER, SRTM v4.1 and GMTED2010, respectively. All stations extend the line of perfect fit, showing excellent coefficient of correlation. This could be due to the large number of used points and well distribution of selected points.
Finally, assessment of DEM’s vertical accuracy is carry out by comparing the elevation profiles of the three DEMs plotted using Excel sheet. The profiles have been chosen to pass through area of different elevations with both steep and gentle slope terrains at a variety of aspects (Figure 5).
It can easily be observed that the three profiles demonstrated similar trend, but with minor different sills (Figure 6). The SRTM profile is much closer to the photogrammetric DEM profile than those of ASTER. Therefore, the plotted profile emphasized SRTM has an accuracy superior to ASTER GDEM2 when compared to the photogrammetric DEM elevations profile as reference profile. ASTER profile obliviously, is lower than DEM based photogrammetric profiles, while SRTM is generally upper than photogrammetric DEM profile, it can be seen that the results obtained in this section further confirm the earlier finding that ASTER GDEM underestimates elevation whereas SRTM overestimates. The quantity of overestimation of SRTM is less than the quantity of underestimation of ASTER GDEM. In other words, SRTM is “closer” to the reference than ASTER GDEM.
Figure 4. Histograms of elevation errors and relevant descriptive statistics: (a) SRTM v4.1 minus reference elevations; (b) ASTER GDEM2 minus reference elevations; (c) Photogrammetric DEM minus reference elevations. Scatter plots of reference elevations vs. (d) SRTM v4.1; (e) ASTER GDEM2; and (f) Photogrammetric DEM.
Figure 5. 3D perspective view of the study area. DEM was draped by the mosaic image. Green line shown transects used for plotting elevation profiles
Figure 6. Profiles of the three DEMs: The red, green and blue profiles represent SRTM v4.1, photogrammetric DEM and ASTER GDEM2, respectively.
4. Conclusion
The accuracies of recent near-global DEMs-SRTM V.4 and ASTER GDEM2 free available digital elevation models were validated against a reference elevation data collected from digital cartography generated using hypsographic and hydrographic data from a 1:50,000 topographical map produced by the SDG, and compared with aerial photogrammetric derived DEM created with photogrammetric techniques from archive aerial photos over the lowest area on earth, where the elevation varied between 700 m above sea level in the north east of the watershed to −210 meter below sea level on the shores of the Dead Sea. DEM differencing frequency histograms, computation of horton statistic, correlation plots, and, profiling are some of the methods employed in the comparison. The validation results reveal a RMSE value of about 5.3 m of ASTER GDEM2 vs. reference data, which are slightly greater than the RMSE values of SRTM (7.6 - 25.0 m); however, photogrammetric RMSE (4.5 m) has the lowest RMSE value of (0.78). Results obtained indicate that, the overall accuracy (in terms of RMSE) of both SRTM, and ASTER GDEM is in line with the reported official accuracy specifications [38] [39] . Furthermore, the photogrammetric DEM accuracy is consistent with the reported previous studies reported that the vertical accuracy of the DEM is estimated as 1/9000th of the flying height [25] . The linear regression analysis revealed strong correlation between the three DEMs and the reference data. The linear regression data showed this correlation to be highly significant for the study area. In fact the value of the slope of the regression line was very close to 1 (0.985, 0.999 and 0.999 for ASTER GEODEM v.2, SRTM v4.1 and photogrammetric DEM, respectively). The visual analyses of the ASTER GEODEM v.2, SRTM v4.1 plotted profiles taking photogrammetric DEM based profile as reference; the results revealed that ASTER GDEM has an underestimation of elevation (i.e. negatively biased) while SRTM has an overestimation of elevation. Results of horizontal profiling showed that the elevation of ASTER GDEM was consistently lower than that of SRTM. According to the results achieved, it is possible to state that photo-based DEM can be used for a range of environmental mapping. Overall, the results obtained in this study indicate that the three DEM’s RMS accuracies are comparable which encourage their use, especially when other expensive high-resolution data are not accessible.
Cite this paper
A’kifAl-Fugara, (2015) Comparison and Validation of the Recent Freely Available DEMs over Parts of the Earth’s Lowest Elevation Area: Dead Sea, Jordan. International Journal of Geosciences,06,1221-1232. doi: 10.4236/ijg.2015.611096
References
- 1. Snehmani, S.M.K., Gupta, R.D. and Ganju, A. (2013) Extraction of High Resolution DEM from Cartosat-1 Stereo Imagery Using Rational Math Model and Its Accuracy Assessment for a Part of Snow Covered NW-Himalaya. Journal of Remote Sensing and GIS (JORSG), 4, 23-34.
- 2. U.S. Geological Survey Rocky Mountain Research Centere (2001) Digital Elevation Models: USGS Digital Elevation Model Information. http://rockyweb.cr.usgs.gov/elevation/dpi_dem.html
- 3. Blaschke, T. and Strobl, J. (2003) Defining Landscape Units through Integrated Morphometric Characteristics. In: Buhmann, E. and Ervin, S., Eds., Landscape Modelling: Digital Techniques for Landscape Architecture, Wichmann-Verlag, Heidelberg, 104-113
- 4. Akbari, A., Noram, B.R. and Ngien, S.K. (2010) Application of Public Domain Satellite-Based DEMs in Natural Hazard Modeling. International Journal of Environmental Science and Development, 7, 140-144. http://dx.doi.org/10.7763/IJESD.2016.V7.756
- 5. Al-Fugara, A., Billa, L., Pradhan, B., Mohamed, T. and Rawashdeh, S. (2011) Coupling of Hydrodynamic Model and Aerial Photogrammetry-Derived Digital Surface Model for Flood Simulation Scenarios Using GIS: Kuala Lumpur Flood, Malaysia. Disaster Advances, 4, 20-28.
- 6. Al-Kouri, O., Al-Fugara, A., Rawashdeh, S., Balqies, S. and Biswajeet, B. (2013) Geospatial Modeling for Sinkholes Hazard Map Based on GIS & RS Data. Journal of Geographic Information System, 5, 584-592. http://dx.doi.org/10.4236/jgis.2013.56055
- 7. Moore, I.D., Grayson, R.B. and Ladson, A.R. (1991) Digital Terrain Modelling: A Review of Hydrological, Geomorphological, and Biological Applications. Hydrological Processes, 5, 3-30.
http://dx.doi.org/10.1002/hyp.3360050103 - 8. Taud, H., Parrot, J. and Alvarez, R. (1999) DEM Generation by Contour Line Dilation. Computers & Geosciences, 25, 775-783. http://dx.doi.org/10.1016/S0098-3004(99)00019-9
- 9. Wilson, J.P. and Gallant, J.C. (2000) Terrain Analysis Principles and Applications. John Wiley & Sons, New York.
- 10. Schenk, T. (1996) Digital Aerial Triangulation. Archives of Photogrammetry and Remote Sensing, 31, 735-745.
- 11. Hohle, J. (2009) DEM Generation Using a Digital Large Format Frame Camera. Photogrammetric Engineering & Remote Sensing, 75, 87-93. http://dx.doi.org/10.14358/PERS.75.1.87
- 12. Favey, E., Geiger, A., Gudmundsson, G.H. and Wehr, A. (2003) Evaluating the Potential of an Airborne Laser-Scanning System for Measuring Volume Changes of Glaciers. Geografiska Annaler, Series A: Physical Geography, 81, 555-561. http://dx.doi.org/10.1111/j.0435-3676.1999.00083.x
- 13. Kervyn, F. (2001) Modelling Topography with SAR Interferometry: Illustrations of a Favourable and Less Favourable Environment. Computers & Geosciences, 27, 1039-1050.
http://dx.doi.org/10.1016/s0098-3004(00)00158-8 - 14. Massonnet, D. and Elachi, C. (2006) High-Resolution Land Topography. Comptes Rendus Geoscience, 338, 1049-1062. http://dx.doi.org/10.1016/j.crte.2006.06.001
- 15. Farr, T.G., Rosen, P.A., Caro, E., Crippen, R., Duren, R., Hensley, S., Kobrick, M., Paller, M., Rodriguez, E., Roth, L., Seal, D., Shaffer, S., Shimada, J., Umland, J., Werner, M., Oskin, M., Burbank, M. and Alsdorf, D. (2007) The Shuttle Radar Topography Mission. Reviews of Geophysics, 45, Article ID: RG2004. http://dx.doi.org/10.1029/2005RG000183
- 16. Falorni, G., Teles, V., Vivoni, E.R., Bras, R.L. and Amaratunga, K. (2005) Analysis and Characterization of the Vertical Accuracy of Digital Elevation Models from the Shuttle Radar Topography Mission. Journal of Geophysical Research, 110, Article ID: F02005. http://dx.doi.org/10.1029/2003jf000113
- 17. ASTER GDEM Validation Team, Tachikawa, T., Kaku, M., Iwasaki, A., Gesch, D., Oimoen, M., Zhang, Z., Danielson, J., Krieger, T., Curtis, B., Hasse, J., Abrams, M., Crippen, R., Hirano, A., Welch, R. and Lang, H. (2003) Mapping from ASTER Stereo Image Data: DEM Validation and Accuracy Assessment. ISPRS Journal of Photogrammetry and Remote Sensing, 57, 356-370.
http://dx.doi.org/10.1016/S0924-2716(02)00164-8 - 18. Guth, P.L. (2006) Geomorphometry from SRTM. Photogrammetric Engineering & Remote Sensing, 72, 269-277. http://dx.doi.org/10.14358/pers.72.3.269
- 19. Miliaresis, G.C. and Paraschou, C.V.E. (2011) An Evaluation of the Accuracy of the ASTER GDEM and the Role of Stack Number: A Case Study of Nisiros Island, Greece. Remote Sensing Letters, 2, 127-135. http://dx.doi.org/10.1080/01431161.2010.503667
- 20. Suwandana, E., Kawamura, K., Sakuno, Y., Kustiyanto, E. and Raharjo, B. (2012) Evaluation of ASTER GDEM2 in Comparison with GDEM1, SRTM DEM and Topographic-Map-Derived DEM Using Inundation Area Analysis and RTK-dGPS Data. Remote Sensing, 4, 2419-2431. http://dx.doi.org/10.3390/rs4082419
- 21. Mukherjee, S., Joshi, P.K., Mukherjee, S., Ghosh, A., Garg, R.D. and Mukhopadhyay, A. (2013) Evaluation of Vertical Accuracy of Open Source Digital Elevation Model (DEM). International Journal of Applied Earth Observation and Geoinformation, 21, 205-217. http://dx.doi.org/10.1016/j.jag.2012.09.004
- 22. Rexer, M. and Hirt, C. (2014) Comparison of Free High Resolution Digital Elevation Data Sets (ASTER GDEM2, SRTM v2.1/v4.1) and Validation against Accurate Heights from the Australian National Gravity Database. Australian Journal of Earth Sciences, 61, 213-226.
http://dx.doi.org/10.1080/08120099.2014.884983 - 23. Hirt, C., Filmer, M.S. and Featherstone, W.E. (2010) Comparison and Validation of the Recent Freely Available ASTER-GDEM Ver1, SRTM Ver4.1 and GEODATA DEM-9s Ver3 Digital Elevation Models over Australia. Australian Journal of Earth Sciences, 57, 337-347.
http://dx.doi.org/10.1080/08120091003677553 - 24. Jarvis, A., Reuter, H.I., Nelson, A. and Guevara, E. (2008) Hole-Filled SRTM for the Globe Version 4. CGIAR-CSI SRTM 90 m Database. http://srtm.csi.cgiar.org
- 25. Maune, D.F., Maitra, J.B. and McKay, E.J. (2007) Accuracy Standards & Guidelines. In: Maune, D., Ed., Digital Elevation Model Technologies and Applications: The DEM Users Manual, 2nd Edition, American Society for Photogrammetry and Remote Sensing, Bethesda, 65-97.
- 26. Ghilani, C.D. and Wolf, P.R. (2006) Adjustment Computations: Spatial Data Analysis. 4th Edition, John Wiley & Sons, Hoboken.
- 27. Congalton, R.G. and Green, K. (1999) Assessing the Accuracy of Remotely Sensed Data Principles and Practices. Lewis Publishers, Boca Raton.
- 28. Slater, J.A., Heady, B., Kroenung, G., Curtis, W., Haase, J., Hoegemann, D., Schockley, C. and Tracy, K. (2009) Evaluation of the new ASTER Global Digital Elevation Model, National Geospatial-Intelligence Agency. http://www.ersdac.or.jp/GDEM/E/image/ASTERGDEM_444ValidationSummaryReport_Ver1.pdf
- 29. Abrams, M., Bailey, B., Tsu, H. and Hato, M. (2010) The ASTER Global DEM. Photogrammetric Engineering and Remote Sensing, 76, 344-348.
- 30. Bolten, A. and Waldhoff, G. (2010) Error Estimation of ASTER GEODEM for Regional Applications—Comparison on ASTER DEM and ALS Elevation Models. Proceedings of the 3rd ISDE Digital Earth Summit, Nessebar, 12-14 June 2010.
- 31. Sertel, E. (2010) Accuracy Assessment of ASTER Global DEM over Turkey. Proceedings of the ASPRS/CaGIS 2010 Fall Specialty Conference, Orlando, 15-19 November 2010.
- 32. Hensley, S., Rosen, P. and Gurrola, E. (2000) Topographic Map Generation from the Shuttle Radar Topography Mission C-Band SCANSAR Interferometry. Proceedings of the SPIE, 412, 179-189.
http://dx.doi.org/10.1117/12.410596 - 33. Welch, R. (1980) Measurements from Linear Array Camera Images. Photogrammetric Engineering and Remote Sensing, 46, 315-318.
- 34. Giuseppe, P. and Francesco, F. (2013) DEM Extraction from Archive Aerial Photos: Accuracy Assessment in Areas of Complex Topography. European Journal of Remote Sensing, 46, 363-378.
http://dx.doi.org/10.5721/EuJRS20134621 - 35. Kamaratakis, E.K. and Chrysoulakis, N. (2006) SRTM vs. ASTER Elevation Products. Comparison for Two Regions in Crete, Greece. International Journal of Remote Sensing, 27, 4819-4838.
http://dx.doi.org/10.1080/01431160600835853 - 36. Jacobsen, K. and Passini, R. (2010) Analysis Faster GDEM Elevation Models. Proceedings of the ISPRS TC 1 Symposium, Calgary, 15-18 June 2010.
- 37. Li, P., Shi, C., Li, Z., Muller, J.P., Drummond, J., Li, X., Li, T., Li, Y. and Liu, J. (2013) Evaluation of ASTER GDEM Using GPS Benchmarks and SRTM in China. International Journal of Remote Sensing, 34, 1744-1771. http://dx.doi.org/10.1080/01431161.2012.726752
- 38. Fujisada, H., Bailey, G.B., Kelly, G.G., Hara, S. and Abrams, M.J. (2005) ASTER DEM Performance. IEEE Transactions on Geoscience and Remote Sensing, 43, 2707-2714.
http://dx.doi.org/10.1109/TGRS.2005.847924 - 39. Rodriguez, E., Morris, C.S. and Belz, J.E. (2006) A Global Assessment of the SRTM Performance. Photogrammetric Engineering and Remote Sensing, 72, 249-260.
http://dx.doi.org/10.14358/PERS.72.3.249








