International Journal of Geosciences
Vol.05 No.03(2014), Article ID:44220,11 pages
10.4236/ijg.2014.53028
Study on Simulation of Foreshock Activity Properties before Strong Earthquake Using Heterogeneous Cellular Automata Models
Meng Li, Feng Yang, Tao Zhang
Earthquake Administration of Xinjiang Uygur Autonomous Region, Urumqi, China
Email: limeng955@sohu.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 September 2013; revised 16 October 2013; accepted 12 November 2013
ABSTRACT
Three different degrees of heterogeneous fault models are simulated by using 2-D random dynamic cellular automata models for analyzing macroscopic behaviors of seismic activity evolution influenced by heterogeneity of fault structures. The results show that the heterogeneities of fault structures can influence evolution properties of the foreshock activity and rupture process, such as the mediate heterogeneous and less heterogeneous structures, which show relatively higher ASR rates and more significant seismic gaps before main shocks. Besides, stress drop distribution ranges of the foreshock events when approaching a main shock show more homogenous (narrower) than that of the foreshock events far from a main shock. So the heterogeneity of fault structures plays an important role in strong earthquake preparation processes.
Keywords:
Cellular Automata Model; Simulation; Heterogeneity; Foreshock Activity

1. Introduction
The behaviors of earthquake activity are complicated and various, which are proved by long-term earthquake prediction. The work on earthquake sequence’s mechanism has been paid more attention to by researchers. Base on rock failure experiment [1] and mathematical analyses [2] [3] , the failure model and earthquake sequence property of different heterogeneous rock structure are studied, and the results show that the three earthquake sequence types of main shock, foreshock-main shock-aftershock and earthquake swarm are obtained from homogeneous to extreme heterogeneous medium respectively. That is why the preparation process of strong earthquake has a direct relation with rock heterogeneous medium. In recent years, some researchers considered the earthquake preparation process to be a critical phenomenon called the critical-point-like model of earthquake [4] [5] . As one of the critical behaviors, the ASR (acceleration strain release) phenomenon often exists before large earthquake occurrence [6] [7] , which is similar to the parameter change of condensed matter physics around the critical point. However, according to Wang Lin-yang’s study [8] , of 117 times mediate or strong earthquakes in China (eastern China Ms ≥ 5.5,western China Ms ≥ 6.0) during years 1970-2003, there are 63 times (51%) general foreshocks and only 13 times (11%) direct foreshocks. In addition, the statistics of worldwide Ms ≥ 7.0 earthquakes show that the probability of foreshock occurrence is 42.2% (40 days before a main shock, range around main shock within 100 km) [9] . It is very important to identify foreshock activity effectively for short- term or middle-term strong earthquake prediction practice. For example, in the daily earthquake monitoring and analysis work, we often face to make a prediction whether a strong shock will occur or not when small or medium shock activity is strengthening, therefore, researchers have paid more attention for the study to properties and identification of precursory foreshocks and its short-term prediction before strong earthquakes.
2. Model Design
We uses a cellular automata model composed by cell (the unit of system) and evolution rule after comparing previous research works [10] -[18] .
2.1. The Setting of Medium Parameter
We set up the fault zone plane model using the generation method of two dimension non-empty cantor set by setting 3 different probability values for each segment in both longitude and latitude directions, and we can get a 81 * 81 cell units model after 4 hierarchic divisions. The probability strength distribution of the model cellular units obeys the fractal dimension distribution. Based on the study of reference [19] , we select three different heterogeneous fault zone plane models (A1, C1 and D1) in reference [19] for the research objects,called model A, model B and model C, respectively. The model corresponding theoretic fractal dimension value is 1.9996, 1.9969 and 1.9915, the model extreme difference ratio of cellular unit probability is 1.69, 4.98 and 14.75,respectively. Obviously the cellular unit strength distribution heterogeneity of three models above increase accordingly. The static friction strength 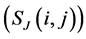 of each unit is obtained after the calculation of each cellular unit ratio by the gross systemic static friction strength which is same for the three models, the model specific setting method and selection of parameter are referred to reference [20] .
of each unit is obtained after the calculation of each cellular unit ratio by the gross systemic static friction strength which is same for the three models, the model specific setting method and selection of parameter are referred to reference [20] .
2.2. Fracture and Stress Redistribution Rules
Set initial stress value of one cell unit on 2-D fault plane as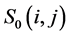 , static frictional strength as
, static frictional strength as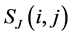 , dynamic frictional strength as
, dynamic frictional strength as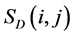 , where
, where 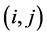 is the number of a cell. Stress increases with random loading, stress increasing ratio as
is the number of a cell. Stress increases with random loading, stress increasing ratio as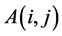 , stress random loading on a cell unit with time step. At the moment of without any cell unit fracturing
, stress random loading on a cell unit with time step. At the moment of without any cell unit fracturing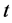 , the stress value of cell unit is
, the stress value of cell unit is
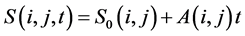 (1)
(1)
At a certain time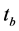 , if stress value of such cell unit
, if stress value of such cell unit 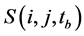 is up to its static frictional strength, namely
is up to its static frictional strength, namely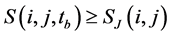 , so the cell unit will fracture, and its stress value drops to dynamic frictional strength. The stress drop of cell unit is
, so the cell unit will fracture, and its stress value drops to dynamic frictional strength. The stress drop of cell unit is
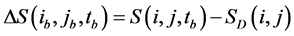 (2)
(2)
When one cell unit fractured, part of stress drop become loss in friction thermal, part of that radiated to neighbor other cells in seismic wave and become as stress loading of these cell units. For each unruptured cell unit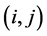 , the increment of stress
, the increment of stress 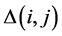 allocated with reciprocal of distance,
allocated with reciprocal of distance,
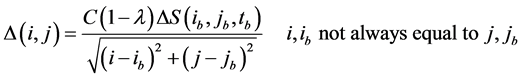 , (3)
, (3)
where the 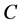 is stress allocation coefficient,
is stress allocation coefficient, 


If several cell units ruptured at the same time influenced by other units, the ruptured units cannot endure stress loading at this moment.
2.3. Earthquake Magnitude
When the stress on a cell unit superseded energy at this moment is:

In order to simplified calculation, we assume every cell unit is with the same elastic constant and the released energy is relative amount. Because of stress adjustment, one cell fracture will lead to other more cells rupturing at the same time until the system reach to a stable state (none ruptured cell), We accumulate fracture power of all the ruptured units, and then a larger earthquake appeared. The magnitude is:

According to Equations (5) and (6), we can calculate average effective stress drop 
3. Results and Analyses
The cell automata in this paper is a 2-D fault plane model made up of 81 × 81 cell units, the static frictional strength and stress distribution rules for each cell unit were assured according to the above model. The system starting with random mode, we chose a stable evolution period (5 × 105 - 20 × 105) as studying sample duration.
3.1. Overall Characteristics of Seismic Activity
Total number of events, magnitude range and accumulated strain release rate 
M-t and evolution curves of system stress level from three models in local period (5 × 105 - 10 × 105) are given in Figure 1. From Figure 1, we can see, with the model from A to C representing the enforcement of the fault zone structural heterogeneity degree, the nonlinearity of system stress level curve increases and dynamic weakening amplitude the curve decreases in turn and event sequences in M-t plots show main-shock type (such as model A), foreshock-main shock-aftershock type (such as model B) and earthquake swarm type (such as model C) features respectively. Besides, we can infer that the deformation features behave from relative brittleness to toughness with structure being more heterogeneous. As pointed by reference [21] , brittleness means distribution of regional stress strength more uniform, toughness means distribution of regional stress strength more
Table 1. General simulation results for different heterogeneous models.
Figure 1. System stress evolution and M-t plots for different heterogeneous models. The plot (a), (b) and (c) is for model A, B, and C respectively.
dispersed. In other words, homogeneous fault structures tend to appear collective rupturing behavior and to form characteristic earthquake (mature fault zone which is relative to a lower mean fracture energy and clustering strong earthquakes in time scale), on the contrary heterogeneous fault structures decline to power law distribution (immature fault zone which performs a higher mean fracture energy and relative uniform strong earthquake distribution in time scale). So distributions of earthquakes from fault structures with different homogeneous showed different deviation features from normal G-R relation. This has a indication meaning for regional seismic risk evaluation.
3.2. Strain Release Features during Foreshock Process
According to calculating results in this paper, features of general seismogenic process from uniformity and non-uniformity model are quite different from each other. In order to analyses stage evolution features of foreshock process with different homogeneous degree fault structure and to provide evidence for earthquake prediction, the author tries to study on foreshock process especially for accelerating release of strain.
Confirming a main shock is the premise of a seismic sequence process research. As pointed out by reference [22] . When average energies of system and main shock size keeping constant, the system reaches to a critical state though energy value is far less than system max geometric possible value. For instance, the strongest earthquake calculated by our models only cover about 30 percent of fault area and average main shocks cover about 10 - 20 percent. In other words, mainshocks are only small parts of the entire fault area.
Taking earthquake as a continuous failure process, we concentrated on the biggest earthquake events calculated by our models. According to intermittent of main shock and seismic activity evolution features, the authors defined this process as a cycle consisting of foreshock, main shock and aftershock. Taking a group of continue earthquake events as a cycle and defined mainshock magnitude as M ≥
In order to study this cycle, we selected three models with different inhomogeneous degree to calculate each foreshock process strain release rate with magnitude > 6.2 as a mainshock. As showed the evolution curves of system stress in Figure 1, m stands for main shock time, l m stands for foreshock process, ml stands for aftershock process. We normalized each foreshock process in time and divided it into four stages: stage one, stage two, stage three and stage four which contains the first 30%, the second 30%, the third 30% and the last 10% duration of a foreshock process, respectively. We can take these four stages as early stage, middle stage, late stage and later stage of foreshock process before a strong earthquake occurrence. Each foreshock events are correlated with main shock in strong earthquake occurrence because cell automata lacks of absolutely time scale and small size of fault grid. This may not match totally with the definition of foreshock process in seismology.
For AMR, there are about three representations: accelerating moment release, increasing of earthquake number and accelerating strain release. Four stage strain release rates of each foreshock process are calculated according to the definition in the paper. For model A, B and C, we get 30, 26 and 25 times foreshock processes respectively. In addition, we calculate the general average strain release rates except for mainshocks for the model A, B and C: 1.022 ± 0.111, 1.632 ± 0.091 and 2.013 ± 0.109, respectively. Moreover, strain release rates don’t behave consistent changing modes or behave randomness in four stages with time scale. This indicates a complicity and fluctuation in foreshock process strain release (Table 2).
As later stage of strong earthquake preparation process, stage 4 has a important significance for strong earthquake prediction. Considering the fluctuation of foreshock activity, the authors definite two kinds of evaluation standards to judge whether or not there is a precursory earthquake: one is 1.1 times of general average strain release rate of each model as a standard 1 (Std1); another is 1.1 times of average strain release rate with four stages of a foreshock processes as standard 2 (Std2). If a rate of stage 4 is bigger than the both two standards above simultaneously, we define there is a precursory earthquake. Statistical results show that:16 precursory earthquakes appear in model A, made up 53% of the model total; 16 precursory earthquakes appear in model B,made up 62% of that; 9 precursory earthquakes appear in model C, made up 36% of that; and the average proportion of three models is about 49%. It is indicated that not every later stage during strong earthquake preparation exists seismic activity enforcement; but some of them even appears seismic activity quietness(less than 0.9 times of the two standards above simultaneously), such as: A13, A19, B5, B8, C21 and C
We compare foreshock magnitude-accumulative frequency distribution between the earlier three stages with the fourth stage of under different model, the results show: stages 4 with precursor earthquake appear moderate size events increase (b value decreasing) during a foreshock process; however, stages 4 of foreshock process without precursory earthquakes do not appear that (plot codes in Figure 2 are correspondent to that in Table 2).
This paper adopted a random stress input way to find randomness of seismic activity. The authors calculated several times with three different models and results show that statistical features of same model is stable, and simulating seismic activity mainly controlled by fault structural heterogeneity but the randomness is related to original condition of system stress.
Evolution of earthquake activity before strong earthquake is complicated according to seismic observation and the simulating results in this paper. For one thing, not every strong earthquake has an enforcement of foreshock activity. For another, a increasing of moderate earthquake events is not necessary when approaching a
Table 2. Strain release rates of foreshock activity processes for different heterogeneous models.
Figure 2. Magnitude-cumulated frequency relation comparison between the 3 earlier stages (black circle curves) and stage 4 (circle curves) of foreshock process events for different heterogeneous models (the code in each plot is consistent with that in Table 2).
strong earthquake. If we can combine up the regional structure condition and earthquake activity, it will help us to recognize moderate earthquakes and earthquakes sequence so that we can make mid-short term prediction for strong earthquakes more effectively.
3.3. Evolution Features of Stress Drop during Foreshock Process
Considering system stress levels increased approaching main shock, earthquakes in later stage can be quite different from same magnitude with different stress background. So we study evolution features of average stress drop during foreshock process, in order to obtain stress conditions and evolution features in focal region before strong earthquakes.
Three models A, B and C are given to calculate evolution result of stress drop and magnitude during foreshock process. No matter how different heterogeneous degree, the smallest event produced by a single cell unit failure. Small and moderate earthquakes may be made up of a single cell unit or several cell units failure, which mean a high stress drop cell unit can serve same magnitude with several different low stress drop cell units, that is magnitude overlapping. With increasing of model heterogeneous degree, the ranges of stress drop and magnitude overlapping widen than it do ever before. Strong earthquakes were made up of many cracked cell units and with increasing of magnitude, the cracked area become larger, which include many cell units with different stress drop values. As an average effect, the range of events average stress drop with event magnitude increasing become smaller until becoming stable. Small events magnitude depend on stress drop of cell units and large earthquake events depend on the focal cracked area or number of ruptured cell units,this is match up with Dysart’s result [25] about the relation between focal crack size and stress drop of natural earthquakes.
In order to comparing statistical characteristics of stress drop of foreshock process, the author divided every foreshock process in Table 2 into two stages in time: stage 1 + 2, stage 3 + 4; and two types: with and without precursor earthquake type (Figure 3).
It is interesting that there isn’t a increasing tendency of stress drop in foreshock process events when approaching a main shock. However, no matter which model was chosen, compared with early and middle stage (stage1 + 2), distribution ranges of stress drop in late and later stage (stage 3 + 4) narrow down and event magnitudes tend to be lager, that is, the distributions of stress drop show uniformity. Of course, there are some differences in distribution ranges of stress drop, for example, the distribution ranges narrow down mainly when events with M > 4 for with precursor earthquake type(Figure 3(a)), but so do when events with M < 4 for without precursor earthquake type (Figure 3(b)). Local stress field features may be one of main causes for these differences.
It is believed that with stress loading and increasing of system stress level, more and more moderate stress drop cell units in cracking state begin to play dominate role. The mechanical properties of unruptured cell unit showed less difference (uniformity state) and increasing correlation length, and then resulted in a uniform distribution of stress drop in late and later foreshock process. As we know, a system with uniformity state near equilibrium is steady, but when out of equilibrium, a system with uniformity state will be unstable. The stress drop of earthquake event tended to become uniform which means system entered an unstable stage under high stress level may cause strong earthquake event. So we can use foreshock process stress drop features to estimate future main shocks.
3.4. Spatial Distribution of Fault Rupture
In order to study distribution characteristics of fault rupture before strong earthquakes, three different model results with different homogeneous degree were given below (Figure 4). For Model A (such as the top plot of A
4. Conclusion and Discussion
According to features of earthquake evolution numerically simulated by three different heterogeneous models, this paper got some main conclusions:
1) Strain release in different stage is complicated and unstable before earthquakes, only half portion of them showed seismic activity reinforced and b value decreased when near a main shock or later stage of foreshock process. In the point of structural heterogeneity, medium heterogeneity structure (model B) shows high percentage of precursory earthquake while extreme heterogeneity structure (model C) is with relatively low percentage and less heterogeneity structure (model A) that is between model B and C.
2) The distribution of stress drop of foreshock events uniformizes and foreshock events’ magnitude is increas- ing gradually when approaching main shock. During foreshock process, distribution ranges of event stress drop narrow down, which are located at high magnitude level with precursory earthquake type while at low magnitude level without precursory earthquake. This provides some useful information for making judgments for stress background and strong earthquake prediction in focal region.


Figure 3. Magnitude-stress drop distribution of foreshock process events for different model heterogeneity (The code in each plot is consistent with that in Table 2, (a) is for type with precursor earthquake and (b) is for type without precursor earthquake).
Figure 4. Cell failure frequency distributions of foreshocks and main shocks for different heterogeneity models (The code in each plot is consistent with that in Table 2, the top plots are for foreshock processes and the bottom ones for main shocks, respectively).
3) Heterogeneity of fault structure caused great influence on spatial rupture process. With less heterogeneous degree, model foreshock process existing in the obvious seismic gap and distribution of main shock shows localized tendency while with high heterogeneous degree it shows discreteness and no seismic gap.
According to simulation results, heterogeneity of fault structure caused different deformation features under the same macro-mechanical characters. Study on heterogeneity will be helpful for understanding more information through different regional geological conditions and evolution process of earthquake, what’s more, it can promote level of seismic hazard assessment and seismic prediction. There are still many factors affecting seismic activities but heterogeneity is an important factor.
Static models are simulated in this paper for spatial migration and time course of earthquake and results only show some characteristics of seismogenic system. If we can build a complex tectonic region model made up of different scale, strike, dip and heterogeneity for fault zone, considering a relationship between stress and crack propagation velocity [26] and a rate- and state-dependent friction law, we will get better results from simulating dynamic process.
Acknowledgements
This study is funded by NSFC, code of the Project is 40774015.
References
- Mogi, K. (1963) Some Discussion on Aftershock, Foreshock and Swarm. Bulletin of the Earthquake Research Institute, University of Tokyo, 41, 615-658.
- Tang, C.A., Liu, H.Y., Qin, S.Q., et al. (2000) Influence of Heterogeneity on Crack Propagation Modes in Brittle Rock. Chinese Journal Geophysics (in Chinese), 43, 116-120. http://dx.doi.org/10.1002/cjg2.15
- Jiao, M.J., Tang, C.A. and Zang, G.M. (2003) Numerical Test of Influence of Mesoscopic Heterogeneity on Macroscopic Behavior of Rock Failure and Seismic Types. Chinese Journal Geophysics (in Chinese), 46, 659-666.
- Main, I.G. (1995) Earthquake as Critical Phenomena: Implications for Probabilistic Seismic Hazard Analysis. Bulletin of the Seismological Society of America, 85, 1299-1308.
- Ben-Zion, Y., Eveva, M. and Liu, Y.F. (2003) Large Earthquake Cycles and Intermittent Criticality on Heterogeneous Faults Due to Evolving Stress and Seismicity. Journal of Geophysical Research, 108. http://dx.doi.org/10.1029/2002JB002121
- Sornette, D. and Sammis, C.G. (1995) Critical Exponents from Renormalization Group Theory of Earthquakes: Implication for Earthquake Prediction. Journal de Physique I, 5, 607-619. http://dx.doi.org/10.1051/jp1:1995154
- Jaume, S.C. and Sykes, L.R. (1999) Evolving towards a Critical Point: A Review of Accelerating Seismic Moment/ Energy Release Prior to Large and Great Earthquake. Pure and Applied Geophysics, 155, 279-306. http://dx.doi.org/10.1007/s000240050266
- Wang, L.Y., Chen, P.Y., Wu, Z.L., et al. (2005) Characteristics of Foreshock and Its Identification. Acta Seismologica Sinica (in Chinese), 27, 171-177.
- Luo, Z.L., Wang, W.J. and Chen, L. (2000) The Time-Frame Coefficient Method to Diagnose Nonlinear Characteristics of Earthquake Sequences in Haicheng-Xiuyan Region, Liaoning Province. Earthquake (in Chinese), 20, 18-27.
- Steacy, S.J. and Mc Closkey, J. (1998) What Controls an Earthquakes Size?—Results from a Heterogeneous Celluar Automaton. Geophysical Journal International, 133, f11-f14. http://dx.doi.org/10.1046/j.1365-246X.1998.1331548.x
- Liu, J., Liu, G.P., Li, L., et al. (1999) Simplified Dynamic Model Based on the Characteristics of Continental Seismicity—Cell Automat Model. Earthquake (in Chinese), 19, 230-238.
- Liu, G.P., Fu, Z.X. and Liu, J. (2000) A Friction Time-Dependent Cellular Automaton Model of Seismicity. Chinese Journal Geophysics (in Chinese), 43, 204-211. http://dx.doi.org/10.1002/cjg2.30
- Liu, G.P. and Fu, Z.X. (2001) Application of the Friction Time-Dependent Cellular Automaton Model of Seismicity to the Study of Heterogeneity of Intensity Distribution of Earthquake. Earthquake (in Chinese), 21, 22-28.
- Li, G., Liu, J., Fu, Z.X., et al. (2004) Simulation of Temporal Evolution of Seismicity before Earthquakes Using Cellular Automaton Model. Earthquake (in Chinese), 24, 34-41.
- Zhu, S.B., Cai, Y.E., Liu, J., et al. (2006) Modeling Seimicity by 3-D Cellular Automaton. Acta Scientiarum Naturalium Universitatis Pekinensis (in Chinese), 42, 206-210.
- Hillers, G., Ben-Zion, Y. and Mai, P.M. (2006) Seismicity on a Fault Controlled by Rate- and State-Dependent Friction with Spatial Variations of the Critical Slip Distance. Journal of Geophysical Research, 111, Article ID: E01403.
- Hillers, G., Mai, P.M., Ben-Zion, Y. andAmpuero, J.P. (2007) Statistical Properties of Seismicity of Fault Zones at Different Evolutionary Stages. Geophysical Journal International, 169, 515-533. http://dx.doi.org/10.1111/j.1365-246X.2006.03275.x
- Hillers, G., Carlson, J.M. and Archuleta, R.J. (2009) Seismicity in a Model Governed by Competing Frictional Weakening and Healing Mechanisms. Geophysical Journal International, 178, 1363-1383. http://dx.doi.org/10.1111/j.1365-246X.2009.04217.x
- Li, M. and Yang, F. (2010) Correlation Fractal Dimension Descriptions on Geometry and Structure Heterogeneity of the Theoretical Model. Inland Earthquake (in Chinese), 24, 193-198.
- Li, M. and Yang, F. (2011) Simulation of Impacts of Fault Structure Heterogeneity on Properties of Seismicity Using Cellular Automata Model. Acta Seismologica Sinica (in Chinese), 33, 672-682.
- Li, P.E. and Yin, Y.Q. (2009) A Simply Model for Earthquake Instability. Earthquake Research in China (in Chinese), 25, 265-273.
- Castellaro, S. and Mulargia, F. (2002) What Criticality in Cellular Automata Models of Earthquakes. Geophysical Journal International, 150, 483-493. http://dx.doi.org/10.1046/j.1365-246X.2002.01709.x
- Zhou, S., Johnston, S., Robinson, R. and Vere-Jones, D. (2006) Tests of the Precursory Accelerating Moment Release Model Using a Synthetic Seismicity Model for Wellington, New Zealand. Journal of Geophysical Research, 111. http://dx.doi.org/10.1029/2005JB003720
- Robinson, R., Zhou, S., Johnston, S. and Ver-Jones, D. (2005) Precursory Accelerating Moment Release (AMR) in a Synthetic Seismicity Catalog: A Preliminary Study. Geophysical Research Letters, 32, Article ID: L07309.
- Dysart, P.S., Snoke, J.A. and Sacks, I.S. (1988) Source Parameters and Scaling Relations for Small Earthquakes in Matsushiro Region, Southwest Honshu, Japan. Bulletin of the Seismological Society of America, 78, 571-589.
- Ben-David, O., Cohen, G. and Fineberg, J. (2010) The Dynamics of the Onset of Frictional Slip. Science, 330, 211-214. http://dx.doi.org/10.1126/science.1194777





