ABSTRACT

It is highly important in Japan to choose a good site for wind turbines, because the spatial distribution of wind speed is quite complicated over steep complex terrain. We have been developing the unsteady numerical model called the RIAM-COMPACT (Research Institute for Applied Mechanics, Kyushu University, Computational Prediction of Airflow over Complex Terrain). The RIAM-COMPACT is based on the LES (Large-Eddy Simulation). The object domain of the RIAM-COMPACT is from several m to several km, and can predict the airflow and gas diffusion over complex terrain with high precision. In the present paper, the design wind speed evaluation technique in wind turbine installation point by using the mesoscale meteorological model and RIAM-COMPACT CFD model was proposed. The design wind speed to be used for designing WTGs can be calculated by multiplying the ratio of the mean wind speed at the hub-height to the mean upper-air wind speed at the inflow boundary, i.e., the fractional increase of the mean hub-height wind speed, by the reduction ratio, R. The fractional increase of the mean hub-height wind speed was evaluated using the CFD simulation results. This method was proposed as Approach 1 in the present paper. A value of 61.9 m/s was obtained for the final design wind speed, U_h, in Approach 1. In the evaluation procedure of the design wind speed in Approach 2, neither the above-mentioned reduction rate, R, nor an upper-air wind speed of 1.7 V_o, where V_o is the reference wind speed, was used. Instead, the value of the maximum wind speed which was obtained from the typhoon simulation for each of the investigated wind directions was adopted. When the design wind speed was evaluated using the 50-year recurrence value, the design wind speed was 48.3 m/s. When a somewhat conservative safety factor was applied, that is, when the 100 year recurrence value was used instead, the design wind speed was 52.9 m/s.

Keywords:

Design Wind Speed, Complex Terrain, Meteorological Model, CFD Model

1. Introduction

With the implementation of the revised “Building Standard Law of Japan” [1] in June 2007, all structures which exceed a height of 60 m are now subject to a performance assessment by a designated institution and the approval of the Minister of Land, Infrastructure, Transport, and Tourism. These requirements are in addition to the application for the approval of the structure as stipulated by the re-revised law. In the case of WTGs (Wind Turbine Generators), these revisions to the law call for calculations of the reference design wind speed at the wind turbine hub-height, which is relevant for the wind resistant design of turbines. Accordingly, the ratio of the wind speed at the hub-height subject to topographical effects to the wind speed at the hub-height free of topographical effects (fractional increase of hub-height wind speed, hereafter) needs to be appropriately defined and evaluated by taking topographical factors into consideration [2] . Hence, the “Guidelines for the Design of Wind Turbine Support Structures/Commentary” [3] were published by the Japan Society of Civil Engineers in 2010. The published Guidelines are based on the “Building Standard Law of Japan” [1] and “Architectural Institute of Japan-Recommendations for Loads on Buildings/Commentary” [4] .

1) For height H smaller than Z_b:

${\text{E}}_{\text{pV}}=1.7{\left(\frac{{\text{Z}}_{\text{b}}}{{\text{Z}}_{\text{G}}}\right)}^{\alpha }$ (1)

2) For height H larger than Z_b:

${\text{E}}_{\text{pV}}=1.7{\left(\frac{\text{H}}{{\text{Z}}_{\text{G}}}\right)}^{\alpha }$ (2)

According to the Guidelines [3] , the design wind speed for a WTG should be evaluated for each of the wind directions which result from the division of the inflow wind directions at the site of interest into 16 wind directions, and the wind directions from which high wind speeds have been observed are not explicitly considered for the evaluation procedure. The Guidelines also state that the evaluation of the design wind speed should employ the appropriate vertical profile of wind speed according to the class of the surface roughness upwind of the site to be evaluated (see Figure 1). In this procedure, it is assumed that the surface roughness extends uniformly over a long distance upwind of the site, and that the values of the wind speed determined from wind tunnel experiments and field observations should be used. Finally, the atmosphere is assumed to be neutrally stratified as observed in high wind conditions, and the wind speed and direction are also assumed to be stationary.

Given this background, the present research proposes a technique for calculating the design wind speed for use in the wind resistant design of WTGs. This technique has been developed using some of our recent research findings. The technique takes into account high wind speed conditions which are similar to those observed in reality and ensures operational safety of the WTGs.

2. Proposed Method

When approval for the construction of WTGs is sought, a crucial factor is to ensure that the WTGs do not collapse under the maximum wind load expected in a given period. Therefore, wind profiles which replicate the actual characteristics of the airflow for high wind conditions at a site of interest should be used in the simulations for evaluating the design wind speed.

The site to be investigated in the present study is located in Japan, and situated in the zone through which typhoons frequently pass, and high winds observed in the past at this location were associated with typhoons. Of the typhoons which hit the site of interest, one with high wind is simulated with a mesoscale meteorological model together with available typhoon data, so that the actual atmospheric conditions from the typhoon can be included in the simulation [5] .

With the use of this simulation result, the wind directions from which high winds are anticipated are identified and additional simulations are conducted for these wind directions with the RIAM-COMPACT Computational Fluid Dynamics (CFD) model [6] - [12] . The use of the RIAM-COMPACT CFD model is motivated by the intention to examine the influence of the terrain near the WTG deployment location on the airflow at the hub-height. For the vertical profile of wind speed at the inflow boundary required for the CFD model, the result from the mesoscale model simulation is used.

Finally, the fractional increase of hub-height wind speed is calculated from the results of the CFD model simulation, and the hub-height design wind speed is determined using the value evaluated from the CFD model together with other variables such as a safety factor under two suggested approaches.

2.1. Typhoon Simulation Using the MM5 Mesoscale Meteorological Model

The mesoscale meteorological model used in the present study is the PSU/NCAR model known as MM5 [5] . This model is a limited-area, nonhydrostatic, terrain-following sigma-coordinate model designed to simulate or predict mesoscale atmospheric circulation. The MM5 model solves a non-hydrostatic, compressible equation system for the atmosphere. The MM5 model has a nesting capability that can resolve the area of interest with fine grid spacing.

2.2. LES Turbulence Simulation with the RIAM-COMPACT CFD Model

In this study, the RIAM-COMPACT natural terrain version model [6] - [12] is used in order to avoid numerical instability and to predict the airflow over complex terrain with high accuracy. The RIAM-COMPACT natural terrain version model uses collocated grids in a general curvilinear coordinate system. The velocity components and pressure are defined at the cell centers, and variables which result from the covariant velocity components multiplied by the Jacobian are defined at the cell faces. As for the computational technique, the Finite-Difference Method (FDM) is adopted, and an LES model is used for the turbulence model. In LES, a spatial filter is applied on the flow field to separate eddies of various scales into Grid Scale (GS) components, which are larger than the computational grids, and Sub-Grid Scale (SGS) components, which are smaller than the computational grids. Large-scale eddies, i.e. the GS components of turbulence eddies, are numerically simulated directly without relying on the use of a physically simplified model. The main effect of small-scale eddies, i.e. the SGS components, is to dissipate energy, and this dissipation is modeled based on the physical considerations of the SGS stress. For the governing equations of the flow, a spatially-filtered continuity equation for incompressible fluid and a spatially-filtered Navier-Stokes Equation are used. Because the present study is on airflow prediction in high wind conditions, the effect of the temperature stratification which is generally present in the atmosphere is neglected.

The computational algorithm and the time marching method are based on a Fractional-Step (FS) method and the Euler explicit method, respectively. The Poisson’s equation for pressure is solved by the Successive Over Relaxation (SOR) method. For discretization of all the spatial terms except for the convective term, a second-order central difference scheme is applied. For the convective term, a third-order upwind difference scheme is applied. An interpolation technique based on 4-point differencing and 4-point interpolation by Kajishima [13] is used for the fourth-order central differencing that appears in the discretized form of the convective term. In the weighting of the numerical dispersion term of the third-order upwind differencing, α = 3.0 is commonly applied in the Kawamura-Kuwahara Scheme [14] . However, α is set to 0.5 in the present study to minimize the influence of numerical dispersion. For LES SGS modeling, the commonly used Smagorinsky model [15] is adopted. A wall-damping function is used with a model coefficient of 0.1. We have developed an LES-based model for analyzing neutral flow over variable topography and applied it to the problem of proper site selection. Model performance was evaluated using data from wind tunnel tests over simple geometries and from a real site [6] - [12] .

3. Case Study

3.1. Description of the Wind Farm

The wind resistant design of WTGs was undertaken for a wind farm located in the south-western part of Wakayama Prefecture, Japan with the cooperation of Eurus Energy Holdings Corporation (see Figure 2). This wind farm consists of ten WTGs with rotor diameters of 62 m. The hub-height and the power output of each of the WTGs are 60 m and 1.3 MW, respectively. The region in which the wind farm is located is frequently hit by typhoons. Therefore, the wind resistant design of the WTGs and their support towers should be based on the prediction of airflow characteristics for the time of a typhoon passage.

Accordingly, a typhoon and the accompanying high winds which occurred in the region under consideration in the past are simulated using the MM5 mesoscale meteorological model, which yields simulated data of the regional scale wind field for the event of interest.

Using the results of the mesoscale simulation, unsteady turbulent flow simulations are performed by the RIAM-COMPACT CFD model for the area in which the topographical relief at and around the wind farm has been reconstructed in detail.

Finally, the design wind speed of the WTGs of the wind farm is calculated based on the results of the unsteady turbulent flow simulations.

3.2. Typhoon Simulation Using the MM5 Mesoscale Meteorological Model

In this study, four nested computational domains are set as shown in Figure 3. Of the typhoons which passed through the region under consideration in the past, Typhoon No. 7 in 1998 (referred to hereafter as “Typhoon No. 9807”) was selected for analysis. When this typhoon approached Japan, it caused high-wind damage to the Hokuriku and Kinki regions, including Wakayama Prefecture. The numerical data that are required for the typhoon simulations performed for the present study were provided by the Japan Meteorological Agency (JMA).

Figure 4 shows a comparison between the simulated and observed trajectories of the center of Typhoon No. 9807. The stars (☆) indicate the trajectory of the location of the lowest pressure in the simulated typhoon, which roughly agrees with that from the JMA best track data (○). The times and wind directions associated with the emergence of high winds are examined using the simulated wind field data for the wind farm and its surrounding region from the time of the passage of Typhoon No. 9807 (Figure 5, Figure 6). The present examination reveals that 1) the wind direction at the WTG deployment site changed from easterly to southerly with the approach of the typhoon and from southerly to westerly upon the passage of the typhoon and 2) the highest wind speeds occurred between 1300 and 1500 LST on 22 September, 1998. Based on the results in Figure 5, numerical unsteady turbulent flow simulations with the RIAM-COMPACT CFD model are performed for the following four wind directions: southeasterly, south-south-easterly, southerly, and west-north-westerly.

3.3. LES Turbulence Simulation with the RIAM-COMPACT CFD Model

The topography in the computational domain is reconstructed using mainly the 50 m elevation data of the Geospatial Information Authority of Japan (GSI). Fine grid spacing is adopted near the wind turbines in order to reconstruct the

topographical features in detail. The computational domain is set up in such a way that airflow characteristics at the turbine location are subject to topographical influences (upwind zone) and that eddies flow out of the computational domain smoothly and airflow at the turbine location is free from the influence of the outflow boundary (leeward zone) (Figure 7). For analyses of airflow over steep topography, a buffer zone is established that surrounds the computational domain. The terrain in the buffer zone is flat with an elevation close to zero meters and connects smoothly to the terrain in the computational domain.

As for the boundary conditions, slip conditions are applied to both the upper boundary and the side boundaries. For the upper boundary, the vertical gradient of the horizontal wind speed components ( $\overline{u}$ , $\overline{v}$ ) and the vertical wind velocity component ( $\overline{w}$ ) are all set to zero. For the side boundaries, the lateral gradient of the streamwise wind velocity component ( $\overline{u}$ ), that of the vertical wind velocity

component ( $\overline{w}$ ), and the spanwise wind velocity component ( $\overline{v}$ ) are all set to zero. For the vertical profile of wind speed at the inflow boundary required for the RIAM-COMPACT CFD model, the result from the MM5 mesoscale model simulation is used.

The computational domain for the present simulation is 8.5 km square, and three observation poles are located in the center of the domain, as shown in Figure 8. The vertical height of the computational domain is approximately 2.9 km. The number of computational grids is 101 × 101 × 51, the horizontal grid width ranges between 32 m and 769 m, and the vertical grid width ranges between 1.7 m and 347 m. The shape of the complex terrain was created based on 50 m Digital Elevation Model (DEM) data provided by the GSI.

As described above, the following four wind directions are considered for analysis with the RIAM-COMPACT model: south-easterly, south-south-easterly, southerly, and west-north-westerly. Figure 9 shows the vertical wind profiles of the horizontal wind speed at the center of the inflow boundary from the time of the occurrence of the largest wind speed at observational pole. Here, the observational pole is located in the center of the wind farm. As suggested by the figure, the vertical wind profile varied according to the wind direction.

The simulation with the RIAM-COMPACT model is performed using the vertical wind profile from the typhoon simulation. In the “Guidelines for the Design of Wind Turbine Support Structures/Commentary [3] ”, the wind speed at an altitude of 550 m or higher is assumed to be constant. Hence, in the simulation, the wind speed at an altitude of 550 m is set to the reference wind speed, U_o = 1.0, and a constant wind speed is used for altitudes higher than 550 m. If the wind speed at any altitude lower than 550 m is larger than that at 550 m, the reference wind speed, U_o = 1.0, is given at that altitude and all higher altitudes. With the conditions described above, the fractional increase of the mean hub-height wind speed, E_tCAL, is evaluated by the RIAM-COMPACT CFD model at the hub-height of each of the WTGs for each of the four wind directions to be investigated (Table 1). Here, the fractional increase of the mean hub-height wind speed, E_tCAL, is defined as the ratio of the mean hub-height wind speed to

the upper-air wind speed (the wind speed at altitudes higher than 550 m) at the inflow boundary, i.e., .

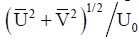4. Results and Discussion

4.1. Statistical Evaluation of the Simulated Typhoon

In this section, the strength of the simulated typhoon is statistically examined. Specifically, the recurrence interval of the magnitude of the wind speed which is

used as the inflow boundary condition in the CFD model is investigated. Using the annual maximum values of the 10-minute average wind speed data that were collected at the Wakayama Meteorological Observatory, the occurrence frequency of the maximum value of the 10-minute average wind speed data is determined. Figure 10(a) shows the relationship between the maximum values of the 10-minute average wind speed data and the reduced variate of the Gumbel analysis. This figure suggests that the trend of the recurrence frequency of the 10-minute average wind speed data differs between the high and low wind speed regimes (there is a change in the slope in the figure). Accordingly, data from only the high-wind regime (wind speeds equal to or larger than 19 m/s) are extracted and a straight-line approximation is made to these data using the least squares method (Figure 10(b)).

The values of the Gumbel parameters a and b, which are determined from Figure 10(b), are a = 1/5.0872 = 0.197 and b = 14.3. The equation for determining the recurrence values of the annual maximum of the 10-minute average wind speed data, U_R, is U_R ≈ 1/a × lnR + b = 5.09 lnR + 14.3. Therefore, the 50 year, 100 year, 200 year, and 500 year recurrence values of U_R are 34.2, 37.7, 41.3, and 45.9 m/s, respectively. The 50 year recurrence value of U_R agrees well with the value of the reference design wind speed of 34 m/s, which is the 50 year recurrence value for Wakayama Prefecture given in the Building Standard Law [1] .

In addition, the maximum value of the 10-minute average wind speed observed at the Wakayama Meteorological Observatory in 1998 is 32.4 m/s and is associated with Typhoon No. 9807. This value matches the 35 year recurrence value of U_R. Therefore, in terms of the recurrence value, the strength of the typhoon simulated by the MM5 mesoscale meteorological model may be considered equivalent to that of a typhoon which hits the area of analysis once every 35 years. From this result together with the result from the Gumbel analysis, the

50 year, 100 year, 200 year, and 500 year recurrence values of the 10-minute average wind speed for the site of analysis can be evaluated by multiplying 32.4 m/s by factors of 34.2/32.4, 37.7/32.4, 41.3/32.4, and 45.9/32.4, respectively. Table 2 summarizes the values of these factors.

4.2. Calculation Method for the Hub-Height Design Wind Speed, U_h

First, the method for evaluating the hub-height design wind speed, U_h, according to the “Guidelines for the Design of Wind Turbine Support Structures/Commentary” is illustrated [3] . The value of U_h can be evaluated using Equation (3.1) from the Guidelines:

${\text{U}}_{\text{h}}={\text{E}}_{\text{tV}}{\text{E}}_{\text{pV}}{\text{V}}_{\text{0}}$ (3)

where V_o is the reference design wind speed shown in Section 3.2 of the Guidelines [3] (V_o for Wakayama Prefecture: 34 m/s as given in Article 87 of the Order for Enforcement of the Building Standards Act, see [1] ), E_tV is the fractional increase of the mean hub-height wind speed, and E_pV is the height correction coefficient for the mean horizontal wind speed. Here, the value of E_pV is given by Equation (1) or (2). The fractional increase of the mean hub-height wind speed evaluated at each WTG from the results of the simulation with the RIAM-COMPACT model is referred to as E_tCAL; E_tCAL is the ratio of U_h to the upper-air wind speed at the inflow boundary of the RIAM-COMPACT model. Because the upper-air wind speed of interest is equal to the value of E_pV from Equation (2) for the case of H larger than Z_G, i.e., E_pV = 1.7V_o, E_tCAL becomes:

${\text{E}}_{\text{tCAL}}={\text{U}}_{\text{h}}/\text{1}{\text{.7V}}_{\text{0}}$ (4)

Substitution of Equation (3) into Equation (4) leads to:

${\text{E}}_{\text{tCAL}}={\text{U}}_{\text{h}}/\text{1}{\text{.7V}}_{\text{0}}={\text{E}}_{\text{tV}}{\text{E}}_{\text{pV}}/\text{1}\text{.7}$ (5)

Thus, E_tCAL includes the fractional increase of the mean hub-height wind speed, E_tV, and the height correction coefficient for the mean horizontal wind speed, E_pV. With the use of V_o = 34 m/s from the “Guidelines for the Design of Wind Turbine Support Structures/Commentary [3] ”, the hub-height design wind speed, U_h, can be evaluated as:

${\text{U}}_{\text{h}}=\text{1}{\text{.7V}}_{\text{0}}{\text{E}}_{\text{tCAL}}=\text{57}{\text{.8E}}_{\text{tCAL}}$ (6)

Below, the final value of the design wind speed, U_h., is evaluated with the following two approaches.

Approach 1:

The value of the design wind speed, U_h, calculated from Equation (6) is corrected using the vertical profile of the wind speed obtained from the typhoon simulation.

Approach 2:

The value of the design wind speed, U_h, is calculated using the maximum horizontal wind speed from each wind direction of interest instead of the upper-air wind speed in Equation (6) (=1.7 V_o).

First, the details of Approach 1 are discussed. As described earlier, the vertical profile of the horizontal wind speed assigned at the inflow boundary of the RIAM-COMPACT model is evaluated in such a way that the influence of the extensive ground surface upwind of the site of interest as well as the meteorological influence of typhoons observed in reality are included in the evaluation. However, it cannot be denied that the evaluated vertical profile of the horizontal wind speed possesses characteristics unique to the vertical profile of the particular typhoon investigated in the present study.

The influence of the vertical profile of the horizontal wind speed on the simulated results increases with decreasing height. Accordingly, the value of the upper-air wind speed needs to be selected with care so that it is as representative as possible of various typhoons. In the present study, the wind speed at 3 km above the ground surface is assumed to vary by only a small amount among various typhoons and is used as the reference wind speed. With the use of the wind speed at 3 km above the ground surface, the reduction ratio, R, of the upper-air wind speed at the inflow boundary of the RIAM-COMPACT model can be evaluated, and Equation (6) can be modified as:

${\text{U}}_{\text{h}}=\text{1}{\text{.7V}}_{\text{0}}{\text{E}}_{\text{tCAL}}=\text{57}{\text{.8E}}_{\text{tCAL}}\text{R}$ (7)

The reduction ratio, R, of the upper-air wind speed is shown in Table 3. Using Table 3, the values of U_h were calculated for all the WTGs, and the maximum value, 61.9 m/s, for the wind directions under consideration occurred at WTG No. 7 with south-south-easterly wind.

Subsequently, the details of Approach 2 are described. Our analysis earlier concluded that the strength of Typhoon No. 9807 is equivalent to that of a typhoon which hits the area under investigation once every 35 years. In order to calculate the final design wind speed using, for example, the 50 year recurrence value rather than the 35 year recurrence value, the final design wind speed can be determined by multiplying the design wind speed evaluated for each wind direction from the typhoon by the factor Q = 1.06 from Table 2. In other words, the design wind speed includes a margin such that the design wind speed is set to 1.06 times the value of U_h evaluated for the strength of Typhoon No. 9807 in this case. In general, the design wind speed, U_h, can be calculated as:

${\text{U}}_{\text{h}}={\text{U}}_{\text{MAX}}{\text{|}}_{\text{each}\text{direction}}{\text{E}}_{\text{tCAL}}\text{Q}$ (8)

In this approach, the design wind speed determined with the 50 year recurrence value is 48.3 m/s. This value of the design wind speed is calculated based on the maximum wind speed of all the WTGs, which occurred at WTG No. 7 with south-south-easterly wind. With the use of a somewhat conservative value of the safety factor, that is, using a 100 year recurrence value, the design wind speed becomes 52.9 m/s. However, it is the designer’s responsibility to select the

appropriate approach and recurrence interval to be used for determining the final design wind speed.

5. Summary

In the present paper, the design wind speed evaluation technique in wind turbine installation point by using the MM5 mesoscale meteorological model and RIAM-COMPACT CFD model was proposed. With the proposed method, a case study was conducted for a wind farm located in the south-western part of Wakayama Prefecture, Japan, with the cooperation of Eurus Energy Holdings Corporation. The findings from the present study are summarized below:

1) The design wind speed to be used for designing WTGs can be calculated by multiplying the ratio of the mean wind speed at the hub-height to the mean upper-air wind speed at the inflow boundary, i.e., the fractional increase of the mean hub-height wind speed, by the reduction ratio, R. The fractional increase of the mean hub-height wind speed was evaluated using the CFD simulation results. This method was proposed as Approach 1 in the present paper. The reduction ratio, R, which takes into account the effect of the wind direction from the time of a typhoon passage, was defined in terms of the wind speed at 3 km above the ground surface. The wind speed at this height was selected because it can be assumed to vary by only a small amount among various typhoons. A value of 61.9 m/s was obtained for the final design wind speed, U_h, in Approach 1. This value corresponds to the value which occurred at WTG No. 7 with south-south-easterly wind and was the maximum of the design wind speeds evaluated at all the WTGs.

2) In the evaluation procedure of the design wind speed in Approach 2, neither the above-mentioned reduction rate, R, nor an upper-air wind speed of 1.7 V_o, where V_o is the reference wind speed, was used. Instead, the value of the maximum wind speed which was obtained from the typhoon simulation for each of the investigated wind directions was adopted. When the design wind speed was evaluated using the 50-year recurrence value, the design wind speed was 48.3 m/s. This design wind speed was based on the maximum wind speed, which occurred at WTG No. 7 with south-south-easterly wind. When a somewhat conservative safety factor was applied, that is, when the 100-year recurrence value was used instead, the design wind speed was 52.9 m/s.

Acknowledgements

This work was supported by JSPS KAKENHI Grant Number 17H02053. Also, a part of the present study was supported by Dr. Takashi Maruyama (Kyoto University) and Dr. Tetsuya Takemi (Kyoto University). The author expresses appreciation to them.

Cite this paper

Uchida, T. (2018) Design Wind Speed Evaluation Technique in Wind Turbine Installation Point by Using the Meteorological and CFD Models. Journal of Flow Control, Measurement & Visualization, 6, 168-184. https://doi.org/10.4236/jfcmv.2018.63014

References

Nomenclature

CFD: Computational Fluid Dynamics

DEM: Digital Elevation Model

FDM: Finite-Difference Method

FS method: Fractional-Step method

GS: Grid Scale

GSI: Geospatial Information Authority of Japan

JMA: Japan Meteorological Agency

LES: Large-Eddy Simulation

LST: Local Standard Time

MM5: PSU/NCAR (Pennsylvania State University/National Center for Atmospheric Research) mesoscale model

RIAM-COMPACT: Research Institute for Applied Mechanics, Kyushu University, COMputational Prediction of Airflow over Complex Terrain

SGS: Sub-Grid Scale

SOR method: Successive Over Relaxation method

WTGs: Wind Turbine Generators