Journal of Flow Control, Measurement & Visualization
Vol.04 No.03(2016), Article ID:69211,10 pages
10.4236/jfcmv.2016.43011
Control of Karman Vortex Street behind a Thin Airfoil at Low Reynolds Number
Shohei Takagi1*, Yasufumi Konishi2, Shigeru Obayashi2, Masato Asai1
1Department of Aerospace Engineering, Tokyo Metropolitan University, Tokyo, Japan
2Institute of Flow Science, Tohoku University, Sendai, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 May 2016; accepted 17 June 2016; published 28 July 2016
ABSTRACT
To control the Karman vortex street formed behind a thin airfoil at a certain incidence, a control cylinder was placed at the suction side apart from the airfoil in the downstream region. Both smoke visualization and hot-wire measurements confirmed that the Karman vortex street was completely suppressed. The mechanism for suppression of the vortex street was examined with a hot-wire survey.
Keywords:
Karman Vortex Street, Vortex Suppresion, Absolute Instability, Convective Instability

1. Introduction
Downstream of a thin flat plate placed in a low-turbulence uniform flow, the basic flow is usually hypothesized to be parallel, where the wake is destabilized by the so-called convective instability. Therefore, infinitesimal disturbances exponentially grow in the wake and the characteristics of growing disturbances can be described by a classical linear stability theory [1] . On the other hand, a street of staggered vortices behind 2-D airfoil models or bluff bodies in a stationary uniform flow is regularly formed in the wake. It is well known that such regular Karman-vortex formation is associated with the so-called global instability of the wake, which selectively induces a monochromatic disturbance [2] [3] . The complex ray theory [4] also shows that the frequency selection of the global mode may be explained from the viewpoint of a logarithmic singularity, which corresponds to a turning point in the global-instability theory and is relevant to the recirculation region in the near wake of the model.
It was observed in a water channel experiment [5] that a Karman-vortex street behind a circular cylinder at a low Reynolds number of approximately 80 was completely suppressed by means of a smaller secondary cylinder placed in the shear layer of the main cylinder. This suppression may be attributed to two primary effects, namely that the secondary cylinder weakens the shear layer, and its wake intrudes into the wake of the main cylinder, suggesting an alteration of that characteristic of the main cylinder wake dominated by the global instability. A numerical simulation [6] corresponding to this experimental observation was made which revealed that the secondary cylinder provided a locally favorable pressure gradient in the wake region of the main cylinder.
The present paper aims at experimentally suppressing the Karman vortex street behind a thin airfoil model making use of a thin secondary cylinder as a control device. The control cylinder is placed not near but well apart from the airfoil model, a configuration which differs from the aforementioned suppression method. In order to examine the mechanism for suppression of Karman-vortex formation by the secondary cylinder, elaborate measurements were made by use of a hot-wire anemometer and smoke-wire visualization techniques.
2. Experimental Arrangement
2.1. Wind Tunnel and Wing Model
All experiments were conducted in the small-scale low-turbulence wind tunnel at the Institute of Fluid Science, Tohoku University, Japan. The test section is a closed octagonal shape with a diagonal length of 290 mm. The residual turbulence level at a freestream velocity of 15 m/s is less than 0.03%. See more detail in Kohama et al. [7] . In order to keep the static pressure in the test-section close to the atmosphere pressure, four diffuser flaps are attached downstream of the test section. The room temperature is kept constant at 25.0˚C and as a result the working air temperature in the test section, for instance 21.5˚C, is also maintained constant.
An NACA0006 airfoil model made of stainless steel was used, whose chord length c and maximum thickness t are 40 mm and 2.4 mm, respectively. The model surface was a matte black coating for visualization. The model was vertically set in the middle test section as shown in Figure 1, and was rotated around the shaft fixed at a quarter chord length from the leading edge of the model. The shaft was connected to a stepper motor at the top surface of the ceiling to set the model angle α relative to the freestream. The precision of the motor stepping was 0.01 degrees per pulse.
As for the coordinate system, x is taken in the streamwise direction and y is in the transverse direction. The origins of x and y are located at the trailing edge of the airfoil at zero incidence. Twelve holes of 1.2 mm diameter were drilled on the ceiling and floor plates positioned at y = ±10, ±20, ±30 and ±34 mm at x = 10 mm to insert a thin control cylinder (occasionally referred to as C.C.). For the present study, one hole at x = 10 mm and y = −30 mm was used for a C.C. with a diameter of 1.0 mm.
The freestream velocity U0 is continuously variable from 1 m/s to 70 m/s. For the present experiment, it was set at 4.2 m/s, corresponding to a Reynolds number of approximately 104, based on the chord length c and U0.
2.2. Hot-Wire Anemometer, Data Acquisition System and 3-D Traversing Mechanism
A single I-type hot-wire probe and a constant-temperature anemometer (CTA) were used to measure the streamwise mean velocity U and fluctuating velocity u in the wake of the model. The hot-wire probe was handmade specifically for this application, having a 5 μm tungsten wire with a sensing length of 1 mm between cop-
Figure 1. Experimental setup in plan view of the test section. The flow runs in from left to right direction. Not to scale.
per plated sleeves softly soldered on the two tapered phosphor-bronze prongs separated apart by 10 mm, and was inclined to intrude into the flow with a slope of 45 degrees from downstream side, because instability in the wake is known to be hypersensitive to the presence of the hot-wire probe. The overheat ratio of operating resistance to cold resistance of the hot-wire at room temperature was set at 1.5. An anti-aliasing filter for the CTA bridge output was used with a cutoff frequency of 5 kHz and a cutoff slope of −100 dB/Oct and the filtered output was recorded into a conventional personal computer at a sampling rate of 10 kHz with a 16 bit A/D converter. Acquired outputs are linearized making use of King’s law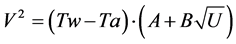 , where
, where 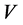 and
and  are the bridge output voltage and local velocity,
are the bridge output voltage and local velocity,  and
and  are the operating temperature of the hot-wire sensor and air temperature in freestream, and
are the operating temperature of the hot-wire sensor and air temperature in freestream, and  and
and  are calibration constants. Placing the hot-wire sensor in the freestream flow, the bridge output was calibrated using a static Pitot tube connected to a pressure transducer Model DM-3501 with overall accuracy in ±0.15% of 500 Pa full scale, supplied by Cosmo Instruments Co., Ltd.
are calibration constants. Placing the hot-wire sensor in the freestream flow, the bridge output was calibrated using a static Pitot tube connected to a pressure transducer Model DM-3501 with overall accuracy in ±0.15% of 500 Pa full scale, supplied by Cosmo Instruments Co., Ltd.
The hot-wire support stem with a diameter of 6 mm inserted through the slitted side wall was mounted on a 3-D traversing mechanism, which is managed under the LabVIEW 2010 software together with a dataacquisition system supplied by National Instruments.
2.3. Smoke-Wire Method and Flow Visualization
Smoke-wire visualization was made, where time-sequential images at a frame rate of 2 kHz were captured by high speed camera SA-X2 with a resolution of 1024 by 1024 pixels supplied by Photron Ltd. Generated smoke was illuminated by a pair of metal halide lamp available commercially. A smoke wire consists of three braided/twisted Nichrome wires with a diameter of 0.05 mm. The longest cross-sectional length of three twisted wires is less than 0.1 mm, which does not exceed the critical Reynolds number of 46 [8] for the Karman vortex shedding at 4.2 m/s, showing no vortex shedding from the wire. Liquid paraffin was coated on the smoke wire for each smoke generation. The smoke wire was placed perpendicular to the freestream and horizontally span- ned the wind tunnel test section upstream of the airfoil model.
3. Results and Discussion
3.1. Profiles of Mean and Fluctuating Velocities
The first test was conducted with the airfoil model set geometrically at zero incidence to the main flow. Then, as the model incidence α was varied from −4 to 4 degrees, a hot-wire probe was scanned across the wake at x/c = 0.4 to measure profiles of mean and fluctuating velocities for U0 = 4.2 m/s. The new origin of α was readjusted from nominal zero to true zero to the axial flow direction so as to be symmetric to measured profiles. This adjustment is −1.2 degrees.
Figure 2 shows the profiles of the mean and fluctuating velocities normalized by U0 measured in the y-direction across the wake at 16 mm (x/c = 0.4) for various corrected α. As the magnitude of both positive and negative incidence is increased up to 3.6 degrees, the maximum deficit of the mean velocity profiles increases slightly, showing that the reverse flow near the trailing edge of the model is magnified. Corresponding fluctuating velocity level in rms values remains quite low. It is noticeable, however, that when the absolute value of α exceeds 3.8˚, rapid growth is observed on the fluctuating velocity profiles as shown in Figure 2(b). Also, the velocity deficit rapidly recovers at α = 4˚. This correspondence is reasonable, because the larger the fluctuating velocity, the faster the deficit recovers.
For subsequent runs, the airfoil model was set at negative incidences so as to avoid intersection of the hot-wire support and the wake of the control cylinder as shown in Figure 1. Figure 3(a), for an incidence of α = −3.9˚ at x/c = 0.4, represents a power spectrum of the velocity fluctuation measured at the rms peak position on the fluctuating velocity profile and Figure 3(b) shows the same spectrum at α = −3.65˚. For the case of α = −3.9˚, a very sharp monochromatic component with a frequency of 348 Hz and its higher harmonics accompanying tower-like shaped sidelobes are observed, while growing fluctuations at α = −3.65˚ consist of broadband components with small amplitudes. This contrast implies that the wake instability between at α = −3.9˚ and α = −3.65˚ is significantly different, although the Strouhal number, based on the main stream velocity and the maximum thickness of the model, for both cases is a value of 0.2. To confirm this implication, the maximum amplitude profiles in terms of the rms values of growing u component measured at various x locations for both cases at α = −3.9˚ and α = −3.65˚ are compared in Figure 4. At α = −3.9˚, the u component starts growing immediately downstream of the trailing edge of the model with a large growth rate and reaches almost 20% of U0 at x/c = 0.4, where the global instability selectively induces a monochromatic fluctuation as shown in Figure 3. On the other hand, at α = −3.65˚ broadband fluctuations are observed to grow at a modest growth rate exemplifying a convective instability. When the incidence at U0 = 4.2 m/s exceeds −3.9˚ negatively, a regular Karman-vortex street is formed, as flow visualization studies reported later will confirm. It might be worthwhile to point out that incipient disturbances leading to the Karman-vortex formation begin growing right downstream of the rear edge of the model although no vortex shedding from the model occurs. This seems to be different from that of bluff bodies like circular cylinders.


Figure 2. Profiles of (a) streamwise mean velocity and (b) rms values of fluctuating u component at various incidences at x = 16 mm (x/c = 0.4). t is the maximum thickness of the model.


Figure 3. Comparison of power spectra of fluctuating u component between (a) at −3.9˚ and (b) −3.65˚ incidences at x = 16 mm (x/c = 0.4).
3.2. Control of Karman Vortex Street and Flow Visualization
Having identified the experimental conditions under which a street of Karman vortices will form, an attempt was made to control or suppress the Karman-vortex formation by means of a thin cylinder, strategically placed in the flow field. At a model incidence of α = −3.9˚, the control cylinder with a diameter of 1 mm made of a phosphor bronze was placed at two different positions of (x, y) = (10 mm, −30 mm) as shown in Figure 1, and (10 mm, −20 mm). These locations are both far enough from the model wake that one might expect little influence on flow behavior in the wake of the airfoil. Figure 5 shows a profile of maximum ums values of the fluctuating velocity u against x with the control cylinder placed at (x, y) = (10 mm, −30 mm), and the other profile without the control cylinder are replotted from Figure 4. The maximum rms values of u component behind the cylinder are also plotted in the figure. As can be observed, insertion of the cylinder far outside of the model wake is effective in suppressing formation of the Karman-vortex street. Additionally, the characteristic of the spatial growth of the u component by means of the cylinder insertion, bears a resemblance to that at an incidence of α = −3.65˚ except for near the trailing edge of the model indicating that the wake is destabilized by a convective instability rather than the global instability. Power spectral analysis of u components at x/c = 0.4 growing in the wake as altered by the cylinder, also endorses that the wake instability favors growth of the broad-band components as shown in Figure 6. The flow around the model was also visualized by use of the smoke-wire technique to confirm whether or not the street of Karman vortices disappears. Visualized flows around the model at α = −3.9˚ with and without the cylinder are compared in Figure 7.
Figure 4. Comparison of spatial growth of u component with maximum rms value at each x location in the wake behind NACA0006 airfoil at α = −3.65˚ and −3.9˚ incidences.
Figure 5. Comparison of streamwise distribution of u component with maximum rms value in the wake behind NACA0006 airfoil at α = −3.9˚ incidence between with and without control cylinder. Also, a maximum rms-value distribution of u component behind the control cylinder is illustrated.
Figure 6. Power spectrum of fluctuating u component at α = −3.9˚ with control cylinder at x/c = 0.4.
Figure 7. Smoke-wire visualization around NACA0006 airfoil at α = −3.9˚. (a) without C.C. (b) with C.C. placed at (x, y) = (10 mm, −30 mm).
Streak lines in Figure 7(a) exhibit the presence of Karman vortices, while Figure 7(b) with the control cylinder present, indicates very weak smoke undulations far downstream of the model along the center line, confirming that the growth of Karman vortices is completely suppressed. Instead, a row of small-scale vortices behind the control cylinder is visible. It is difficult to extract the reason why the control cylinder, located considerably apart from the cylinder, plays the role as Karman-vortex suppressor from comparison of visualized images shown in Figure 7.
3.3. Effect of Control Cylinder
Rapid growth of fluctuating velocities behind the model leading to the formation of Karman vortices is associated with the global instability in the recirculation region. In order to unravel the mechanism of Karman-vortex suppression by means of insertion of the control cylinder, attention should be directed to the profiles of the mean velocity across the wake with, and without, the cylinder. This idea comes from the speculation that insertion of the control cylinder may alter the basic flow in relation with the reverse flow sensitive to local flow direction near the trailing edge of the model. Figure 8 compares three profiles of the mean velocity in the wake at x/c = 0.4 both with, and without the control cylinder, for an incidence of α = −3.9˚, together with a case of α = −3.65˚ with no cylinder. For an incidence of α = −3.9˚, the maximum velocity deficit without the control cylinder recovers earlier than the case with the cylinder as mentioned before. Here, it is worthwhile to make careful comparison of the mean velocity profiles between two cases at an incidence of α = −3.9˚. The y location of the maximum velocity deficit due to insertion of the cylinder is found to be shifted approximately +0.1 mm, where the cylinder seems to play a role of a displacement body at the suction side of the model. Namely, the local flow at the suction side is deflected in the positive y direction, and in consequence, the relative angle between local-flow direction and the model axis is reduced by tan−1(0.1/16) = 0.36˚. In other words, the control cylinder generates favorable pressure gradient at the suction side near the trailing edge of the model.
Another comparison of two mean-velocity profiles between at α = −3.65˚ in the absence of control cylinder and α = −3.9˚ in the presence of cylinder is made in Figure 8. These are almost identical, although the y location of the maximum velocity deficit is slightly different. This identical profile suggests that insertion of the control cylinder with a diameter of 1 mm placed at (x, y) = (10 mm, −30 mm) changes actual angle of attack of the model from α = −3.9˚ to α = −3.65˚. It turns out that this decreased angle roughly coincides with the deflected angle 0.36˚ mentioned above.
It is also noteworthy to compare the predictions of potential theory with experimental observation. Potential theory asserts that the transverse velocity V induced by insertion of the control cylinder should be negligibly small. From this theory, when a cylinder with a diameter of a is immersed in a uniform flow U, v/U at the trans-
Figure 8. Comparison of the mean velocity profile between both with and without the control cylinder for an incidence of α = −3.9˚ together with a case of α = −3.65˚ with no cylinder at x/c = 0.4.
versal location y = r is (a/r)2 = 1/642 ≅ 0.00024, which corresponds to a deflection of only 0.014 degrees from the uniform flow, where the location r includes a displacement 2 mm of the trailing edge from the zero incidence. This deflected angle is extremely low compared with the real flow accompanying vortex shedding as shown in Figure 2(b) and Figure 7(b).
4. Conclusion
In summary, control of the Karman vortex street formed behind a thin airfoil at a certain incidence, the influence of a control cylinder placed well apart from the airfoil in the downstream region was studied. Both flow visualization and hot-wire surveys consistently showed that the Karman vortex street could be completely suppressed. It was concluded that the suppression effect appeared to derive from an effective decrease of the actual incidence angle caused by insertion of the control cylinder.
Acknowledgements
This work was partly supported by the Grant for Core Research for Evolutional Science and Technology (CREST) from the Japan Science and Technology Agency, and partly by a Grant-in-Aid (C) Nos. 22560778 and 25420846 for Scientific Research from the Ministry of Education, Culture, Sports, Science and Technology, Japan. Part of the work was carried out under the Collaborative Research Project of the Institute of Fluid Science, Tohoku University.
Cite this paper
Shohei Takagi,Yasufumi Konishi,Shigeru Obayashi,Masato Asai, (2016) Control of Karman Vortex Street behind a Thin Airfoil at Low Reynolds Number. Journal of Flow Control, Measurement & Visualization,04,114-123. doi: 10.4236/jfcmv.2016.43011
References
- 1. Sato, H. and Kuriki, K. (1960) The Mechanism of Transition in the Wake of a Flat Plate Placed Parallel to a Uniform Flow. Journal of Fluid Mechanics, 11, 321-352. http://dx.doi.org/10.1017/S0022112061000561
- 2. Monkewitz, P.A., Huerre, P. and Chomaz, J.-M. (1993) Global Linear Stability Analysis of Weakly Non-Linear Shear Flows. Journal of Fluid Mechanics, 251, 1-20. http://dx.doi.org/10.1017/S0022112093003313
- 3. Chomaz, J.-M. (2005) Global Instabilities in Spatially Developing Flows. Annual Review of Fluid Mechanics, 37, 357- 392. http://dx.doi.org/10.1146/annurev.fluid.37.061903.175810
- 4. Itoh, N., Takagi, S. and Ikeda, T. (2012) Instability and Frequency Selection of the Wake behind a Flat Plate. Transactions of Japan Society for Aeronautical and Space Sciences, 55, 356-363. http://dx.doi.org/10.2322/tjsass.55.356
- 5. Strykoski, P.J. and Sreenivasan, K.R. (1990) On the Formation and Suppression of Vortex “Shedding” at Low Reynolds Numbers. Journal of Fluid Mechanics, 218, 71-107. http://dx.doi.org/10.1017/S0022112090000933
- 6. Mittal, S. and Raghuvanshi, A. (2007) Control of Vortex Shedding behind Circular for Flows at Low Reynolds Numbers. International Journal of numerical Methods in Fluids, 35, 421-447. http://dx.doi.org/10.1002/1097-0363(20010228)35:4<421::AID-FLD100>3.0.CO;2-M
- 7. Kohama, Y., Kobayashi, R. and Ito, H. (1982) Performance of Small-Scale Low-Turbulence Wind Tunnel. The Memoirs of the Institute of High Speed Mechanics (Tohoku University), 48, 119-142. (In Japanese)
- 8. Jackson, C.P. (1987) A Finite-Element Study of the Onset of Vortex Shedding in Flow Past Variously Shaped Bodies. Journal of Fluid Mechanics, 182, 23-45. http://dx.doi.org/10.1017/S0022112087002234
Nomenclature
A: Calibration constant in King’s law
a: Radius of control cylinder [mm]
B: Calibration constant in King’s law
c: Chord length of model [mm]
r: Radial distance from control-cylinder center [mm]
Ta: Air temperature [˚C]
Tw: Hot-wire temperature [˚C]
t: Maximum thickness of airfoil model [mm]
U: Mean velocity in x direction [m/s]
U0: Mean velocity in uniform flow [m/s]
u: Fluctuating velocity in x direction [m/s]
u': rms value of u [m/s]
V: Bridge output voltage of constant temperature anemometer [volt]
v: Transversal velocity induced by control cylinder [m/s]
x: Streamwise distance [mm] from trailing edge of model at zero incidence
y: Transversal distance [mm] from trailing edge of model at zero incidence
α: Angle of attack of model [˚]
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
NOTES
*Corresponding author.









