Journal of Flow Control, Measurement & Visualization
Vol.02 No.04(2014), Article ID:50972,7 pages
10.4236/jfcmv.2014.24018
Experimental and Numerical Investigation of a Rayleigh-Bénard Convection Affected by Coriolis Force*
Claudia Zimmermann, Rodion Groll
Center of Applied Space Technology and Microgravity, University of Bremen, Bremen, Germany
Email: groll@zarm.uni-bremen.de
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 March 2014; revised 17 April 2014; accepted 21 August 2014
ABSTRACT
In this paper the influence of an impressed Coriolis force field on the configuration of a turbulent Rayleigh-Bénard convection problem is investigated in an experimental and numerical study. The main purpose of both studies lie on the analysis of a possible stabilising effect of a Coriolis acceleration on the turbulent unsteady structures inside the fluid. The relative Coriolis acceleration which is caused in the atmosphere by the earth rotation is realised in the experimental study by a uniform-rotational movement of the setup in a large-scale centrifuge under hyper-gravity. The same conditions as in the atmosphere in the beginning of a twister or hurricane should be realised in the experiment. The investigated Rayleigh numbers lie between 2.33 × 106 ≤ Ra ≤ 4.32 × 107.
Keywords:
Rayleigh-Bénard Convection, Compressible Flow, Coriolis Force, PIV, Large-Eddy Simulation

1. Introduction
A Rayleigh-Bénard (RB) convection or Rayleigh-Bénard (RB) problem describes thermally driven flow against gravity between two horizontal, heated walls. The fluid is accelerated by local density differences and a resulting pressure gradient. Directly at the heated walls the temperature distribution is determinate by increasing temperature gradients, while convective mass exchange is dominant in the center region. Turbulent shear layers parallel to the direction of gravity develop between the walls. The first studies of a RB problem between horizontal, heated walls were performed by the French physicist Henri Claude Bénard and the English physicist Lord Rayleigh [1] [2] around the beginning of the 20th century. Since then, numerous studies investigated convective flows in different configurations in an experimental as well as theoretical and numerical way. As for example,
Maystrenko et al. [3] investigate the boundary layer thickness of a RB convection in air. Complementary to [3] , Ebert et al. [4] and du Puits et al. [5] measure the temperature distribution and local heat flux of a convective flow in a rectangular enclosure. Shishkina et al. [6] analyse the thermal dissipation rate and the development of plumes in a cylindrical RB cell with help of a Direct Numerical Simulation (DNS) for different Rayleigh numbers. The purpose of the presented experimental and numerical study is to investigate how the turbulent structures inside the fluid are possibly changed by a Coriolis force affecting the fluid inside the setup similar to a twister or hurricane in the atmosphere. Concerning the numerical study, a compressible Large-Eddy Simulation (LES) is performed.
2. Test Case Configuration
The experimental RB cell consists of a rectangular, air-filled container with horizontal, heated walls. The container is heated isothermally from below and cooled from above with a constant temperature difference between both walls DT = Thot – Tcold. The container has a length (L) of 0.58 m, a height (H) of 0.2 m and a depth (D) of 0.58 m. The sidewalls consist of polymethyl methacrylate (PMMA) and have all a thickness of 0.01 m. Despite an insulating effect of the PMMA side walls, a possible heat loss through the side walls has to be considered. An almost atmospheric pressure condition is generated inside the cell. An overview of the centrifuge system (left picture) and a photograph (right picture) of the experiment installed in the centrifuge is presented in Figure 1.
The blue coloured parts in Figure 1, left picture, form the base frame of the centrifuge system. The green coloured parts mark the rotator shaft with two rotating arms. At the end of each arm a free running pendant is located. The experimental cell is installed at the right pendant. At the opposite pendant a counterbalance is fixed. The initial temperature field in the cell is assumed to be T = TIF = Tcold = 293.15 K. The container can be characterised by the parameters of the Rayleigh number Ra, the Prandtl number Pr, the Nusselt number Nu and its aspect ratios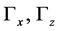 . The mentioned parameters are defined as
. The mentioned parameters are defined as
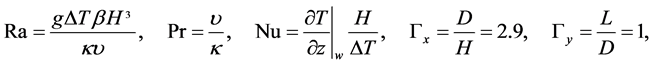 (1)
(1)
where 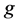 is the gravitational acceleration,
is the gravitational acceleration, 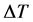 the temperature difference between the hot and cold wall, β the thermal expansion rate,
the temperature difference between the hot and cold wall, β the thermal expansion rate, 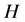 the height of the container,
the height of the container, 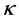 the thermal diffusivity coefficient,
the thermal diffusivity coefficient, 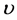 the kinematic viscosity and
the kinematic viscosity and 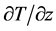 the temperature gradient directly at the cold/hot wall (marked by index “
the temperature gradient directly at the cold/hot wall (marked by index “ ”). The Nusselt number characterises the heat flux in the container. All parameters are defined on the mean temperature
”). The Nusselt number characterises the heat flux in the container. All parameters are defined on the mean temperature . The Prandtl number lies at Pr = 0.71. If a critical value of temperature difference is reached, the fluid starts moving controlled by DT. To investigate the influence of a Coriolis force field on the turbulent structures inside the fluid, two different modes are analysed. First, the RB cell is studied in a non-rotation mode. Second, the RB cell is analysed while rotating uniformly under hyper-gravity. The rotational movement of the test cell causes relative accelerations and a higher gravitational force of gres = 1.4 g acting on the fluid. Thus, different Rayleigh numbers are realised in both modes. In case of the non-rotation mode and DT = 3 K a Rayleigh-number of Ra = 2.33 × 106 is realised, for
. The Prandtl number lies at Pr = 0.71. If a critical value of temperature difference is reached, the fluid starts moving controlled by DT. To investigate the influence of a Coriolis force field on the turbulent structures inside the fluid, two different modes are analysed. First, the RB cell is studied in a non-rotation mode. Second, the RB cell is analysed while rotating uniformly under hyper-gravity. The rotational movement of the test cell causes relative accelerations and a higher gravitational force of gres = 1.4 g acting on the fluid. Thus, different Rayleigh numbers are realised in both modes. In case of the non-rotation mode and DT = 3 K a Rayleigh-number of Ra = 2.33 × 106 is realised, for 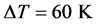 it lies at
it lies at 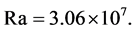 In case of the rotation mode and DT = 3 K a Rayleigh-number of Ra = 3.29 × 106 is realised, for DT = 60 K it lies at Ra = 4.32 × 107. Figure 2 displays in the left picture a sketch of the test case installed in the centrifuge with relevant geometrical lengths L1 = 3.724 m, L2 = 4.72 m, L3 = 0.361 m, L4 = 1.411 m, L5 = 0.4 m, L6 = 5.1030 m, height H = 2.75 m, deflection angle α = 46.167˚ and two sensors S1, S2. The centrifuge system rotates with 13.704 revolutions per minute (rpm). The experimental setup has a total weight of 107.5 kg. It is helpful to divide the complete setup in two different systems. The system of the RB cell, marked by
In case of the rotation mode and DT = 3 K a Rayleigh-number of Ra = 3.29 × 106 is realised, for DT = 60 K it lies at Ra = 4.32 × 107. Figure 2 displays in the left picture a sketch of the test case installed in the centrifuge with relevant geometrical lengths L1 = 3.724 m, L2 = 4.72 m, L3 = 0.361 m, L4 = 1.411 m, L5 = 0.4 m, L6 = 5.1030 m, height H = 2.75 m, deflection angle α = 46.167˚ and two sensors S1, S2. The centrifuge system rotates with 13.704 revolutions per minute (rpm). The experimental setup has a total weight of 107.5 kg. It is helpful to divide the complete setup in two different systems. The system of the RB cell, marked by 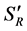 and
and 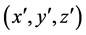 in the following, is relative rotating to the inertial system of the centrifuge axis, marked by
in the following, is relative rotating to the inertial system of the centrifuge axis, marked by 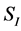 and (x, y, z). The right picture in Figure 2 shows a close-up sketch of the RB cell installed in the centrifuge.
and (x, y, z). The right picture in Figure 2 shows a close-up sketch of the RB cell installed in the centrifuge.
The Computational Test Case
In the 3-dimensional numerical simulation presented, the computational geometry of the container is analogously chosen to the experimental cell and displayed schematically in Figure 3, left picture. The lateral walls are modelled with a condition of adiabatic walls. The velocity field at all walls is zero due to a non-slip-condi- tion. The total pressure is considered by a zero gradient-option at all walls. The initial pressure field is assumed to be constant at 1 × 105 Pa.
Figure 1. Left: Overview of the centrifuge system. Right: Photograph of the experimental RB cell installed in the centrifuge.
Figure 2. Left: Sketch of the experimental cell installed in the pendant of one rotating arm (system SI). Right: Close-up of the RB cell (system
Figure 3. Left: Configuration of the computational geometry. Right: Computational mesh resolution with (200 × 200 × 110) cells.
The simulation assumes a non-Boussinesq fluid. Temperature dependent fluid properties are calculated by the Sutherland model [7] . The computational mesh consists of a structured Cartesian grid with 27 blocks. It contains of (200 × 200 × 110) cells in 
3. Results
3.1. Velocity Structure Visualisation in the Experiment
To record the flow profile in the experiment, the flow is visualised by tracer particles of magnesium carbonate (MgCO3). Only visualised data is estimated at this point from the experiment. A camera, which is fixed in front of the container at point K (see Figure 2 and Figure 4, right picture), records the moving flow particles.
An overview of the estimated flow region in the experimental cell as well as a sketch of the camera installation are illustrated in Figure 4. The recorded videos of the fluid movement are estimated on basis of a Particle Image Velocimetry (PIV) as it is stated in [9] . Because of a significantly varying image contrast, only a small region of the recorded videos could be estimated on basis of the PIV method (see Figure 4 left picture, red dashed rectangle). The estimated region has a height of 0.15 m and a width of 0.12 m. The flow resistance and inertia of the tracer particles should not exceed a critical value and have the same density as air. It is assumed that, in an ideal case, a tracer particle can be modelled by a spherical object. The flow resistance of a spherical particle can be circumscribed for a 2-dimensional case by the law of Stokes

where μ is the dynamic viscosity of air, r the radius of the spherical particle and u its approaching velocity. The highest realisable temperature difference between the heated walls is DT = 60 K the lowest one is

with a supposed mean approaching velocity

Hence, the used tracer particles shall have at most a radius of 

where St is the stokes number and H the height of the setup. The sketches in Figure 5 picture possible displacements of a fluid particle in the RB cell due to an acting Coriolis force.
Figure 4. Left: Region of estimated flow structures in the experimental cell (red dashed rectangle). Right: Sketch of the container-camera installation in the experiment.
Figure 5. Possible displacements of a fluid particle in the container due to an acting Coriolis force.
If a particle is moving parallel to the rotation axis of the centrifuge, no effect of an acting Coriolis force can be seen. In all other cases a Coriolis acceleration affects the flow movement inside the cell. The left sketch in Figure 5 pictures a displacement of a fluid particle which is moving along the 













3.2. Nusselt Number Values Obtained in the Simulated Process
In the study of King et al. in [10] boundary layers of rapidly rotating convection cells are investigated for different Rayleigh and Prandtl numbers in a numerical as well as experimental study. The numerical study uses an incompressible simulation. A stabilising effect of the Coriolis force on the convection is stated. The results of [10] obtained in the non-rotating mode agree for a Prandtl number of 

In this study, the LES performed uses a compressible coupled model. The analysed fluid is air and the Prandtl number lies at 
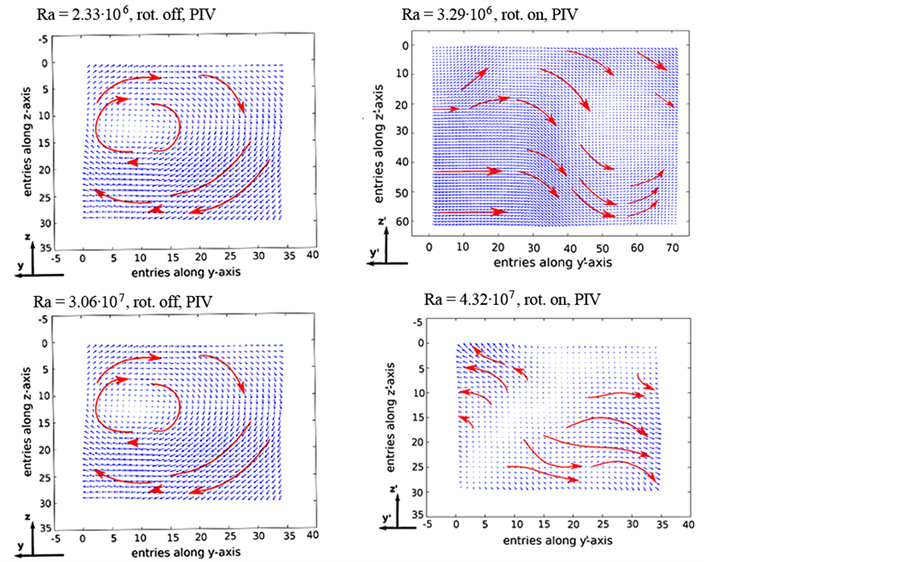
Figure 6. Time-averaged 2-dim. velocity field. Experimental results (PIV). Plane located at
Figure 7. Nusselt number versus Rayleigh number. Left: Cold wall. Right: Hot wall. 
3.3. Velocity Structures Estimated in the Simulated Process
In the study of [10] , a rapidly rotating convection cell is investigated in an incompressible numerical simulation. Gravity and the rotation axis of the cell are both vertical. It is observed that a rapidly rotating convection is typically organised by the Coriolis force into tall, thin, coherent convection columns that are aligned with the rotation axis [10] . In the presented study, the angular velocity of the centrifuge is chosen as ω = 1.435 rad/s. Furthermore, the rotation axis of the centrifuge is also vertical as gravity, but the container itself is turned by an angle of α = 46.167˚ relative to the rotation axis of the centrifuge. Consequently, the rotation axis is turned relative to the vertical axis of the container. This aspect has an additionally effect on the development of flow structures inside the fluid due to an acting influence of gravity component g which points now in an angle α relative to the heated walls and one of the perpendicular acting component gres (see Figure 2, right picture). On the basis of DT = 3 K and a top view of the container, instantaneous snapshots of mean velocity structures in both modes are displayed in Figure 8. As in [10] , the velocity structures in the rotation mode are axially aligned and tall, thin, coherent convection structures appear. But, due to the turned rotation axis, the arrangement
Figure 8. Instantaneous snapshots of mean velocity structures in the container, top view. ∆T = 3 K. Left: Non-rotation mode. Middle and Right: Rotation mode, components
of velocity structures show a wave-like character. In comparison to a non-rotating RB cell (left picture in Figure 8) no typical large-scale convection cells appear. The velocity structures seem to be smaller, mixed and more irregular. Compared to the non-rotating RB cell a stabilising effect of the Coriolis force could not be observed directly.
4. Conclusion
An experimental and a numerical study were performed for a turbulent RB convection in an air-filled enclosed container where the horizontal walls were heated isothermally, but with a constant temperature difference. The setup was accelerated in a large-scale centrifuge to investigate a possible influence of a Coriolis force on the development of turbulent structures inside the fluid. Compared to a non-rotating RB cell, which shows typically large-scale convection cells, the velocity structures in the rotation mode seemed to be smaller, mixed and more irregular. Furthermore, the development of turbulent structures rose. However, the structures became larger and seemed to be more regular with increasing Rayleigh numbers. Higher Nusselt number values could not be observed in the rotation mode compared to the non-rotation mode. Thus, comparing the rotating RB cell directly to the non-rotating cell, a stabilising effect of the Coriolis force could not be observed in both studies.
Acknowledgements
This study was funded by the Zentrale Forschungsförderung of the University Bremen.
References
- Bénard, H. (1900) Les tourbillons cellulaires dans une nappe liquide. Revue Générale des Sciences Pures et Appliquées, 11, 1261-1271, 1309-1328.
- Rayleigh, Lord (1916) On the Convective Currents in a Horizontal Layer of Fluid When the Higher Temperature Is on the under Side. Philosophical Magazine, Series 6, 32, 529-546.
- Maystrenko, A., Resagk, C. and Thess, A. (2007) Structure of the Thermal Boundary Layer for Turbulent Rayleigh- Bénard Convection of Air in a Long Rectangular Enclosure. Physical Review E, 75, 066303-1-066303-11. http://dx.doi.org/10.1103/PhysRevE.75.066303
- Ebert, A., Resagk, C. and Thess, A. (2008) Experimental Study of Temperature Distribution and Local Heat Flux for Turbulent Rayleigh-Bénard Convection of Air in a Long Rectangular Enclosure. Journal of Heat and Mass Transfer, 51, 4238-4248. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2008.01.017
- Du Puits, R., Resagk, C., Tilgner, A., Busse, F.H. and Thess, A. (2007) Structure of Thermal Boundary Layers in Turbulent Rayleigh-Bénard Convection. Journal of Fluid Mechanics, 572, 231-254. http://dx.doi.org/10.1017/S0022112006003569
- Shishkina, O. and Wagner, C. (2006) Analysis of Thermal Dissipation Rates in Turbulent Rayleigh-Bénard Convection. Journal of Fluid Mechanics, 546, 51-60. http://dx.doi.org/10.1017/S0022112005007408
- Sutherland, W. (1893) The Viscosity of Gases and Molecular Force. Philosophical Magazine, Series 5, 36, 507-531. http://dx.doi.org/10.1080/14786449308620508
- Zimmermann, C., Groll, R. and Rath, J.H. (2012) Modelling Turbulent Heat Transfer of a Rayleigh-Bénard Problem with Compressible Large-Eddy Simulation. In: Hanjalić, K., Nagano, Y., Borello, D. and Jarkirlić, S., Eds., Proceedings of the Seventh International Symposium On Turbulence, Heat and Mass Transfer, ICHMT, Begell House Inc., West Redding, USA, 615-623. http://dx.doi.org/10.1615/ICHMT.2012.ProcSevIntSympTurbHeatTransfPal.480
- Mori, N. and Chang, K.A. (2002) Introduction to MPIV-PIV Toolbox in MATLAB® - Version 0.965, http://www.oceanwave.jp/softwares/mpiv/index.php?FrontPage
- King, E.M., Stellmach, S., Noir, J., Hansen, U. and Aurnou, J.M. (2009) Boundary Layer Control of Rotating Convection Systems. Nature, 457, 301-304. http://dx.doi.org/10.1038/nature07647
- Grossmann, S. and Lohse, D. (2000) Scaling in Thermal Convection: An Unifying Theory. Journal of Fluid Mechanics, 407, 27-56. http://dx.doi.org/10.1017/S0022112099007545
- Stevens, R.J.A.M., van der Poel, E.P., Grossmann, S. and Lohse, D. (2013) The Unifying Theory of Scaling in Thermal Convection: The Updated Prefactors. Journal of Fluid Mechanics, 730, 295-308. http://dx.doi.org/10.1017/jfm.2013.298
Nomenclature
Roman Symbols
ac: Coriolis acceleration vector [m/s2]
a,ZF: Centrifugal acceleration vector in point A [m/s2]
a, ZP: Centripetal acceleration vector in point A [m/s2]
g: Gravitational acceleration vector [m/s2]
u: Approaching velocity of a tracer particle [m/s]
m: Mass [kg]
x, y, z: Cartesian coordinates with respect to system SI
x', y', z': Cartesian coordinates with respect to system S'R
D: Depth of the RB cell [m]
Fw: Flow resistance [N]
H: Height of the RB cell setup [m]
L: Length of the RB cell [m]
L1,...L6: Lengths in the centrifuge system [m]
SI: Inertial system
S'R: Relative to SI rotating system
S1, S2: Sensors in the centrifuge system
T: Temperature [K]
Tmean: Mean temperature between heated walls [K]

r: Radius of a tracer particle [m]
V: Volume of a fluid particle [m3]
Greek Symbols
α: Angle [°]
β: Thermal expansions coefficient [1/K]
μ: Dynamic viscosity [kg/ms]
ν: Kinematic viscosity [m2/s]
κ: Thermal diffusivity coefficient [m2/s]
ρ: Density [kg/m3]
ω: Angular velocity vector [rad/s]
ΔT: Temperature difference between heated walls [K]
Dimensionless numbers
Nu: Nusselt number
Ra: Rayleigh number
Pr: Prandtl number
Γ: Aspect ratio
St: Stokes number
NOTES
*Short paper.