Open Journal of Optimization
Vol.04 No.03(2015), Article ID:59378,12 pages
10.4236/ojop.2015.43010
A New Approach of Solving Linear Fractional Programming Problem (LFP) by Using Computer Algorithm
Sumon Kumar Saha1, Md. Rezwan Hossain2, Md. Kutub Uddin3, Rabindra Nath Mondal4
1Department of Applied Mathematics, Gono Bishwabidyalay (University), Dhaka, Bangladesh
2Department of Business Development, Allcare Limited, Dhaka, Bangladesh
3Department of Mathematics, University of Dhaka, Dhaka, Bangladesh
4Department of Mathematics, Jagannath University, Dhaka, Bangladesh
Email: sumonaftermath@gmail.com, rezwan28@gmail.com, rnmondal71@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 June 2015; accepted 1 September 2015; published 4 September 2015
ABSTRACT
In this paper, we study a new approach for solving linear fractional programming problem (LFP) by converting it into a single Linear Programming (LP) Problem, which can be solved by using any type of linear fractional programming technique. In the objective function of an LFP, if β is negative, the available methods are failed to solve, while our proposed method is capable of solving such problems. In the present paper, we propose a new method and develop FORTRAN programs to solve the problem. The optimal LFP solution procedure is illustrated with numerical examples and also by a computer program. We also compare our method with other available methods for solving LFP problems. Our proposed method of linear fractional programming (LFP) problem is very simple and easy to understand and apply.
Keywords:
Linear Programming, Linear Fractional Programming Problem, Computer Program

1. Introduction
Various optimization problems in engineering and economics involve maximization (or minimization) of the ratio of physical or economic function, for instances cost/time, cost/volume, cost/benefit, profit/cost or other quantities measuring the efficiency of the system. Naturally, there is a need for generalizing the simplex technique for linear programming to the ratio of linear functions or to the case of the ratio of quadratic functions in such a situation. All these problems are fragments of a general class of optimization problems, termed in the literature as fractional programming problems. This field of LFP was developed by Hungarian mathematician Matros [1] [2] in 1960. Several methods are proposed to solve this problem. Charnes and Kooper [3] have proposed their method depended on transforming this (LFP) to an equivalent linear program, they say the feasible region 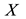 is nonempty and bounded,
is nonempty and bounded, 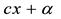 and
and 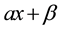 do not vanish simultaneously in
do not vanish simultaneously in 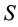 then they used the variable transformation
then they used the variable transformation 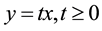 in such a way that
in such a way that 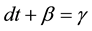 where
where 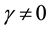 is a specified number and transform LFP to an LP problem. Multiplying the numerator and denominator and the system of inequalities by
is a specified number and transform LFP to an LP problem. Multiplying the numerator and denominator and the system of inequalities by 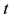 and
and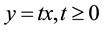 , they obtain two equivalent LP problems and name them as EP and EN. If EP or EN has an optimal solution and other is inconsistence, then LFP also has an optimal solution. If any of the two problems EP or EN is unbound, then LFP is also unbound. So if the first problem is not unbound, one needs to solve the other. That’s why one needs to solve two LPs by Big-M or two-phase simplex method, which is a very lengthy process. On the other hand, the simplex type algorithm is introduced by Swarup [4] and Swarup, Gupta and Mohan [5] .
, they obtain two equivalent LP problems and name them as EP and EN. If EP or EN has an optimal solution and other is inconsistence, then LFP also has an optimal solution. If any of the two problems EP or EN is unbound, then LFP is also unbound. So if the first problem is not unbound, one needs to solve the other. That’s why one needs to solve two LPs by Big-M or two-phase simplex method, which is a very lengthy process. On the other hand, the simplex type algorithm is introduced by Swarup [4] and Swarup, Gupta and Mohan [5] .
In that method one needs to compute 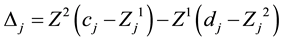 in each step and continues this process
in each step and continues this process
until the value of 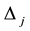 satisfying the required condition. We see that it has to deal with the ratio of two linear functions, that’s why its computational process is complicated and also when the constraints are not in canonical form then it becomes lengthy. Another method is called updated objective function method derived from Bitran and Novaes [6] is used to solve this linear fractional program by solving a sequence of linear programs only re-computing the local gradient of the objective function. But to solve a sequence of problems sometimes may need many iterations and at some cases say,
satisfying the required condition. We see that it has to deal with the ratio of two linear functions, that’s why its computational process is complicated and also when the constraints are not in canonical form then it becomes lengthy. Another method is called updated objective function method derived from Bitran and Novaes [6] is used to solve this linear fractional program by solving a sequence of linear programs only re-computing the local gradient of the objective function. But to solve a sequence of problems sometimes may need many iterations and at some cases say, 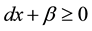 and
and 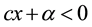
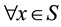 , Bitran-Novaes method is failed. Singh [7] in his paper makes a useful study about the optimality condition in fractional programming. Tantawy [8] develops a technique with the dual solution. Hasan and Acharjee [9] also develop a method for solving LFP by converting it into a single LP, but for the negative value of
, Bitran-Novaes method is failed. Singh [7] in his paper makes a useful study about the optimality condition in fractional programming. Tantawy [8] develops a technique with the dual solution. Hasan and Acharjee [9] also develop a method for solving LFP by converting it into a single LP, but for the negative value of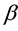 , their method fails. Tantawy [10] develops another technique for solving LFP which can be used for sensitivity analysis. Effati and Pakdaman [11] propose a method for solving the interval-valued linear fractional programming problem. Pramanik et al. [12] develops a method for solving multi-objective linear plus linear fractional programming problem based on Taylor Series approximation.
, their method fails. Tantawy [10] develops another technique for solving LFP which can be used for sensitivity analysis. Effati and Pakdaman [11] propose a method for solving the interval-valued linear fractional programming problem. Pramanik et al. [12] develops a method for solving multi-objective linear plus linear fractional programming problem based on Taylor Series approximation.
In this paper, our intent is to develop a new technique for solving any type of LFP problem by converting it into a single linear programming (LP) problem because at some cases in the denominator and numerator when 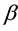 is negative, available methods are failed to solve the linear fractional problem. We also develop a FOR- TRAN computer program for solving it and analyze the solution by numerical examples.
is negative, available methods are failed to solve the linear fractional problem. We also develop a FOR- TRAN computer program for solving it and analyze the solution by numerical examples.
2. Mathematical Formulation of LP and LFP
The mathematical expression of a general linear programming problem is as follows:
Maximize (or Minimize)
Subject to
where one and only one of the signs (≤, =, ≥) holds for each constraint and the sign may vary from one constraint to another. Here 



set or feasible regionof (LP).
In matrix vector notation the above problem can be expressed as:
Maximize (or Minimize)
Subject to
where 









The mathematical formulation of an LFP (in matrix vector notation) is as follows:
Maximize
Subject to
where 










2.1. Solving LFP by Our Method
If 



We convert the LFP into an LP in the following way assuming that
Case I:
For objective function,
where, 

For constraint,
where
So the new LP is: Maximize
Subject to
2.2. Calculation for the Unknown Variable of the LFP
From the above LP, we get
This is our required optimal solution. Putting the value of 
Case II:
For objective function,
Same as above procedure, we have
where, 


For constraints, following the same procedure as above, we get
where
Case III:
For objective function:
Same as above procedure, we have
where, 

For constraints, following the same procedure as above, we get
where
3. Algorithm
If 




else



4. Numerical Examples
Here we illustrate some numerical examples to demonstrate our method.
Example 1:
Minimize
Subject to
Solution: Here we have, 



related to the third constraint. So, we have the new objective function.
Minimize
Now for the first constraint,
For the second constraint,
For the third constraint,
Converting the LP in standard form we have
Maximize
Subject to
Now we get the following table (Table 1 and Table 2):
Table 1. Initial table for Example 1.
Table 2. Final table for Example 1.
So we have, 
Now
Putting this value in the original objective function, we have
Min
Now, we solve the above problem by computer program.
Output:
Minimum value of the Objective Function = −1.090909.
X1 = 7.000000;
X2 = 0.000000.
We see that our hand calculation result and computer oriented solution is the same. This shows that our computer program is correct.
Example 2:
Maximize
Subject to
Solution: Here we have, 


Now,
So, we have the new objective function
Maximize
Now for the first constraint,
For the first constraint,
Converting the LP in standard form we have
Maximize
Subject to
Now we get the following tables (Table 3 and Table 4):
Table 3. Initial table for Example 2.
Table 4. Final table for Example 2.
So we have, 
Now
Putting this value in the original objective function, we have
Maximum
By using computer technique we get the following result.
Output:
Maximum value of the Objective Function = 3.000000.
X1 = 3.000000;
X2 = 0.000000.
Note: This problem cannot be solved by any available method because the value of β is negative.
Example 3:
Maximize
Subject to
Solution: Maximize
Subject to
Here we have, 


So we have the new objective function
Maximize
Now for the first constraint,
For the second constraint,
Converting the LP in standard form, we have
Maximize
Subject to
Now we get the following tables (Table 5 and Table 6):
Table 5. Initial table for Example 3.
Table 6. Final table for Example 3.
So we have
Now,
Putting this value in the original objective function, we have
Maximum
Using computer program, we get the following result.
Output:
Maximum value of the Objective Function = 1.800000.
X1 = 0.000000;
X2 = 1.000000.
Example 4: Production Problem of a Certain Industry.
Suppose an industry has Tk. 3,00,00,000/= by which it can produce six different products Palm oil, Coconut oil, Mustard oil, Soyabean oil, Sunflower oil and Dalda. The net refined oil from per metric ton cobra, master seeds, sunflower seeds, palm crude oil, soyabean crude oil are respectively 300 kg, 400 kg, 400 kg, 980 kg, 970 kg. The industry has some production loss for palm oil and soyabean oil, which are respectively 2% and 3%. The industry has a fixed establishment cost is Tk. 5,00,000. The management of industry wishes to produce maximum 600 metric tons different types of oil. The cost for different raw materials to produce per metric ton crude oil/ seed/cobra in taka as follows (Table 7).
In addition the industry has the following limitations on expenditures:
Maximum investment for crude oil/seeds/cobra is Tk. 20,000,000/-;
Maximum investment for transportation is Tk. 5,00,000/-;
Maximum investment for storage is Tk. 15000/-;
Maximum investment for customs duties and vat is Tk. 6,000,000/-;
Maximum investment for chemicals is Tk. 55,000/-;
Maximum investment for electricity and gas is Tk. 120,000/-;
Maximum investment for maintains is Tk. 30,000/-;
Maximum investment for labor is Tk. 10,000/-;
Maximum investment for management is Tk. 25,000/-.
Table 7. Cost for different raw materials.
The objective is to maximize the ratio of return to investment. This leads to a linear fractional program as shown below.
Formulation of Example 4.
The three basic steps in constructing an LFP model are as follows:
Step 1. Identify the unknown variables to be determined (decision variables) and represent them in terms of algebraic symbols.
Step 2. Identify all the restrictions or constraints in the problem and express them as linear equations or inequalities, which are linear functions of the unknown variables.
Step 3. Identify the objective or criterion and represent it as a ratio of two linear functions of the decision variables, which is to be maximized (or minimized).
Now we shall formulate the above problem as follows:
Step 1. Identify the decision variables.
For this problem the unknown variables are the metric tons of refined oil produced for different product. So, let






Step 2. Identify the constraints.
In this problem constraints are the limited availability of found for different purposes as follows:
1) Since the management of industry wishes to produce maximum 600 metric tons different types of oil, so we have
2) Since the industry has maximum investment for crude oil/ seeds/ cobra is Taka 2,00,00,000/-, so we have
3) Since the industry has maximum investment for transportation is Taka 500,000/-, so we have
4) Since the industry has maximum investment for storage is Taka 15,000/-, so we have
5) Since the industry has maximum investment for customs duties and vat is Taka 6,000,000/-, so we have
6) Since the industry has maximum investment for chemical cost is Taka 6,000,000/-, so we have
7) Since the industry has maximum investment for electricity and gas is Taka 120,000/-, so we have
8) Since the industry has maximum investment for maintains is Taka 30,000/-, so we have
9) Since the industry has maximum investment for labor is Taka 200,000/-, so we have
10) Since the industry has maximum investment for delivery is Taka 10,000/-, so we have
11) Since the industry has maximum investment for management is Taka 25,000/-, so we have
We must assume that the variables 
Step 3. Identify the objective function.
In this case, the objective is to maximize the ratio of total return and investment by different crops. That is
Now we have expressed our problem as a mathematical model. Since the objective function is the ratio of return to investment and all of the constraints functions are linear, the problem can be modeled as the following LFP model:
Subject to
The problem consists of 6 decision variables and 11 constraints. To solve it by hand calculations it involves 17 variables and 11 constraints, which cannot be accommodated in available size of papers. Moreover, in real life, there may be some problems which may be involved with hundreds of constraints and variables and hence these cannot be solved by hand calculations. To overcome difficulties one has to require computer oriented solutions. Now, applying the computer program, we have obtained the following solutions.
Output:
X1 = 22.774542;
X2 = 0.000000;
X3 = 0.000000;
X4 = 0.000000;
X5 = 11.660869;
X6 = 0.000000.
Maximum value of the Objective Function = 1.655239.
5. Comparison
In this section, we compare our method with all other available methods and we find that our method is better than any other available method. The reasons are as follows:
・ We can solve any type of linear fractional programming problems by this methodology.
・ We can easily transfer the LFP problem into a LP problem.
・ Its computational steps are so easy from other methods.
・ In this method, we need to solve one LP but by other methods one needs to solve more than one LP, and thus our method saves valuable time.
・ The final result converges quickly in this method.
・ In this method there is one restriction that is
・ In some cases of the denominator and numerator say, 



・ Using computer program, we get the optimal solution of the LFP problem very quickly.
6. Conclusion
In this paper, we have provided a new method for solving linear fractional programming problem (LFPP). While all other existing methods are failed in the case of negative value of
Cite this paper
Sumon KumarSaha,Md. RezwanHossain,Md. KutubUddin,Rabindra NathMondal, (2015) A New Approach of Solving Linear Fractional Programming Problem (LFP) by Using Computer Algorithm. Open Journal of Optimization,04,74-86. doi: 10.4236/ojop.2015.43010
References
- 1. Martos, B. (1960) Hyperbolic Programming, Publications of the Research Institute for Mathematical Sciences. Hungarian Academy of Sciences, 5, 386-407.
- 2. Martos, B. (1964) Hyperbolic Programming, Naval Research Logistics Quarterly, 11, 135-155.
http://dx.doi.org/10.1002/nav.3800110204 - 3. Charnes, A. and Cooper, W.W. (1962) Programming with Linear Fractional Functions. Naval Research Logistics Quarterly, 9, 181-186.
http://dx.doi.org/10.1002/nav.3800090303 - 4. Swarup, K. (1964) Linear Fractional Functional Programming. Operations Research, 13, 1029-1036.
http://dx.doi.org/10.1287/opre.13.6.1029 - 5. Swarup, K., Gupta, P.K. and Mohan, M. (2003) Tracts in Operation Research. 11th Edition.
- 6. Bitran, G.R. and Novaes, A.J. (1973) Linear Programming with a Fractional Objective Function. Operations Research, 21, 22-29.
http://dx.doi.org/10.1287/opre.21.1.22 - 7. Sing, H.C. (1981) Optimality Condition in Fractional Programming. Journal of Optimization Theory and Applications, 33, 287-294.
http://dx.doi.org/10.1007/BF00935552 - 8. Tantawy, S.F. (2007) A New Method for Solving Linear Fractional Programming problems. Australian Journal of Basic and Applied Science, 1, 105-108.
- 9. Hasan, M.B. and Acharjee, S. (2011) Solving LFP by Converting It into a Single LP. International Journal of Operations Research, 8, 1-14.
- 10. Tantawy, S. (2008) An Iterative Method for Solving Linear Fraction Programming (LFP) Problem with Sensitivity Analysis. Mathematical and Computational Applications, 13, 147-151.
- 11. Effati, S. and Pakdaman, M. (2012) Solving the Interval-Valued Linear Fractional Programming Problem. American Journal of Computational Mathematics, 5, 51-55.
http://dx.doi.org/10.4236/ajcm.2012.21006 - 12. Pramanik, S., Dey, P.P. and Giri, B.C. (2011) Multi-Objective Linear Plus Linear Fractional Programming Problem Based on Taylor Series Approximation. International Journal of Computer Applications, 32, 61-68.



























































































































