Open Journal of Optimization
Vol.1 No.2(2012), Article ID:26134,5 pages DOI:10.4236/ojop.2012.12006
Investigation of Probability Generating Function in an Interdependent M/M/1/:((; GD) Queueing Model with Controllable Arrival Rates Using Rouche’s Theorem
Shekhawati Engineering College, Rajasthan Technical University, Kota, India
Email: prof.drvnmaurya@gmail.com, prof_vnmaurya@yahoo.in
Received September 28, 2012; revised November 2, 2012; accepted November 14, 2012
Keywords: Interdependent Queueing Model; Bivariate Poisson Process; Controllable Arrival Rates; Probability Generating Function; Laplace Transform; Rouche’s Theorem; Performance Measures
ABSTRACT
Present paper deals a 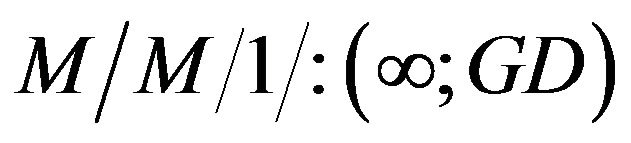 queueing model with interdependent controllable arrival and service rates wherein customers arrive in the system according to poisson distribution with two different arrivals rates-slower and faster as per controllable arrival policy. Keeping in view the general trend of interdependent arrival and service processes, it is presumed that random variables of arrival and service processes follow a bivariate poisson distribution and the server provides his services under general discipline of service rule in an infinitely large waiting space. In this paper, our central attention is to explore the probability generating functions using Rouche’s theorem in both cases of slower and faster arrival rates of the queueing model taken into consideration; which may be helpful for mathematicians and researchers for establishing significant performance measures of the model. Moreover, for the purpose of high-lighting the application aspect of our investigated result, very recently Maurya [1] has derived successfully the expected busy periods of the server in both cases of slower and faster arrival rates, which have also been presented by the end of this paper.
queueing model with interdependent controllable arrival and service rates wherein customers arrive in the system according to poisson distribution with two different arrivals rates-slower and faster as per controllable arrival policy. Keeping in view the general trend of interdependent arrival and service processes, it is presumed that random variables of arrival and service processes follow a bivariate poisson distribution and the server provides his services under general discipline of service rule in an infinitely large waiting space. In this paper, our central attention is to explore the probability generating functions using Rouche’s theorem in both cases of slower and faster arrival rates of the queueing model taken into consideration; which may be helpful for mathematicians and researchers for establishing significant performance measures of the model. Moreover, for the purpose of high-lighting the application aspect of our investigated result, very recently Maurya [1] has derived successfully the expected busy periods of the server in both cases of slower and faster arrival rates, which have also been presented by the end of this paper.
1. Introduction
The probability generating function approach plays a vital role in the study of queueing problems as it is crucially useful in performance analysis of a wide range of queueing models. As an example, the probability generating function approach facilitates to determine the expected busy and idle periods and system size distribution. In the queueing literature, it has been enthusiastically observed that most of the previous researchers [2-7] and references therein have presumed that the parameters of arrival and service rates in the queueing systems are independent to each other. However, it is not so in general because we find many queueing situations in our real life where the arrival and service rates are correlated with an elevated extent. We remark here that the arrival rate of a variety of queueing systems is usually controlled in order to reduce the queue length. Queueing models with controllable arrival rates have been studied by a few noteworthy researchers [3,8-10] which reveals the fact that there is still an increasing demand of analyzing an interdependent queueing models with controllable arrival rates. Srinivasa Rao et al. [8] have confined to obtain the average system size and average waiting time of an
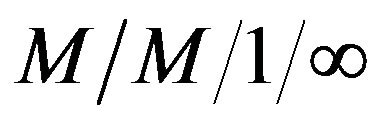 interdependent queueing model with controllable arrival rates under steady state conditions. Of late, Pal [4] considered the same queueing model which was already examined by Srinivasa Rao et al. [8] with a version of its limited waiting space and he succeeded to investigate the cost per unit time of a served customer in the system. Recently, Thiagarajan M. and Srinivasan A. [9] focused their attention to explore the
interdependent queueing model with controllable arrival rates under steady state conditions. Of late, Pal [4] considered the same queueing model which was already examined by Srinivasa Rao et al. [8] with a version of its limited waiting space and he succeeded to investigate the cost per unit time of a served customer in the system. Recently, Thiagarajan M. and Srinivasan A. [9] focused their attention to explore the  interdependent queueing model with bulk arrivals and controllable arrival rates. In this sequential work, we consider here an interdependent
interdependent queueing model with bulk arrivals and controllable arrival rates. In this sequential work, we consider here an interdependent 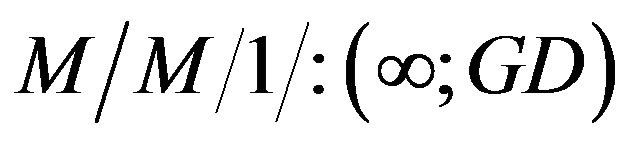 queueing model incorporating bivariate Poisson process and controllable arrival rates in order to investigate the probability generating functions in faster and slower arrival rates.
queueing model incorporating bivariate Poisson process and controllable arrival rates in order to investigate the probability generating functions in faster and slower arrival rates.
2. Description of the Model
In the present study, we consider an interdependent  queueing model with bivariate Poisson process and controllable arrival rates. The arrival pattern of customers are controlled by the system that it allows two arrival rates
queueing model with bivariate Poisson process and controllable arrival rates. The arrival pattern of customers are controlled by the system that it allows two arrival rates 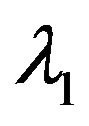 and
and ;
; . Without loss of generality we assume that whenever the system size attains a fixed number S, the arrival rate reduces to
. Without loss of generality we assume that whenever the system size attains a fixed number S, the arrival rate reduces to  from
from  and the arrival rate
and the arrival rate 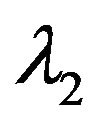 remains unchanged till the system size is greater than
remains unchanged till the system size is greater than . But as soon as the system size reduces to R, the arrival rate
. But as soon as the system size reduces to R, the arrival rate  changes back to
changes back to 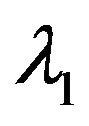 and the same pattern of change of arrival rates is repeated during the complete busy period of the system. Moreover, we assume that both
and the same pattern of change of arrival rates is repeated during the complete busy period of the system. Moreover, we assume that both  and
and 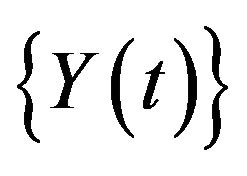 representing respectively the arrival and service processes are interdependent and these discrete random variables follow a bivariate Poisson distribution [11] with their probability mass function
representing respectively the arrival and service processes are interdependent and these discrete random variables follow a bivariate Poisson distribution [11] with their probability mass function 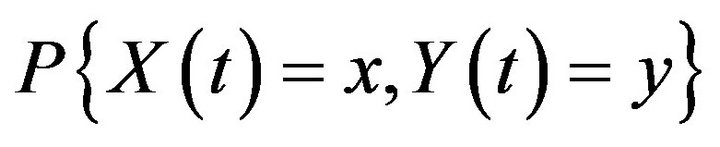 defined as given below
defined as given below

with following feasible conditions:

and .
.
Here 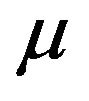 is the mean service rate and
is the mean service rate and ![]() is the covariance between arrival and service processes.
is the covariance between arrival and service processes.
3. Postulates of the Model
In addition to our assumptions in previous section-2 of the model, we have here underlying postulates for the purpose of our current study and analysis:
Postulate 3.1: The probability that there is one arrival and no service completion during a small interval of time  is
is ; when the system has arrival rate
; when the system has arrival rate .
.
Postulate 3.2: The probability that there is neither arrival and nor service completion during a small interval of time  is
is , when the system has arrival rate
, when the system has arrival rate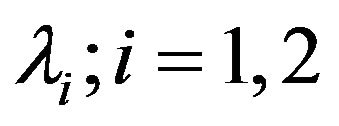 .
.
Postulate 3.3: The probability that there is no arrival and one service completion during a small interval of time  is
is , whatever be the arrival rate
, whatever be the arrival rate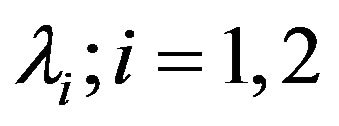 .
.
Postulate 3.4: The probability that there is one arrival and one service completion during a small interval of time  is
is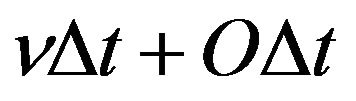 ; whatever be the arrival rate
; whatever be the arrival rate .
.
4. Differential-Difference Equations
Before proceeding further, we use symbol 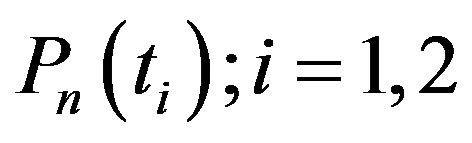 be the probability that there are n customers in the system at time
be the probability that there are n customers in the system at time  when system allows the arrival rate
when system allows the arrival rate .
.
Now it is fairly easy to observe that 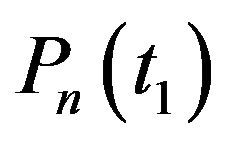 exists when
exists when  however both
however both  and
and 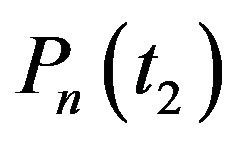 exist when
exist when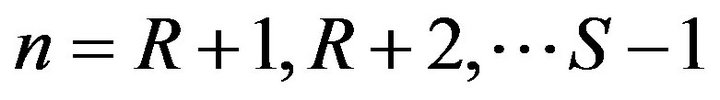 ; but only
; but only  exists when
exists when 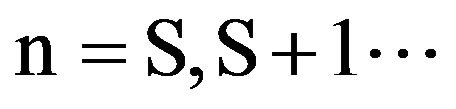
We further assume that the initial system size is 1 and R + 1 respectively when system has arrival rate . Let
. Let  and
and  be the busy period density respectively when the system has arrival rate
be the busy period density respectively when the system has arrival rate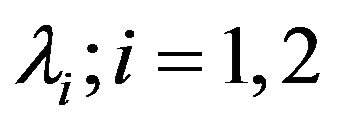 .
.
Now in view of an absorbing barrier at empty system during its faster arrival rate  the governing differential difference equations of the system size for the model are as following:
the governing differential difference equations of the system size for the model are as following:
![]() (4.1)
(4.1)
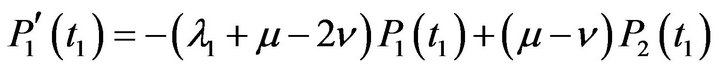 (4.2)
(4.2)
 (4.3)
(4.3)
The differential difference equation for the system size 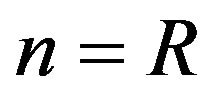 is as following:
is as following:
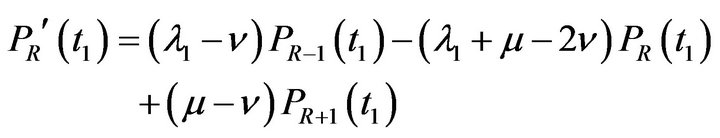 (4.4)
(4.4)
Moreover, the differential difference equations for the system size  are as following:
are as following:
 (4.5)
(4.5)
And the differential difference equation governing the state 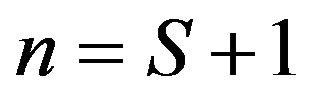 is as follows
is as follows
![]() (4.6)
(4.6)
Similarly, in view of an absorbing barrier at  system size during its slower arrival rate
system size during its slower arrival rate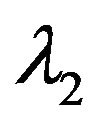 , we have the differential difference equations governing for the system size
, we have the differential difference equations governing for the system size 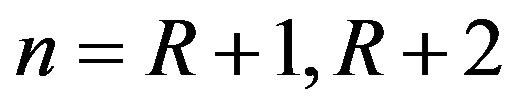 as following:
as following:
 (4.7)
(4.7)
 (4.8)
(4.8)
As in the earlier case of faster arrival rate, it is fairly easy to obtain the differential difference equations governing the states for 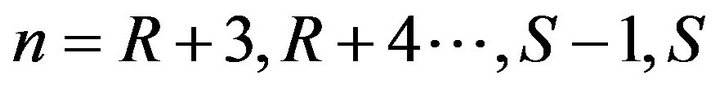 in slower arrival rate of the model which are given as following
in slower arrival rate of the model which are given as following
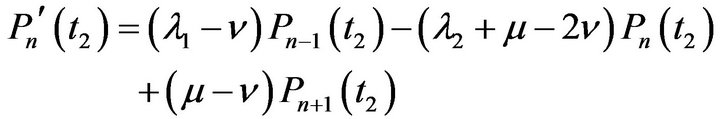 (4.9)
(4.9)
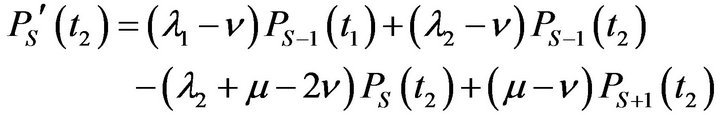 (4.10)
(4.10)
Moreover, the differential difference equations governing the states of the system for . in slower arrival rate are as follows
. in slower arrival rate are as follows
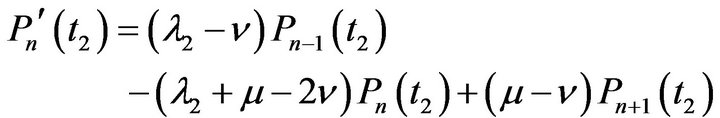 (4.11)
(4.11)
5. Determination of Probability Generating Function in Faster Arrival Rate
We define following probability generating function for the busy period of server in faster arrival rate:
 (5.1)
(5.1)
and we use symbol  for the Laplace transform of
for the Laplace transform of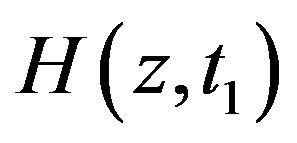 in following equation:
in following equation:
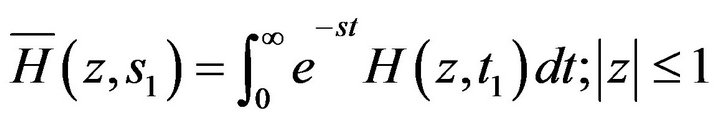 (5.2)
(5.2)
Multiplying by 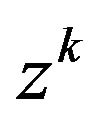 for
for  in respective differential difference Equations (4.1) to (4.6) and then summing over k and simplifying we obtain following partial differential equation
in respective differential difference Equations (4.1) to (4.6) and then summing over k and simplifying we obtain following partial differential equation
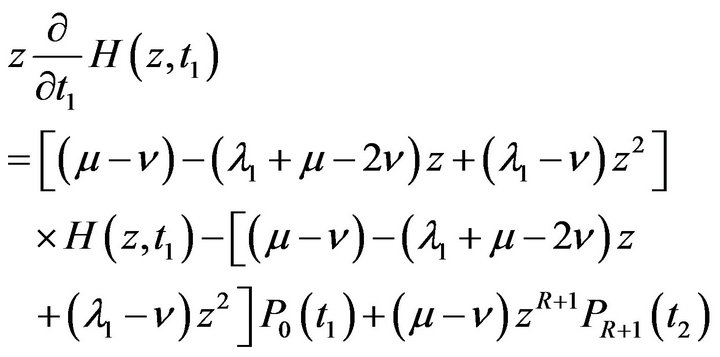 (5.3)
(5.3)
Taking Laplace transform of both sides of partial differential difference Equation (5.3), it is fairly easy to obtain
 (5.4)
(5.4)
As we know the fact that the converges in the region of the unit circle;
converges in the region of the unit circle;  and
and  whenever the denominator of RHS of equation (5.4) has zeros in the unit circle;
whenever the denominator of RHS of equation (5.4) has zeros in the unit circle; .
.
The two zeros of the denominators are as following:
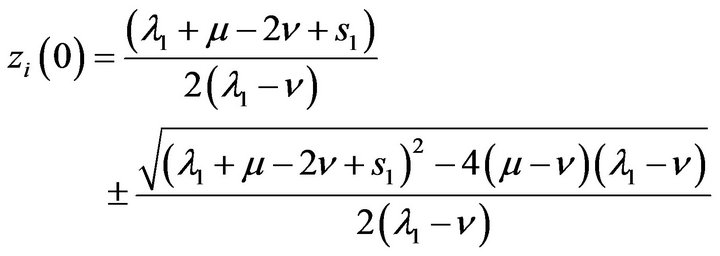 (5.5)
(5.5)
From Equation (5.5), we can observe here that

Moreover, we have
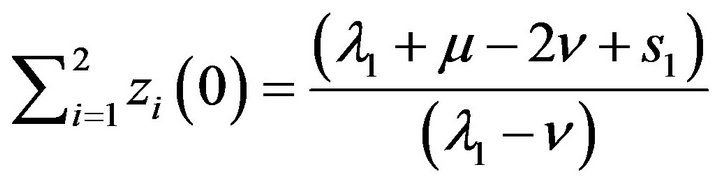 (5.6)
(5.6)
 (5.7)
(5.7)
On making use of Rouche’s theorem in Equation (5.4), it is fairly easy to evaluate 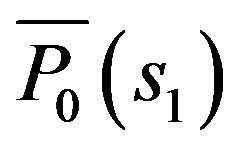 as following:
as following:
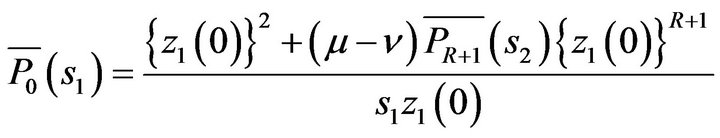 (5.8)
(5.8)
In view of Equation (5.8),  from Equation (5.5) yields as following:
from Equation (5.5) yields as following:
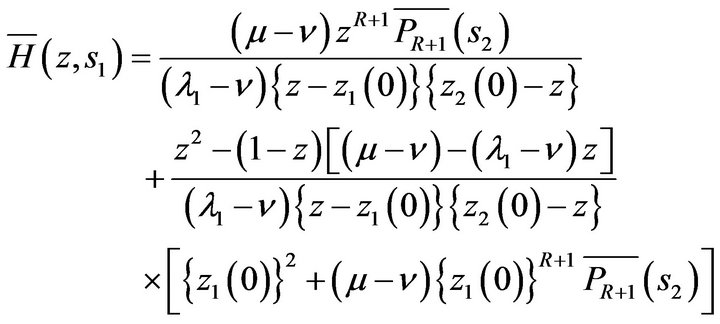 (5.9)
(5.9)
Equation (5.9) can be used in view of Gross and Harris [12] to explore the expected busy periods  in faster arrival rate as discussed by Maurya [1] and it is expressed as following:
in faster arrival rate as discussed by Maurya [1] and it is expressed as following:
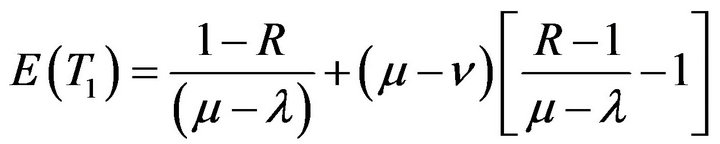 (5.10)
(5.10)
6. Determination of Probability Generating Function in Slower Arrival Rate
In this section, we define following probability generating function for the busy period of slower arrival rate:
 (6.1)
(6.1)
and we use symbol  for the Laplace transform of
for the Laplace transform of 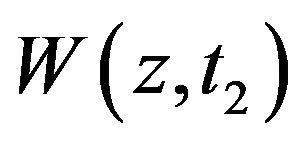 in following equation:
in following equation:
 (6.2)
(6.2)
Multiplying through differential difference Equations (4.7) to (4.11) by appropriate power of 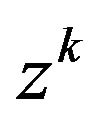 for
for 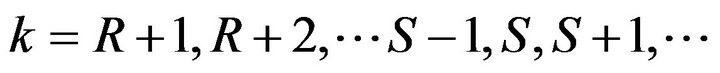 and then summing over k and proceeding as in earlier case of faster arrival rate
and then summing over k and proceeding as in earlier case of faster arrival rate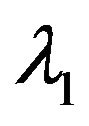 , it is fairly easy to obtain
, it is fairly easy to obtain  as following:
as following:
 (6.3)
(6.3)
where 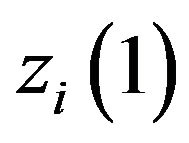 is given by following equation:
is given by following equation:
 (6.4)
(6.4)
It is remarkable that 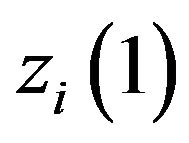 in Equation (6.4) possesses following three properties:
in Equation (6.4) possesses following three properties:
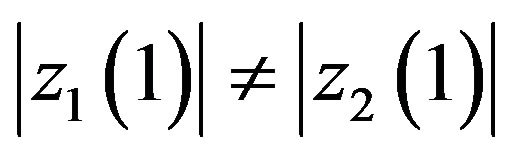 (6.5)
(6.5)
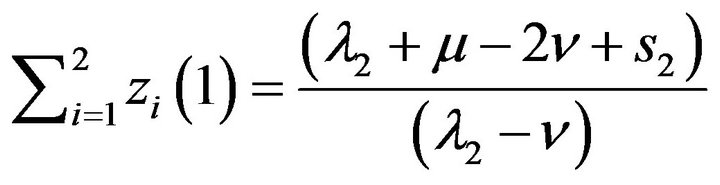 (6.6)
(6.6)
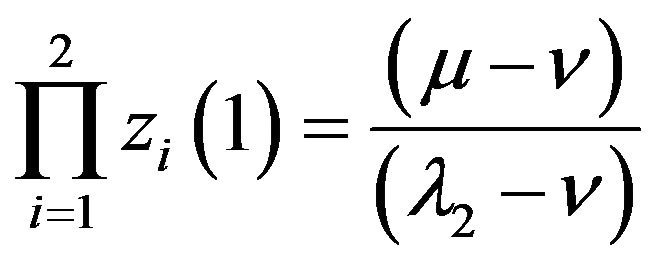 (6.7)
(6.7)
Applying Rouche’s theorem in Equation (6.3), we may have 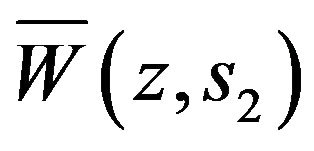 as following:
as following:
 (6.8)
(6.8)
We remark here that using equation (6.8) in the light of Gross and Harris [12], Maurya [1] succeeded to evaluate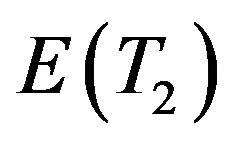 ; the expected busy period in slower arrival rate which is expressed as following:
; the expected busy period in slower arrival rate which is expressed as following:
 (6.9)
(6.9)
7. Conclusions
The probability generating function is the most important mathematical technique to examine the transient and steady state behavior of queueing models, particularly to explore many significant performance measures in study of wide range of queueing models which has been been evidenced by recent work of Maurya [1,6,7] and references therein and therefore it plays considerably a vital role in analyzing queueing problems. In the present paper, we have successfully investigated the probability generating functions for two different cases of slower and faster arrival rates of an interdependent 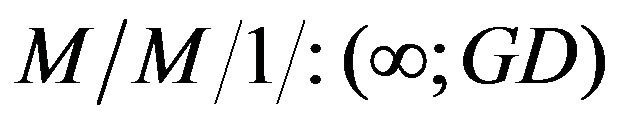 queueing model with controllable arrival rates taking into account that the two parameters of arrival and service rates follow the bivariate Poisson process. In order to emphasize the application aspect of the investigated result in the present paper, it is much relevant to remark here that by using the probability generating function approach, recently Maurya [1] considered the same queueing model and explored the expected busy periods of the server in both cases of faster and slower arrival rates. Moreover, we remark here that cost per unit time in both cases of faster and slower arrival rates of the queueing model taken into present consideration can be determined. In addition to this, it is highly expected that the research of the present investigation can be further extended by incorporating the concept of some other versions of control policies, server breakdown and multi-phase services.
queueing model with controllable arrival rates taking into account that the two parameters of arrival and service rates follow the bivariate Poisson process. In order to emphasize the application aspect of the investigated result in the present paper, it is much relevant to remark here that by using the probability generating function approach, recently Maurya [1] considered the same queueing model and explored the expected busy periods of the server in both cases of faster and slower arrival rates. Moreover, we remark here that cost per unit time in both cases of faster and slower arrival rates of the queueing model taken into present consideration can be determined. In addition to this, it is highly expected that the research of the present investigation can be further extended by incorporating the concept of some other versions of control policies, server breakdown and multi-phase services.
REFERENCES
- V. N. Maurya, “Determination of Expected Busy Periods in Faster and Slower Arrival Rates of an Interdependent
 Queueing Model with Controllable Arrival Rates,” International Journal of Engineering Research & Technology, Vol. 1, No. 5, 2012, pp. 1-5.
Queueing Model with Controllable Arrival Rates,” International Journal of Engineering Research & Technology, Vol. 1, No. 5, 2012, pp. 1-5. - I. J. B. F. Adan and J. Resing, “A Note on a Fluid Queue Driven by an
 Queue,” The Annals of Mathematical Statistics, Vol. 27, 1956, pp. 768-778.
Queue,” The Annals of Mathematical Statistics, Vol. 27, 1956, pp. 768-778. - P. Purdue, “The
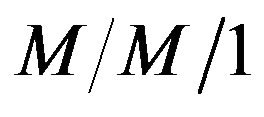 Queue in a Markovian Environment,” Operations Research, Vol. 22, No. 3, 1974, pp. 562-569. doi:10.1287/opre.22.3.562
Queue in a Markovian Environment,” Operations Research, Vol. 22, No. 3, 1974, pp. 562-569. doi:10.1287/opre.22.3.562 - S. Pal, “The Cost Analysis of
 Interdependent Queueing Model with Controllable Arrival Rates,” Ganita Sandesh, Vol. 17, No. 2, 2003, pp. 13-20.
Interdependent Queueing Model with Controllable Arrival Rates,” Ganita Sandesh, Vol. 17, No. 2, 2003, pp. 13-20. - V. N. Maurya, “A Study of Use of Stochastic Processes in Some Queueing Models,” Ph. D. Thesis, Department of Mathematics & Statistics, Dr. Ram Manohar Lohia Avadh University, Faizabad, 2000.
- V. N. Maurya, “Performance Analysis of an
 Queueing Model with Second Phase Optional Service and Bernoulli Vacation Schedule,” International Journal of Emerging Research in Management and Technology, Vol. 1, No. 2, 2012.
Queueing Model with Second Phase Optional Service and Bernoulli Vacation Schedule,” International Journal of Emerging Research in Management and Technology, Vol. 1, No. 2, 2012. - V. N. Maurya, “Sensitivity Analysis on Significant Performance Measures of Bulk Arrival Retrial Queueing
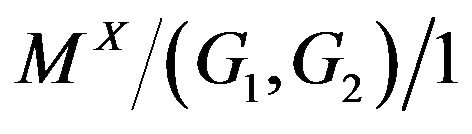 Model with Second Phase Optional Service and Bernoulli Vacation Schedule,” International Journal of Engineering Research and Technology, Vol. 1, No. 10, 2012.
Model with Second Phase Optional Service and Bernoulli Vacation Schedule,” International Journal of Engineering Research and Technology, Vol. 1, No. 10, 2012. - K. Srinivasa Rao, T. Shobha and P. Srinivas Rao, “The
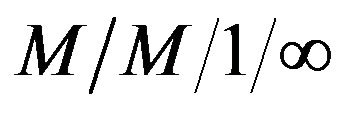 Interdependent Queueing Model with Controllable Arrival Rates,” Opsearch, Vol. 37, No. 1, 2000.
Interdependent Queueing Model with Controllable Arrival Rates,” Opsearch, Vol. 37, No. 1, 2000. - M. Thiagarajan and A. Srinivasan, “The
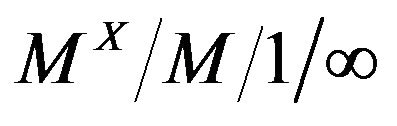 Interdependent Queueing Model with Controllable Arrival Rates,” Journal of Decision and Mathematical Sciences, Vol. 11, No. 1-3, 2006, pp. 7-24.
Interdependent Queueing Model with Controllable Arrival Rates,” Journal of Decision and Mathematical Sciences, Vol. 11, No. 1-3, 2006, pp. 7-24. - V. N. Maurya, “On the Expected Busy Periods of an Interdependent
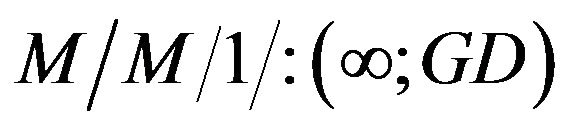 Queueing Model Using Bivariate Poisson Process and Controllable Arrival Rates,” Proceedings of 2nd International Conference on Computer Research and Development, IEEE Computer Society, Kuala Lumpur, 7-10 May 2010, pp. 558-564. doi:10.1109/ICCRD.2010.119
Queueing Model Using Bivariate Poisson Process and Controllable Arrival Rates,” Proceedings of 2nd International Conference on Computer Research and Development, IEEE Computer Society, Kuala Lumpur, 7-10 May 2010, pp. 558-564. doi:10.1109/ICCRD.2010.119 - L. Norman and S. K. Johnson, “Discrete Distributions,” John Wiley & Sons, New York, 1969.
- D. Gross and C. M. Harris, “Fundamentals of Queueing Theory,” John Wiley, New York, 1974.

