Graphene
Vol.05 No.02(2016), Article ID:65466,18 pages
10.4236/graphene.2016.52007
The Dissimilarities between Graphene and Frame-Like Structures
Rasheed Atif, Fawad Inam
Department of Mechanical and Construction Engineering, Faculty of Engineering and Environment, Northumbria University, Newcastle, UK

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 February 2016; accepted 10 April 2016; published 13 April 2016
ABSTRACT
Modeling and simulation allow methodical variation of material properties beyond the capacity of experimental methods. Due to the hexagonal structure of graphene, it is considered as frame-like structure. In the frame, covalent C-C bonds are taken as beams joined together with carbon atoms placed at the joints. Uniaxial beam elements, defined by their cross-sectional area, material properties, and moment of inertia represent the covalent bonds. The parameters of the beam elements are determined by establishing equivalence between structural and computational mechanics. However, the bonds connecting the carbon atoms do not have physical existence as they are a compromise between attractive and repulsive forces. Also, defects at nanoscale make graphene different from frame-like structure. In addition, the topography of graphene makes it non-linear structure and even the axial loading changes to eccentric loading. Here we show that, by using basic statics principles, disparities between graphene and frame-likes structures can be highlighted.
Keywords:
Modeling, Graphene, Frame-Like Structure, Topographical Features, Stress Concentration

1. Introduction
The numbers of publications of Carbon Nanotubes (CNTs) and graphene in the last decade are shown in Figure 1(a) and Figure 1(b). The trends indicate that the number of publications of state-of-the-art CNTs in 2014 is lower than that in 2013. On the contrary, there is an exponential rise in the use of graphene in the last decade. Novoselov et al. [1] experimentally produced Single Layer Graphene (SLG) using scotch-tape method and a low cost method to synthesize graphene on large scale was presented by Stankovich et al. [2] allowing the extension of the applications of graphene to industrial scale. In 2014, 2009 research papers were published on graphene.

Figure 1. Number of yearly publications of (a) CNTs and (b) graphene during 2005-2014 (Thomson Reuters).
However, to the best of our knowledge, no article is yet published in which SLG was used. One of the reasons could be that the SLG is not yet at everyone’s disposal. Nevertheless, the trends indicate that the graphene would surpass other carbonaceous materials no sooner it becomes easily and economically available. Therefore, extensive theoretical research has been carried out in the last decade to justify the use of graphene in eclectic applications.
As graphene is a two-dimensional structure, each carbon atom can undergo chemical reaction from the sides. It is one of the reasons for high chemical reactivity of graphene. The carbon atoms on the edge of SLG have three incomplete bonds that impart especially high chemical reactivity to edge carbon atoms. In addition, defects within graphene sheet are high energy sites and preferable localities for chemical reactants to attack. All these factors make graphene a very highly chemically reactive entity. The carbon atoms are connected through strong covalent bonds. There is sp2 orbital hybridization between Px and Py that forms σ-bond [3] . The orbital Pz forms π-bond with half-filled band that allows free motion of electrons. These interatomic forces play a crucial part in defining the proficiency of graphene as reinforcement in polymers.
As atoms keep oscillating with characteristic oscillating frequencies, the oscillatory period of carbon atoms for some bounded trajectories reaches terahertz frequencies [4] . To define the trajectory of atoms, Newton’s equation of motion in MD can be used as given in Equation (1) and the relation between force f1 and potential energy E is given in Equation (2), where mI, rI, and fI are mass of, position of, and force on Ith atom, respectively,
and 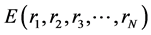 is potential energy of the N-atom system. The potential energy arises from the bonded
is potential energy of the N-atom system. The potential energy arises from the bonded
and non-bonded interactions among atoms and molecules. Polymer Consistent Force Field (PCFF) can be used to specify such interactions [5] . The PCFF defines the potential energy components as given in Equation (3) [6] .
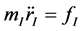 (1)
(1)
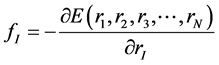 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
The first four terms of Equation (3) represent bond, angle, torsion, and dihedral energy, respectively. The other six terms represent cross-terms among various valance energy components, mainly bond and angle. The last two terms define energy arising from Columbic and Van der Walls interactions, respectively. The influence of thermal vibrations on potential energy is addressed by the cross-terms. The total energy of N atoms is represented by Hamiltonian function (H) which can be defined in terms of potential energy (Equation (3)) and is given in Equation (4) while the kinetic energy component is given in Equation (5), where PI and MI are momentum and mass of Ith atom, respectively [6] .
In current study, various factors of graphene structure are discussed such as atomic bonds, atomic structure, topographical features, type of loading, torque transmission, and stress concentration effect. To corroborate the influence of specimen geometry on the mechanical properties, epoxy samples were produced of different curvatures and subjected to compression loading. The following study differentiates between the hexagonal structure of graphene and frame-like structure.
2. Experimental Section
2.1. Materials
Bisphenol A-epichlorohydrin based epoxy having density of ~1.3 g/cm3 and dimethylbenzylamine isophoronediamine based low viscosity fast curing hardener with ~1.1 g/cm3 density were used in current study. The epoxy matrix used consisted of EPOPHENTM EL5 bisphenol A based liquid epoxy and EPOPHENTM EHA57 diamine hardener, purchased from Polyfibre, UK. This epoxy system is a multi-purpose resin offering good all-round properties with the epoxy group content of 4.76 - 5.25 mol/kg. The viscosity of liquid epoxy and hardener are 12,000 - 15,000 cps and 45 cps at room temperature, respectively. To prepare epoxy material, the mix proportions are 50 parts by weight of hardener to 100 parts by weight of liquid epoxy. The gelation time of the resin was 43 min at room temperature.
2.2. Samples Production
The epoxy and hardener were initially degassed separately for 1 h each. The epoxy and hardener were mixed using sonication that was carried out using tip sonicator of power 750 W and frequency 250 kHz (Vibra-cell model VC 750, USA). The operation mode was 70% power with 10 s vibration and 5 s break. Although the sonication was carried out at room temperature, however, temperature of the system rose due to high energy vibration produced by tip sonicator. Vacuum degassing was carried out for 15 min. The resin was poured into silicone molds (without any release agent) and cured at room temperature for 6 h followed by post-curing at 80˚C for 6 h.
2.3. Characterization
The epoxy samples were subjected to compression loading using Instron universal testing machining (Model 3382). The displacement rate was kept 1 mm/min. Five specimens were tested for each composition. The test results were used to corroborate the theoretical explanations. The atomic bonds, graphene structure, and topographical features of graphene are discussed in detail. The influence of topography on centric and eccentric loading is discussed. In addition, the torque transmission in the graphene structure is correlated with the graphene structure. As covalent bonds do not show plastic character, therefore, the stress concentration effect in the presence of notches will be pertinent and significantly influence the mechanical properties of graphene.
3. Results and Discussion
Various theoretical and computational approaches have been employed to explore graphene including but not limited to, quantum mechanical-based methods [7] , Continuum Mechanics (CM) [8] , Molecular Mechanics (MM) [9] , Molecular Dynamics (MD) [10] , atomistic modelling [11] , Density Functional Theory (DFT) [12] , and multiscale modelling [13] . Due to the hexagonal structure of graphene, it is considered as frame-like structure. In the frame, covalent C-C bonds are taken as beams joined together with carbon atoms placed at the joints. Uniaxial beam elements, defined by their cross-sectional area, material properties, and moment of inertia represent the covalent bonds. The parameters of the beam elements are determined by establishing equivalence between structural and computational mechanics. However, the bonds connecting the carbon atoms do not have physical existence as they are a compromise between attractive and repulsive forces. Also, defects at nanoscale make graphene different from frame-like structure. In addition, the topography of graphene makes it non-linear structure and even the axial loading changes to eccentric loading.
3.1. Atomic Bonds
No two atoms, to the best known knowledge, can touch each other and whenever they are juxtaposed, they show ambivalence between attraction and repulsion as shown in Figure 2. It is because there are attractive forces between nucleus of an atom and electrons of the other atom because of the opposite charges, and vice-versa. However, because of the similar charges, there are repulsive forces between nucleus of an atom and nucleus of the other atom and electrons of one atom and electrons of the other atom. The energetics of inter-atomic interactions can be defined using Lennard-Jones potential as given in Equation (6) [14] [15] ,
 (6)
(6)
where rij is the separation distance between atoms i and j, and rcut is the cut-off distance. These forces change with varying distance between the atoms as shown in Figure 3. A compromise between attractive and repulsive forces is established and atoms settle down at a certain gap known as equilibrium bond length. A similar structure is observed in graphene as shown in Figure 4.
Figure 2. Attractive and repulsive forces between atoms.
Figure 3. Variation in attractive and repulsive forces between atoms with distance [16] .
Figure 4. Carbon atoms joined together by strong covalent bonds [16] .
3.2. Atomic Structure
The schematic diagram of hexagonal unit cell of the atomic structure of graphene is shown in Figure 5. When carbon atoms form a hexagonal network in two dimensions, a graphene sheet is obtained as shown in Figure 6. This graphene structure is considered as frame-like structure for simulation purposes as shown in Figure 7. The bonds between graphene are considered as beams and carbon atoms are considered as joints. However, the structural variations and defects make it different from ideal frame-like structure. For example, in the graphene structure, the hexagonal network is not always repeated.
The graphene has many other stable configurations apart from honeycomb hexagonal lattice structure. For example, different chemisorbed configurations of epitaxial graphene coexist on single crystal Ni(111) such as top-FCC, top-HCP, and top-bridge [17] . In addition, there are structural defects [18] in graphene that significantly influence physical and chemical properties of graphene [19] . Some of the atomic scale defects are schematically shown in Figures 8(a)-(d), which include atomic vacancies, heptagon-pentagon topological defects, adatoms, and dopants. These defects can be inherited by graphene during growth [20] and can be introduced advertently by resonance plasma [21] , chemical treatment [22] , and irradiation [23] .
Surface defects are also introduced during functionalization, oxidation, and reduction [24] . For example, in reduced graphene oxide, the graphene layers are found to comprise of a few nanometers interspersed defect areas dominated by clustered heptagons and pentagons [24] . The first-principles calculations show that atomic-scale defects result in both intravelley and intervalley scattering of graphene and Fermi velocity is decreased in the vicinity of the defects due to enhanced scattering [25] . The electronic properties of graphene are strongly varied by structural defects that deform the original honeycomb lattice [26] .
3.3. Topographical Features
The exploitation of topographically modified geometries in synthetic and bioinspired materials is a novel area of research [27] [28] . The topographically modified carbonaceous materials are produced by various methods and have found numerous applications [29] [30] . It was shown that the superior electronic properties of graphene are sensitive to topography [31] . The graphene sheets have coiled structure that helps them to store sufficient amount of energy [32] . The individual sheet and chunk of sheets together are subjected to plastic deformation at the application of external load. The applied energy is utilized in undertaking plastic work that enhances the ability of graphene to absorb more energy [33] . Graphene has shown inclination for stable folding and bending energy at folds is compensated by intersheet adhesion (Van der Waals interactions) [34] . The individual layers of graphene, under external loadings and thermal stresses, undergo out-of-plane wrapping [35] , rippling [36] , folding [37] , scrolling [38] , and crumpling [39] , making graphene a tough material. Wang et al. showed that wrinkle’s wavelength and amplitude are directly proportional to volumetric dimensions of graphene as clear from Equation (7) and Equation (8), where λ is wrinkle wavelength, ν is Poisson’s ratio, L is length of graphene sheet, t is thickness of graphene sheet, ε is edge contraction on a suspended graphene sheet, and A is wrinkle amplitude [40] .
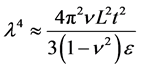 (7)
(7)
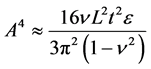 (8)
(8)
As defects significantly influence graphene properties and are produced during synthesis process, therefore the properties of graphene are sensitive to synthesis method. In addition, as the defects have a non-uniform distribution, therefore the properties of graphene also become dependent on the sheet size. Similarly, out-of-plane
Figure 5. Schematic diagram of hexagonal unit cell of graphene structure.
Figure 6. Graphene sheet comprising of 2D hexagonal network of carbon atoms combined by strong covalent bonding.
Figure 7. Graphene being perceived as frame-like structure with bonds as beams and carbon atoms as joints.
Figure 8. Structural defects in graphene: (a) vacancy; (b) pentagon-heptagon; (c) adatom; and (d) dopant.
wrapping, rippling, folding, scrolling, and crumpling can significantly influence the properties of graphene. As the variation in topographical features is unpredictable and defects may appear randomly, therefore the properties of graphene become significantly dependent on the location of graphene sample under consideration. On the contrary, the ideal frame-like structure repeats itself exactly in all directions. The graphene size, shape, and topography can be controlled simultaneously [41] . Chen et al. synthesized well-aligned millimeter-sized tetragon-shaped and hexagon-shaped graphene on a polycrystalline copper substrate using low pressure CVD [41] . CVD is an efficient approach to produce high quality and large surface area graphene on metallic substrates [42] . Graphene can be grown epitaxially on single crystal copper substrate [43] . Graphene shape and orientation strongly depend on crystallographic orientation of copper substrate [44] . The dendritic graphene with multiple branches can be obtained by diffusion-limited growth dynamics [45] . The graphene shape can also be controlled using surface condition of substrate. For example, wet-loaded samples produce tetragonal shaped and dry-loaded samples produce hexagonal shaped graphene [41] . The graphene shape can also be controlled by processing temperature [46] .
3.4. Stress and Strain Distribution under Axial Loading
The distribution of stresses and strains in structural element depends on the way of load application. The distribution of stresses and strains in structural elements can be measured using tensile tests, strain gage tests, photoelastic methods, and dynamic mechanical analyzer, and modeling approaches [47] . When uniform load is applied or concentrated load applied through rigid plates, the load is distributed uniformly in the structural member and uniform deformation is observed as shown in Figure 9(a) and Figure 9(b). However, when concentrated load is applied directly to structural member, the distribution of stresses and strain will not be uniform in the structural member and load will be concentrated at the point of loading as shown in Figure 10(a) and Figure 10(b). Except in the immediate vicinity of the points of application of the loads, the stress distribution may be assumed independent of the actual mode of the application of the loads as shown in Figure 11 and Figure 12. The stress distribution in concentrated loading is quite different at the ends compared with uniform loading where stress distribution is the same at the ends in transverse direction. However, in both the cases, the stress distribution at the middle of the member is the same irrespective of the type of loading. This principle is known as Saint-Venant’s principle after the French mathematician and engineer Adhemar Barre de Saint-Venant (1797- 1886) [48] . Although Saint-Venant’s principle makes it possible to replace a given loading by a simpler one for the purpose of computing the stresses in a structural member, it however may not be applied to graphene. For long, slender members, such as graphene, another configuration is possible and indeed will prevail, if the load is sufficiently large; the member buckles and assumes a curved shape. When member buckles, the loading
Figure 9. (a) Concentrated loading applied through rigid plates; (b) The stress distribution remains the same throughout the specimen.
Figure 10. (a) Concentrated loading applied without rigid plates; (b) The stress is concentrated at the point of loading.
Figure 11. Stress distribution under point loading.
Figure 12. Stress distribution under uniform loading.
conditions and stress and strain distribution significantly vary and affect the overall properties of the structural member.
3.5. Centric vs. Eccentric Loading
When structural member buckles, the applied axial loading varies from centric to eccentric loading. Consider a structural member with cross-sectional area A and subjected to loading P and P' as shown in Figure 13(a). As there are two forces involved, it is called as two force member. As both the forces are acting along the axis of the member, this type of loading is called as axial loading. As the cross-sectional area is exactly perpendicular to axis of loading, the stress (P/A) is called as normal stress and is taken as average value of stress over the cross- section rather than the stress at a specific point of the cross-section. However, it should be noted that when uniform distribution of stress is assumed, then it follows from elementary statics that the resultant P of the internal forces passes through the centroid C of the section. This means that a uniform distribution of stress is possible only if the line of action of the concentrated loads P and P' passes through the centroid of the section considered. This type of loading is called centric loading and is assumed to take place in all straight two-force members found in beams, trusses, and frame-like structures.
When the structure buckles, the loading condition varies. Consider a two-force member loaded axially as shown in Figure 13(b). From the conditions of equilibrium, the internal forces in a given section must be equivalent to a force P applied at the centroid of the section and a moment M = Pd as shown in Figure 13(c). This axial loading is called as eccentric loading in which the distribution of forces and corresponding stresses can neither be uniform nor symmetric. The graphene being a slender specimen will undergo buckling and topographical features will further complicate the stress distribution. Montazeri and Rafii-Tabar observed an exponential drop in bending rigidity and lower axial Young’s modulus with increasing temperature in graphene-PMMA nanocomposites [49] . It can be attributed to eccentric loading and bond breakage. Graphene has sp2 hybridization which is stronger than sp3 hybridization found in diamond [50] . Therefore, graphene shows superior mechanical properties. However, at the application of elevated temperatures, C-C bonds deteriorate and protrude out of the graphene plane. These misaligned bonds do not offer their intrinsic mechanical strength in the axial direction.
To experiment the influence of curved specimens on the strength of material, monolithic epoxy samples were produced by casting in silicone molds. The samples were cured at room temperature for 6 h followed by post- curing at 80˚C for 6 h. Samples of two different geometries were produced: straight samples as shown in Figure 14(a), and curved specimen as shown in Figure 14(b). The specimens were ground on grinding papers to make the ends perpendicular to the axis of load application. The specimens were subjected to compression axial loading with displacement rate of 1 mm/min. The stress-strain trends achieved are shown in Figure 14(c). The samples showed brittle fracture between strains of 0.05 - 0.06 that may be attributed to the brittleness of thermoset-
Figure 13. Two-force member under axial centric loading and axial eccentric loading.
Figure 14. Epoxy samples: (a) straight sample; and (b) curved sample; (c) stress- strain trends of epoxy samples.
ting monolithic epoxy. The curved specimen showed a significant lower value of strength and stiffness than straight specimen. In addition, the curved specimen got fractured earlier than the straight specimen. It may be attributed to the geometry of the sample as compositions and testing conditions were the same. In curved specimen, not only axial loading is acting, but also moment is produced due to eccentric loading which caused the drop in strength and stiffness of the curved specimen.
It has been shown that graphene does not show smooth and flat surface. The graphene structure contains ripples and wrinkles. Abedpour et al. used both analytical and MD-based numerical simulations and correlated the surface topography of graphene with thermal fluctuations [51] . The Monte Carlo-based simulations predicted the formation of spontaneous ripples on graphene surface at finite temperatures. The ripple amplitude is comparable with the interatomic distance of graphene C-C covalent bonds (~0.142 nm) and was found independent of the total length of graphene sheet. It was also observed that the spontaneous ripples had a characteristic wavelength of about 8 nm [52] . Therefore, rippling being the intrinsic feature of graphene sheet is expected to strongly influence the mechanical properties of graphene. Therefore, if graphene is subjected to axial loading, it will not be centric loading as shown in Figure 15(a). Instead, the graphene will undergo eccentric loading (Figure 15(b) and Figure 15(c)). During this eccentric loading, the carbon bonds undergo moment along with axial loading. This moment can significantly alter the behavior of graphene.
3.6. Torque Transmission
When graphene is subjected to eccentric axial loading, the axial load will be accompanied by a moment as shown in Figure 16. The influence of moment on the properties of graphene will be defined by the way it is transferred into the graphene structure. If we consider a frame-like structure, the moment transmission depends on the shaft. For example, the shear stress distribution and torque transmission of solid and hollow shafts are different because of the polar moment of inertia as shown in Figure 17 and Figure 18, respectively. The polar
moment of inertia of solid shaft is 0.5πc4 and that of hollow shaft is
solid and a hollow shaft of the same cross-section, the efficiency of moment transmission in hollow shaft is greater than that in solid shaft. This is the reason that the drive shafts of vehicles are made hollow. Considering the carbon bonds as forces and not consisting of material, what would be the values of moment on atoms 2 and 3 in Figure 19? It may be highly unlikely that x = y = 1.
Figure 15. Graphene structures under axial loading. There is high probability that graphene will undergo eccentric loading due to topographical features.
Figure 16. Carbon atoms in graphene subjected to eccentric axial loading undergoes torque.
Figure 17. (a) Solid shaft subjected to moment; (b) Shear stress distribution in solid shaft.
Figure 18. (a) Hollow shaft subjected to moment; (b) Shear stress distribution in hollow shaft.
Figure 19. Carbon atom 1 in graphene structure subjected to moment M. What would be the values of moment on locations 2 and 3? Would it be the case that x = y = 1?
3.7. Stress-Strain Calculations
To calculate stress, applied load is divided by area. However, area calculation in graphene sheet would not be easy as shown in Figures 20(a)-(d). If we consider graphene as flat sheet as shown in Figure 20(a), the surfacearea becomes 50 nm2. However, the graphene undergoes wrinkling, rippling, folding, scrolling, and crumpling. In simple words, the graphene sheet cannot be considered as flat structure and surface area significantly alters in non-flat sheet. If we consider semicircles in graphene sheet as shown in Figures 20(b)-(d), the surface area increases up to 23.6%. Accordingly, the stress calculation will be significantly affected by the input area. Therefore, the stress calculation in graphene sheet considering a flat frame-like structure may yield erroneous stress values. Similarly, the strain calculations would also be affected by the original length. If we consider flat sheet,
its length is 


though stress-strain calculations look quite simple, however, they will find worth when graphene will be used in the production of nano-sensors that would be sensitive to any variation in stress and/or strain. As the topographical features of graphene are a function of number of factors, such as synthesis method and temperature, therefore the precise calculations of stress and strain would not be as easy as in the case of simple frame-like structure.
3.8. Stiffness Comparison
The stiffness comparison of ferrous, non-ferrous, and graphene is shown in Figure 22. The steels show a specific upper and lower yield points which is not prominent in non-ferrous metals and alloys such as aluminum. The profile of graphene is considered based on the energy profile as shown in Figure 3. The energy profile is flipped vertically to compare it with stress-strain curves of steel and aluminum. The tensile testing machines are usually strain (or displacement) controlled and not stress (or load) controlled. It means that machine displaces the sample at a constant speed and force changes accordingly to sustain that speed. As material flows, the load is varied based on internal mechanisms in the material. For example, dislocations in metals are initially pinned and force is increased to unpin the dislocations. Just before the inception of the unpinning of the dislocations, upper yield point is observed. Once the dislocations are free to move, the load drops and lower yield point is reached after which the material flows spontaneously at the same loading until single slip system remains active. With the passage of time, multiple slip systems become active and strain-hardening takes place by Lomer-Cottrell dislocations and jogs on screw dislocations which impede the dislocation glide. The load is further increased till Ultimate Tensile Strength (UTS) is reached. After UTS, the cross-slip and climb become mobile and load drops till fracture takes place. However, it should be noted that all these mechanisms are not available in graphene being single layer and non-metallic. Therefore, the load-displacement trend will be defined by the interplay between attractive and repulsive forces between the atoms. When the graphene is subjected to tensile loading, the distance between the atoms will change at a constant rate. As there are no inherent mechanisms available in graphene to resist deformation except the attractive forces between atoms, therefore the load will follow the energy profile as shown in Figure 3 which is flipped vertically in Figure 22 for comparison with steel and aluminum curves. It should be noted that in both ferrous and non-ferrous metals, there are elastic and plastic regions.
However, in graphene, bonds do not deform plastically. They are either there or not. Therefore, graphene behaves as elastic material from origin A till end point B. Accordingly, the stiffness becomes a function of the location of the curve where the slope is calculated from. In addition, the slope will become a function of defects, topographical features, and stress concentration. Therefore, measuring elastic constants in graphene is not as straightforward as in simple frame-like structure.
Figure 20. Difference in surface areas of flat and topographically modified surfaces. Surface area significantly increases with textured topography.
Figure 21. Strain calculations: change in length should be divided by 

Figure 22. Comparison of stress-strain curves of ferrous, non-ferrous, and graphene.
3.9. Stress Concentration
When a structural member contains a discontinuity, such as a hole, high localized stresses occur near the discontinuity as shown in Figure 23. The maximum stress (
For a circular hole (a = b), 

notch becomes elliptical and pointed. Therefore, a very narrow crack oriented normal to the tensile axis will result in a very high stress concentration. The effect of stress raiser is much more pronounced in a brittle material than in a ductile material. In a ductile material, plastic deformation occurs when the yield stress is exceeded at the point of maximum stress. Further increase in load produces a local increase in strain at the critically stressed region with little increase in stress. Because of strain hardening, the stress increases in regions adjacent to the stress raiser, until if the material is sufficiently ductile, the stress distribution becomes essentially uniform.
Thus, a ductile material loaded statically will not develop the full theoretical stress-concentration factor. However, redistribution of stress will not occur to any extent in a brittle material. Therefore, a stress concentration of close to theoretical value will result in a brittle material. According to Griffith crack theory, discontinuities in brittle materials will significantly lower the mechanical properties [54] . Therefore, when graphene sheet contains a notch as shown in Figure 24, it will behave as ideally brittle material since bonds do not undergo plastic deformation. Therefore, under the influence of applied loading and in the presence of notch, the mechanical properties of graphene will suffer severe degradation. This degradation will be more severe than in frame-like structure as latter exhibits plastic character which is absent in the graphene structure.
Figure 23. Variation in stress as moving away from crack tip.
Figure 24. Notched-graphene sheet.
4. Conclusion
In conclusion, the topographical features, atomic defects, torque transmission, totally elastic behavior, and stress concentration are the important factors which make graphene and frame-like structures disparate. Therefore, if the objective is to model graphene to simulate its properties or in graphene based materials, aforementioned factors should be taken into account. If graphene is to be considered as frame-like structure, it should be treated either as crystalline hexagonal structure with localized glassy regions, or as glassy phase with localized ordered structure. The extent of either region should be a function of synthesis method of graphene, thermal fluctuations, and other service conditions.
Acknowledgements
The authors would like to thank the Department of Mechanical and Construction Engineering, Northumbria University, UK for the provision of research facilities, without which the analysis of relevant data was not possible.
Cite this paper
Rasheed Atif,Fawad Inam, (2016) The Dissimilarities between Graphene and Frame-Like Structures. Graphene,05,55-72. doi: 10.4236/graphene.2016.52007
References
- 1. Novoselov, K.S., Geim, A.K., Morozov, S.V., Jiang, D., Zhang, Y., Dubonos, S.V., et al. (2004) Electric Field Effect in Atomically Thin Carbon Films. Science, 306, 666-669. http://dx.doi.org/10.1126/science.1102896
- 2. Stankovich, S., Dikin, D.A., Dommett, G.H.B., Kohlhaas, K.M., Zimney, E.J., Stach, E.A., et al. (2006) Graphene- Based Composite Materials. Nature, 442, 282-286. http://dx.doi.org/10.1038/nature04969
- 3. Choi, W. and Lee, J.-W. (2012) Graphene Synthesis and Applications. CRC Press, Boca Raton.
- 4. Chan, Y. and Hill, J.M. (2010) Some Novel Plane Trajectories for Carbon Atoms and Fullerenes Captured by Two Fixed Parallel Carbon Nanotubes. The European Physical Journal D, 59, 367-374. http://dx.doi.org/10.1140/epjd/e2010-00173-9
- 5. Sun, H. (1998) COMPASS: An Ab Initio Force-Field Optimized for Condensed-Phase Applications Overview with Details on Alkane and Benzene Compounds. The Journal of Physical Chemistry B, 102, 7338-7364. http://dx.doi.org/10.1021/jp980939v
- 6. Rahman, R. (2013) The Role of Graphene in Enhancing the Stiffness of Polymeric Material: A Molecular Modeling Approach. Journal of Applied Physics, 113, Article ID: 243503. http://dx.doi.org/10.1063/1.4812275
- 7. Yanovsky, Y.G., Nikitina, E.A., Karnet, Y.N. and Nikitin, S.M. (2009) Quantum Mechanics Study of the Mechanism of Deformation and Fracture of Graphene. Physical Mesomechanics, 12, 254-262. http://dx.doi.org/10.1016/j.physme.2009.12.007
- 8. Lu, Q., Gao, W. and Huang, R. (2011) Atomistic Simulation and Continuum Modeling of Graphene Nanoribbons under Uniaxial Tension. Modelling and Simulation in Materials Science and Engineering, 19, Article ID: 054006. http://dx.doi.org/10.1088/0965-0393/19/5/054006
- 9. Theodosiou, T.C. and Saravanos, D.A. (2014) Numerical Simulation of Graphene Fracture Using Molecular Mechanics Based Nonlinear Finite Elements. Computational Materials Science, 82, 56-65. http://dx.doi.org/10.1016/j.commatsci.2013.09.032
- 10. Ni, Z., Bu, H., Zou, M., Yi, H., Bi, K. and Chen, Y. (2010) Anisotropic Mechanical Properties of Graphene Sheets from Molecular Dynamics. Physica B: Condensed Matter, 405, 1301-1306. http://dx.doi.org/10.1016/j.physb.2009.11.071
- 11. Liu, Y. and Xu, Z. (2014) Multimodal and Self-Healable Interfaces Enable Strong and Tough Graphene-Derived Materials. Journal of the Mechanics and Physics of Solids, 70, 30-41. http://dx.doi.org/10.1016/j.jmps.2014.05.006
- 12. Liu, F., Ming, P. and Li, J. (2007) Ab initio Calculation of Ideal Strength and Phonon Instability of Graphene under Tension. Physical Review B, 76, Article ID: 064120.
- 13. Mortazavi, B. and Rabczuk, T. (2015) Multiscale Modeling of Heat Conduction in Graphene Laminates. Carbon, 85, 1-7. http://dx.doi.org/10.1016/j.carbon.2014.12.046
- 14. Rafiee, M.A., Rafiee, J., Wang, Z., Song, H., Yu, Z. and Koratkar, N. (2009) Enhanced Mechanical Properties of Nanocomposites at Low Graphene Content. ACS Nano, 3, 3884-3890. http://dx.doi.org/10.1021/nn9010472
- 15. Ebrahimi, S., Ghafoori-Tabrizi, K. and Rafii-Tabar, H. (2012) Multi-Scale Computational Modelling of the Mechanical Behaviour of the Chitosan Biological Polymer Embedded with Graphene and Carbon Nanotube. Computational Materials Science, 53, 347-353. http://dx.doi.org/10.1016/j.commatsci.2011.08.034
- 16. Patterson, J. and Bailey, B. (2010) Solid-State Physics: Introduction to the Theory. 2nd Edition, Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-02589-1
- 17. Bianchini, F., Patera, L.L., Peressi, M., Africh, C. and Comelli, G. (2014) Atomic Scale Identification of Coexisting Graphene Structures on Ni(111). The Journal of Physical Chemistry Letters, 5, 467-473. http://dx.doi.org/10.1021/jz402609d
- 18. Meyer, J.C., Kurasch, S., Park, H.J., Skakalova, V., Künzel, D., Gross, A., et al. (2011) Experimental Analysis of Charge Redistribution Due to Chemical Bonding by High-Resolution Transmission Electron Microscopy. Nature Materials, 10, 209-215. http://dx.doi.org/10.1038/nmat2941
- 19. Skowron, S.T., Lebedeva, I.V., Popov, A.M. and Bichoutskaia, E. (2015) Energetics of Atomic Scale Structure Changes in Graphene. Chemical Society Reviews, 44, 3143-3176. http://dx.doi.org/10.1039/C4CS00499J
- 20. Rutter, G.M., Crain, J.N., Guisinger, N.P., Li, T., First, P.N. and Stroscio, J.A. (2007) Scattering and Interference in Epitaxial Graphene. Science, 317, 219-222. http://dx.doi.org/10.1126/science.1142882
- 21. Ruffieux, P., Melle-Franco, M., Groning, O., Bielmann, M., Zerbetto, F. and Groning, P. (2005) Charge-Density Oscillation on Graphite Induced by the Interference of Electron Waves. Physical Review B, 71, Article ID: 153403. http://dx.doi.org/10.1103/PhysRevB.71.153403
- 22. Osvath, Z., Vertesy, G., Tapaszto, L., Weber, F., Horvath, Z.E., Gyulai, J., et al. (2005) Atomically Resolved STM Images of Carbon Nanotube Defects Produced by Ar + Irradiation. Physical Review B, 72, Article ID: 045429. http://dx.doi.org/10.1103/PhysRevB.72.045429
- 23. Chen, J.-H., Li, L., Cullen, W.G., Williams, E.D. and Fuhrer, M.S. (2010) Tunable Kondo Effect in Graphene with Defects. Nature Physics, 7, 535-538. http://dx.doi.org/10.1038/nphys1962
- 24. Gómez-Navarro, C., Meyer, J.C., Sundaram, R.S., Chuvilin, A., Kurasch, S., Burghard, M., et al. (2010) Atomic Structure of Reduced Graphene Oxide. Nano Letters, 10, 1144-1148. http://dx.doi.org/10.1021/nl9031617
- 25. Yan, H., Liu, C.C., Bai, K.K., Wang, X., Liu, M., Yan, W., et al. (2013) Electronic Structures of Graphene Layers on a Metal Foil: The Effect of Atomic-Scale Defects. Applied Physics Letters, 103, Article ID: 143120. http://dx.doi.org/10.1063/1.4824206
- 26. Yan, H., Chu, Z.D., Yan, W., Liu, M., Meng, L., Yang, M., et al. (2013) Superlattice Dirac Points and Space-Depen- dent Fermi Velocity in a Corrugated Graphene Monolayer. Physical Review B, 87, Article ID: 075405. http://dx.doi.org/10.1103/physrevb.87.075405
- 27. Matan, K., Williams, R.B., Witten, T.A. and Nagel, S.R. (2002) Crumpling a Thin Sheet. Physical Review Letters, 88, Article ID: 076101. http://dx.doi.org/10.1103/PhysRevLett.88.076101
- 28. Balankin, A.S. and Orlando, S.H. (2008) Entropic Rigidity of a Crumpling Network in a Randomly Folded Thin Sheet. Physical Review E, 77, Article ID: 051124. http://dx.doi.org/10.1103/PhysRevE.77.051124
- 29. Patel, M.U.M., Luong, N.D., Seppälä, J., Tchernychova, E. and Dominko, R. (2014) Low Surface Area Graphene/ Cellulose Composite as a Host Matrix for Lithium Sulphur Batteries. Journal of Power Sources, 254, 55-61. http://dx.doi.org/10.1016/j.jpowsour.2013.12.081
- 30. Zhang, K., Duan, X., Zhu, X., Hu, D., Xu, J., Lu, L., et al. (2014) Nanostructured Graphene Oxide-MWCNTs Incorporated Poly(3,4-ethylenedioxythiophene) with a High Surface Area for Sensitive Determination of Diethylstilbestrol. Synthetic Metals, 195, 36-43. http://dx.doi.org/10.1016/j.synthmet.2014.05.005
- 31. Cranford, S.W. and Buehler, M.J. (2011) Packing Efficiency and Accessible Surface Area of Crumpled Graphene. Physical Review B, 84, Article ID: 205451. http://dx.doi.org/10.1103/PhysRevB.84.205451
- 32. Cranford, S. and Buehler, M.J. (2011) Twisted and Coiled Ultralong Multilayer Graphene Ribbons. Modelling and Simulation in Materials Science and Engineering, 19, Article ID: 054003. http://dx.doi.org/10.1088/0965-0393/19/5/054003
- 33. Lee, D., Zou, X., Zhu, X., Seo, J.W., Cole, J.M., Bondino, F., et al. (2012) Ultrafast Carrier Phonon Dynamics in NaOH-Reacted Graphite Oxide Film. Applied Physics Letters, 101, Article ID: 021604. http://dx.doi.org/10.1063/1.4736572
- 34. Becton, M., Zhang, L. and Wang, X. (2013) Effects of Surface Dopants on Graphene Folding by Molecular Simulations. Chemical Physics Letters, 584, 135-141. http://dx.doi.org/10.1016/j.cplett.2013.08.027
- 35. Zhao, J., Yang, B., Zheng, Z., Yang, J., Yang, Z., Zhang, P., et al. (2014) Facile Preparation of One-Dimensional Wrapping Structure: Graphene Nanoscroll-Wrapped of Fe3O4 Nanoparticles and Its Application for Lithium-Ion Battery. ACS Applied Materials & Interfaces, 6, 9890-9896. http://dx.doi.org/10.1021/am502574j
- 36. Bao, W., Miao, F., Chen, Z., Zhang, H., Jang, W., Dames, C., et al. (2009) Controlled Ripple Texturing of Suspended Graphene and Ultrathin Graphite Membranes. Nature Nanotechnology, 4, 562-566. http://dx.doi.org/10.1038/nnano.2009.191
- 37. Cranford, S., Sen, D. and Buehler, M.J. (2009) Meso-Origami: Folding Multilayer Graphene Sheets. Applied Physics Letters, 95, 2013-2016. http://dx.doi.org/10.1063/1.3223783
- 38. Meyer, J.C., Geim, A.K., Katsnelson, M.I., Novoselov, K.S., Booth, T.J. and Roth, S. (2007) The Structure of Suspended Graphene Sheets. Nature, 446, 60-63. http://dx.doi.org/10.1038/nature05545
- 39. Parviz, D., Metzler, S.D., Das, S., Irin, F. and Green, M.J. (2015) Tailored Crumpling and Unfolding of Spray-Dried Pristine Graphene and Graphene Oxide Sheets. Small, 11, 2661-2668. http://dx.doi.org/10.1002/smll.201403466
- 40. Wang, X., Jin, J. and Song, M. (2013) An Investigation of the Mechanism of Graphene Toughening Epoxy. Carbon, 65, 324-333. http://dx.doi.org/10.1016/j.carbon.2013.08.032
- 41. Chen, Q., Liu, W., Guo, S., Zhu, S., Li, Q., Li, X., et al. (2015) Synthesis of Well-Aligned Millimeter-Sized Tetragon-Shaped Graphene Domains by Tuning the Copper Substrate Orientation. Carbon, 93, 945-952. http://dx.doi.org/10.1016/j.carbon.2015.05.108
- 42. Bae, S., Kim, H., Lee, Y., Xu, X., Park, J.-S., Zheng, Y., et al. (2010) Roll-to-Roll Production of 30-Inch Graphene Films for Transparent Electrodes. Nature Nanotechnology, 5, 574-578. http://dx.doi.org/10.1038/nnano.2010.132
- 43. Ago, H., Kawahara, K., Ogawa, Y., Tanoue, S., Bissett, M.A., Tsuji, M., et al. (2013) PS-13-15. Epitaxial Growth and Electronic Properties of Large Hexagonal Graphene Domains on Cu(111) Thin Film. 2013 International Conference on Solid State Devices and Materials, Vol. 1, Fukuoka, 25-27 September 2013, 438-439.
- 44. Murdock, A.T., Koos, A., Britton, T.B., Houben, L., Batten, T., Zhang, T., et al. (2013) Controlling the Orientation, Edge Geometry, and Thickness of Chemical Vapor Deposition Graphene. ACS Nano, 7, 1351-1359. http://dx.doi.org/10.1021/nn3049297
- 45. Hao, Y., Bharathi, M.S., Wang, L., Liu, Y., Chen, H., Nie, S., et al. (2013) The Role of Surface Oxygen in the Growth of Large Single-Crystal Graphene on Copper. Science, 342, 720-723. http://dx.doi.org/10.1126/science.1243879
- 46. Dai, G.-P., Wu, M.H., Taylor, D.K. and Vinodgopal, K. (2013) Square-Shaped, Single-Crystal, Monolayer Graphene Domains by Low-Pressure Chemical Vapor Deposition. Materials Research Letters, 1, 67-76. http://dx.doi.org/10.1080/21663831.2013.772078
- 47. Warren, C. and Budynas, Y.R.G. (2002) Roark’s Formulas for Stress and Strain. 7th Edition, McGraw-Hill, New York.
- 48. Beer, F.P., Johnston, E.R.J., DeWolf, J.T. and Mazurek, D.F. (2012) Mechanics of Materials. 6th Edition, McGraw- Hill, New York.
- 49. Montazeri, A. and Rafii-Tabar, H. (2011) Multiscale Modeling of Graphene- and Nanotube-Based Reinforced Polymer Nanocomposites. Physics Letters A, 375, 4034-4040. http://dx.doi.org/10.1016/j.physleta.2011.08.073
- 50. Bhushan, B., Ed. (2010) Springer Handbook of Nanotechnology. 3rd Edition, Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-02525-9
- 51. Abedpour, N., Neek-Amal, M., Asgari, R., Shahbazi, F., Nafari, N. and Tabar, M.R.R. (2007) Roughness of Undoped Graphene and Its Short-Range Induced Gauge Field. Physical Review B, 76, Article ID: 195407. http://dx.doi.org/10.1103/PhysRevB.76.195407
- 52. Fasolino, A., Los, J.H. and Katsnelson, M.I. (2007) Intrinsic Ripples in Graphene. Nature Materials, 6, 858-861. http://dx.doi.org/10.1038/nmat2011
- 53. Dieter, G.E. (1988) Mechanical Metallurgy. SI Metric Edition, McGraw-Hill, New York.
- 54. Griffith, A.A. (1921) The Phenomena of Rupture and Flow in Solids. Philosophical Transactions of the Royal Society of London, Series A, Containing Papers of a Mathematical or Physical Character, 221, 163-198. http://dx.doi.org/10.1098/rsta.1921.0006

























