Advances in Remote Sensing
Vol.04 No.03(2015), Article ID:59401,9 pages
10.4236/ars.2015.43018
Comparison of Simulated Backscattering Signal and ALOS PALSAR Backscattering over Arid Environment Using Experimental Measurement
Saeid Gharechelou, Ryutaro Tateishi, Josaphat Tetuko Sri Sumantyo
Center for Environmental Remote Sensing (CEReS), Chiba University, Chiba, Japan
Email: acfa3286@chiba-u.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 March 2015; accepted 4 September 2015; published 7 September 2015
ABSTRACT
The purpose of this paper is to simulate the backscattered signal by experimental data and field working then, comparing with the backscattered signal from actual L-band SAR data over arid to semi-arid environments. The experimental data included the laboratory-measured dielectric constant of soil samples and the roughness parameter. A backscattering model used to simulate the backscattering coefficient in sparse vegetation land cover. The backscattering coefficient (σ˚) simulated using the AIEM (advanced integral equation model) based on the experimental data. The roughness data were considered by the field observation, chain method measuring and photogrammetry simulation technique by stereo image of ground real photography. The simulated backscattering coefficients were compared with the real extracted backscattering coefficient (σ˚) from the ALOS PALSAR single and dual polarization mode data. The most problem in backscattering simulation was the vegetation water content. Therefore, the water-cloud model using the water index result of optical data applied on the simulated backscatter model for enhancement the backscattering heterogeneity from vegetation water contents due to the mix pixel of vegetation in spars vegetation. At the results the AIEM model overestimated the backscattering simulation, it might be cause of high sensitivity of this model to roughness. The ALOS PALSAR HV polarization mode is more sensitive than the HH mode to vegetation water content. The water-cloud model could improve the result and the correlation function of the samples was increased but, the difficulties were the input the A and B parameters to model.
Keywords:
AIEM, SAR Backscattering, ALOS PALSAR, Sparse Vegetation, Backscattering Simulation, Arid Environment, Dielectric Measurement

1. Introduction
A numbers of radar backscattering models have been reported in the past several years. The backscattering model in literature developed to estimate the soil surface parameter. Those of them most frequently used by other researcher included the two semi-empirical models by Oh et al. [1] - [4] , and Dubois et al. [5] and the physical model the Integral Equation Model (IEM) developed by Fung et al. [6] . These models are supposed to regenerate the radar backscattering coefficient (σ˚) by forward model. The computed backscattered signal after comparison by actual SAR data and estimated the correlation function will be used for invention radar backscattering coefficient to the estimation of soil surface parameters such as soil water content and roughness. In the model, the radar backscattering coefficient link to soil parameters such as dielectric constant and roughness and to SAR sensor parameters (e.g. incidence angle, radar wavelength and polarization), which is correlated to the bare land cover. However, the results of previous work have shown the experimentally which radar backscattering is most sensitive to surface roughness and it is working better in low incident angle (Ulaby et al., 1986, Dobson and Ulaby 1986, Oh et al., 1992, Baghdadi et al., 2002, Zribi and Dechambre 2002, Holah et al., 2005). Moreover, the inconsistencies researchers are observed in several studies between SAR backscattering coefficients and those simulated results by the models, interpretation the inversion results was inaccurate [7] - [10] . The empirical and semi-empirical models are working based on the experimental data and most frequent was tested over wet and humid area by C band radar data such as RADARSAT-1 and 2 and ENVISAT and recently x-band data such as TerraSAR data over bare soil [10] - [12] . The radar scattering model, integral equation method (IEM) model of Fung et al., 1992 has been most commonly used validated at fine scales in a laboratory setting (Licheri et al., 2001; Macelloni et al., 2000) using uniform media but has not been shown to consistently predict radar backscatter at broad scales [13] . Some of the more successful studies include those by Bindlish and Barros; 2000, [14] , Baghdadi, et al., 2004, 2006, 2011. The advanced integral equation model (AIEM) proposed by Fung et al., [15] .
The rare study has been done over the arid environment and mostly tested over the bare land. Objectives of this research were to apply the semi-empirical AIEM model to test over sparse vegetation in arid environment, and identifying the factors affecting to the prediction model particularly the vegetation water content change in vertical due to mixed pixel of grassland and herbaceous to sparse vegetation. This approach is used to the ALOS PALSAR sensor in L-band in single and dual polarization and more focused on the physical and properties experiment such as dielectric constant, vegetation water content according the land cover type.
The varieties of backscattering coefficient (σ˚) of simulated model give rise to a wide variety of surface roughness, dielectric constants and water content of soil surface and vegetation water content in vegetated land cover [16] . Meanwhile, most frequently cases study the researcher overcomes the vegetation affected to the radar backscattering coefficient because of this complexity. Therefore, in this research, objective is more focused on land condition not on sensor parameters.
The purpose of this research is most often focused on the experimentally dielectric constant measurement and field observation because there is a significant relationship with it and the backscattering and compare with actual SAR data. In addition, study the simulated backscattered in sparse vegetation in arid environment which to clarify and improvement the vegetation water content change in vertical and its influenced in backscattering according the land cover conditions. This paper is ground-based observation, and experimentally determined values of real and imaginary parts of the complex dielectric constant for applying to forward backscattering model for simulation the backscattered signal. The backscattering coefficient at each ground sample position is then simulated using the advanced integral equation model (AIEM). Thus, the simulated backscattered signal improved by water-cloud model [17] for considering the vegetation water content in vertical profile and compared with the actual value of σ˚ obtained from ALOS PALSAR data. The information from this study can be useful for dielectric constant modeling and back scattering modeling as well as microwave sensor calibration and design.
2. Material and Methods
2.1. Study Area and Dataset
The study area is located in the northern part of Iran. This area is an alluvial plain with a small topographic relief on the northern part while in southern part performed flat area (Figure 1). The climate type of study area is arid
Figure 1. Study area location using Landsat 7 composite (RGB, 432) image, and the red polygon shows the city border.
and semi-arid, conferring to the temperature and humidity regime of soil classification, the soil of this region is categorized as Aridisols. In the US soil taxonomy, the soil is categorized as the Aridisols class (from Latin aridus, “dry”), which exhibit at least some subsurface horizon development [18] . Land use in this area are mainly range, wildlife recreation, abandoned farm land, and the land cover in study area consists mainly of bare land and sparse vegetation.
The ALOS PALSAR image acquired from September 16, 2010 in the fine beam mode (FBD) and fine single mode (FBS) [19] . We selected the September visited SAR image due to the driest month and always there is less amount of precipitation. The information of the SAR data is shown in Table 1. Before using the SAR data, radiometric calibration, speckle noise removing and geometric correction were done (Figure 2).
2.2. Field Observation and Sample Collection
The field work was done during September 10 to 13, 2012, (the same month that ALOS data was acquired) (Figure 3). Since the two years difference time between satellite observation and field work, we investigated the meteorological dataset (e.g. observed humidity, rain, temperature) vegetation index which was derived by optical sensor and land use change. There was not observed any changes on September between two of different years for meteorological data (Table 1) and land use of study area has not been changing due to the most part of study area is located in the Kavir National Park and it is the conservative area for wildlife recreation.
Thirty-five soil samples from depths of 0 - 10 cm were collected using soil sampling tool kit from different Land units of study area, i.e. location where different soil types and land cover was minded to create the land unit map. Soil moisture was measured by TDR (Time domain reflectance) in the field. The soil sample was taken randomly from top soil in land unit type. For select the worth soil sample representation, we was tried to takings the four samples in four different direction with ten meter distance regarding the PALSAR image resolution and after the mixed them made the one sample. Once completed, a one-half kilogram of soil was taken and send to the laboratory for dielectric constant measurement. The soil samples in the laboratory, once moisture were measured again by TDR and weighted sensibly same as field moisture condition. The soil physical and chemical properties were obtained from laboratory testing (Table 1).
Roughness measurement was made using the different technique in field and GIS environment such as chain method measurement in field and photogrammetry technique by stereo images of ground photos. From these measurement and simulation the two roughness parameters, root mean square of surface height (h_rmas) and correlation length (L) were calculated. According the research target and filed observation of land cover the surface roughness is categorized in three level of low (<1.5 cm), medium (1.5 - 3 cm) and high (3 - 4.5 cm). The most of study area was in low category (<1.5 cm) corresponding to clay pan and medium in sparse vegetation, very less area which are covered by abandoned farm in north part of study area and the parts in south that covered by desert geomorphological shape.

Figure 2. The ALOS PALSAR image HH mode (a) and HV mode (b) in dB and green rectangle shows study area.

Figure 3. Field sampling; the yellow pins are some selected soil samples position, pink polygon is the land unit map and yellow line is the PALSAR foot print (a) and laboratory experiment soil moisture measurement by TDR (b).
Table 1. Physical properties of soil surface in study area.
2.3. Laboratory Measurement of the Dielectric Constant
In this study, we measured the dielectric constant for thirty-five undestroyed soil samples using the network analyzer coupled with an open air probe (Agilent 85070E dielectric tool kit) (Figure 4) [20] . The measurement frequency was from 0.3 to 3 GHz with 200 sampling points [21] . This frequency range was used in order to be consistent with observations from the ALOS/PALSAR satellite launched by JAXA in 2006 [19] .
The real and imaginary parts (ε' and ε") of the complex dielectric constant of samples in different soil types and land cover type were determined experimentally under laboratory conditions. Dielectric permittivity (ε*) is a complex function with real and imaginary components and is defined as [22] :
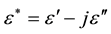 (1)
(1)
where j is the square root of −1. The real part (ε') is often expressed as the relative permittivity (εr), which is the ratio of the electric-field storage capacity to that of free space [23] . The relative permittivity is a frequency dependent variable and decreases with increasing frequency [24] . The imaginary part (ε") of the dielectric permittivity is usually expressed in terms of dielectric losses, which include dispersive losses, as well as free-water relaxation and bound-water relaxation losses [21] .

Figure 4. The sample result of dielectric constant in the real (ɛ') and imaginary (ɛ") part (a) and and the dielectric measure- ment tool kit (b).
2.4. Backscattering Model
For assessing the effect of soil moisture on radar signal and comparison with satellite-derived SAR data, the first step is to remove the part of the backscattering cross section that can be attributed to known models. This is done that the residual effects of the model and observation can be analyzed, as well as to compare the models with the observations. For these models, the dielectric constant, surface parameter and sensor parameters need to be computed. There are several backscattering models proposed by different researchers (theoretical, physical and empirical models), such as the SPM (small perturbation model), and the POM (physical optic model) introduced by F. T. Ulaby et al. in microwave remote sensing [22] , the DM (Dubois model) proposed by Dubois et al. [5] , and the IEM (integral equation model) and AIEM (advanced integral equation model) proposed by Fung et al. [5] . Different models have different application fields (Table 2) [24] [25] .
The POM model is useable when the RMS surface slope is small relative to the wavelength and the Dubois model is appropriate for frequencies between 1.5 GHz and 11 GHz [5] . The comparison of the above models illustrate the model based on the IEM is the most appropriate model for different surface types [5] . This approach was reported by Fung and Chen as well [5] , where the phase of Green’s function in a higher order term was ignored. This phase was later retained by Hsieh and Fung by fully including the phase effect in Green’s function to achieve better accuracy in bistatic scattering and multiple surface scattering, especially in regions where the incident and scattering angles are not equal, which was primarily the case for the AIEM [24] [26] . Hence, we applied the AIEM to simulate the single backscattering coefficient of arid soil by only considering the surface scattering term. The single backscattering coefficient of the AIEM model is expressed as:
 (2)
(2)
where ρ = V or ℎ polarization, θ is the incident angle, κχ = κsinθ, κz = κcosθ, fVV = 2RV/cosθ, and fℎℎ = 2Rℎ/cosθ. The expressions w and w(n) are the surface spectra corresponding to the two-dimensional Fourier transformations of the surface correlation coefficient and its nth power.
Exponential statistical distribution and Gaussian and the χ-power law distribution can all be used to describe the natural surface as described by Fung and Chen [5] , who also showed that, for moderately rough surfaces, an exponential statistical distribution performs better than the Gaussian or the χ-power law distributions (χ = 1.5). In view of the relatively smooth surface the exponential statistical distribution have chosen for describing the surface of the AIEM model [20] , [22] , and [26] . The incident angle used in the model is assumed to be 35˚, to comparing with the incident angles of the PALSAR image.
2.5. Water Cloud Model
Generally, the water cloud model (Attema and Ulaby, 1978) for a given incident angle θi is given as:
Table 2. Application field of different backscattering coefficient models.
where κ = 2π/λ is the wave-number, λ is the wavelength of electromagnetic wave.
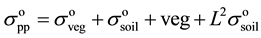 (3)
(3)
where
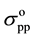 is the co-polarized total backscatter coefficient, σ˚ veg is the backscatter contribution of the vegetation cover. The
is the co-polarized total backscatter coefficient, σ˚ veg is the backscatter contribution of the vegetation cover. The
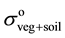 is the volume backscattering including vegetation elements and the soil surface, σ˚ is the backscattering contribution of the soil surface and L2 is the two-way vegetation attenuation [24] . The term of
is the volume backscattering including vegetation elements and the soil surface, σ˚ is the backscattering contribution of the soil surface and L2 is the two-way vegetation attenuation [24] . The term of
 is represent the interaction of the incident radiation between the vegetation and the underlying soil. In the past years, numbers of the model have been reported by Ulaby et al. (1982, 1982); Bindlish and Barros (2001) [14] [17] . Ulaby et al. (1978, 1986) concluded that, for a given radar configuration, the backscatter from the bare soil is a linear function of the surface soil moisture [24] [25] . Prevot et al. (1993) proposed a water cloud model with four empirical coefficients, A, B, as a vegetation parameters. The parameter A corresponds to the albedo of the vegetation and B is an attenuation factor. Hence, the equation is modified to the parameters A, B, are generally estimated by nonlinear least square regression analysis and fitting the model against experimental data sets. (Prevot et al., 1993; Xu et al., 1996; Bindlish and Barros, 2001) [25] . In this study we applied the Bindish and Barros (2001) empirical model to derive the vegetation water content [13] . The A, and B parameters is based on Bindish model while a little changed because of geophysical characteristics of land cover of study area and the albedo is high in arid and semi-arid area. The equation (3) which use as a vegetation correlation model into the soil backscattering.
is represent the interaction of the incident radiation between the vegetation and the underlying soil. In the past years, numbers of the model have been reported by Ulaby et al. (1982, 1982); Bindlish and Barros (2001) [14] [17] . Ulaby et al. (1978, 1986) concluded that, for a given radar configuration, the backscatter from the bare soil is a linear function of the surface soil moisture [24] [25] . Prevot et al. (1993) proposed a water cloud model with four empirical coefficients, A, B, as a vegetation parameters. The parameter A corresponds to the albedo of the vegetation and B is an attenuation factor. Hence, the equation is modified to the parameters A, B, are generally estimated by nonlinear least square regression analysis and fitting the model against experimental data sets. (Prevot et al., 1993; Xu et al., 1996; Bindlish and Barros, 2001) [25] . In this study we applied the Bindish and Barros (2001) empirical model to derive the vegetation water content [13] . The A, and B parameters is based on Bindish model while a little changed because of geophysical characteristics of land cover of study area and the albedo is high in arid and semi-arid area. The equation (3) which use as a vegetation correlation model into the soil backscattering.
 (4)
(4)
where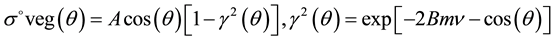 , and mv is the vegetation water content, which is derived by Landsat data or other optical data and using water content index [25] . The A and B parameters are vegetation parameter of the semi-empirical model 0.0082 and 0.011 respectively [13] [19] . For mv parameter the normalized different water index (NDWI) was applied. This index is sensitive to changes in vegetation canopy water content because reflectance [17] . The NDWI index applied in Landsat image at same time of PALSAR image to retrieve the vegetation water content (Figure 5). The value of NDWI index ranges from −1 to 1 from dry to wet. The common range for green vegetation is −0.1 to 0.4. The dry area shows by low value and red color and highest value shoes by blue color (Figure 5(a)). The both indexes of NDWI and NDVI has almost similarity in highest and lowest value from north to south part study area based on vegetation cover and vegetation water contents (Figure 5).
, and mv is the vegetation water content, which is derived by Landsat data or other optical data and using water content index [25] . The A and B parameters are vegetation parameter of the semi-empirical model 0.0082 and 0.011 respectively [13] [19] . For mv parameter the normalized different water index (NDWI) was applied. This index is sensitive to changes in vegetation canopy water content because reflectance [17] . The NDWI index applied in Landsat image at same time of PALSAR image to retrieve the vegetation water content (Figure 5). The value of NDWI index ranges from −1 to 1 from dry to wet. The common range for green vegetation is −0.1 to 0.4. The dry area shows by low value and red color and highest value shoes by blue color (Figure 5(a)). The both indexes of NDWI and NDVI has almost similarity in highest and lowest value from north to south part study area based on vegetation cover and vegetation water contents (Figure 5).
3. Results and Discussion
Comparison of the Backscattering Coefficients
The dielectric constant data is an input parameter in the AIEM, with an incident angle of 34˚, the same as for obtaining the SAR image. The average values of roughness parameter of the RMS height (s), 0.35 cm, and the correlation length (L), 2.5 cm, were used as the inputs for the model. The backscattering coefficients of HH and VV polarization of PALSAR data were derived using the AIEM model. The backscattering coefficients of the ALOS PALSAR images after speckle noise removing and radiation calibration for conversion in dB were extracted according to the coordinates of ground truth samples for comparison. In this step before extract the σ˚ of samples we applied the focal function with 3 *3 window for be an average of the values of the neighbor pixel. The comparisons of backscattering coefficient of model simulation and image values of the samples with

Figure 5. The result of normalized different water index (NDWI) and normalized different vegetation index using Landsat data.
HH and VV polarization results are shown in Figure 6(a) for HH polarization and Figure 6(b) for VV polarization.
The relationship between the simulated and σ˚ image shown in Figure 6 and the correlation coefficient for HH and HV mode is 0.3844 and 0.4229, respectively. The correlation between the modeled value and image value was relatively weak, possibly due to the influence of mixed pixels containing bare land and sparse vegetation or agriculture in some areas. As has shown in Figure 1, the study area consisted of a mixture of sparse vegetation and bare soil distributed randomly, resulting in these mixed pixels. Some researchers tried to improve this problem with apply the water-cloud model to consider about the vegetation affect and mixed pixel [24] -[28] . For improving the effect of mixed pixel we applied the water-cloud model, Equation (4). With applying this model the vegetation information was updated according the ground soil samples and plot against the backscattering coefficient (σ˚) of PALSAR image. The results are shown in Figure 7.
However, the result has been improved and the σ˚ is increasing and is bigger than the σ˚ of the PALSAR image at sample pixel. It might be due to the different reason but, we can mention about the complexity affected of two layer scatter of soil and vegetation in sparse vegetation land scape. And the second might be cause of the surface roughness average value which we had used this research. The Figure 8 shows the comparison of the mix pixel of land cover in three different image with NDVI, NDWI and PALSAR HV mode by the ground real photo of its location. It shows however the land cover is the sparse vegetation in some parts with the grassland vegetated cover can be affected in backscattering intensity and it is clearly defined the role of vegetation water content which the detailed land cover with apply the vegetation water cloud model.
4. Conclusion
The most result of this research is focus on backscattering simulation using experiment data and its characteristics over sparse vegetation of land cover in arid environment. The backscattering coefficients based on the experimental and field data which simulated using AIEM model were successfully compared and analyzed with ALOS PAOLSAR backscattering. As a result, the AIEM model showed overestimation of backscattering signal which computed the around 15 dB range over plane area in dry season. This overestimation was due to the partly wetland and saline soil in lowland area, in addition affected by heterogeneity of surface roughness at different land cover. The AIEM model was very sensitive to surface roughness therefore, more accurate surface roughness data with higher spatial resolution needs to be applied to the laboratory dielectric constants and compared with the backscattering coefficient extracted from radar imagery. The backscattering coefficients of HV polarization mode seem to be more sensitive than HH polarization on the water content, however, the HH shown has better correlation with soil moisture change. This may be due to the vegetation water content in mixed pixels over different land cover including sparse vegetation and grassland. It seems to be necessary to apply additional model(s) for improving the simulation, such as a cloud model. The result of water-cloud model for improvement the vegetation effect of mixed pixel has been improved the correlation function. The result of water cloud model causes to reduce the variance of simulated backscattering coefficient points and lessen the range of the dB of it. The σ˚ of cloud model result was increased in mix pixel points, it might be due to the different reason but, the complexity affected of two layer volumetric scatter of soil and vegetation in sparse vegetation land scape might be considered. And the second might be cause of the surface roughness average value which we had used

Figure 6. Simulated backscattering coefficient compared to the ALOS PALSAR images of the 23 ground samples, with HH polarization on (a) and HV polarization on (b).

Figure 7. Comparison of the improved backscattering coefficient by water-cloud model with simulated backscattered coefficient of 23 samples in HH (a) and HV (b) polarization.
Figure 8. The mix land cover of the vegetation area (b) and sparse vegetation in (a) of ground photo (d) and compare with the normalized different water index (a); normalized different vegetation index (b) and HV mode of PALSAR image.
this research and it should be considered about the more precise rough data. The A and B parameters in water- cloud model was the other difficulties to input model and may it need to measure the vegetation water content in laboratory for more accurate. The result also has shown land covers have a good agreement with the experimental result of soil samples and backscattering characteristics. In the field work data the result shown the more numbers of sampling points are needed or wide range of sampling would be allowed to investigate the more creditable correlation with SAR backscattering signal. The recently-launched ALOS 2, which has similar frequency and polarizations to ALOS PALSAR but has a higher spatial resolution (up to 1 m × 3 m resolution), might help overcome these problems due to mixed pixels either integrated with high resolution optical image.
Cite this paper
SaeidGharechelou,RyutaroTateishi,Josaphat Tetuko SriSumantyo, (2015) Comparison of Simulated Backscattering Signal and ALOS PALSAR Backscattering over Arid Environment Using Experimental Measurement. Advances in Remote Sensing,04,224-233. doi: 10.4236/ars.2015.43018
References
- 1. Oh, Y., Sarabandi, K. and Ulaby, F.T. (1992) An Empirical Model and an Inversion Technique for Radar Scattering from Bare Soil Surfaces. IEEE Transactions on Geoscience and Remote Sensing, 30, 370-382.
http://dx.doi.org/10.1109/36.134086 - 2. Oh, Y., Sarabandi, K. and Ulaby, F.T. (1994) An Inversion Algorithm for Retrieving Soil Moisture and Surface Roughness from Polarimetric Radar Observation. Proceedings IGARSS’94, Pasadena, USA, IEEE Catalog Number 94CH3378-7, 3, 1582-1584.
http://dx.doi.org/10.1109/igarss.1994.399504 - 3. Oh, Y., Sarabandi, K. and Ulaby, F.T. (2002) Semi-Empirical Model of the Ensemble-Averaged Differential Mueller Matrix for Microwave Backscattering from Bare Soil Surfaces. IEEE Transactions on Geoscience and Remote Sensing, 40, 1348-1355.
http://dx.doi.org/10.1109/TGRS.2002.800232 - 4. Oh, Y. (2004) Quantitative Retrieval of Soil Moisture Content and Surface Roughness from Multipolarized Radar Observations of Bare Soil Surfaces. IEEE Transactions on Geoscience and Remote Sensing, 42, 596-601.
http://dx.doi.org/10.1109/TGRS.2003.821065 - 5. Dubois, P.C., Van Zyl, J. and Engman, T. (1995) Measuring Soil Moisture with Imaging Radars. IEEE Transactions on Geoscience and Remote Sensing, 33, 915-926.
http://dx.doi.org/10.1109/36.406677 - 6. Fung, A.K., Li, Z. and Chen, K.S. (1992) Backscattering from a Randomly Rough Dielectric Surface. IEEE Transactions on Geoscience and Remote Sensing, 30, 356-369.
http://dx.doi.org/10.1109/36.134085 - 7. Mattia, F., Le Toan, T., Souyris, J.-C., De Carolis, G., Floury, N., Posa, F. and Pasquariello, G. (1997) The Effect of Surface Roughness on Multifrequency Polarimetric SAR Data. IEEE Transactions on Geoscience and Remote Sensing, 35, 954-966.
http://dx.doi.org/10.1109/36.602537 - 8. Zribi, M., Taconet, O., Le Hegarat-Mascle, S., Vidal-Madjar, D., Emblanch, C., Loumagne, C. and Normand, M. (1997) Backscattering Behavior and Simulation: Comparison over Bare Soils Using SIR-C/X-SAR and ERASME 1994 Data over Orgeval. Remote Sensing of Environment, 59, 256-266.
- 9. Baghdadi, N. and Zribi, M. (2006) Evaluation of Radar Backscatter Models IEM, OH and Dubois Using Experimental Observations. International Journal of Remote Sensing, 27, 3831-3852.
http://dx.doi.org/10.1080/01431160600658123 - 10. Baghdadi, N., Chaaya, J.A. and Zribi, M. (2011) Semi-Empirical Calibration of the Integral Equation Model for SAR Data in C-Band and cross Polarization Using Radar Images and Field Measurements. IEEE Geoscience and Remote Sensing Letters, 8, 14-18.
http://dx.doi.org/10.1109/LGRS.2010.2050054 - 11. Baghdadi, N., Gherboudj, I., Zribi, M., Sahebi, M., Bonn, F. and King, C. (2004) Semi-Empirical Calibration of the IEM Backscattering Model Using Radar Images and Moisture and Roughness Field Measurements. International Journal of Remote Sensing, 25, 3593-3623.
http://dx.doi.org/10.1080/01431160310001654392 - 12. Baghdadi, N., Holah, N. and Zribi, M. (2006) Calibration of the Integral Equation Model for SAR Data in C-Band and HH and VV Polarizations. International Journal of Remote Sensing, 27, 805-816.
http://dx.doi.org/10.1080/01431160500212278 - 13. Bindlish, R. and Barros, A.P. (2000) Multifrequency Soil Moisture Inversion from SAR Measurements with the Use of IEM. Remote Sensing of Environment, 71, 67-88.
http://dx.doi.org/10.1016/S0034-4257(99)00065-6 - 14. Rocco, P., Mihai, A., Tanase, K.L., Jeffrey, P.W. (2014) Evaluation of IEM, Dubois, and Oh Radar Backscatter Models Using Airborne L-Band SAR. IEEE Transactions on Geoscience and Remote Sensing, 52, 4966-4979.
- 15. Fung, A.K., Li, Z. and Chen, K.S. (1992) Backscattering from a Randomly Rough Dielectric Surface. IEEE Transactions on Geoscience and Remote Sensing, 30, 356-369.
http://dx.doi.org/10.1109/36.134085 - 16. Thoma, D.P., Moran, M.S., Bryant, R., Rahman, M., Holifield-Collins, C.D., Skirvin, S., Sano, E.E. and Slocum, K. (2006) Comparison of Four Models to Determine Surface Soil Moisture from C-Band Radar Imagery in a Sparsely Vegetated Semiarid Landscape. Water Resources Research, 42, W01418.
http://dx.doi.org/10.1029/2004wr003905 - 17. Kamal, K., Hari, P.S.R. and Arora, M.K. (2015) Study of Water Cloud Model Vegetation Descriptors in Estimating Soil Moisture in Solani Catchment. Hydrological Processes, 29, 2137-2148.
http://dx.doi.org/10.1002/hyp.10344 - 18. USDA.
http://www.nrcs.usda.gov - 19. Jaxa.
http://www.eorc.jaxa.jp/ALOS/en/about/palsar.htm - 20. Agilent.
http://www.keysight.com - 21. Gharechelou, S., Tateishi, R. and Sumantyo, J.T.S. (2015) Interrelationship Analysis of L-Band Backscattering Intensity and Soil Dielectric Constant for Soil Moisture Retrieval Using PALSAR Data. Journal of Advances in Remote Sensing, 4, 15-24.
http://dx.doi.org/10.4236/ars.2015.41002 - 22. Ghosh, A., Bihari, J. and Pyne, S. (1998) Dielectric Parameters of Dry and Wet Soils at 14.89 GHz. Indian Journal of Radio & Space Physics, 27, 130-134.
- 23. Campbell, J.E. (1990) Dielectric Properties and Influence of Conductivity in Soils at One to Fifty Megahertz. Soil Science Society of America Journal, 54, 332-341.
http://dx.doi.org/10.2136/sssaj1990.03615995005400020006x - 24. Ulaby, F.T., Moore, M.K. and Fung, A.K. (1986) Microwave Remote Sensing: Active and Passive. Vol. 3, Artech House, Norwood.
- 25. Li, Y.-Y., Zhao, K., Ren, J.-H., Ding, Y.-L. and Wu, L.-L. (2014) Analysis of the Dielectric Constant of Saline-Alkali Soils and the Effect on Radar Backscattering Coefficient: A Case Study of Soda Alkaline Saline Soils in Western Jilin Province Using RADARSAT-2 Data. The Scientific World Journal, 2014, Article ID: 563015.
- 26. Verhoest, N.E.C., Lievens, H., Wagner, W., Mozos, J.á., Moran, M.S. and Mattia, F. (2008) On the Soil Roughness Parameterization Problem in Soil Moisture Retrieval of Bare Surfaces from Synthetic Aperture. Journal of Sensors, 8, 4213-4248.
http://dx.doi.org/10.3390/s8074213 - 27. Jackson, T.J., Chen, D.Y., Cosh, M., Li, F.Q., Anderson, M., Walthall, C., Doriaswamy, P. and Hunt, E.R. (2004) Vegetation Water Content Mapping Using Landsat Data Derived Normalized Difference Water Index for Corn and Soybeans. Journal of Remote Sensing of Environment, 92, 475-482.
http://dx.doi.org/10.1016/j.rse.2003.10.021 - 28. Gorrab, A., Zribi, M., Baghdadi, N., Lili-Chabaane, Z. and Mougenot, B. (2014) Multi-Frequency Analysis of Soil Moisture Vertical Heterogeneity Effect on Radar Backscatter. 1st International Conference on Advanced Technologies for Signal and Image Processing, Sousse, 17-19 March 2014, 379-384.
http://dx.doi.org/10.1109/atsip.2014.6834640









