Advances in Parkinson's Disease
Vol.05 No.04(2016), Article ID:72267,10 pages
10.4236/apd.2016.54012
Parkinson’s Disease Treatment as Seen from a Mechanical Point of View
Sarah Gebai, Mohamad Hammoud*
SDM Research Group, Mechanical Department, School of Engineering, Lebanese International University, Beirut, Lebanon

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 25, 2016; Accepted: November 21, 2016; Published: November 25, 2016
ABSTRACT
Tremor is considered as the most common faced abnormal involuntary movement disorder and the source of functional disability. Parkinson disease (PD) is a slowly progressive degenerative disorder of the central nervous system caused by the lack in the level of dopamine. Levodopa is the most effective dopaminergic medication used to manage Parkinson symptoms. However, it will be the source of the motor fluctuation after several years. An uncommon type of medication is suggested to suppress the resting tremor of PD patients. In this paper, a vibration absorber is used as a mechanical treatment and designed to reduce critical angular displacement amplitude at the resonance frequency. Human hand is modeled dynamically at the musculoskeletal level to reflect Parkinsonism. Motion is considered due to shoulder, elbow, Biceps brachii and wrist muscles activation. Absorber’s geometry, materials properties and parameters are well chosen to satisfy the tuning condition. The solution to the equation of motion for the hand is shown in the frequency and time domains to check the performance of the absorber in reducing the flexion angular motion at the wrist joint. Results show that the absorber was very effective over a good frequency bandwidth. It was able to reduce 93% of tremors amplitude at the wrist joint in the frequency domain. This type of absorber has low cost, can operate without power requirements, and has a simple design. Since its effectiveness was proved when tested numerically, it is recommended to proceed to the manufacturing process and the experimental study.
Keywords:
Parkinson’s Disease, Hand Modeling, Resonance, Dynamic Absorber, Tremor Suppression

1. Introduction
Hand motion is divided into two categories, the intentional-voluntary and unintentional-involuntary hand motion. Neurologically disordered persons suffer from involuntary tremor disability which can worsen their life’s quality. It prevents them from achieving physical tasks like writing, drinking and eating, etc. Drug and surgical therapy are able to regulate the muscle and reduce Parkinson’s disease (PD) tremor but leaving serious side effects. To improve the life of those people, an effective alternative treatment could be found to suppress involuntary tremor at their proximal joints.
The British physician, Dr. James Parkinson, was the first to describe PD (Paralysis Agitans) in 1817 [1] . It is described as a slowly progressive degenerative disorder of the central nervous system. Clinically, PD is associated with motor symptoms as resting tremor, postural reflexes impairment, rigidity, freezing, bradykinesia, akinesia and dyskinesia. Idiopathic, secondary or acquired and “Parkinson plus” can be the three general etiologic groups of Parkinsonism [2] . The most common form of PD is the idiopathic Parkinson. The most common chronic diseases of the late adulthood are respectively the cerebrovascular diseases, PD and arthritis [2] .
Human body can sustain certain level of vibration, but over long period of time deterioration will begin and natural processes and systems will fail. Vibrational energy waves in human body are absorbed by tissue, organs and skeletal systems before its being dissipated leading to the voluntary and involuntary contraction of muscles. Vibration at resonant frequency can cause tissue degeneration, organ failure, severe discomfort and reduction in the ability to perform precise motor movement. Local muscle fatigue occurs when muscles try to react against vibrational energy to maintain the balance at resonance.
Tremor is a rhythmic or semi rhythmic, oscillatory movement of body part which results from alternating simultaneous antagonistic muscle group contractions [3] [4] . Movement disorders cause patients with pathological tremor to have significant uncontrollable hand tremor movement [5] [6] . Pathological tremor tends to have constant frequency with small variations [7] . There is no treatment that can cure patients and control tremor completely, but there are different methods that can lessen tremor to improve life quality. Parkinsonian tremor was hypothesized to be the result of abnormal activity within the basal ganglia. Levodopa is the most effective dopaminergic medication for PD patients which is converted in the brain into dopamine. The recommended drug dose increases with the increased symptom severity, but high doses can produce involuntary tremor and can lead to serious side effects. In the United States, about 630,000 people had diagnosed PD in 2010. The national economic burden of PD exceeds $14.4 billion in 2010 (approximately $22,800 per patient) [8] .
In this paper, we are trying to help biomedical community by presenting a promising mechanical treatment in order reduce the rest tremor (3 - 5 Hz [9] ) in hand of PD patients. A tremor suppression device is designed to do the function of the muscles in counteracting against tremor when attached to the forearm. Passive vibration controller, requiring no input power, is suggested to control hand movements at the rest conditions. A biodynamic hand model is provided at the musculoskeletal level to model the hand as mass, springs and dampers. Based on the modeled hand system, the vibration absorber is sized and tuned at the problematic tremor’s frequency. The performance of the absorber is analyzed in the time and frequency domain responses at the wrist joint to check its effectiveness.
The rest of the paper is organized as follows: Section 2 includes the biodynamic modeling of the human hand by considering the flexion angular motion in the horizontal plane. Section 3 describes the design of the vibration absorber to be used in reducing the rest tremor. Section 4 shows the effect of the absorber attached to the forearm of the hand where the results are presented in the frequency and time domains. Section 5 includes the conclusions and future work.
2. Skeletal Hand Model
The musculoskeletal model of the hand is important for studying the tremor disorder and can be used for tremor suppression techniques [10] [11] . Oscillations can be translated into the movements of masses and springs due to the nature of the complex joint-muscle-tendon system [12] . Most researchers have agreed on modeling bones and corresponding soft tissues as rigid bodies connected by frictionless joints with fixed axes or centers of rotation [13] [14] [15] .
In the current study, human hand is modeled as a three degree-of-freedom (DOF) system: the upper arm, forearm and the palm rigid segments to describe the flexion-extension motion at proximal joints. The model is considered in the horizontal plane to reflect the rest tremor at the musculoskeletal level which usually consists of the skeletal dynamics and muscle dynamics. The flexion motion only which represents muscles contraction was taken into account. The model was based on a modification of Hashemi et al. [16] model by considering motion at the wrist joint. The wrist joint must be considered since it’s the most joint related to the tremulous limbs of patients [17] . Hand segments are connected in between by single DOF frictionless: shoulder (pivot), elbow (hinge) and wrist (saddle) joints (Figure 1). The system is pinned to the fixed trunk by shoulder joint. Sizing human hand segments is based on the density, length and position of the centroid for the right hand determined experimentally by Drillis et al. [18] . Based on these parameters, then the calculated mass and mass moment of inertia of each segment are shown in Table 1. The total mass of the considered hand is 3.77 kg.
Active inputs to the hand can be described as muscular activity [19] [20] which are considered as sinusoidal function(s) [21] . The four muscles modeled to produce movement are: the single joint shoulder, elbow and wrist joint muscle and the double joint Biceps brachii muscle as shown in Figure 2. The Biceps brachii is a bi-articular muscle that can cross both the shoulder and elbow joints [22] . Theoretically, muscles can be assumed to be regulated independently [16] . Damping and stiffness coefficient of muscles are assumed to be linearly proportional [23] . Equation of motion describing the dynamics of the hand at its proximal joints is derived [24] - [30] and used for designing the tremor suppression device.
Table 1. Calculated mass and mass moment of inertia of each segment.
Figure 1. Dynamic hand modeling.
Figure 2. Musculoskeletal hand modeling.
3. Vibration Absorber
Vibration absorber is a passive vibration controller added as a secondary system to reduce the steady-state vibrational motion of the structure at a particular frequency. Passive undamped TVA has a simple design and installation and is easy to implement, but is effective over narrow-band of frequencies. The absorber’s proof mass absorbs vibrational energy of the primary system. Its spring transfer energy to the proof mass and must be capable to withstand the full force of excitation and its corresponding deflection. Absorber’s parameters (mass-spring) are chosen to minimize vibration at an undesired frequency, usually the forcing frequency. At the tuning condition, when the absorber’s natural frequency is designed to be exactly equal to the driving frequency, the absorber transmits aforce (moment) having the same magnitude and opposite sense of the problematic force (moment) to cancel it out. Absorber’s mass, spring size and spring deflection represent geometric limitation in the design of a vibration absorber system [31] . The bandwidth describing the frequency range of operation of the absorber can be widened by adding a damping element [31] . The damper dissipates energy of a vibrating system and converts this mechanical energy into heat. The conventional damped TVA has a mass connected to a parallel connected spring and damper and attached to the primary mass.
The derived equation of motion describing the dynamics of the controlled system is as follows:
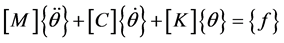 (1)
(1)
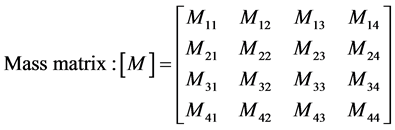 (2)
(2)
where,
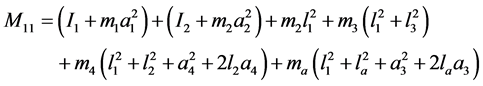
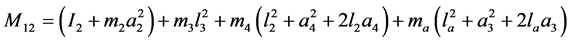
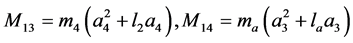
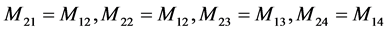
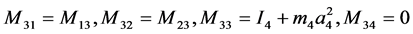
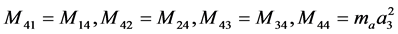
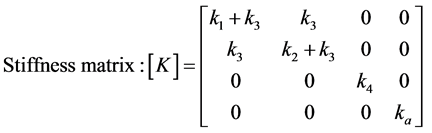 (3)
(3)
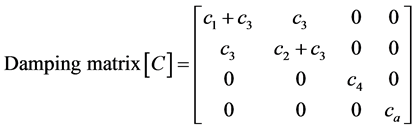 (4)
(4)
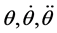 are the angular displacement, velocity and acceleration vectors at hand joints. The lengths l1, l2, l4, masses m1, m2, m4, and positions at centroid a1, a2, a4, correspond to the upper arm, forearm and the palm, respectively. k1, k2, k3, k4 and c1, c2, c3, c4 are respectively the stiffness and damping coefficients of the shoulder, elbow, biceps brachii, wrist joint muscles. la is the position of absorber’s joint along the forearm measured from the elbow joint, a3 is the position from absorber’s proof mass to its joint along the beam and m3 is the mass of controller device holding the absorber. ka and ca are the stiffness and damping coefficients of absorber’s beam material. f is the input moments exerted from muscular activity.
are the angular displacement, velocity and acceleration vectors at hand joints. The lengths l1, l2, l4, masses m1, m2, m4, and positions at centroid a1, a2, a4, correspond to the upper arm, forearm and the palm, respectively. k1, k2, k3, k4 and c1, c2, c3, c4 are respectively the stiffness and damping coefficients of the shoulder, elbow, biceps brachii, wrist joint muscles. la is the position of absorber’s joint along the forearm measured from the elbow joint, a3 is the position from absorber’s proof mass to its joint along the beam and m3 is the mass of controller device holding the absorber. ka and ca are the stiffness and damping coefficients of absorber’s beam material. f is the input moments exerted from muscular activity.
The suggested mechanical vibration absorber is designed as cold rolled stainless steel alloy (type 301) cantilevered beam with a copper mass attach along its length with the dimensions shown in Figure 3. Absorber’s geometry is sized using Dunkerley’s semi- empirical formula [32] to satisfy the tuning condition [31] at system’s fundamental resonance frequency (3.486 Hz) of resting tremor. The selected beam’s material is chosen since it can produce an absorber of short length due to its relatively low modulus of elasticity and its high yielding and fatigue strength can protect it against failure. The proof mass is selected to be copper because of its high density, so a small volume is needed to attain the designed mass value 149.5 g. An additional 50 g is considered in order to take into account the absorber’s device mass needed to hold the absorber. The absorber is set 8.5 cm away from the wrist joint along the forearm to avoid interference with the palm’s oscillation. Little damping coefficient can be provided from beam’s material [33] . Its stiffness coefficient is calculated to satisfy the root of a wrist joint’s response [25] [26] [27] [28] .
4. Results
The behavior of the modeled hand system is described in the frequency and time domains to show the effect of the designed absorber (Figure 3). Equation of motion describing the dynamics behavior is implemented using MATLAB to calculate its response and show the results. The behavior at the wrist joint will be presented only due to its importance. The responses are obtained using the following equations:
Figure 3. Designed passive vibration absorber.
Frequency domain 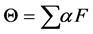 (5)
(5)
Time domain 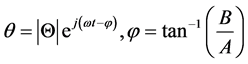 (6)
(6)
where, 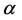 is the Receptance transfer function, F is the muscular moment amplitude,
is the Receptance transfer function, F is the muscular moment amplitude, 

The frequency domain response can serve in analyzing the angular displacement amplitude due to each excitation frequency. Figure 4(a) shows the frequency domain response at the wrist joint before and after adding the absorber which is tuned at 3.486 Hz. High tremor’s amplitude is shown at the resonance frequencies of the uncontrolled and controlled systems. The uncontrolled hand system was vibrating with critical amplitude of 9.59˚ at 3.486 Hz as shown clearly in Figure 4(b). This amplitude is decreased to 2.81˚ after adding the tuned absorber at the resonance frequency. It is shown that the absorber can reduce tremor’s amplitude around the tuning frequency, from


Figure 4. Flexion angular motion at the wrist joint in the frequency domain (a) wide range of frequencies; (b) zoom-in in the range of resting tremor frequencies.
Figure 5. Flexion angular motion at the wrist joint in the time domain.
3.158 Hz to 3.597 Hz, which presents the bandwidth of the absorber around the rest tremor’s frequency.
The time domain response is presented to see the behavior of the angular displacement with respect to time. Figure 5 shows the time domain response at the wrist joint when the muscles are excited at resonance. The absorber is usually designed to reduce the steady state motion. However, it is shown that the absorber was also able to reduce homogenous response which lasts in 7 seconds. At the steady state, the absorber causes 93% reduction of the tremor’s amplitude at the wrist joint.
5. Conclusions and Future Work
This paper aims to benefit from concept of mechanical vibration absorbers used to reduce the undesired oscillations of structures and study their effect in suppressing the involuntary hand tremor. A numerical study is done to test the performance of the passive vibration absorber in reducing the symptoms of PD without series side effects. Based on the collected experimental data of a human hand, a dynamic model at the musculoskeletal level was done. Then, a suitable vibration absorber is designed and tuned to cause 93% reduction in the tremor’s flexion motion at the wrist joint. This absorber is numerically effective in reducing the rest hand tremor with a device of total mass 200 g where all its parameters and material properties are specified. Passive absorbers have low cost, simple design and require no external power source. It can be used as an alternative approach to medical and surgical treatments.
The effect of the mechanical vibration absorber can be tested experimentally after the numerical evidence of its effectiveness in reducing the angular motion at the wrist joint. The absorber’s device can be manufactured based on the parameters calculated from a real Parkinson’s patient to satisfy its tuning condition.
Cite this paper
Gebai, S. and Ham- moud, M. (2016) Parkinson’s Disease Treat- ment as Seen from a Mechanical Point of View. Advances in Parkinson’s Disease, 5, 97-106. http://dx.doi.org/10.4236/apd.2016.54012
References
- 1. Parkinson, J. (1817) The Shaking Palsy. Sherwood, Neely and Jones, London.
- 2. McDowell, F.H. and Cedarbaum, J.M. (1993) The Extrapyramidal System and Disorders of Movement. Clinical Neurology, 3, 57-59.
- 3. Deuschl, G., Bain, P. and Brin, M. (1998) Consensus Statement of the Movement Disorder Society on Tremor. Movement Disorders, 13, 2-23.
https://doi.org/10.1002/mds.870131303 - 4. Elble, R.J. and Koller, W.C. (1990) Unusual Forms of Tremor. Tremor, The Johns Hopkins University Press, Baltimore, 154-157.
- 5. Hussein, M., As’arry, A., Zain, M.M., Mailah, M. and Abdullah, M.Y. (2009) Experimental study of Human Hand-Arm Model Response. Mechatronics and Its Applications. ISMA'09. 6th International Symposium, 1-6.
- 6. Kazi, S., As’arry, A., Zain, M.M., Mailah, M. and Hussein, M. (2010) Experimental Implementation of Smart Glove Incorporating Piezoelectric Actuator for Hand Tremor Control. WSEAS Transactions on Systems and Control, 5, 443-453.
- 7. O’Suilleabhain, P.E. and Matsumoto, J.Y. (1998) Time-Frequency Analysis of Tremors. Brain, 121, 2127-2134.
https://doi.org/10.1093/brain/121.11.2127 - 8. Kowal, S.L., Dall, T.M., Chakrabarti, R., Storm, M.V. and Jain, A. (2013) The Current and Projected Economic Burden of Parkinson’s Disease in the United States. Movement Disorders, 28, 311-318.
https://doi.org/10.1002/mds.25292 - 9. Morrison, S., Kerr, G. and Silburn, P. (2008) Bilateral Tremor Relations in Parkinson’s Disease: Effects of Mechanical Coupling and Medication. Parkinsonism & Related Disorders, 14, 298-308.
https://doi.org/10.1016/j.parkreldis.2007.09.004 - 10. Zhang, D., Poignet, P., Widjaja, F. and Ang, W.T. (2011) Neural Oscillator Based Control for Pathological Tremor Suppression via Functional Electrical Stimulation. Control Engineering Practice, 19, 74-88.
https://doi.org/10.1016/j.conengprac.2010.08.009 - 11. Bó, A., Poignet, P., Zhang, D. and Ang, W.T. (2009) FES-Controlled Co-Contraction Strategies for Pathological Tremor Compensation. In 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, 1633-1638.
https://doi.org/10.1109/IROS.2009.5354397 - 12. Grimaldi, G. and Manto, M. (2008) Tremor: From Pathogenesis to Treatment. Synthesis Lectures on Biomedical Engineering, 3, 1-212.
https://doi.org/10.2200/S00129ED1V01Y200807BME020 - 13. Seireg, A. and Arvikar, R.J. (1973) A Mathematical Model for Evaluation of Forces in Lower Extremeties of the Musculo-Skeletal System. Journal of biomechanics, 6, 313IN19323-322IN20326.
https://doi.org/10.1016/0021-9290(73)90053-5 - 14. Chao, E.Y. and An, K.N. (1978) Determination of Internal Forces in Human Hand. ASCE Journal of Engineering Mechanics, 104, 255-272.
- 15. Zajac, F.E. and Gordon, M.E. (1989) Determining Muscle’s Force and Action in Multi-Articular Movement. Exercise and Sport Sciences Reviews, 17, 187-230.
- 16. Hashemi, S.M., Golnaraghi, M.F. and Patla, A.E. (2004) Tuned Vibration Absorber for Suppression of Rest Tremor in Parkinson’s Disease. Medical and Biological Engineering and Computing, 42, 61-70.
https://doi.org/10.1007/BF02351012 - 17. Yao, P., Zhang, D. and Hayashibe, M. (2012) Simulation of Tremor on 3-Dimentional Musculoskeletal Model of Wrist Joint and Experimental Verification. 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 4823-4826.
- 18. Drillis, R., Contini, R. and Bluestein, M. (1964) Body Segment Parameters. Artificial Limbs, 8, 44-66.
- 19. Cnockaert, J.C., Lensel, G. and Pertuzon, E. (1975) Relative Contribution of Individual Muscles to the Isometric Contraction of a Muscular Group. Journal of Biomechanics, 8, 191-197.
https://doi.org/10.1016/0021-9290(75)90024-X - 20. Wright, V. and Johns, R.J. (1960) Physical Factors Concerned with the Stiffness of Normal and Diseased Joints. Bulletin of the Johns Hopkins Hospital, 106, 215-231.
- 21. Deuschl, G., Raethjen, J., Lindemann, M. and Krack, P. (2001) The Pathophysiology of Tremor. Muscle & Nerve, 24, 716-735.
https://doi.org/10.1002/mus.1063 - 22. Lan, N. (1997) Analysis of an Optimal Control Model of Multi-Joint Arm Movements. Biological Cybernetics, 76, 107-117.
https://doi.org/10.1007/s004220050325 - 23. Maia, N.M. and e Silva, J.M. (1997) Theoretical and Experimental Modal Analysis. Research Studies Press, Baldock.
- 24. Gebai, S., Hammoud, M., Hallal, A. and AL Shaer, A. (2016) Structural Control and Biomechanical Tremor Suppression: Comparison between Different Types of Passive Absorber. Journal of Vibration and Control, in Press.
- 25. Gebai, S., Hammoud, M. and Khachfe, H. (2016) Using a Dual Vibration Absorber to Suppress Rest Hand Tremor of Elderly. The Fifth International Conference on Global Health Challenges, GLOBAL HEALTH 2016, Venice, 9-13 October 2016.
- 26. Gebai, S., Hammoud, M., Hallal, A. and Khachfe, H. (2016) Tremor Reduction at the Palm of a Parkinson’s Patient Using Dynamic Vibration Absorber. Bioengineering, 3, 18.
https://doi.org/10.3390/bioengineering3030018 - 27. Gebai, S., Hammoud, M., Hallal, A., AL Shaer, A. and Khachfe, H. (2016) Biomechanical Treatment for Rest Tremor of Parkinson’s Patient. IEEE International Multidisciplinary Conference on Engineering Technology, IMCET’16, Beirut, 2-4 November 2016.
- 28. Gebai, S. and Hammoud, M. (2016) Reduction of Parkinsonism Disorder Symptoms Using Passive Dual Absorbers. Third Middle East Conference on Biomedical Engineering, MECBME’16, Beirut, 6-7 October 2016, 88-91.
https://doi.org/10.1109/mecbme.2016.7745415 - 29. Gebai, S., Hammoud, M., Shaito, A. and Hallal, A. (2016) A Novel Design of Tuned Vibration Absorber for Tremor in Hand of Parkinsonian Patients. Master Thesis, Lebanese International University, Beqaa Valley.
- 30. Gebai, S., Hammoud, M., Hallal, A., Al Shaer, A. and Khachfe, H. (2016) Passive Vibration Absorber for Tremor in Hand of Parkinsonian Patients. 3rd International Conference on Advances in Computational Tools for Engineering Applications, ACTEA2016, Beirut, 13-15 July 2016, 167-172.
- 31. Inman, D.J. (2008) Engineering Vibrations. Prentice Hall, Upper Saddle River.
- 32. Jeffcott, H.H. (1918) The Periods of Lateral Vibration of Loaded Shafts. The Rational Derivation of Dunkerley’s Empirical Rule for Determining Whirling Speeds. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 95, 106-115.
https://doi.org/10.1098/rspa.1918.0052 - 33. Hirsch, G. and Bachmann, H. (1995) Wind-Induced Vibrations. In: Vibration Problems in Structures, Birkh?user, Basel, 73-112.�






