International Journal of Nonferrous Metallurgy
Vol.2 No.3(2013), Article ID:33899,6 pages DOI:10.4236/ijnm.2013.23016
Axisymmetric Strain Stability in Sheet Metal Deformation
Tver State Technical University, Tver, Russia
Email: brovman@mail.ru
Copyright © 2013 Tatjana V. Brovman. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 31, 2012; revised February 7, 2013; accepted February 18, 2013
Keywords: Plastic Axisymmetric Deformation; Loss of Stability; Side Strain Development
ABSTRACT
Production of axisymmetric pieces by technology of sheet metal drawing is widespread nowadays. So the calculation analysis of capacity and forces necessary for deformation is of special interest. The length of cylindrical pieces with axisymmetric deformation is limited by loss of stability and buckling due to the development of side strains. A new technological process is based on making considerable number of folds—18 - 26 with the amplitude of 0.8 - 0.9 mm— before the deformation or immediately after the partial one. That reduces the stiffness of billets and prevents from development of large size buckles. A new technological process is developed for producing a long run of high-quality products.
1. Introduction
Axisymmetric deformation of sheet metal blanks are widely used in the manufacture of cylindrical pieces made of flat metal sheets.
Such products as various vessel bodies, nozzles, connecting pipes are made of low carbon steels as well as of copper, brass, magnesium alloys and other metals.
This paper examines only the deformation of the products with axial symmetry, which are increasingly used in industry.
Regularities of plastic deformation are studied in research papers [1-4]. They demonstrate that under the pressure of a cylindrical die on the center of the workpiece which was initially shaped like a disk, the plane stress is developed, with only two of the six tensor components being nonzero. Due to tensile radial stress and compressive tangential stress [1,2] the buckling of deformable workpiece accompanied with folds is possible. Usually this leads to waste metal and therefore it is necessary to limit the length of a product, to use drawing with subsequent additional deformation (secondary drawing operation, rolling).
To prevent the occurrence of folds the blank holders are used, but this significantly increases the deformation strain to an extent of the occasional overdrawing occurrence in a deformable work piece. Sometimes drawing with the billet or its edge parts heating (near the maximum diameter) is used. For some metals billet heating can increase the allowed length of a product by 1.5 - 2.0 times.
Magnesium alloy sheets are thought to be used for deep drawing only with the billet heating. But as the thickness of a sheet metal to be deformed is small (up to 1 - 3 mm) and is exposed to chilling it has to be heated directly on a die. That complicates the design of the equipment, enhances significantly power consumption and makes it difficult to ensure safety conditions.
In this paper we discuss some features of the sheet blanks axsymmetric strain. A new drawing technique which allows to improve the technology and to expand significantly the range of products is proposed and investigated.
2. Kinematically Admissible Velocity Fields by Drawing Deformation
The graphic pattern of drawing deformation is illustrated in Figure 1, where one can see matrix 1, deformed billet 2 with outer radius R0 and inner one R1, thickness h and punch 3 which moves along axis Z with constant velocity Vz = ‒V0.
Kinematically admissible velocity field determines the upper limit of deformation ca capacity N and the associated moving die force P. Such a velocity field is to satisfy: a) the incompressibility condition, b) velocity boundary conditions, c) the condition under which the deformation capacity is positive [1]. The volume of a deformable billet can be divided into two parts. One of them having a cylindrical shape with inner radius R1 moves with velocity Vz = ‒V0 together with moving die 3 [2,3]. In this zone Vr is equal to 0 (the coordinate axes location is shown in Figure 1). As this part of a billet moves like a rigid body, its capacity of plastic deformation is equal to zero [3]. The second zone includes the part of a billet which has a shape of a ring with thickness h limited by radius r = R1 + h and r = R0. Some features of this deformation are considered in paper [4]. In this area the kinematically admissible velocity field could be
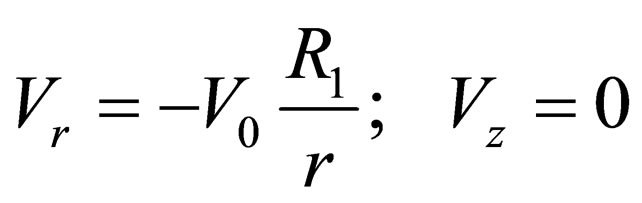 (1)
(1)
with the strain-rate tensor components
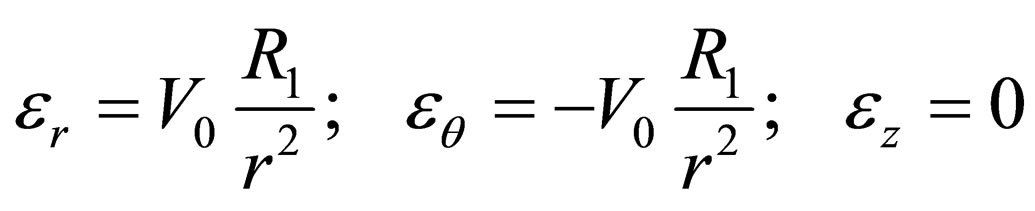
(the other tensor components are equal to zero). Value  is velocity under
is velocity under  and the second invariant of strain-rate tensor is equal to
and the second invariant of strain-rate tensor is equal to
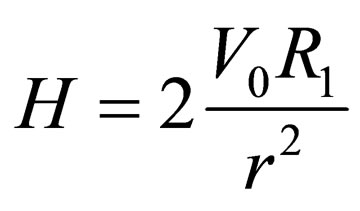
This velocity field can be assumed as kinematically admissible only if there exists surface z(r) separating the two selected deformation zones. On this surface the normal rate components are to be equal, (tangential components may differ and their difference determines the capacity of the shear). Such a surface exists and is a paraboloid [5]. As a result, it is possible to determine the deformation capacity
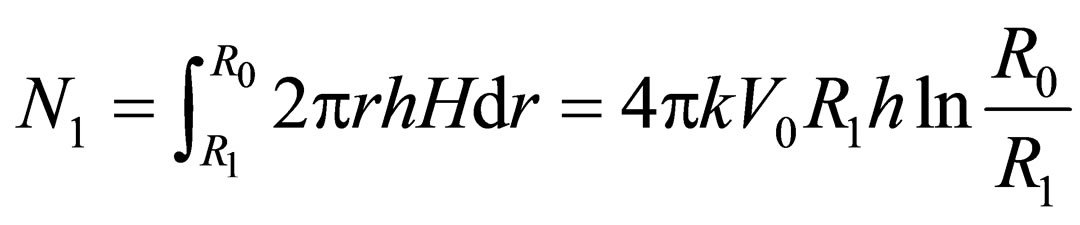
where 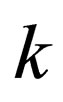 is yield point in shear, and shear capacity over the surface of paraboloid is
is yield point in shear, and shear capacity over the surface of paraboloid is
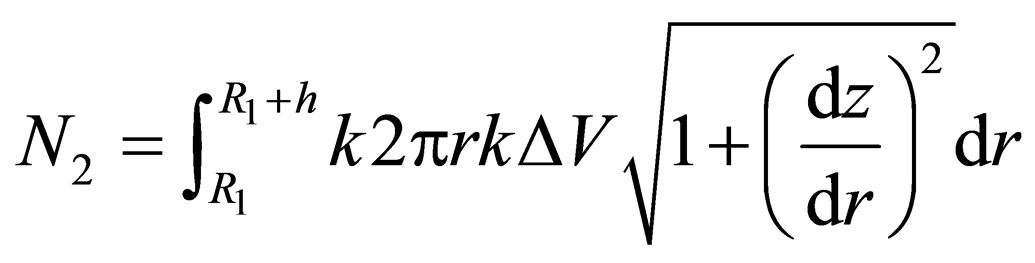
with paraboloid equation:
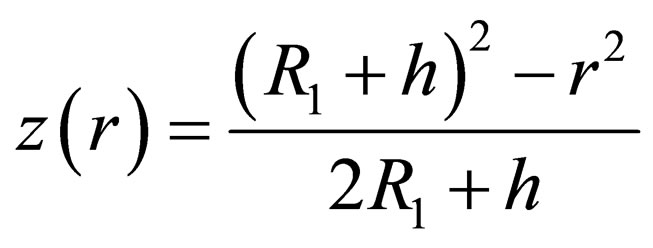 (2)
(2)

Figure 1. Drawing Scheme.
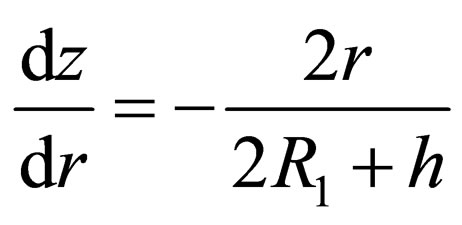
tangential components break at the boundary of two zones
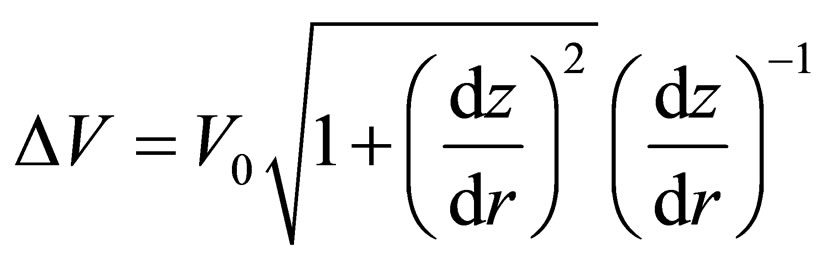
with shear capacity

Full capacity with provision for friction load at the surface of lower die is
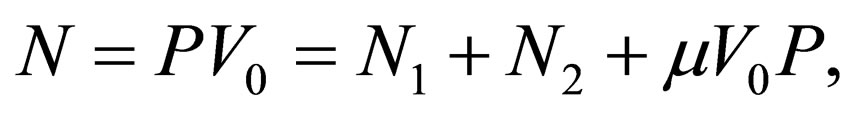
where 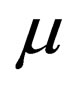 is coefficient of sliding friction. Moving die force is
is coefficient of sliding friction. Moving die force is
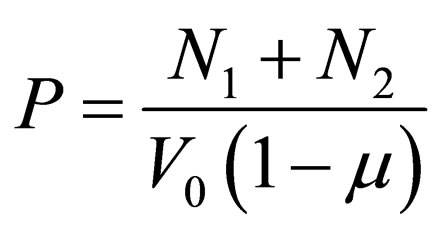 (3)
(3)
If the deformation is carried out with the use of blankholder, with force T, the friction load increases and force P is equal to
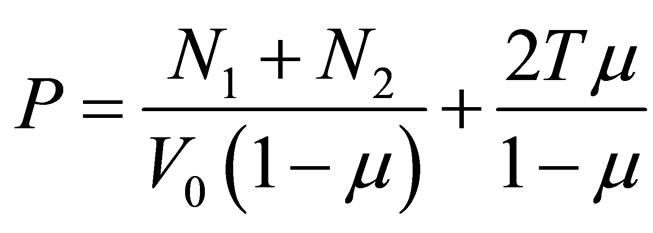 (4)
(4)
Usually 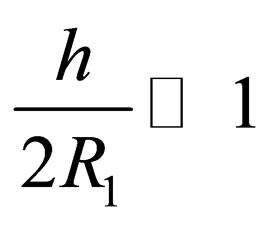 and the force is
and the force is
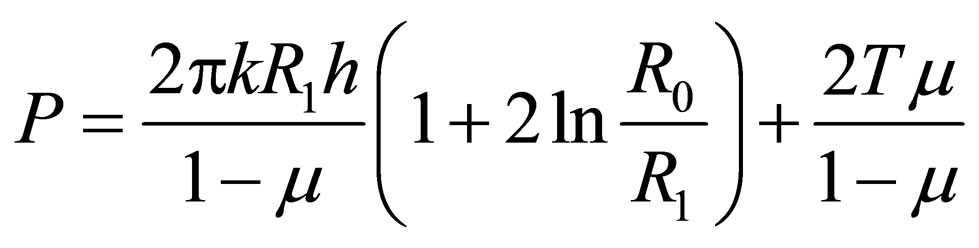 (5)
(5)
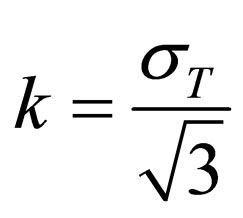
If the steel sheet deformation is carried out without the use of blankholder, as shown in Figure 1 (with Т = 0,
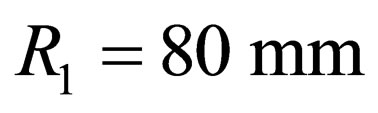 ,
, 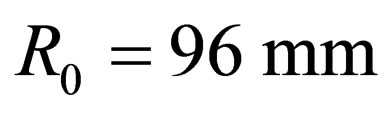 ,
,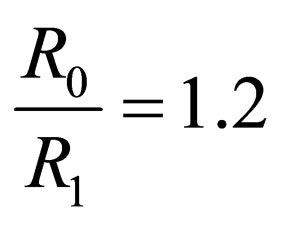 ; h = 1 mm, m = 0.10,
; h = 1 mm, m = 0.10,  ,
,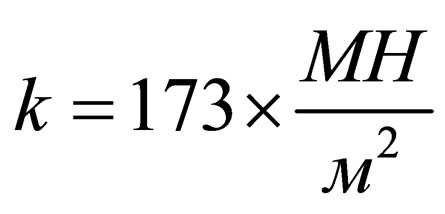 ), the value of force according to (5) is P= 0.13 MN.
), the value of force according to (5) is P= 0.13 MN.
As usual, the kinematically admissible velocity field determines the upper limit of forces (i.e., overstated values of P). According to experimental data, in case of drawing this overstatement amounts to 20% - 25%. This is acceptable for the choice of equipment in most cases.
3. Workpiece Buckling in the Drawing Deformation
In the process of deep drawing a sheet shaped initially like a disk undergoes tangential compressive stress that can lead to loss of stability. Thereby folds occur on the part of a surface, as shown in Figure 2. Paper [1] indicates that the location and number of folds depends on the metal anisotropy, for example for some alloys the number of waves is four, with the location being at an angle of 45˚ to the rolling direction of a sheet. But the number may come up to six [1].
Usually, the fold occurrence, i.e. wavy surface with amplitude of up to 10 - 20 mm, leads to inability to output products and to rejected material. From Saint-Venan condition end equation of equilibrium
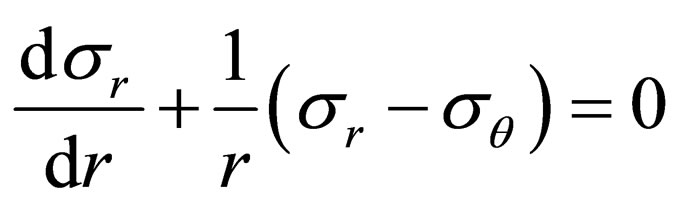 (6)
(6)
and condition of plasticity
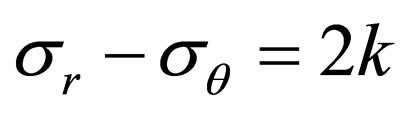
it is clear that stress is 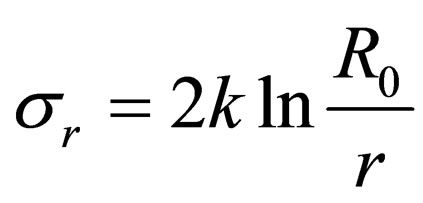
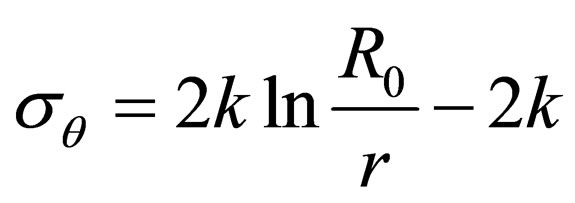 (7)
(7)
where the integration constant is determined by the condition of 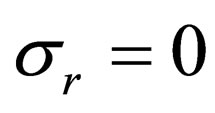 with
with 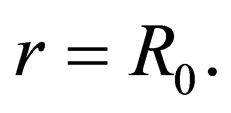 Tangential stress with
Tangential stress with 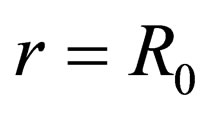 is equal to
is equal to .
.
The minimum allowable value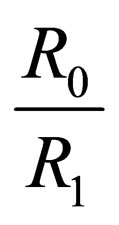 , (under which folds occur) is determined by parameters:
, (under which folds occur) is determined by parameters: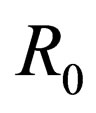 ,
, 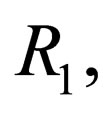 h,
h,  ЕТ with the dimensions: m (for the first three) и МН/m2 for yield limit
ЕТ with the dimensions: m (for the first three) и МН/m2 for yield limit 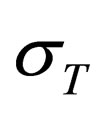 and plastic deformation hardening modulus
and plastic deformation hardening modulus . Here
. Here 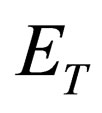 is a value characterizing metal hardening in plastic deformation.
is a value characterizing metal hardening in plastic deformation.
Out of these five variables it is possible to form three dimensionless parameters:
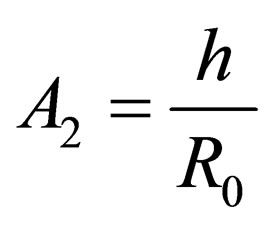
 and
and 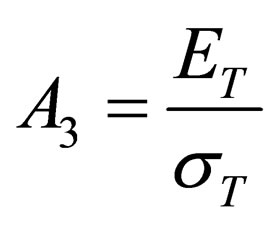
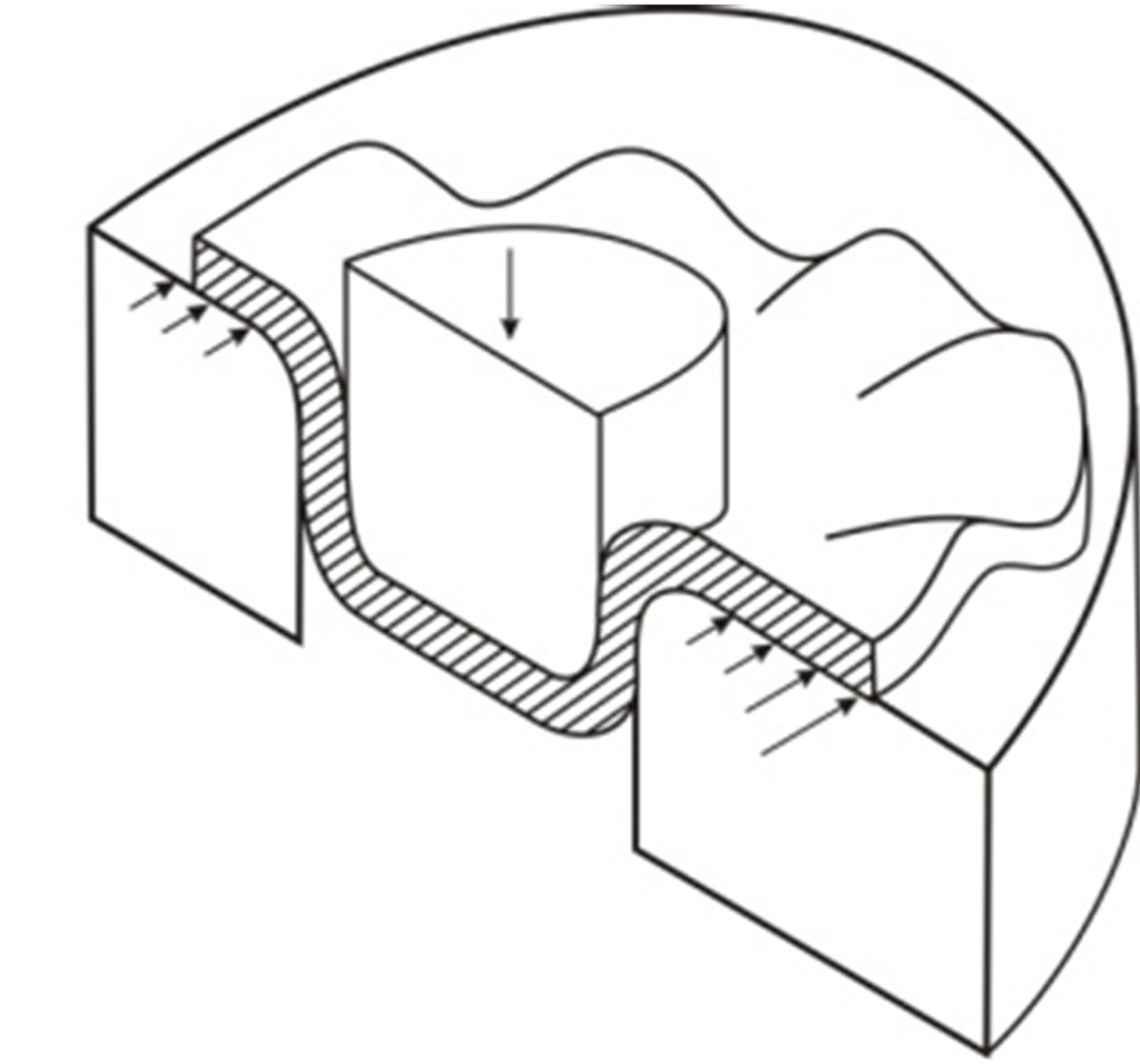
Figure 2. Development of Folds.
As well as to determine approximately strain-hardening characteristic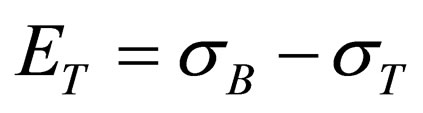 , where
, where 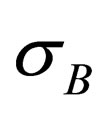 is ultimate strength.
is ultimate strength.
According to  theorem the relationship between the above-mentioned parameters must take the following form
theorem the relationship between the above-mentioned parameters must take the following form 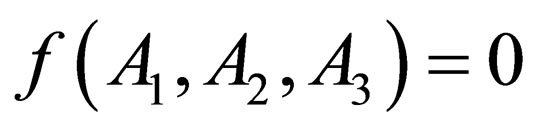 . Having solved it for
. Having solved it for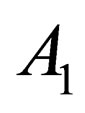 , we get
, we get
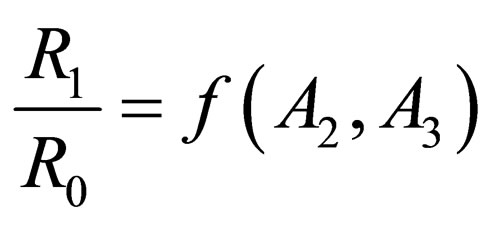 (8)
(8)
Based on the data of many deformation experiments with carbon steel sheets of 0.5 mm, 1.00 mm, 1.5 mm and 2.0 mm thicknesses the graphs  were plotted as given on Figure 3.
were plotted as given on Figure 3.
The relationship (8) can be determined with the empirical formula for a maximum permissible (minimum) value
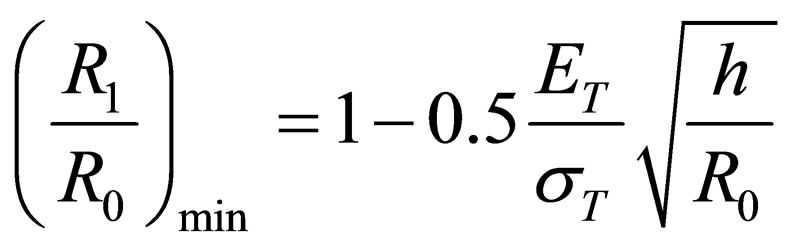 (9)
(9)
To provide the sheet stability the following condition should be fulfilled:
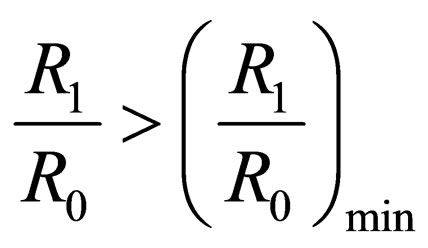 (10)
(10)
Since the maximum possible upset length is equal to
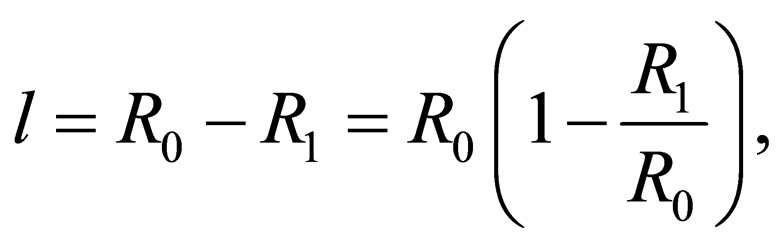 it follows from (9) that the maximum possible length of work is
it follows from (9) that the maximum possible length of work is
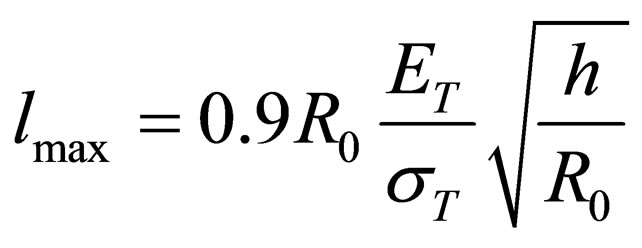 (11)
(11)
For example, for a steel sheet of h = 1 mm thickness
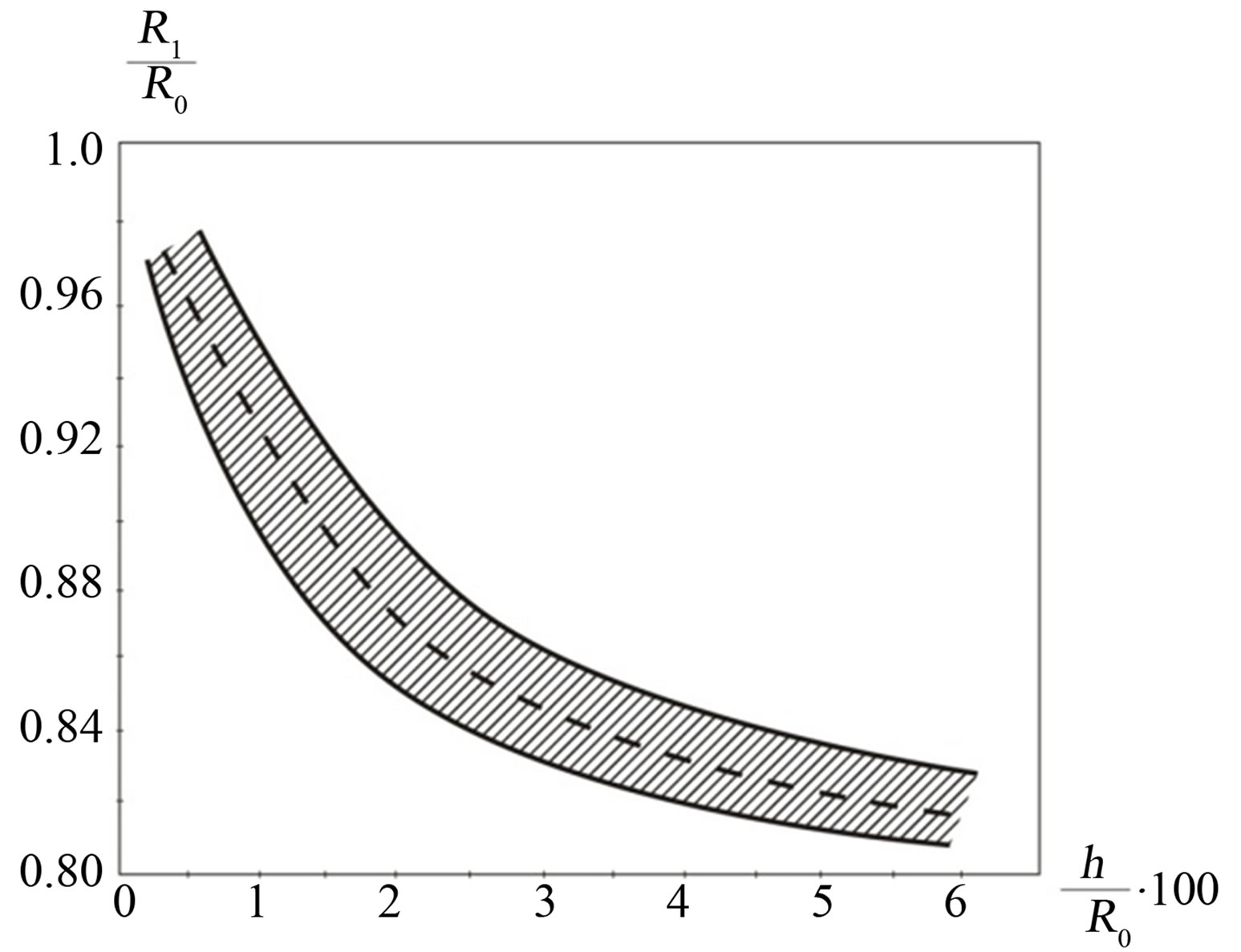
Figure 3. Graph of Function .
.
with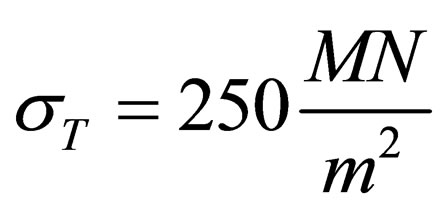 ,
, 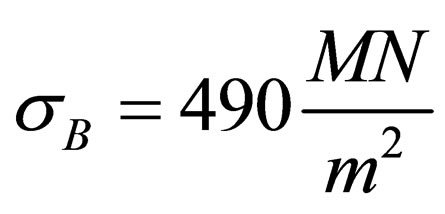 ,
, 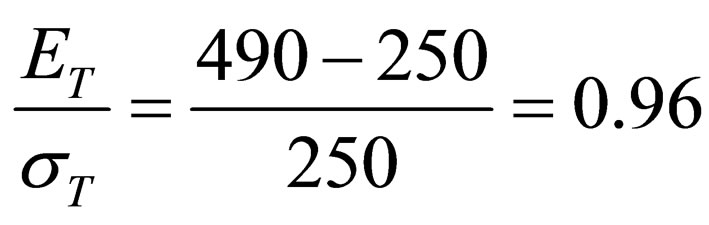 ;
; 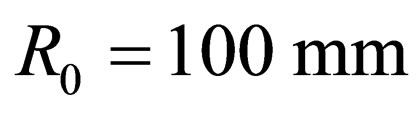 .
.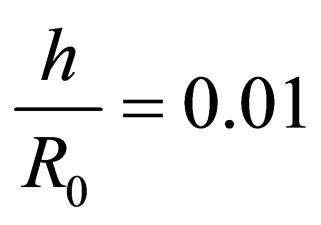 according to Formula (9) we get
according to Formula (9) we get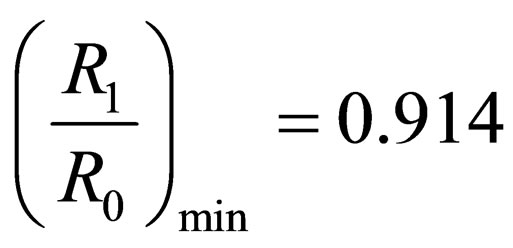 ,
,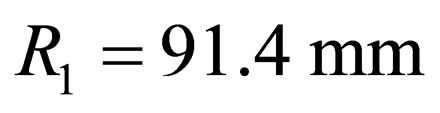 ; l = 8.6 mm.
; l = 8.6 mm.
Formula (9) can be applied if 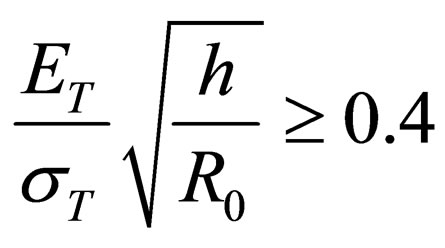 and the experimental data spread is considerable which is seen from Figure 3. The dotted line here divides the data span into two parts. Below the dottedline there is a zone for specially selected samples with thickness differences of no more than 0.02 mm. The higher the gage interference, the more often the buckling failure and buckle development happen. Therefore it is important to increase the dimensional accuracy of sheets used for deep drawing. Empirical formula (9) gives that if
and the experimental data spread is considerable which is seen from Figure 3. The dotted line here divides the data span into two parts. Below the dottedline there is a zone for specially selected samples with thickness differences of no more than 0.02 mm. The higher the gage interference, the more often the buckling failure and buckle development happen. Therefore it is important to increase the dimensional accuracy of sheets used for deep drawing. Empirical formula (9) gives that if
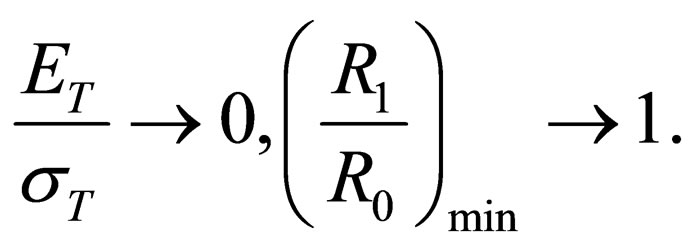 It conforms to the test which shows what should be applied for metal (alloys) drawing with high hardening: the higher
It conforms to the test which shows what should be applied for metal (alloys) drawing with high hardening: the higher 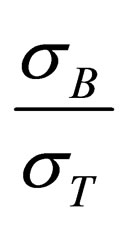 is, the easier the deformation can be made, and the larger work length can be produced when drawing. Metals with minor hardening with graph of function
is, the easier the deformation can be made, and the larger work length can be produced when drawing. Metals with minor hardening with graph of function 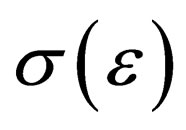 being close to a perfectly plastic body graph (i.е. when
being close to a perfectly plastic body graph (i.е. when  ) are unfit for deep drawing.
) are unfit for deep drawing.
Steel sheets with up to 0.05% - 0.15% temper and not more than 20 - 30 µm grain size with extension strain of no less than 40% are often used fro drawing.
According to the above-mentioned the holder allows to increase l value and decrease parameter 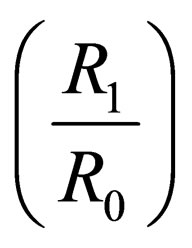 . However, the ring crack wastage increases as shown on Figure 4. There can be seen ring cracks being the reasons of up to 10% and more increase of waster number which aggravates the manufactures’ economic indexes signifycantly.
. However, the ring crack wastage increases as shown on Figure 4. There can be seen ring cracks being the reasons of up to 10% and more increase of waster number which aggravates the manufactures’ economic indexes signifycantly.
4. New Method of Drawing
Based on the research conducted a new technological drawing process has been suggested (see Patent Application of Russian Federation №2011123174/02, MPK 7В1D 22/02 from 08 June 2011).
The method consists in forming a series of waves (ridges) along a ring on a disk-form billet, see Figure 5. The amplitude of the waves is small (usually not more than (1/2)h) but their quantity is large up to 16 - 28 waves located along the ring as can be seen on Figure 5. All the deepenings (waves) are reasonable to be made simultaneously with one die then the billet should be upturned and deformed by drawing, the clearance between the sheet being deformed and the punch should exceed the “waves” amplitude 1.5 - 2.0 times in order to avoid sheet jamming. With drawing deformation the buckled sheet compressive deformation relieves (its hardness is reduced).
Experiments were made with samples of diameters 70 - 120 mm and height 80 - 140 mm of low carbon steels.
The waves may be located not along the billet edge as shown on Figure 5(а) but in its middle as on Figure 5(b). Even making 0.5 - 1 mm amplitude waves on a billet parallel portion gives a positive result after partial drawing deformation.
Various wave variants are also shown on Figures 5(c) and (d), e. The depth for 0.5 mm sheets of carbon steel was 0.5 mm, the number of waves being 18 - 26. “The loss of stability” with large wave formation, e.g. shown on Figure 2, does not occur and there is a possibility of manufacturing products with a length 2 - 3 times higher the admissible length of a conventional drawing.
The deformation is sure to result in increasing the wave amplitude, sometimes 1.5 times (there occurs their compression with “wave” shortening sometimes in 2 - 3 times), but the new waves of large amplitude do not emerge (e.g. as those shown on Figure 2).


Figure 4. Blanks with Cracks.
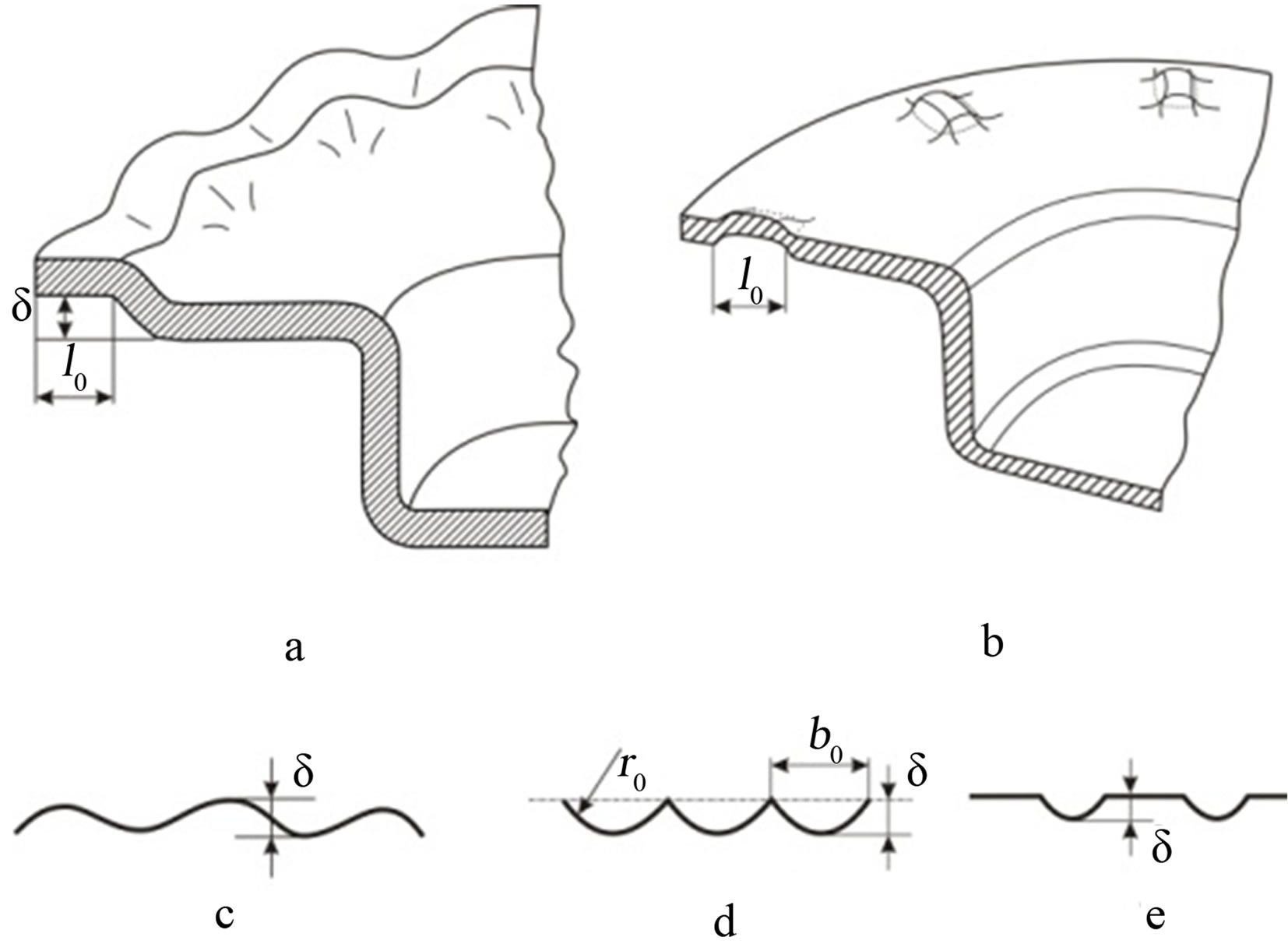
Figure 5. New Method of Drawing.
The main idea of the method consists in making a large number (18 - 26) of waves of small amplitude on a sheet (disk) in advance in order to avoid the potential of emerging 4 - 8 “waves” (buckles) of large amplitude (up to 10 - 20 mm). It decreases the rigidity of a deformed billet, with the amplitude being able to reach 1.5 mm after drawing, which does not lead to sharp changes of the whole product pattern (it usually happens with the stability loss) and allows to manufacture the required product of high quality.
Figure 6 shows the samples manufactured at OAO TsBPR (the town of Tver, Russia) with the new method used.
These Filter Casing Blanks were made from low carbon steel (st.08 according Russian standart 1050 - 88). Quality of Carbon was 0.05% - 0.25%. Part of filter Casings was made of semi-killed steel (st.3). Diameters of these Casing Blanks were 96 mm and their height was 92 mm. Artificial waves were made with length 28 mm and amplitudes 1 mm. Quanlity of Filters was good and reject was decreased twice till 0.75%.
The artificial waves (ridges) are certain to remain on the product. The method is sure not to be used in cases when even small waves on the product cannot be allowed. But in many cases such waves with amplitude of less than 1mm do not at all make the product quality worse and therefore are possible. So the above-mentioned Tver plant manufactured more than 10 thousand filter casings (Figure 6) of high quality. An analogy may be drawn to the case of bar pressing (see Figure 7). When a straight cantilever bar is compressed with stress P (Figure 7(а)), according to Euler formula
 (a)
(a) (b)
(b)
Figure 6. Filter Casing Blanks Produced with New Method.
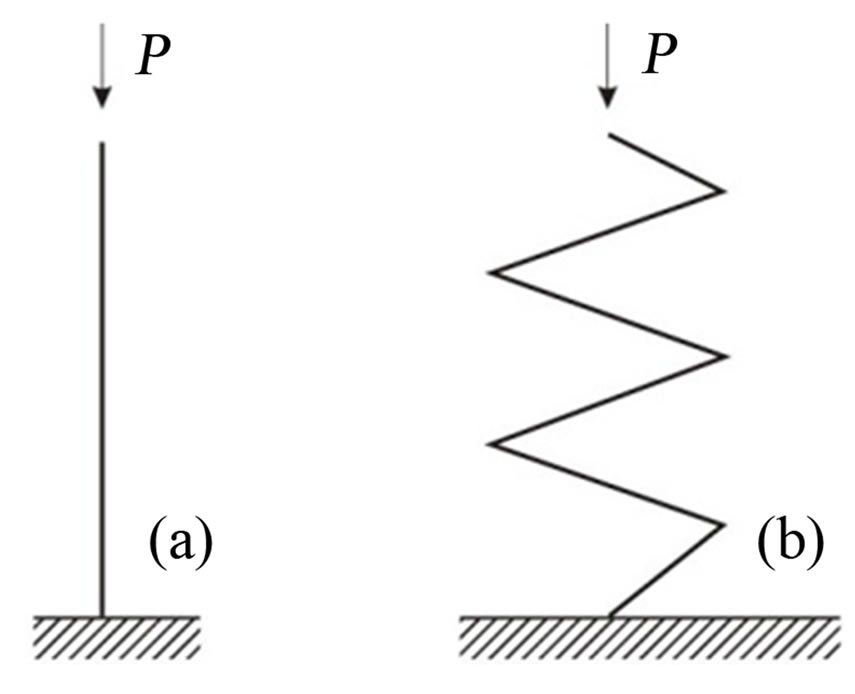
Figure 7. Scheme of Stability under Deformation.

it loses stability when being subject to compressive deformation, (where F is an area of bar section, J is its moment of inertia, l is a bar length).
With further compression a bar loses its configuration, with the deflection increasing rapidly up to 0.5 l and more.
If a bar can be manufactured as shown on Figure 7(b), it keeps its whole configuration in higher deformations 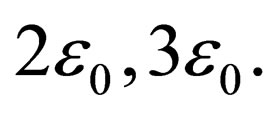 Its rigidity is a considerably less than that of a straight bar but no sharp changes of the whole form occur.
Its rigidity is a considerably less than that of a straight bar but no sharp changes of the whole form occur.
(Both the rings and deformable bodies of Figure 7(b) can certainly “buckle” but, as a rule, in cases when the deformation is several times more than value 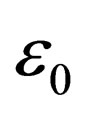 for a straight bar).
for a straight bar).
In some cases the manufactured rigidity reduction of the billet being drawn can be rational.
5. Conclusions
The following conclusions can be deduced from the above-said study:
1) The axially symmetric sheet blank deformation under drawing has been examined.
The kinematically admissible velocity field for force upper limits has been built.
2) A new method of drawing which included making ridges-waves of small amplitude on a blank before drawing has been proposed and studied. But the number of such waves should be considerable and it gives the possibility to avoid the formation of more significant form distortions of a billet.
3) The method was used for producing oil filter casings and getting a high-quality product. More than 10 thousand filter casings of good qualities of carbon steel were produced with use of new method.
REFERENCES
- R. Hill, “Mathematical Theory of Plasticity,” Clarendon Press, Oxford University Press, 1950, 407 pages.
- L. A. Shofman, “Theory and Calculation of Cold Forming,” Machine-Building, Moscow, 1964, 375 pages. [in Russian]
- M. Ja. Brovman, “Application of the Theory of Plasticity in Rolling,” Metallurgiya, Moscow, 1991, 265 pages. [in Russian]
- H. Vergus and R. Sowerby, “The Pure Plastic Bending of Laminated Sheet Metals,” Journal of Mechanical Sciences, Vol. 17, No. 1, 1975, pp. 31-51.
- T. V. Brovman, “Sheet Stamping Forces Calculation,” Vestnik Mashinostroyenia, No. 3, 2004, pp. 61-63. [in Russian]

