International Journal of Nonferrous Metallurgy
Vol. 2 No. 2 (2013) , Article ID: 30450 , 16 pages DOI:10.4236/ijnm.2013.22007
Alumina/Iron Oxide Nano Composite for Cadmium Ions Removal from Aqueous Solutions
1Fabrication Technology Department, Advanced Technology and New Materials Research Institute (ATNMRI), City of Scientific Research and Technological Applications (SRTA-City), Previously “Mubarak City for Scientific Research and Technology Applications (MuCSAT)”, Alexandria, Egypt.
2Dharyya College for Arts and Sciences, Qassim University, Al Qassim, Saudi Arabia
3Surface Chemistry and Catalysis Laboratory, Physical Chemistry Department, National Research Center, Cairo, Egypt
Email: *amona1911@yahoo.com
Copyright © 2013 Mona Mahmoud Abd El-Latif et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 31, 2012; revised February 7, 2013; accepted February 15, 2013
Keywords: Activated Alumina; Magnetic Properties; Cadmium Ions Removal; Equilibrium Isotherms; Kinetics
ABSTRACT
Magnetic alumina nano composite (MANC) was prepared for combination of the adsorption features of nano activated alumina with the magnetic properties of iron oxides to produce a nano magnetic adsorbent, which can be separated from the medium by a simple magnetic process after adsorption. MANC was characterized using XRD, SEM, TEM, EDX and surface area (BET). Quantum design SQUID magnetometer was used to study the magnetic measurement. The present study was conducted to evaluate the feasibility of MANC for the removal of cadmium ions from aqueous solutions through batch adsorption technique. The effects of pH, adsorbent dose, temperature, contact time and initial Cd2+ concentration on cadmium ions adsorption were studied. Equilibrium data were fitted to Langmuir, Freundlich and Temkin isotherms. The equilibrium data were best represented by the Langmuir isotherm. The kinetic data were fitted to pseudo-first-order, pseudo-second-order, Elovich and intraparticle diffusion models, and it was found to follow closely the pseudo-second-order model. Thermodynamic parameters were calculated for the Cd2+ ion-MANC system and the positive value of ΔH° showed that the adsorption was endothermic in nature. Furthermore, a single-stage batch adsorber was designed for the removal of Cd2+ ions by MANC based on the equilibrium data obtained.
1. Introduction
Water is the most precious natural resource that exists on our planet although we as humans recognize this fact; we discharged it by polluting our rivers, lakes and underground water. The release of heavy metals into the environment is a potential threat to water and soil quality as well as to plant, animal and human health. Heavy metals can be bioaccumulated through food chain transfers and unlike organic toxicants are not amenable to biological degradation [1]. Over the last two decades there has been a sharp rise in the global use of Cd for batteries and a steady decline in its use for other applications, such as pigments, polyvinyl chloride stabilizers, and plating. This trend in the use of Cd products and compounds has inspired a number of international agreements to manage and control the release of Cd to the environment and limit human and environmental exposure to Cd can cause kidney damage in mammals and humans [2,3]. Also, cadmium (Cd) is one toxic heavy metal of particular environmental concern, because it can be introduced into and accumulated in soils through agricultural application of sewage sludge, fertilizers, and/or through land disposal of Cd-contaminated municipal and industrial wastes. Cd is a known human carcinogen and may induce lung insufficiency, bone lesions and hypertension [4]. The high toxicity of cadmium has resulted in governments imposing ever tighter environmental legislation limiting wastewater discharge and the removal of heavy metals such as Cd from wastewater has been a major preoccupation of environmental professionals for many years. In particular, ever increasing world populations are likely to place increasing stress on a limited clean water resource placing a greater focus on clean up and reuse of contaminated wastewater streams [1]. Among the various methods proposed for this purpose adsorption proved to be of the most promising ones [5,6]. Several natural (e.g. natural zeolites, bentonites, metal oxides) and synthetic (e.g. synthetic zeolites, resins, metal phosphates and silicates, synthetic oxides/hydroxides/hydroxyoxides) materials have been investigated as sorbents for heavy metal removal from solutions achieving different levels of success [7-13]. Moreover, considerable research work has been done on various industrial waste materials in order to develop suitable sorbents for water treatment; so fly ash [14,15], blast fumace slug [16], biomass [17,18] and bagasse fly ash [19], among others have been tested as sorbents for heavy metal removal with various levels of success. Although, Adsorption processes are widely used for treatment of polluted surface and groundwaters and also play a significant role in advanced wastewater treatment. In adsorption, Adsorbents remove adsorbates by means of concentrating them on the large inner surface so that adsorbents with higher specific surface area possess superior adsorption capacity. A small particle size of the adsorbent can offer not only a greater specific surface area but also better mass transfer efficiency. However, a high pressure drop may be encountered with the compact adsorbent in a packed bed adsorption column if the particle diameter is smaller than 0.5 mm [5]. Because of the disadvantages caused by the small particle size, the batch stirred adsorption system with intensive mixing, which enhances the adsorption rate, is usually adopted for the use of powder adsorbents. However, the separation technology of ultra-fine particles, especially nano-scale particles, is still under development and presents difficulties to a certain extent. As a result of these disadvantages using such small particles as adsorbents, there is a great deal of interest in the preparation of nanosized magnetic particles and understanding of their properties, which are drastically different from those of the corresponding bulk materials [20]. The magnetic particle technology has a high potential to be applied in adsorption systems. In order to remove the target pollutants or compounds from the streams, the magnetic particles can be modified by the combination or modification of functional groups or inorganic compounds yielding magnetic adsorbents [21]. It is well known that porous ceramics are used in a wide range of applications including catalysts, effective absorbents, ionic conductors, filtering membranes, coatings and insulating aerogels [22-25]. Alumina is one of the most widely used ceramics due to its high specific surface area, very good thermal stability and amphoteric properties [26]. Due to these characteristics porous alumina is generally a very good candidate as a catalyst carrier as well as an adsorbent. Although alumina is used very frequently as a ceramic matrix for metal-composite materials, only a few works have been published concerning its participation in magnetic composites.
This work aims to evaluate the prepared magnetic alumina nano-composite (MANC) in removal of cadmium ions from aqueous solutions. The effects of various operating parameters such as solution pH, adsorbent dose, temperature, initial Cd2+ concentration and contact time on cadmium ions adsorption were investigated. Also the effect of loading of alumina by iron oxide on cadmium ions adsorption was studied. Adsorption isotherms, kinetics and thermodynamics of the sorption process were studied. Further, a single-stage batch adsorber was designed for the removal of cadmium ions by MANC based on the equilibrium data obtained.
2. Materials and Methods
2.1. Materials
All chemicals used in this study were of analytical grade. Ferric chloride (FeCl3) and (FeSO4∙7H2O) were supplied from Adwic Company, Cadmium chloride (CdCl2∙2.5H2O), was supplied from Aldrich Company and Aluminium oxide Al2O3, Activated Neutral, Brock Mann 1, STD Grade, CA, 150 Mesh.
2.2. Preparation of Magnetic Alumina Nano Composite (Adsorbent)
The nano composite (MANC) was prepared from a suspension of activated alumina in 400 mL solution of FeCl3 (7.8 g, 28 mmol) and FeSO4∙H2O (3.9 g, 14 mmol) at 343 K. A solution of NaOH (100 mL, 5 mol∙L−1) was added drop wise to precipitate the iron oxides. The amount of activated alumina was adjusted in order to obtain the Activated Alumina/iron oxide with weight ratio of 3:1. The 3:1 weight ratio of activated alumina to Fe oxide was chosen to avoid a decreasing in adsorption capacity of the composites due the high content of iron oxide. The obtained materials were dried in a digital dryer of (Carbolite, Aston Lane, Hope Sheffield, 5302RP, England) at 373 K for 3 h.
2.3. Characterization of Magnetic Alumina
The adsorbent(MANC) was characterized by using X-ray diffraction analysis (XRD), Scanning electron microscopy (SEM), transmission electron microscope (TEM), Quantum design SQUID magnetometer and BET surface area. X-ray diffraction analysis was carried out using Xray diffractometer (Schimadzu-7000, USA) to evaluate the phase composition, XRD spectra were obtained with a 30 kW rotating anode diffractometer fitted with a copper target. XRD spectra were obtained between 20˚ and 80˚ (2θ) in continuous scan with 4◦/min using the standard θ - 2θ geometry.
The morphology of the synthesized powders was studied using the SEM/EDX analysis which was performed using scanning electron microscope Jeol JMS 6360 LA, and the sample was prepared by coating with gold. Also, Jeol transmission electron microscope (TEM) with Max. Mag. 600 k× and resolution 0.2 nm was used to study the morphology of the prepared MANC. The samples were prepared by sonication for 30 min. Also the textural characteristics of MANC including surface area, pore size analyzer (BET) were determined using standard N2-adsorption techniques (Beckman Coulter, SA3100, USA). A quantum design SQUID magnetometer was used to obtain hysteresis loops of products at 25◦C and in fields up to 15 kOe nano composite.
2.4. Adsorbate
A stock solution of Cd2+ was prepared (1000 mg∙L−1) by dissolving required amount of, CdCl2∙2.5H2O in distilled water. The stock solution was diluted with distilled water to obtain desired concentration ranging from 100 to 1000 mg/L. pH was adjusted using 0.1 N HCl or 0.1 N NaOH. The remaining concentration of Cd2+ in each sample before and after adsorption was determined by using prodigy prism high dispersion inductive coupled plasmaatomic emission spectroscopy (ICP-AES, USA).
2.5. Batch Mode Adsorption Studies
The effects of experimental parameters such as, pH (2 - 9) using pH meter (Denver Instrument Co., USA), adsorbent dosage (0.25 - 3.0 g∙L−1), temperature (22◦C - 55◦C), initial Cd2+ ions concentration (100 - 1000 mg∙L−1) and contact time (0 - 300 min) on the adsorptive removal of Cd2+ ions were studied in a batch mode operation. For kinetic studies, 250 mL of Cd2+ solution of known different initial concentrations and pH = 6 was taken in a 250 mL screw-cap conical flask with a fixed adsorbent dosage (1 g∙L−1) and was agitated in a orbital shaker (yellow line OS 10 Control, Germany) for a contact time varied in the range 0 - 300 min at a speed of 250 rpm at 295 K. At various time intervals, the adsorbent was separated and the concentration of Cd2+ was determined. For adsorption isotherms, 250 ml of different initial Cd2+ ion concentrations (100 - 1000 mg∙L−1) were agitated with 1 g∙L−1 adsorbent dosage in an orbital shaker at 250 rpm for 240 min. The adsorbent was separated and the metal under consideration was determined as mentioned previously. The concentration retained in the adsorbent phase (qe, mg∙g−1) was calculated by using the following equation
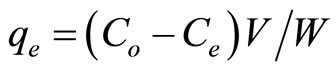 (1)
(1)
where Co is the initial Cd2+ concentration and Ce is the Cd2+ concentration (mg∙L−1) at equilibrium, V is the volume of solution (L) and W is the mass of the adsorbent (g).
3. Results and Discussion
3.1. Characterization of Magnetic Alumina Nano Composite
3.1.1. X-Ray Analysis and Microstructure
The X-ray diffractograph in Figure 1(a) represent the pattern of pure alumina used in the experimental work. Figure 1(b) represent the XRD pattern of iron oxide indicating the cubic iron oxide phase (d = 2.5, 2.91, 2.07, 1.60) which can be related to maghemite or magnetite. In Figure 1(c) the XRD pattern indicates the crystal structure of MANC particles, where the peak at 2θ = 35.55˚ is corresponding to iron oxide phase JCPDS card (19-0629) and that at 2θ = 43.22˚, 62.5˚ and 66.1˚ are corresponding to alumina JCPDS card (10-173). It is obvious that these peaks appear broader indicating smaller crystallite size of the produced MANC particles than that of the starting alumina particles and this may be devoted to the method of preparation of the composite which cause dispersion of alumina particles. The crystallite size of both phases of produced composite can be calculated from peaks at 2θ = 35.55˚ corresponding to iron oxide phase and peak at 2θ = 43.22˚ corresponding to Al2O3 phase using Sherrer Equation (2).
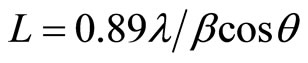 (2)
(2)
where β is the FWHM of diffraction peak, λ is the wave length of X-ray (0.154 nm), L is the crystallite size, and θ is the Bragg peak position.
The crystallite size was found to be 13.6 nm and 17.5 nm for both Al2O3 and Fe3O4 respectively.
3.1.2. Magnetic Properties
The magnetization curve obtained from the SQUID magnetometer is shown in Figure 2" target="_self"> Figure 2. The saturation magnetization Ms value is 12.12 emu/g, the remanance
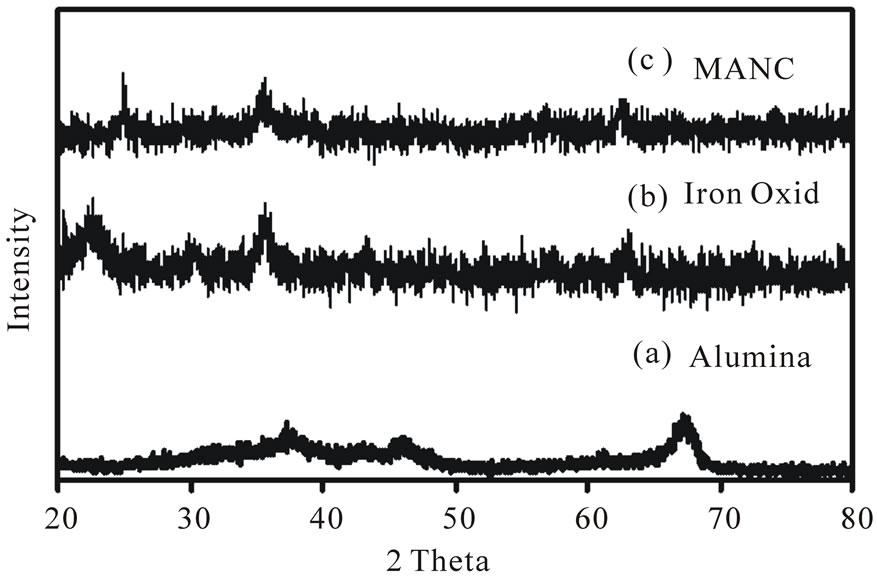
Figure 1. XRD diffractograph. (a) Alumina, (b) Iron oxide and (c) MANC.

Figure 2. Hysteresis loop of MANC taken at 25◦C.
Mr is 2.679 emu/g and the coericivity Hc is 44.89 Oe. This behaviour indicates that magnetic loaded alumina showed paramagnetic properties and its separation from treatment aqueous media can be achieved by applying magnetic field [27]. The magnetite content can be calculated on the basis of being the saturation magnetization of bulk magnetite is 94 emu/g. Because the magnetization of the produced composite is only due to Fe3O4, the mass percentage of Fe3O4 in MANC can be estimated from the value of Ms considering the saturation magnetization of Fe3O4 as reference saturation magnetization. So the content of Fe3O4 in MANC is 12.12 weight percent.
3.1.3. Morphology and Microstructure
The SEM image of MANC was shown in Figure 3(a). The particles are nearly uniformly spherical and the particle size can be measured in the range of 25 - 29 nm. In addition the energy dispersive X-ray spectroscopy (EDX) is shown in Figure 3(c), (EDX) shows the atomic percent of Al and Fe are 29.89 and 36.39 respectively. The EDX spectra reveal that the Fe3O4 phase is abundant on the surface of MANC deduced from the high atomic ratio of iron.
Transmission electron microscope (TEM) was used to investigate the nature of magnetic nanoparticles in the produced composite. The produced composite showed uniform spherical nanoparticles with diameter range between 7 and 18 nm, the magnetite nanoparticles are finally divided and well distributed within the composite as shown in Figure 3(b). It was not possible to distinguish between the iron oxide and aluminium oxide phase’s structure.
3.1.4. Textural Analysis
The surface area and the pore structure of MANC sample were determined from nitrogen isotherm analysis, as shown in Figure 4. MANC displayed a type-IV iso-
 (a)
(a) (b)
(b) (c)
(c)
Figure 3. Morphology and microstructure of MANC. (a) SEM image; (b) TEM image and (c) EDX spectra.
therm, characteristic for mesoporous materials. Using these data, the specific surface area SBET was calculated to be 298 m2∙g−1, the pore size 25 Å, and the total pore volume 0.29 mL∙g−1.
3.2. The Effects of Experimental Parameters
3.2.1. Effect of pH
Metal-ion adsorption is known to be dependent on the pH of solution. The effect of pH on the adsorption of Cd2+ by MANC was studied by varying the initial pH of the solution over the range of 2 - 9. The calculation from the solubility product equilibrium constant (Ksp) demonstrated that the best pH range of 2 - 9 for Cd2+ for adsorption [28]. Figure 5 illustrated that removal efficiency increased with increase pH. The uptake of Cd2+ by MANC increased as the pH increased from 2 to 9. Although a maximum uptake was noted at a pH of 9, as the pH of the solution increased to >7, Cd2+ started to precipitate out from the solution. Therefore, experiments were not conducted over pH 7 to avoid precipitation [29]. The increased capacity of adsorption at pH > 7 may be a combination of both adsorption and precipitation on the surface of the adsorbent. It is considered that MANC had a maximum adsorption capacity at a pH = 6, if the precipitated amount is not considered in the calculation. Therefore, the optimum pH for Cd2+ was determined to be 6 and used in all experiments. The same trend has also been reported in the removal of Cd2+ ions by other adsorbent materials such as Bamboo charcoal [30] and crosslinked carboxymethyl konjac glucomannan [31].

Figure 4. Nitrogen isotherm analysis of MANC.

Figure 5. Effect of different pH on the removal of Cd2+ onto MANC (Initial Cd2+ ions concentration = 250 mg∙L−1, adsorbent dose = 1 g/l, solution temp. = 22◦C ± 2◦C, contact time = 60 min and agitation speed = 250 rpm.
The metal ions in the aqueous solution may undergo salvation and hydrolysis. The process involved for metal adsorption is as follows [32]:
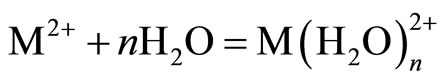 , (3)
, (3)
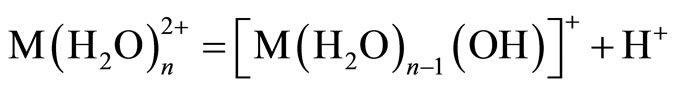 , (4)
, (4)
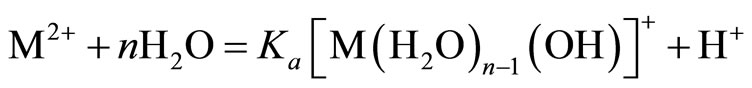 . (5)
. (5)
The pKa value for Cd2+ is 10.1. Perusal of the literature on metal speciation shows that the dominant species is M(OH)2 at pH > 6.0 and M2+ and M(OH)+ at pH < 6.0. Maximum removal of metal was observed at pH 6 for adsorption. On further increase of pH adsorption decreases probably due to the formation of hydroxide of cadmium because of chemical precipitation [33-35].
3.2.2. Effect of Adsorbent Dosage
Adsorbent dosage is an important parameter because it determines the capacity of an adsorbent for a given initial concentration of the adsorbate. The effect of adsorbent dosage was studied on Cd2+ ions removal from aqueous solutions by varying the amount of MANC from 0.25 to 3.0 g∙L−1, while keeping other parameters (pH, agitation speed, temperature, initial Cd2+ ion concentration and contact time) constant. Figure 6 showed that the percent removal of Cd2+ ion increased from 96.06% to 99.99% for MANC as the adsorption dosage was increased from 0.25 to 3 g∙L−1. On the other hand, the amount adsorbed per unit mass of the adsorbent decreased considerably. The decrease in unit adsorption with increase in the dosage of adsorbent was due to adsorption sites remaining unsaturated during the adsorption process [36]. For the rest of the study 1 g∙L−1 adsorbent dosage is considered as optimum dosage for cadmium removal using MANC.
3.2.3. Effect of Contact Time and Initial Cd2+ Ions Concentration
Figure 7 shows the effect of contact time on the
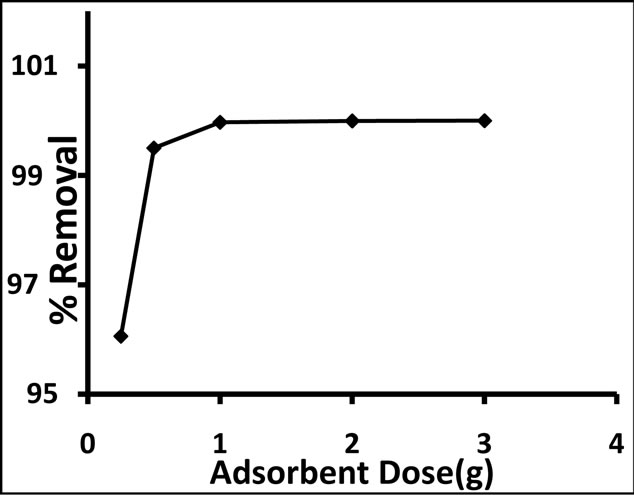
Figure 6. Effect of adsorbent dose on the removal of Cd2+ onto MANC (Initial Cd2+ ions concentration = 250 mg∙L−1, pH = 6, solution temp. = 22◦C ± 2◦C, contact time = 60 min and agitation speed = 250 rpm).
adsorbed amount of Cd2+ by MANC from solutions with different initial concentrations of Cd2+ (100 - 1000 mg/ L) at 22◦C. The adsorption increased sharply with contact time in the first 40 min and attained equilibrium within 240 min. It is also clear from Figure 7(a) that by increasing the initial Cd2+ ions concentration the percentage of Cd2+ removal decreased, although the actual amount of Cd2+ adsorbed per unit mass of MANC increased as shown in Figure 7(b). At low initial solution concentration, the surface area and the availability of adsorption sites were relatively high, and the Cd2+ ions were easily adsorbed. At higher initial solution concentration, the total available adsorption sites are limited, thus resulting in a decrease in percentage removal of Cd2+ ions. The increased in the equilibrium adsorption amount of Cd2+ at higher initial concentration can beattributed to enhance the driving force. The equilibrium adsorption amount of Cd2+ was found to increase from 100 to 501 mg∙g−1 as the initial concentration increased from 100 to 1000 mg∙L−1.
The same trend has also been reported in the removal of Cd2+ ions by Bamboo charcoal [30]. The higher adsorption capacity and rate of Cd2+ on MANC indicated its suitability to treat wastewater polluted with Cd2+.
 (a)
(a) (b)
(b)
Figure 7. Effect of contact time and initial Cd2+ ions concentration on: (a) the removal of Cd2+ and (b) adsorption capacity onto MANC (adsorbent dose = 1 g/L, pH = 6, solution temp. = 22◦C ± 2◦C, contact time = 60 min and agitation speed = 250 rpm).
3.2.4. Effect of Temperature
Temperature plays key roles on the adsorption process [37]. First, increasing the temperature decreases the viscosity of the solution which, in turn, enhances the rate of diffusion of the adsorbate molecules across the external boundary layer of the adsorbent and resulted in higher adsorption. Second, changing the temperature may affect the equilibrium adsorption capacity of the adsorbent. For instance, the adsorption capacity will decrease upon increasing the temperature for an exothermic reaction; while it will increase for an endothermic one. Hence, a study of the temperature-dependent adsorption processes provides valuable information about the standard Gibbs free energy, enthalpy and entropy changes accompanying adsorption. In this study, a series of experiments were conducted at 22◦C, 35◦C, 45◦C and 55◦C to investigate the effect of temperature on Cd2+ adsorption and determine thermodynamic parameters. Figure 8 shows the amount of Cd2+ adsorbed onto MANC nano adsorbents at different temperatures. As seen in the figure, the amount of Cd2+ adsorbed increases as the temperature increased. This increase suggests that the adsorption process is an endothermic one. The increase in the Cd2+ adsorption with temperature may be due to the increase in ions mobility, which in turn increases the number of ions that interacted with active sites at the adsorbent surfaces. Similar trends are also observed by other researchers for aqueous phase adsorption [38,39].
3.2.5. Effect of Loading of Alumina by Iron Oxide
The adsorption tests showed that the magnetic alumina nano-composite possesses the same adsorption capacity as pure activated alumina, suggesting that the presence of Fe oxide in the composite is not inhibiting the adsorption of metals. Figure 9" target="_self"> Figure 9 compares the adsorption capacity of magnetic alumina nanocomposite and activated alumina. From this figure, the composites showed high adsorption capacities for the Cd2+ in aqueous solution and, more

Figure 8. Effect of temperature on adsorption capacity onto MANC (Initial Cd2+ ions concentration 500 mg∙L−1 adsorbent dose = 1g/L, pH = 6, agitation speed = 250 rpm and contact time = 60 min, 240 min).
important, no reduction of the adsorption was produced by the formation of the composite.
3.3. Adsorption Isotherms
Adsorption isotherms describe qualitative information on the nature of the solute-surface interaction as well as the specific relation between the concentration of adsorbate and its degree of accumulation onto adsorbent surface at constant temperature. Adsorption isotherms are critical in optimizing the use of adsorbents, and the analysis of the isotherm data by fitting them to different isotherm models is an important step to find the suitable model that can be used for design purposes [40]. There are several isotherm equations available for analyzing experimental sorption equilibrium data, the most famous adsorption models for single-solute systems are the Langmuir and Freundlich models. The experimental data obtained in the present work was tested with the Langmuir, Freundlich and Temkin, isotherm models. Linear regression is frequently used to determine the best-fitting isotherm, and the applicability of isotherm equations is compared by judging the correlation coefficients.
3.3.1. Langmuir Isotherm
The theoretical Langmuir sorption isotherm [41] is valid for adsorption of a solute from a liquid solution as monolayer adsorption on a surface containing a finite number of identical sites. The model is based on several basic assumptions: 1) the sorption takes place at specific homogenous sites within the adsorbent; 2) once a Cd2+ occupies a site; 3) the adsorbent has a finite capacity for the adsorbate (at equilibrium); 4) all sites are identical and energetically equivalent. Langmuir isotherm model assumes uniform energies of adsorption onto the surface without transmigration of adsorbate in the plane of the surface. Therefore, the Langmuir isotherm model was chosen for estimation of the maximum adsorption capacity corresponding to complete mono-layer coverage on the sorbent surface. The Langmuir isotherm model is
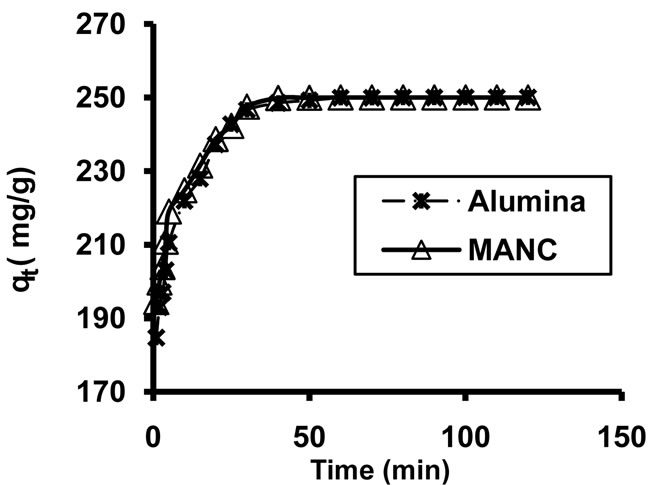
Figure 9. Effect of iron oxide loading on the adsorption of Cd2+ (Initial Cd2+ ions concentration = 250 mg∙L−1 adsorbent dose = 1 g/L, pH = 6, solution temp. = 22◦C ± 2◦C, contact time = 60 min and agitation speed = 250 rpm).
represented in the linear form as follows [41]
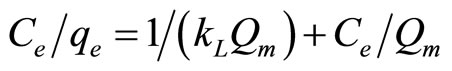 (6)
(6)
where KL is the Langmuir adsorption constant (L∙mg−1) and Qm is the theoretical maximum adsorption capacity (mg∙g−1). Figure 10 shows the Langmuir (Ce/qe vs. Ce) plot for adsorption of Cd2+ ions. The value of Qm and KL constants and the correlation coefficient for Langmuir isotherm are presented in Table 1" target="_self"> Table 1. The correlation coefficient was high (R2 = 0.976) as shown in Table 1. This result indicates that the experimental data fitted well to Langmuir sorption isotherm with maximum adsorption capacity 625 mg/g.
The essential characteristics of Langmuir dimensionless constant separation factor or equilibrium parameter, RL, which is defined by the following Equation [42]:
 (7)
(7)
where Co is the initial Cd2+ ions concentration, mg/L. The RL parameter is considered as more reliable indicator of the adsorption. There are four probabilities for the RL value: 1) for favorable adsorption 0 < RL < 1, 2) for unfavorable adsorption RL > 1, 3) for linear adsorption RL = 1 and 4) for irreversible adsorption RL =0. In the present study, the values of RL (Table 2) are observed to be in the range 0 - 1, indicating that the adsorption process is favorable for MANC.
3.3.2. The Freundlich Isotherm
The Freundlich isotherm model is the earliest known relationship describing the sorption process [43]. The model applies to adsorption on heterogeneous surfaces with interaction between adsorbed molecules and the application of the Freundlich equation also suggests that sorption energy exponentially decreases on completion of the sorption centers of an adsorbent. This isotherm is an empirical equation which can be employed to describe heterogeneous systems and is expressed in the linear form as follows

Figure 10. Langmuir isotherm plot for adsorption of Cd2+ onto MANC.

Table 1. Langmuir, Freundlich and Tempkin isotherm parameters and correlation coefficients for the adsorption of Cd2+ from aqueous solutions onto magnetic alumina nano-composite.
 (8)
(8)
where KF is the Freundlich constant (L∙g−1) related to the bonding energy. KF can be defined as the adsorption or distribution coefficient and represents the quantity of Cd2+ adsorbed onto adsorbent for unit equilibrium concentration. 1/n is the heterogeneity factor and n is a measure of the deviation from linearity of adsorption. Its value indicates the degree of non-linearity between solution concentration and adsorption as follows: if the value of n is equal to unity, the adsorption is linear; if the value is lower than unity, this implies that adsorption process is chemical; if the value is higher unity adsorption is a favorable physical process [44].
Figure 11 shows the plot of log(qe) versus log(Ce) to generate the intercept value of KF and the slope of 1/n (Table 1). The value of n is higher than unity, indicating that adsorption of Cd2+ onto MANC is a favorable physical process [44]. The correlation coefficients, R2 = 0.921. This result indicates that the experimental data did not fit well to Freundlich model.
3.3.3. The Temkin Isotherm
Temkin isotherm model contains a factor that explicitly takes into account adsorbing species-adsorbate interactions [45]. This model assumes the following: 1) the heat of adsorption of all the molecules in the layer decreases linearly with coverage due to adsorbate-adsorbent interactions, and 2) adsorption is characterized by a uniform distribution of binding energies, up to some maximum binding energy. The derivation of the Temkin isotherm assumes that the fall in the heat of sorption is linear rather than logarithmic, as implied in the Freundlich equation. The Temkin isotherm has commonly been applied in the following form (Equation (9))
 (9)
(9)
Equation (9) can be linearized as
 (10)
(10)
where BT = RT/bT, T is the absolute temperature in degree K, R the universal gas constant, 8.314 J∙mol−1∙K−1, KT is the equilibrium binding constant (Lmg−1), BT is related to the heat of adsorption and bT is Temkin constant (J∙mol−1). A plot of qe vs lnCe at studied temperature is given in Figure 12. The constants obtained for Temkin isotherm are illustrated in Table 1. Examination of the data shows that the Temkin isotherm is not applicable to

Table 2. RL values for different Cd2+ ions concentrations.
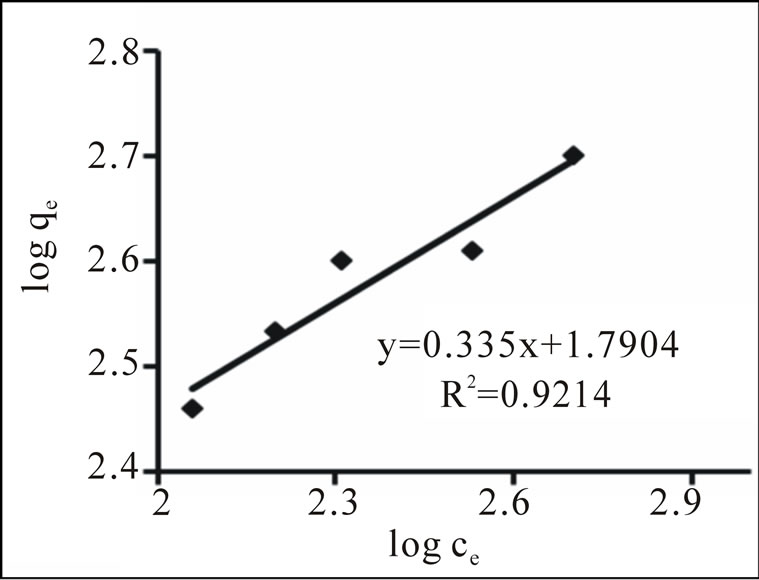
Figure 11. Freundlich isotherm plot for adsorption of Cd2+ onto MANC.
the Cd2+ adsorption onto MANC because of the small correlation coefficient.
Table 1 summarizes all the constants and correlation coefficients, R2 of the three isotherm models. The Langmuir model yielded the best fit with R2 which were higher than 0.97. Confirmation of the experimental data into the Langmuir isotherm equation indicated the homogeneous nature of magnetic alumina nano-composite surface, i.e., each Cd2+ ion/magnetic alumina nano composite (MANC) adsorption had equal adsorption activation energy. The results also demonstrated the formation of monolayer coverage of cadmium ions at the outer surface of MANC. The good correlation coefficients showed that Langmuir model is more suitable than Freundlich and Temkin for adsorption equilibrium of cadmium ions onto MANC. Values of the adsorption capacity of other adsorbents from the literature are given in Table 3 for comparison [46-50]. It is clear from this table that the adsorption capacity of MANC for Cd2+ is higher than the other adsorbents.
3.4. Adsorption Kinetics
Kinetic models can be helpful to understand the mechanisms of metal adsorption and evaluate performance of the adsorbents for metal removal. The kinetics of Cd2+ adsorption onto MANC is required for selecting optimum operating conditions for the full-scale batch process. The kinetic parameters, which are helpful for the prediction of adsorption rate, give important information for designing and modeling the adsorption processes. Thus, Lagergren pseudo-first-order [51], pseudo-second-order [52], Elovich [53-55] and intraparticle diffusion [56,57] kinetic models were used for the adsorption of Cd2+ onto MANC. The conformity between experimental data and the model-predicted values was expressed by the correlation coefficients (R2, values close or equal to 1, the relatively higher value is the more applicable model).
3.4.1. The Pseudo First-Order Equation
The Lagergren pseudo-first-order model [51] is the earliest known equation describing the adsorption rate based on the adsorption capacity, which can be expressed in a linear form as
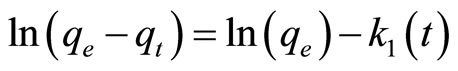 (11)
(11)
where qe and qt are the amount of cadmium ions adsorbed (mg∙g−1) on the MANC at the equilibrium and at time t, respectively, and k1 is the rate of constant adsorp-

Figure 12. Temkin isotherm plot for adsorption of Cd2+ on to MANC.
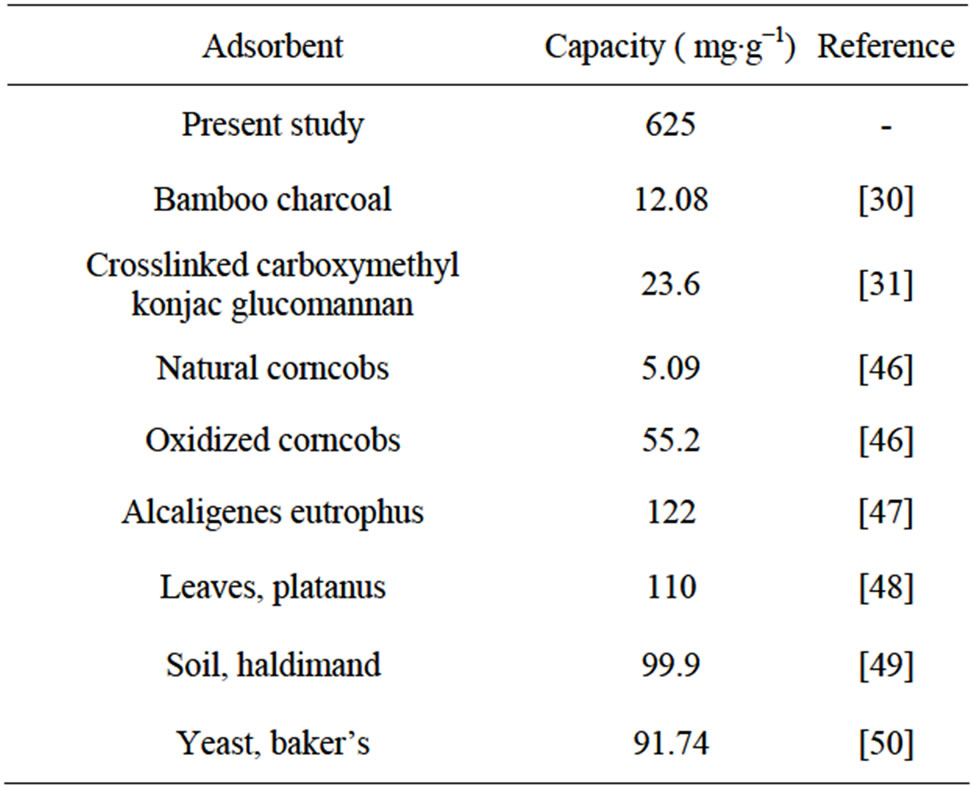
Table 3. Materials used as adsorbent for Cd2+ ions.
of ln(qe − qt) versus t for different concentrations of the tion (min−1). Values of k1 were calculated from the plots Cd2+ ion as shown in Figure 13. The values k1 and qe are given in Table 4.
The pseudo-first order equation was used to correlate the experimental data, based on the following mechanistic scheme:
 (12)
(12)
One cadmium ion was assumed to sorb onto one adsorption site of the MANC.
As noticed from Table 4 pseudo-first order kinetic predicts a lower value of the equilibrium adsorption capacity than the experimental value. Hence, this equation cannot provide an accurate fit of the experimental data.
3.4.2. The Pseudo Second-Order Equation
A linear form of pseudo second-order model is shown in Equation (13)
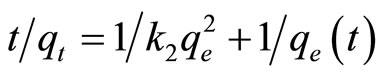 (13)
(13)
where k2 is the rate constant of pseudo second-order adsorption (g∙mg−1∙min−1). The constants can be obtained
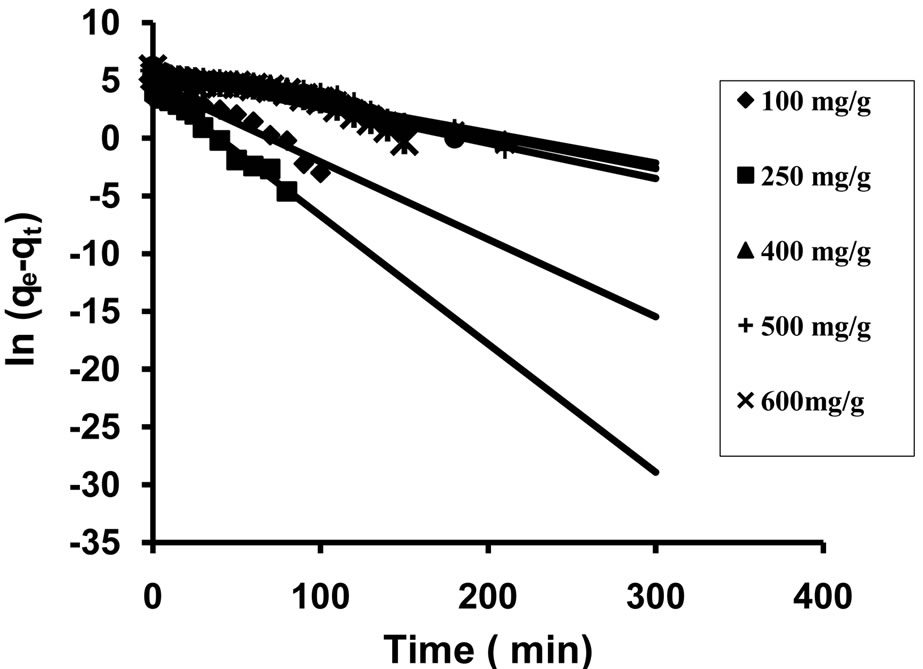
Figure 13. First-order plots of Cd2+ adsorption onto MANC.
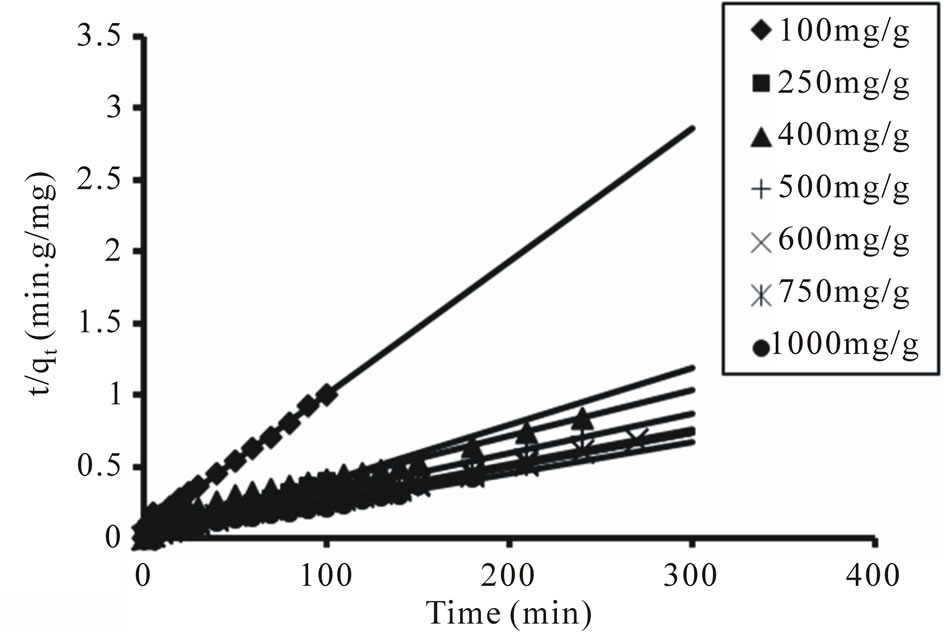
Figure 14. Second-order plots Cd2+ adsorption onto MANC.
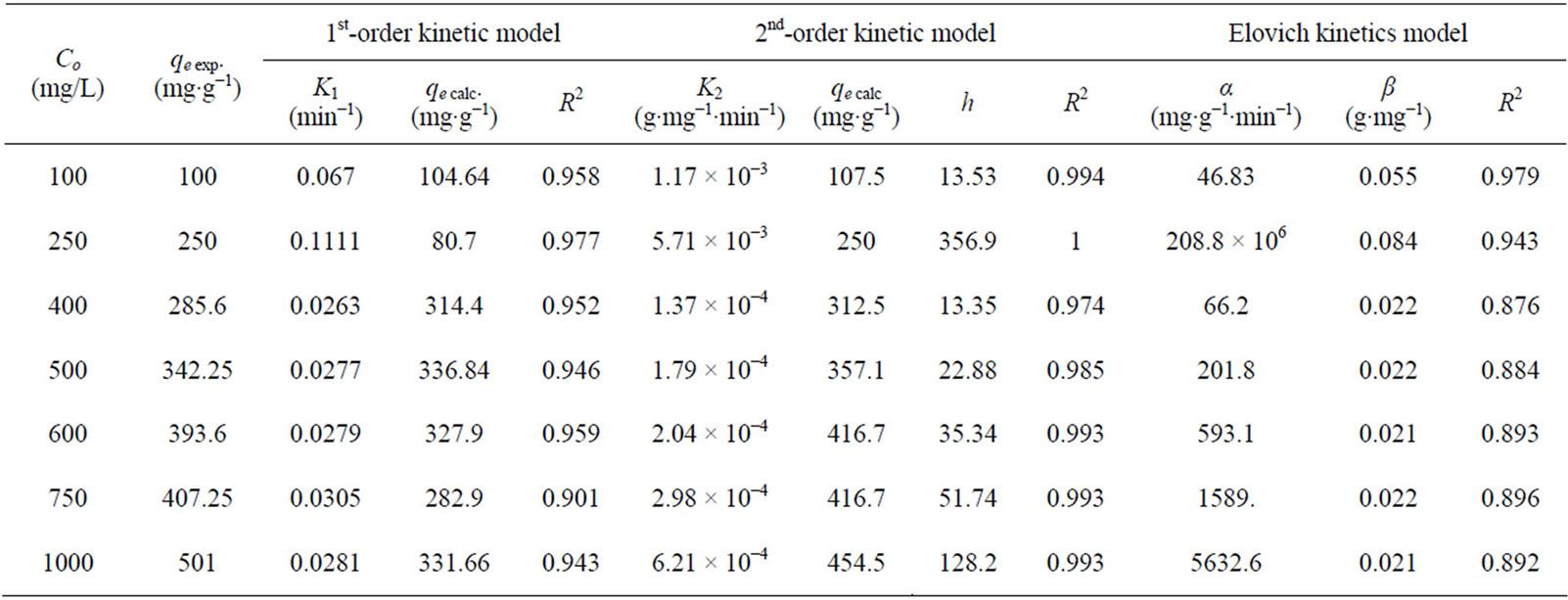
Table 4. The pseudo first-order, second-order and Elovich kinetic parameters for Cd2+ at different initial cadmium ions concentration by MANC.
from plotting (t/qt) versus t Figure 14. The values k2, qe and the initial adsorption rate h 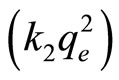 are given in Table 4.
are given in Table 4.
The pseudo-second order model assumes that cadmium is sorbed onto two active sites:
 (14)
(14)
The equilibrium adsorption capacities, qe, obtained with this model are slightly more reasonable than those of the pseudo-first order when comparing predicted results with experimental data. Moreover, the values of R2 also indicated that this equation produced better results (Table 4) at all concentrations and adsorbent doses, R2 values for pseudo-second-order kinetic model were found to be between 0.974 and 1. This indicates that the Cd2+ MANC adsorption system obeys the pseudo-second order kinetic model for the entire sorption period.
3.4.3. Elovich Kinetic Equation
The Elovich equation is of general application to chem. isorptions kinetics. The equation has been applied satisfactorily to some chemisorption processes and has been found to cover a wide range of slow adsorption rates. The same equation is often valid for systems in which the adsorbing surface is heterogeneous, and is formulated as:
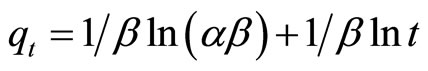 (15)
(15)
where α (mg/g∙min) is the initial adsorption rate and β is related to the extent of surface coverage and the activation energy involved in chemisorption (g/mg).
The Elovich equation assumes that the active sites of adsorbent are heterogeneous [58], and therefore exhibit different activation energies for chemisorption. Teng and Hsieh [59] proposed that constant α is related to the rate of chemisorptions and β is related to the surface coverage.
The Elovich equation is based on a general secondorder reaction mechanism for heterogeneous adsorption processes [58].
Plot of qt versus ln(t) should yield a linear relationship if the Elovich is applicable with a slope of (1/β) and an intercept of (1/βln(αβ) (Figure 15). The Elovich constants obtained from the slope and the intercept of the straight line reported in Table 4. The correlation coefficients R2 are very wavy and ranged from low value to high value without definite role (Table 4).
3.4.4. Intra-Particle Diffusion Model
The adsorption mechanism of adsorbate onto adsorbent follows three steps: film diffusion, pore diffusion and intra-particle transport. The slowest of three steps controls the overall rate of the process. Generally, intra-particle diffusion is often rate-limiting in a batch reactor, while for a continuous flow system film diffusion is more likely the rate-limiting step. In order to investigate the possibility of intra-particle diffusion resistance affecting the adsorption intra-particle diffusion model [56] was explored
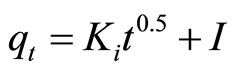 (16)
(16)
where Ki (mg∙g−1∙min−0.5) is the intra-particle diffusion rate constant. Figure 16 represents a plot of qt vs t0.5, it shows two separate regions the initial part is attributed to the bulk diffusion while the final part to the intra-particle diffusion. Values of I give an idea about the thickness of boundary layer (Table 5), i.e. the larger the intercept the greater is the boundary layer effect [60]. The data indicate that intra-particle diffusion controls the adsorption rate. Simultaneously, external mass transfer resistance cannot be neglected although this resistance is only significant for the initial period of time [61].

Figure 15. Elovich plots of Cd2+ adsorption onto MANC.
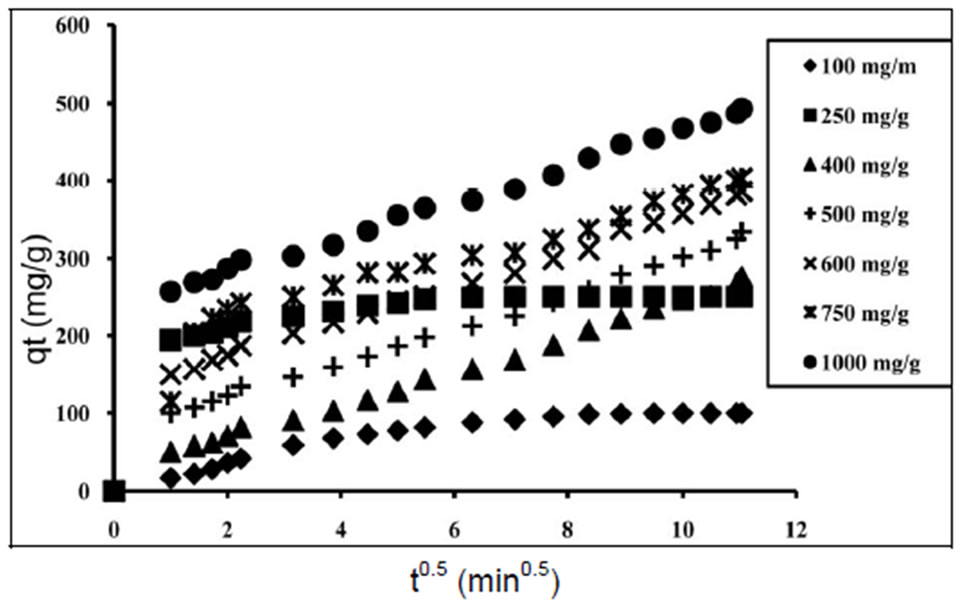
Figure 16. Intra-particle diffusion plots of Cd2+ adsorption onto MANC.

Table 5. The intra-particle diffusion parameters for Cd2+ at different initial cadmium ions concentration by MANC.
The data exhibit multi-linear plots, revealing that the process is governed by two or more steps (Figure 16). The first linear portion (phase I) at all concentrations, can be attributed to the immediate utilization of the most readily available sorbing sites on the sorbent surface. Phase II may be attributed to very slow diffusion of the Cd2+ from the MANC surface site into the inner pores. Thus, initial portion of Cd2+ ions sorption by MANC may be governed by the initial intra-particle transport of Cd2+ controlled by surface diffusion process and the later part controlled by pore diffusion. The values of ki1 and ki2 (diffusion rate constants for phases I and II, respectively) obtained from the slope of linear plots are listed in Table 5.
3.5. Thermodynamics Studies
Thermodynamic parameters were evaluated to confirm the adsorption nature of the present study.
The variation in temperature, influencing the distribution of adsorbate between solid and liquid phases, was examined in the range 295 - 328 ˚K. Moreover the increase in Cd2+ sorption with a rise in temperature can be explained on the basis of thermodynamic parameters such as change in enthalpy (ΔH°), entropy (ΔS°) and free energy (ΔG°). The change in enthalpy (ΔH°) and entropy (ΔS°) are calculated by using the van’t Hoff equation [62].
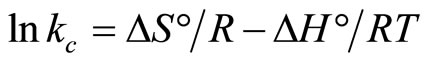 (17)
(17)
where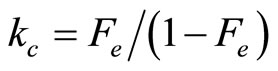 , and
, and ; is the fraction adsorbed at equilibrium, while T is the temperature in degree K and R is the gas constant [8.314 (J/mol K)].
; is the fraction adsorbed at equilibrium, while T is the temperature in degree K and R is the gas constant [8.314 (J/mol K)].
The plot of lnkc vs 1/T gives a straight line with acceptable coefficient (R2) as shown in Figure 17. From the slope and the intercept of van’t Hoff plots, the values of ΔH° and ΔS° were computed, while the Gibbs free enrgy change ΔG° was calculated using the following equation [63]:
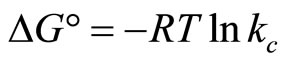 (18)
(18)
The thermodynamic parameters for the sorption of cadmium ions onto MANC at various temperatures were calculated and summarized in Table 6. The positive value of ΔH° indicates that the studied sorption processes are endothermic in nature. Furthermore the negative values of ΔG° demonstrate the spontaneous behavior of the sorption processes [63]. The decrease in the value of ΔG° with the increase of temperature shows that the reaction

Figure 17. Effect of temperature on Cd2+ kinetic sorption for MANC (Initial Cd2+ ions concentration = 500 mg∙L−1 adsorbent dose = 1 g/l, pH = 6, agitation speed = 250 rpm and contact time = 60 min, 240 min.

Table 6. Thermodynamic parameters and activation energy for Cd2+ sorption onto MANC.
is more spontaneous at higher temperature which indicates that the sorption processes are favored by the increase in temperature [64]. It is noteworthy that adsorption process with ΔGo values between −20 and 0 kJ/mol corresponds to spontaneous physical process, while that with values between −80 and −400 kJ/mol corresponds to chemisorptions [65,66]. From the ΔGo values obtained in this study, it can be deduced that the adsorption mechanism is dominated by physisorption. This also is supported by the fact that ΔHo < 40 kJ mol, indicating physical adsorption process [65].
Finally, the positive value of ΔS° suggest that the increased randomness at the solid-solution interface during the sorption process. The adsorbed solvent molecules which are displaced by the adsorbate species gain more translational entropy than ions lost by adsorbate, thus allowing for prevalence of randomness in the system [67]. Normally, adsorption of gases leads to a decrease in entropy due to orderly arrangement of the gas molecules on a solid surface. However, the same may not be true for the complicated system of sorption from solution [68].
Energy of activation was calculated and illustrated in Table 6 according to a relationship between Ea and ΔH° for reactions in solution by the following equation [69]:
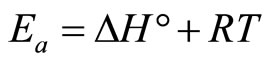 (19)
(19)
Energies of activation below 42 kJ∙mol−1 generally indicate diffusion-controlled processes and higher values represent chemical reaction processes [54]. In terms of Ea, diffusion or transport controlled reactions are those governed by mass transfer or diffusion of the adsorbate from the bulk solution to the adsorbent surface and can be described using the parabolic rate law [70]. Conversely, the reaction is surface controlled if the reaction between the adsorbate and adsorbent is slow compared with the transport or diffusion of the adsorbate to the adsorbent. For surface controlled reactions, the concentration of the adsorbate next to the adsorbent surface is equal to the concentration of the adsorbate in the bulk solution and the kinetic relationship between time and adsorbate concentration should be linear [71]. In our study, the small value of the activation energy below 42 kJ∙mol−1 confirms the fact that the process of the removal Cd2+ using MANC is diffusion controlled.
3.6. Single-Stage Batch Adsorber
Adsorption isotherm studies can also be used to predict the design of single stage batch adsorption systems [72- 74]. The schematic diagram for a single-stage adsorption process is shown in Figure 18. The solution to be treated contains V (L) of water and an initial Cd2+ concentration Co (400 mg/L) which is to be reduced to Ce in the adsorption process. In the treatment stage, the amount of adsorbent W (g) added is added to solution and the Cd2+ ions concentration on the solid changes from q0 = 0 to qe. The mass balance for the dye in the single stage is given by
 (20)
(20)
The Langmuir isotherm data may now be applied to Equation (19) since the Langmuir isotherm gave the best fit to experimental data.
 (21)
(21)
Figure 19 shows a series of plots derived from Equation (20) for the adsorption of Cd2+ ions on the adsorbent and depicts the amount of effluent which can be treated to reduce the cadmium ions content by 90%, 80%, 70%, 60% and 50% using various masses of the adsorbent.
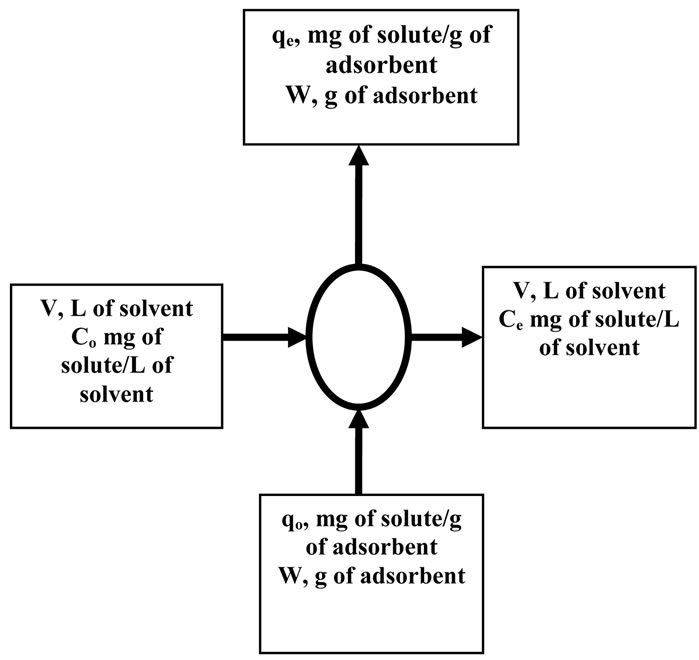
Figure 18. A single-stage batch adsorber.
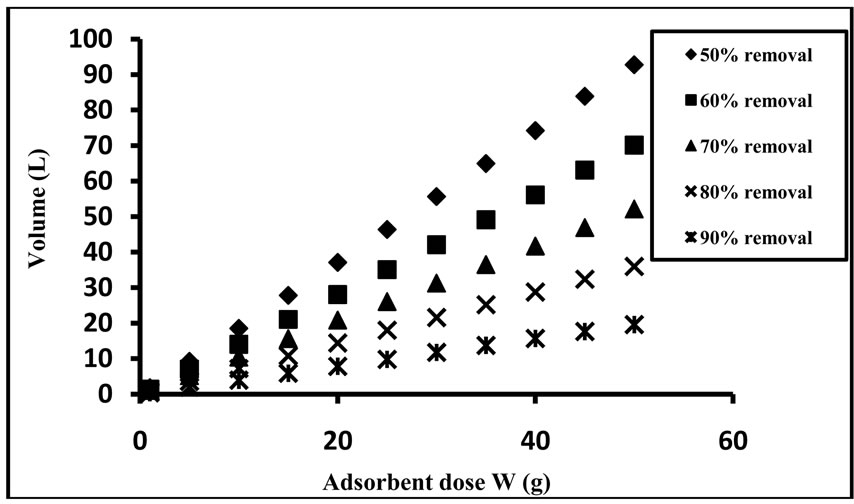
Figure 19. Volume of effluent treated against adsorbent dose for different percentages of Cd2+ removal.
4. Conclusions
The prepared Magnetic composite MANC was found to be in nano-scale with high surface area 298 m2∙g−1 and its magnetic behavior was paramagnetic, which makes its removal from treatment media by applying magnetic field possible. These properties made this composite an excellent candidate for removal of cadmium ions from water. Removal of cadmium ions on Magnetic alumina nano composite (MANC) is pH dependent and the maximum removal was attained at pH 6. The equilibrium adsorption is practically achieved through a time of 240 min. It was also a function of initial adsorbent dose and cadmium ions concentration, Also adsorption equilibrium data follows; Langmuir sorption isotherm with maximum adsorption capacity 625 mg∙g−1. The data indicate that the adsorption kinetics follow the pseudosecond-order model with intraparticle diffusion as one of the rate determining steps. The adsorption process was spontaneous and increased with increase in temperature showing endothermic nature of the adsorption.
REFERENCES
- L.-G. Yan, X.-Q. Shan, B. Wen and G. Owensb, “Adsorption of Cadmium onto Al13-Pillared Acid-Activated Montmorillonite,” Journal of Hazardous Materials, Vol. No. 1-3, 156, 2008, pp. 499-508. doi:10.1016/j.jhazmat.2007.12.045
- J. Wase and C. Forster, “Biosorbents for Metal Ions,” Taylor & Francis Inc., Bristol, 1997.
- E. W. Shin, K. G. Karthikeyan and M. A. Tshabalala, Adsorption Mechanism of Cadmium on Juniper Bark and Wood,” Bioresource Technology, Vol. 98, No. 3, 2007, pp. 588-594. doi:10.1016/j.biortech.2006.02.024
- ATSDR, “Toxicological Profile for Cadmium,” Agency for Toxic Substances and Disease Registry, Department of Health and Human Services, USA, 1999.
- V. K. Gupta, M. Gupta and S. Sharma, “Process Development for the Removal of Lead and Chromium from Aqueous Solutions Using Red Mud—An Aluminium Industry Waste,” Water Research, Vol. 35, No. 5, 2001, pp. 1125-1134. doi:10.1016/S0043-1354(00)00389-4
- S. J. T. Pollard, G. D. Fowler, C. J. Sollars and R. Perry, “Low-Cost Adsorbents for Waste and Wastewater Treatment,” Science of the Total Environment, Vol. 116, No. 1-2, 1992, pp. 31-52. doi:10.1016/0048-9697(92)90363-W
- E. Erdem, N. Karapinar and R Donat, “The Removal of Heavy Metal Cations by Natural Zeolites,” Journal of Colloid and Interface Science, Vol. 280, No. 2, 2004, pp. 309-314. doi:10.1016/j.jcis.2004.08.028
- O. Abollino, M. Aceto, M. Malandrino, C. Sarzanini and E. Mentatsi, “Adsorption of Heavy Metals on Na-Montmorillonite. Effect of pH and Organic Substances,” Water Research, Vol. 37, No. 7, 2003, pp. 1619-1627. doi:10.1016/S0043-1354(02)00524-9
- K. A. Matis, A. I. Zouboulis, G. P. Gallios, T. Erwe and C. Blocher, “Application of Flotation for the Separation of Metal-Loaded Zeolites,” Chemosphere, Vol. 55, No. 1, 2004, pp. 65-72. doi:10.1016/j.chemosphere.2003.11.030
- L. C. A. Oliveira, R. V. R. A. Rios, J. D. Fabris, K. Sapag, V. K. Garg and R. M. Lago, “Clay-Iron Oxide Magnetic Composites for the Adsorption of Contaminants in Water,” Applied Clay Science, Vol. 22, No. 4, 2003, pp. 169-177. doi:10.1016/S0169-1317(02)00156-4
- D. Zamboulis, S. I. Pataroudi, A. I. Zouboulis and K. A. Matis, “The Application of Sorptive Flotation for the Removal of Metal Ions,” Desalination, Vol. 162. No. 3, 2004, pp. 159-168. doi:10.1016/S0011-9164(04)00039-6
- F. Pagnanelli, F. Veglio and L. Toro, “Modelling of the Acid-Base Properties of Natural and Synthetic Adsorbent Materials Used for Heavy Metal Removal from Aqueous Solutions,” Chemospere, Vol. 54, No. 7, 2004, pp. 905-915. doi:10.1016/j.chemosphere.2003.09.003
- Y. Xu and L. Axe, “Synthesis and Characterization of Iron Oxide-Coated Silica and Its Effect on Metal Adsorption,” Journal of Colloid and Interface Science, Vol. 282, No. 1, 2005, pp. 11-19. doi:10.1016/j.jcis.2004.08.057
- S. E. Bailey, T. J. Olin, R. M. Bricka and D. D. Adrian, “A Review of Potentially Low-Cost Sorbents for Heavy Metals,” Water Research, Vol. 33, No. 11, 1999, pp. 2469-2479. doi:10.1016/S0043-1354(98)00475-8
- R. Ciccu, M. Ghiani, A. Serci, S. Fadda, R. Peretti and A. Zucca, “Heavy Metal Immobilization in the Mining-Contaminated Soils Using Various Industrial Wastes,” Minerals Engineering, Vol. 16, No. 3 , 2003, pp. 187-192. doi:10.1016/S0892-6875(03)00003-7
- S. V. Dimitrova and D. R. Mehandriev, “Lead Removal from Aqueous Solutions by Granulated Blast-Furnace Slag,” Water Research, Vol. 32, No. 11, 1998, pp. 3289-3292. doi:10.1016/S0043-1354(98)00119-5
- K. C. Sekhar, C. T. Kamala, N. S. Chary, A. R. K. Sastry, T. Nageswara Rao and M. Vairamani, “Removal of Lead from Aqueous Solutions Using an Immobilized Biomaterial Derived from a Plant Biomass,” Journal of Hazardous Materials, Vol. 108, No. 1-2, 2004, pp. 111-117.
- N. Chubar, J. R. Carvalho and M. J. N. Correia, “Cork Biomass as Biosorbent for Cu(II), Zn(II) and Ni(II),” Colloids Surfaces A: Physicochemical and Engineering Aspects, Vol. 230, No. 1, 2003, pp. 57-65. doi:10.1016/j.colsurfa.2003.09.014
- K. T. Park, V. K. Gupta, D. Mohan and S. Sharma, “Removal of Chromium(VI) from Electroplating Industry Wastewater Using Bagasse Fly Ash—A Sugar Industry Waste Material,” The Environmentalist, Vol. 19, No. 2, 1999, pp. 129-136.
- M. A. Karakassides, D. Gournis, A. B. Bourlinos, P. N. Trikalitisb and T. Bakasc, “Magnetic Fe2O3-Al2O3 Composites Prepared by a Modified Wet Impregnation Method,” Journal of Materials Chemistry, Vol. 13, No. 4, 2003, pp. 871-876. doi:10.1039/b211330a
- C.-F. Changa, P.-H. Lin and W. Holl, “Aluminum-Type Superparamagnetic Adsorbents: Synthesis and Application on Fluoride Removal,” Colloids Surfaces A: Physicochemical and Engineering Aspects, Vol. 280, No. 3, 2006, pp. 194-202. doi:10.1016/j.colsurfa.2006.02.011
- L. M. Sheppard, “Ceramic Transactions,” In: K. Ishizaki, L. M. Sheppard, S. Okada, T. Hamasaki and B. Huybrechts, Eds., Porous Materials, American Ceramic Society, Westerville, 1993, p. 3.
- I. Nettleship, “Applications of Porous Ceramics,” Key Engineering Materials, Vol. 122-124, No. 1, 1996, pp. 305-324. doi:10.4028/www.scientific.net/KEM.122-124.305
- G. R. Doughty and D. Hind, “The Applications of IonConducting Ceramics,” Key Engineering Materials, Vol. 122-124, No. 1, 1996, pp. 145-162. doi:10.4028/www.scientific.net/KEM.122-124.145
- M. Schmidt and F. Schwertfeger, “Applications for Silica Aerogel Products,” Journal of Non-Crystalline, Vol. 225, No. 1, 1998, pp. 364-368. doi:10.1016/S0022-3093(98)00054-4
- L. Ji, J. Lin, K. Ltan and C. Zeng, “Synthesis of High- Surface-Area Alumina Using Aluminum Tri-sec-butoxide-2,4-pentanedione-2-propanol-nitric Acid Precursors,” Journal of Material Chemistry, Vol. 12, No. 19, 2000, pp. 931-939.
- A. M. Ibrahim, M. M. Abd El-Latif and M. M. Mahmoud, “Synthesis and Characterization of Nanosize Cobalt Ferrite Prepared by Convenient Heating Polyol Method and Microwave Heating Technique,” Journal of Alloys and Compounds, Vol. 506, No. 1 , 2010, pp. 201-204. doi:10.1016/j.jallcom.2010.06.177
- C. N. Sawyer, P. L. McCarty and G. F. Parkin, “Chemistry of Environmental Engineering,” 5th Edition, McGrawHill, New York, 2002.
- A. Denizli, G. Ozkan and M. Yakup Arica, “Preparation and Characterization of Magnetic Polymethylmethacrylate Microbeads Carrying Ethylene Diamine for Removal of Cu(II), Cd(II), Pb(II), and Hg(II) from Aqueous Solutions,” Journal of Applied Polymer Science, Vol. 78, No. 3, 2000, pp. 81-89. doi:10.1002/1097-4628(20001003)78:1<81::AID-APP110>3.0.CO;2-J
- F. Y. Wang, H. Wang and J. W. Ma, “Adsorption of Cadmium(II) Ions from Aqueous Solution by a New LowCost Adsorbent-Bamboo Charcoal,” Journal of Hazardous Materials, Vol. 177, No. 1-3, 2010, pp. 300-306. doi:10.1016/j.jhazmat.2009.12.032
- C. Niu, W. Wu, Z. Wang, S. Li and J. Wang, “Adsorption of Heavy Metal Ions from Aqueous Solution by Crosslinked Carboxymethyl Konjac Glucomannan,” Journal of Hazardous Materials, Vol. 141, No. 1, 2007, pp. 209-214. doi:10.1016/j.jhazmat.2006.06.114
- A. Akil, M. Mouflith and S. Sebti, “Removal of Heavy Metal Ions from Water by Using Calcined Phosphate as a New Adsorbent,” Journal of Hazardous Materials, Vol. 112, No. 2, 2004, pp. 183-190. doi:10.1016/j.jhazmat.2004.05.018
- G. Wulfsberg, “Principles of Descriptive Chemistry,” Brookes/Cole Publishing, Montery, 1987.
- N. Khalid, S. A. Chaudhri, M. M. Saeed and J. Ahmed, “Separation and Preconcentration of Lead and Cadmium with 4-(4-Chlorophenyl)-2-phenyl-5-thiazoleacetic Acid and Its Application in Soil and Seawater,” Separation Science and Technology, Vol. 31, No. 2, 1996, pp. 229-239. doi:10.1080/01496399608000692
- S. Schiewer and B. Volesky, “Modeling of the ProtonMetal Ion Exchange in Biosorption,” Environmental Science and Technology, Vol. 29, No. 12, 1995, pp. 3049-3058. doi:10.1021/es00012a024
- A. Shukla, Y. H. Zhang, P. Dubey, J. L. Margrave and S. S. Shukla, “The Role of Sawdust in the Removal of Unwanted Materials from Water,” Journal of Hazardous Materials, Vol. 95, No. 1-2, 2002, pp. 137-152. doi:10.1016/S0304-3894(02)00089-4
- N. N. Nassar, “Rapid Removal and Recovery of Pb(II) from Wastewater by Magnetic Nanoadsorbents,” Journal of Hazardous Materials, Vol. 184, No. 1-3, 2010, pp. 538-546. doi:10.1016/j.jhazmat.2010.08.069
- Y. H. Huang, C. L. Hsueh, C. P. Huang, L. C. Su and C. Y. Chen, “Adsorption Thermodynamic and Kinetic Studies of Pb(II) Removal from Water onto a Versatile Al2O3- Supported Iron Oxide,” Separation and Purification Technology, Vol. 55, No. 1, 2007, pp. 23-29. doi:10.1016/j.seppur.2006.10.023
- A. K. Bhattacharya, T. K. Naiya, S. N. Mandal and S. K. Das, “Adsorption, Kinetics and Equilibrium Studies on Removal of Cr(VI) from Aqueous Solutions Using Different Low-Cost Adsorbents,” Chemical Engineering Journal, Vol. 137, No. 3, 2008, pp. 529-554.
- I. A. W. Tan, A. L. Ahmad and B. H. Hameed, “Adsorption of Basic Dye on High-Surface-Area Activated Carbon Prepared from Coconut Husk: Equilibrium, Kinetic and Thermodynamic Studies,” Journal of Hazardous Materials, Vol. 154, No. 1-3 , 2008, pp. 337-346. doi:10.1016/j.jhazmat.2007.10.031
- I. Langmuir, “The Constitution and Fundamental Properties of Solids and Liquids,” Journal of American Chemical Society, Vol. 38, No. 11, 1916, pp. 2221-2295. doi:10.1021/ja02268a002
- M. M. Abd El-Latif and A. M. Ibrahim, “Removal of Reactive Dye from Aqueous Solutions by Adsorption onto Activated Carbons Prepared from Oak Sawdust,” Desalination and Water Treatment, Vol. 20, No. 1-3, 2010, pp. 102-113.
- H. M. F. Freundlich, “Ueber Die Adsorption in Loesungen,” Zeitschrift für Physikalische Chemie (Leipzig), Vol. 57, No. A, 1907, pp. 385-470.
- M. M. Abd El-Latif and M. F. Elkady, “Equilibrium Isotherms for Harmful Ions Sorption Using Nano Zirconium Vanadate Ion Exchanger,” Desalination, Vol. 255, No.1-3, 2010, pp. 21-43. doi:10.1016/j.desal.2010.01.020
- M. J. Temkin and V. Pyzhev, “Kinetics of the Synthesis of Ammonia on Promoted Iron Catalysts,” Acta Physiochimica (URSSR), Vol. 12, 1940, pp. 327-356.
- R. Leyva-Ramos, L. A. Bernal-Jacome and I. Acosta-Rodriguez, “Adsorption of Cadmium(II) from Aqueous Solution on Natural and Oxidized Corncob,” Separation and purification Technology, Vol. 45, No. 1, 2005, pp. 41-49. doi:10.1016/j.seppur.2005.02.005
- A. H. Mahvi and L. Diels, “Biological Removal of Cadmium by Alcaligenes Eutrophus CH34,” International journal of Environmental Science andTechnology, Vol. 1, No. 3, 2004, pp. 199-204.
- A. H. Mahvi, J. Nouri, G. A. Omrani and F. Gholami, “Application of Platanus Orientalis Leaves in Removal of Cadmium from Aqueous Solution,” World Applied Sciences Journal, Vol. 2, No. 1, 2007, pp. 40-44.
- K. A. Bolton and L. J. Evans, “Cadmium Adsorption Capacity of Selected Ontario Soils,” Canadian Journal of Soil Science, Vol. 5, No. 3, 1996, pp. 183-189. doi:10.4141/cjss96-025
- P. Hanzlik, J. Jehlicka, Z. Weishauptova and O. Sebek, “Adsorption of Copper, Cadmium and Silver from Aqueous Solutions onto Natural Carbonaceous Materials,” Plant Soil Environmental, Vol. 50, No. 6, 2004, pp. 257-264.
- S. Lagergren, “About the Theory of So-Called Adsorption of Soluble Substances Zur Theorie der Sogenannten Adsorption Geloster Stoffe,” Kungliga Svenska Vetenskapsakademiens Handlingar, Vol. 24, No. 4, 1898, pp. 1-39.
- Y. S. Ho, G. McKay, D. A. J. Wase and C. F. Foster, “Study of the Sorption of Divalent Metal Ions on to Peat,” Adsorption Science and Technology, Vol. 18, No. 7, 2000, pp. 639-650. doi:10.1260/0263617001493693
- S. H. Chien and W. R. Clayton, “Application of Elovich Equation to the Kinetics of Phosphate Release and Sorption in Soils,” Soil Science Society America Journal, Vol. 44, No. 2, 1980, pp. 265-268. doi:10.2136/sssaj1980.03615995004400020013x
- D. L. Sparks, “Kinetics of Reaction in Pure and Mixed Systems,” In: D. L. Sparks, Ed., Soil Physical Chemistry, CRC Press, Boca Raton, 1986, pp. 83-145.
- J. Zeldowitsch, “Über Den Mechanismus der Katalytischen Oxidation Von CO a MnO2,” URSS, Acta Physiochim, Vol. 1, No. 2, 1934, pp. 364-449.
- W. J. Weber and J. C. Morris, “Kinetics of Adsorption on Carbon from Solution,” Journal of the Sanitary Engineering Division American Society of Civil Engineering, Vol. 89, No. 2, 1963, pp. 31-60.
- K. Srinivasan, N. Balasubramanian and T. V. Ramakrishan, “Studies on Chromium Removal by Rice Husk Carbon,” Indian Journal Environment and Health, Vol. 30, No. 4, 1988, pp. 376-387.
- C. W. Cheung, J. F. Porter and G. Mckay, “Sorption Kinetic Analysis for the Removal of Cadmium Ions from Effluents Using Bone Char,” Water Research, Vol. 35, No. 3, 2001, pp. 605-612. doi:10.1016/S0043-1354(00)00306-7
- H. Teng and C. Hsieh, “Activation Energy for Oxygen Chemisorption on Carbon at Low Temperatures,” Indusstrial Engineering and Chemical Research, Vol. 38, No. 1, 1999, pp. 292-297. doi:10.1021/ie980107j
- K. Kannan and M. M. Sundaram, “Kinetics and Mechanism of Removal of Methylene Blue by Adsorption on Various Carbons—A Comparative Study,” Dyes Pigments, Vol. 51, No. 1, 2001, pp. 25-40. doi:10.1016/S0143-7208(01)00056-0
- C. L. Lu, J. G. Lv, L. Xu, X. F. Guo, W. H. Hou, Y. Hu and H. Huang, “Crystalline Nanotubes of γ-AlOOH and γ-Al2O3: Hydrothermal Synthesis, Formation Mechanism and Catalytic Performance,” Nanotechnology, Vol. 20, No. 2, 2009, pp. 1-6. doi:10.1088/0957-4484/20/21/215604
- J. M. Murray and J. G. Dillard, “The Oxidation of Cobalt(II) Adsorbed on Manganese Dioxide,” Geochima et Cosmochima Acta, Vol. 43, No. 2, 1979, pp. 781-787. doi:10.1016/0016-7037(79)90261-8
- M. G. Zuhra, M. I. Bhanger, A. Mubeena, N. T. Farah and R. M. Jamil, “Adsorption of Methyl Parathion Pesticide from Water Using Watermelon Peels as a Low Cost Adsorbent,” Chemical Engineering Journal, Vol. 138, No. 1-3, 2008, pp. 616-621. doi:10.1016/j.cej.2007.09.027
- M. Syed, I. Muhammad, G. Rana and K. Sadullah, “Effect of Ni2+ Loading on the Mechanism of Phosphate Anion Sorption by Iron Hydroxide,” Separation and Purification Technology, Vol. 59, No. 1, 2008, pp. 108-114. doi:10.1016/j.seppur.2007.05.033
- Y. Seki and K. Yurdakoc, “Adsorption of Promethazine Hydrochloride with KSF Montmorillonite,” Adsorption, Vol. 12, No. 1, 2006, pp. 89-100. doi:10.1007/s10450-006-0141-4
- Y. Yu, Y. Y. Zhuang and Z. H. Wang, “Adsorption of Water-Soluble Dye onto Functionalized Resin,” Journal of Colloid Interface Science, Vol. 242, No. 2, 2001, pp. 288-293. doi:10.1006/jcis.2001.7780
- N. Dizge, C. Aydiner, E. Demirbas, M. Kobya and S. Kara, “Adsorption of Reactive Dyes from Aqueous Solutions by Fly Ash: Kinetic and Equilibrium Studies,” Journal of Hazardous Materials, Vol. 150, No. 3, 2008, pp. 737-746. doi:10.1016/j.jhazmat.2007.05.027
- H. Oualid, S. Fethi, C. Mahdi and N. Emmanuel, “Sorption of Malachite Green by a Novel Sorbent, Dead Leaves of Plane Tree: Equilibrium and Kinetic Modeling,” Chemical Engineering Journal, Vol. 143, No. 1, 2008, pp. 73-84. doi:10.1016/j.cej.2007.12.018
- J. H. Noggle, “Physical Chemistry,” 3rd Edition, Vol. 11, Harper Collins Publishers, New York, 1996.
- W. Stumm and R. Wollast, “Coordination Chemistry of Weathering. Kinetics of the Surface Controlled Dissolution of Oxide Minerals,” Reviews of Geophysics, Vol. 28, No. 1, 1990, pp. 53-69. doi:10.1029/RG028i001p00053
- K. G. Scheckel and D. L. Sparks, “Temperature Effects on Nickel Sorption Kinetics at the Mineral-Water Interface,” Soil Science Society of America Journal, Vol. 65, No. 3, 2001, pp. 719-728. doi:10.2136/sssaj2001.653719x
- M. M. Abd El-Latif, A. M. Ibrahim and M. F. El-Kady, “Adsorption Equilibrium, Kinetics and Thermodynamics of Methylene Blue from Aqueous Solutions Using Biopolymer Oak Sawdust Composite,” Journal of American Science, Vol. 6, No. 6, 2010, pp. 267-283.
- M. Alkan, B. Kalay, M. Dogan and O. Demirbas, “Removal of Copper Ions from Aqueous Solutions by Kaolinite and Batch Design,” Journal of Hazardous Materials, Vol. 153, No. 1-2, 2008, pp. 867-876. doi:10.1016/j.jhazmat.2007.09.047
- B. H. Hameed, D. K. Mahmoud and A. L. Ahmad, “Sorption Equilibrium and Kinetics of Basic Dye from Aqueous Solution Using Banana Stalk Waste,” Journal of Hazardous Materials, Vol. 158, No. 2-3, 2008, pp. 499-506. doi:10.1016/j.jhazmat.2008.01.098
NOTES
*Corresponding author.

