Computational Water, Energy, and Environmental Engineering
Vol.3 No.3(2014), Article ID:48051,8 pages
DOI:10.4236/cweee.2014.33012
An Automated Negotiation Protocol Based On Game Theory
Chenming Li, Wei Huang, Zhenli Ma, Fengzhou Wang, Xiaodong Wei, Lizhong Xu*
College of Computer and Information Engineering, Hohai University, Nanjing, China
Email: *lzhxu@hhu.edu.cn, banjamin2006@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 1 May 2014; revised 12 June 2014; accepted 8 July 2014
ABSTRACT
With the goal of meeting one-to-many negotiation mechanism in the process of inter-basin water transfer, according to features of all interest subjects in analysis of inter-basin water transfer, a one-to-many synchronous bidding negotiation model based on bidding rules of game theory is structured, which analyzes and negotiates the functions, code of conduct and information expression of each subject. In order to optimize overall interests and individual interests, and a series of parameters in the negotiation, the paper propose various rules corresponding to the negotiation model so that the efficiency of each interest subject and fair distribution of negotiation proceeds can be safeguarded in the inter-basin water transfer system.
Keywords:Game Theory, Automated Negotiation Protocol, Inter-Basin Water Transfer

1. Introduction
On the middle level, the feature of inter-basin water transfer project in water conservancy industry is a multilateral game under severe uncertainty. The disadvantage of traditional water resources administration focuses on departments, with regions as auxiliary. The division of vertical is serious and the benefit of regions is greater than the constraints of departments. Many departments are established and it is difficult to keep the interest of all parties balanced. Take South-to-North Water Diversion Project, for example, the first phase of the project entering Beijing delayed water supply for 5 years, which was caused by multi-game. Consequently, a reasonable negotiation mechanism has not been found so far. This chapter is set in eastern route scheduling of South-to-North Water Diversion Project, on the condition of quasi-market operation, aimed at the formation process of interbasin water allocation plan. With water resources allocation of quasi-market economy as the background, under complex network framework, the game involving multiple interest groups in the process of inter-basin water transfer is researched and a multiple Agent automatic communication protocol with supervision is designed. In the protocol administrator Agent as a middleman uses complete information dynamic game model to evaluate the lower scheduling scheme. The lower Agent uses the imperfect information dynamic game—Bayesian Equilibrium and analyzes which strategy the high quality interest subject chooses in the process of autonomous negotiation, which is beneficial to provide reference bases for inter-basin water resources allocation scheme.
2. Game of All Interests Subject in Inter-basin Water Transfer
South-to-North water diversion has feature of half-market [1] . The scheduling scheme is influenced by a few natural factors at the same time, such as artificial interference, weather, season, hydrogeological conditions and so on. Besides, Water quantity supplied by water providers is limited and water demanders along the water transfer routes restrict mutually. The inconsistency or conflict of the supply and demand forms a game problem about interests of multiple aspects under uncertain conditions. For this kind of complex engineering operation scheduling, it is complicated and involves many factors, meanwhile, requirements and goals are different, even contradictory. For example, 1) how to distribute the problems under compatible/incompatible interests; 2) local autonomy and macroeconomic control; 3) unity of opposites between local interests and global interests; 4) multi-dimension coordination and interaction; 5) complementary configuration and satisfactory configuration; 6) comprehending complementation, compromising in conflicts and concerning about all-win; 7) considering short, medium and long term local water resources configuration and global water resources configuration; 8) social , economic and political factors ; and so on. All of them make it difficult to determine the inter-basin water transfer scheme consultation mechanism [2] .
Game theory is a branch of applied mathematics which researches interactional actions among different subjects [3] . It is a mathematical theory and method researching the phenomenon with the nature of competition or struggle. Game is divided into cooperative game and non-cooperative game [4] . The difference between cooperative game and non-cooperative game is whether there is a binding agreement between the parties. If so, it is cooperative game. If not, it is non-cooperative game.
Based on time series of the behavior, game theory is divided into static game and dynamic game. Static game is that the participant makes a choice at the same time or makes a choice not at the same time but the later actor doesn’t know exactly what the early actor do.
Dynamic game is in the game participant’s actions is in a sequence and the later actor can observe what action the early actor chooses [5] .
According to how well the participant knows about other participants, it is divided into complete information game and incomplete information game [6] . Complete game is every participant has accurate information about other participants’ characteristics, the strategy and profit function.
Incomplete information game means if the participant doesn’t have precise information about other participants’ characteristics, the strategy and profit function or the precise information about other participants’ characteristics, the strategy and profit function is not sufficient. It is called incomplete information game in this case.
The Game Analysis of All Interests Subject in Inter-Basin Water Transfer
In the process of inter-basin water transfer scheduling, what all interests’ parts focus on is adjustable water quantity and water price. As the basic signal of supply and demand in water resources market and the important means of allocating water resources, water price play a very important role in the process of water transfer operation and management. Reasonable water price will effectively promote the optimized allocation of water resources and improve efficiency of use. It also ensures positive operation and sustainable development of water transfer project. However, water price is influenced by complex factors, especially; large-scale inter-basin water transfer project (area) has the strong characters of public welfare. So the water price follows the basic law of socialist market economy .The influence of government public management goal, consumer’s willingness to pay and basic tolerance capacity should also be taken a full account.
The assumption in literature [7] is used by this paper: water price consists of cost and fixed profit, but the cost includes government fees and operation cost of water supply enterprise. Assume that the operation cost is fixed and lack of elasticity for the same water supply enterprise, water supply price is decided by government charge. The higher government charge is, the higher cost of water supply enterprise is. Accordingly water supply price is higher. According to water price, the users can decide how much water they use. Water supply development enterprises weigh benefit on the basis of how much government charges and consumer uses, so they can decide whether to invest on the project. The goal water supply enterprise pursues is higher profits (realized by higher water price). However, government not only pursues higher water price income, but also considers the interests of users in order to meet basic water demands of users and make sure that all users in any income levels can afford basic water demands costs. Of course, if government charge is too high. It will make water supply enterprise unprofitable and the enterprise will not invest. Therefore, the effectiveness of government should be a function of both water price income and water consumption users satisfy (the government stipulate that water price income is the sum of water supply enterprise cost and the fixed profit regulated with government permission). As a consequence the utility of government is:
 (1)
(1)
In the function: W—government charge ratio.
L—the amount of water provided by water supply enterprise in accordance with the price passed by government.
The profits obtained by government and water supply enterprise are expressed in
utility
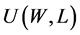 and profit
and profit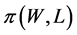 . For water supply enterprise Agent, the best
interest L is:
. For water supply enterprise Agent, the best
interest L is:
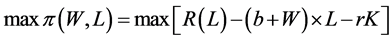 (2)
(2)
In the formula: b is variable cost of water supply enterprise and r is capital cost rate. Concrete analysis can refer to literature [7] . The individual Agent of the automated negotiation protocol in this paper calculates its own negotiating price based on the series of feasible water price acquired by means of gaming, which is negotiate price.
Transferable water is the core problem of inter-basin water transfer [8] . The intake area usually overemphasizes water supply, but ignores the research of actual water demand. Water transfer area is easy to emphasize too much the relative importance of social and economic development of local region, and then it increases the regional water requirement in the future. Strictly speaking, in order to determine the transferable water quantity, under the guidance of sustainable development to sustainable, it should integrate water transfer area and intake area into a big unified system of inter-basin water resources. The development model of society-economy-environment-resource is established, which is confirmed on based on the principle of system optimal comprehensive efficiency. This paper obtains macroeconomic control protocol by gaming between south water supply aggregation and north water supply aggregation through middle leader Agent [9] -[12] . The game model is:
1) Suppose there are two kinds of negotiators, honest negotiator (H) and dishonest negotiator (L), in negotiation market. In the negotiation, the honest negotiator will provide real material according to the actual situation of own department. The negotiation cost is set to C. The dishonest negotiator will provide false material in order to win the favor of the boss or for special interests of the department. Cheating cost is set to △C; hence the cost of dishonest negotiator is C+△C.
2) The honest negotiator gets a successful negotiation with probability P. The benefit acquired is RH and the net benefit of the honest contractor is RH-C. The benefit of global scheduling is R.
3) The dishonest negotiator wins the bid with probability P as well. The benefit
is RL and the net benefit is RL − (C + △C). At this time completing scheduling
plan will take on some risks it is difficult to ensure income. The benefit of global
scheduling is set to . If the real type of the dishonest negotiator
is recognized by leader Agent with probability (1 − P) so that the scheduling
plan is not executed. Hence the benefit is −(C − ΔC) and the loss R0
of global benefit is exonerated.
. If the real type of the dishonest negotiator
is recognized by leader Agent with probability (1 − P) so that the scheduling
plan is not executed. Hence the benefit is −(C − ΔC) and the loss R0
of global benefit is exonerated.
4) Because this game is incomplete information, leader Agent doesn’t know whether bidders are honest. Therefore, the benefit function is unknown. For the convenience of analysis, the Harsanyi transformation is needed. Leader L selects the type of negotiator at first step and assumes negotiator Agent know his own type.
According to this model, the game tree is structured as shown in figure 1 [13] . The first stage of game is launched by leader Agent. The second stage is decided whether negotiation is needed by supply and requisition parties. The intention of negotiation depends on expected revenue coming from the whole regulation scheme.
For the honest Agent, the expected revenue of negotiation is:
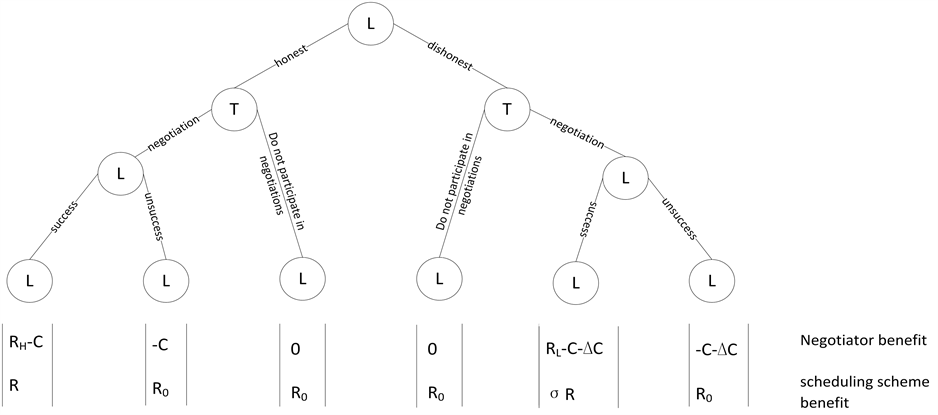
Figure 1. Scheduling scheme negotiation game figure.
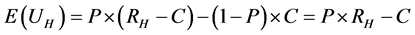 (3)
(3)
For the dishonest Agent, the expected revenue of negotiation is:
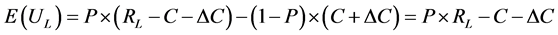 (4)
(4)
When negotiator find that the benefit of global scheduling scheme is greater than negotiation cost, the negotiation starts. In the third stage leader Agent decides whether the negotiation is successful based on the degree of honesty. According to real-time water storage of system, weather forecast and water storage expected time of negotiations location, Leader Agent generates probability P(H) and P(L), which respectively represent the number of honest negotiator and dishonest negotiator in the system. Therefore, PH = PL, P(H) + P(L) = 1. According to Bayes’ theorem, the probability of honest negotiator is:
 (1)
(1)
In the same way, the probability of dishonest is:
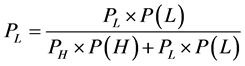 (2)
(2)
When leader Agent’s expectations for expected revenue of scheduling plan, which
is equal or greater than zero, is![]() , he will declare the negotiation is successful.
In order to prevent the scheduling plan influenced by dishonest Agent from executing,
it ought to impose severe punishment on dishonest Agent by the means of supervising.
Suppose degree of punishment is D. At this time, unsuccessful negotiation benefit
of dishonest negotiator is
, he will declare the negotiation is successful.
In order to prevent the scheduling plan influenced by dishonest Agent from executing,
it ought to impose severe punishment on dishonest Agent by the means of supervising.
Suppose degree of punishment is D. At this time, unsuccessful negotiation benefit
of dishonest negotiator is , the expected revenue changes into:
, the expected revenue changes into:
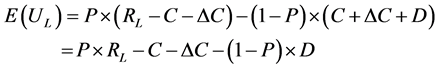 (7)
(7)
When ∆C and C is big enough, it can ensure dishonest Agent behavior in whole system is restricted in the negotiation.
3. Automated Negotiation Protocol Model Based on Game Theory
3.1. Basic Framework of Negotiation Protocol
According to game analysis in the above section, it regards the Agent interaction of the eastern line scheduling system in south-to-north water diversion as multi-attribute negotiation centering on multi-object [14] . The above game is researched by using the negotiation protocol of one-side to one-side multi-objective bilateral synchronous quotation, and multiple Agent automated negotiation protocol model is established as follow [15] -[17] :
Symbol s(Seller) represents seller, b(Buyer) represents buyer and L(Leader) represents
government Agent in the process of negotiation.
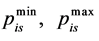 represents number interval accepted the ith objective of
Agents and
represents number interval accepted the ith objective of
Agents and
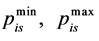 presents number interval accepted the ith objective of
presents number interval accepted the ith objective of
![]() (Agent buyer). However,
(Agent buyer). However,
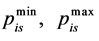 is an accepted potential number interval for
is an accepted potential number interval for
![]() and
and
![]() (Agent seller), and the difference is the rest limit value of ith objective in the
trade.
(Agent seller), and the difference is the rest limit value of ith objective in the
trade.
![]() represents the quotation of ith objective which
represents the quotation of ith objective which
 submits to
submits to
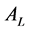 (Agent Leader) at negotiation time t.
(Agent Leader) at negotiation time t.
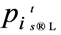 represents the quotation of ith objective which submits
to
represents the quotation of ith objective which submits
to
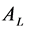 at time t. t is a sequential time series in the process
of negotiation and it is represented by natural number. L generates prompts by comparing
the quotation of both sides and transmits synchronously unmatched consequence and
prompts in this round in both directions.
at time t. t is a sequential time series in the process
of negotiation and it is represented by natural number. L generates prompts by comparing
the quotation of both sides and transmits synchronously unmatched consequence and
prompts in this round in both directions.
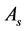 and
and
 estimate opponent’s quotation distribution through analysis of prompts, and amend
effectiveness distribution,
estimate opponent’s quotation distribution through analysis of prompts, and amend
effectiveness distribution,
 and
and , of own ith objective dynamically.
, of own ith objective dynamically.
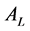
sets a time limit
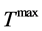 consuming in the negotiation for both negotiating sides. When this moment arrives,
both negotiating sides will withdraw from the negotiation and a punishment scheme
will be provided by
consuming in the negotiation for both negotiating sides. When this moment arrives,
both negotiating sides will withdraw from the negotiation and a punishment scheme
will be provided by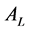 . When
. When
![]() >
>![]() , it indicates that the buyer and seller
doesn’t agree on quotation of the ith objective.
, it indicates that the buyer and seller
doesn’t agree on quotation of the ith objective.
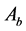 and
and
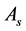
perform an analysis through the prompts coming from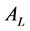 , and generate negotiation decision at next
time by combining with the own retaining information. Then, they will submit quote
information in next round. When
, and generate negotiation decision at next
time by combining with the own retaining information. Then, they will submit quote
information in next round. When
![]()
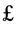
![]() (quotation of all subgoals satisfied),
quotation of both sides is compatible.
(quotation of all subgoals satisfied),
quotation of both sides is compatible.
 calculates concrete worth of transactions and declares
negotiation is completed successfully. If negotiating parties find the maximum negotiating
time
calculates concrete worth of transactions and declares
negotiation is completed successfully. If negotiating parties find the maximum negotiating
time
 is coming in the process,
is coming in the process,
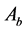 and
and
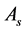 submit the last quotation. Finally, Agent L puts forward trade agreement based on
own principle.
submit the last quotation. Finally, Agent L puts forward trade agreement based on
own principle.
3.2. Action Definition of Negotiation Agent
1) The actions of
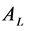 at time t are defined as follows:
at time t are defined as follows:
a) When the quotation submitted by
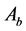 and
and
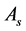 meets
meets
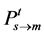

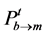 ,
,
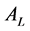 calculates transaction price and declares negotiation
is completed successfully.
calculates transaction price and declares negotiation
is completed successfully.
b) When the quotation submitted by
 and
and
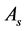 meets
meets
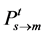
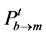 ,
,
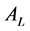 generates prompts and conveys to both sides simultaneously
and respectively. It is ready to receive quote information from both sides at next
time and prompts quotation deadline.
generates prompts and conveys to both sides simultaneously
and respectively. It is ready to receive quote information from both sides at next
time and prompts quotation deadline.
c) When
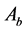 and
and
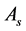 submit quotation and inform it is the last time for submitting,
submit quotation and inform it is the last time for submitting,
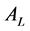 relays the news that the negotiation is coming to an end.
It needs to submit the last quotation and declare to start the last matching calculation
by negotiating.
relays the news that the negotiation is coming to an end.
It needs to submit the last quotation and declare to start the last matching calculation
by negotiating.
d)
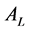 finds the quotation in this round is not matched by calculating,
and the next step to negotiate has touched the maximum negotiating deadline set
by
finds the quotation in this round is not matched by calculating,
and the next step to negotiate has touched the maximum negotiating deadline set
by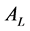 , namely at time of
, namely at time of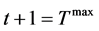 . It provides the prompts of last negotiating
quotation to for
. It provides the prompts of last negotiating
quotation to for
 and both sides.
and both sides.
e) When
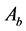 and
and
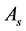 submit quotation for the last time,
submit quotation for the last time,
 conveys the information that negotiation is over and declares
the protocols draw up based on
conveys the information that negotiation is over and declares
the protocols draw up based on
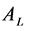 own principle.
own principle.
2) The actions of
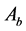 and
and
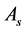 at time t are defined as follows:
at time t are defined as follows:
a) When the information of
 about successful negotiation and transaction price is received, it completes consultation
and sets out to make own scheduling plan.
about successful negotiation and transaction price is received, it completes consultation
and sets out to make own scheduling plan.
b) When the information of
 last quotation submitted by the opponent, it submits own last quotation and terminates
negotiation.
last quotation submitted by the opponent, it submits own last quotation and terminates
negotiation.
c) When the information of
 about the unmatched results and prompts in this round is received, it judges opponent’s
current strategy and then submits its own new quotation.
about the unmatched results and prompts in this round is received, it judges opponent’s
current strategy and then submits its own new quotation.
d) When the information of
 about the unmatched results and prompts in this round is received and next negotiation
has touched the maximum negotiating deadline, namely at time of
about the unmatched results and prompts in this round is received and next negotiation
has touched the maximum negotiating deadline, namely at time of .
.
It prompts and conveys last negotiating quotation to .
.
e) When the information of
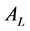 about the unmatched results and prompts in this round is received and it has touched
the reservation price in the negotiation, namely at time of
about the unmatched results and prompts in this round is received and it has touched
the reservation price in the negotiation, namely at time of
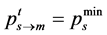 or
or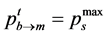 , it submits the last quotation and terminates negotiation.
, it submits the last quotation and terminates negotiation.
3.3. Negotiating Utility Function and Calculation of Negotiating Price
For multi-attribute negotiation, utility maximization of result is the objective of all negotiating parties which is assessed through utility function. This paper adopts related content in comprehensive literature [14]. The general utility function is built as follow:
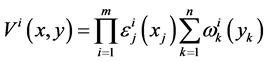 (8)
(8)
In the formula,
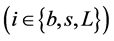 represents negotiating Agent, j
represents negotiating Agent, j
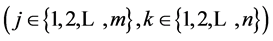 represents negotiation properties with different functions, and
represents negotiation properties with different functions, and
![]() represents the importance of attribution j and attribution k for Agent. Negotiating
Agent uses genetic algorithm respectively for next round of quotation. The strategy
uses concession strategy in literature [5] . Quotation
calculation is simplified as follows:
represents the importance of attribution j and attribution k for Agent. Negotiating
Agent uses genetic algorithm respectively for next round of quotation. The strategy
uses concession strategy in literature [5] . Quotation
calculation is simplified as follows:
1) the concession intention of
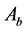 and
and
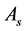
It means that at any time t in the negotiation process of
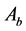 and
and
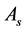 middle
middle
 gets the gaps between both sides by receiving and calculating, which is added to
the punishment of unsuccessful negotiation. It expressed by
gets the gaps between both sides by receiving and calculating, which is added to
the punishment of unsuccessful negotiation. It expressed by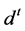 , shown in Formula (9):
, shown in Formula (9):
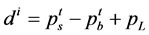 (9)
(9)
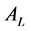 will prompt quotation of
will prompt quotation of
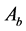 and
and
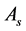 according to
according to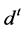 .
.
2)
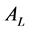 penalty value
penalty value
 is penalty parameter, the leader calculates dynamically
based on variety of national ecological conditions. It is shown as follow:
is penalty parameter, the leader calculates dynamically
based on variety of national ecological conditions. It is shown as follow:
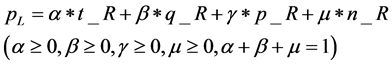 (10)
(10)
In the formula, t_R, q_R, p_R and n_R respectively represents the constraint conditions
satisfaction degree of time, quality, price and quantity. α, β, γ and
![]() are constant weight factor, whose value is related to leader’s emphasis degree of
each constraint condition.
are constant weight factor, whose value is related to leader’s emphasis degree of
each constraint condition.
3) quotation of
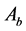 and
and
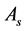 in next round If
in next round If
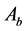 or
or
 finds its own quotation and the prompts don’t accord with the requirement, quotation
of
finds its own quotation and the prompts don’t accord with the requirement, quotation
of
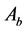 and
and
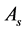 in next round is:
in next round is:
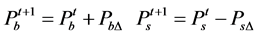 (11)
(11)
In the formula,
![]() and
and
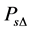 is the concession strategy.
is the concession strategy.
4. The Simulation Validation of Protocol
4.1. Experimental Results
In order to validate the effectiveness of brief automated negotiation protocol above, Agent simulation is established. In the protocol test, manager 3 is the representative of water supply (seller) and manager 15 is the representative of water demand (buyer). Then, South-to-North office under The State Council is the leader (coordinator) representative in the automated negotiation simulation. It is tested the effectiveness of protocol by intelligent software automated negotiation.
The steps of each game party: according to current condition to determine own decision types, determining own and opponent’s cost function, combing with coordinator’s penalty function to determining own quotation strategy, calculating payoff function, building game matrix and selecting final quotation.
Table 1. the comparison of simulation result of concession protocol and automated negotiation protocol.
4.2. Analysis of Simulation Results
In order to validate the effectiveness of automated negotiation protocol. For the situation of water supply side and water demand side in inter-basin water transfer, This paper adopts concession protocol and automated negotiation protocol in literature [14] to negotiate for 50 times. The detailed statistical result of simulation is shown in table 1.
In table 1, total times represents respective negotiation times of concession protocol and automated protocol. Success represents successful negotiation times by using this protocol to make a deal finally. Average rounds represent average negotiation times in the negotiation, namely recording how many rounds in every negotiation and averaging the data lastly. Success at deadline means the successful negotiation times at maximum negotiation time, which is used to weigh the importance of penalty function in the negotiation. According to final simulation result, these two kinds of protocol can make Agent interactive. However, automated interactive protocol gets more successful cases under market conditions with the background of inter-basin water transfer system. It also costs less time. The reason of this simulation result is that concession protocol is applied in the background of network trading under full market condition. Both sides of the deal have full freedom to determine own price based on their whishes. The reason for successful negotiation is the negotiated outcome that is satisfied by both sides. Nonetheless, automated negotiation protocol aims at the environment of quasi-market (half quasi-market), and both sides of the deal not only proceed from their own interests, but also considers the penalty given by intermediary agent. For example, the goals pursued by water supply sides is high profits (realized through high water price), and the social responsibility of water supply area should be taken into account, which is reflected in penalty function of intermediary Agent in the protocol. Water shortage area gents need to consider the interests of local users. They use limited funds to meet the basic needs of local users in order to keep local area from using groundwater on account of high costs. In this process, the profit of callout side should be considered. Therefore, a superintendent who ensures to complete some trades is needed on both sides of the deal in order to meet basic social requirement. In the automated negotiation protocol, the penalty given by the superintendent can guarantee both sides prefer to come to an agreement in order to make the negotiation beneficial to regional water resources. Under the special background of real-time scheduling in South-to-North water transfer, the effect of automated interaction protocol is superior to concession negotiation.
5. Conclusion
For the benefit game of scheduling in South-to-North water transfer project, the contradiction is sharp and it lacks effective negotiation mechanism. In this paper, from the view of persons’ (all interest subjects) demand, the allocation schemes of mid-and-long term is acquired through mutual game of related interest subjects (multiple Agent) in complex network. Based on analyzing features of inter-basin water transfer, an automated negotiation protocol on the basis of game theory uses a complete information dynamic game model. It obtains water price on behalf of water supply side and government, using the imperfect information dynamic game (Bayesian equilibrium theory) to obtain adjustable water during the negotiation. This protocol can make supplying and demanding parties come to a satisfactory executable global water resources allocation scheme agreement under half-supervision mechanism. Finally, the simulation is realized on Agent Builder simulation platform. It preliminarily validates the feasibility and effectiveness. Compared with original protocol, automated negotiation protocol has a high success rate and a high speed, which establishes the foundation for designing effective automated negotiation mechanism later.
Acknowledgements
This study is supported by the National Natural Science Foundation of China (No. 51179047).
References
- Wang, Y.S. and Yang, Y.Y. (2005) The South-North Water Diversion Project in China. Yangtze River, 36, 2-5.
- Zhang, Y. and Lv, D.H. (2013) Inter-Basin Water Diversion Project Consultation Mechanism Study of Water resources Allocation, Water Conservancy Science and Technology and Economy, 19, 30-32.
- Zhang, X.Y. (2008) Game Logic and Its Application Research. Nanjing University, Nanjing.
- Jiang, P.F. (2007) Cooperative Game Solution and Application Research. Shandong University, JiNan.
- Wu, X.M. (2008) The Theory of Static and Dynamic Game of Logic. Seeking Truth, 35, 51-55.
- He, S.N. (2010) The Logical Analysis of Incomplete Information Game. Journal of Zhoukou Normal College, 27, 104-107.
- Zhang, H. and He, H.C. (2006) Multiple Agent Automatic Negotiation Strategy and Algorithm. Computer Application, 26, 1935-1937.
- Gao, C. and Shi, S.P. (2012) Adjustable Water Analysis of Water Diversion Project. Water Resources and Hydropower Engineering, Water Resources and Hydropower Engineering, 31, 31-32.
- Wooldridge, M.J. (2000) Reasoning about Rational Agents. The MIT Press, Cambridge MA.
- Liu, D.Y. and Yang, K. (2000 The Current Situation and the Development Trend of the Agent. Journal of Software, 11, 315-321.
- Tardo, J. and Valente, L. (1996) Mobile agent Security and Telescript. Proceedings of 1996 IEEE COMPCON’96, Santa Clara, 58-63.
- Wooldridge, M.J. (2002) An Introduction to Multiagent Systems. Wiley, Hoboken.
- Yue, J.P. and Feng, S. (2009) The Computer System Application. Overview of Game Tree Search Algorithm, 9, 203-207.
- Wei, X.D. (2006) Based on the Multi-Agent Eastern Fast Water Research and Simulation. Hohai University, Nanjing.
- Kaveh, M. and Ariel, D. (2012) Cooperative Institutions for Sustainable Common Pool Resource Management: Application to Groundwater. Water Resources Research, 48, 1-15.
- Brooks, J.P., Adeli, A. and McLaughlin, M.R. (2014) Microbial Ecology, Bacterial Pathogens, and Antibiotic Resistant Genes in Swine Manure Wastewater as Influenced by Three Swine Management Systems. Water Research, 57, 96-103. http://dx.doi.org/10.1016/j.watres.2014.03.017
- Kucukmehmetoglu, M. (2012) An Integrative Case Study Approach between Game Theory and Pareto Frontier Concepts for the Transboundary Water Resources Allocations. Journal of Hydrology, 450, 308-319.
NOTES
![]()
*Corresponding author.


