Crystal Structure Theory and Applications
 Vol.3 No.1(2014), Article ID:44361,8 pages DOI:10.4236/csta.2014.31004

Investigating Double-Regime Crossover in Y1Ba2Cu3 − xRxO7 − δ Superconductors

Mohamed H. Badr*, Lubna M. Sharaf El-Deen, Mohamed El-Hofy, Aly A. Haswa

Physics Department, Faculty of Science, Minufiya University, Shebin El-Koom, Egypt

Email: *mhbadr0@hotmail.com

Copyright © 2014 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 2 February 2014; revised 1 March 2014; accepted 18 March 2014

ABSTRACT

The effect of Pr and Gd doping on the transport properties of Cu-deficient YBCO superconductors has been studied. Two series of Y1Ba2Cu3 − xRxO7 − δ, where R = Pr or Gd, were prepared by the conventional solid-state reaction technique. Resistance measurements showed a suppression of Tc with increasing of Prand Gd-contents in addition to a normal-state metal-to-insulator transition. Moreover, a superconductor-to-insulator transition has been observed at ambient pressure for temperatures less than 50 K for Pr with x = 0.3 and for Gd with x > 0.3. The overall complex behaviours of the resistivity data have been preliminary explained in terms of localization of charge carriers, structural disorders, and magnetic ordering of magnetic moments.

Keywords:High Tc Superconductivity; Metal-Insulator Transition; Superconductor-Insulator Transition

1. Introduction

Elemental substitutions play an important role in understanding the nature of superconductivity in high Tc superconductors. Substitutions of Cu by X ions in RBCXO system, where R is a rare earth and X is Mn, Cr, Fe, Co, Ni, Al, and Ga, have been studied [1] -[11] . The studies have revealed that substitutions with nonmagnetic ions caused a huge decrease in the critical transition temperature as compared to magnetic ions. Many non-magnetic mechanisms have been proposed to explain the phenomena in addition to pair-breaking due to magnetic impurities in accordance with Abrikosov and Gorkov theory. The dependence of resistivity on temperature proved to be difficult to explain not only for different compounds, but within the same family as well [12] . Metal to insulator transition (MIT) has been observed upon substitutions at Y-, Ba-, and Cu-sites in diverse superconducting systems [13] -[21] . Moreover, evidence of MIT due to other reasons such as changes in oxygen content, pressure, film thickness, and doping at grain boundaries has been reported [22] -[26] . In this work we investigated the effect of doping magnetic ions of R = Pr and Gd on Cu-deficient Y1Ba2Cu3 − xRxO7 − δ system with x = 0.1, 0.2, and 0.3 and x = 0.1, 0.2, 0.3 and 0.4, respectively. Our aim is to study and compare the MIT and the observed incomplete superconductor to insulator (SIT) crossovers in the two systems and investigate its origin.

2. Experimental Details

The polycrystallized samples were prepared by the conventional solid state reaction method. Raw powders of Y2O3 (99.99%, Aldrich Chemical Co. Ltd.), Gd2O3 (99.9%, Aldrich Chemical Co. Ltd.), Pr6O11 (99.9%, Sigma Chemical Co.), BaCO3 (99%, NTL Nentech Ltd.), and CuO (99%, Aldrich Chemical Co. Ltd.), were mixed according to the nominal chemical formula Y1Ba2Cu3 − xPrxO7 – δ with x = 0, 0.1, 0.2, and 0.3 and Y1Ba2Cu3 − xGdxO7 – δ with x = 0, 0.1, 0.2, 0.3, and 0.4. The powders were dried for 10 hr at 120˚C and mixed according to the required stoichiometric compositions. Then, they were manually ground using an agate mortar for 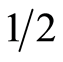hr followed by mechanical milling for 5 hr to ensure homogeneity. Calcination of homogenous mixtures took place at 900˚C for 10 hr in porcelain crucibles. Then, the calcined powders were subjected to a second cycle of grinding under same conditions mentioned above. Using a hydraulic press with a pressure of 6 tons/cm2, we obtained tablets of 13 mm in diameter and 2 - 3 mm in thickness. The obtained tablets were sintered at 950˚C for 10 hr with an oxygen flow during the cooling process. Finally, the sintered tablets were reground manually for hr followed by mechanical milling for 3 hr. The sintered powders were pressed again and retreated thermally under same pervious conditions. The X-ray diffraction (XRD) patterns were recorded at room temperature using a Bruker D8 Advance diffractrometer with Cu target, and it’s Kα radiation. The 2θ scanning speed of detector was 3˚/min with a step width of 0.02˚ and running condition of 40 KV and 40 mA. The X-ray diffraction patterns were analyzed using the XPowder software [27] . The DC resistance was measured using the conventional four-point probe method in the temperature range 40 - 300 K using a closed cycle helium cryostat (APD Cryogenics, USA), programmable current source (Keithley 224), sensitive digital voltmeter (Keithley 182), and autotuning temperature controller (LakeShore 321).

3. Results and Discussion

The X-ray diffraction patterns between 20˚ and 80˚ for Y1Ba2Cu3 − xPrxO7 – δ and Y1Ba2Cu3 − xGdxO7 – δ were shown in Figures 1 and 2, respectively. The intensity of peaks for different values of Prand Gd-contents, x, were normalized and shifted for clarity purposes. As seen, the pure sample, x = 0.0, showed the well known Y123 pattern with all peaks indexed in the orthorhombic structure. The calculated a, b, and c lattice parameters for x = 0.0 were given as 3.8374, 3.8867, and 11.6650 Å, respectively. It is worth mentioned to observe the extra two peaks, denoted by (+), appeared for x ≥ 0.1 in both series. These peaks matched the insulating Y2BaCuO5 phase with characteristic planes (311) and (112). Table 1 showed the dependence of lattice constants, orthorhombicity (tendency towards orthorhombic phase related to the quantity), difference in peak position of (020) and (200) reflections (∆pp), and grain-size diameter (D) with Prand Gd-contents.

Since the ionic radius of Pr (1.13 Å) is greater than that of Gd (1.05 Å) and Cu (0.93 Å), one should expect a systematic increase in lattice parameters with the increase of x if both occupied the Cu sites. Moreover, the expected increase in the parameters should be stronger for Pr doping (denoted as Pr(Cu)) than that of Gd(Cu). Referring to Table 1 and checking the expected increase, it is noticed that such expectations did not exist. The absence of such expectations is an established knowledge that both dopants would occupy the A-sites rather than Cu-sites. This is consistent with the formation of the impurity insulating Y2BaCuO5 phase and its increase with increasing of doping content..Linear fitting have beenused to investigate the overall variation of lattice parameters with Prand Gd-contents in the range x = 0 - 0.3. The rate of change of parameters with x was given for Pr(Cu) as 0.08, 0.004, and 0.014 for a-, b-, and c-parameters, respectively. Whereas for Gd(Cu) it was given as 0.113, 0.016, and 0.043 for a-, b-, and c-parameters, respectively. These rates confirm that the lattice constant b is nearly invariant for both systems and that the effect of Gd(Cu) on lattice parameters is stronger than that of Pr(Cu) even though the ionic radius of the latter is greater than the former. For Gd(Cu) with x = 0.4, it was noticed that the a-parameter decreased sharply which could be attributed to the observed strong formation of the insulating phase, Figure 2.

The two peaks denoted by (*) in Figures 1 and 2 referred to the (020) and (200) indices that describe the orthorhombic nature of the structure. The peak positions of these diffraction peaks have been measured and the

Table 1. The variation of lattice parameters (a, b, and c), orthorhombicity, difference in peak position of (020) and (200) reflections (∆pp), and grain-size diameter (D) with Prand Gd-contents, x.                                             

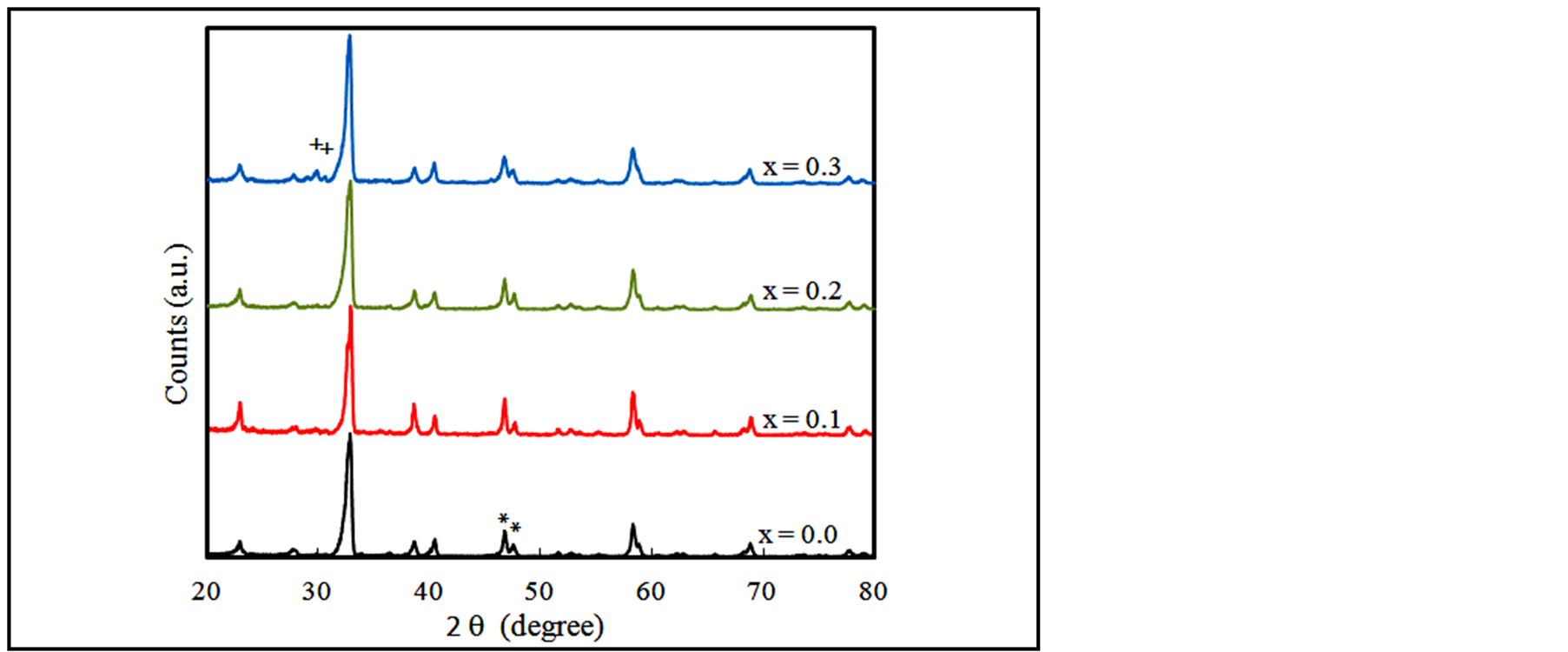
Figure 1. Normalized XRD pattern of Y1Ba2Cu3 − xPrxO7 − δ with x = 0.0, 0.1, 0.2, and 0.3. The peaks denoted by (+) referred to Y2BaCuO5 phase while (*) peaks referred to (020) and (200) indices.                                

Figure 2. Normalized XRD pattern of Y1Ba2Cu3 − xGdxO7 − δ samples with x = 0.0, 0.1, 0.2, 0.3, and 0.4. The peaks denoted by (+) referred to Y2BaCuO5 phase while (*) peaks referred to (020) and (200) indices.                   

variation of resulting position difference (∆pp) with Pr and Gd contents was given in Table 1. It is clear that there is a lattice distortion for x > 0.1 for Pr(Cu) and x > 0.0 for Gd(Cu) that was mainly due to changes in a-parameter, since b-parameter was less affected by the substitution. This behavior was reflected on the resistivity measurements as would be discussed later. Furthermore, the decrease in ∆pp with increasing of x-content reflected the tendency of the structure towards the tetragonal phase, and a consequent decrease in the critical transition temperature with increasing of x could be expected. Also, Table 1 lists the dependence of grain size on Prand Gd-contents. As observed, the grain size diameter decreased from 280 to 190 Å for Pr(Cu) and from 270 to 180 Å for Gd(Cu) as x increased from 0.1 to 0.3. This decrease will be reflected on the nature of the transition width as will be discussed later.

Figure 3 shows the variation of normalized resistance with temperature for Y1Ba2Cu3 − xPrxO7 – δ samples with x = 0.0, 0.1, 0.2, and 0.3. As shown, the x < 0.3 samples still showed a metallic-normal state behaviour 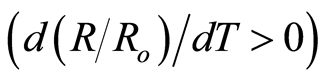as expected for polycrystalline Y123 system. This could be attributed to weak holes localization (as discussed below) due to the assumption that Pr unoccupied the Cu sites, as mentioned above. The increase in the normal state resistance as x increased from 0 to 0.2 could be attributed to the corresponding absence of Cu ions. Whereas, the sample with x = 0.3 showed a normal-state metallic to insulating transition (MIT) (with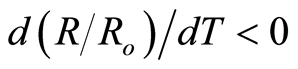) down to about 82 K. Then, a superconducting behaviour existed (with a decrease of normalized resistance by about 58% from its value at the onset of transition) in the small temperature range 82 - 50 K. This incomplete superconducting state, no Tc(offset), was lost for T < 50 K and a crossover from superconducting to insulating transition (SIT) took place in the form of a twofold increase in normalized resistance as the temperature decreased below 50 K by just 16 K. The dependence of the critical transition temperatures and transition width on Pr-content, x, was shown in Figure 4. Moreover, the pure sample, x = 0, showed a transition width of about 1.1 K which confirms the well coupling of grains in the sample. Furthermore, increasing x resulted in a decrease in critical transition temperatures with an increase in the transition width, ∆Tc.

On the other hand, the variation of normalized resistance with temperature of Y1Ba2Cu3 – xGdxO7 – δ samples with x = 0.0, 0.1, 0.2, 0.3, and 0.4 was shown in Figure 5. Unlike Pr(Cu), the normal-state MIT 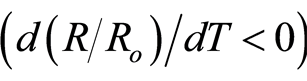existed for all values of x > 0 and the insulating nature increases systematically with the increase of x. This could be attributed to strong holes localization of Gd(Cu). The sample with x = 0.4 showed an onset of superconductivity at around 83 K and the state existed down to about 50 K with a strong reduction in normalized resistance by about 96% in the temperature range 83 - 50 K. The incomplete superconducting state was lost for T < 50 K and SIT appeared with the gain of about 95% of the value of normalized resistance at the onset of transition over the small temperature range 50 - 40 K. To confirm the SIT in our system, we have prepared and measured the sample with x = 0.5, as shown in Figure 5. As expected, this sample followed the nor

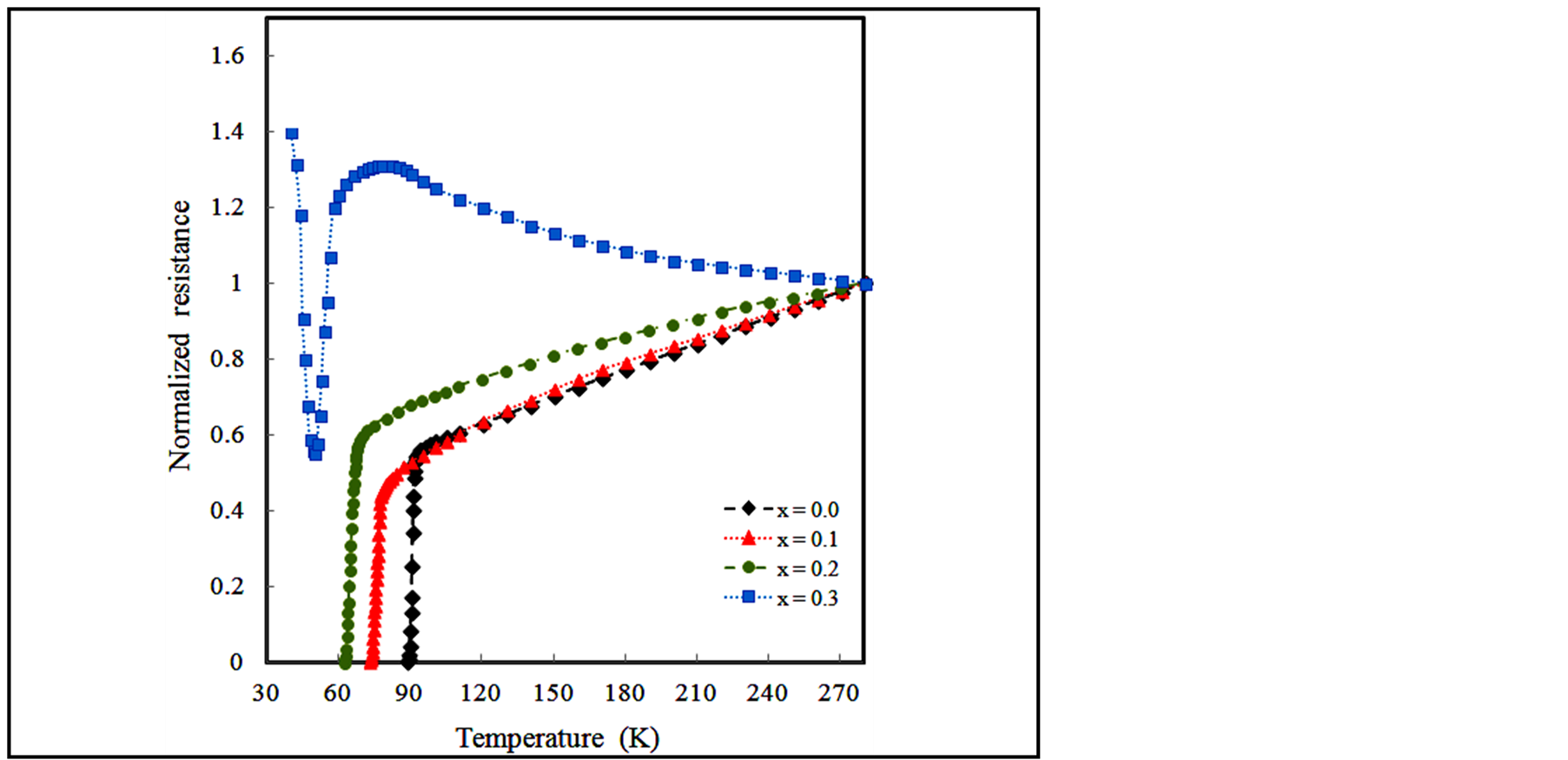
Figure 3. Variation of normalized resistance with temperature of             Y1Ba2Cu3 − xPrxO7 − δ samples with x = 0.0, 0.1, 0.2, and 0.3.                   

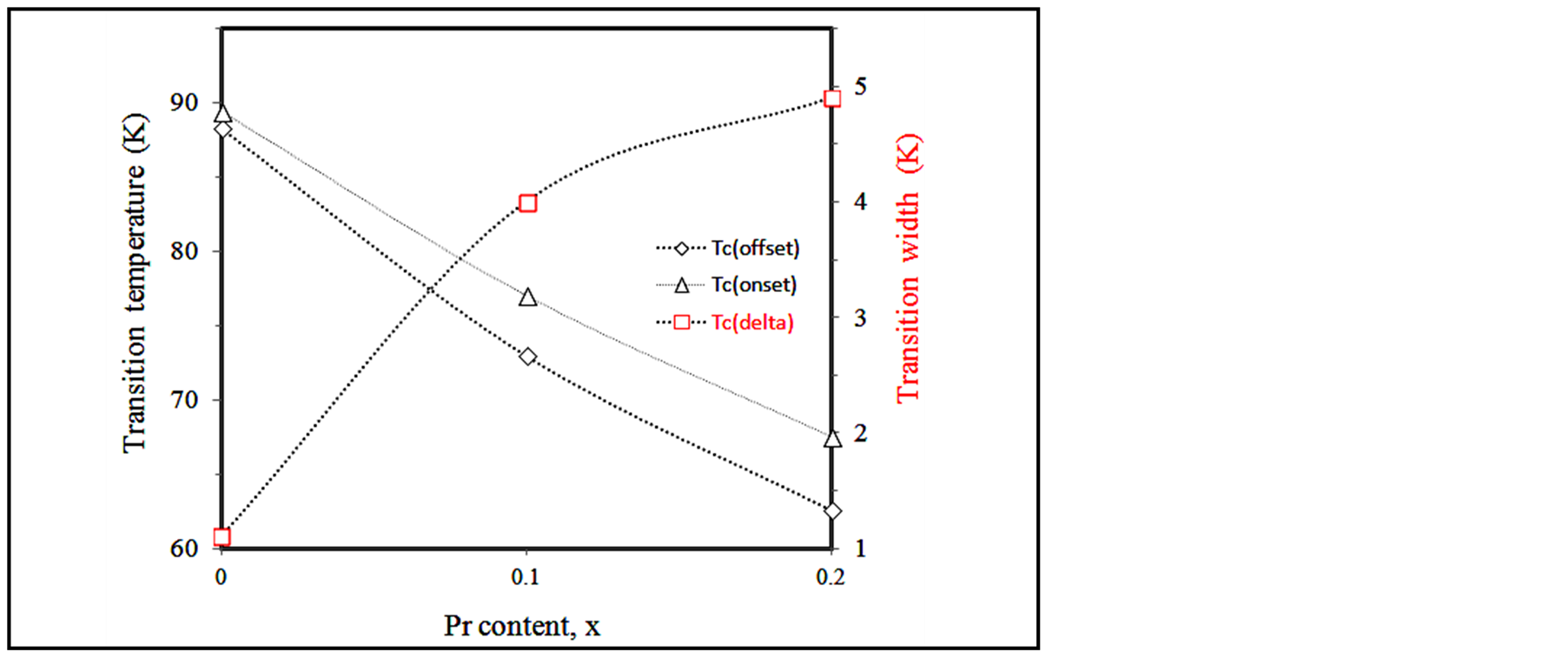
Figure 4. Dependence of the critical transition temperatures and transition width on Pr-content, x.                                              

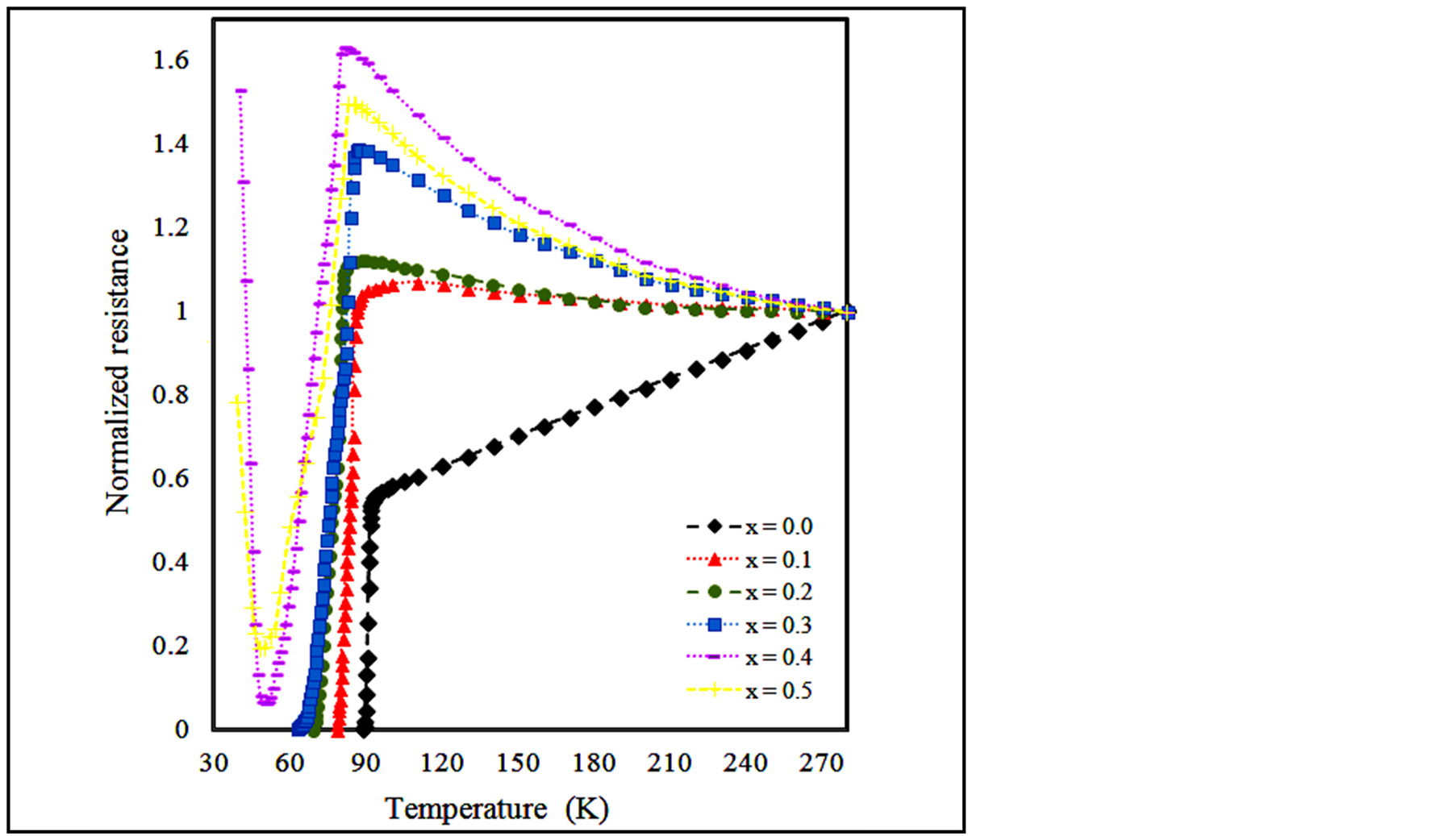
Figure 5. Variation of normalized resistance with temperature of             Y1Ba2Cu3 − xGdxO7 − δ samples with x = 0.0, 0.1, 0.2, 0.3, 0.4, and 0.5.        

mal-state nonmetallic pattern with MIT tendency in addition to SIT at lower temperatures. It is important to observe that the normalized resistance at the onset of superconducting state decreased with just 87% as compared to 96% for x = 0.4 over the same temperature range. This suggests the tendency of the system to show less (or loss of) superconducting behaviour with further increase in x due to the gradual decrease in charge carriers concentration. The variation of the critical transition temperatures and transition width with Gd-content, x, was shown in Figure 6. As seen, increasing the Gd-content resulted in a decrease in critical transition temperatures with an increase in the transition width, ∆Tc. The transition width was more affected by Gd(Cu) than Pr(Cu), Figure 4, which could be attributed to very small grain coupling due to participation of the insulating Y2BaCuO5 phase in these grain boundaries, Figures 2 and 3.

Some points should be clarified, namely, the tendency of the normal-state to transit from metallic to insulating transition (MIT) with increasing of Prand Gd-contents, the incomplete superconducting states, and the loss of

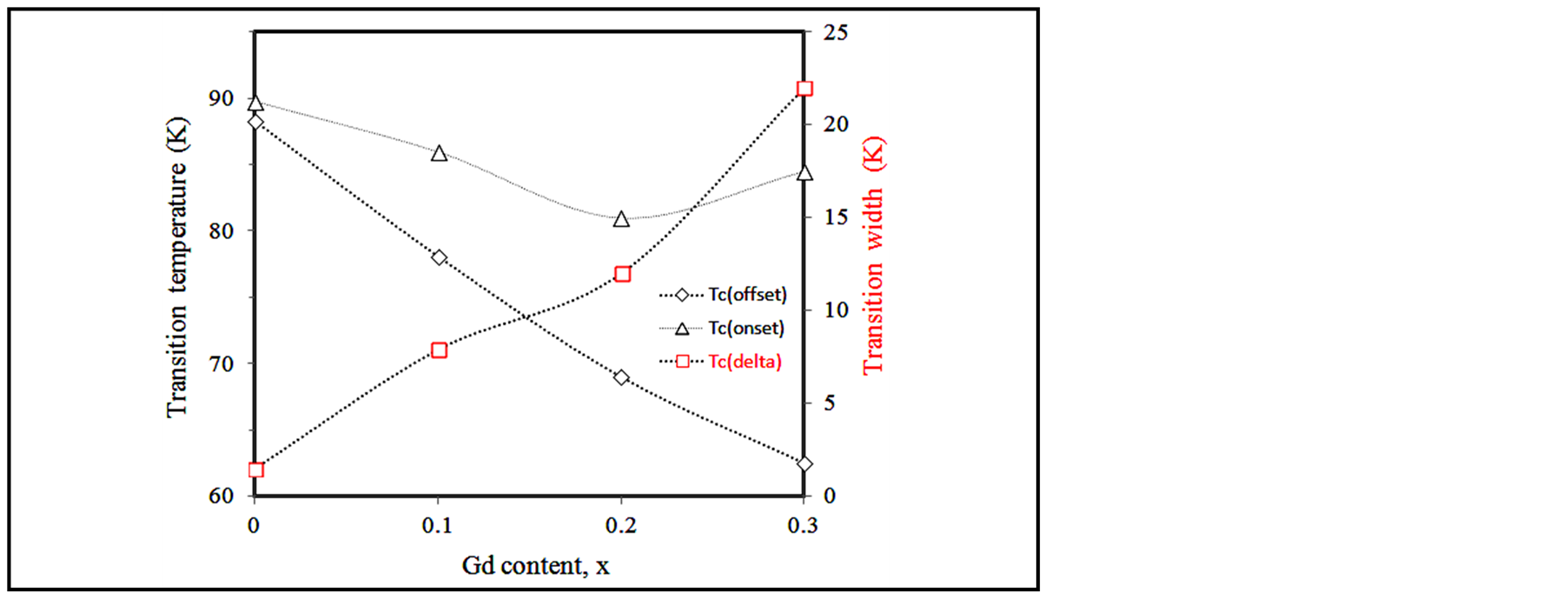
Figure 6. Dependence of critical transition temperatures and transition width on Gd-content, x, of prepared Y1Ba2Cu3 − xGdxO7 − δ samples.                 

the incomplete superconducting transition (SIT) for x = 0.3 in case of Pr(Cu) and for x > 0.3 for Gd(Cu). As known, high-temperature superconductors (HTS) cuprates with optimal doping are highly anisotropic with twodimensional (2D) charge carriers concentration in the normal and superconducting states. A shift from optimal doping makes it easier for carriers to hope in 3D (rather than the 2D ab-plane) through the “hard” c-axis where the effective mass anisotropy 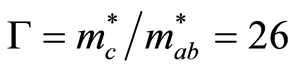for Y123 [28] . This involves a suppression of charge carriers with a consequent normal-state 2D to 3D crossover, namely, metal to insulator transition, MIT. This means that HTS cuprates stretch out to the metal-insulator edge [29] . Let us now study the origin of the shift in optimal structure in our systems. First, since the possibility of Pr and Gd to occupy the Cu-sites is minimal, that would cause a structure distortion leading to a shift in oxygen content from its optimal value, and therefore a decrease in mobile hole concentration, i.e., metallic to insulator transition. The deficiency in oxygen content is reflected in the tendency of the structure towards the tetragonal phase, Table 1. This view agrees with the work of Chang et al. [30] who concluded that mobile holes concentration decreases quite linearly with the increase of rare earth ionic radius.

Secondly, let us comment on the observed incomplete superconductivity for high Pr and Gd contents. Ahn et al. [31] have studied the effect of the polarization field formed by ferroelectric oxide lead zirconate titanate layer on GdBa2Cu3O7 – x HTS thin film. They observed a dip in the normal-state nonmetallic behaviour started at around 50 K and have been attributed to nonuniformity in the thickness of the HTS thin film. The observed incomplete superconducting state in our samples could be explained as follows. These samples are characterized by the strong development of the insulating Y2BaCuO5 phase, Figures 1 and 2, and wide transition width, Figures 4 and 6. We suggest here that both characters are responsible for the absence of zero-resistance where the wide transition width is a signature of increasing lattice imperfections and the number of grain sizes [32] . In our samples, the lattice distortion and the intensity of the insulating phase increased with increasing of x. Moreover, the decrease in grain size with increasing of x, Table 1, implies an increase in the number of grain sizes. This would suppress the superconducting tunneling between grains.

Thirdly, as indicated by Figures 4 and 6, we observe that the offset critical temperature of Pr(Cu) is less than Gd(Cu). Furthermore, while Pr(Cu) with x = 0.3 showed incomplete superconducting state, the same content showed a complete transition in case of Gd(Cu) substitution, Figures 3 and 5. These observations could not be explained purely in terms of the magnetic nature of Pr and Gd ions. Whereas, the reported critical temperaturesoffset are greater than that required for ordering magnetic moments. The observed negative impact of Pr(Cu) as compared to Gd(Cu) could be attributed to the Pr3+-Pr4+ mixed valent state and Gd3+ [16] . These electronic configurations require the depletion of charge carriers (holes localization) in the CuO2 planes due to Pr(Cu) to be stronger than that of Gd(Cu).

Finally, let us examine the superconducting to insulator transition (SIT) observed at low temperatures. Kobayashi et al. [33] have observed SIT in λ-BETS2FexGa1 − xCl4 (λ-type BETS alloys; BETS = bis(ethylenedithio) tetrathiafulvalene) with x = 0.43 at ambient pressure and with x = 0.55 at 1 k bar. The observed SIT have been considered as an intrinsic property of the crystals. Explanation of the observed superconductor-insulator transition below 50 K in our samples with high x contents is a difficult task. It could be attributed to the established high crystal structural disorder along with the rule played by grain boundaries, such as segregation of Pr and Gd ions at grain boundaries [34] . Another reason might be due to ordering of magnetic moments of Pr and Gd ions [35] [36] . Further work is needed to identify the nature of the observed transitions in these systems.

4. Conclusion

We have investigated the effect of partial doping of Pr and Gd on the electrical resistance of Cu-deficient Y123 superconductors. Resistance measurements showed a suppression of the critical transition temperature with increasing of Gd-content and this suppression increased in case of Pr doping. A normal-state metal-to-insulator crossover has been observed with x > 0 and x = 0.3 for Gd(Cu) and Pr(Cu), respectively. Moreover, Pr(Cu) with x = 0.3 showed incomplete superconducting transition, while the same content showed a complete transition in case of Gd(Cu). Furthermore, a superconductor-to-insulator crossover has been observed for Pr with x = 0.3 and for Gd with x > 0.3 at temperatures less than 50 K. To the best of our knowledge, no SIT has been reported in the studied two systems before. The observed crossovers were preliminary explained in terms of localization of charge carriers, structural disorders, and magnetic ordering of magnetic moments.

References

  1. Jamadar, T.A. and Ghosh, A.K. (2009) Metal to Insulator Transition in Mn Substituted Underdoped NdBa2Cu3O7−y: Evidence of Strong Charge Localization. Physica C, 469, 1971-1976.
  2. Babu, T.G.N. and Greaves, C. (1993) Critical Hole Density for Superconductivity in Sr-Containing Phases Related to YBa2Cu3O7: Structure, Superconductivity and Cation Substitutions in YSr2Cu2.8Cr0.2O7. Physica C, 207, 44-50.
  3. Skakle, J.M.S. (1998) Crystal Chemical Substitutions and Doping of YBa2Cu3Ox and Related Superconductors. Materials Science and Engineering: R: Reports, 23, 1-40.
  4. Tarascon, J.M., Greene, L.H., Barboux, P., McKinnon, W.R. and Hull, G.W. (1987) 3d-Metal Doping of the HighTemperature Superconducting Perovskites La-Sr-Cu-O and Y-Ba-Cu-O. Physical Review B, 36, 8393-8400. http://dx.doi.org/10.1103/PhysRevB.36.8393
  5. Mendels, P., Bobroff, J., Collin, G., Alloul, H., Gabay, M., Marucco, J.F., Blanchard, N. and Grenier, B. (1999) Normal-State Magnetic Properties of Ni and Zn Substituted in YBa2Cu3 O6 +x: Hole-Doping Dependence. Europhysics Letters, 46, 678-684. http://dx.doi.org/10.1209/epl/i1999-00319-x
  6. Tarascon, J.M., Barboux, P., Miceli, P.F., Greene, L.H., Hull, G.W., Eibschutz, M. and Sunshine, S.A. (1988) Structural and Physical Properties of the Metal (M) Substituted YBa2 Cu3-xMxO7-y Perovskite. Physical Review B, 37, 7458- 7469. http://dx.doi.org/10.1103/PhysRevB.37.7458
  7. Xiao, G., Streitz, F.H., Gavrin, A. and Chien, C.L. (1988) Superconductivity and Magnetism in Transition Element Substituted YBa2Cu3O7 Compounds. Journal of Applied Physics, 63, 4196. http://dx.doi.org/10.1063/1.340222
  8. Xiao, G., Streitz, F.H., Gavrin, A., Du, Y.W. and Chien, C.L. (1987) Effect of Transition-Metal Elements on the Superconductivity of Y-Ba-Cu-O. Physical Review B, 35, 8782-8784. http://dx.doi.org/10.1103/PhysRevB.35.8782
  9. Kistenmacher, T.J. (1988) Substitution for Copper in YBa2 Cu3Oy: The First 3%. Physical Review B, 38, 8862-8867. http://dx.doi.org/10.1103/PhysRevB.38.8862
  10. Goldschmidt, D., Direktovitch, Y., Knizhnik, A. and Eckstein, Y. (1996) Similar Depression of Tc by Zn and Ni Impurities in1:2:3 (Ca0.4La0.6)(Ba1.35La0.65)(Cu1-zMz)3Oy. Physical Review B, 54, 13348-13351. http://dx.doi.org/10.1103/PhysRevB.54.13348
  11. Garcı́a, S., Cobas, R., Musa, J.E. and Baggio-Saitovitch, E.M. (2000) Normal-State Behavior of the Resistivity in the Superconducting YBa2(Cu1-xLix)3O7-x System: An Evidence of Scattering by the Spin Fluctuations. Physica C, 341, 1895-1896.
  12. Ito, T., Takagi, H., Ishibashi, S., Ido, T. and Uchida, S. (1991) Normal-State Conductivity between Cupric Oxide Planes in Copper Oxide Superconductors. Nature, 350, 596-598. http://dx.doi.org/10.1038/350596a0
  13. Beschoten, B., Quitmann, C., Kelley, R., Onellion, M. and Güntherodt, G. (1996) Metal-Insulator Transition and Electronic Structure in Pr-Doped Bi2Sr2(Caz Pr1 −z)Cu2O8+y. Physica B, 223, 519-521.
  14. Tarascon, J.-M., Barboux, P. and Hull, G.W. (1989) Bismuth Cuprate High-Tc Superconductors Using Cationic Substitution. Physical Review B, 39, 4316-4326. http://dx.doi.org/10.1103/PhysRevB.39.4316
  15. Clayhold, J., Hagen, S.J. and Ong, N.P. (1989) Approaching the Mott-Hubbard Insulator in the 85-K Superconductor Bi2(Sr,Ca)3Cu2O8+d by Doping With Tm. Physical Review B, 39, 7320-7323. http://dx.doi.org/10.1103/PhysRevB.39.7320
  16. Akhavan, M. (1995) Normal Electrical Resistivity of the Superconductor-Insulator d1−xPrxBa2Cu3O7−y(0⩽x⩽1) System. Physica C, 250, 25-29.
  17. Tomkowicz, Z., Lunkenheimerb, P., Knebelb, G., Bałandac, M., Pacynac, A.W. and Zaleskid, A.J. (2000) InsulatorMetal Transition by the Substitution of Ho, Y or Ca for Pr in PrBa2Cu3O7−δ. Physica C, 331, 45-56.
  18. Ando, Y., Boebinger, G.S., Passner, A., Wang, N.L., Geibel, C., Steglich, F., Kimura, T., Okuya, M., Shimoyama, J., Kishio, K., Tamasaku, K., Ichikawa, N. and Uchida, S. (1997) Low-Temperature Normal-State Resistivity of High-Tc Cuprates. Physica C, 282, 240-243.
  19. Prabhakaran, D. and Subramanian, C. (1997) Metal-Insulator Transition in the Pr Substituted Bi-2212 Bulk Textured Crystals. Physica C, 291, 73-78.
  20. Chattopadhyay, M.K., Ghatak, S.K. and Dey, T.K. (1997) Metal-Insulator Transition in YBa2−xCaxCu3O7−δ System. Physica C, 281, 211-217.
  21. Cao, X.W., Tang, Y.J. and Ho, J.C. (1996) Superconducting Tc and Normal-State Resistivity in Nd1−xPrxBa2Cu3O7−δ System. Physica C: Superconductivity, 259, 361-364. http://dx.doi.org/10.1016/0921-4534(96)00061-5
  22. Semba, K., Matsuda, A. and Mukaida, M. (2000) Carrier-Concentration-Drivensuperconductor-to-Insulator Transition in YBa2Cu3O6+x. Physica B: Condensed Matter, 281-282, 904-905. http://dx.doi.org/10.1016/S0921-4526(99)00907-2
  23. Li, X., Sun, X., Wu, W., Chen, Q., Shi, L., Zhang, Y., Kotaka, Y. and Kishio, K. (1997) Variations of Normal State Resistivity and Cu2+ Localized Spin Moment in the Single Crystal Bi2Sr2 CaCU2O8+x. Physica C: Superconductivity, 279, 241-245. http://dx.doi.org/10.1016/S0921-4534(97)00141-X
  24. Fujita, T., Hori, J., Iwata, S., Yoshino, Y., Kurisaki, H., Goko, T., Yamane, K. and Nakamura, F. (2001) Superconductor-Insulator Transition in Under-Doped Cuprates. Physica C: Superconductivity, 364-365, 274-277. http://dx.doi.org/10.1016/S0921-4534(01)00771-7
  25. Goldman, A.M. (2003) Superconductor-Insulator Transitions in the Two-Dimensional Limit. Physica E: Low-Dimensional Systems and Nanostructures, 18, 1-6. http://dx.doi.org/10.1016/S1386-9477(02)00932-3
  26. M’chirgui, A., Zouaoui, M., Ben Azzouz, F., Yangui, B. and Ben Salem, M. (2003) Electron Localization Induced by Grain Boundary Disorder in the Normal State of High-Tc Superconductors. Physica C: Superconductivity, 125, 71-76. http://dx.doi.org/10.1016/S0038-1098(02)00714-7
  27. Martin, J.D. (2005) Using XPowder: A Software Package for Powder X-Ray Diffraction Analysis. www.xpowder.com
  28. Ferrell, D., Williams, C., Wolf, S., Bansel, N. and Kogan, V. (1988) Experimental Evidence for a Transverse Magnetization of the Abrikosov Lattice in Anisotropic Superconductors. Physical Review Letters, 61, 2805-2805. http://dx.doi.org/10.1103/PhysRevLett.61.2805
  29. Mandal, P., Poddar, A., Ghosh, B. and Choudhury, P. (1991) Variation of Tc and Transport Properties with Carrier Concentration in Yand Pb-Doped Bi-Based Superconductors. Physical Review B, 43, 131 02-13111. http://dx.doi.org/10.1103/PhysRevB.43.13102
  30. Chang, B.C., Yang, C.Y., Hsu, Y.Y. and Ku, H.C. (2007) Origin of Metal-Insulator Transition in the Weak-Ferromagnetic Superconductor System RuSr2RCu2O8 (R = Rare Earths). Physica C: Superconductivity, 460-462, 503-505. http://dx.doi.org/10.1016/j.physc.2007.03.334
  31. Ahn, C., Gariglio, S., Paruch, P., Tybell, T., Antognazza, L. and Triscone, J. (1999) Electrostatic Modulation of Superconductivity in Ultrathin GdBa2Cu3O7−x Films. Science, 248, 1152-1155. http://dx.doi.org/10.1126/science.284.5417.1152
  32. Shaltiel, D., Bezalel, M., Golosovsky, M., Kwok, W.K. and Fendrich, J.A. (1999) Induced Microwave Absorption by Magnetic Modulation in Untwinned and Twinned YBaCuO Crystals and Its Comparison with Resistivity Measurements. Physica C: Superconductivity, 315, 23-35. http://dx.doi.org/10.1016/S0921-4534(99)00190-2
  33. Kobayashi, H., Akutsu, H., Ojima, E., Sato, A., Tanaka, H., Kobayashi, A. and Cassoux, P. (1999) Supercondutor-toInsulator Transition of λ-BETS2FexGa1−xCl4. Synthetic Metals, 103, 1837-1838. http://dx.doi.org/10.1016/S0379-6779(98)00489-5
  34. Durrell, J.H., Eom, C.-B., Gurevich, A., Hellstrom, E.E., Tarantini, C., Yamamoto, A. and Larbalestier, D.C. (2011) The Behavior of Grain Boundaries in the Fe-Based Superconductors. Reports on Progress in Physics, 74, 124511- 124549. http://dx.doi.org/10.1088/0034-4885/74/12/124511
  35. Ishikawa, M. and Fischer, Ø. (1977) Destruction of Superconductivity by Magnetic Ordering in Ho1.2Mo6S8. Solid State Communications, 23, 37-39. http://dx.doi.org/10.1016/0038-1098(77)90625-1

NOTES

*Corresponding author.

Journal Menu >>