Advances in Aging Research
Vol.03 No.05(2014), Article ID:51453,11 pages
10.4236/aar.2014.35047
Second Law of Thermodynamics Formalism Applied to Finite Duration through Cycles of Living Dissipative Systems
Jorge Antonio Montemayor-Aldrete1, Pablo Ugalde-Vélez2, Marcelo Del Castillo-Mussot1, Gerardo Jorge Vázquez1, Ernesto Federico Montemayor-Varela3
1Departamento de Estado Sólido, Instituto de Física, Universidad Nacional Autónoma de México, México, D.F., México
2Departamento de Materiales (CBI), Universidad Autónoma Metropolitana Azcapotzalco, México, D.F., México
3Instituto Nacional de Perinatología, México, D.F., México
Email: jorge@fisica.unam.mx
Academic Editor: Krishna Midde, University of California San Diego, USA
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 September 2014; revised 20 October 2014; accepted 7 November 2014
A simple and general theory to describe basic irreversible thermodynamic aspects of aging in all dissipative living is presented. Any dissipative system during its operation continuously loses efficiency by the production of structural or functional defects because of the second law of thermodynamics. This continuous loss of efficiency occurs on all the dissipative systems through the realization of specific functional cycles, leading to a maximum action principle of any system involving the Planck’s constant during their total dissipative operation. We applied our theory to the calculation of men and women lifespans from basal metabolic rate per unit weight and to the calculation of a new aging parameter per cycle of some human organs or physiological functions. All microscopic theory of the aging of living beings should be consistent with the second law of the thermodynamics. In other words, the operation of the biological self-organized structures only implies a delay in which the dissipative biological systems outside of equilibrium approach inexorably to the thermodynamic equilibrium obeying the second law of the thermodynamics.
Keywords:
Aging, Functional Damage, Entropy Production Rate, Dissipative Structures, Dissipative Cycles

From Schrödinger’s classic work published in 1944 [1] it became clear that life, and not only the not-living systems like cyclic thermal machines, obeys the first and second laws of thermodynamics. Relative to the human body he writes, “Energy is needed to replace not only the mechanical energy of our bodily exertions, but also the heat we continually give off to the environment. That our body gives off heat is not accidental, but essential. This is precisely the manner in which we dispose of the surplus entropy we continually produce in our physical life process, and seems to suggest that the higher temperature of the warm-blooded animal includes the advantage of enabling it to get rid of its entropy at a quicker rate so that it can afford a more intense life process”. The basic same ideas were expressed in a different paragraph using similar expressions: “organization of living organisms is maintained by extracting ‘order’ from the environment” and he also asks: “How would we express in terms of the statistical theory the marvelous faculty of a living organism, by which it delays the decay into thermodynamical equilibrium (death)?” Finally, he introduced the idea of an “aperiodic crystal”, and the microcode of which Schrödinger spoke have become the DNA and the genetic code of today. It is well known that Watson and Crick, co-discoverers of the structure of DNA, each respectively acknowledged the mentioned book as a source of inspiration for their initial researches.
The next step of the theoretical conception of living systems or non-living dissipative systems in a thermodynamical scheme was due to the Prigogine work in 1945, when the theorem of minimum entropy production applicable to non-equilibrium stationary states is published [2] . According to Prigogine this theorem gives a clear explanation of the analogy relating the stability of equilibrium thermodynamical states and the stability of biological systems, such as that expressed in the concept of “homeostasis” proposed by Claude Bernard. The notion of “dissipative structure” was elaborated by him in 1967 [3] , and in 1971, he concluded: “The formation of dissipative coherent structures, for sufficient far-from-equilibrium conditions, appears as a quite unexpected manifestation of ‘disorder to order’ processes, far from equilibrium, but conforming to the second law of thermodynamics” [4] . In the words, Professor Stig Claesson [5] states that: “Prigogine has been particularly captivated by the problem of explaining how ordered structures-biological systems, for example-can develop from disorder… which display order in both time and space, and which are stable to perturbations. Prigogine has called these systems dissipative systems, because they are formed and maintained by the dissipative processes which take place because of the exchange of energy between the system and its environment, and because they disappear if that exchange ceases… The method which Prigogine has used to study the stability of the dissipative structures to perturbations is of very great general interest. It makes it possible to study the most varied problems, such as city traffic problems, the stability of insect communities, the development of ordered biological structures… to mention but a few examples”.
Additionally, to the previous information, it is an almost universal experimental fact that stationary states corresponding to dissipative structures do not last forever, despite being stable against fluctuations. Gradually, stationary states start to monotonically decline and eventually stop working to reach the thermodynamic equilibrium. For non-living dissipative systems, these processes could be defined as a process of intrinsic progressive loss of functionality, which conducts to ceasing of working properly, and eventually to failure [6] . For the living dissipative systems, this process of intrinsic progressive loss of organic function is reflected at the population level as an increase in the likelihood of death and a decline in the production of offspring [7] [8] .
Given the generality of the finite duration of stationary states in dissipative structures within irreversible thermodynamic processes, the following steps in a thermodynamical scheme, it is obligated. Let us try to use the second law of thermodynamics to describe the following facts. Section 2 contains a thermodynamical background necessary for our model. In Section 3, we present some empirical thermodynamical observations of living systems and present our very general theoretical formalism of an average dissipation rate theory taking into account the cyclic nature of living beings. In Section 4, we analyze in our formalism data comparing lifespans of human beings (females and males) and different human organs and physiological functions. Section 5 is devoted to conclusions.
First, let us make a brief synthesis of relevant general thermodynamical results.
The first law reads,
 (1)
(1)
where the internal energy of the system is ,
,
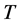 is temperature in
Kelvin scale,
is temperature in
Kelvin scale,
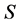 the entropy,
the entropy,
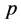 the pressure acting
on the homogeneous system and
the pressure acting
on the homogeneous system and
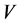 the volume. The second law defines entropy as
the volume. The second law defines entropy as
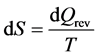 (2)
(2)
with
 as the reversible heat flow.
as the reversible heat flow.
Also we know [9] [10] that the rate of entropy production
denoted by , also
can be expressed as a function of generalized fluxes
, also
can be expressed as a function of generalized fluxes
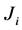 and generalized forces
and generalized forces :
:
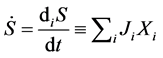 (3)
(3)
From this equation, it is possible to define the Raleigh’s dissipation function
[10] ,
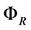 as
as
 (4)
(4)
This represents the heat generation inside a system, and could be experimentally measured. For biological dissipative structures far from thermodynamic equilibrium, it is convenient to write Equation (4) per unit volume or per unit weight;
 (5)
(5)
Prigogine [9] [11] , by starting from Equation (3), shows that
 (6)
(6)
where



However, in contrast to inequality for linear irreversible thermodynamics


3. Average Dissipation Rate Theory
3.1. General Empirical Facts
It has been experimentally observed long time ago that during the time development
of living systems, the dissipative Raleigh function per unit volume

The general schematic behavior of self-organized living dissipative structures is
shown in
Figure 2, where the specific (per unit volume) production rate of entropy
versus time is presented. In more detail, the curve shows four chronological stages:
1) An initial transient stage, where


In our formalism, the initial time is the instant when the “egg” is formed, which depends on the type of living being. For instance, in a mammal, we consider that time starts with the fetus development, and for the birds, the
Figure 2. Schematic diagram of specific (per unit volume) production rate of entropy vs. time showing four chronological sta- ges; 1—initial growing, 2—stationary or steady-state stage, (adult- hood), 3—aging in the mature stage, and 4—catastrophic failure or destruction. The rectangle should have the same area to apply Calculus mean value theorem.
process depends on the heat received by the egg in the incubation process.
It is widely observed that most living dissipative systems perform functional cycles. For example in mammals breathing, heartbeat, digestive processes, etc. are cyclic processes. Of these, the most important functional cycle is the relative to the rate of arrival of nutrients and oxygen to each and every one of the cells that make up every living system. The heartbeats promote, throughout the body, a distribution of free energy per unit time which allows meeting the needs of the dissipative system. Clearly, for each process that occurs within the system, the length of each cycle varies with the age of each living being and that may depend on the specific activities carried out at all times. As a first approximation, the case of the cyclic dissipative systems will be analyzed, under the assumption that a large population of them can be represented by average values through their working life. Based on the second law of thermodynamics, is considered here that any living being gradually wears down and eventually stops working as it previously did (in a similar way that occurs for an internal combustion engine, which also operates through cycles).
During their operation dissipative systems perform internal processes of a cyclic
nature that could be repeated hundreds, thousands or thousands of millions of times,
etc. The dissipative structures go through a maximum number of cycles,

If we consider the whole process to take place at a constant temperature
In mathematical language

where




where




Thus, the total operation time of the dissipative system is given by

Which shows in a direct way that a dissipative system has a maximum of continuous
time operation inversely proportional to the specific dissipative Raleigh’s function
of the system, and directly proportional to their
3.2. Cyclic Nature of Dissipative Systems
It is clear that many dissipative structures realize functional cycles, which repeat over and over during its whole period of operation, before fail. Assuming, for simplicity, that the cycles are identical, then, from Equation (9):

Here



In the sake of mathematical simplicity, constant or average duration of the functional cycles through life will be assumed, even though we know that during adulthood metabolism decreases in time, which causes that the time duration of cycles also diminish.
The existence of an upper limit to the number of the operation cycles implies also the existence of accumulative damage and aging processes. This damage and aging processes cause the continuous decreasing on the power that the dissipative can handle through time and from empirical observation is clear that the aging rate is different and characteristic for each type of system.
For auto-organized systems, there are many phenomenological observations, which show that the macroscopic symptoms of aging begin to appear after the auto-organized dissipative structure attains adulthood [13] . This stage corresponds to the stage 2 of Figure 2 previously defined. In the stage 3, the specimen already arrived to adulthood, and the production rate of specific entropy will be a decreasing function of time.
Taking into account such empirical information from macroscopic signs of aging it
is possible to make an approximation about the derivative in time




where


Here



which clearly states that every dissipative structure necessarily suffers accumulative
damage during its operation. We can say that the dissipative system has some functional
memory, in the sense that cannot be rejuvenated. That is,


Neglecting the contribution of the collapse stage 4 (assuming that this last stage is extremely short as compared with the stage 3), also from Equation (14) it is easy to define a new physical macroscopically variable related to the steady-state of entropy production; the fractional remaining functionality:

Therefore,

From this equation, it is clear that when the dissipative system collapses,


By using Equation (17) into Equation (14)

which describes the time evolution of




which could be expressed as a function of the total cycle number at failure condition


Here





This equation shows, as expected, that fractional remaining functionality has high
values, when the functional damage is low. For animals, these equations allow to
see that at the time





3.3. Maximum Action Principle
Here, by using our formalism, it is possible to obtain an equation for the maximum
entropy changes in a dissipative system as multiples of the Boltzmann’s constant.
For this purpose, let us employ another physical meaning of Equation (9) if we use
Equation (5), together with


where




where

Therefore, the total entropy generated during the continuous dissipative operation
of the dissipative system,


Notice that physically and mathematically Equation (23) resembles the uncertainty principle due to Heisenberg;

where



By using Equation (25), into Equation (24) it is possible to obtain

where


In the following paragraphs, a comparison between the theoretical results here obtained with experimental data, and other theoretical considerations will be made.
4. Comparison between Experimental Data and Theory
4.1. Average Lifespan of Human Females and Males
First, we will give a quantitative thermodynamic explanation to experimental facts
that on average (for all current country populations) women live several years more
than men. Later, we will discuss some thermodynamic implications of aging of humans
and their internal organs. On one hand, from Figure 3, [15] it is immediate that the average basal
metabolic rate in man throughout his existence is 40









On the other hand, taking into account the female and male life expectancy of all the members of the European Union (EU) [18] and their respective population, we obtain the average ratio for the female and male life
expectancy for the EU,

Therefore, the percentage difference between the theoretical and the experimental data is 2.5%, which is an excellent result.
There are two reasons for employing EU data; their data availability and very few premature deaths of that relatively rich, healthy and homogeneous population as compared to other regions of the world population. Premature deaths are due to crimes, war, disease, and malnutrition. For instance, in Sub-Saharan Africa, one of the worse health problems (if not the worst) is underweight infancy.
4.2. Aging Rates of Human Organs
Relative to the thermodynamic implications of aging of humans and their internal organs, in Figure 4, experimental data for Average Percent Physiological Function Remaining of different human organs and physiological functions, (as given by Cutler [13] ) are shown as a percentage of maximum lifespan potential; In principle, all these organs obey the Equation (16), but since they form part of the whole system, in reality, they are interdependent.
From data of Cutler et al. [13] as shown in Figure 4, by using Equation (16) we can calculate the
values for the aging parameter,





The data on
Table 1 allow to describe the time dependence of the percentage functional
remaining,


Figure 4. Experimental data for the average percentage remaining functionality (PFR) for different human organs and functions as a function of the percentage of maximum lifespan potential (as given by Cutler [13] ). We point out that these straight lines also appeared in the original work.
Table 1. Aging parameters, a, which characterize the functional decay of the dissipative system in each cycle corresponding to different organs in human bodies.
We identified general four chronological stages of self-organized living dissipative
structures of the specific (per unit volume) production rate of entropy: 1) an initial
more or less exponential transient stage, 2) stationary or steady-state stage, (adulthood),
with slow aging, 3) aging in the mature stage” with an approximate linear decrease
of

Based on the proposal of an average dissipation rate model for non-linear irreversible
thermodynamics for dissipative structures, which goes through functional cycles,
we conclude that the systems necessarily generate a maximum quantity of entropy
(characteristic of each type) and, therefore, last a maximum quantity of time
The second law of thermodynamics has been used to explain the finite time duration
of stationary states and simultaneously, both the processes of intrinsic progressive
loss of functionality for non-living dissipative systems, and the processes of intrinsic
progressive loss of organic function in the living dissipative systems. Some of
the theoretical results (as Equation (10)) show in a direct way that all kinds of
dissipative system have a maximum of continuous time operation inversely proportional
to the specific dissipative Raleigh’s function of the system, and directly proportional
to their
We hope that future developments of simple concepts developed here, such as fractional
remaining functionality (Equation (16)), could to make a contribution to develop
programs for preventive health care. Different values for corresponds to distinct
aging rates on a given subsystem of human bodies. Then for a given organ (fundamental
or not) it is possible to collect data of a human population and select the people
with lower values for

Figures of the type of Figure 4 and the use of Equation (16), in principle allow to compare the general state of health of a concrete human being of x age with regard to the general state of health at the same age corresponding with an average of humans being that later have arrived to the 100-year-old age. And also to determine the maximum duration of the person’s life that moves away from the values that correspond to the possibility of arriving to a 100-year-old age. In short, for example, after evaluating the alpha corresponding to the centennials and knowing the average of the numerical values for the heart functionality in a 100-year-old population we can determine the value that would throw the use of Equation (16) for a specific person of x age. It would allow it to evaluate the difference among the heart functionality from the centennials to that age and the subject in question. If we consider that the value of the heart functionality of the centennials is a limit value; then the use of Equation (16) for a specific person will determine us statistically their maximum duration of life. This analysis type can be a complementary useful tool, cheap and effective that cooperates to the standard evaluation procedures of the future health of big groups of human beings. For the time evolution of the basal metabolism on children is necessary a further independent study.
Analogous to the quantum Heinsenberg’s principle, we presented an empirical principle for maximum action of any dissipative system involving the Planck’s constant.
We made use of average values of the basal metabolic rate per unit weight of European man and women to conclude that, on average, the human female last longer than the human males, with only a 2.5% of relative error. Also, we calculated the aging parameter measuring the functional decay of the dissipative system in each cycle from specific production of entropy of some human organs or physiological functions.
We assumed constant duration of the cycles in adulthood, even though we know that during adulthood, metabolism decreases in time. Then it will be desirable to refine our formalism to include different values of the average and the variance of the duration of the cycles in different stages of the living structures.
The substitution of organs as a way to increase the span of human life, we would have as limit the time implied by the aging rhythm of the original brain. In the same way that the inclusion of new pieces in an old car does not increase to infinite the lifespan of the car, since during the replacement process, a stage will be attained were the car rejuvenated no longer corresponds with the original car.
All microscopic theory of the aging of living beings should be consistent with the second law of the thermodynamics. In other words, the operation of the biological self-organized structures, is not more than an efficient mechanism of degradation of the free energy that we receive from the sun, and it only implies a delay in which the dissipative biological systems outside of equilibrium approach inexorably to the thermodynamic equilibrium obeying the second law of the thermodynamics.
JAMA specially wants to thanks to Prof. M. López de Haro for many years of deep discussions and arguments and by his contribution to final shaping of the ideas here developed.
- Schrödinger, E. (1992) What Is Life? With Mind and Matter and Autobiographical Sketches. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139644129
- Prigogine, I. (1945) Etude thermodynamique des phénomènes irréversibles. Thèse d’agrégation présentée en 1945 à l’Université Libre de Bruxelles. Desoer, Liège, 1947. Académie Royale de Belgique. Bulletin de la Classe des Sciences, 31, 600.
- Prigogine, I. (1969) Structure, Dissipation and Life. Theoretical Physics and Biology, Versailles, 1967. North-Holland Publ. Company, Amsterdam.
- Glansdorff, P. and Prigogine I. (1971) Structure, Stabilitéet Fluctuations, Masson, Paris. Thermodynamic Theory of Structure Stability and Fluctuations. Wiley and Sons, London.
- The Nobel Prize in Chemistry (1977) Ilya Prigogine. Award Ceremony Speech. Presentation Speech by Professor Stig Claesson of the Royal Academy of Sciences. (Translation from the Swedish Text)
- Feinberg, A.A. and Widom, A. (2000) On Thermodynamic Reliability Engineering. IEEE Transactions on Reliability, 49, 136-146.
- Kirkwood, T.B. and Austad, S.N. (2000) Why Do We Age? Nature, 408, 233-238. http://dx.doi.org/10.1038/35041682
- Partridge, L. and Gems, D. (2002) Ageing: A Lethal Side-Effect. Nature, 418, 921-921. http://dx.doi.org/10.1038/418921a
- Prigogine, I. (1967) Thermodynamics of Irreversible Process. Charles C. Thomas Publisher, Springfield.
- Glaser, R. (1999) Biophysics. Springer-Verlag, New York.
- Glansdorf, P. and Prigogine, I. (1971) Thermodynamical Theory of Structures, Stability and Fluctuations. Wiley Interscience, New York.
- Guytton, A.C. (1976) Textbook of Medical Physiology. 5th Edition, W. B. Saunders Company, Philadelphia-London- Toronto, 952.
- Cutler, R.G. (1978) Evolutionary Biology of Senescence. In: Behnke, J.A., Finch, C.E. and Moment, G.B., Eds., The Biology of Aging, Plenum Press, New York, 311-360. http://dx.doi.org/10.1007/978-1-4613-3994-6_20
- Sommerfeld, A. (1972) “Mechanics” Lectures on Theoretical Physics, Volume I. Paperback Edition, 6th Printing, Academic Press, Inc., Waltham, 181.
- Durnin, J.V.G.A. (1981) Basal Metabolic Rate in Man. University of Glasgow Glasgow Scotland. Joint FAO/WHO/ UNU Expert Consultation on Energy and Protein Requirements Rome, 5-17 October. http://www.fao.org/docrep/meeting/004/m2845e/m2845e00.htm
- Sparreboom, A. and Verweij, J. (2003) Paclitaxel Pharmacokinetics, Threshold Models, and Dosing Strategies. Journal of Clinical Oncology, 21, 2803-2804. http://dx.doi.org/10.1200/JCO.2003.99.038
- (2006) Health and Food. Fieldwork November, December 2005. Special Eurobarometer. European Commission. http://ec.europa.eu/public_opinion/archives/ebs/ebs_246_en.pdf
- WHO (2013) WHO Life Expectancy. http://apps.who.int/gho/data/node.main.688?lang=en






